bemenet ![]() feldolgozás
feldolgozás ![]() eredmény.
eredmény.
Programozás BASIC nyelven
1983 - Dr. Kocsis András
Tartalom
Könyvünknek kettős a funkciója: egyrészt tankönyv a BASIC programozási nyelv tanfolyami oktatásához, másrészt egyéni tanulásra szolgáló könyv.
Ajánljuk műszaki és gazdasági területen dolgozó szakembereknek, valamint más olyan felhasználóknak, akik feladataik számítógépes megoldásához a BASIC programozási nyelvet kívánják felhasználni önállóan, számítástechnikai szakemberek bevonása nélkül. Ennek ellenére olvasóinkról feltételezzük, hogy a számítástechnika alapvető fogalmait (a számítógép főbb egységei, az operációs rendszerek feladatai stb.) már ismerik.
A könyv szerkezetét úgy alakítottuk ki, hogy a feladatok megoldásához szükséges BASIC nyelvi lehetőségeket a könyvön végighaladva egyszerűen, gyorsan meg lehessen találni és el lehessen sajátítani. Az egyes fejezetek sorrendje az interaktív (terminál melletti) programkészítés folyamatát követi.
A könyv első része a BASIC nyelvi programozáshoz elengedhetetlenül szükséges alapismereteket tartalmazza. Ha valaki életében először akar BASIC programot írni, a feladat megoldásához szükséges részeket átolvasva megírhatja a programot. A könyv végén megtanulhatja a programtesztelést, és közben befejezheti a programot.
Célunk az, hogy a BASIC nyelvi lehetőségek alkalmazását teljes, zárt problémák megoldásán mutassuk be. Így az olvasónak elegendő a saját feladatához legközelebb álló feladattípust megkeresni, és segítségével saját problémáját megoldhatja. A könyv elején az egyszerűbb, a végén a bonyolultabb feladattípusok találhatók. A felosztás alapja a bemeneti adatok szerkezete (egyedi adatok, összetartozó adatok).
A többi magas szintű nyelvtől eltérően a BASIC nyelv szabványosított változata e könyv nyomdába adásáig nem jelent meg. Részben ez az oka annak, hogy mind a mai napig igen sokféle BASIC nyelvi változat van forgalomban, és újabbak is jelennek meg. A változatosság másik oka, hogy a BASIC nyelv népszerűsége a mikroszámítógépek megjelenésével együtt megnőtt, és sokszor eltérő tulajdonságú BASIC-változatokat készítenek a különböző mikroszámítógépekhez. Ez részben azzal magyarázható, hogy a gyártók olyan BASIC-változatot adnak gépükhöz, amely a gép lehetőségeit a legjobban kihasználja, illetve a gép által nem támogatott lehetőségeket kihagyják a nyelvből.
Ez a látszólag "bábeli nyelvzavar" a BASIC nyelvben valójában nem okoz gondot a nyelv ismerőjének. Az egyes nyelvi változatok közötti különbség ugyanis nem nagy. Alapjában véve minden nyelvi változat nagyon hasonlít a könyvünkben tárgyalt változathoz.
A főbb eltérések a géptípus hardver tulajdonságaiból fakadnak. Mikroszámítógépekhez ritkán tartozik háttértároló, ezért az ilyeneknek adatállomány-kezelési lehetőségük nincs. Ha van is kazettás tárolójuk, ezt a gép program-könyvtározásra alkalmazza, adatok tárolására nem.
A BASIC egyes változatai pontos rajzot is képesek készíteni.
A különbségek teljes feltárása lehetetlen lenne, ezért azt tanácsoljuk az olvasónak, hogy mielőtt a rendelkezésre álló gépet és a BASIC-változatot használni kezdené, a nyelv kézikönyvét tanulmányozza át, hogy tisztában legyen vele, mire számíthat, mire nem.
Köszönetemet fejezem ki minden kollégámnak, aki segített a könyvben alkalmazott módszer meghatározásában és a tartalom felépítésének kialakításában. Külön is köszönetét mondok Gerő Péter kollégámnak, aki a nyelv oktatására alkalmas tárgyalásmód kialakításában segített.
A szerző
1. Bevezető ismeretek a BASIC programozási nyelvhez
A számítógép a felhasználója számára valamilyen adatfeldolgozást végez el. Ennek során bemeneti adatokból feldolgozó műveletekkel egy eredmény-adathalmazt állít elő. Ez a három fogalom minden számítástechnikai feladatmegoldásban szerepel:
bemenet
feldolgozás
eredmény.
A cél mindig az eredmény-(vagy kimeneti)adatok előállítása. Ezeket az adatokat a rendelkezésre álló bemeneti adatokból kell előállítani a feldolgozás műveleteivel.
Vizsgáljuk meg ezt a három fogalmat egy kicsit bővebben is! Mindenesetre feltételezzük, hogy az olvasó ezekkel a fogalmakkal már találkozott, esetleg pontosan ismeri is őket. Mégis szükségesnek tartjuk, hogy az egységes értelmezés kedvéért néhány fontosabb meghatározást rögzítsünk.
Anélkül, hogy a feladatmegoldás eredményközpontúságát szem elől tévesztenénk, a bemenetnél kezdjük az ismertetést. A számítógépes feladat bemenetét adatok alkotják. A feladattól függően a bemenet lehet néhány (egy és kb. 10 közötti) egymástól független adat vagy egymással összefüggő nagyszámú adat. Ez utóbbi esetben az adatok az összefüggés miatt logikai szerkezetet hoznak létre. Ezt a szerkezetet célszerű általánosan megvizsgálni, mivel ez majd a feldolgozáskor figyelembe vehető. Ha például az a feladatunk, hogy számlák adataiból valamilyen eredményadatot készítsünk el, akkor a számlák adatai alkotják a feldolgozás bemeneti adatállományát. A bemeneti adatállomány részei a számlák. A számlák adatokat tartalmaznak: az áru megnevezése, a szállítás időpontja, az áru ára stb. Példánkban egy számla adatait együttesen rekordnak nevezzük. A példaként felsorolt adatok pedig a rekord mezői. Egy bemeneti állomány azonos típusú számlákból (vagy más adategyüttesből) áll. Ezért az adatállomány rekordjai is azonosak. Ha pedig így van, akkor biztosak lehetünk abban, hogy például az adott állományon belül a harmadik mező az áru árát tartalmazza. A későbbiekben látni fogjuk, hogy ez a rekordonkénti feldolgozás során jól hasznosítható. Ezért célszerű a bemeneti adatok szerkezetét feltárni.
A feldolgozás műveletek sorozatából áll, amely a bemeneti adatokból elkészíti az eredmény- (kimeneti)adatokat. A feldolgozás műveleteit és ezek sorrendjét a feladatnak megfelelően kell összeállítani. Az egy adott feladat megoldását szolgáló műveletsorozatot algoritmusnak nevezzük. A feldolgozási algoritmus feladatfüggő.
Egy feladat több különböző algoritmussal, hasonló feladatok ugyanazzal az algoritmussal is megoldhatók, vagyis nem kell minden feladathoz új algoritmust kitalálni.
Az algoritmust a feladat megoldójának kell megfogalmaznia. Ez azt jelenti, hogy az algoritmust olyan egyszerű lépésekre kell felbontani, amilyeneket egy számítógép el tud végezni.
A számítógép számára a számítógépi műveletekből összeállított algoritmus a program. Másképpen: a program a számítógép nyelvére lefordított algoritmus.
A program utasításokból épül fel. Amikor a programot futtatjuk, az utasítások végrehajtódnak, és hatásukra a számítógép elvégzi a kijelölt műveleteket.
A harmadik fogalom az eredmény- vagy kimeneti adat. A kimeneti adat általában közvetlenül a felhasználónak szól, ezért mint kiírás jelenik meg. Ez lehet egyetlen számérték vagy egy mondat, táblázat stb., de lehet egy következő feldolgozás bemeneti adatállománya is. Ekkor nyilvánvalóan az adat tárolódik, hogy a következő lépésben elérhető legyen.
A fentiek illusztrálására tekintsünk egy egyszerű feladatot. Határozzuk meg például öt szám számtani átlagát.
A feldolgozási algoritmus: a bemeneti adatokat (B1, ..., B5) össze kell adni, az összeget (S) el kell osztani a tagok számával (5), és eredményként az igényelt adatot kapjuk, vagyis a számtani átlag (A):
S = B1 + B2 + B3 + B4 + B5 = 5 + 8 + 6 + 5 + 7 = 31
A= S/5 = 31/5 = 6.2
A BASIC programozási nyelv
A BASIC programozási nyelvet a magyar származású John G. Kémény és Thomas E. Kurtz fejlesztette ki Dartmouth College-ben 1963-64-ben. A BASIC a Beginner's All Purpose Symbolic Instruction Code (kezdők általános célú szimbolikus utasításkódja) kifejezés rövidítése.
A BASIC nyelvet egyrészt a kezdő számítástechnikai szakembereknek, másrészt olyan nem számítástechnikai szakembereknek fejlesztette ki Kémény és Kurtz, akik a számítástechnikát szakmai feladataik megoldására alkalmazzák.
A minta a FORTRAN nyelv volt. Némi egyszerűsítéssel emberközelibbé alakították, így a használata könnyebb lett. Általában minden számítógépgyártó saját BASIC rendszert (vagy rendszereket) nyújt a felhasználóknak. Ezek a változatok szolgáltatásaik skálájában térnek el egymástól. Vannak "szűkebb" és "bővebb" rendszerek. A nyelv szabványosításának hiánya miatt egy adott gépen elkészített program egy másik gépen nem biztos, hogy futtatható, mert talán olyan utasítást is tartalmaz, amelyet a másik gép nem "ért". Az viszont lényeges jellemzője valamennyi BASIC változatnak, hogy azonos műveletre azonos utasítása van (például az eredményt valamennyi BASIC változatban a PRINT utasítással lehet kiíratni).
A BASIC fordító a program utasításait egyenként lefordítja és végrehajtja. Ennek következtében a megírt programot egy lépcsőben, vagyis azonnal le lehet futtatni. A programkészítője közvetlenül - és természetesen gyorsan - kipróbálhatja az éppen befejezett programját.
A BASIC nyelvet azért látták el ilyen fordítóval, hogy interaktív módon lehessen alkalmazni. Az interaktív programozás azt jelenti, hogy a program készítője a program megtervezése után a program kódját terminálon viszi be a számítógépbe, és a végrehajtott művelet után ide érkezik az eredmény. Az interaktivitás miatt a programok gyorsan javíthatók, a kapott eredmények hamar értékelhetők, és a program szükség esetén gyorsan módosítható.
A BASIC nyelv a kis- és mikroszámítógépeken terjedt el leginkább. Ennek egyrészt az az oka, hogy ezeknek a gépeknek az erőforrás helyzetéhez (a fordító kis tárigénye, kis méretű adatállományok használata) jól idomul a nyelv, másrészt a kis- és mikrogépekre tervezett kisebb feladatok hatékonyan elvégezhetők BASIC nyelven.
2. A feladatmegoldás módszere és folyamata
2.1. Az alkalmazott programozási módszer
Ha felmerül egy feladat (pl. a babkávé fogyasztását kell megjósolni az elkövetkező öt évre, vagy egy termékszerkezet rendelésállománya alapján a gyártókapacitást és az alkatrészszükségletet kell meghatározni, vagy egy vállalat dolgozóinak bérét kell kiszámítani a teljesítmények alapján), amelyet számítógéppel akarunk megoldani, akkor a feladat megfogalmazása után a megoldásig a következő lépéseket kell elvégezni:
Az első négy munkafázissal a 2.2 alfejezetben részletesen foglalkozunk.
A 3. és 4. fejezetben konkrét problémák megoldásában alkalmazzuk ezeket a lépéseket, a tesztelést könyvünk 5. fejezete tárgyalja.
A futtatás, az eredmények értékelése a felhasználó feladata, a programozással nem függ össze szorosan, ezért ezzel könyvünk külön nem foglalkozik.
A programozási feladatok megoldásához olyan módszert mutatunk be, amely az elemzési, tervezési és kódolási szakaszban is hasznosan alkalmazható. Az alapmódszer: a moduláris programozás.
A moduláris programozás lényege, hogy a feladatot részfeladatokra kell felbontani, ezeket önállóan kell kódolni, majd az egyes modulokból össze kell állítani a kész programot.
Választhattuk volna a strukturált programozás valamelyik módszerét is. Ezt azonban két okból nem tettük:
A strukturált programozás módszerét természetesen nem hagyjuk ki teljesen könyvünkből. A modulok jóval egyszerűbb belső tervezését és kódolását strukturált programozási módszerrel végezzük el.
Mielőtt a feladatmegoldás egyes lépéseit ismertetnénk, egy fontos alapfogalmat kell tisztázni, a modul fogalmát.
A modul a programnak egy része, amely
A moduláris programozás leglényegesebb lépése a feladat modulokra bontása. Ez azt jelenti, hogy a feladatot logikai funkciókra kell bontani, és az egyes logikai funkciók fogják a modulokat megvalósítani. Egy modul több típusú funkciót láthat el. Attól függően, hogy a modul milyen logikai funkciót lát el a programon belül, a modulokat három típusba sorolhatjuk:
A vezérlőmodul irányítja, vezérli egy vagy több modul, vagy az egész program végrehajtását. Ez "hívja" az egyes eljárásmodulokat, azaz meghatározza, hogy az eljárásmodulok milyen sorrendben hajtódjanak végre. A vezérlőmodul az alárendelt (vezérelt) modulokat a feladat megoldásához szükséges sorrendben hívja. Egy programon belül akár több vezérlőmodul is lehet:
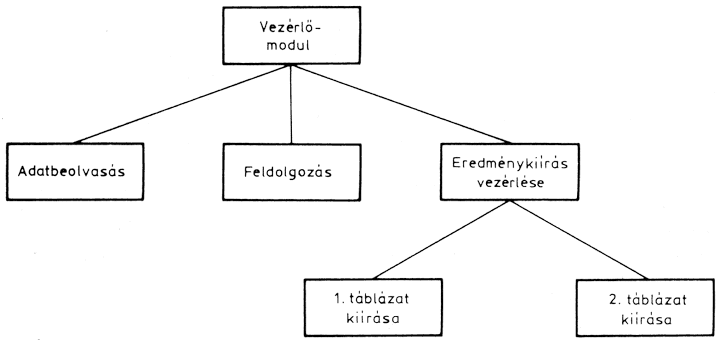
Természetesen a két vagy több vezérlőmodul között lehet hierarchikus (alá-fölé rendeltségi) viszony, de lehetnek a modulok függetlenek is egymástól. Az ábrán látható példán az eredménykiírást két modulra bontottuk: az 1. és 2. táblázat kiírására.
A fő vezérlőmodul hívja az "eredménykiírás" vezérlőmodult, majd ez az 1. és a 2. táblázat kiírómodulját. A két vezérlőmodul tehát hierarchikusan kapcsolódik egymáshoz.
Egyszerű szerkezetű programoknál - és ez elmondható a BASIC nyelv alkalmazóinak feladatairól is - a vezérlőmodul el is hagyható. Ilyenkor a modulok a megoldásnak megfelelő logikai sorrend szerint egymást hívják.
Az ábrán bemutatott kibővített feladatból el lehet hagyni az "eredmény kiírás" vezérlőmodult. Ha a feladat úgy szól, hogy előbb az 1., utána a 2. táblázatot kell kiírni, akkor a modu-lok sorosan hajtódnak végre:
Adatbeolvasás
![]()
Feldolgozás
![]()
1. táblázat kiírása
![]()
2. táblázat kiírása
Ha azonban a feladat úgy szól, hogy bizonyos feltételnél az 1., egyébként a 2. táblázatot kell kiírni, akkor ezt a feltételt a kiírást megelőző modul befejezésekor meg kell vizsgálni. Ezt az esetet a következő ábra mutatja:
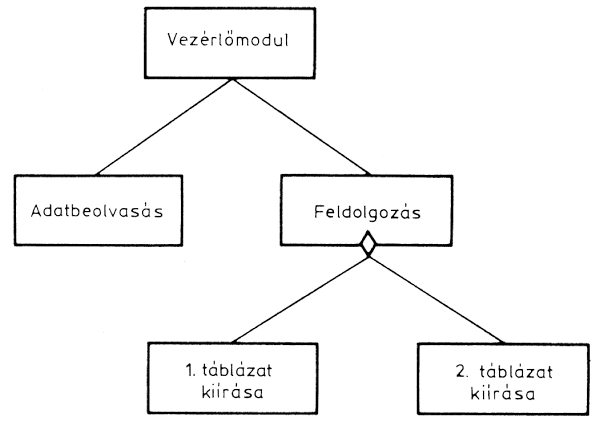
Alternatívát tartalmazó szerkezet
A hívómodul alján levő rombusz jelzi, hogy valamilyen feltételtől függően a hívómodul csak az egyik modult aktivizálja. Itt végeredményben nem csináltunk mást, mint azt, hogy a vezérlőmodul funkcióját megtartottuk, de beolvasztottuk a "feldolgozás" modulba.
Az adatmodul a program adatainak meghatározására szolgál. Lényegében passzív modul, csupán adatokat tartalmaz. A BASIC nyelvben sokkal egyszerűbb az adatok meghatározása, mint más magas szintű nyelvekben. Az adatmeghatározás szigorúan véve csupán vektorok és tömbök terjedelmének meghatározására szolgál. Adatmodulnak tekintjük azonban az olyan modulokat is, amelyekben adatbeolvasás vagy változók induló értékének meghatározása, vagy konstansok definiálása megy végbe. Adatmeghatározás két módon lehetséges a programban:
Célszerű, ha a program elején az összes adatot egyszerre definiáljuk, mert így az adatmeghatározások egy helyen lesznek.
Az eljárásmodulok valamilyen logikai feladatot hajtanak végre. Ezek a modulok végzik el pl. az adatok beolvasását, a különböző feldolgozási műveleteket és a kiírásokat. Egy programon belül eljárásmodulból van a legtöbb, és ezek összessége hajtja végre a tulajdonképpeni feldolgozást. A feladat megoldása szempontjából ezek a leglényegesebbek.
2.2. A feladatmegoldás folyamata
2.2.1. A feladat elemzése
A feladat elemzése a felülről lefelé haladás elvének megfelelően történik, eredménye pedig a feladat modulszerkezetének kialakítása. Ezt megelőzi a feladat megoldhatóságának vizsgálata.
Könyvünkben a Myers dekompozíciós eljárás egyszerűsített változatát fogjuk követni. A feladat elemzése a következő négy lépésben történik:
1. A felülről lefelé haladás (top-down) elvének megfelelően először a feladat nagyvonalú szerkezetét vázoljuk fel. A feladat tanulmányozása után össze kell gyűjteni azokat a funkciókat, amelyeket a feladatot megoldó programnak el kell látnia. Itt a megoldás módjára még nem utalunk, csupán a főbb tevékenységeket jelöljük meg, ezek felsorolása egyúttal a feladat nagyvonalú felépítését is rögzíti. Tekintsünk példaként egy trendszámítási feladatot, amelynek az a célja, hogy a tetszőleges folyamatra vonatkozó, tetszőleges időléptékű lineáris és exponenciális trendszámítást el lehessen végezni.
Első lépésben erről a feladatról a főbb funkciókat kell megállapítani:
- az adatok bevitele, értelmezése,
- a lineáris trendszámítás és kiírása,
- exponenciális trendszámítás és kiírás.
2. A következő lépésben az adatáramlást kell megtervezni. Mivel a program nem más, mint különböző adattranszformációk végrehajtása, látnunk kell, hogy az elemzés kulcsfontosságú szakasza az adatáramlás megtervezése. Fel kell tárni azokat az adattranszformációkat, amelyeknél a bemeneti és a tárolt adatokból elkészül az eredmény. Az adatáramlás tervezése történhet előre - a bemenettől a kimenet felé - vagy visszafelé. Az utóbbi esetben a feladat céljául szolgáló eredményből kell visszafelé elindulni, és meghatározni, hogy a kívánt kimenet elkészítéséhez milyen közvetlen adattranszformációk szükségesek, s hogy azt milyen adattranszformációknak kell megelőzniük. Ezt folytatni kell mindaddig, amíg el nem jutunk a lehetséges bemeneti adatig.
Példánkban ahhoz, hogy a trendszámítás eredménye a felhasználó számára értelmezhető legyen, meg kell adni a trendszámítás tárgyát, mennyiségét (kg, tonna, fő stb.), időléptékét (év, hó stb.), s el kell különíteni a tényidőszakokat az előre jelzett időszakoktól.
A bemeneti adatok közül az idősor adataiból el kell végezni a trendszámítást. A számítás eredményét a paraméteradatokkal együtt kell kiírni, majd a szemléletesebb ábrázolás kedvéért diagram formájában ki kell rajzolni, tehát az eredményekből a grafikus ábrázoláshoz szükséges adatokat ki kell számolni. Ezt mind a lineáris, mind az exponenciális trendszámításhoz el kell végezni.
Az adatáramlás az alábbi főbb műveleteket foglalja magában:
- a bemeneti adatok olvasása és értelmezése,
- a trendszámítás,
- a trendszámítás eredményének kiírása,
- a trendszámítás eredményének grafikus ábrázolása.
Az utolsó három műveletet mind a lineáris, mind az exponenciális trendszámításhoz végre kell hajtani. Ennek alapján a feladat megoldásaként a következő újabb modulszerkezetet kaptuk:
Adatok beolvasása
Lineáris tenderszámítás
Eredmény kiírás
Eredményrajzolás
Exponenciális tenderszámítás
Eredménykiírás
Eredményrajzolás3. A modulokat meg kell határozni. A 2. lépés eredményeként már kialakult egy előzetes modulszerkezet, most pedig a kapott modulok funkcióját kell röviden kifejteni.
Az első modult az alábbiak szerint lehet röviden leírni: beolvassa és funkció szerint tárolja a tényidőszak adatait, az adatok dimenzióját, időértékét és a trendszámítás tárgyát.4. Az elemzés utolsó lépéseként a megoldás modul szerkezetét kell meghatározni. Ez a lépés a modulok kapcsolódását rögzíti, de eredményezheti a további bontásukat is.
Ezzel a feladat elemzése lezárult. Jól érzékelhető a felülről lefelé haladás elve. Az első lépés eredményeként példánkban még csupán 3 funkciót határoztunk meg, a másodikban már hetet, a harmadikban pontosítottuk a modulok definícóját. Az elemzés során meghatároztuk a modulszerkezetet, és ezzel a lépéssel már a programtervezéshez jutottunk el.
2.2.2. A program tervezése
A programtervezés a feladat elemzése után kezdődik, és annak eredményeit használja fel. A programtervezésben egy fontos feladat a program szerkezetének további finomítása, a feladatelemzés során kapott modulszerkezet tovább bontása. A meglevő funkciókat újabb részfunkciók megállapításával újabb hierarchikus szinteken bontjuk tovább. A bontást addig célszerű folytatni, amíg minden szinten lehetőleg zárt funkciót ellátó modulokat kapunk. Ezek a funkciók alkotják a program moduljait.
A feladatelemzés olyan modulszerkezetet eredményezett, amely a feladat természetes megoldási menetét követi. A programtervezésnél a modulszerkezet finomítását a feladat szerkezetének megfelelően kell végrehajtani. Programtervezéskor a finomítást a felülről lefelé haladás elve szerint végezzük.
A bontás mélysége nem lesz egyenletes a feladat minden funkcióját tekintve. A bonyolultabb funkciókat több szinten kell alkotóelemeikre bontani, míg az egyszerűbbeket 1-2 szinten is már a megfelelő részletességig lehet finomítani.
A bontás eredményeként kapott modulok között kapcsolat van. Ezeknek a kapcsolatoknak kell biztosítaniuk, hogy a modulok végrehajtása a helyes sorrendben történjen, és az adatok a kívánt módon haladjanak a programon belül.
A modulok közötti kapcsolat sokféle lehet. Ezek közül csupán kettőt vizsgálunk: a vezérlő- és az adatkapcsolatot.
A programtervezés eredményeként létrehozott modulokat és a közöttük fennálló kapcsolatokat (struktúrát) egyezményes jelek segítségével ábrázoljuk:
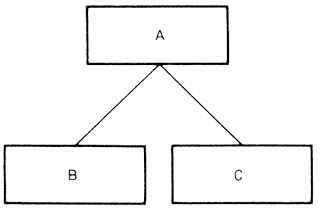 |
A hívja B-t, majd C-t: Az A modul előbb a B, majd a C modult hívja. Ha az A modul a B és a C modul vezérlőmodulja, akkor A valódi (a programban kódolt) modul. Ha a B és C modul csupán az A modul tovább bontása, akkor A modul nem létezik, ilyenkor csak a B és a C modul valódi, és ezek valamilyen sorrendben végrehajtódnak. |
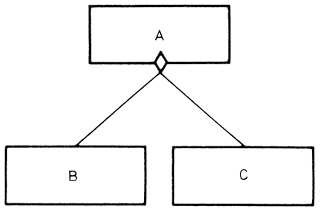 |
Az A modul egy feltételtől függően vagy a B, vagy a C modult hívja. Természetesen az A modul valóságos modul, mert valóságos feladatot (feltételvizsgálat) lát el a programon belül. A B és C modul végrehajtása a vizsgált feltételtől függ. |
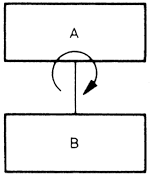 |
Az A modul ciklikusan hívja a B modult. Erre akkor van szükség, ha egy adatcsoport valamennyi elemén ugyanazt a műveletet kell elvégezni (pl. egy vállalat dolgozóinak bérét ugyanazzal az eljárással kell kiszámítani). Az A modul annyiszor hívja a B modult, ahányszor a műveleteket végre kell hajtani. |
 |
A B modul önmagát hívja (rekurzív hívás). Ez lényegében az előző pontban leírt szerkezet egyszerűsített változata, ha a vezérlő A modult elhagyjuk, és a ciklikus hívás vezérlő logikáját a B modulba építjük. |
A bemutatott modulszerkezeti jelekkel szinte valamennyi feladat szerkezete ábrázolható. Alkalmazásukra a 3. és 4. fejezetben mutatunk példákat.
A szerkezettel kapcsolatban két olyan fogalmat is kell vizsgálni, amelyet helyesen működő programok készítéséhez ismerni kell.
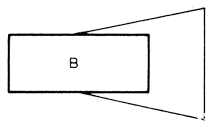
Egy modul vezérlési hatáskörébe azok a modulok tartoznak, amelyeket a modul közvetlenül vagy közvetve képes hívni. A következő ábrán a B modul a D és E modult tudja közvetlenül, az F és G modult csak közvetve (az E modulon keresztül) hívni. Ezért azt mondjuk, hogy a B modul vezérlési hatáskörébe a B,D,E,F,G modul tartozik, de a H modul például nem.
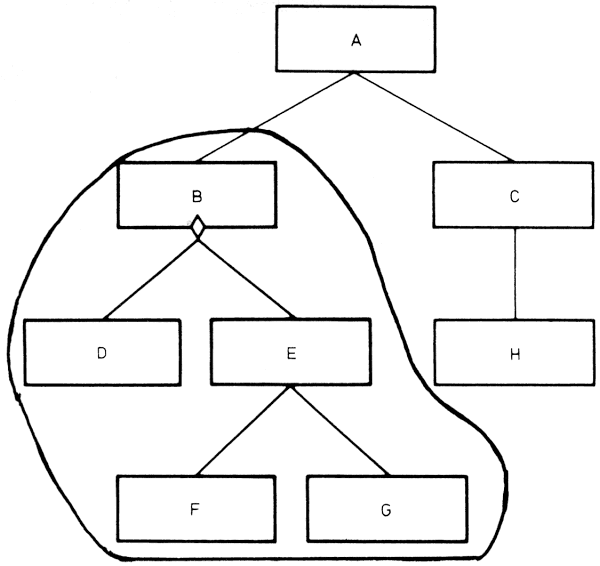
Egy modul döntési hatáskörébe azok a modulok tartoznak, amelyek végrehajtása döntéstől függ. Ilyen döntést láthatunk a B modulban.
A modulszerkezet kialakítása akkor helyes, ha egy döntés hatáskörébe tartozó modulok a döntést tartalmazó modul vezérlési hatáskörének részhalmazát alkotják.
Ha például a bemutatott döntés hatáskörébe a B,C,D és E modul tartozna, akkor a tervezés helytelen lenne, mert a C modul nem tartozik a B modul vezérlési hatáskörébe. Ha a B modulban létrejöhet olyan feltétel, hogy a C modult kellene hívnia, akkor a B modul ezt nem tudja megtenni, mert a C modul nem tartozik a vezérlési hatáskörébe, tehát nem tudja hívni. Ilyenkor a programot át kell tervezni, hogy a vezérlési és döntési hatáskörök összhangba kerüljenek.
Ha a fentiekkel ellentétben a döntés hatáskörébe csak a B,D és E modul tartozik, akkor a döntési hatáskörbe tartozó modulok a vezérlési hatáskör (B,D,E,F és G) részhalmazát alkotják, tehát a tervezés ebből a szempontból helyes.
A modulok végrehajtásának sorrendjét a vezérlőmodul, illetve ha több van, akkor a vezérlőmodulok megfelelő kialakításával kell biztosítani.
A funkciókat megvalósító modulokat balról jobbra haladva kell berajzolni a modulszerkezeti ábrába, így a végrehajtás is majd balról jobbra haladva történik.
A programtervezéshez tartozik annak az eldöntése is, hogy a program egyetlen program legyen, vagy több önálló programból álljon. Ha egyetlen program módszerét választjuk, akkor egy állományban tároljuk a teljes programot, a másik esetben pedig annyi programállományunk lesz, ahány önálló programból az egész eljárás összerakható.
Felmerül a kérdés, hogy mikor melyik megoldás a célszerűbb. Bonyolult, hosszú programnál, illetve feladatnál - különösen akkor, ha vezérlőmodulokat is tartalmaz a programterv - cél-szerű több programra felosztani az egészet. Ilyenkor sem érdemes modulonként külön programot készíteni. Végrehajtásnál a szekvenciálisán következő modulokat érdemes egy programba összevonni. A vezérlőmodulokat pedig célszerű egyesíteni és egyetlen önálló programként elkészíteni. Ez utóbbit nevezzük főprogramnak.
Hasonló vagy azonos funkciók ellátására érdemes típusprogramot tervezni. Ezt csak egyszer kell megtervezni és elkészíteni, és ezek után több feladat megoldásában is alkalmazható. Ezzel sok fáradságot és időt lehet megtakarítani. A többször felhasználható modulprogramok modulkönyvtárat alkotnak.
Összefoglalva megállapíthatjuk, hogy a program modulokra bontásának számos előnye van:
2.2.3. A modulok tervezése
Az egész program megtervezése után a program "építőköveinek" - a moduloknak - a tervezése következik. A modultervezés célja, hogy elkészítsük a modul külső specifikációját (azonosítását), és leírjuk azokat a belső folyamatokat, amelyek végrehajtásával a modul teljesíti funkcióját.
A külső specifikációhoz tartozik a modul neve, amellyel a programozó az adott modult azonosítja. Ide tartozik a modul típusának (vezérlő, adat, eljárás) meghatározása is. Végül azt is definiálni kell, hogy a modul milyen módon kapcsolódik a környezetéhez, vagyis hogyan lehet hívni, és mi történik a befejezéskor.
Általánosan követendő szabályként javasoljuk az olyan modulok tervezését, amelyek fő jellemzője, hogy egyetlen bejáratuk és egyetlen kijáratuk van. Ez azt jelenti, hogy a modul végrehajtása mindenféleképpen ugyanazon a kezdő programsoron indul, és ugyanazon a záró programsoron fejeződik be. Ez a modulok zártságát, áttekinthetőségét fokozza, és nem lebecsülendő az sem, hogy ilyen esetekben a módosítás könnyebben elvégezhető.
A modul belső tervezése három fő lépésből áll:
A bemenet és kimenet tervezését konkrét példákon szemléltetjük a 3. és 4. fejezetben. Itt részletesen foglalkozunk a feldolgozás folyamatának általánosítható szempontjaival.
A feldolgozási folyamat, az adattranszformáció algoritmusa a program szempontjából alapvető jelentőségű. A program valamennyi funkcióját az egyes modulok feldolgozási lépései valósítják meg. A feldolgozás egymás után következő (szekvenciális) műveletek elvégzését jelenti.
A feldolgozási folyamatot folyamatábrával tesszük képszerűbbé és könnyebben áttekinthetővé. Sok olyan művelet van, amely rendszerint több feldolgozási folyamatban is előfordul. Ezeket célszerű egységes folyamatábra-jellel jelölni. Így alakultak ki a folyamatábra - szimbólumok, amelyek a feldolgozás menetétől függetlenül egy-egy művelettípust jelölnek. A folyamatábra - szimbólumokat egységesítették, majd szabványosították - hazánkban is - és ez elősegíti, hogy a szakemberek egy-egy feldolgozásról közös, rajzos nyelven beszélhessenek.
A következőkben áttekintjük a gyakrabban használt folyamatábra-szimbólumokat:
| Tárolóeszközök: | Perifériák és velük kapcsolatos műveletek: |
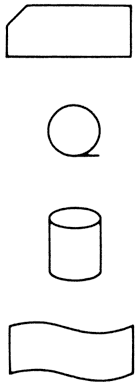 |
Lyukkártyaállomány |  |
Sornyomtató, bemeneti bizonylat, kiírás | |
| Mágnesszalag-állomány | Képernyős terminál | |||
| Mágneslemez-állomány | Billentyűzet kézi adatbevitel | |||
| Lyukszalag |
| Műveletek: |
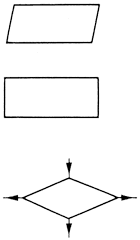 |
Bemeneti vagy kimeneti művelet |  |
Külön meghatározott művelet, amely önmaga is egy több lépéses folyamatábra lehet. Akkor használjuk, ha a folyamatábrában egy, már meghatározott műveletsorozatot nem akarunk részletezni. | |
| Tetszőleges műveleti jelkép. | Határoló jelkép. A folyamat kezdetén és végén alkalmazzuk. |
|||
Döntés. A döntés valamilyen vizsgálaton alapszik. A vizsgálat eredményeként a program végrehajtása 2-3 irányban haladhat tovább. |
Adatátvitel - jelölés távadatfeldolgozásnál. |
| Rajztechnikai jelek: |
 |
Folyamatvonal a folyamatvégrehajtás irányával. | 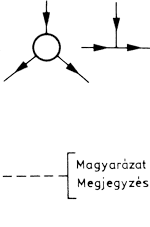 |
Kapcsolójel. A folyamatvonal elágazását vagy találkozását jelöli. | |
| Folyamatvonalak keresztezése. | Magyarázó jelkép, amely valamilyen folyamatábra-jelhez kapcsolódik. Akkor használjuk, ha a kívánt szöveg nem fér el a szimbólumban. A kiegészítő szöveget a magyarázó jelkép jobb oldalára írjuk. |
A folyamatábra-jelölések egyszerűek és könnyen érthetők. Rajzolásuk megkönnyítésére a kereskedelemben folyamatábra-sablonok kaphatók.
Megengedett algoritmustípusok (a feldolgozási folyamat tervezésének módszere)
A modul funkcióját megvalósító folyamat sokféleképpen mehet végbe. A strukturált programozás egyik kidolgozója, Dijkstra, három alapvető algoritmustípus alkalmazását ajánlja. A továbbiakban ezeket, illetve az ezekre visszavezethetőket fogjuk mi is felhasználni. Alkalmazásukat a következőkkel lehet indokolni:
Ezek után vizsgáljuk meg a három alapvető algoritmustípust.
Szekvencia
Két vagy több utasításból álló utasítássorozat.
Egy szekvencia tetszőleges típusú és számú műveletet tartalmazhat.Feltételes elágazás
Valamilyen feltételtől függően két utasítássorozat közül csak az egyik hajtódik végre. Ennek az algoritmustípusnak három alfaja van. Az első két esetben a feltétel két értéket vehet fel (igaz, hamis), s ha az egyik feltételértékhez külön utasítássorozat tartozik, akkor ezt IF-THEN (ha ..., akkor ...) típusú algoritmusnak nevezzük.
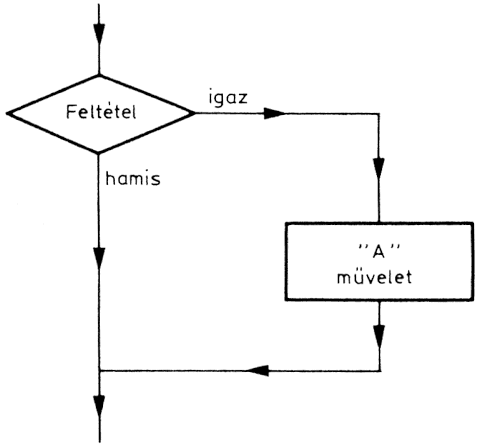
Az ábrán látható, hogy ha a feltétel teljesül, akkor az művelet végrehajtódik, ha hamis, akkor nem.
A feltételes elágazás második esetében a feltétel mindkét ágában van egy-egy utasítássorozat. Ha a feltétel teljesül, akkor az egyik ág, ha a feltétel nem teljesül, akkor a másik ág utasítássorozata hajtódik végre. Ez az IF-THEN-ELSE (ha..., akkor. . ., egyébként...) algoritmus.
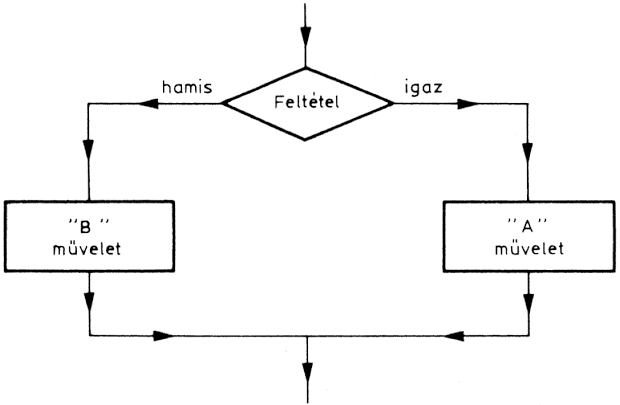
Tegyük fel, hogy OTP átutalási betétszámláról kell egy bizonyos összeget egy megadott címre átutalni. A feladat az OTP átutalási díjának meghatározása. Ismeretes, hogy az OTP bármelyik fiókjánál vezetett OTP-számlára való átutalásnál nem számol fel díjat, míg más esetben az átutalási díj 3,- Ft. A díj megállapításának tehát az a feltétele, hogy a címzett számla OTP- számla-e vagy sem. Ha nem, akkor az OTP díjat számol fel, ha azonban OTP-számla, akkor az átutalás díjmentes.
Ha például a szabály úgy módosulna, hogy az OTP-számlára való átutalásnál az OTP 1,- Ft díjat számolna fel, akkor a feltételének "igen" ágában is el kellene helyezni egy műve-letet (1 Ft felszámolása), és így egy IF-THEN-ELSE szerkezetet kapnánk.
A feltételes elágazási algoritmus harmadik típusában is egy feltételt kell vizsgálni, de ennek kettőnél több értéke lehet. Ez a CASE (abban az esetben, ha ...) algoritmus. Általánosított folyamatábrája az alábbi ábrán látható.
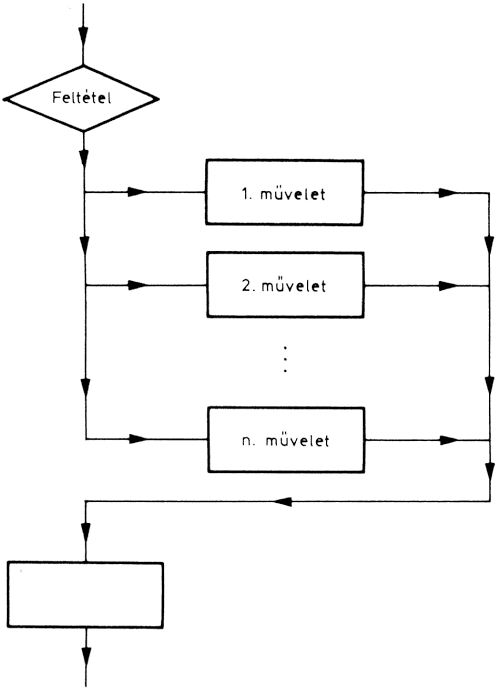
A feltétel-változó értékétől függően más és más műveletsorozatot kell elvégezni. Ez tulajdonképpen az IF-THEN-ELSE szerkezet kiterjesztése kettőnél több kimenetű feltétel esetén.
Ciklus
Ha több hasonló típusú adaton kell ugyanazt a műveletet elvégezni, akkor ezt ciklikusan kell megvalósítani. A ciklikus műveletek végét valamilyen feltétel határozza meg.
A ciklikus műveletek a feltételvizsgálat helyétől függően két formában hajthatók végre:
Az elöl tesztelő vagy DO-WHILE típusú szerkezetben a ciklikus művelet elvégzése előtt kell megvizsgálni azt a feltételt, aminek alapján el lehet dönteni, hogy szükség van-e még a művelet elvégzésére.
Tegyük fel, hogy számokat kell terminálról beolvasni, és ezek összegét kell képezni. Az összegezést természetesen csak addig kell csinálni, amíg jön be adat. Ha minden adat beérkezett, akkor a következő műveletre (például átlagszámítás) kell áttérni. A ciklus végrehajtásának az a feltétele, hogy van-e még adat, vagy valamilyen speciális jel érkezett be, amely azt mutatja, hogy a bevitel befejeződött. Ekkor a ciklust már nem kell végrehajtani. A hátul tesztelő (DOUNTIL) típusú szerkezetnél először a művelet megy végbe, és csak utána vizsgáljuk, hogy végre kell-e még hajtani. Lényeges különbség az elöl tesztelő szerkezethez képest, hogy a feltételvizsgálat akkor történik meg, amikor már a ciklikus művelet végrehajtódott.
A DOUNTIL típusú szerkezetet akkor lehet alkalmazni, ha a befejezési feltételt hordozó változó a ciklikus művelet során változtatja értékét. Ha ez a változó a befejezési feltétel értékét kapja meg, akkor a hátul tesztelő vizsgálat a ciklus végrehajtását leállítja. Ha tudjuk például, hogy 30 adatot kell feldolgozni, akkor a még feldolgozandó adatok számát a ciklikus művelet után eggyel csökkenteni kell. Ha ez a szám 0, akkor több feldolgozásra váró adat nincs, tehát a ciklus befejeződik.
2.2.4. A kódolás
A kódolás a folyamatábrában rögzített műveletek megfogalmazása az adott programnyelven, jelen esetben BASIC nyelven. A kódolást modulonként külön-külön, a folyamatábra alapján kell elvégezni. A folyamatábra lefordításánál figyelembe kell venni az adott - jelen esetben a BASIC - nyelv lehetőségeit, sajátosságait. Ezért nem csupán szóról szóra kell fordítani - mint a beszélt nyelveknél -, hanem a nyelv szerkezeti sajátosságait is figyelembe kell venni. Ebben a pontban a kódírás alapszabályait tekintjük át.
A programozási nyelvekben a folyamatábra műveleteit utasításokkal írjuk le. Egy utasítás egy mondatnak felel meg. Az utasítások a BASIC nyelvben "mondattanilag" két részből állnak: a kulcsszóból, amely a mondat állítmányának felel meg, és az utasítás tárgyából, amely azt mutatja, hogy melyik adaton kell elvégezni a kulcsszóval meghatározott műveletet.
Hivatkozáshoz és a végrehajtás sorrendjének egyértelmű meghatározásához az utasítások sorszámot is kapnak.
Egy BASIC utasítás tehát három részből áll: sorszám, utasításkulcsszó, az utasítás tárgya.
Fontos szintaktikai szabály, hogy az egyes részek között legalább egy szóközt kell hagyni - bár ez nem minden implementációban feltétel - (többet is lehet).
Helyes sorok:
100 LET A=8
vagy
100 LET A = 8
vagy
200 IF B=10 THEN GO TO 500
Helytelen sorok:
100 L E T A = 8
vagy
1 0 0 LET A=8
A BASIC (és az egyéb programozási nyelvi) utasításokat sorokba újuk. Általában egy sorba egy utasítást írunk. Könyvünk további részében - néhány rendkívüli esetet kivéve - ezt a szabályt fogjuk alkalmazni. Megjegyezzük, hogy egy sorba több utasítást is írhatunk, de egy utasítást sohasem lehet két sorba írni! Az egy sorba írt, ún. többszörös utasításokat kettősponttal kell elválasztani egymástól.
Az alábbi rövid programrészletben minden utasítás külön sorban van:
10 LET A=5
20 LET B=10
30 PRINT A+B
Ugyanezt leírhatjuk egy sorba is:
10 LET A=5: LET B=10: PRINT A+B
A jelentése ennek is ugyanaz. Vegyük észre, hogy a többszörös utasításnak egy sorszáma van; jelentőségét a sorszám tárgyalásánál világítjuk meg.
A BASIC nyelvben egy sor hossza - implementációtól függően - 120-255 karakter lehet.
Egy sorba tehát csak annyi utasítást lehet összevonni, hogy az összes karakter száma (beleértve a sorszámot és a szóközöket is) ne legyen ennél több. Ugyanez vonatkozik az egyedül álló utasításokra is.
Felhívjuk a figyelmet arra, hogy a többszörös utasításokat csak kivételes esetekben célszerű használni, mert ezek - egy program áttekinthetőségében és javíthatóságában - komoly nehézségeket okozhatnak. Ezeket a kivételeket majd példával szemléltetjük.
Most pedig vizsgáljuk meg az utasítások részeit!
A sorszám
A program utasítássorait sorszámmal kell ellátni. A program futásakor az egyes utasítások a legalacsonyabb sorszámtól a sorszámok növekvő sorrendjében hajtódnak végre. Egy sorban csak a sor elején lehet egy sorszám. Többszörös utasításoknál a sorban levő első utasítás kap sorszámot, a többi nem.
Mint már említettük, a sorszám az utasítás azonosítója, ezzel hivatkozhatunk rá. Ha egy sorban például valamilyen szintaktikai (formai) hiba van, akkor a fordító a hibaüzenetben a hibás sor számát íja ki. Így a programozó rögtön tudja, hol keresse a hibát.
Programon belül is csak az utasítás sorszámára hivatkozhatunk. A vezérlésátadó utasítások utasítástárgyában mindig sorszám szerepel. Az alábbi GO TO utasítás például azt jelenti, hogy a programot a 150-es sorszámú sorban kell folytatni:
100 GO TO 150
Többszörös utasításoknál csak a sor kezdőutasítására lehet a vezérlést átadni ("ugrani"), közbenső utasításra nem.
A sorszámot a program készítője határozza meg. A program első utasítása kapja a legalacsonyabb sorszámot, a többi utasítást a végrehajtás sorrendjének megfelelően növekvő sorszámmal kell ellátni.
A sorszám téves begépelése az utasítás végrehajtási sorrendjét megváltoztathatja, és a program hibásan fog működni.
Vigyázzunk arra is, hogy két utasítás ne kapja ugyanazt a sorszámot, mert ilyenkor a másodiknak bevitt sor törli az a már meglévő azonos sorszámú sort.
A sorszám szerinti végrehajtást néhány utasítás megváltoztathatja. Ezeket - a többi utasítással együtt - a következő fejezetekben részletesen bemutatjuk.
Bár az utasítások végrehajtási sorrendjét nem a begépelésük és a programkódon belüli elhelyezkedésük sorrendje határozza meg, hanem a sorszámuk, mégis célszerű az utasításokat a végrehajtás sorrendjében begépelni. Ezzel a program áttekinthetőbb, futási ideje pedig rövidebb lesz.
A legkisebb adható sorszám 1, a legnagyobb adható sorszám implementációfüggő:
Ajánlatos az utasításokat ötösével vagy tízesével sorszámozni. Ha ugyanis a helyes működés érdekében az utasítások közé újabb utasítást kell beszúrni, akkor ez az utasítás (vagy utasítások) megkaphatja a fel nem használt sorszámot. Ha egyesével számozzuk az utasításokat, akkor egy kényszerű beszúrásnál át kell sorszámozni az egész programot.
Az utasításkulcsszó
Az utasításkulcsszó műveletet határoz meg. Utasításkulcsszó csak kijelölt szó lehet. Használatukat a 3. fejezetben ismertetjük. Az utasításkulcsszavakat csak a BASIC nyelv szintaktikája által megengedett formában lehet megadni. Van egy olyan utasításkulcsszó, amelyet elhagyhatunk (kivéve a Spectrum BASIC-ben). Ez az értékadó utasításkulcsszó, a LET. Az alábbi utasítás azt jelenti, hogy az A változó értéke 10 legyen:
20 LET A=10
A LET utasításkulcsszó elhagyásával az utasítás ugyanazt jelenti:
20 A=10
Figyeljük meg, hogy az utasításkulcsszó megadása azért mellőzhető, mert azt az utasítás tárgyában levő egyenlőségjel pótolja.
Van olyan utasításkulcsszó, amely nem műveletet jelöl, hanem csupán valamilyen jelzést, üzenetet ad át a fordítónak. Ilyen a megjegyzést jelölő REM utasításkulcsszó:
30 REM ITT KEZDODIK A NYOMTATAS
Ez az utasítás azt jelenti, hogy a számítógépnek semmilyen műveletet sem kell elvégeznie, áttérhet a következő sor első utasításának végrehajtására. Az utasítás tárgyában levő szöveget a programozó saját maga számára beírja, hogy a program nevezetes pontjait megjelölje.
Az utasítás tárgya
Általában valamilyen adat, amelyre az utasítás vonatkozik. Van olyan utasítás, amelyhez nem tartozik utasítástárgy. Az utasítás tárgyának típusait részletesen a 3. és 4. fejezetben ismertetjük.
A kódolás módszere
A programkódot célszerű először kódlapra (vagy más papírra) megírni, és csak ellenőrzés után begépelni. Nem javasoljuk a rögtönzött kódolást a folyamatábra alapján, mert az még rövid, egyszerű moduloknál is nagyon sok hibát eredményezhet.
2.2.5. A dokumentáció
A dokumentációnak írásban kell rögzítenie a program célját, a feladat megoldási és az adatok tárolási módját, a bemeneti, kimeneti adatokat, és általában minden olyan adatot, amely lehetővé teszi, hogy más szakember is megismerje, megértse programunkat. Lényeges, hogy a dokumentáció segítse a program készítőjét vagy javítóját, hogy a programot - ha módosítani kell - 1-2 év után is megértse.
A programdokumentáció a programról rendelkezésre álló írásos információ. Az alkalmazott módszernek megfelelően az alábbi dokumentumok készülnek a programmal párhuzamosan:
Valamennyi programdokumentummal kapcsolatban általános követelmény, hogy hozzáférhető legyen az érdekeltek számára. Ezért a felhasználók számának és igényeinek megfelelő példányszámban és minőségben kell a dokumentumokat elkészíteni. A dokumentáció legyen tömör, világos szerkezetű.
Végül, de nem utolsósorban a dokumentáció legyen érvényes. Ez csak úgy lehetséges, ha a program módosítását valamennyi dokumentumra átvezetjük.
A felsorolt dokumentumok közül az első néggyel nem érdemes külön foglalkozni, mert a program létrehozásának ezek a lépései egyébként is csak írásban készíthetők el, tehát egyúttal dokumentációként is szolgálnak.
A programkód listája a program egyes sorainak a listája abban a formában, ahogy a program tárolódik. A programlista önmagában nem könnyen áttekinthető, nem beszédes dokumentum, ha csak a programutasításokat tartalmazza. Olvashatóságát növeli, ha a REM üzenő-utasítással különböző magyarázatokat, közléseket helyezünk el benne. REM utasításokkal a program elejére beírhatjuk a program nevét.
A REM utasítással üzeneteket helyezhetünk el a program kritikus pontjain vagy az egyes programszakaszok elején. A közbeékelt üzeneteket "üres" REM utasításokkal emelhetjük ki a környezetből.
A programlistában elhelyezett üzenetekre is vonatkozik, hogy a program módosításával egyidejűleg ezeket is módosítani kell. Ezért csak annyi REM utasítást helyezzünk el a programban, amennyinek a karbantartását ésszerű ráfordítással el tudjuk végezni.
A programlista áttekinthetőségét növeli a srukturált kódolás. Ez azt jelenti, hogy az egyes sorok, illetve sorcsoportok utasításkulcsszavait a sorszám után bizonyos számú szóközzel (bekezdéssel) eltolva írjuk be (ezt több BASIC implementáció lehetővé teszi). Ezzel a kódsorok kiemelhetők és elkülöníthetők egymástól.
A felhasználói kézikönyv a program felhasználójának készül. Megmutatja, hogy a programot hogyan lehet használni az adott feladat megoldására. Tartalmaznia kell a futáshoz szükséges bemeneti adatokat és bevitelük módját, a futtatás parancsait, az eredményadatok kezelését, a program üzemszerű szolgáltatásait. Meg kell adnia a különböző hibáknál kiadott hibaüzenetek értelmezését és a hiba elhárításához szükséges tevékenységeket.
3. Feladatok megoldása egyedi adatokkal
A számítógéppel megoldandó feladatok körében több szempontból is jól elkülöníthető csoportot alkotnak az egyedi adatok feldolgozását célzó feladatok. Erre a csoportra az a jellemző, hogy a feladaton belül viszonylag kevés (legfeljebb 100) és lényegében egymástól független adatot kell feldolgozni. A hangsúly inkább az utóbbin van, ami azt jelenti, hogy a feladat szinte valamennyi adatát külön kell kezelni és feldolgozni. Ez a feladattípus jól elkülönül az 4. fejezetben ismertetendő összetartozó adatok feldolgozásától, ahol nagy és egymáshoz logikailag kapcsolódó adattömegen kevés műveletet kell végezni.
Az egyedi adatok feldolgozására az is jellemző, hogy sok a számítás a feladatokban. Ezek az ún. "központiegység-igényes" feladatok. A bemeneti adatkezelés és az eredménykiírás - az adatok alacsony száma miatt - egyszerű.
Az egyedi adatok feldolgozási csoportjába tartoznak általában a tudományos, a mérnöki, a gazdasági és egyéb számítások, ezért ezekről a tipikus alkalmazási területekről vesszük a példáinkat is.
3.1. Soros (szekvenciális) feladatok
A soros vagy szekvenciális feladatok sajátsága, hogy a bemeneti adatok feldolgozása egy megadott, kötött lépéssorozatban történik. A valóságban kevés olyan soros feladat van, amelynek megoldására a számítógépet hatékonyan lehet felhasználni. A soros algoritmusok tanulmányozására azért van szükség, mert minden később bemutatott bonyolultabb feladat építőelemként tartalmaz soros algoritmusokat. Mielőtt konkrét példánkat megoldanánk, néhány fontos fogalmat ismertetünk.
Az egyszerű adattípusok
A feldolgozandó adat egy feladaton belül kétféle lehet: változó és konstans.
A számítástechnikában - a matematikában kialakult fogalomhoz hasonlóan - a változó olyan adat, amely értékét változtathatja a feldolgozás közben. Ezért jellemzője nem egy konkrét érték, hanem a logikai funkció, amit a feldolgozásban betölt. A változóra egy szimbólum segítségével hivatkozunk, amely önállósítja és elkülöníti a változót a többi adattól.
A számítástechnikában a változónak mindig konkrét számértéke van, a változó tehát csak logikai szerepet nem tölthet be. A változó értéke a tárban tárolódik. Ha a változóval végzett művelet során értéke megváltozik, akkor ez természetesen a tárolt értéket is módosítja. Az értékváltozás után a régi érték elvész, és mindig csak az új marad meg.
A konstans értékét nem változtatja a feldolgozás folyamán, így fő jellemzője az értéke. Szimbolikus hivatkozást nem igényel, a programban minden előfordulásnál közvetlenül az értékével szerepelhet.
A numerikus változók a legtöbb BASIC implementációban csak meghatározott neveket kaphatnak. A változó neve egy vagy két karakter hosszúságú lehet. Az első karakter mindig az ábécé valamelyik betűje, a második - ha van ilyen - csak számjegy lehet:
Helyes változónevek:
- X
- N8
- A
Helytelen változónevek:
- X11 - (három karakteres)
- AB - (a második karakter nem szájegy)
- 1C - (az első karakter nem betű)
A Spectrum BASIC-ben bármilyen betűt vagy számot tartalmazhatnak, az egyetlen megkötés az, hogy az első helyen egy betű szerepeljen. Betűközt is használhatunk a könnyebb megértés érdekében, de ez nem lesz a név része. Ugyanígy semmi különbség sincs, ha kis vagy nagybetűt használunk.
A továbbiakban más típusú változókat is megismerünk (indexelt, szöveges), amelyek nevét hasonlóan lehet képezni, de megkülönböztetésül kiegészítő jeleket kell a változónévhez adni.
A BASIC nyelvben a változókat nem szükséges a program elején meghatározni. A programban bárhol lehet új változókat bevezetni. A legtöbb BASIC implementáció minden változónak automatikusan 0 értéket ad, ha valamilyen utasítás nem rendelt értéket hozzá (de pl. a Spectrum BASIC hibaüzenetet ad, ha olyan változóra hivatkozunk, aminek még nem adtunk értéket). Így tehát minden változó eleve "nullázva" kerül a programba. Ha ez nem megfelelő a program helyes működéséhez, akkor a változóhoz a kívánt értéket kell hozzárendelni (pl. LET értékadó utasítással).
Tegyük fel, hogy az A változó értékét induláskor 6-ra kell beállítani. Ezt a
20 LET A=6
utasítással lehet elérni, amely az A változó értékét korábbi értékétől függetlenül 6-ra állítja be. Ha azt akarjuk, hogy az A változó vegye fel a B változó értékét (A legyen B-vel egyenlő), akkor a
30 LET A=B
utasítást adjuk meg. Felhívjuk a figyelmet, hogy az a változó, amelynek értékét megadni vagy módosítani kívánjuk, mindig az egyenlőségjel bal oldalán, míg az új értéket kifejező konstans, változó vagy kifejezés az egyenlőség jobb oldalán áll. Tehát a
40 LET B=A
utasítás nem egyenértékű az előző utasítással. Ekkor ugyanis - pont fordítva - a B változó veszi fel A értékét.
Ha az új értéket egy kifejezés képviseli, akkor azt kell az egyenlőségjel jobb oldalára írni:
60 LET A=B+C-1
Figyeljük meg, hogy a jobb oldalon végül is egy számérték van, s ezt a bal oldalon álló változó felveszi.
Az értékadásnak más módjai is vannak. Ezekkel a további fejezetekben ismerkedünk meg.
Feldolgozási lépések
A feldolgozás során az adatokkal számításokat, illetve logikai műveleteket végzünk. A számítási műveletek a BASIC-ben egyszerűen megadhatók:
| Ősszeadás: | A+B |
| Kivonás: | A-B |
| Szorzás: | A*B |
| Osztás: | A/B |
| Hatványozás: | A^2 vagy régebbi implementációkban: A**2 |
Számítási műveletet sohasem lehet "önállóan" megadni. A kapott eredményt mindig valahol tárolni kell. Ha például A és B szorzatát kell képezni, akkor a kapott értéket a további felhasználás érdekében meg kell őrizni.
Erre felhasználhatunk egy harmadik változót:
70 LET C=A*B
vagy a számítás bármelyik változóját, ha értékére tovább nincs szükség:
70 LET A=A*B
A művelet elvégzése után A értéke az A*B szorzat lesz.
Az eredmények kiírása
A feldolgozás eredményeit a PRINT kulcsszavú utasítással lehet kiírni. A PRINT utasítás hatására a megjelölt adat az éppen használt terminálra íródik ki.
Ha előre meghatározható szöveget vagy változónevet akarunk kiíratni, akkor ezt a PRINT utasításban idézőjelek közé kell írni. Ha a változó tartalmát kell kiíratni, akkor az utasításban a változó nevét kell megadni.
Ha például az "Eredő ellenállás" szöveget akarjuk kiíratni, akkor ezt a
100 PRINT "Eredo ellenallas"
utasítással lehet elérni.
Ha a feladat C változó értékének a kiíratása, akkor a
110 PRINC C
utasítást kell megadni. Ha az érték mellett a C változó nevét is ki akarjuk íratni, akkor a
120 PRINT "C=";C
utasítással oldhatjuk meg a feladatot. Ennek hatására a program az alábbi kiírást végzi el (tegyük fel, hogy C értéke 125):
C=125
A PRINT utasítás tárgyában idézőjelbe tett karaktereket a program változatlanul kiírja, az idézőjel nélkülieket változóknak tekinti, s ezek tartalmát úja ki.
A program befejezése
A program végét az END vagy STOP utasítással lehet jelölni (A Spectrum BASIC-ben nincs END), de használata nem kötelező. Az END hatására a programvégrehajtás megáll.
Használata egyszerű:
500 END
Most már hozzákezdhetünk az I. probléma megoldásához.
I. probléma
Adva van az alábbi ábrán látható ellenállásokból álló hálózat:
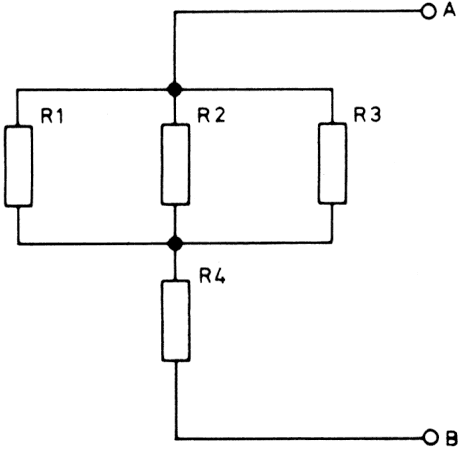
Meg kell határozni az A és B pont közötti eredő ellenállást. Az ellenállások értékei a következők:
R1 = 1000 ohm
R2 = 2000 ohm
R3 = 500 ohm
R4 = 200 ohm
A program az alábbi formában írja ki az eredő ellenállás értékét:
AZ EREDO ELLENALLAS (OHM): x
1. A probléma elemzése
A probléma az eredő ellenállás meghatározása ismert adatokból. A megoldás számítógéppel elvégezhető.
A programnak az alábbi főbb funkciókat kell megvalósítania:
A belső adatáramlásra jellemző, hogy a négy bemeneti adatból egyetlen értéket kell kiszámítani - az elektromosság egyik törvényszerűsége értelmében -, majd ezt az adatot ki kell írni. A program moduljait a fő tevékenységek alapján lehet meghatározni:
A megoldás modulszerkezete ezek után könnyen megállapítható:
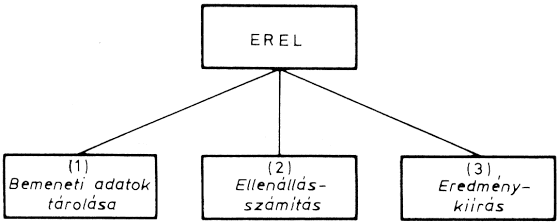
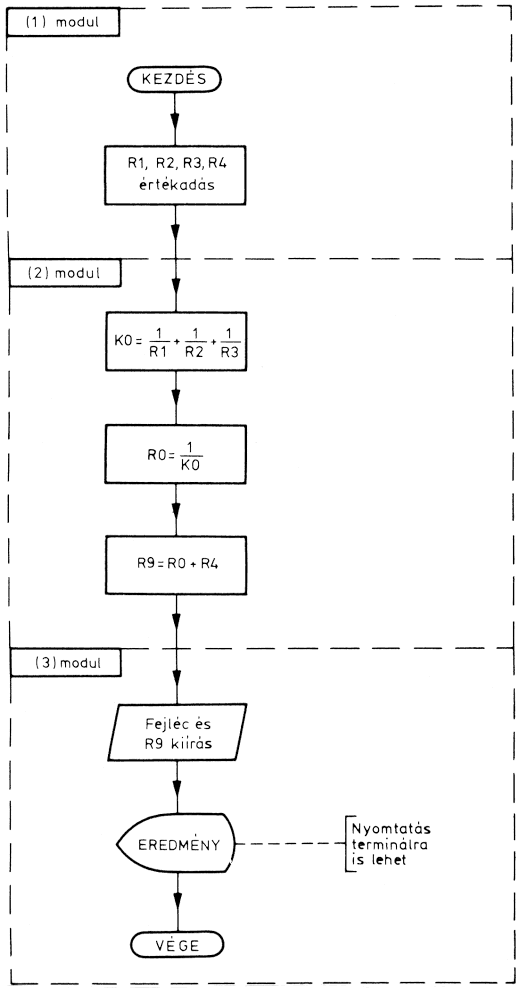
Az elemzésnél a feladat főbb funkcióit feltártuk. Most már áttérhetünk a program megtervezésére. A program neve legyen EREL (ERedő ELlenállás).
2. A program tervezése
A probléma egyszerűsége miatt nincs szükség a modulszerkezet további finomítására. Így az elemzés során kapott modulszerkezetet a programtervezés alapjának is tekinthetjük.
A modulok között adatkapcsolat van. Az (1) modul a bemeneti adatokat (ellenállások értékei) átadja a (2) modulnak, amely ezekből kiszámítja az eredőt, és ezt az értéket továbbítja a (3), a kiírómodulnak.
Látható, hogy a modulokat egyszerű szekvencia szerint [(1), (2), (3)] kell végrehajtani. Ezért vezérlőmodulra nincs szükség.
3. A modulok tervezése
A programtervezésnél a modulokat és tevékenységüket specifikáltuk, most az egyes modulok megtervezése következik.
(1) A bemeneti adatok tárolása
A modul adat típusú, mert egyetlen funkciója a négy ellenállásérték tárolása. A modulnak önálló bemeneti adatai nincsenek, a kimeneti adatokat az ellenállások értékei adják.
A modul algoritmusa az R1, R2, R3, R4 változó értékeinek megadása. Mivel az ellenállások értékei nem változnak a program folyamán, kezelhetnénk konstansként is. De ha azt is figyelembe vesszük, hogy ezt a programot ugyanilyen hálózat más értékű ellenállásainak eredőellenállás-számítására is felhasználhatjuk, akkor célszerűbb az ellenállásokat változóként jelölni.(2) Ellenállás-számítás
A modul eljárás típusú, mert feldolgozást végez. A modul bemenete a négy ellenállásérték, kimeneti adata az R9 eredő ellenállás.
Az alkalmazott algoritmus a soros és párhuzamos ellenállásokból álló hálózat eredőellenállás-számítására vonatkozó ismert kifejezésre épül:
Először határozzuk meg a tört nevezőjében álló kifejezést, jelöljük K0-val, majd ennek vegyük a reciprokát. Ezzel a jobb oldal első tagját kiszámítottuk. Az R4 érték hozzáadásával megkapjuk R9-et.
(3) Eredménykiírás
Ez a modul is eljárásmodul, mert adatkivitelt végez. A modul bemeneti adata a (2) modulból származó R9 eredő ellenállás értéke. A kimeneti adat ugyanez, de kiírva.
A specifikáció szerint a modulnak egy megadott szöveg után ki kell írnia az eredő ellenállás értékét. Ezt egy lépésben el lehet végezni. Az eredménykiírás mindig azon a terminálon megy végbe, amelyen dolgozunk. A kiírás után a program befejeződik.
A modulok folyamata:
4. A kódolás
A következő lépésben a modulspecifikációk alapján az egyes modulokat kódoljuk.
(1) A bemeneti adatok tárolása
Ez a program kezdőmodulja. Ezért a modul elejére (dokumentációs célokból) REM utasítások segítségével elhelyezzük a program nevét. A tényleges modul kezdetén pedig - szintén REM utasítással - a modul nevét adjuk meg. Ezután az egyes ellenállások értékeit kell megadni. Ezt legegyszerűbben a LET értékadó utasítással végezhetjük el. A LET utasításokkal minden változónak (ellenállás) a kívánt értéket adjuk.(2) Ellenállás-számítás
A modul folyamatábrájában foglalt értékadásokat szintén LET utasításokkal lehet kódolni. Figyeljük meg azonban a különbséget, hogy itt nem közvetlenül számértéket rendelünk hozzá egy változóhoz, hanem az érték egy kifejezés kiszámításával keletkezik. A folyamatábra tagjait egy-egy utasítással lehet kódolni. A modul elejére itt is elhelyezzük a modul címét.
A (2) modul mindig az (1) modul után hajtódik végre, ezért az utasításokat az (1) modul végéhez folyamatosan sorszámozhatjuk.(3) Eredménykiírás
A modul kiírási feladatát egyetlen PRINT utasítással el lehet végezni. Ezt a modult is célszerű a modul nevével bevezetni. Ez a program utolsó modulja, ezért a modul végére END (STOP) utasítást is írhatunk. A kiírómodul a számítási modul után következik, ezért a sorszámozást a (2) modultól lehet folytatni.
Az elkészült kód a következő:
10 REM *** EREL ***
20 REM BEMENETI ADATOK TAROLSASA
30 LET R1=1000
40 LET R2=2000
50 LET R3=500
60 LET R4=200
70 REM ELLENALLAS SZAMITAS
80 LET K0=1/R1+1/R2+1/R3
90 LET R0=1/K0
100 LET R9=R0+R4
120 PRINT "AZ EREDO ELLENALLAS (OHM): ";R9
5. A megoldás értékelése
A program elkészült, a futás eredményes. Csupán azt kell ellenőrizni, hogy a program logikailag is helyesen működik-e. Példánkban ennek legegyszerűbb módja, ha az eredő ellenállás értékét magunk is kiszámítjuk: 485.714 ohm
Megállapíthatjuk, hogy programunk helyesen működik, a problémát megoldja.
A feladat megoldása után a programot LIST paranccsal kilistázhatjuk, és SAVE "filenév" paranccsal háttértárra menthetjük.
3.2. Soros feladatok összetett aritmetikai műveletekkel
Ebben az alfejezetben az előzőekben bemutatott problémához hasonló szerkezetű problémákat ismertetünk. Lényeges különbség a két feladattípus között, hogy most bonyolultabb számolási műveletekkel találkozhatunk. Ebben a fejezetben a hangsúlyt a bonyolult képletek BASIC nyelven való megfogalmazására helyezzük.
A képleteket matematikai szabályok szerint írjuk le. Amikor valamilyen konkrét értéket kell kiszámítanunk, akkor a számolást a kifejezésben levő műveletek szabályai szerint végezzük el. A matematikai kifejezéseket BASIC nyelvre is le lehet fordítani. A műveleti jeleket a 3.1. fejezetben ismertettük. A kifejezések felépítéséhez zárójelet is lehet használni. A BASIC jelkészletében mind a nyitó, mind a záró zárójel megvan.
A kifejezésekben levő zárójelek a műveletek elvégzési sorrendjét határozzák meg. A sorren-det prioritási szabályok írják le. A matematikában is használt prioritási szabályok érvényesek a BASIC nyelvben felépített kifejezésekben is. E szerint a zárójelben levő kifejezésnek van a legmagasabb prioritása. Ebből következik, hogy egy zárójeles részt is tartalmazó kifejezés értékének kiszámításakor a fordító a zárójeles rész tartalmát számítja ki először.
Ha több szintű zárójelet tartalmaz a kifejezés, akkor a legbelső kifejtésével kezdődik a számítás, majd fokozatosan halad kifelé. Ha több azonos szintű "belső" zárójeles kifejezés található a "külső" zárójelben, akkor ezek kifejtése balról jobbra halad. Pl:
((A1+B1)*(A2+B2))^K
A zárójeles kifejezésrészen belül vagy a zárójel nélküli kifejezésben az egyes műveletek sorrendjében a következő prioritási szabályok érvényesülnek:
Ha egy kifejezésben több azonos szintű szabályba tartozó művelet van, akkor a műveletek kifejtése balról jobbra halad:
A*B/C
értelmezése:
vagy
A*B+C*D
vagy
A+B/C
Ha a kívánt műveleti sorrend nem egyezik a prioritási szabályokkal, akkor zárójelet használunk.
Figyeljük meg egy bonyolultabb kifejezés BASIC nyelvre való lefordítását:
Ennek BASIC alakja:
(A*(B+(C+D)/E))*F^2
értelmezése:
A BASIC-ben nincs korlátozva a zárójelek szintjeinek száma. Tetszés szerinti hosszúságú kifejezés adható meg egyetlen utasításként, csupán a sor - adott BASIC implementációban megengedett - maximális hosszát kell szem előtt tartani.
A kifejezéseket lehet lépésenként is kódolni - ahogy bemutattuk -, de ez nem indokolt, hiszen a BASIC bármilyen bonyolult kifejezést képes értelmezni.
Megjegyezzük, hogy gyökvonást - a törtkitevőjű hatvány értelmezésének alapján - a megfelelő törtkitevőre való hatványozással is végezhetünk.
Számábrázolás BASIC-ben
A BASIC - implementációtól függően - a nagyon nagy és nagyon kicsi intervallumba eső értékeket fixpontos (valós) formában írja ki. A Spectrum BASIC a [0.00001, 99999999], a Commodore 64 BASIC-je a [0.001, 999999999] intervallumba eső számokat valós formában írja ki, az intervallumon kívül 10-es alapú lebegőpontos alakban ír ki minden számot a következőképpen:
(előjel)X.XXXXXXXeE±n
Az előjel után 8 számjegyből álló mantissza, majd az E után az előjelhelyes karakterisztika.
A BASIC nyelv egyik fontos korlátja, hogy adatokat csak 1^38 < N < 1^38 tartományban fogad el.
Adatokat is meg lehet lebegőpontos formában adni. Kiírásnál azonban a fordító a fenti szabályokat az adat megadás formájától függetlenül alkalmazza.
II. probléma
Tekintsünk egy termelő beruházást, amelybe a T=0 időpontban 100 millió forintot fektettünk be. A beruházás éves bevétele 40 MFt, üzemeltetési költsége pedig 20 millió forint. Határozzuk meg a jelenérték elvének (a magyarázatot lásd a probléma elemzésében) figyelembevételével, hogy 5, illetve 10 év alatt megtérül-e a beruházás. A kamatláb értéke 12%.
A program az alábbi adatokat írja ki:
Beruházásgazdaságossági számítás
Beruházás = 100 MFt
Jövedelem = 40 MFt/év
Üzemeltetés = 20 MFt/év
Kamatláb = 12%1. Számítás
Évek száma: 5
Hozam: X MFt2. számítás
Évek száma: 10
Hozam: X MFt
A problémában az egyéb tényezők hatásától eltekintünk. Az egyszerűség kedvéért a beruházási összeget úgy tekintjük, hogy az a T=0 időpontban, a jövedelem és az üzemeltetési költség pedig a tárgyév végén egy összegben merül fel. A megoldásnál az infláció hatását sem vesszük figyelembe.
1. A probléma elemzése
A feladat meghatározása alapján a bevételeket és a kiadásokat a T=0 időpontra vonatkoztatva vizsgáljuk. Így lehet csak összehasonlítani például a 3. évben felmerülő üzemeltetési költséget és az 5. évben jelentkező jövedelmet. Ezt úgy érhetjük el, hogy valamennyi T=0 időpont után felmerülő összeget (akár kiadás, akár bevétel) a T=0 időpontra diszkontálunk, vagyis a jövőbeli összegek jelenértékét számítjuk ki. A diszkontált hozadékot, illetve költséget 12%-os éves kamat mellett számítjuk ki. A diszkontálás szabálya szerint a T=0 után két évvel jelentkező 40 MFt-os jövedelem a T=0-ban nem 40 MFt-ot, hanem kevesebbet ér. Ma pontosan olyan összeget ér - jelenérték -, ami a 2 éves 12%-os kamatos kamattal együtt 40 MFt-ot tenne ki:
J/(1+K)^2
ahol
J = az éves jövedelem (40 MFt),
K = a kamatláb (12%).
Ha ugyanis ez az alacsonyabb összeg a T=0 időpontban rendelkezésre állna, akkor a 12%-os kamatos kamattal 2 év után éppen 40 MFt-ra nőne. Ugyanígy határozhatjuk meg az üzemeltetési költségek jelenértékét is.
A T=0 után 2 évvel jelentkező 20 MFt kiadás a T=0-ban alacsonyabb értéket képvisel. Ez egy olyan összeget jelent, amely a két éves kamatos kamattal 20 MFt:
U/(1+K)^2
ahol
U = az éves üzemeltetési költség (20 MFt).
Az összes jövedelem az egyes évek T=0-ra diszkontált jövedelmeinek az összege:
A kifejezés jobb oldalán, a zárójelben levő rész egy N tagú véges mértani sorozat összege. Ennek figyelembevételével kapjuk a
kifejezést.
Hasonlóan kapható meg a T=0-ra diszkontált üzemeltetési költség az 1 ,... , N években:
A beruházás T=0-ra diszkontált hozama a jövedelem és a kiadás különbsége:
A feladat szerint azt kell kiszámítani, hogy N=5 év és N=10 év esetén H értéke mennyi. Ha adott N mellett H<100 MFt, akkor a beruházás N év alatt nem térült meg. Ha H>100 MFt, akkor a beruházás megtérült.
A probléma értelmezése után nézzük meg, hogy a számítás programját hogy lehet elkészíteni. A programnak az alábbi főbb funkciókat kell ellátnia:
A program adatait a program kezdetén kell megadni. Ezekből a szükséges számítások elvégezhetők, és a kapott eredményadatokat ki kell írni. Az év változó értékét egy alkalommal változtatni kell (5 és 10 év).
A fontosabb funkciók alapján a program a következő fő modulokból áll majd:
A modulszerkezetet a fenti soros modulok fogják alkotni:
2. A program tervezése
A bemeneti adatok modulban kell megadni a feladat változóit (beruházás, éves jövedelem, üzemeltetési költség, kamatláb és az évek száma). A következő modulban ki kell számítani az első 5 év utáni hozamot. A (3) modul feladata a specifikáció szerinti alapadatok és az öt év utáni hozam kiírása. Így ezt a modult két további modulra lehet bontani. A 10 év utáni számítási modul megegyezik az 5 év utáni számítási modullal. Az utolsó kiírási modul már csak a 10 év utáni számolási eredményeket írja ki, ezért tovább bontása felesleges. A finomított modulszerkezetet mutatja az ábra:
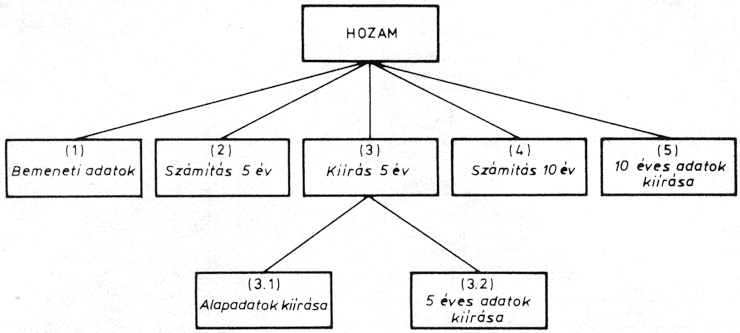
A program moduljai között adatkapcsolat van, mert a modulok balról jobbra haladva adatokat adnak át egymásnak. A program szekvenciálisán végrehajtható modulokból áll, ezért vezérlőmodulokra nincs szükség.
Megemlítjük, hogy a programszerkezetet többféleképpen is elkészíthettük volna. Jó megoldás lett volna az is, ha egy modulba a számításokat, a másikba pedig az összes kiírást gyűjtjük össze. Azért választottuk azonban az ábrán látható szerkezetet, mert a feladat - és főleg a kiírás - szerkezetét ez követi a legjobban.
3. A modulok tervezése
(1) Bemeneti adatok
A modul adat típusú, mert adatokat határoz meg. Bemeneti adata nincs, kimenetét a B, J, U, K és N adat képezi. A modul az induló adatokat, azaz a B (a beruházás összege), a J (éves jövedelem), az U (éves üzemeltetési költség), a K (kamatláb 12%, illetve 0.12) és az N (évek száma) változók indulóértékeit tárolja.(2) Számítás 5 év
A modul eljárás típusú. Bemeneti adatai (J, U, K, N) az (1) modulból származnak. A modul egyetlen kimeneti adata a kiszámított hozam (H). Az algoritmus itt is egyetlen lépésből, a hozam kifejezés szerinti kiszámításából áll.(3.1) A lapadatok kiírása
A modul eljárás típusú. Bemeneti adatai (B, J, U, K) az (1) modulból származnak. A modul kimenete a terminálra kiírt szövegrész. A modul algoritmusa a B, J, U, K adatokból és a hozzájuk tartozó szövegek kiírási utasításaiból áll.(3.2) 5 éves adatok kiírása
Ez a modul is eljárás típusú. Bemeneti adatai részben az (1) modulból (N), részben a (2) modulból (H) származnak. A modul kimenete itt is a terminálra kiírt szövegrész. A kiírás folyamata három lépésből áll: a rövid cím, az N és a hozam (H) kiírásából.(4) Számítás 10 év
A modul teljes leírása megegyezik a (2) moduléval, de az a különbség, hogy ebben a mo¬dulban N értékét N=10-re kell módosítani.(5) 10 éves adatok kiírása
A modul hasonlít a (3.2) modulhoz, csak annyi az eltérés, hogy most N=10 éves adatokat kell kiírni. A modul műveleteit a programbefejezés lépésével kell kiegészíteni.
4. A kódolás
(1) Bemeneti adatok
A modul elejére felírjuk a program (HOZAM), majd a modul nevét. Az értékadásokat a LET utasításokkal kódoljuk:10 REM * HOZAM *
20 REM BEMENETI ADATOK
30 LET B=100
40 LET J=40
50 LET U=20
60 LET K=.12
70 LET N=5(2) Számítás 5 év
A hozam (H) kiszámítását egyetlen utasítással elvégezhetjük, mert közbenső adatokra (részeredményekre) nincs szükség. A kifejezést változók helyett konstansokkal is ki lehet számolni. A változókkal kódolt kifejezés azért előnyösebb és sokkal rugalmasabb, mint a konstansokkal való kódolás, mert általánosabb, és tetszés szerinti változó ért ékre érvényes. A modul kódja:80 REM SZAMITAS 5 EV
90 LET H=(J-U)*((1+K)^N-1)/(K*(1+K)^N)(3.1) A lapadatok kiírása
A kiírásokat PRINT utasításokkal kódoljuk. A cím után - formai szempontból - célszerű 1-2 üres sort hagyni, hogy a kiírási kép jobban áttekinthető legyen. Üres sort tárgy nélküli ("üres") PRINT utasítással lehet elérni, hiszen befejezett sor után egy új PRINT utasítás megjelenésekor soremelés történik. Ha az utasításnak nincs tárgya, akkor nincs kiírás. A 130-160. utasításokban a változó kiíratása után is szövegrészt íratunk ki. Ezt ugyanúgy idézőjelek közé kell tenni, mint az első szövegrészt. Látható, hogy egyetlen sorban tetszés szerinti számú változó és szövegkonstans kiírását kódolhatjuk. A fordító minden páratlan sorszámú idézőjel utáni karaktersorozatot kiír a következő idézőjelig. Ha ezután áll valamilyen karakter (sorozat), akkor ezt a fordító változónak tekinti, és ennek értékét úja ki.
A modul kódolása:110 PRINT "BERUHAZAS GAZDASAGOSSAGI SZAMITAS"
120 PRINT
130 PRINT "A BERUHAZAS OSSZEGE = ";B;" MFT"
140 PRINT "EVES JOVEDELEM = ";J;" MFT"
150 PRINT "EVES UZEMELTETESI KOLTSEG = ";U;" MFT"
160 PRINT "KAMATLAB = ";100*K;"%"
170 PRINT(3.2) 5 éves adatok kiírása
A kiíratásokat ebben a modulban is PRINT utasításokkal lehet elvégeztetni:180 REM 5 EVES ADATOK KIIRASA
190 PRINT "1. SZAMITAS"
200 PRINT "EVEK SZAMA: ";N
210 PRINT "HOZAM = ";H;" MFT"(4) Számítás 10 év
(5) 10 éves adatok kiírása
A két modul kódolása megegyezik a (2) és a (3.2) modul kódolásával:220 REM SZAMITAS 10 EV
230 LET N=10
240 LET H=(J-U)*((1+K)^N-1)/(K*(1+K)^N)
250 PRINT
260 REM 10 EVES ADATOK KIIRASA
270 PRINT "2. SZAMITAS"
280 PRINT "EVEK SZAMA: ";N
290 PRINT "HOZAM = ";H;" MFT"
Ezzel a program elkészült, ezután kipróbáljuk, hogyan működik. Kézi számítással ellenőrizhetjük, hogy például az 5 év utáni hozam kiszámítása a megadott adatokkal helyes-e. Ha erről meggyőződtünk, akkor a kapott eredmények helyesek, a probléma megoldásához felhasználhatók.
A hozamértékekből látható, hogy 5 év alatt a beruházás nem térül meg, 10 év után viszont a hozam 13 millió forinttal meghaladja a beruházás összegét. Tehát a beruházás az 5. és a 10. év közötti időszakban térül meg.
A kiírás formai módosítása
A táblázat formailag nem kifejezetten szép, olvasása nehézkes, mert a számértékek összevissza vannak benne. Előnyösebb lenne, ha a kiírás elkülönülő részeiben a számértékek egymás alatt, a szöveges részhez közel helyezkednének el. Ehhez csupán azt kell meghatároznunk, hogy milyen távolságra kerüljenek a számértékek a szövegektől. Ezt a leghosszabb szövegrészhez kell igazítani, és ennek a végétől elég 3-4 szóköznyi távolságot kihagyni. Nyomtatáskor a változó értékének jobbra tolását úgy lehet elérni, hogy szóközt is nyomtatunk a szöveg után, azaz a szöveget szóközökkel bővítjük. A változóértékek első számjegyükkel akkor esnek egymás alá, ha a szövegsorok karakterszáma (szöveg és szóköz összesen) megegyezik.
Ennek megfelelően a programot módosítjuk, és a következő új kódot kapjuk:
10 REM * HOZAM *
20 REM BEMENETI ADATOK
30 LET B=100
40 LET J=40
50 LET U=20
60 LET K=0.12
70 LET N=5
80 REM SZAMITAS 5 EV
90 LET H=(J-U)*((1+K)^N-1)/(K*(1+K)^N)
100 REM ALAPADATOK KIIRASA
110 PRINT "BERUHAZAS GAZDASAGOSSAGI SZAMITAS"
120 PRINT
130 PRINT "A BERUHAZAS OSSZEGE = ";B;" MFT"
140 PRINT "EVES JOVEDELEM = ";J;" MFT"
150 PRINT "EVES UZEMELTETESI KOLTSEG = ";U;" MFT"
160 PRINT "KAMATLAB = ";100*K;"%"
170 PRINT
180 REM 5 EVES ADATOK KIIRASA
190 PRINT "1. SZAMITAS"
200 PRINT "EVEK SZAMA: ";N
210 PRINT "HOZAM = ";H;" MFT"
220 REM SZAMITAS 10 EV
230 LET N=10
240 LET H=(J-U)*((1+K)^N-1)/(K*(1+K)^N)
250 PRINT
260 REM 10 EVES ADATOK KIIRASA
270 PRINT "2. SZAMITAS"
280 PRINT "EVEK SZAMA: ";N
290 PRINT "HOZAM = ";H;" MFT"
Változók módosítása a program közben (READ, DATA utasításpár)
Gyakran szükséges, hogy a feldolgozást több különböző bemeneti adattal elvégezzük, közben figyeljük az eredmény viselkedését; vagy az a célunk, hogy több esetben ismerjük meg az eredményt. Ezt programmódosítással is megoldhatjuk, de ez meglehetősen nehézkes eljárás. Sokkal egyszerűbb, ha a különböző adatokat eleve "beépítjük" a programba.
Erre szolgál a READ (olvasd) és a DATA (adatok) utasításpár. Az adatokat a DATA utasítás tárgyában soroljuk fel, és a felsorolás sorrendjében a READ utasítással olvassuk ki. A READ utasítás a kiolvasott adat értékét a READ utasítás tárgyában levő változóhoz rendeli.
A DATA utasítást célszerű a program végén elhelyezni. A DATA szó után vesszővel elválasztva, olyan sorrendben soroljuk fel a használni kívánt adatokat, ahogy a kiolvasásuk megtörténik.
Tegyük fel, hogy a II. probléma programjában az évet mint változót akarjuk megadni, és két konkrét számértékkel kívánjuk a számolást elvégezni. Ekkor a következő formájú DATA utasítást kell megadni:
310 DATA 5,10
A READ utasítást oda kell elhelyezni, ahol szükség van a változó értékének megadására. A READ utasítás tárgyában meg kell adni azt a változót (vagy változókat), amelyeknek értékét a DATA-ból kiolvasott adattal kell egyenlővé tenni. Esetünkben a 70-es sorszámú utasítás helyett a
70 READ N
utasítást kell megadni. Ez az első READ-előfordulás a programban, ezért N az első helyen szereplő adat értékével (5-tel) lesz egyenlő.
Ugyanígy módosítani kell a 230-as sorszámú utasítást. Ennek hatására a következő (10-es) értéket adja N-nek.
A leírtak alapján a program módosított kódolása a következő:
10 REM * HOZAM *
20 REM BEMENETI ADATOK
30 LET B=100
40 LET J=40
50 LET U=20
60 LET K=0.12
70 READ N
80 REM SZAMITAS 5 EV
90 LET H=(J-U)*((1+K)^N-1)/(K*(1+K)^N)
100 REM ALAPADATOK KIIRASA
110 PRINT "BERUHAZAS GAZDASAGOSSAGI SZAMITAS"
120 PRINT
130 PRINT "A BERUHAZAS OSSZEGE = ";B;" MFT"
140 PRINT "EVES JOVEDELEM = ";J;" MFT"
150 PRINT "EVES UZEMELTETESI KOLTSEG = ";U;" MFT"
160 PRINT "KAMATLAB = ";100*K;"%"
170 PRINT
180 REM 5 EVES ADATOK KIIRASA
190 PRINT "1. SZAMITAS"
200 PRINT "EVEK SZAMA: ";N
210 PRINT "HOZAM = ";H;" MFT"
220 REM SZAMITAS 10 EV
230 READ N
240 LET H=(J-U)*((1+K)^N-1)/(K*(1+K)^N)
250 PRINT
260 REM 10 EVES ADATOK KIIRASA
270 PRINT "2. SZAMITAS"
280 PRINT "EVEK SZAMA: ";N
290 PRINT "HOZAM = ";H;" MFT"
300 REM *********
310 DATA 5,10
Mint látható, az adatokat egy sor csillaggal elválasztottuk az (5) modultól, mert azok annak nem részei. A program futása után változatlan eredményeket kapunk, hiszen csak az adatmegadást módosítottuk.
A READ, DATA utasításpárt több változó tetszés szerinti számú értékének megadására is fel lehet használni. Tegyük fel, hogy a hozamot négy különböző jövedelem (J), üzemeltetési költség (U) és kamatlábérték mellett, az alábbi táblázat szerint akarjuk megvizsgálni:
1. 2. 3. 4. Jövedelem (MFt) 40 40 35 35 Üzemeltetési költség (MFt) 20 18 20 18 Kamatláb (%) 12 10 12 10
Az adatoszlopokat a felírt sorrendben kívánjuk olvasni. Ehhez a program négy pontján - a négy művelet előtt - négy azonos felépítésű READ utasítást kell elhelyezni:
READ J,U,K
A program végén pedig - a kiolvasások sorrendjének megfelelően - az adatokat kell elhelyezni:
1000 DATA 40,20,12
1010 DATA 40,18,10
1020 DATA 35,20,12
1030 DATA 35,18,10
Az első READ utasításban a K=40, J=40, az U=20, és a K=12 értékadás megy végbe. A következő READ utasítás végrehajtásakor a sorrendben következő adatokat olvassa ki a program.
Ebből következik, hogy a READ, DATA utasításpárt nagyon gondosan kell alkalmazni. Ha például az egyik READ utasításban a változókat felcseréljük, akkor helytelen értékadások mennek végbe. De ugyanígy az adatokat sem szabad felcserélni.
Egy READ utasítás annyi READ utasítássá bontható fel, amennyi változót tartalmaz. Például a
100 READ J
110 READ U
120 READ K
utasítássorozat egyenértékű a
100 READ J,U,K
utasítással. De mint látható, a szabály fordítottja is igaz, mert több összetartozó READ utasítást is össze lehet egyetlen READ utasítássá vonni.
Ugyanez érvényes a DATA utasításra is. Az első két DATA utasítást például összevonhatjuk:
1000 DATA 40,20,12,40,18,10
A program működését ez nem változtatja meg, ráadásul a program kevesebb sorból áll. Dokumentálási szempontból és a jó áttekinthetőség kedvéért azonban az a célszerű, ha a DATA szerkezet követi a READ szerkezetét, vagyis ha egy READ utasításhoz egy DATA utasítás tartozik. Kivéve, ha a programban kevés READ utasítás, s ezek tárgyában csak néhány változó van. A fenti példában is bemutattuk, hogy ilyenkor egy, esetleg két DATA utasítás is elegendő.
Végül megjegyezzük, hogy a DATA nem végrehajtható utasítás. Ha tehát a fordító DATA utasításhoz ér, akkor nem veszi figyelembe, és a következő utasításra tér át. A DATA utasításban levő adatokat a READ utasítás aktivizálja.
3.3. Alternatívák kezelése
Vannak olyan problémák, amelyek megoldási módja a bemeneti vagy közbenső adatok értékétől függ. Ha az adatok valamilyen rögzített tartományba eső értéket vesznek fel, akkor egy A szekvenciális algoritmus szerint, ettől eltérő esetben pedig B algoritmus alapján kell megoldani a feladatot. Az A és B lépéssorozatokat tehát alternatív műveleteknek kell tekinteni. Valamilyen adatértéktől függően (feltétel) vagy az egyik, vagy a másik műveletet hajtja végre a program. Bizonyos esetekben a probléma megoldása kettőnél több algoritmuságat is tartalmazhat. Az alternatívák kezelésére példaként az X/Y hányados képzését említjük. Nyilvánvaló, hogy az osztást Y<>0 esetben lehet csak elvégezni. Ha Y=0, akkor az osztás nem végezhető el, és ezt a felhasználóval egy erre vonatkozó üzenettel tudatni kell, vagy a hányadosnak valamilyen megegyezéses értéket (például nullát) kell adni.
Egy másik eset, amikor egy szállítóvállalat terméke egységárát a rendelési mennyiségtől teszi függővé. Ilyenkor meg kell vizsgálni, hogy a rendelt mennyiség melyik árintervallumba esik, és a számla kiállításánál ezt az árat kell figyelembe venni.
Kitűnik, hogy a fenti feladatokban - és ezt a további példákban is tapasztalhatjuk - van egy (vagy esetleg több) adat, amelynek értéke eldönti, hogy melyik algoritmuságon haladjunk. Ez a változó (vagy változók) a probléma feltétele vagy feltételváltozója, s ez meghatározza a további végrehajtás menetét. A megoldásba tehát be kell iktatni olyan lépést is, amelyben megvizsgáljuk a feltételváltozó értékét, és a vizsgálat eredményeként el lehet dönteni, hogy melyik lépéssorozaton kell haladni.
Az osztási példában az Y osztó lehet a feltételváltozó. Ha az Y=0 feltételt vizsgáljuk, akkor a feltétel teljesülésénél az osztás nem végezhető el, ellenkező esetben viszont igen. Vizsgálhatjuk az Y<>0 feltételt is. Ekkor a feltétel teljesülésénél elvégezhető az osztás.
Tekintsünk egy példát, melyben egy termék egységárát a szállító a rendelt mennyiségtől (R) függően állapítja meg. Tegyük fel, hogy a szállító 3 árintervallumot állapít meg. Az árintervallumokat az M1 és M2 mennyiség határolja a következő táblázat szerint:
Mennyiség (R) Ár
ahol az M1 és M2 az árengedmény határait rögzítő mennyisége, az A1, A2 és A3 a rendelt mennyiségtől függő árak.
Ahhoz, hogy az egységárat megállapíthassuk, az alábbi vizsgálatokat kell elvégezni:
R<=M1
M1<R<=M2
M2<RA1
A2
A3
BASIC utasítások az alternatívák kódolásához
Először a GO TO utasítást mutatjuk be (A GO TO utasítást több BASIC implementációban GOTO-nak kell írni). A GO TO utasítás segítségével lehet elérni, hogy a program a sorrendben következő helyett a GO TO utasítás tárgyában megadott sorszámú utasításra ugorjon, és onnan folytassa a végrehajtást. A GO TO utasítás felépítése a következő:
x GO TO sorszám
Amikor a program a végrehajtáskor eléri az X sorszámú utasítást, akkor a GO TO utasítás végrehajtásának eredményeként nem az X után következő legalacsonyabb sorszámú utasítás hajtódik végre, hanem a vezérlés átkerül a GO TO utasítás tárgyában megadott sorszámú utasításra. A GO TO tehát a programon belül ugrást hajt végre. Az a sorszám, ahová a program ugrik, lehet kisebb, mint a GO TO sorszáma (ekkor ismétlést hajt végre a program), vagy lehet nagyobb is (valamilyen utasítássorozat átugrása).
A GO TO utasítást önmagában csak különleges esetben szabad használni. Többnyire valamilyen IF (IF-THEN, IF-THEN-ELSE, CASE) szerkezetben alkalmazzuk. Ezt a következőkben részletesen is bemutatjuk. A GO TO önálló használata a program szerkezetét áttekinthetetlenné teszi.
A BASIC nyelvben az alternatívák kódolására az IF utasítás használható. Az IF utasítás felépítése a következő:
x IF kifejezés1 összehasonlító művelet kifejezés2 THEN utasítás
vagy
x IF kifejezés1 összehasonlító művelet kifejezés2 THEN sorszám
Az utasítás kulcsszavai az IF ... THEN (és a GO TO). Az utasítás lényege, hogy két kifejezést hasonlít össze, és az összehasonlítás eredményétől függő utasítássorozatot hajtja végre. Ha az 1. és a 2. kifejezés között az utasításban foglalt feltétel teljesül, akkor a program a THEN utáni részt hajtja végre. Ha a feltétel nem teljesül, akkor a program a következő sorszámú (és új sorban levő) utasításra tér át. Több BASIC implementáció megengedi, hogy a THEN után ne csak egy utasítás álljon, ennek ellenére a THEN után leggyakrabban GO TO áll, ezért THEN után a GO TO el is hagyható (csak sorszámot kell írni).
Az utasításban szereplő kifejezések olyan tetszőleges BASIC aritmetikai kifejezések lehetnek, amelyek változói a program előző részében értéket kaptak. Csak meghatározott értékű kifejezéseket lehet összehasonlítani. Például az
IF B^2-4*A*C>0 THEN ...
feltétel vizsgálatának csak akkor van értelme, ha a programban az A, B és C értékét előzőleg már meghatároztuk.
Az összehasonlító műveletek megegyeznek a matematikában használatos műveleti jelekkel, csupán formájukban van kisebb eltérés:
= egyenlő < nagyobb <= kisebb vagy egyenlő > nagyobb >= nagyobb vagy egyenlő <> nem egyenlő
A THEN kulcsszó után állhat GO TO utasítás, de bármilyen más utasítást megadhatunk. Ha az IF utasítás sorába a THEN után több utasítást írunk, akkor ezeket kettősponttal kell elválasztani. Például:
100 IF B^2-4*A*C=0 THEN LET X=0: GO TO 200
A THEN után annak az utasításnak a sorszáma is állhat, ahol - az összehasonlító művelet teljesülése esetén - a végrehajtást folytatni kell. Ez egyenértékű a THEN helyett álló GO TO-val.
A THEN után egy újabb IF utasítás is állhat. Egy ilyen utasítás nagyon jól használható arra, hogy megvizsgáljuk, egy B változó beleesik-e egy adott (A1, A2) intervallumba:
100 IF B>=A1 THEN IF B<=A2 THEN LET C=B*P1: GO TO 300
110 LET C=B*P2
Ha az első feltétel teljesül, akkor a program áttér a következő vizsgálatára. Ha az első feltétel nem teljesül, akkor a következő sorszámú (110) utasításra lép. Ha az első feltétel teljesül, de a második nem, a program ekkor is a következő sorra tér át. A második THEN utáni utasítást csak akkor hajtja végre a program, ha az első és a második feltétel teljesül. Láthatjuk, hogy a program lefolyása független a feltételek sorrendjétől.
Az IF-THEN szerkezet megvalósítása
Az IF-THEN szerkezet olyan algoritmusban használható, amikor a feltétel teljesülésekor valamilyen A műveletsorozatot kell végrehajtani, és utána a B műveletsorozatra kell áttérni. Ha a feltétel nem teljesül, akkor az A műveletsorozatot nem kell végrehajtani, hanem rögtön a B műveletre kell áttérni. A B műveletsorozatot mindenképpen végrehajtja a program, ezért ezt közös résznek nevezzük. Az IF-THEN szerkezet folyamatát mutatja a következő ábra:
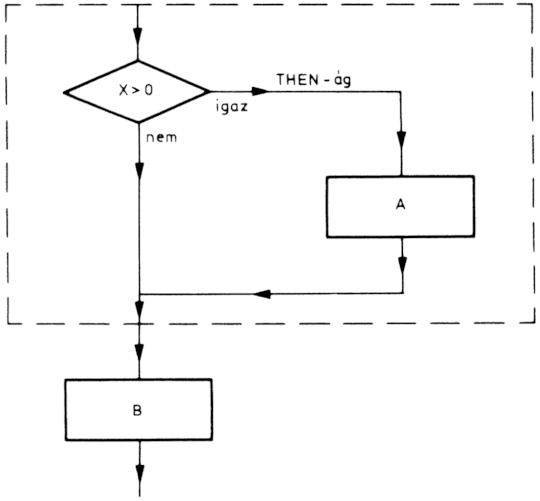
Az IF-THEN szerkezet kódolása többféleképpen oldható meg. A lehetséges változatok közül kettőt mutatunk be. Az első kódolási mód kissé "szószátyár", azaz viszonylag sok REM utasítást tartalmaz. Ezáltal azonban a kód jól strukturált lesz, áttekinthetőbb, és javítja a dokumentáltságot:
k IF feltétel THEN m
GO TO n
m REM * THEN-ag *
...
n REM * IF veg *
Az IF-THEN szerkezet zárt részt alkot a program kódjában. A kódrészt az IF utasítás vezeti be, és az "IF veg" megjegyzéssel zárjuk le. A THEN után következő műveletsorozatot az m sorszámtól kezdve, két sorral az IF utasítás alatt (így m=k+20 lehet) helyezzük el. A műveletet egy REM utasítással nyitjuk meg, s ide beírjuk, hogy itt kezdődik a THEN-ág. Mind a REM utasítás, mind a THEN-ág kódját 2-2 szóközzel jobbra tolva írjuk (ha ezt az adott implementáció megengedi), hogy jobban elkülönüljön. A THEN-ág utolsó utasítása után az n sorszámú, az "IF veg"-et tartalmazó REM utasítás következik, és a vezérlés átkerül a következő műveletsorozat kezdetére.
Ha a feltétel nem teljesül, akkor a program a következő sorra tér át. Logikailag azonban a következő műveletsorozatnak kell következnie, amit úgy érhetünk el, hogy egy GO TO utasítást helyezünk az IF utasítást követő (például k+10 sorszámú) sorba, s ez az n sorszámú utasításra - gyakorlatilag a következő műveletsorozatra - helyezi át a vezérlést.
Ez utóbbi lépésnek az a lényege, hogy az IF-THEN zárt szerkezeti egységnek egyetlen "kijárata" legyen, az n sorszámú utasítás. Ez az egy "egykijáratúság" módosításánál nagyon megkönnyíti a helyzetünket.
Bemutatunk még egy szerkezetet is az IF-THEN kódolására. Ez akkor használható ésszerűen, ha a THEN-ág csupán egy-két utasításból áll. Ilyenkor felesleges a bonyolultabb megoldást használni, nélküle is áttekinthető kódot kapunk:
k IF feltétel THEN then-ag
THEN-ág egy-két utasítását a THEN kulcsszó után, kettősponttal elválasztva helyezzük el. Az utolsó THEN-ági utasítás után a IF-THEN szerkezetet követő (közös) ág következik, ezért GO TO utasításra nincs szükség, mert a program ettől függetlenül is a következő sorban levő műveletsorozat első utasítására lép. Ha a feltétel nem teljesül, akkor is a következő műveletsorozatra tér át a program, tehát a kódolás helyesen valósítja meg az IF-THEN szerkezetet.
Az IF-THEN-ELSE szerkezet megvalósítása
Az IF-THEN-ELSE szerkezet olyan algoritmushoz használható, amelyben egy feltétel teljesülésekor a THEN-ágban levő A műveletsort kell elvégezni, és a C közös részre kell áttérni. Ha a feltétel nem teljesül, az A helyett egy B műveletsort kell elvégezni; ez az ELSE-ág. Ezután a közös C részre kell áttérni:
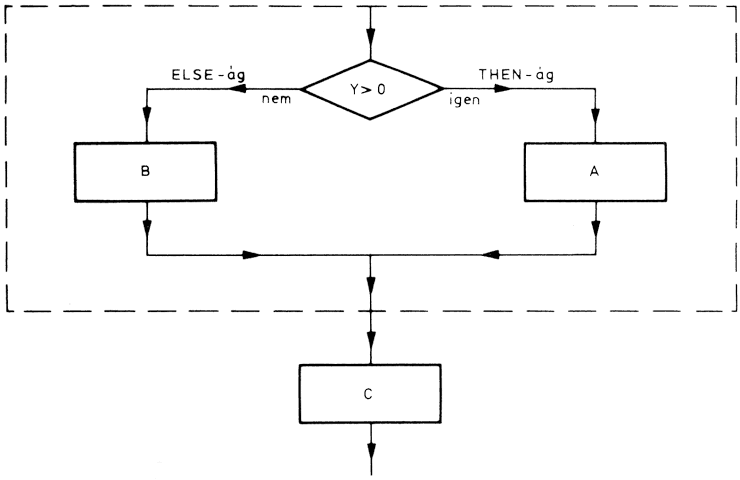
Az IF-THEN-ELSE szerkezet kódolására az IF-THEN szerkezet kódolásánál bemutatott szerkezetekhez hasonló megoldásokat mutatunk be. Mindhárom megoldás alapja, hogy IF-THEN típusú utasításra épül, mert a legtöbb BASIC-változatban nincs IF-THEN-ELSE típusú utasítás. A strukturált változat:
k IF feltétel THEN GO TO m
GO TO n
m REM * THEN-ag *
...
GO TO p
n REM * ELSE-ag *
...
p REM * IF veg *
Az IF-THEN-ELSE szerkezet is zárt részt alkot a programon belül. Az IF utasítás nyitja meg, és az "IF-vég" megjegyzés zárja le. Az IF-THEN-ELSE részen belül - a jobb áttekinthetőség kedvéért - a sorokat jobbra tolva gépeljük be, ha ezt az adott BASIC implementáció megengedi. A THEN-ág és az ELSE-ág kódját pedig "két lépcsővel" toljuk jobbra.
A THEN-ág kódolása az IF-THEN szerkezetnél bemutatott módszerhez hasonlóan megy végbe, csak a befejezés tér el. A THEN-ág után most nem a közös rész (C műveletsor), hanem az ELSE-ág kódja következik, ezért egy GO TO utasítással át kell ugrani a p sorszámú utasításra, ahol az IF-THEN-ELSE kijárata (a közös rész kezdete) van.
Ha a feltétel nem teljesül, akkor az ELSE-ágra kell áttérni. Ezt az IF utasítás után következő sorban elhelyezett GO TO utasítással lehet elérni. Ekkor az ELSE-ág végrehajtódik, és a vezérlés közvetlenül átkerül a p sorszámú megjegyzésre, illetve innen a közös ágra.
Az olyan BASIC-változatokban, amelyekben IF-THEN-ELSE típusú utasítás is van, a THEN és az ELSE után meg kell adni, hogy melyik sorszám alatt kezdődnek az egyes ágak. A THEN- és az ELSE-ágat hasonló, strukturált módon lehet kódolni. Ilyenkor az IF utáni GO TO utasítás feleslegessé válik.
Az IF-THEN-ELSE szerkezet kódolását is lehet egyszerűsíteni, ha a THEN-ág csupán egy-két utasítást tartalmaz (a feltétel jó megválasztásával eldönthető, hogy melyik ág legyen a THEN-ág). Az egyszerűsített szerkezete:
m IF feltétel THEN then-ag: GO TO n
REM * ELSE-ag *
...
n REM * IF-veg *
A THEN-ág utasításait a THEN kulcsszó után, kettősponttal elválasztva írjuk le. Ezután a közös rész végrehajtása következik. A következő sorban az ELSE-ág kezdődik, ezért a sor végén egy GO TO n utasítással az IF szerkezet végére kell ugrani, s ezután már a közös rész következik. Ha a feltétel nem teljesül, akkor az IF-THEN-ELSE szerkezetnek megfelelően, az ELSE-ág hajtódik végre, az ELSE-ág befejezése után pedig a közös rész kerül sorra. Könyvünk a továbbiakban csak a strukturált IF-THEN-ELSE szerkezetet alkalmazza.
A CASE szerkezet kódolása
A CASE szerkezetet olyan algoritmusoknál lehet alkalmazni, amelyeknél egy változó lehetséges értékeitől függően nemcsak két műveletsor (THEN és ELSE) valamelyikét, hanem több műveletsorból kell egyet végrehajtani. Ezért a CASE szerkezet az IF-THEN-ELSE szerkezet kiterjesztéseként is felfogható. Ezt a tulajdonságot a továbbiakban felhasználjuk.
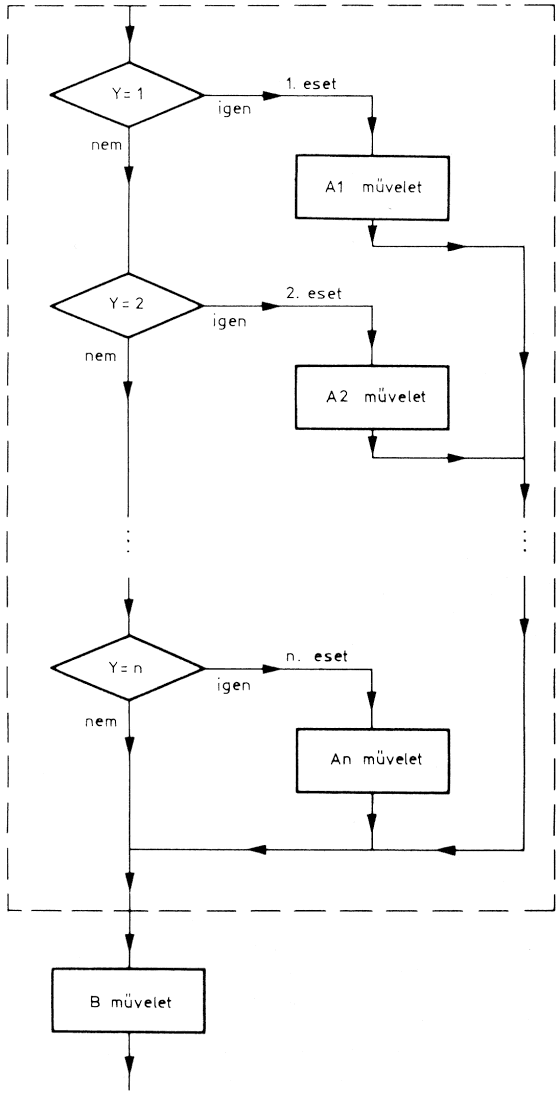
A BASIC-ben a CASE szerkezet - ha van az adott BASIC implementációban - az ON GO TO (lásd később) vagy az IF-THEN utasítással kódolható. Az utóbbi nyújtja az általánosabb és rugalmasabb megoldást, ezért ennek a használatát mutatjuk be. A CASE szerkezet kódolására is lét megoldást ismertetünk. A CASE szerkezet strukturált változata:
REM * CASE-kezdet *
IF feltétel1 THEN GO TO m1
IF feltétel2 THEN GO TO m2
...
IF feltételn THEN GO TO mn
GO TO p
m1 REM * 1. eset *
...
GO TO p
m2 REM * 2. eset *
...
GO TO p
...
mn REM * n. eset *
...
p REM * CASE-vég *
A CASE szerkezet is zárt egységet alkot a programon belül. Az 1. feltétel IF utasítása nyitja meg, és a "CASE-vég" megjegyzés zárja le. A CASE szerkezet elején egymás után helyezkednek el az egyes feltételeket vizsgáló IF utasítások. Ha a változó értéke valamelyik feltételnek nem tesz eleget, akkor a vezérlés a következő vizsgálatra kerül át. Ha a változó egyik feltételnek sem felel meg, akkor a közös rész végrehajtása következik, tehát a p sorszámú - utolsó - utasításra kell ugrani. Ha a változó valamelyik feltételnek eleget tesz, akkor a vezérlés az adott feltételhez tartozó műveletsorra ugrik át. Ennek végrehajtása után a közös rész következik, erre egy GO TO utasítással kell áttérni.
Az N-edik esetnél ez a GO TO felesleges, mert a vezérlés mindenféleképpen a közös részre kerül a p sorszámú megjegyzés után. Látható, hogy a CASE szerkezetet is úgy kódoljuk, hogy az "egykijáratúság" biztosítva legyen. A kijárat a p sorszámú utasítás.
A CASE szerkezetet is lehet nem strukturált módon kódolni, ha az egyes esetek egyöntetűen felépíthetők egy-két utasításból:
REM * CASE-kezdet *
IF feltétel1 THEN 1.eset: GOTO p
IF feltétel2 THEN 2.eset: GOTO p
...
IF feltételn THEN n.eset
p REM * CASE-vég *
E megoldás szerint az egyes esetek kódját a megfelelő feltételt vizsgáló IF utasításban, a THEN kulcsszó után helyezzük el. Ha az i-edik feltétel teljesül, akkor az i. esethez tartozó műveletsor hajtódik végre. Ha valamelyik i eset végrehajtódott, akkor a CASE részből egy GO TO p utasítással ki kell lépni.
Összefoglalásként megállapíthatjuk, hogy az alternatívákat megvalósító IF-THEN, IF-THEN-ELSE és CASE szerkezetek kódolása mindenképpen nehézkes, mert kétdimenziós folyamatábrát kell egydimenziós utasítássorrá átalakítani. Ez minden esetben nehézséget okoz, és csak kompromisszumok árán (például lemondunk a jó áttekinthetőségről) oldható meg.
III. probléma
Állóeszközök amortizációval csökkentett nettó értékét kell meghatározni. Az állóeszköz beszerzésének éve és ára (bruttó ár) alapján ki kell számítani, hogy jelenleg mennyi az állóeszköz nettó értéke.
A vizsgált állóeszközök leírási időszaka 5 év. A leírás lineáris, azaz az állóeszközök nettó értéke az eredeti (bruttó) érték évenként 20%-kal csökkentett értéke (1 év után a bruttó érték 80%-a, 2 év után 60%-a). 5 év után, amikor a nettó értéknek nullára kellene csökkennie, az állóeszközöket könyvelési okokból 100,- Ft eszmei értékre írják le, és azután ezen az értéken tartják nyilván.
Az eredményt az alábbi formában kell kiírni:
NETTÓ ÉRTÉK SZÁMÍTÁSA
Bruttó érték:
A beszerzés éve:
Életkor:
Nettó érték:
19xx év
X év
X eFt
vagy nullára leírt állóeszköznél:
NETTÓ ÉRTÉK SZÁMÍTÁSA
Bruttó érték:
A beszerzés éve:
Életkor:
Nettó érték:X eFt
19xx év
X év
0.1 eFt
(eszmei érték)
Egy-egy alkalommal egymás után több állóeszköz nettó értékét kell meghatározni.
1. A probléma elemzése
A probléma leírása szerint az állóeszközök bruttó értéke és a beszerzés éve alapján a nettó értéket kell kiszámítani az ide vonatkozó szabályok alkalmazásával. Az eredményt a megadott formában kell kiírni. A specifikáció szerint nemcsak egyetlen állóeszköz nettó értékét kell kiszámítani, hanem olyan megoldásra van szükség, amelyben a feladat bemeneti adatait rugalmasan lehet cserélni.
A probléma megoldásához egy olyan számítógépes programra van szükség, amely a bruttó értékből, a beszerzési évből és a folyó év számából a nettó értéket határozza meg. A felhasználó az állóeszközök adatait kartonokon tárolja, ezért ebben az esetben számítógépes adattárolásra nincs szükség.
A program elején a számításhoz szükséges bemeneti adatokat meg kell adni, és ezekből kell a nettó értéket kiszámítani, végül az eredményt ki kell írni.
A fentiek alapján már meghatározható, hogy a feladat megoldásához milyen modulok kellenek. Először szükség van egy bemeneti adat modulra, az amortizáció számításhoz egy másik modulra, végül egy kiírás modulra. A modulok az ábrán látható egyszerű szerkezetet alkotják. A programnak az AMOR nevet adjuk.
2. A program tervezése
A program szerkezete kialakult. Vizsgáljuk meg, hogy a modulszerkezet hogyan finomítható tovább.
A bemeneti adatok modulban csupán egy állóeszköz beszerzési évének és bekerülési árának adatait kell meghatározni. Ez elég egyszerű feladat ahhoz, hogy egyetlen modul lássa el. A modul feladata a kiinduló adatok rögzítése úgy, hogy az állóeszközre vonatkozó adatokat (B és E) minél egyszerűbben lehessen módosítani. Ehhez a READ, DATA utasításpárt fogjuk alkalmazni. A modulban kell meghatározni a J (folyó évszám) adatot is.
Az amortizációszámítást a következő kifejezés szerint végezhetjük el:
ha (J-E)<5
ahol
N = a nettó érték eFt-ban,
B = a bruttó érték eFt-ban,
J = a folyó év (csak kerek évszámot használunk),
E = a beszerzés éve.
A kiírásnál az állóeszköz életkorát is meg kell határozni, ezért a (J-E) helyett a K (életkor) változót vezetjük be. A nullára leírt (5 éves vagy régebbi) állóeszközök nettó értékét pedig az
N=0.1
ha K>=5
értékadással határozzuk meg. Az állóeszköz életkora dönti el, hogy melyik kifejezést alkalmazzuk a nettó érték kiszámításánál. A feltételváltozó tehát a K (életkor) változó lesz. Láthatjuk, hogy alapjában véve ez a modul is egyszerű, ezért további finomításra nincs szükség.
Ehhez hasonlóan könnyen belátható, hogy a kiírás modul bontására nincs szükség, mert csak a címet és a négy adatot kell egyszerű formában kiírni. Látnunk kell azonban, hogy az utolsó sor formája és tartalma a K változótól függ.
A modulok között adatkapcsolat van, az adatok balról jobbra haladnak. Az adatátadással egyidejűleg vezérlésátadás is végbemegy.
3. A modulok tervezése
(1) Bemeneti adatok
A modul adat típusú. Bemeneti adatait a B és az E, kimenetét pedig három adat: B, E, J alkotja.
A modul folyamata a J konstans értékadásával kezdődik. A következő lépésben kell meghatározni a B és az E értékét. A READ, DATA megoldást választjuk, mert ez rugalmasabb utasítás, mint az értékadás (LET), és így egyszerre több állóeszköz adatait is meg lehet adni. Az első lépésben csak egy állóeszköz adatainak biztosítsunk helyet.(2) Amortizációszámítás
A modul eljárás típusú. Bemeneti adatai: a B, E és J változó az (1) modulból. A modul állítja elő az életkor (K) és a nettó érték (N) kimeneti adatokat.
A specifikáció szerint a programnak a következő feladatokat kell megvalósítania. Először a K (életkor) értékét kell meghatároznia, mert a K-ra a továbbiakban szükség lesz. Ezután következik a nettó érték számítása (N), illetve az N = 100 Ft eszmei értékadás 5 évnél régebbi állóeszközök esetén. K értékétől függ, hogy melyik műveletet kell elvégezni. Fogalmazzuk meg a feltételt K<5 formában (de lehet másképp is). Ha a feltétel teljesül, akkor ki kell számítani az amortizációval csökkentett nettó értéket. Ha a feltétel nem teljesül (ELSE), akkor a nettó értéknek 0.1 eFt értéket kell adni. A soron következő lépések (a következő modul) függetlenek K értékétől, ezért a két ág a modul végén egyesül.(3) Kiírás
A modul eljárás típusú. Bemeneti adatai B és E az (1) modulból, valamint K és N a (2) modulból.
A modul kimenete a cím és az eredmények kiírása. A műveletek végrehajtásakor először a címet (aláhúzással), majd a B, E és K adatot kell a megfelelő szöveggel kiírni. A következő sor kiírási formája attól függ, hogy az állóeszköz nettó értéke nagyobb-e nullánál, vagy eléri-e a nullát, illetve eszmei értéken tartják-e nyilván. A megfelelő kiírási formát az állóeszköz nettó értéke vagy kora határozza meg. A (2) modulban hasonló döntést kellett hozni; ott az életkor volt a döntés feltétele. Az egységesség kedvéért célszerű ebben a modulban is ugyanazt a változót használni feltételváltozóként. Hiszen ha a (2) modul bármilyen hiba folytán tévesen számítaná ki a nettó értéket, és a (3) modul e téves nettó érték alapján döntené el a kiírás formáját, akkor a hiba megkétszereződne. Ha azonban a feltételváltozó mindkét modulban ugyanaz, akkor a hiba valószínűsége kisebb (hacsak a K nem hibás). Ez utóbbi esetben a program ellenőrzése és karbantartása is egyszerűbb.
Ha egy programon belül többször kell vizsgálni ugyanannak a feltételnek a teljesülését, akkor mindig az eredeti feltételt és ne a feltételvizsgálat eredményeként kialakult adatot vizsgáljuk, mert az hibához vezethet. Ezért a kiírási kép kiválasztásához itt is az életkort alkalmazzuk feltételváltozóként. Ha K<5, akkor a számított nettó értéket, ha K>=5, akkor az eszmei értéket tartalmazó N változó értékét (100,- Ft) kell kiírni, de zárójelben meg kell jegyezni, hogy ez az eszmei érték. Ezután a program véget ér.
4. A program kódolása
(1) A bemeneti adatok
A modul a program első modulja, ezért a program nevét ide helyezzük el. A folyó évet értékadással határozzuk meg, mert változtatására évente csupán egy alkalommal van szükség. A B (bruttó érték) és az E (beszerzési év) adat a READ, DATA utasításpárral kap értéket. A DATA utasítást is ebbe a modulba helyezzük el, hogy egy helyen legyen a READ utasítással. Módosítási igénynél a DATA utasítás adatait kell csak kicserélni. A modul kódja a következő:10 REM * AMOR *
20 REM BEMENETI ADATOK
30 LET J=1982
40 READ B,E
50 DATA 1000,1976(2) Amortizáció számítás
A modul kódja a K meghatározásával kezdődik. Ezek után az IF-THEN-ELSE szerkezet kódolása megy végbe:60 REM AMORTIZACIO SZ.
70 LET K=J-E
80 IF K<5 THEN LET N=(B*(5-K))/5: GO TO 100
90 LET N=0.1(3) A kiírás
Példánkban először a címet íjuk ki. A cím után egy sort üresen hagyunk. Ezután következik a B, E és a K kiírása szöveges megjelöléssel. A nettó értéket a K-tól függő formában, IF-THEN szerkezetet alkalmazva íratjuk ki. Ezután a programot befejezzük:100 REM KIIRATAS
110 PRINT "NETTO ERTEK SZAMITAS"
120 PRINT
130 PRINT "BRUTTO ERTEK: ";B;" EFT"
140 PRINT "A BESZERZES EVE: ";E;" EV"
150 PRINT "ELETKOR: ";K;" EV"
160 PRINT "NETTO ERTEK: ";N;" EFT";
170 IF K>=5 THEN PRINT " (ESZMEI ERTEK)";
180 PRINT: PRINT
5. Az eredmény értékelése
Ezzel a program elkészült. Futtathatjuk és ellenőrizhetjük, hogy megfelelően működik-e. Az első futtatásnál azt keressük, hogy egy 1976-ban 1000 eFt-ért beszerzett gépnek mennyi a nettó értéke 1982-ben. A futtatás eredményeként leolvashatjuk, hogy a 6 éves állóeszköz 100,- Ft eszmei értéken van nyilvántartva.
Több állóeszköz nettó értékének kiszámítása egyetlen futással
A felhasználóban jogosan merül fel az az igény, hogy a program 5-10-20, esetleg több állóeszköz nettó értékét számítsa és úja ki, mert az egyenkénti adatcsere lassúnak bizonyulhat. Ezt viszonylag kis módosítással elérhetjük. A READ utasításnak azt a tulajdonságát kell kihasználni, hogy a DATA utasításban levő adatokat minden olvasásnál sorban előrehaladva olvassa ki.Ezért, ha a DATA utasításban valamennyi állóeszköz adatait elhelyezzük, akkor már csak azt kell elérni, hogy a READ utasítás minden feldolgozás végén egy újabb adatpárt olvasson ki. A legegyszerűbb megoldás, ha a feldolgozás befejeztével - a (3) modul végén - visszaugrunk az (1) modul READ utasítására.
Ennek eredményeként minden feldolgozás után újabb adatpár olvasódik be, és a program az adatpárnak megfelelő állóeszköz nettó értékét határozza meg. Amikor elfogynak az adatok, a fordító hibát érzékel (a READ utasításhoz nincs több adat), a program hibaüzenetet ír ki, és a futás leáll.
Kódolási szinten úgy módosítunk, hogy a DATA utasítást kiegészítjük a szükséges adatokkal (pl. három állóeszköz adataival), és a (3) modul végén egy GO TO utasítást helyezünk el.
10 REM * AMOR *
20 REM BEMENETI ADATOK
30 LET J=1982
40 READ B,E
50 DATA 1000,1976
55 DATA 500,1982,3500,1981
60 REM AMORTIZACIO SZ.
70 LET K=J-E
80 IF K<5 THEN LET N=(B*(5-K))/5: GO TO 100
90 LET N=0.1
100 REM KIIRATAS
110 PRINT "NETTO ERTEK SZAMITAS"
120 PRINT
130 PRINT "BRUTTO ERTEK: ";B;" EFT"
140 PRINT "A BESZERZES EVE: ";E;" EV"
150 PRINT "ELETKOR: ";K;" EV"
160 PRINT "NETTO ERTEK: ";N;" EFT";
170 IF K>=5 THEN PRINT " (ESZMEI ERTEK)";
180 PRINT: PRINT: PRINT
190 GO TO 40
A program (3) moduljának végére három PRINT utasítást is beszúrtunk, hogy az egyes kiírásokat jól elválasszuk egymástól.
Felhívjuk az olvasó figyelmét, hogy bár a fenti egy lehetséges megoldás, de az úgynevezett veszélyes programszerkezetek közé tartozik, mert a GO TO utasítás ciklust képez a programban, és a programozó nem ellenőrzi, hogy a ciklus mikor fejeződik be. Az ellenőrzést a fordítóra bíztuk, és az akkor állítja le a programot, amikor elfogynak az adatok. Formailag sem szép a programlista, mert a címet mindig kiírja, és a futás végén hibaüzenetet ad ki. Könyvünk a 3.5 alfejezetben a ciklikus problémák megoldására szabályosabb szerkezetet mutat be, de más szerkezetek alkalmazásával is ki lehet kerülni az ilyen megoldást.
Adatbevitel terminálról, programfutás közben
Vannak olyan feladattípusok, amelyeknél az az igény merül fel, hogy a felhasználó a program futásakor adja meg egyes változók értékét.
Az eddig megismert LET és READ, DATA értékadó utasítások segítségével az adatok változtatása nehézkes, mert a program módosításával jár. A futás közbeni gyors adatbevitelre az INPUT utasítás alkalmas. Az INPUT utasítás formája:
x INPUT változó1, változó2,...
Amikor a program a végrehajtáskor eléri az INPUT utasítást, egy kérdőjelet ír ki, ezzel jelzi, hogy adatbevitelre vár. A kérdőjel kiírásával egyidejűleg a programfutás leáll, és csak az INPUT utasítás tárgyában levő változók értékének begépelése, valamint a RETURN (ENTER) billentyű lenyomása után folytatódik. Ha kevesebb értéket gépelünk be, mint amennyit az utasítás vár, akkor a program a RETURN billentyű lenyomása után újabb kérdőjelet ír kijelezve, hogy még vár adatokat. A megfelelő számú adat begépelése után az INPUT utasítás az utasítás tárgyában levő változókhoz rendeli hozzá a felsorolás sorrendjében a begépelt értékeket. Tehát az INPUT utasítás kettős funkciót lát el: adatbevitelt és értékadást.
Ha több változó szerepel az INPUT utasításban, akkor ezeket vesszővel kell elválasztani:
20 INPUT C1,C2,C3
Ugyanígy - a legtöbb BASIC implementációban - a begépelt adatokat is vesszővel kell elválasztani.
Ha egy program több INPUT utasítást tartalmaz, akkor több alkalommal kell adatot beadni a program futása közben. Az INPUT utasítás előtt ajánlatos egy PRINT utasítással kiírni, milyen adat beadása következik, hogy a felhasználó tudja, mikor, melyik adatot, és milyen mértékegységben kell beadni. A legtöbb BASIC-ben az INPUT utasítás is meg tud jeleníteni tájékoztató szöveget:
20 INPUT "szöveg",C1,C2,C3
Például, ha az AMOR programban egy INPUT utasítás kérésére a berendezés bruttó értékét kell megadni, akkor ezt a műveletet a következőképpen érdemes kódolni:
40 PRINT "AZ ALLOESZKOZ BRUTTO ERTEKE (EFT): "
45 INPUT B
Megtehetjük azt is, hogy a szöveges adatmegjelölés és az adat egy sorba kerüljön. Ez úgy érhető el, hogy a PRINT utasítás végére ; (pontosvesszőt) jelet írunk. Ennek hatására nincs soremelés. Az előző két utasítás így módosul:
40 PRINT "AZ ALLOESZKOZ BRUTTO ERTEKE (EFT): ";
45 INPUT B
Mielőtt az INPUT utasítás alkalmazását bemutatnánk, még egy fogalmat kell megismernünk.
A szöveges változók
Egyes feladatok megoldása azt is igényli, hogy a program ne csak numerikus, hanem szöveges változókat is tudjon kezelni. Szükség lehet például nevek bevitelére, tárolására vagy ezek ábécérend szerinti rendezésére, kiírására. A BASIC nyelv rendelkezik ilyen képességekkel. Egy szöveges adat 0-255, a BASIC által megengedett karakterből állhat, de van olyan BASIC implementáció is, amely nem korlátozza a szöveges változóban tárolható karakterek számát.
Szöveges adat például egy név:
KOVACS PAL
vagy lakáscím:
SZEP UTCA 2.
és így tovább. A szöveges adatot meghatározáskor idézőjelek közé kell tenni, hogy a program pontosan tudja értelmezni, hol kezdődik, és hol fejeződik be. A numerikus adatoknál erre nincs szükség, mert ezeknek csak egyetlen számból (szóköz nélkül) álló számértéke lehet. A szöveges adatra (string) viszont a hosszúsága is jellemző, ezért kell egyértelműen behatárolni.
A szöveges adatok a numerikus adatokhoz hasonlóan lehetnek:
A szöveges konstans a program során nem változtatja tartalmát. Ilyen szöveges konstans a PRINT utasítás tárgyában megadott szöveg:
110 PRINT "NETTO ERTEK SZAMITAS"
Az idézőjelek közé tett szöveges adat a program során nem változik, ezért konstans.
Ha a szöveges adat tartalma a program során megváltozik, vagy értékét ugyan nem változtatja meg, de többször kell rá hivatkozni, akkor a szöveges adatot változóként kezeljük. Ekkor a szöveges adat változónevet kap. A szöveges adatok változónevét a numerikus változók nevéhez hasonlóan képezzük, azzal az eltéréssel, hogy a változónév végére $ jelet kell írni. A $ jel utal a szöveges adattípusra.
Ilyen lehet például:
A$
C5$
A Sinclair BASIC a szöveges változók neveire szigorúbb korlátozást követel meg: egy stringváltozó neve egyetlen betű és az azt követő $ jel lehet.
A szöveges változók a már ismert módokon kaphatnak értéket. Értékadás történhet a LET utasítás segítségével:
200 LET B$="NETTO ERTEK SZAMITAS"
Értékadásra felhasználható a READ, DATA utasításpár is:
100 READ C$
...
1000 DATA "ABA DENES","BALINT GEZA"
1010 DATA "CAKO LAJOS","DENES ZOLTAN"
Vegyük észre, hogy a változó értékét mindkét értékadásnál idézőjelek közé kell tenni. (Több BASIC implementációban a DATA sorokban el lehet hagyni az idézőjeleket, ha a tárolt szöveges dadatok nem tartalmaznak szóközt.)
A szöveges változó értékét az INPUT utasítással is meg lehet határozni:
70 INPUT N$
Az INPUT utasítással való értékadáskor a változó tartalmát nem kell idézőjelek közé írni, de a Sinclair BASIC kirakja az idézőjeleket, jelezvén, hogy szövegfüzért vár.
A szöveges változó tartalmát ugyanúgy lehet kiíratni, mint a numerikus változóét. Például:
PRINT N$
Megemlítjük, hogy szöveges adatokkal is lehet bizonyos műveleteket végezni, így például szöveges adatokat össze lehet adni (egymás után láncolni):
10 READ A$,B$,C$,D$
20 PRINT A$+B$+C$+D$
30 DATA "KISS PETER"," ","3500"," FT"
Az eredmény:
KISS PETER 3500 FT
Az összehasonlító művelet a szöveges adatokra is értelmezhető. Ezzel könyvünk részletesen nem foglalkozik.
IV. probléma
Egy vállalatnál havibéres dolgozók havi bérszámfejtését kell elvégezni. A vállalat 1 vagy 2 hónapos idénymunkára veszi fel a dolgozókat. Adva van a dolgozó neve, alapbére, a bérkiegészítés (290,- Ft dolgozónként) és az esetleges letiltás. Meg kell határozni a nyugdíjjárulékot (N0), majd mindezek alapján az összes kifizetést.
A nyugdíjjárulék a havibér összegétől függően progresszív, a levonást Az alábbi táblázat mutatja (az 1983. jan. 1. előtti előírások alapján):
Havi alapbér (Ft) Nyugdíjjárulék (%) 1 - 8000 3 1801 - 2300 4 2301 - 3000 5 3001 - 4000 6 4001 - 5000 7 5001 - 6000 8 6001 - 7000 9 7001 - 10
A dolgozók adatait kartonon tartják nyilván. Ezeken szerepel a név, az alapbér és a letiltás is. A bérszámfejtés eredményét a következő formában kell kiírni:
ELSZÁMOLÁS
<név>
Járandóságok
Alapbér
Bérkiegészítés
Összes járandóság
Levonások
Nyugdíjjárulék
Letiltás
Összes levonás
Összes kifizetés
x Ft
290 Ft
x Ft
x Ft
x Ft
x Ft
x Ft
1. A probléma elemzése
Minden dolgozó adatait külön kartonon tartják nyilván, ezért a bérszámfejtést személyenként célszerű végezni. A személyi adatok gépi tárolására nincs szükség, mert idényjellegű foglalkoztatásról van szó.
Legegyszerűbb megoldásként egy olyan programot készítünk, amely a futás elején bekéri a szükséges alapadatokat, majd ezután a bérfizetési adatokat kiszámítja és kiírja. Ezzel a program befejeződik. A programot annyiszor kell futtatni, ahány dolgozó van.
A program számára - a kiírási igényből kiindulva - a következő adatokat kell megadni:
A bérkiegészítés különböző áremelések kompenzációja, a 290,- Ft/fő az egész programban konstansként szerepel.
A programban ki kell számítani
A feladat megoldásához szükség van egy bemeneti adat modulra, amely bekéri a bemeneti adatokat (D$, A, L). A feldolgozás fenti négy feladatát egy feldolgozómodulnak kell elvégeznie.
Végül kell egy kiíró modul is. A feladat szerkezete hasonlít az eddig megismert szerkezetekre, ezért a modulszerkezet is hasonló lesz: Addazbeolvasás ![]() Feldolgozás
Feldolgozás ![]() Kiírás.
Kiírás.
2. A program tervezése
Vizsgáljuk meg egyenként a modulokat, hogy további felbontásuk szükséges-e. Az adatbeolvasó modul három adatot olvas be a terminálról. Adatellenőrzési igény nincs, így a modul elég egyszerű és zárt ahhoz, hogy ne bontsuk tovább.
A feldolgozó modul négy feladatot lát el. Elméletileg az a legjobb megoldás, ha mind a négy feladat külön modult alkot. Ez a megoldás - a nyugdíjjárulék kiszámításának kivételével - nagyon rövid modulokat eredményez.
A kiíró az adatok kiírásával egyetlen funkciót valósít meg, ezért további bontására nincs szükség. A program modulszerkezete az ábrán látható:
Az egyes modulok végrehajtási sorrendje soros, ezért vezérlőmodulokra nincs szükség.
Az (1)-(2.1), a (2.2)-(2.3), a (2.3)-(2.4) és a (2.4)-(3) modulkapcsolatok adat jellegűek, a többieknél adatátadás nincs, csak vezérlésátadás.
3. A modulok tervezése
(1) Adatbeolvasás
Bár ez a modul adatokat definiál, az adatmeghatározás módján (beolvasás terminálról) van a hangsúly, ezért a modul eljárás típusú.
A modul kívülről származó adatai:
- a dolgozó neve (D$),
- alapbére (A),
- letiltás (L).
Ugyanezek az adatok jelennek meg a modul kimenetén is. A modul művelete a fenti három adat beolvasása. A beolvasást INPUT utasítással hajtjuk végre. Minden INPUT utasítás előtt ki kell írni, hogy milyen adat begépelését kéri a program.
(2.1) Összes járandóság
A modul eljárás típusú. Bemeneti adata az alapbér (A) az (1) modulból. Ehhez hozzá kell adni a konstans 290 forintot, így megkapjuk a modul kimenetét képező összes járandóságot (J).(2.2) Nyugdíj járulék
Ez a modul is eljárás típusú. A modul bemenete az alapbér (A) az (1) modulból, kimenete pedig az az összeg (N0), amit az alapbérből nyugdíjjárulékként le kell vonni.N0=A*S
ahol
S = az alapbér összegétől függő szorzószám.
Meg kell vizsgálni, hogy az alapbér összege a nyugdíjjárulék-táblázat melyik intervallumába esik, majd az ennek megfelelő S értékkel kell megszorozni, így megkapjuk az N0 értéket.
Láthatjuk, hogy egynél több és egymással összefüggő feltételvizsgálatot kell elvégezni. Ezt CASE szerkezettel lehet megvalósítani. A modul végrehajtásakor először azt kell vizsgálni, hogy A beleesik-e az első intervallumba. Ha igen, akkor a nyugdíjjárulék összege az alapbér 3%-a lesz. Megfigyelhetjük, hogy a két vizsgálat közül az első felesleges, mert 1,- Ft-nál kisebb bér nem létezik. Ha az1 <= a <= 1800
feltétel nem teljesül, áttérünk a következő intervallum vizsgálatára. Ekkor azt kell vizsgálni, hogy A-ra teljesül-e az
1801<= a <= 2300
vagy az ezzel egyenértékű
1800< a <= 2300
feltétel.
A második intervallum vizsgálatánál is felesleges az első feltételvizsgálat (A>1800), mert az első intervallumvizsgálat eredményeként már kiderült (A<=1800 nem teljesül). Tehát ez ismét elhagyható.
Ha az intervallumvizsgálatot alulról felfelé haladva folyamatosan végzi a program, akkor minden vizsgálatnál elhagyható az alsó határ vizsgálata, mert az adott intervallumvizsgálatra csak akkor kerülhet sor, ha már bebizonyosodott, hogy nem esik egyik alacsonyabb intervallumba sem az alapbér.
Ha a vizsgálatot a felső intervallumnál kezdjük, akkor a felső határ vizsgálata hagyható el az intervallumvizsgálatoknál.
Ez az egyszerűsítés azon alapszik, hogy az intervallumok folytonosan kapcsolódnak egymáshoz, és a program a vizsgálatot alulról felfelé vagy felülről lefelé haladva, folyamatosan végzi. Ezek alapján készíthető el a modul folyamatábrája:

Minthogy az utolsó intervallum felülről nyitott, a felső határ vizsgálata is feleslegessé válik. Ha tehát az alapbér meghaladja a 7000,- Ft-ot, akkor a nyugdíjjárulék további vizsgálat nélkül is meghatározható.
(2.3) Összes levonás
A modul eljárás típusú. Bemeneti adatai az (1) modulból származó letiltás (L) és a (2.2) modulban kiszámított nyugdíjjárulék (N0). Ezt a két értéket kell összeadni, és megkapjuk az összes levonást (C).
Ez az összeg a modul kimenete.(2.4) Összes kifizetés
A modul eljárás típusú. Bemeneti adatai az összes járandóság (J) a (2.1) modulból és az összes levonás (C) a (2.3) modulból. A kettő különbsége adja az összes kifizetés összegét. Ez a különbség (K) a modul kimeneti adata.(3) Kiírás
A modul eljárás típusú. Bemeneti adatai a megelőző modulokból származnak:
- a név (D$) és
- az alapbér (A) az (1) modulból,
- az összes járandóság (J) a (2.1) modulból,
- a nyugdíjjárulék (N0) a (2.2) modulból,
- a letiltás (L) az (1) modulból,
- az összes levonás (C) a (2.3) modulból,
- az összes kifizetés (K) a (2.4) modulból.
A modul kimenetét a specifikáció szerinti formában kiírt adatok alkotják. A kiírás szövegeit kétlépcsős töréssel kell kinyomtatni. Célszerű a két lépcsőnek megfelelően két, szóközökből álló szövegkonstanst (M$, N$) meghatározni (az egyik legyen 3, a másik legyen 6 karakter hosszúságú), és a beljebb kezdett sorokat ezekkel kezdve nyomtatni. Így a sor eleji szóközszámolást csak egyszer kell elvégezni.
4. A kódolás
(1) Az adatbeolvasás
A modul elején a már ismert módon helyezzük el a program nevét. Ezután következik a címkiírás, majd a három adatbevitel. Minden adatbevitel előtt ki kell nyomtatni, hogy milyen adatot kell beadni. Az adat megnevezése után célszerű még egy sort emelni, hogy a nyomtatós terminálon jobban lehessen látni a szöveget. A modul kódja a következő:10 REM * BER *
20 REM ADATBEOLVASAS
30 PRINT "ADATBEVITEL"
40 PRINT
50 PRINT "NEV: ";
60 INPUT D$
70 PRINT "---------------"
80 PRINT "ALAPBER (FT): ";
90 INPUT A
100 PRINT "LETILTAS (FT): ";
110 INPUT LSinclair BASIC-ben az INPUT eltérő működése miatt a modult az alábbiak szerint érdemes elkészíteni:
10 REM * BER *
20 REM ADATBEOLVASAS
30 PRINT "ADATBEVITEL"
40 PRINT
50 PRINT "NEV: ";
60 INPUT D$
65 PRINT D$
70 PRINT "---------------"
80 PRINT "ALAPBER (FT): ";
90 INPUT A
95 PRINT A;" FT"
100 PRINT "LETILTAS (FT): ";
110 INPUT L
115 PRINT L;" FT"(2.1) Összes járandóság
A modul egyetlen összeadásból áll:120 REM OSSZES JARANDOSAG
130 LET J=A+290(2.2) Nyugdíjjárulék
A modult a strukturált CASE szerkezet alapján kódoltuk (ber ez ennél a feladatnál nem indokolt):140 REM NYUGDIJ JARULEK
150 REM CASE KEZDET
160 IF A<=1800 THEN GO TO 240
170 IF A<=2300 THEN GO TO 270
180 IF A<=3000 THEN GO TO 300
190 IF A<=4000 THEN GO TO 330
200 IF A<=5000 THEN GO TO 360
210 IF A<=6000 THEN GO TO 390
220 IF A<=7000 THEN GO TO 420
230 GO TO 450
240 REM 1. ESET
250 LET N0=A*0.03
260 GO TO 470
270 REM 2. ESET
280 LET N0=A*0.04
290 GO TO 470
300 REM 3. ESET
310 LET N0=A*0.05
320 GO TO 470
330 REM 4. ESET
340 LET N0=A*0.06
350 GO TO 470
360 REM 5. ESET
370 LET N0=A*0.07
380 GO TO 470
390 REM 6. ESET
400 LET N0=A*0.08
410 GO TO 470
420 REM 6. ESET
430 LET N0=A*0.08
440 GO TO 470
450 REM 8. ESET
460 LET N0=A*0.1
470 REM CASE VEGA modul elején a feltételvizsgálatok kaptak helyet, majd ezek után az egyes esetekhez tartozó műveletek kódja következik.
(2.3) Összes levonás
A modul egyetlen összeg képzéséből áll:500 REM OSSZES LEVONAS
510 LET C=N0+L(2.4) Összes kifizetés
A modul egyetlen kivonásból áll:520 REM OSSZES KIFIZETES
530 LET K=J-C(3) Kiírás
A modul elején létrehoztuk a "bekezdés" szövegváltozókat (M$, N$). Ezek hosszát az adott képernyős terminálon egy sorban megjeleníthető karakterek számához kell igazítani. Ezután a program 2 soremelést hajt végre, hogy a kiírást az adatbevitelektől elkülönítse. A cím kinyomtatásához is felhasználtuk a szóközből álló szövegváltozókat.540 REM KIIRAS
550 LET M$=" "
560 LET N$=M$+" "
570 PRINT: PRINT
580 PRINT N$;M$;"ELSZAMOLAS"
590 PRINT
600 PRINT D$
610 PRINT M$;"JARANDOSAGOK"
620 PRINT N$;"ALAPBER: ";A;" FT"
630 PRINT N$;"BERKIEGESZITES: 290 FT"
640 PRINT N$;"OSSZES JARANDOSAG: ";N$;J;" FT"
650 PRINT
660 PRINT M$;"LEVONASOK"
670 PRINT N$;"NYUGDIJJARULEK: ";N0;" FT"
680 PRINT N$;"LETILTAS: ";L;" FT"
690 PRINT N$;"OSSZES LEVONAS: ";N$;C;" FT"
700 PRINT
710 PRINT N$;"OSSZES KIFIZETES: ";N$;N$;K;" FT"
5. Az eredmény értékelése
A programot néhány eltérő adattal kipróbáljuk, hogy helyesen működik-e. Ha a specifikáció szerint működik, felhasználhatjuk a probléma megoldásában. A bérszámfejtő a terminál előtt ülve a dolgozók kartonján található adatok alapján dolgozónként elvégezheti a bérszámfejtést. A program a bérkifizetéshez és a befizetésekhez szükséges adatokat személyenként kiírja. A kiírt táblázat bizonylatként kezelhető. (A program némileg egyszerűsített formában végzi el a bérszámfejtést, de a hiányzó csökkentő és növelő összegek bevitelével a bérszámfejtés szabályossá tehető, és a valóságban is alkalmazható. Ez a kiegészítés a program terjedelmét is növeli, ezért bemutatását nem tartottuk célszerűnek.)
Az egyszerűsített CASE szerkezet alkalmazása a (2.2) modulban
A fejezet elején utaltunk rá, hogy a CASE szerkezet egyszerűsített formában is kódolható, ha az egyes esetekben levő műveletek csak 1-2 utasításból állnak. Ebben a programban ez igaz, hiszen a műveletek egyetlen szorzásból állnak. Az egyszerűsített szerkezet kódja a következő:
140 REM NYUGDIJ JARULEK
150 REM CASE KEZDET
160 IF A<=1800 THEN LET N0=A*0.03: GO TO 240
170 IF A<=2300 THEN LET N0=A*0.04: GO TO 240
180 IF A<=3000 THEN LET N0=A*0.05: GO TO 240
190 IF A<=4000 THEN LET N0=A*0.06: GO TO 240
200 IF A<=5000 THEN LET N0=A*0.07: GO TO 240
210 IF A<=6000 THEN LET N0=A*0.08: GO TO 240
220 IF A<=7000 THEN LET N0=A*0.09: GO TO 240
230 LET N0=A*0.1
240 REM CASE VEG
Látható, hogy a CASE szerkezet egyszerűsített formájú kódolása jelentősen csökkentette a modul hosszát.
Egy speciális CASE szerkezet kódolása
Ha egy feladat CASE szerkezetében a feltételváltozó értéke csak 1, 2, .., n természetes szám lehet, akkor a CASE szerkezet megvalósításához az ON GO TO utasítás is használható, melyet a legtöbb BASIC implementáció (de a Sinclair BASIC nem) ismer:
x ON kifejezés GO TO sorszám1,sorszám2,...,sorszámn
Ez az utasítás a feltételváltozó értékeinek megfelelő sorszámra adja át a vezérlést.
Az utasítás végrehajtásakor a fordító kiszámítja a kifejezés értékét (amely egyetlen változó is lehet). Ha a kifejezés értéke 1, akkor a GO TO után írt első sorszámra adja át a vezérlést, ha 2, akkor a másodikra, és így tovább. A GO TO után írt sorszámokon kezdődnek azok a műveletek, amelyeket a változó értékétől függően kell elvégezni:
40 REM CASE KEZDET
50 ON X GO TO 100,200,300
60 GO TO 400
100 REM 1. ESET
110 LET Y=2
...
180 GO TO 400
200 REM 2. ESET
210 LET Y=3
...
280 GO TO 400
300 REM 3. ESET
310 LET Y=4
...
400 REM CASE VEG
Az ON GO TO utasítás szükségtelenné teszi a feltételváltozó intervallum- vagy értékvizsgálatát. Az utasítás gátja, hogy csak akkor használható, ha a feltételváltozó értéke 1,2,... természetes szám, vagy ha valamilyen módon átalakítható erre az értéktartományra.
Ha a feltételváltozó értéke nagyobb, mint ahány sorszám szerepel az utasításban, akkor a vezérlés a következő sorra kerül át.
Dekódolás az ON GO TO utasítás segítségével
Az ON GO TO utasítás egyik alkalmazási területe a dekódolás. Tegyük fel, hogy a személyek foglalkozását az alábbi kódolás szerint tároltuk:
Foglalkozás: Kód: rendszerszervező 1 programozó 2 gépkezelő 3
Legyen az a részfeladat, hogy a kódolásnak megfelelően szöveggel újuk ki a személyek tárolt nevét és a foglalkozását. Ehhez el kell olvasni a személy nevét (D$) és foglalkozási kódját (F). Majd a kód kiértékelését egy CASE szerkezetben el kell végezni.
A program kódolásához felhasználhatjuk az ON GO TO utasítást, így a következő kódot kapjuk:
200 READ N$,F
210 REM CASE KEZDET
220 ON F GO TO 250,280,310
230 PRINT "ADATHIBA"
240 GO TO 500
250 REM 1. ESET
260 LET F$="RENDSZERSZERVEZO"
270 GO TO 330
280 REM 2. ESET
290 LET F$="PROGRAMOZO"
300 GO TO 330
310 REM 3. ESET
320 LET F$="GEPKEZELO"
330 REM CASE VEG
340 PRINT N$
350 PRINT F$
360 PRINT
370 GO TO 200
400 DATA "KOZAK GEZA",2,"KELEMEN ODA",1
410 DATA "LAPOS ELEK",1,"HUDAK BELA",3
Láthatjuk, hogy az ilyen feladatok az ON GO TO felhasználásával lényegesen kevesebb utasítással valósíthatók meg, mint az IF utasításokkal.
3.4. A szubrutinok
Az előző részekben is láthattuk, hogy a programok modulokból épülnek fel. Az eddig bemutatott feladatok többsége olyan volt, hogy a programok moduljai különböztek egymástól. Vannak azonban olyan feladatok, amelyekben egy műveletsorozatot vagy egy modult a programban többször is végre kell hajtani. Itt nem valamilyen műveletsorozat ciklikus ismétlésére gondolunk, hanem azt az esetet tanulmányozzuk, amikor ugyanazt a műveletsorozatot (modul) a program több pontján kell végrehajtani. A program készítőjében jogosan merül fel az az igény, hogy ilyenkor az ismétlődő modult csak egyszer kelljen kódolni, és a megfelelő helyekről - ahol végre kell hajtani - hívni lehessen. Ezt a lehetőséget szerencsére szinte valamennyi programozási nyelv, így a BASIC is biztosítja.
A többször használt modult vagy műveletsorozatot szubrutinnak nevezzük.
Egy programban több szubrutin is lehet, és valamennyi többször is hívható a programon belül. A szubrutint tartalmazó programot ugyanúgy kell tervezni, mint bármely más programot.
A szubrutint csak egyszer kell kódolni, és több helyről lehet hívni, ezért a szubrutinokat megfelelő sorszámmal a program végére, a DATA utasítások elé (ha van ilyen a programban) javasolt elhelyezni. A szubrutinok a modulokhoz hasonlóan logikailag zárt egységet alkotnak. Egy szubrutin állhat egy vagy több modulból, de lehet egy modulrészlet is.
A szubrutin kezdetét semmilyen szubrutinnyitó utasítás nem jelzi, így a program olvasója sem veszi észre egy utasításról, hogy az szubrutinkezdés-e vagy sem. A szubrutin kezdő utasítását csak sorszáma alapján határozhatjuk meg, mert hívásakor a hívó utasításban (lásd később) a szubrutin kezdő utasításának sorszámát kell megadni. A szubrutint minden esetben RETURN utasítással kell befejezni. Ennek hatására még visszatérünk.
A programnak azon a pontján, ahol egy szubrutint végre kell hajtani,
x GOSUB sorszám
szubrutinhívó utasítást adunk meg.
A GOSUB utasításkulcsszó jelöli a szubrutin hívását. Az utasítás tárgyában levő szám azt a sorszámot jelöli, ahol a szubrutin kezdődik (ebből a sorszámból lehet megtudni a program tanulmányozásakor, hogy melyik sornál kezdődik a szubrutin). Az utasítás hatására a vezérlés átkerül a megadott sorszámra. Vegyük észre, hogy eddig a működése megegyezik a GO TO utasítás hatásával.
Ezután a hívott szubrutin végrehajtódik. Amikor a program eljut a szubrutin végét jelölő RETURN utasításhoz, akkor a szubrutin befejeződik, és a vezérlés visszakerül a hívó GOSUB utasítást követő utasításra. A program végrehajtása ezután az ún. főágban folytatódik. Láthatjuk, hogy a szubrutinhívást a GOSUB utasítás valósítja meg, a visszatérés a főágra pedig a RETURN utasítás hatására megy végbe.
A szubrutint tartalmazó programokat így kell felépíteni:
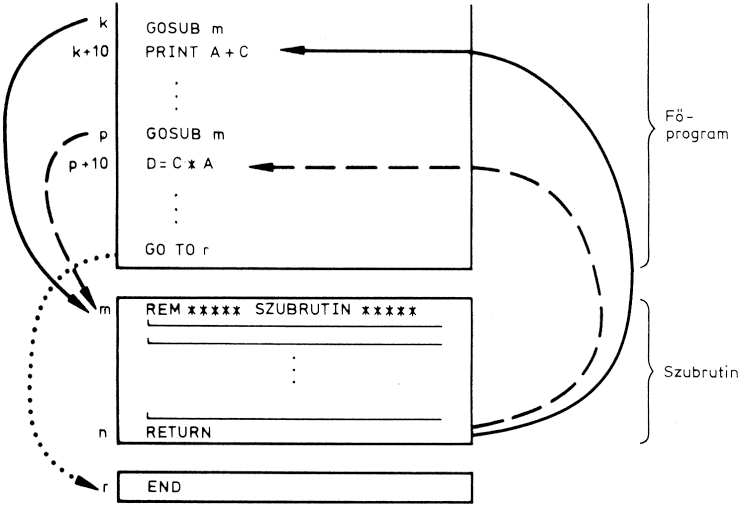
Jól látható, hogy bárhonnan is hívjuk a szubrutint, a végrehajtás után a vezérlés mindig az aktuálisan hívó GOSUB utáni utasításra tér vissza. Felhívjuk a figyelmet arra, hogy a főág (a szubrutinokat és DATA-t nem tartalmazó programrész) végrehajtása után a program rátérne az első szubrutin végrehajtására, anélkül, hogy erre szükség lenne. Ilyenkor eljutna a RETURN-ig, de nem tudna sehova sem visszatérni, mert GOSUB hívás nélkül került a szubrutinba. Ezért a fordító hibaüzenetet ad ki, és a végrehajtást befejezi. Bár ez a program helyes működését nem befolyásolja, formai szempontból mégis célszerű, ha a főág befejezése után GO TO utasítással a program utolsó - END (STOP) - utasítására adjuk át a vezérlést.
Menjünk most vissza a HOZAM nevű programra (II. probléma). Ebben a programban két modul van, amely a program futásakor két alkalommal is végrehajtódik. Ezek a számítás 5 év és a számítás 10 év modulok, amelyek eltérő nevük ellenére ugyanazt a műveletet tartalmazzák. A másik ilyen az 5 éves adatok kiírása, valamint a 10 éves adatok kiírása modul. Az elsőből és a másodikból is kialakíthatunk egy-egy szubrutint. A számítás szubrutinkódja:
370 REM SZAMITAS SZUBRUTIN
380 LET H=(J-U)*((1+K)^N-1)/(K*(1+K)^N)
390 RETURN
A programban ezt a szubrutint kétszer kell hívni. Az egyik esetben N=5 (5 év utáni hozam), a másikban N=10. Így tehát N értékét minden hívás előtt meg kell határozni. Ezt a műveletet a szubrutin paraméterezésének nevezzük. Ha ezt elmulasztjuk, akkor a program N=0 értéket feltételez vagy hibaüzenettel leáll - BASIC implementációtól függően. A többi változó értéke adott, így ezekkel nem kell foglalkozni.
A kiírásmodulban szerepel az, hogy 1. vagy 2. kiírás (számítási sorszám). A szubrutinban ezt is paraméterezni kell. A sorszám kiírási utasításában a kiírás sorszámát S változóval jelöljük, és értékét a GOSUB hívás előtt meghatározzuk. A kiírási szubrutin a következő:
400 REM KIIRAS SZUBRUTIN
410 PRINT
420 PRINT S;". SZAMITAS"
430 PRINT "EVEK SZAMA: ";N
440 PRINT "HOZAM = ";H;" MFT"
450 RETURN
A szubrutinok meghatározásával a teljes programot át kell alakítani. Ahol eddig számítást kellett végrehajtani, ott most számítási szubrutinhívás (GOSUB 370) szerepel. Előtte azonban N értékét be kell állítani. Ahol eddig évfüggő kiírás volt, oda most kiírási szubrutinhívás (GOSUB 400) kerül. Ezelőtt a kiírási sorszámot kell beállítani (S paraméterezése).
A programot ennek megfelelően át kell kódolni. Vegyük észre azonban, hogy a program modulszerkezete nem változott, mert ugyanazokból a modulokból épül fel, és a modulok végrehajtási sorrendje sem változott.
A módosított program kódja:
10 REM * HOZAM *
20 REM BEMENETI ADATOK
30 LET B=100
40 LET J=40
50 LET U=20
60 LET K=0.12
70 REM SZAMITAS 5 EV
80 LET N=5
90 GOSUB 370
100 REM ALAPADATOK KIIRASA
110 PRINT "BERUHAZAS GAZDASAGOSSAGI SZAMITAS"
120 PRINT
130 PRINT "A BERUHAZAS OSSZEGE = ";B;" MFT"
140 PRINT "EVES JOVEDELEM = ";J;" MFT"
150 PRINT "EVES UZEMELTETESI KOLTSEG = ";U;" MFT"
160 PRINT "KAMATLAB = ";100*K;"%"
170 PRINT
180 REM 5 EVES ADATOK KIIRASA
190 LET S=1
200 GOSUB 400
210 REM SZAMITAS 10 EV
310 LET N=10
320 GOSUB 370
330 REM 10 EVES ADATOK KIIRASA
340 LET S=2
350 GOSUB 400
360 STOP
370 REM SZAMITAS SZUBRUTIN
380 LET H=(J-U)*((1+K)^N-1)/(K*(1+K)^N)
390 RETURN
400 REM KIIRAS SZUBRUTIN
410 PRINT
420 PRINT S;". SZAMITAS"
430 PRINT "EVEK SZAMA: ";N
440 PRINT "HOZAM = ";H;" MFT"
450 RETURN
Látható, hogy minden szubrutinhívás előtt elvégeztük a paraméterezést. A program némileg egyszerűsödött, de semmivel sem lett rövidebb. A szubrutinok ugyan rövidek, de a szubrutinhívásokkal sok "adminisztráció" (paraméterezés, RETURN-ök) jár együtt. Nem szerencsés, hogy az alapadatok kiírása beékelődik a szubrutinhívások közé, holott következhetne rögtön a bemeneti adatok modul után is, mert itt csak a konstansok íródnak ki.
A program modulszerkezetét ennek megfelelően átalakíthatjuk, de ez az eredményre nem lesz hatással:
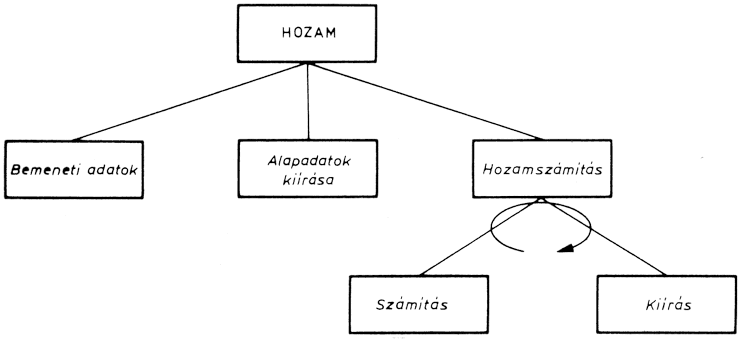
Belátható, hogy a számítási és a kiírási modul lényegében összevonható egyetlen szubrutinba, hiszen a számítás után mindig kiírás következik, és mindkét modult egy-egy hívás alkalmával paraméterezzük. Ezt az összevont szubrutint többször (programunkban kétszer) hívjuk. Az új összevont szubrutin kódja a következő:
370 REM SZAMITAS ES KIIRAS
380 LET H=(J-U)*((1+K)^N-1)/(K*(1+K)^N)
390 PRINT
400 PRINT S;". SZAMITAS"
410 PRINT "EVEK SZAMA: ";N
420 PRINT "HOZAM = ";H;" MFT"
430 RETURN
A módosított programtervnek megfelelően a kódolt program pedig ilyen formájú lesz:
10 REM * HOZAM *
20 REM BEMENETI ADATOK
30 LET B=100
40 LET J=40
50 LET U=20
60 LET K=0.12
70 REM ALAPADATOK KIIRASA
80 PRINT "BERUHAZAS GAZDASAGOSSAGI SZAMITAS"
90 PRINT
100 PRINT "A BERUHAZAS OSSZEGE = ";B;" MFT"
110 PRINT "EVES JIVEDELEM = ";J;" MFT"
120 PRINT "EVES UZEMELTETESI KOLTSEG = ";U;" MFT"
130 PRINT "KAMATLAB = ";100*K;"%"
140 PRINT
150 REM HOZAM SZAMITAS
160 LET N=5
170 LET S=1
180 GOSUB 370
190 LET N=10
340 LET S=2
350 GOSUB 370
360 STOP
370 REM SZAMITAS ES KIIRAS
380 LET H=(J-U)*((1+K)^N-1)/(K*(1+K)^N)
390 PRINT
400 PRINT S;". SZAMITAS"
410 PRINT "EVEK SZAMA: ";N
420 PRINT "HOZAM = ";H;" MFT"
430 RETURN
Ezzel a módosítással már rövidebb programot kaptunk. A program szerkezete jobban kihasználja a szubrutin szerkezetét, mint az előző változat, ugyanakkor valamivel merevebb lett, mert a szubrutinba két modult összevontunk. Emellett nagyon jól látszik a rövidebb programnak az az előnye, hogy most a hozam értékét újabb N-re könnyebben tudjuk kiszámítani, hiszen egy harmadik számításhoz nem kell megismételni a számítás és a kiírás kódját, csak a két paraméterező utasítást kell elhelyezni.
Az INT függvény
Van olyan feladat vagy részfeladat, amelyben egy x számról le kell "választani" a szám törtrészét, és csak az egész részt kell a továbbiakban felhasználni. Ezt az
LET Y=INT(X)
függvény úja le. A kifejezés azt jelenti, hogy az y függvényérték az x független változó egész (integer) részével egyezik meg. Egészen pontosan y az a legnagyobb egész szám (vagy zérus), amely nem nagyobb x-nél.
Például:
INT(16.53) = 16
INT(0.408) = 0
INT(-4.2) = -5
A BASIC nyelvben az egész (integer) függvény beépített függvényként szerepel, ezért a programozó ezt a függvényt alkalmazhatja. A függvényekkel a 3.6 pontban foglalkozunk részletesen, itt csupán ezt az egy függvényt mutatjuk be. A BASIC-ben az egész függvény
x LET Y=INT(Z)
formában adható meg, és hatása megegyezik a fent leírtakkal. A Z helyett állhat kifejezés vagy egy konstans is. Ha a zárójelben kifejezés van, akkor a fordító előbb kiszámítja a kifejezés értékét, majd ennek egész részét képezi, és Y-t a kapott értékkel egyenlővé teszi.
V. probléma
Egy kifizetőhely (pénztár) különböző összegű személyi kifizetéseket teljesít személyek által bemutatott vagy belső bizonylatok alapján. A kifizetett összegek forintra vannak kerekítve, így fillért nem tartalmaznak. A feladat az, hogy minden összeget a lehető legkevesebb fizetőeszközzel (bankjeggyel vagy érmével) fizessenek ki, hogy minél egyszerűbben lehessen kezelni és ellenőrizni (megszámolni).
Minden kifizetésnél meg kell határozni az egyes címletekből kifizetett részösszegeket és a végösszeget, s azt, hogy melyik címletből hány darab kell a kifizetéshez. A megadott összeg és a részösszegekből képzett végösszeg legyen vizuálisan összehasonlító és ellenőrizhető, hogy a címletek meghatározott értéke helyes-e. Az eredményeket az alábbi formában kell kiírni (bizonylataim); (az 1000 forintos megjelenése előtt):
A KIFIZETENDŐ ÖSSZEG: x Ft
CÍMLETEK DB ÖSSZEG 500
100
50
20
10
5
2
1
x
x
x
x
x
x
x
x
x
x
x
x
x
xÖSSZESEN:
Ennek alapján megtörténhet a kifizetés.
1. A probléma elemzése
A feladat értelmében a pénztáros az igényelt összeget vagy a saját, vagy a jelentkező által bemutatott bizonylat alapján a lehető legkevesebb pénzdarab (bankjegy és érme) felhasználásával azonnal kifizeti.
Ez a követelmény nyilvánvalóan akkor elégíthető ki, ha az adott összeget minél nagyobb címletű pénzdarabokból állítjuk össze, hiszen minél nagyobb B számmal osztunk el egy A számot, annál kisebb lesz a hányadosa. Így tehát először azt kell meghatározni, hogy maximálisan hány 500 Ft-os, majd a maradékhoz hány 100 forintos, illetve kisebb címletű bankjegyre van szükség. Az 1 forintosnál kisebb címleteket nem kell figyelembe venni, mert az összegek forintra vannak kerekítve. Ez a sorozatos címletekre bontás, illetve osztás számítógéppel jól elvégezhető.
Egy másik követelmény szerint a kifizetéseket azonnal kell teljesíteni, de az esetek egy részében a kifizetendő összeg csak a pénz felvételére jogosult személy érkezésekor válik ismertté, tehát gyorsan kell cselekedni. Ehhez pedig az kell, hogy a címletekre bontást a számítógép azonnal végezze el. Ez úgy valósítható meg, hogy a pénztáros az igény jelentkezésekor az összeget begépeli, és a számítógép válaszul - a specifikációban megadott táblázatos formában - kiírja a címleteket. A feladathoz egy olyan programot kell készíteni, amely a futás elején bekéri a kifizetendő összeget, és kiírja a kifizetési bizonylatot.
A kiírási tervben látható, hogy a fizetendő összeget kétszer kell kinyomtatni a bizonylatra. A specifikáció szerint erre azért van szükség, hogy a beadott összeg és a címletekből újra felépített (számított) összeg azonossága vizuálisan ellenőrizhető legyen, azaz a kifizető meggyőződhessen róla, hogy valóban a kért összeg lesz-e kifizetve. Bár ez az ellenőrzési módszer a mai, nagy megbízhatóságú számítógépeknél felesleges, beépítése mégsem hiba. A lényeg azonban az, hogy bár a két összeg számszerűleg megegyezik, a származása más (bemeneti adat és számított adat), és ezt a program készítésekor figyelembe kell venni.
A feladat szerkezete hasonlít az eddig megismert feladatok szerkezetéhez. A program kezdetén meg kell adni a kifizetendő összeget. Ezt a feladatot majd az adatbeviteli modul látja el. A következőkben ki kell számítani, hogy az egyes címletekből hány darabra van szükség (címltek számítása modul). Ezt a második modul végzi el. Végül az eredményt a harmadik modulban ki kell írni.
2. A program tervezése
Az adatbeviteli modul funkciója - a IV. probléma programjának adatbeviteli moduljához hasonlóan - egyszerű, további bontásra nincs szükség.
A címletek számítása modulnak a következő funkciókat kell ellátnia:
A műveleteket mindig az előző címletszámolás eredményeként megmaradt összegen kell elvégezni. Ez a számolás minden címlet meghatározásához szükséges, ezért egy modulba összefogható. Az is belátható, hogy a megoldó algoritmus mindig ugyanaz, de változik az induló összeg és a címletérték. Tehát szükség van egy vezérlőmodulra, amely sorozatosan hívja (500 Ft ![]() 1 Ft) a címletdarabszám modult, és minden híváshoz megadja az induló adatokat.
1 Ft) a címletdarabszám modult, és minden híváshoz megadja az induló adatokat.
A kiírási modul is egyszerű. Egyetlen táblázat kiírását valósítja meg, továbbfinomítása nem indokolt. A program moduljai és modulszerkezete a következő ábrán látható:
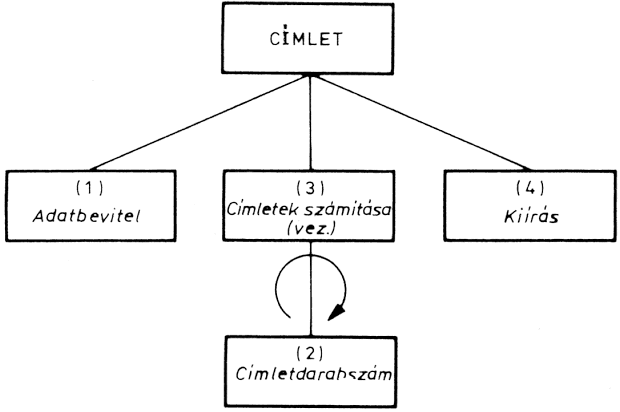
Az adatbeviteli modul és a címletek számítása modul között adatkapcsolat van, mert az előbbi modul adja át a számoláshoz az induló adatot. A címletek számítása (vez.) és a címletdarabszám szám modul közt a vezérlőkapcsolaton van a hangsúly, de a címlet darab szám modul paraméterezése miatt adatkapcsolat is van. Az adatbeviteli és a kiírási modul, valamint a címletek számítása (vez.) és a kiírás modul (darabszámok és részösszegek) között adatkapcsolat van.
3. A modulok tervezése
(1) Adatbevitel
A modul eljárás típusú. Bemeneti adata a felhasználó által begépelt összeg. Ez egyúttal a modul kimeneti adata is a címletek és a kiírás modul számára. Először a felhasználó számára ki kell írni, hogy mit vár a program, majd az összeget (KI) INPUT utasítással be kell vinni.(2) Címletdarabszám
A modul eljárás típusú. A programterv alapján látható, hogy a modul szubrutint fog alkotni a programon belül, mert ugyanazt a funkciót kell ellátnia valamennyi számba jöhető címletnél (500, 100, 50, 20, 10, 5, 2, 1 Ft). A modul minden hívásánál a következő bemeneti adatokat kell a modul számára megadni:
- induló összeg (K),
- címletnévérték (C).
A modulnak minden egyes esetben az alábbi kimeneti adatokat kell szolgáltatnia:
- az adott címlet darabszáma (D),
- a részösszeg (címletnévérték * darabszám) (R),
- a maradék összeg (M).
A címlet darabszáma az aktuális kiinduló összegből és a címletnévért ékből kapható meg:
H = K/C.
Kimenetként csak egész darabszám fogadható el, ezt az integer függvény felhasználásával kapjuk meg:
D = INT(H).
Ki kell még számítani a részösszeget is:
R = D*C.
Végül meg kell határozni, hogy az induló összegből mennyi maradt, amit a kisebb címletekkel kell kifizetni. A maradék:
M = K-R .
A modul következő hívásakor M lesz a kiinduló összeg, azonban ezt a modul kezdetén K-val jelöltük, ezért M értékét átmásoljuk K-ba: LET K=M .
Ezt annál is inkább megtehetjük, mert a modul végén a kiinduló összegre már nincs tovább szükség.(3) Címletek számítása (vez.)
A modul vezérlő típusú, mert a (2) modul végrehajtását vezérli, de emellett eljárásokat is végrehajt.
A modul egyik bemeneti adata (K1) az (1) adatbeviteli modulból származik. A K1 adatot meg kell őrizni, mert ez a kiíráshoz szükséges. A (2) modul minden végrehajtás után ettől a modultól is kap bemeneti adatokat (címletdarabszám: D, részösszeg: R és a maradék összeg: K).
A modul kimeneti adata a kifizetendő összeg (K1) és a (2) modul minden egyes hívásához az aktuális címletnévérték (C). A kiíráshoz ez a modul szolgáltatja a címletdarabszám és a részösszeg adatokat. Ezeket így jelöljük:
CÍMLETEK DB ÖSSZEG 500
100
50
20
10
5
2
1
D2
D3
D4
D5
D6
D7
D8
R2
R3
R4
R5
R6
R7
R8Első lépésként a kiinduló összeg értékét határozzuk meg:
K = K1
K1-et azért nem használhatjuk fel közvetlenül, mert erre a kiírásnál még szükség lesz. Az alkalmazott algoritmus ugyanis olyan, hogy K1 értékét minden címletszámítás után aktualizálja, ezért K1 értéke már az első számítás után elveszne.
Ezután azt kell meghatározni, hogy hány darab 500 forintos kell az adott összeg kifizetéséhez. Tehát C=500 értékadásra van szükség, majd hívni kell a (2) modult. Ez kiszámítja a darabszámot (D) és a részösszeget (R). A (2) modul végrehajtása után ezeket az adatokat meg kell menteni, mert a következő címletszámítási eljárás végrehajtásakor ezek az értékek elvesznek, hiszen a következő számítás végén a D és R változó a 100 forintosok darabszámát és részösszegét tartalmazza.
Ezért kell elvégezni a
D1 = D (az 500 forintosok darabszáma),
R1 = R (az 500 forintosok részösszege)
értékadásokat.
Ezután át lehet térni a 100 forintosok darabszámának meghatározására. A C=100 értékadás után ismét hívni kell a (2) modult, majd a darabszámot és a részösszeget ki kell menteni.(4) Kiírás
A modul eljárás típusú. Bemeneti adatai közül a kifizetendő összeg (K1) az (1) modulból, a többi adat (címlet, darabszámok, részösszegek és a számított végösszeg) a (3) modulból származik.
A modul eredménye a kiírt táblázat. A modul műveletei a már ismert kiírási műveletek. Az egyes sorokat a specifikáció szerinti sorrendben kell kiírni.
4. A kódolás
(1) Az adatbevitel
A modult a IV. probléma BÉR programjának adatbeviteli moduljához hasonlóan kódolhatjuk. Az adatbevitelhez itt is az INPUT utasítást alkalmazzuk:10 REM * CIMLET *
20 REM ADATBEVITEL
30 PRINT "OSSZEG: ";
40 INPUT K1(2) A címletdarabszám
A szubrutinok kódolásához megismert szabályok értelmében a szubrutint a program végén helyezzük el, és a modult a RETURN utasítás zárja le. A kódban alkalmaztuk az INT (egész) függvényt is. A modul kódja a következő:1000 REM CIMLET DARABSZAM
1010 LET D=INT(K/C)
1020 LET R=D*C
1030 LET M=K-R
1040 LET K=M
1050 RETURN(3) A címletek számítása (vez.)
A címletek darabszámának kiszámításához a (2) modult kell hívni a GOSUB utasítással.50 REM CIMLETEK SZAMITASA (VEZ.)
60 LET K=K1
70 LET C=500: GOSUB 1000
80 LET D1=D: LET R1=R
90 LET C=100: GOSUB 1000
100 LET D2=D: LET R2=R
110 LET C=50: GOSUB 1000
120 LET D3=D: LET R3=R
130 LET C=20: GOSUB 1000
140 LET D4=D: LET R4=R
150 LET C=10: GOSUB 1000
160 LET D5=D: LET R5=R
170 LET C=5: GOSUB 1000
180 LET D6=D: LET R6=R
190 LET C=2: GOSUB 1000
200 LET D7=D: LET R7=R
210 LET C=1: GOSUB 1000
220 LET D8=D: LET R8=R(4) Kiírás
A háromoszlopos táblázat kiírását az eddig bemutatott PRINT lehetőségekkel is megoldhatjuk, szövegek (vagy adatok) és megfelelő számú szóközök egymás után helyezésével. Ezt azonban már ismerjük és tudjuk, hogy háromoszlopos kiírásnál a kódolást nagyon megnehezíti a karakterpozíciók kiszámolása.
Használjuk fel inkább a PRINT utasítás táblázatok kiírásánál hasznosítható lehetőségét. Ha a PRINT utasítás tárgyában levő változókat vagy szövegkonstansokat vesszővel választjuk el, akkor a fordító a vessző előtti adat (szám vagy összeg) kinyomtatására - implementációtól függően - 10-16 karakter hosszúságú oszlopokat tart fenn. Az oszlop elejére kerül az adat annyi pozícióban, ahányból áll, majd az oszlop végéig nincs nyomtatás, a következő adat az ez utáni pozíción kezdődik. Ha a vessző előtti adat hossza meghaladja az oszlopszélességet, akkor a fordító nem egy, hanem két oszlopot biztosít ennek az adatnak. Ha a vessző(k) előtt nem szerepel kiírni való adat, akkor a vesszők számának megfelelő számú oszlop üresen marad.
A modulban levő táblázat kiíratásához ezt a táblázatnyomtatási lehetőséget használtuk fel. A modul kódja:230 REM KIIRATAS
240 PRINT
250 PRINT "A KIFIZETENDO OSSZEG: ";K1;" FT"
260 PRINT
270 PRINT "CIMLETEK","DB","OSSZEG"
280 PRINT "500",D1,R1
290 PRINT "100",D2,R2
300 PRINT "50",D3,R3
310 PRINT "20",D4,R4
320 PRINT "10",D5,R5
330 PRINT "5",D6,R6
340 PRINT "2",D7,R7
350 PRINT "1",D8,R8
360 PRINT "OSSZESEN:",,R1+R2+R3+R4+R5+R6+R7+R8
370 STOPA Spectrum BASIC mindössze két oszlopot biztosít a képernyőm, ezért ott célszerűbb a TAB függvényt (ld. később) használni.
5. Az eredmény értékelése
Ha a programot kipróbáljuk, és helyesnek bizonyul, akkor használatba lehet venni. A felhasználó a kifizetés előtt elindítja a programot (RUN paranccsal), majd az összeg kérdésre begépeli a kifizetendő összeget, és ezután a program kiírja a táblázatot.
A táblázat utolsó sorában levő összeget a pénztáros leolvassa. Ha ez egyezik a begépelt összeggel, akkor a program helyesen működik. Ha az eredmény helyes, akkor a táblázat szerinti címleteket össze kell válogatni és az igénylőnek átadni. Ezzel a feladat befejeződött.
Végül példaként 9896,- Ft kifizetéséhez szükséges műveleteket mutatjuk be:
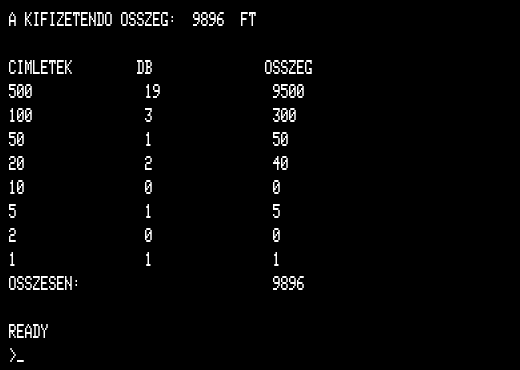
A programszerkezet kialakítása szubrutinokból
Az eddig bemutatott programoknál - a legutóbbi CÍMLET program kivételével - csak eljárás és adat típusú modulokat használtunk fel. A programok egyszerűsége ezt lehetővé tette. A program eljárás- és adatmoduljai lineáris szerkezetet alkottak, és a programot a modulok lineáris sorrendjében fel lehetett építeni. Ezért valójában nem is volt szükség vezérlőmodulra, amely az egyes modulok végrehajtásának sorrendjét vezérelte volna. Bonyolult szerkezetű programoknál azonban a vezérlőmodul használata szinte elkerülhetetlen. A modulok végére általában nagyon bonyolult döntési eljárásokat kellene elhelyezni, hogy a soron következő modult kiválasszák. Vezérlőmodul használatakor a döntési eljárást csak egyszer kell felépíteni a vezérlőmodulban, és ennek alapján a vezérlőmodul a megfelelő sorrendben hívja a többi modult.
Hogyan valósítható meg a vezérlőmodul által vezérelt programszerkezet? A vezérlőmodul a modulszerkezet csúcsán helyezkedik el, amint ezt már a korábbi modulszerkezeti ábrákon is láthattuk. A vezérlőmodul az adat- és eljárásmodulok végrehajtásának sorrendjét vezérli, ezért eredményt általában nem szolgáltat, és így a felhasználó a létét nem érzékeli.
Tegyük fel, hogy először az A, majd a B modult kell végrehajtani. A vezérlőmodulnak tehát ezt a sorrendet kell vezérelnie. Vezérlőszerkezet többféle módon valósítható meg:
Az első módszert nem érdemes használni, mivel a másodikkal egyenértékű, de ez utóbbi egyszerűbb.
Tekintsük a második esetet, és nézzünk erre egy példát. A vezérlőmodul GOSUB utasításokból fog állni, és többszörösen hívott modulok esetén a modulok paraméterezését, illetve a modulok eredményeinek kimentését is tartalmazza:
100 REM * VEZERLOMODUL *
110 (paraméterbeállítás)
120 GOSUB 1000
130 (paraméterkimentés)
140 (paraméterbeállítás)
150 GOSUB 2000
160 (paraméterkimentés)
170 GO TO 3000
1000 REM * A MODUL *
...
1500 RETURN
2000 REM * A MODUL *
...
2500 RETURN
3000 END
A vezérlőmodul végén a program utolsó sorában levő befejező (END) utasításra kell ugrani. Az adat- és eljárásmodulok - természetesen - változatlanok, akár van vezérlőmodul, akár nincs (kivéve a RETURN utasítást a modul végén).
A vezérlőmodul létrehozása kényelmetlenséget is okoz. Egyrészt meg kell tervezni, és kódolni kell, ami többletmunkát jelent. Ez a többletmunka azonban különösen bonyolultabb programoknál megtérül a vezérlés egyszerűbb irányítása következtében. Másrészt nehezebb a vezérlőmodulos programot olvasni, mivel hol az adat- és eljárásmodulokat, hol a főmodult kell olvasni.
Tiszta vezérlőmodulos szerkezetet ritkán alkalmaznak. A vezérlőmodult és a csak egyszer használt modulokat gyakran lineáris szerkezetbe vonják össze, és csak a többször használt modulok végrehajtását teszik vezéreltté (mint a korábbi programokban).
3.5. Ciklikus tevékenységek végrehajtása
A számítógépek egyik legfontosabb alkalmazási területe műveletek ismételt elvégzése változó adattal. Ilyenkor a műveletet vagy műveletsort nem kell annyiszor kódolni a programban, ahányszor végre kell hajtani, hanem csak egyszer, és végrehajtását a kívánt számban kell ismételni. A programban ismételten végrehajtott részt ciklusnak nevezzük.
Vegyük a következő példát. Egy utasszállító gép utasai bőröndjeiket személy poggyászként feladják. Tegyük fel, hogy a bőröndök össztömege nem haladhatja meg az 1000kg-ot, és a tömegtöbbletet teherszállító repülő szállítja el. A jegykezelőnek az a feladata, hogy figyelje az össztömeget, és ha az túllépi az 1000 kg-ot, akkor több bőröndöt ne vegyen fel, hanem a teherszállító gépre irányítsa át. Ezt legegyszerűbben úgy tudja megoldani, hogy a feladott bőröndök tömegét minden jegykezelés után összegezi. Ha az össztömeg nagyobb, mint 1000 kg, akkor a további bőröndöket a teherszállító gépre irányítja.
Milyen lépésekből áll ez a művelet?
Ebben a példában a tömegösszegezés a ciklikus tevékenység. A ciklikus tevékenységet akkor kell befejezni, amikor az össztömeg nagyobb, mint 1000 kg. A ciklusban az össztömeg a ciklusváltozó, amelynek értéke meghatározza, hogy a ciklust meddig kell folytatni. A ciklus kezdetén előkészítő tevékenységet is kell végezni: az össztömeget 0-ra kell állítani a beszállás kezdetén (új ívet kell elővenni, vagy a kalkulátort nullázni kell).
Vázoljuk fel a ciklus általános szerkezetét! Egy ciklus három részből áll:
A ciklusszerkezetet kétféle algoritmusban valósíthatjuk meg, attól függően, hogy hol helyezkedik el a ciklusfeltétel-vizsgálat:
Az elöl tesztelő (DO-WHILE) típusú ciklusszerkezet: Mint a nevében is benne van, az elöl tesztelő ciklusban a feltételvizsgálat a ciklusmag végrehajtása előtt történik meg, és a ciklusmagot mindaddig végre kell hajtani, amíg a végrehajtási feltétel fennáll. Ha a feltétel már nem teljesül, akkor a ciklus befejeződik, és a vezérlés a ciklus után következő utasításra kerül.
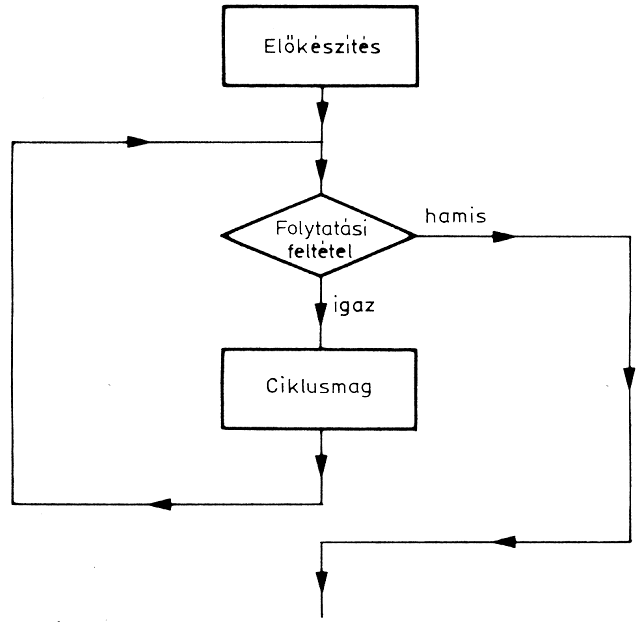
A hátul tesztelő (DO-UNTIL) típusú ciklusszerkezet: Ebben az esetben a feltételvizsgálat a ciklusmag után megy végbe, és azt kell vizsgálni, hogy a befejezés feltétele fennáll-e. Ha ez még nem áll fenn, akkor a ciklust folytatni kell. Ha a befejezés feltétele fennáll, akkor a ciklus befejeződött.
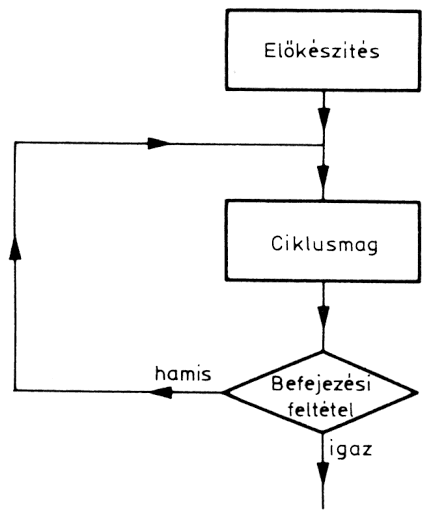
A két szerkezetet összehasonlítva látható, hogy a feltételvizsgálat helye és a vizsgálat jellege eltér egymástól. Az elöl tesztelő (DO-WHILE) szerkezetben a folytatás feltételét kell vizsgálni (példánkban: ha az össztömeg kisebb, mint 1000 kg, akkor a ciklust folytatni kell), a hátul tesztelő (DO-UNTIL) szerkezetben a befejezés feltételét kell vizsgálni (példánkban: ha az össztömeg nagyobb 1000 kg-nál, akkor a ciklust be kell fejezni).
Többnyire bármelyik szerkezetet lehet használni. Vannak azonban olyan feladatok, ahol vagy az egyiket, vagy a másikat lehet használni (ezért is van kétféle szerkezet). Ha a ciklus befejezése valamilyen speciális adat beérkezéséhez kötődik, akkor csak DO-WHILE (elöl tesztelő) szerkezetet lehet használni. Ez az ún. végfeltétel adat. Ha beérkezik, akkor ezt már nem kell feldolgozni, és a ciklusból ki kell lépni.
A ciklikus tevékenységek kódolásához is célszerű a ciklus szerkezetét kifejező kódolási formát alkalmazni. Az elöl tesztelő ciklusszerkezet kódolása:
m REM CIKLUSKEZDET
IF folytatási feltétel THEN n
GO TO p
n REM CIKLUSMAG
...
GO TO m
p REM CIKLUSVEG
A ciklus kezdetét és végét megjegyzéssel is kiemeljük. A ciklus eleién helyezkedik el a folytatási feltétel vizsgálata. Ha a feltétel teljesül, akkor a ciklusmag hajtódik végre. (Vegyük észre, hogy a CIKLUSMAG az IF utasítás THEN-ága!). Ha nem teljesül, akkor a vezérlés a ciklus végére kerül. A ciklusmag után egy GO TO utasítással visszaadjuk a vezérlést a ciklus kezdetére.
A hátul tesztelő ciklusszerkezet kódja:
REM CIKLUSKEZDET
n REM CIKLUSMAG
...
IF befejezési feltétel THEN GO TO p
GO TO n
p REM CIKLUSVEG
Az elv hasonló a DO-WHILE szerkezet kódjához. A befejezési feltétel IF utasításának THEN-ágába most nem a folytatást, hanem a befejezést kell elhelyezni.
A bemutatott két szerkezeten kívül a BASIC-ben a FOR és a NEXT utasításpárral is lehet ciklust kialakítani. Ezt a ciklusképzési eljárást külön meg kell vizsgálni.
A FOR, NEXT utasításpár
Ha a ciklusmagban van olyan változó, amelynek értéke minden ciklusmag végrehajtása során egyenletesen (lineárisan) változik (nő vagy csökken), és értéke alapján a ciklus befejezése eldönthető, akkor a ciklus kódolásához a FOR, NEXT utasításpár felhasználható. Az említett változó pedig a ciklusváltozó lesz. A FOR, NEXT utasításpárral felépített ciklusban azt kell meghatározni, hogy a ciklusváltozó milyen kezdőértékétől milyen lépésenként haladva, milyen végfeltétel-értékig kell a ciklust végrehajtani. A program a ciklusmagot mindaddig végrehajtja, amíg a ciklusváltozó értéke meg nem haladja a záróértékét. A ciklusváltozó értékének módosítását a program minden ciklusmag végrehajtásakor automatikusan elvégzi. A programozónak nem kell vizsgálati utasítást kódolnia, mert az ellenőrzést az utasítás automatikusan elvégzi, és ha a folytatási feltétel nem teljesül, a gép a ciklust befejezi.
A FOR utasítás vezeti be a ciklust. Definiálja a ciklusváltozót, valamint ennek kezdő- és záróértékét. A FOR utasítás formája:
x FOR ciklusváltozó=kifejezés1 TO kifejezés2 [STEP kifejezés3]
ahol
A változtatás lehet növelő jellegű, + előjellel (ezt nem kell kiírni) vagy csökkentő jellegű, - előjellel:
20 FOR S=1 TO 10 STEP 0.5
Az utasítás hatására a FOR után következő ciklusmag S = 0.5-es lépésekkel mindaddig vég-rehajtódik, amíg túl nem lépi a 10-et. S = 10.5 esetén a ciklusmag már nem hajtódik végre, és a ciklus befejeződik.
A változtatás negatív irányú is lehet:
40 FOR S=8 TO -8 STEP -1
Ebben az esetben az S értéke minden ciklusmag végrehajtásakor 8-ról csökken egyesével -8-ig. Az utolsó ciklusmag S = -8 értéknél hajtódik végre, majd a ciklus befejeződik. A ciklusmagot a
x NEXT ciklusváltozó
utasítás zárja le. Hatására a program visszaadja a vezérlést a FOR utasításnak, amely kiszámítja a ciklusváltozó új értékét (ha még szükséges). A ciklusmag utolsó végrehajtása után a vezérlés a NEXT utasítás utáni utasításra kerül át.
A FOR, NEXT utasításokból felépített ciklus befejezésekor a ciklusváltozó értéke azt az értéket veszi fel, amellyel az utolsó ciklusmag végrehajtódott.
Minden FOR utasításhoz egy és csakis egy NEXT utasításnak kell tartoznia.
VI. probléma
Készítsünk egy olyan programot, amely tetszés szerinti N szám faktoriálisát számítja ki, kivéve, ha N > 10^38, vagyis meghaladja a BASIC-ben megadható legnagyobb számértéket. Az N szám értékét a felhasználó adja meg.
Az eredményt az alábbi formában úja ki a program:
FAKTORIÁLISSZÁMÍTÁS
N!=X
1. A feladat elemzése
Mint ismeretes, egy adott N egész szám faktoriálisa az 1,2,..., N-1, N számok szorzata. Mivel a faktoriális csak egész számok esetében értelmezhető, törtrészt nem lehet elfogadni. Ekkor hibaüzenetet kell kiírni, és fel kell szólítani a felhasználót, hogy csak egész számot adjon meg.
A faktoriális csak nem negatív számokra van értelmezve, ezért negatív szám megadása sem engedélyezhető. Ekkor azt kell kérni a felhasználótól, hogy csak nem negatív számot adjon meg.
A feladat szerint bármely nem negatív egész szám faktoriálisát lehet kérni, ezért kiszámításához olyan módszer szükséges, amely az egymás után következő természetes számokat automatikusan előállítja, és ezek szorzatát képezi, majd ezt leállítja akkor, ha a kért faktoriális létrejött. A számítás után a kapott eredményt ki kell nyomtatni.
A programban szükség van egy adatbeviteli modulra, amely a kívánt N értéket beolvassa és az adatellenőrzést elvégzi. Ezután a faktoriális számításához kell egy modul. Végül a kiíráshoz is szükséges egy önálló modul.
2. A program tervezése
A program 3 modulból áll. Az egyszerű vezérlési szerkezet miatt vezérlőmodulra nincs szükség. Az egyes modulok funkciója elég zárt ahhoz, hogy további finomításra ne legyen szükség. Az egyes modulok között adatkapcsolat áll fenn.
Az adatbeviteli modul funkciója az N beolvasása és az adat ellenőrzése. Törtszám és negatív szám begépelésekor újabb adatot kell kérni. Az ellenőrzésnél azonban még egy lényeges dolgot kell tisztázni. Ha ugyanis egy adatot több szempontból kell ellenőrizni, akkor felmerül a kérdés, hogy a program hogyan végezze ezt.
A program az ellenőrzéseket szekvenciálisán végzi, azaz egyszerre csak egy jellemzőt tud vizsgálni, és megállapítja, hogy ebből a szempontból hibás-e vagy sem, majd áttér a következő ellenőrzésre. A kérdés az, hogy ilyen esetben, amikor a hibás adat újra begépeléssel könnyen javítható, végezze-e el a program mindkét (egész és nem negatív) ellenőrzést, írja-e ki (esetleg) mindkét hibatípust, és ezután kérjen újra begépelést, vagy már az első hibánál kéRjen új adatot, és a második szempontú ellenőrzést már ne végezze el.
Az első megoldás a korrektebb, mert teljes tájékoztatást ad a hibákról, míg a második megoldás többszörös hiba esetén is csak egyetlen hibát mutat ki, viszont a program sokkal egyszerűbb. E megoldás hátránya az is, hogy többszörös hibánál az adatbevitelt annyiszor kell megismételni, ahányféle hiba van az adatban. De ez a gyors futás miatt nem okoz problémát. Feladatunkhoz az utóbbi megoldást alkalmazzuk.
A faktoriálisszámítás modul kiszámítja az N faktoriálisát, és a kiírás modul a végeredményt a kívánt formában kiírja.
3. A modulok tervezése
(1) Az adatbevitel
A modul adat típusú, bár az ellenőrzések révén eljárást is hajt végre. Bemeneti adata a terminálról beolvasott N adat, kimeneti adata pedig egy helyes és ellenőrzött N szám.
Az adatbevitelt a már ismert formában kell megvalósítani. Ki kell írni, hogy milyen adatot kell megadni, majd az ellenőrzéseket kell végrehajtani. Először az előjelet kell ellenőrizni, mivel ez jelent nagyobb gondot (bár tulajdonképpen esetünkben csaknem egyformán súlyos a két hiba). Ezt N<0 vizsgálattal lehet elvégezni.
Az ellenőrzés tehát egy vizsgálattal kezdődik. Hiba esetén ki kell írni a hibaüzenetet, hogy csak nem negatív szám adható meg, és fel kell szólítani a felhasználót, hogy ilyen értéket gépeljen be. Ezután vissza kell térni az adatbevitelre, majd ismét ellenőrzés következik, egészen addig, amíg a begépelt adat helyes nem lesz.
Második lépésként azt kell ellenőrizni, hogy a megadott szám egész-e. Egy N számról úgy tudja a program eldönteni, hogy egész-e vagy sem, hogy azN-INT(N)
különbséget képezzük. Ha
N-INT(N)=0,
akkor N egész szám, ellenkező esetben nem. A vizsgálat után hasonló módon kell a hibakezelést elvégezni, de ekkor arra kell felszólítani a felhasználót, hogy egész számot adjon meg. A hibakezelés után vissza kell térni az adatbevitelre. Ellenkező esetben a (2) faktoriálisszámítás modult kell végrehajtani.
(2) Faktoriálisszámítás
A modul eljárás típusú. Bemeneti adata az N, kimenete az N faktoriálisa.
A feladat specifikációja és az elemzés szerint olyan algoritmusra van szükség, amely a faktoriálisszámítást lépésenként végzi el, és bármelyik ismétlési lépés után leállítható, annak megfelelően, hogy melyik szám faktoriálisát kell kiszámítani. Ezt nyilvánvalóan ciklussal lehet megvalósítani. Mivel bármely szám faktoriálisát kérheti a felhasználó, a ciklusmagban egy-egy szám faktoriálisának kiszámítását kell elvégezni. Méghozzá nyilvánvalóan minden ciklusműveletnél az előzőnél eggyel nagyobb szám faktoriálisát érdemes kiszámítani:FS=FS-1*S
ahol
FS=S!
FS-1=(S-1)!A következő lépésben pedig (S+1)! kiszámítása következhet. Tehát a faktoriálisszámítás lépésenként történik, rekurzív módon, az előző ciklus eredményétől kiindulva.
Ha a ciklusváltozónak S-et választjuk, akkor az értékét 1-től N-ig kell növelni egyesével, így S értéke minden egyes ciklusmag végrehajtása után eggyel nagyobb természetes szám lesz, és ha eléri N-et, a számítást le kell állítani.
Az ismertetett algoritmus a 0! értékének számítását nem tartalmazza, hiszen ezt nem is számítás, hanem definíció határozza meg. A0! = 1! = 1
egyenlőségek felhasználásával az algoritmus mégis megadható úgy, hogy a 0! értékét is helyesen adja.
A ciklus elvi tervezése után tervezzük meg a teljes ciklusszerkezetet.
Az előkészítés folyamán be kell állítani a számítás indulóértékeit. Egy sorszám fogja mindig megmutatni, hogy melyik szám faktoriálisát számítja ki éppen a program. Jelöljük ezt S-sel. Mivel a faktoriálisszámítás 1-től indul, induláskor az értékadás: S=1.
A faktoriálisszámítás elve, hogy minden lépésben az előző (S-1) értékhez tartozó faktoriálist kell megszorozni az S aktuális értékével, ezért a faktoriálisszámításhoz is kell egy indulóérték, méghozzá F0=1, mivel a számítás 1-től indul.
A ciklusmagban történik a sorozatos faktoriálisszámítás: F1=F0*S, ahol F0=(S-1)!
S = az a szám, amelynek faktoriálisát az aktuális lépésben ki kell számítani.
A ciklusmagban - a művelet végrehajtása után - a ciklusváltozó értékét (S) eggyel növelni kell: S=S+1 értékadással, hogy a következő faktoriálisszámítást el lehessen végezni.
A következő lépésben az F1 értéke lesz az előző faktoriális (F0), ezért a ciklusmag végén a "régi" értéket hordozó F0-nak F1 értékét kell felvennie: F0=F1. Így most már F0 = S! és F0 kiinduló értéke lehet az (S+1)! kiszámításának. Ezzel persze F1 értéke még nem változott meg egyazon cikluson belül, tehát például kiíráshoz felhasználható.
Minden ciklusmag végrehajtása után ellenőrizni kell, hogy az S=N fennáll-e. Ha igen, akkor a modul befejeződött, és a (3) kiírás modul következhet. Ha nem, akkor folytatni kell a számítást.
A (2) modul algoritmusát három változatban készítjük el:
- a DO-WHILE (elöl tesztelő),
- a DO-UNTIL (hátul tesztelő) és
- a FOR, NEXT szerkezetek felhasználásával.
a) A modul algoritmusa DOWHILE (elöl tesztelő) szerkezettel
A vizsgálat a ciklusmag előtt helyezkedik el. Olyan feltételt kell vizsgálni, amelynek teljesülése esetén a ciklikus számítást folytatni kell. Erre az S<N feltétel alkalmas. Így a ciklusmag mindaddig végrehajtódik, míg S túl nem lépi N-et.b) A modul algoritmusa DO-UNTIL (hátul tesztelő) szerkezetben
Ebben a szerkezetben olyan ciklusfeltételt kell megfogalmazni, amelynek teljesülése esetén a ciklus befejeződik. Erre az S>N feltétel alkalmas. Ha ugyanis N! már kiszámítódott, akkor az S=S+1 értékadás miatt S>N teljesül, és a ciklus befejeződhet. Ha a feltétel nem teljesül, akkor a ciklus folytatódik.c) A modul algoritmusa FOR, NEXT szerkezetben
Valamennyi közül a legegyszerűbb, mivel nincs benne feltételvizsgálat. A program ugyanis ezt automatikusan elvégzi.(3) Kiírás
A modul eljárás típusú. Egyik bemeneti adata a (2) faktoriálisszámítás modul eredményadata (N!), a másik pedig az az N, amely az (1) adatbevitel modulból származik. A modul eredményadata a kiírás. A modul csupán kiírási műveleteket tartalmaz.
4. Kódolás
(1) Adatbevitel
Az adatbevitel modul a kezdőmodul, tehát a programnév is itt kap helyet.10 REM * FAKTOR *
20 PRINT "MELYIK SZAM FAKTORIALISAT KERI? ";
30 INPUT NEzután kódoljuk a bemeneti adat ellenőrzését is:
50 IF N<0 THEN PRINT "A FAKTORIALIS CSAK NEM NEGATIV SZAMRA ERTELMEZHETO'": PRINT: GO TO 20
60 IF N-INT(N)<>0 THEN PRINT"CSAK EGESZ SZAM FAKTORIALISA LETEZIK!": PRINT: GO TO 20(2) Faktoriálisszámítás
A modul kódolását a modultervekhez hasonlóan 3 változatban készítettük el.a) A DO-WHILE (elöl tesztelő) szerkezet kódja
A kódolásban a ciklus szerkezete jól felismerhető.70 REM FAKTORIALIS SZAMITAS
80 LET S=1
90 LET F0=1: LET F1=1
100 REM CIKLUS KEZDET
110 IF S<=N THEN GO TO 130
120 GO TO 180
130 REM CIKLUSMAG
140 LET F1=F0*S
150 LET S=S+1
160 LET F0=F1
170 GO TO 110
180 REM CIKLUSVEGb) A DO-UNTIL (hátul tesztelő) szerkezet kódja
A fentiekhez hasonlóan a DO-UNTIL szerkezetű kód elkészíthető:70 REM FAKTORIALIS SZAMITAS
80 LET S=1
90 LET F0=1: LET F1=1
100 REM CIKLUS KEZDET
110 REM CIKLUSMAG
140 LET F1=F0*S
150 LET S=S+1
160 LET F0=F1
170 IF S>N THEN GO TO 190
180 GO TO 110
190 REM CIKLUSVEGc) A FOR, NEXT szerkezet kódolása
A szerkezet az alábbi kódot eredményezi:70 REM FAKTORIALIS SZAMITAS
80 LET F0=1: LET F1=1
90 FOR S=1 TO N
100 LET F1=F0*S
110 LET F0=F1
120 NEXT SHa a három kódolást összehasonlítjuk, akkor láthatjuk, hogy a harmadik kódolási forma a legrövidebb és a legáttekinthetőbb. Ezután a DO-UNTIL szerkezet következik, a leghosszabb a DO-WHILE szerkezetű modul. Ebben az esetben tehát a FOR, NEXT szerkezet használata a legelőnyösebb, mivel a sorok száma ekkor a legkevesebb.
(3) Kiírás
A modul kódja:200 REM KIIRAS
210 PRINT: PRINT "FAKTORIALIS SZAMITAS"
220 PRINT N;"! = ";F1
5. Az eredmények értékelése
A programot kipróbálása után használatba vehetjük. Elindítása után megadjuk azt a számot, amelynek faktoriálisát keressük, majd a program elvégzi a számítást, és az eredményt kiírja:
FAKTORIALIS SZAMITAS
6! = 720
Ha nem egész számot vagy negatív számot adunk meg, akkor a program hibát jelez, és ezt teszi mindaddig, amíg nem kap helyes adatot.
Ha a kért szám faktoriálisára fennáll nagyobb mint 10^38, akkor a fordító hibaüzenetet ad ki, mert a túl nagy számot nem tudja kezelni.
A II. Probléma kiegészítése
A II. probléma leírása szerint a T=0 időpontban 100 millió forintot fektetünk be egy beruházásba, amelynek bevétele évente 40 millió Ft, és az üzemeltetés költsége 20 millió forint. Most arra keresünk választ, hogy hány év alatt térül meg a beruházás, illetve hány év múlva lehet a beruházott összeg kétszeresét megkeresni.
A számítás eredményeit az alábbi formában kell kiírni:
BERUHÁZÁSGAZDASÁGOSSÁGI SZÁMÍTÁS
A BERUHÁZÁS ÖSSZEGE
ÉVES JÖVEDELEM
ÉVES ÜZEMELTETÉSI KÖLTSÉG
KAMATLÁB
40 MFT
20 MFT
12%
A BERUHÁZÁS ÖSSZEGE MEGTÉRÜL
MEGKÉTSZEREZŐDIK
x1 ÉV MULVA
x2 ÉV MULVA
A következőkben csak a probléma új részére keressük a megoldást. A II. probléma programjában már megoldott lépéseket itt nem tárgyaljuk.
1. A probléma elemzése
A feladat analitikus megoldása az lenne, ha a
kifejezést N-re megoldanánk H=B és H=2*B behelyettesítéssel. Nehézséget jelent azonban, hogy a kamat csak teljes évre vonatkozik, ezért csak egész N-ek fogadhatók el a megoldásban. Ezzel a megszorítással viszont nem valószínű, hogy a feladat megoldható, mivel nem biztos, hogy a H=B vagy a H=2*B hozam éppen egész értékű N-nél áll elő. Ezért így a feladat nem oldható meg. Inkább egy közelítő megoldást alkalmazunk.
A feltételt "enyhíthetjük" azzal, hogy nem egyenlőséget figyelünk, hanem intervallumot, vagyis N-et különböző egész értékekkel helyettesítjük, és így figyeljük, hogy H beleesik-e a kijelölt intervallumba. Ha az intervallum túl kicsi, akkor lehet, hogy ismét nem kapunk megoldást. Ha az intervallum túl széles, akkor lehet, hogy a számítást túl korán abbahagyjuk. Legyen például az intervallum +20% szélességű. így a megoldásokat elfogadjuk, ha
0.8B <= 1.2B
illetve
1.6B <= 2.4B
fennáll. Ha van olyan megoldás, amely egész értékű N-nél kismértékben túllépi a 0.8B-t, akkor a számolás befejeződik.
Ettől függetlenül még lehet egy másik, az előzőnél nagyobb N (ha N értékét a közelítő számítás folyamán növeljük), amely jobb megoldást ad, vagyis ezzel az N-nel számított H közelebb van az egyhez, mint az előzővel számított H. De ezt az új N-et már nem keressük, mivel már találtunk egy "jót". Tehát ez a módszer sem kielégítő.
Ehelyett egy olyan megoldást készítünk, amely az egyes N értékeket és a hozzájuk tartozó H hozamokat táblázatos formában kiírja minden N-re, és a felhasználó kiválaszthatja a megfelelő eredményt. Ezzel az eredeti kiírás képét is megváltoztatjuk.
A kérdés csupán az, hogy a számítássorozatot milyen N-től milyen N-ig végezzük el. A HOZAM program szerint a megtérülés valahol 5 és 10 év között várható. Nincs adatunk arra vonatkozóan, hogy a tőke mennyi idő múlva duplázódik meg. Próbáljuk meg N=20-ig végezni a számítást. Így első közelítésben az 5 <= N <= 20 intervallumban fog változni.
Olyan program szükséges, amely
N = [5...20]
értékek esetében kiszámítja a H értéket, és mind az N, mind a H értékeket kiírja az alábbi formában:
ÉVEK SZÁMA HOZAM (MFT) x x.x
sorozatos számítást kell végrehajtani, amely a
kifejezés értékét a megadott N-ek esetében szolgáltatja.
A feladat megoldásához szükségesek a HOZAM program (1) bemeneti adatok és (3.1) alapadatok kiírása moduljai. Ezek után egy olyan modul kell, amely a különböző N értékekhez kiszámítja H értékét, és ezeket ki is írja. Az ilyen sorozatos számítást, kiírást célszerű egy modulban összefogni, a szétválasztás sok adatátadást igényelne a modulok között.
2. A program tervezése
A program elkészítéséhez az (1) bemeneti adatok és a (3.1) alapadatok kiírása modul a HOZAM programból átvehető, csupán a (4) hozamszámítás és kiírás modult kell itt megtervezni. Ez a modul a táblázatszámítást és -kiírást fogja ciklusban elvégezni. A modul további bontása szükségtelen, mivel a funkciók száma kevés. Az új modul az (1) modullal van adatkapcsolatban. A programnak a MEGTER (megtérülés számítása) nevet adjuk.
3. A modulok tervezése
(1) Bemeneti adatok
A modul változatlan, csupán az N értékadás felesleges, mivel ezt a (3) modulba érdemes áthelyezni a feladat módosulásának megfelelően.(2) A lapadatok kiírása
A modul teljes egészében átvehető a HOZAM programból, ahol (3.1) néven szerepel.(3) Hozamszám és kiírás
A modul eljárás típusú. Bemeneti adatai az (1) modulból származnak, kimenete a kiírt táblázat.
A modul kezdetén a táblázat fejlécét kell kiírni, mivel erre csak egyszer van szükség. Ezután a számításokat és a kiírásokat ciklikusan érdemes elvégezni.
Az előkészítés során be kell állítani az adatok indulóértékét. Itt csupán az N=5 értékadás szükséges.
A ciklusmagba két művelet kerül:
- az első kifejezés értékének kiszámítása,
- az aktuális N és H értékek kinyomtatása.
A műveletsorozatot akkor kell befejezni, ha az N=20 feltétel teljesül, és erre az évszámra a számítást elvégeztük. Így tehát az N a ciklusváltozó is.
4. Kódolás
(1) Bemeneti adatok
A modul a modultervezésnek megfelelő módosítással átvehető:10 REM * MEGTER *
20 REM BEMENETI ADATOK
30 LET B=100
40 LET J=40
50 LET U=20
60 LET K=0.12(2) Alapadatok kiírása
A modul kódja:70 REM ALAPADATOK KIIRASA
80 PRINT "BERUHAZAS GAZDASAGOSSAGI SZAMITAS"
90 PRINT
100 PRINT "A BERUHAZAS OSSZEGE: ";B;" MFT"
110 PRINT "EVES JOVEDELEM: ";J;" MFT"
120 PRINT "EVES UZEMELTETESI KOLTSEG: ";U;" MFT"
130 PRINT "KAMATLAB: ";100*K;"%"
140 PRINT(3) Hozamszámítás és kiírás
A fejléc kiírása a már ismert módon elvégezhető. A két oszlop elválasztását a programra bízzuk úgy, hogy az oszlopok adatait a PRINT utasításban vesszővel választjuk el.
A ciklust a FOR, NEXT utasításpárral kódolhatjuk, mivel a ciklusváltozó az egyes lépések során egyenletesen változtatja értékét.150 REM HOZAMSZAMITAS ES KIIRAS
160 PRINT "EVEK SZAMA","HOZAM (MFT)"
170 FOR N=5 TO 20
180 LET H=(J-U)*((1+K)^N-1)/(K*(1+K)^N)
190 PRINT N,H
200 NEXT N
210 PRINT
5. Az eredmény értékelése
A program kipróbálása és esetleges javítása esetén kapott eredményekből látható, hogy legalább 9 évig kell üzemeltetni a beruházást, hogy megtérüljön. Ugyanakkor még 20 év után is csak másfélszeres hozamra lehet számítani.
A tőkekétszerezéshez szükséges időt az alkalmazott megoldásban viszonylag nehezen kapjuk meg. Fel kell venni egy olyan elég nagy intervallumot (N értéket), amelyen belül a hozam biztosan eléri a befektetés kétszeresét. Így viszont esetleg 100 soros táblázatot ír a program, ami túl nagy ahhoz, hogy könnyen lehessen kezelni. Ehelyett próbálkozzunk először durva kereséssel, azaz csak minden 5. évre számíttassuk ki a hozamot, és az eredmények alapján keressük meg, hogy melyik 5 éves intervallumban éri el a hozam a tőke kétszeresét, majd a programot módosítsuk úgy, hogy a megadott intervallumon belül az évenkénti hozamokat úja ki. A durva kereséshez a 170. számú sort kell módosítani:
170 FOR N=5 TO 100 STEP 5
Látható, hogy a hozam az 50. év után szinte alig változik. Mi ennek a magyarázata? Vizsgáljuk meg a hozam számítására alkalmazott kifejezést:
Kis átrendezéssel a
kifejezést kapjuk. A jobb oldal jobb oldali törtje N növelésével 1-hez tart, mivel a -1 elhanyagolhatóvá válik. Így végül is nagy N-eknél a hozam a
H=(J-U)/K
kifejezéssel közelíthető. A feladatban használt számértékeket behelyettesítve a H maximuma:
H=(40-20)/0.12 = 166.6
Tehát a tőkekétszerezés - az adott értékekkel - elvileg is lehetetlen. Ezt a számítógépes eredmények is alátámasztják.
Változók abszolút értékének meghatározása
Vannak olyan feladatok, amelyekben valamely változó abszolút értékét kell meghatározni. Az ilyen változókat kifejezésekben két függőleges vonal között íjuk le, és tudjuk, hogy értéke sohasem negatív. A BASIC programozási nyelvben egy változó vagy egy kifejezés abszolút értékét az
ABS(kifejezés)
függvény állítja elő. Hatására a fordító kiszámítja a kifejezés értékét, és ha negatív, akkor előjelét pozitívra változtatja. Például a
100 LET X=ABS(A-B)
esetében az X sohasem lesz negatív A és B értékétől függetlenül.
3.6. könyvtári és felhasználói függvények használata
Az öt aritmetikai műveletijei felhasználásával (és konstansok, illetve változók, valamint zárójelek igénybevételével) lehet aritmetikai kifejezéseket létrehozni. A törtkitevős hatványozás szabályának alkalmazása lehetővé teszi a gyökvonást is. Közismert, hogy vannak olyan függvé-nyek, amelyek ezekből az alapműveletekből nem építhetők fel. Ilyenek a logaritmus, a trigonometrikus függvények vagy a véletlenszám-generálás, hogy csak néhányat említsünk.
Hogy a felhasználó ilyen függvényeket is tudjon használni, a BASIC-be ezek könyvtári függvényként be vannak építve. BASIC-beli nevükkel lehet őket hívni, és a függvénynév után zárójelben kell megadni a független változó értékét:
függvénynév(kifejezés)
A függvény értéke a kifejezés által meghatározott pontbeli érték, például:
200 LET A=COS(3.14/2)
Példánkban a függvényérték A=0 (ha a PI értékét kellő pontossággal adjuk meg).
A BASIC-ben levő függvények egy része matematikai értelemben is függvény:
| ATN(kifejezés) | a kifejezés arctg-ét számítja ki; |
| COS(kifejezés) | a kifejezés cosinusát számítja ki (ívmértékben); |
| SIN(kifejezés) | a kifejezés sinusát számítja ki (ívmértékben); |
| EXP(kifejezés) | az e (2.71828) kifejezés szerinti hatványát számítja ki; |
| LOG(kifejezés) | a kifejezés természetes (2 alapú) logaritmusát számítja ki (Spectrum BASIC-ben: LN); |
| RND | 0 és 1 közötti egyenletes eloszlású véletlenszámot generál. Több BASIC implementációban formális paramétert is kell híváskor adni: RND(0) |
| INT(kifejezés) | a kifejezés értékénél kisebb legnagyobb egész számot adja meg; |
| SGN(kifejezés) | a kifejezés előjelének megfelelően vagy 1-et (a kifejezés pozitív), vagy -1-et (a kifejezés negatív), vagy 0-t (a kifejezés zérus) ad; |
| SQR(kifejezés) | a kifejezés négyzetgyökét számítja ki; |
| ABS(kifejezés) | a kifejezés abszolút értékét adja meg; |
| TAB(kifejezés) | a kurzort a kifejezés értéke által meghatározott pozícióra állítja (csak PRINT utasításban használható); |
| LEN(karaktersorozat) | a karaktersorozat hosszát adja meg karakterszámban. |
A második csoportba olyan függvények tartoznak, amelyek lényegében nem is függvények - csupán függvény formában használatosak -, és a felhasználónak nyújtanak valamilyen külön szolgáltatást. A legtöbb BASIC-ben egy ilyen függvény van (de még az sem mindegyikben):
| PI | konstans, a PI = 3.14592... értékét tartalmazza, |
A fentieken kívül a felhasználó is definiálhat függvényeket az 5 alapműveletből és a BASIC könyvtári függvényeiből. Ezek a felhasználói függvények. A felhasználói függvényeket használatuk előtt definiálni kell a programban az alábbi utasítással:
x DEF FN betű(kif1 [,kif2, kif3, kif4, kif5])=kifejezés
ahol
| DEF | a függvénydefiniáló utasítás kulcsszava, |
| FNbetű | a felhasználói függvény neve, amelyben a betű azonosítja a függvényt. |
| kif1 ... kif2 | legfeljebb egy változót tartalmazó, a BASIC-ben megengedett kifejezések. Ezek tartalmazzák a függvény független változóit. |
| kifejezés | azokat a műveleteket tartalmazza, amelyek segítségével a függvény értékét ki lehet számítani a független változókból. A kifejezés magában foglalja a független változókat vagy egy részüket. |
Tegyük fel például, hogy a felhasználó az
y=xe^-x
függvény értékét egy programban többször ki akarja számítani. Ezt elvégezheti közvetlenül is az
500 LET Z=X*EXP(-X)
alakú utasítással. Minden kiszámítási helyen az X helyére a megfelelő konstanst kell beírni. Például:
1200 LET Z=1.75*EXP(-1.75)
vagy ha X-hez előzőleg hozzárendeltük a megfelelő értéket, akkor az eredeti utasítást felhasználhatjuk.
Egyszerűbb azonban, ha a függvényt FN A jelű felhasználói függvényként definiáljuk:
400 DEF FN A(X)=X*EXP(-X)
és a programban ezután az FN A(X) függvénnyel helyettesítjük a kifejezést:
500 LET Z=FN A(X)
Ez utóbbi utasításnak az a hatása, hogy a fordító az adott X értékhez kiszámítja az FN A(X) függvény értékét a szerint a műveletsorozat szerint, ahogy azt az FNA függvény definiálásakor megadtuk.
A felhasználói függvény használatakor a független változónak konkrét számértéket is adhatunk:
500 LET Z=FN A(1.75)
Végül bemutatjuk a II. probléma megoldása során ismertetett hozamszámítási kifejezés függvényként való definiálását. A hozam kiszámítása:
H=(J-U)*((1+K)^N-1)/(K*(1+K)^N)
A kifejezés jobb oldalán négy változó található, ezért a hozam kiszámítására egy négyváltozós függvényt kell definiálni:
500 DEF FN B(J,U,K,N)=(J-U)*((1+K)^N-1)/(K*(1+K)^N)
Ha a változók közül néhányat konstansnak tekintünk, akkor a függvény egyszerűsíthető. A II. problémánál csak az évek számát (N) tekintettük változónak. Ezzel a függvénydefiniálás a következőképpen egyszerűsödik:
500 DEF FN B(N)=(J-U)*((1+K)^N-1)/(K*(1+K)^N)
A program folyamán a hozamértékeket az FN B függvény segítségével lehet kiszámítani:
90 LET H=FN B(5)
...
240 LET H=FN B(10)
VII. probléma
Egy vállalat beszerez egy adott típusú munkagépet, amely 3 műszakban dolgozik a vasárnapok és az ünnepnapok kivételével (306 nap). A gép várható élettartama 5 év. A vállalat vezetősége tudni szeretné, hogy az 5 év alatt mennyi lesz a gép hasznos ideje, és mennyi az állásideje.
A felhasználói tapasztalatokból megállapították, hogy az üzembe helyezéstől az első hibáig átlagosan 1450 üzemóra telik el. A hiba előfordulása egyenletes valószínűséggel következik be a 0-2900 munkaóra-intervallumban. Az első javítás időtartama 8 óra (tulajdonképpen 7.5 és 8.5 óra közötti idő, de tekinthetjük kereken 8 órának). A további véletlenszerű meghibásodásokig eltelt idő minden alkalommal az előző időtartam 97,5 százaléka. A javítási idő pedig minden alkalommal 8%-kal nő. A gép az első évben 100 üzemóra karbantartást (állásidő) igényel, amely évente - az előző évihez képest - 10%-kal növekszik.
A kérdés az, hogy várhatóan mennyi lesz az összes állásidő, és mennyi a hasznos idő. A megadott adatokkal a feladat analitikusan megoldható, de a vállalat vezetősége tudni szeretné, hogy a véletlen mennyire befolyásolja az állásidőt, hogy alakul szélsőségesen kedvezőtlen és kedvező esetben. Vagyis tudni szeretné, hogy mennyire szóródik az állásidő. Végeredményben a várható minimális és maximális állásidőt és az átlagos értéket kell megbecsülni.
1. A probléma elemzése
A specifikálás szerint a feladat úgy oldható meg, hogy a gép állásidejét (vagy hasznos idejét) a rendelkezésre álló adatok alapján szimuláljuk. Vagyis papírral, ceruzával és véletlenszám-táblázat segítségével a gép állásidejével kapcsolatos eseményeket végigkövetjük az öt esztendő folyamán, és közben figyeljük az összes állásidőt, valamint az összes hasznos időt. Ezt a következőképpen végezhetjük el:
A gép állásidejét kétféle esemény befolyásolja:
A meghibásodás véletlenszerűen következik be. Először a meghibásodási eseményhez rendelhető valószínűségi változó a 0...2900 intervallumban vehet fel értéket. A második meghibásodás valószínűségi változója már csak 0...2827.5 a harmadik meghibásodás valószínűségi változója pedig újabb 2,5%-kal rövidebb intervallumban vehet fel értéket (0..2756.8), és így tovább.
A véletlenszerű meghibásodás miatt bekövetkező állásidő a hiba utáni javítás munkaideje. Ez az első hibánál 8 óra, majd minden alkalommal 8%-kal növekszik.
Hiba Javítási idő (óra) 1.
2.
3.
4.8
8.64
9.33
10.07
A másik esemény a tervszerű karbantartás, amely az adatok szerint az első évben 100 óra. Ezután évente 10%-kal növekszik:
Karbantartás: 1. év
2. év
3. év
4. év
5. év100
110
121
133.1
146.4Összesen: 609.5 üzemóra
Ezzel a karbantartás okozta munkaóra-kiesést meg is határoztuk.
Hogy végül is mennyi lesz az állásidő az 5 év során, a véletlentől is függ, vagyis attól, hogy a véletlenszerű meghibásodások milyen időközökben és összesen hányszor fordulnak elő. Példaként hasonlítsunk össze két eseménysorozatot az első 1200 órában:
1. eset |
2. eset |
||
Hiba előfordulása (óraszám) |
javítási idő (óra) |
Hiba előfordulása (óraszám) |
javítási idő (óra) |
500. 600. |
8 8.64 |
1200. - |
8 - |
Láthatjuk, hogy a két esetben az állásidő több mint 100%-kal tér el egymástól, s mindkettő bekövetkezésének reális esélye van.
A feladatot úgy tudjuk megoldani, hogy a véletlenszerű időtartamok hosszát véletlenszámokkal határozzuk meg, majd kiszámítjuk az állásidőt, ezután az új valószínűségi változó értékét határozzuk meg egy véletlenszámmal, és így tovább.
A karbantartás időtartama állandó, és úgy tekinthetjük, hogy bármikor elvégezhető az év során, s nem befolyásolja a véletlen meghibásodások szabályszerűségét. Ezért a karbantartási időt egy összegben levonhatjuk az elvi időalapból (36 720 óra). Így feladatunk az ábrán bemutatott folyamattal megoldható:

Lényegében a periódusokat kell szimulálni és kigyűjteni a hasznos időt és az állásidőt.
Minden perióduson belül meg kell határozni a hiba bekövetkezését véletlenszámmal és a determinisztikus javítási időt. A hiba bekövetkezésének meghatározásához ismerni kell a hasznos időtartam elvi hosszát (az az időtartam, amelyen belül a gép biztosan elromlik). Az i-edik meghibásodás előtti hasznos időszak elvi hosszát az (i-1)-edik időtartamból lehet kiszámítani:
Hi=Hi-1*0.975
Számszerűleg az első szakasz hosszából határozható meg:
Hi=H0*0.975^(i-1)
ahol H0=2900.
Ennek alapján a (0, Hi) intervallumban egyenletes eloszlású véletlenszámot kell generálni (táblázatból kiolvasni), amelynek értéke lesz a hasznos idő. Majd a javítási időt kell kiszámítani, ami a hibátlan működések intervallumhosszának kiszámításához hasonló módon történhet:
Ji=J*1.08^(i-1)
ahol J=8.
Ezzel feladatunk nagyon egyszerűvé vált, mert a hasznos időtartamok és a javítási idők az előző értékekből ciklikusan számíthatók. Az ilyen feladat pedig számítógépen könnyen megoldható, beleértve a véletlenszám-generálást is, amely az RND könyvtári függvénnyel megoldható.
Mivel a minimális és maximális állás- és hasznos időre szükség van, egyetlen szimulálási folyamattal nem oldható meg a feladat. Célszerű a szimulálást legalább 100-szor megismételni, és a 100 esetből a legkedvezőtlenebbet és a legkedvezőbbet ki kell emelni. Ki kell számítani a 100 eset átlagát is, amelynek az analitikusan számítható átlagos értékhez kell közelítenie.
A feladat számítógéppel megoldható. Az indulóadatok a program elején rögzíthetők, így a program beavatkozás nélkül lefuthat, és a végeredményt kiírhatja az alábbi formában:
GÉPKIHASZNÁLÁS-SZÁMÍTÁS
1. LEGKEDVEZŐTLENEBB ESET
ÁLLÁSIDŐ (ÓRA):
HASZNOS IDŐ (ÓRA):
ÖSSZES IDŐ (ÓRA):
MEGHIBVÁSODÁSOK SZÁMA:
x.x
x.x
36720
x
2. LEGKEDVEZŐBB ESET
ÁLLÁSIDŐ (ÓRA):
HASZNOS IDŐ (ÓRA):
ÖSSZES IDŐ (ÓRA):
MEGHIBVÁSODÁSOK SZÁMA:
x.x
x.x
36720
x
3. ÁTLAGOS ESET
ÁLLÁSIDŐ (ÓRA):
HASZNOS IDŐ (ÓRA):
ÖSSZES IDŐ (ÓRA):
MEGHIBVÁSODÁSOK SZÁMA:
x.x
x.x
36720
x
Megjegyezzük, hogy az "összes idő" mindenütt az 5 éves időszak összes munkaórája: 36 720 óra. Az átlagos értékekhez elég az állásidő átlagát kiszámítani, és azt levonva az összes munkaórákból megkapjuk az átlagos hasznos időt.
A feladat megoldásához szükség van egy adatdefiniáló modulra, amely az indulóértékeket rögzíti, majd egy olyan ciklusra, amelyben az 5 éves időszakokat kell 100-szor szimulálni. Minden szimulálás végén meg kell vizsgálni, hogy a legkedvezőbb vagy a legkedvezőtlenebb eset jött-e létre.
A szimuláláson belül hasznos idő és javítási idő számítási ciklusokat kell végrehajtani 5 éves időszakokra, és a hasznos idő, az állásidő, a meghibásodások száma adatokat gyűjteni kell a legkedvezőbb, legkedvezőtlenebb értékek kiválasztásához és az átlag kiszámításához.
2. A program tervezése
Az adatdefinidlási modulban az indulóadatokat kell rögzíteni:
A szimulációs modul vezérli a szimulálások végrehajtását 100 alkalommal és minden szimulációs menet után a minimális, illetve maximális állásidő kiválasztását.
Az 5 éves időszak szimulálás modul két további modulból áll. Az egyik végzi a periódusszámításokat, a másik pedig az állásidő, a hasznos idő és összes időadatok összegezését.
Az átlagszámítás modul a szimulálás befejezése után az állásidő átlagát számítja ki. A programot a kiírás modul fejezi be.
A program két egymásba ágyazott ciklust tartalmaz. Vizsgáljuk meg ezeket külön is, mivel több modult érintenek. A külső ciklus a szimulálás. Erről tudjuk, hogy 100-szor kell végrehajtani, ezért FOR, NEXT szerkezetű ciklusként célszerű implementálni.
A ciklus kimeneti adatai:
A minimális és a maximális adatokat a min., max. és gyűjtés modul válogatja ki a szimulációs menetekből. Az összes hasznos időt a H5, az összes állásidőt az A5 változó tartalmazza. A H5-öt minden ciklus kezdetén nullázni kell, hogy csak az adott szimulációs menet hasznos idejét tartalmazza. Az A5 változó értékét pedig nem nullázni kell, hanem a karbantartási idők összegére kell beállítani: A5=609.5
Ugyanez lesz a T0 változó indulóértéke is, amely az összes eltelt időt tartalmazza a szimuláció folyamán: T0=609.5
A ciklus cikluson kívüli előkészítést nem igényel.
A ciklusmag tartalmazza:
a H5, N, A5, T0 és K kezdeti értékadást
K=609.5
A5=K
T0=K
N=1 (meghibásodások száma)
H5=0
a periódusszámításokat, az A5, H5, T0 és N összegezéseit,
az A5, H5, T0 és N feldolgozását,illetve az A5 min. és max. keresését.
A belső ciklus a periódusszámítás és a hozzá tartozó összegezések. Ez a ciklus a hasznos idő - javítás periódusok hosszát számítja véletlenszám-generátor felhasználásával egészen addig, míg az összóraszám eléri a 36 720-at.
A ciklus kimenete az A5, H5, T0 és N aktuális értéke egy 5 éves időszakon belül. Ezeket a ciklus előtt indulóértékre kell állítani. Ez a külső ciklus keretében már megtörténik, más előkészítő lépésre nincs szükség.
A belső ciklusmag az alábbi funkciókat látja el:
az N aktuális értékének megfelelően kiszámítja a hibátlan működésű szakasz (H1) teljes hosszát és a véletlen által befolyásolt értékét (H2)
H1=H0-0.975^(N-1)
H2=H1*RND
(A véletlenszámot azért kell H1-gyel megszorozni, hogy (0, H1) intervallumba eső véletlen-számot kapjunk. A BASIC ugyanis (0,1) intervallumba eső véletlenszámokat generál);
a javítási idő N-től függő értékét kiszámítja:
J1=J*1,08^N-1;
N értékét növeli minden periódus után;
a kapott időket gyűjti:
H5=H5+H2,
A5=A5+J1,
T0=T0+A5+H5.
A ciklust addig kell folytatni, amíg a T0>=36720 feltétel nem teljesül. Ha T0>=36720,
akkor értékét vissza kell állítani 36 720-ra az A5 és H5 értékeivel együtt.
A ciklus szerkezete hátul tesztelő, és a ciklusváltozó a T0 adat. A ciklus két modulból áll (periódusszámítás és összegezések). Ezek ciklikusan követik egymást, vezérlőmodult nem igényelnek. A program modulszerkezete:
A (2.1) vezérlőmodul kódolása felesleges, mivel a két alárendelt modul egymást is tudja hívni.
3. A modulok tervezése
(1) Adatdefiniálás
A modul adat típusú. Bemeneti adatai az itt definiált H0, J és K. Ugyanezek a modul kimeneti adatai is. A modul értékadási műveletekből áll.(2) Szimuláció
A modul vezérlő típusú. Nem kap bemeneti adatokat, funkciója az ötéves ciklusok szimulálásának irányítása úgy, hogy a szimuláció 100-szor megtörténjék.
A belső ciklus kimeneti adatait a kezdőértékre állítja a H5 nullázással és T0=K, A5=K, N=1 értékadásokkal. Ezután hívja a periódusszámítást és az összegezést. Minden ötéves periódus szimulációja után a legkedvezőbb és legkedvezőtlenebb eset kiválasztását és az eredmények gyűjtését végző modult hívja.(2.1) 5 éves időszak szimulálás
(2.1.1) Periódusszámítás
A modul eljárás típusú. Bemeneti adatai az (1) modulban definiált adatok (H0, J, K). A kimeneti adatok pedig az aktuális periódus hasznos idő (H2) és állásidő (J1) adatai. Ezeket a modul minden periódusszámítás alkalmával átadja az összegezések modulnak.
A modul a belső ciklusmag tárgyalásánál bemutatott hasznos és állásidő számításokat végzi el. Először a hasznos idő véletlen hosszát határozza meg az N aktuális értéke és egy véletlenszám alapján, majd a javítási időt N értékének megfelelően. Ezután a következő periódust fogja számolni (hacsak be nem fejeződik a ciklus), ehhez N értékét eggyel növeli, mivel az adatok értéke N-től függ. A modult a külső ciklusból hívható szubrutinként kell kódolni, hogy jelenléte a kódban ne "zavarja" a (2) modult.(2.1.2) Összegezések
A modul eljárás típusú. Bemeneti adatai a H2 hasznos idő és a J1 állásidő a (2.1.1.) modulból. Az ezekből készített összeg a modul eredménye.
A modul a ciklusmag-tevékenységek közül az állásidők összegét: A5=A5+J1,
a hasznos idők összegét: H5=H5+H2
és az összes eltelt időt: T0=T0+A5+H5
gyűjti az első lépésben, majd ellenőrzi a belső ciklus ciklusvége feltételét. Ha a T0>36720 feltétel teljesül, akkor a ciklus befejeződik, és a vezérlést vissza kell adni a hívó- (2) modulnak. Előtte azonban a T0 értékét vissza kell állítani 36720-ra. Ugyanis többnyire az fordul elő, hogy az utolsó periódusszámítás hasznos és állásidejét hozzáadva T0-hoz T0>36720.
A túllépést jelöljük D-vel: D=T0-36720. A feladat viszont az, hogy pontosan ötéves időszakokat szimuláljunk, mivel ezek hasonlíthatók össze. Ezért a túllépést le kell vonni, s ezzel együtt csökkenteni kell az A5 és H5 értékeket is. Tegyük fel, hogy D<=J1, akkor csak az A5-öt (állásidőt) kell D-vel csökkenteni.
Ha D>J1, akkor az állásidőt J1-gyel kell csökkenteni: A5=A5-J1, és a hasznos időt pedig a D-J1 különbséggel: H5=H5-(D-J1).
Ha T0<36720, akkor a periódusszámítást folytatni kell, és a vezérlés visszakerül a (2.1.1) modulra.(2.2) Min., max. és gyűjtés
A modul eljárás típusú. Bemeneti adata a periódusszámítások eredménye, az A5 (ötéves összes állásidő). A teljes futás alatt 100 ilyen adatot kap, ezek közül kell a legkisebbet és a legnagyobbat tárolni. A modul kimeneti adata egyrészt a minimális és a maximális értékű A5, valamint a 100 darab A5 összege, amelyből a (3) modul az A5 átlagát számítja ki.
A modul adatai közül:
- ki kell választani a legkisebb értéket (a legkedvezőbb érték) és a hozzá tartozó periódusszámot (N),
- ki kell választani a maximális értéket (a legkedvezőtlenebb érték) és a hozzá tartozó periódusszámot (N),
- és összegezni kell ezeket az adatokat az átlagszámításhoz.
Vizsgáljuk meg először a minimum és maximum kiválasztási elvét és folyamatát. Az adatok egymás után érkeznek a modulhoz, de ezeket nem tároljuk, vagyis mindig csak az aktuális adat van jelen. Tehát minden A5 adatról csak azt tudjuk eldönteni, hogy egy korábbi A5-nél kisebb-e vagy sem. Ha kisebb, akkor a továbbiakban ezt az értéket tároljuk úgy, mint minimális értéket (M0) egészen addig, amíg nem érkezik egy még kisebb A5 érték. Minden egyes adatmegőrzésnél az öt év során lejátszódó hibajavítási periódusok darabszámát is tárolni kell. Ez az N-ből határozható meg. A (2.1.1) modulból ismeretes, hogy az N pillanatnyi értéke a következő periódus sorszámát tartalmazza, ezért az N0=N-1 értéket kell megőrizni.
Kérdéses még, hogy a minimális A5 értéket tároló M0 változó milyen kezdőértéket kapjon; figyelembe véve, hogy minden szimuláció végén össze kell hasonlítani A5 értékével. Indulóértéke nem lehet nulla, mivel A5>0 minden esetben, és így M0 végig 0 lenne, ami nyilván félrevezető.
A legbiztosabb, ha M0 értéke egy olyan nagy szám, amely az A5 maximumánál nagyobb, így már az első esetben lesz csere, és M0 valóban a minimális értéket fogja tárolni a futás végén. Várhatóan kb. 40 szakasz zajlik le, és az állásidő átlagértékét 15 órára becsüljük, így biztosan lesz olyan állásidő (A5), amelynek értéke 1300-nál kisebb lesz. Ezért M0 = 1300 legyen.
Az A5 maximum keresése hasonlóan végezhető el, azzal a természetes különbséggel, hogy az A5 aktuális maximumát tároló Ml értékét akkor kell módosítani, ha A5>M1. Ezzel egyidejűleg az N1=N-1 periódusszámot is tárolni kell. M1 indulóértéke lehet 0 is, mivel így már az első A5 adat után M1=A5 lesz, és a továbbiakban a maximum tárolása biztosítva van.
Az M0 és M1 indulóérték beállítását a szimulációs ciklus elé kell felvenni, hogy csak egyszer kapjanak induló értéket. Ezért az (1) modult ezzel a két értékadással ki kell egészíteni, ami a modul lényegét nem befolyásolja. Az N0 és N1 indulóérték beállítása szükségtelen, mivel értékük nem összehasonlítás alapján, hanem egyszerű értékadással változik meg.
A fentieken kívül az A5 adatok összegét is képezni és tárolni kell. Erre szolgál az A9 változó. Az N-1 értékek összegét az N9 tárolja.
A modult szubrutinként kell kódolni a (2.1.1) és (2.1.2) modulokhoz hasonlóan. Ezért a vezérlést a modul a (2) vezérlőmodulnak adja vissza.(3) Átlagszámítás
A modul eljárás típusú. Bemeneti adata az A5 állásidők összegét tartalmazó A9 érték és az N-1 hibaszámok összegét tároló N9 érték a (2.2) modulból. Kimeneti adatai az A5 állásidők átlaga:A8=A9/100
és az átlagos hibaszám:
N8=N9/100
A modul ezt a két műveletet tartalmazza.
(4) Kiírás
A modul eljárás típusú. Bemeneti adatai három csoportba oszthatók a táblázat alapján:
Legkedvezőtlenebb: Legkedvezőbb: Átlagos: Ezek, valamint a táblázat szövegrészei a modul kimeneti adatai.
A modul a bemutatott formájú táblázatot készíti el. Az állásidő, a hasznos idő, az összes idő és a meghibásodások száma együttesen háromszor fordul elő - azonos formában -, ezért a szövegrészeket szövegkonstansokként érdemes definiálni.
4. A program kódolása
(1) Adatdefiniálás
A program neve GEPKI. Ezután az indulóérték-adásokat kódoljuk:10 REM * GEPKI *
20 REM ADATDEFINIALAS
30 LET H0=2900
40 LET J=8: LET K=609.5
60 LET M0=1300: LET M1=0
70 LET A9=0: LET N9=0(2) Szimuláció
A modul a program két ciklusa közül a külsőt vezérli. Mint már említettük, FOR, NEXT típusú ciklusszerkezetben kódoltuk. A modul által vezérelt (2.1.1), (2.1.2) és (2.2) modulokat a modul által hívott (700-as, illetve 1000-es sorok) szubrutinokként kódoltuk. A modul kódja:80 REM SZIMULACIO
90 FOR S=1 TO 100
100 LET A5=K: LET H5=0
110 LET T0=K: LET N=1
120 GOSUB 700
130 GOSUB 1000
140 NEXT S(2.1.1) Periódusszámitás
A modul az 5 éves időszak szimulálásának első része. A modult szubrutinként kódoltuk a (2.1.2) összegezések modullal együtt. A kódolásnál figyelembe vettük, hogy a modulban kezdődik a hátul tesztelő szimulációs ciklus. A modul kódja:700 REM PERIODUS SZAMITAS
710 REM CIKLUS KEZDET
720 LET H1=H0*0.975^(N-1)
730 LET H2=H1*RND
740 LET J1=J*1.08^(N-1)
750 LET N=N+1(2.1.2) Az összegezések
A modul kezdetén a (2.1.1) modulban megkezdett ciklus folytatása, valamint a ciklus befejezését tesztelő vizsgálat van. Ezután kódoltuk a T0 visszaállítását. Itt fejeződik be a (2.1.1) modullal közös szubrutin, ezért a végén RETURN utasítás látható:760 LET H5=H5+H2
770 LET A5=A5+J1
780 LET T0=T0+H2+J1
790 IF T0<36720 THEN GO TO 710
800 REM CIKLUS VEG
810 LET D=T0-36720
820 IF D<=J1 THEN LET A5=A5-D: GO TO 850
830 LET A5=A5-J1
840 LET H5=H5-(D-J1)
850 RETURN(2.2) Min., max. és gyűjtés
Ez a modul önálló szubrutint alkot a programon belül. A modul kódja:1000 REM MIN, MAX GYUJTES
1010 IF A5<M0 THEN LET M0=A5: LET N0=N-1
1020 IF A5>M1 THEN LET M1=A5: LET N1=N-1
1030 LET A9=A9+A5
1040 LET N9=N9+N-1
1050 RETURN(3) Átlagszámítás
A modul két átlagszámítást tartalmaz:300 REM ATLAGSZAMITAS
310 LET A8=A9/100
320 LET N8=N9/100(4) Kiírás
A kiírás modul a kívánt szerkezetű táblázatot nyomtatja ki. A modul kódja:330 REM KIIRAS
340 LET A$=" ALLASIDO (ORA): "
350 LET H$=" HASZNOS IDO (ORA): "
360 LET T$=" OSSZES IDO (ORA): "
370 LET M$=" MEGHIBASODASOK SZAMA: "
380 PRINT
390 PRINT " GEPKIHASZNALAS SZAMITAS"
400 PRINT
410 PRINT "1. LEGKEDVEZOTLENEBB ESET"
420 PRINT A$;M1
430 PRINT H$;36720-M1
440 PRINT T$;36720
450 PRINT M$;N1
460 PRINT
470 PRINT "2. LEGKEDVEZOBB ESET"
480 PRINT A$;M0
490 PRINT H$;36720-M0
500 PRINT T$;36720
510 PRINT M$;N0
520 PRINT
530 PRINT "3. ATLAGOS ESET"
540 PRINT A$;A8
550 PRINT H$;36720-A8
560 PRINT T$;36720
570 PRINT M$;N8
580 PRINT
590 STOP
5. Értékelés
A program tesztelése után futtathatjuk, és a futás végén a az alább látható eredményt kapjuk:
Az első tapasztalatunk, hogy a program meglehetősen sokáig fut, és közben látszólag nem történik semmi. Ennek az az oka, hogy a belső ciklus átlag 36 lépést hajt végre, a külső pedig ezt 100-szor ismételteti. Összességében tehát kb. 3600 számítást hajt végre a program a kiírás előtt.
Látható, hogy a legkedvezőbb és legkedvezőtlenebb eset között lényeges különbség van. Ez arra hívja fel a figyelmet, hogy a véletlenek hatására a gép kihasználása nagyon jól is alakulhat. Az állásidő átlagos értéke közel áll a várható értékek alapján analitikusan kiszámítható értékhez:
Számított átlag:
Szimulált átlag:
eltérés:2032.8
2123.4
-90.6
Ez természetesen nem meglepő, hiszen a 100-szor végzett szimuláció eredményeinek átlaga már közelítő eredményt ad a nagyobb mintával számított átlageredményekhez.
A program többszöri futtatása során ugyanazokat az eredményeket kapjuk, mert a futás során ugyanazokat a véletlenszámokat kapja változatlan sorrendben. Ez lehetővé teszi, hogy a program eredményeit bármikor reprodukálni lehessen.
Ha minden futás végén újabb véletlenszerű eredményeket akarunk kapni, akkor a program elejére a
RANDOMIZE
utasítást kell elhelyezni, amelynek eredményeként a program véletlenszerű helyen kezdi el olvasni a véletlenszám-táblázat elemeit. A RANDOMIZE utasítást csak kipróbált, jól működő programba szabad beírni, hogy a hibák felderítését ne akadályozza.
A számítógépet nemcsak műszaki és gazdasági számítások vagy más adatfeldolgozási feladatok elvégzésére lehet felhasználni, hanem szórakoztató szerepet is játszhat. A számítógép mint "játszótárs" a kétszemélyes játékokban terjedt el. A játékok elterjedését nagymértékben segítette az interaktív üzemmód megjelenése. A mikroszámítógépek gyors térhódítása következtében a számítógépet mind nagyobb számban alkalmazták, és ez megnövelte a számítógéppel játszók táborát. Ma már külön célszámítógépek is készülnek, amelyek egyetlen funkciója a játék. Ezek sorában a mozgásjátékok (tv-pingpong) voltak az elsők; a mai legfejlettebb gépi játszótársak a sakkgépek.
De térjünk vissza az általános célú számítógépeken játszható játékokra. Itt nagy szerepet kap interaktív használata miatt a BASIC nyelv, és az is segítette a BASIC nyelvű játékok elterjedését, hogy nagyon sok olyan ember (egyetemi hallgató, kutató stb.) használja, aki "játékos kedvű", és napi feladatain kívül szívesen "elszórakozik" a számítógéppel. Ennek köszönhető, hogy a számítógépes játékok programozása és a BASIC nyelv összetartozó fogalmak.
A számítógép alkalmas játszótárs, mert interaktív (kérdést ír ki, a játékos válaszol), a játékos akcióira (lépéseire) gyorsan válaszol, statisztikával értékeli a játékos eredményeit, és végül: nem csal.
A számítógépes játék fő jellemzői:
Nagyon sok számítógépes játék van forgalomban, és számuk egyre bővül. Programozásuknak néhány egyedi sajátossága is van. Ezek közül az egyik leglényegesebb a nagyfokú interaktivitás, vagyis számos kérdés és válasz. A játékprogramok sok alternatívát kezelnek, és nagyon sok funkciót tartalmaznak, ami a program szerkezetét bonyolulttá teszi.
VIII. Probléma
A közismert hadihajócsata játék számítógépen játszható, módosított változatát kell elkészíteni. Most csak a számítógép jelöl ki hajókat egy 66x66 négyzetből álló hálóban, amelyeket a játékosnak el kell találnia. A fordítottját - a játékos helyez el hajókat a csatamezőben, és a program vadászik ezekre - az egyszerűség kedvéért kihagyjuk a problémából.
A játék célja, hogy a játékos legfeljebb 20 lövéssel eltalálja az álló vagy mozgó hajókat. A játékszabályok:
A játék kezdetén ki kell írni a játékszabályokat a játékos számára:
Egy 66 x 66-os csatamezőben kell egy ismeretlen helyen levő hajót eltalálni a célpont koordinátáinak megadásával. A program a becsapódás és a hajó távolságát közli. Több hajóból álló flottára is vadászhat, de a hajókra egyenként kell vadászni. Minden ellenséges hajóra 20 lövedéket lőhet ki. A hajók állhatnak, vagy kérheti, hogy mozogjanak. Csak akkor mozgassa az ellenség hajóit, ha már sok csatát megnyert, mert mozgó célpontot nehezebb eltalálni.
Ezután meg kell kérdezni az ellenséges flotta hajóinak számát:
Hány hajóból álló flottával óhajt megküzdeni?
Erre a játékos tetszés szerinti értéket adhat meg. Ezután kezdődik a hajók vadászata. A vadászat kezdete előtt ki kell írni a hajó sorszámát:
A(z) j. hajó következik!
Majd azt kell megkérdezni, hogy a hajó álljon vagy mozogjon.
Mozogjon az ellenséges hajó?
A játék folyamán vagy olyan kérdéseket szabad feltenni, amelyekre valamilyen számmal kell válaszolni, vagy eldöntendő kérdéseket kell feladni. Igenlő válasz esetén 1-et, tagadás esetén 0-t kell begépelni.
Ezután következik maga a vadászat. A játékos megadja az egyes lövések becsapódási pontjainak a koordinátáit. Hogy a játékos pontosan tudja, milyen lépést vár tőle a program, ki kell írni:
A(z) i. lövés koordinátái:
Ezután a játékos begépeli a lövés X,Y koordinátáit, majd a program kiírja a becsapódási pont és a hajó közötti távolságot a négyzetháló négyzeteinek élhosszúságában kifejezve:
A becsapódás távolsága: x.
Ha ez nulla, akkor a játékos a hajót eltalálta. Ezt külön is tudatni kell:
Ön elsüllyesztette az ellenség k. kajóját.
Ezt követően újabb hajó vadászata következik mindaddig, amíg van hajó. Ha a hajók elfogytak, a játék befejeződik.
Ha a lövés nem talált, akkor újabb lövést ad le a játékos. Ha a 20. lövés sem talált, akkor a csata sikertelen volt. Ezt a játékossal közölni kell:
Ez nem sikerült! A hajó az x0, y0 koordinátákról indult.
Ha a játékos mozgó hajóval csatázik, akkor előfordulhat, hogy a mozgó hajó a csata befejezése előtt (lövésszám<20) elhagyja a csatamezőt. Ezt is ki kell írni:
A hajó az x0,y0 pontról indult, és elhagyta a csatamezőt az x1,y1 ponton. Az ellenség megmenekült!
A csata befejeztével a csatát a játékos eredményeinek megfelelően értékelni kell. Először az alapadatokat kell kiírni:
Az elsüllyesztett hajók száma:
Az elmenekült hajók száma:
A sikertelen vadászatok száma:
Majd az eredmények értékelése következik. Ha a játékos valamennyi hajót elsüllyesztette:
Ön egy zseniális admirális. Tökéletes győzelmet aratott!
Ha a hajók felét (vagy annál többet, de nem mindet) eltalálta:
Ön jól harcolt, csak kissé még rutintalan.
A felénél kevesebb hajót talált el:
Ön egy átlagos képességű hadvezér.
Ha valamennyi hajó elmenekült:
Tanuljon meg célozni!
Ha a játékos nem talált el egy hajót sem:
Ön tehetségtelen, keressen más elfoglaltságot!
A játék végén a játékosnak legyen lehetősége újabb játékra, ezért az
Óhajt még játszani?
kérdés jelenjen meg, és a játékos a válaszával dönthet. Ha már nem akar tovább játszani, akkor a játék befejeződik az alábbi kiírással:
Köszönöm a játékot!
Viszontlátásra!
1. A probléma elemzése
Már a probléma megfogalmazásából észrevehető, hogy a játék sok interakciót tartalmaz, azaz sok üzenet jelenik meg, és sok adatot kér a program.
Ez a játék csak akkor élvezhető, ha az "ellenfél" (a számítógép) lépései kiismerhetetlenek, vagyis a játékos a korábbi játékok lefolyásából nem következtethet arra, hogy a program hol helyezi el a hajót a csatamezőben, illetve mozgó hajó esetében milyen irányban és sebességgel mozog a hajó.
A játékon belüli véletlenszerűség az RND véletlenszám-generáló függvénnyel érhető el. De ez nem elég, mert tudjuk, hogy az RND függvény minden futáskor ugyanazt a véletlenszámsort szolgáltatja, és így a játékok nem lennének függetlenek egymástól. Ezt a RANDOMIZE utasítással lehet kivédeni.
A játék élvezhetőségének kevésbé lényeges feltétele, hogy a mozgó hajó sebessége arányos legyen a csatamező méretével, azaz ne legyen se túl lassú, se túl gyors. Az első esetben a játékos nem érzékeli a mozgást, a másodikban pedig nem tudja követni, és így a játék érdektelenné válik. A tapasztalatok szerint a sebesség legcélszerűbb értéke a
0.5 ... 3.5 négyzetél/időegység
intervallumba esik. A sebesség konkrét értékét minden hajó vadászatánál véletlenszerűen kell meghatározni. Ugyanez vonatkozik a mozgás irányára is.
Kérdés az, hogy mit tekintsünk egységnyi időnek. A legélethűbb megoldás az lenne, ha az egységnyi idő 5,10, 20, ... stb. másodperc lenne. Ez az eljárás azonban több nehézséget is felvet. A megoldás arra ösztönzi a játékost, hogy minél rövidebb időt töltsön el két lövés között gondolkodással, ugyanis hosszú töprengés után a hajó relatíve nagy távolságot mozdul el. Ez a játékot megzavarhatja. Emellett a programot is lényegesen bonyolultabbá teszi az idő állandó figyelése és a mozgatás folyamatos véghezvitele. A játékos szempontjából megnyugtatóbb megoldás, ha a két lövés között eltelt időt tekintjük egységnyi időnek. Vagyis a játékos minden lövése után a sebességnek megfelelő mértékben kell a hajót továbbvinni. Ez a játékos számára azt az érzetet kelti, hogy a hajó hozzá képest egyenletes sebességgel mozog. Emellett a program bonyolultsági foka sem nő.
A becsapódás helye és a hajó közötti távolság könnyen megállapítható, mivel minden pontot X és Y koordinátákkal adunk meg. Ügyelni kell azonban arra, hogy a program és a játékos is csak egész számmal jelölhet koordinátát. Ez különösen a találat érzékelésekor fontos.
Egy hajó akkor menekül meg, amikor elhagyja a csatamezőt, vagyis az
X1 > 66 vagy X1 < 1,
vagy
Y1 > 66 vagy Y1< 1,
vagy több feltétel is teljesül egyidejűleg.
A játék végén az eredmény kiértékeléséhez szükség van az egyes események előfordulási számára:
A legjobb eredmény elérésekor T = E,
a második legjobb esetben T > E >= T/2,
a harmadik helyen 0 < E < T/2.
A rosszul célzó játékosnál T = M.
Végül a legrosszabb eredmény a T = S+M.
Könnyen belátható, hogy valamennyi lehetséges eredmény besorolható valamelyik kategóriába, tehát nincs olyan csata, amely nem értékelhető egyértelműen, illetve sehogy.
Mindezekből megállapítható, hogy a problémaleírásban megfogalmazott játék programozható.
A feladat - első közelítésben - három funkcionális egységre bontható:
Mivel a specifikáció szerint a játéknak programon belül akárhányszor ismételhetőnek kell lennie, be kell építeni egy vezérlőegységet, amely a csata és a befejezés közül azt hívja, amelyet a játékos kíván. Ezzel megkapjuk a feladat szerkezetét.
2. A program tervezése
A program megtervezéséhez nézzük először az egyes modulokat, majd a vezérlési szerkezetet. A játékszabályok modul egyetlen funkciót lát el: a játékszabályok kiírását a program kezdetén. Ez a modul tovább nem bontható.
Az újrajátszás vezérlése modulnak az a feladata, hogy a játékos kívánságának megfelelően vagy a csata lejátszása, vagy a befejezés modult hívja. Ez elég egyszerű vezérlési szerkezet ahhoz, hogy egyetlen modul tartalmazza.
A játékban többször hívható csata lejátszása modul azonban több feladatot lát el:
Ezek a funkciók elég jelentősek ahhoz, hogy a megvalósításukhoz külön modulokat rendeljünk.
A befejezés modul a specifikáció szerinti búcsúzást írja ki. Ez a funkció további bontást nem tesz szükségessé.
Az első finomítás után a az alábbi modulszerkezetet kapjuk.
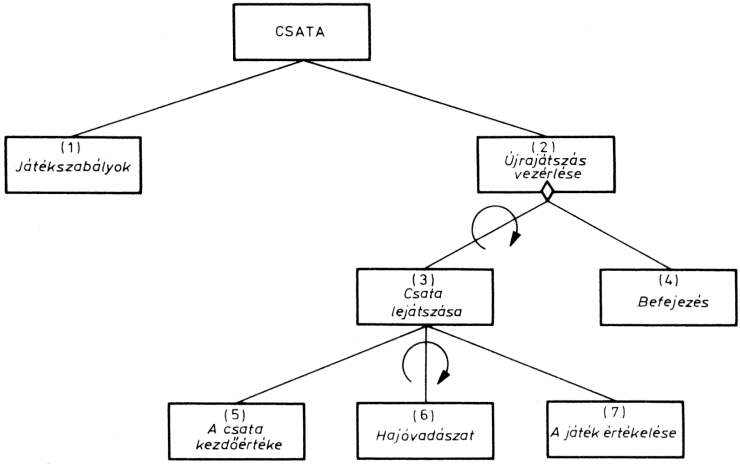
Vizsgáljuk meg most az újonnan kapott (5), (6) és (7) modulokat.
Az (5) a csata kezdőértékei modul a flotta hajóinak számát rögzíti a játékos igénye szerint. Ezt a modult felesleges felbontani.
A ciklikusan végrehajtható (6) hajóvadászat modulnak több funkciója van:
Mindkét funkció megvalósítása önálló modulokat igényel.
A (8) hajóparaméterek modul állítja be minden hajóvadászat kezdetén a soron következő hajó adatait:
Jól érzékelhető, hogy mindhárom feladat egyetlen funkció részeit alkotja. Ugyanakkor az is látható, hogy elég nagyok és zártak ahhoz, hogy a programban önálló modulokként vegyük őket figyelembe.
Ezzel a lépéssel a (8) hajóparaméterek modult tovább bontottuk. A modulok szerkezetének meghatározásakor figyelembe kell venni, hogy a harmadiknak felírt funkciót csak akkor kell végrehajtani, ha a játékos mozgó hajót kíván eltalálni.
Vizsgáljuk meg részletesebben az utóbbi modulok funkcióit! A hajó helyzetét a program véletlenszerűen úgy tudja kijelölni a 66x66-os négyzethálóban, hogy mind az X0, mind az Y0 koordinátát véletlenszám-generálással állítja elő. Figyelembe kell venni, hogy az RND utasítás csak a [0,1] intervallumba eső számot képes generálni. Ezért a kapott véletlenszámot meg kell szorozni 66-tal, hogy a kívánt intervallumba essen. Mindig csak egész számú koordinátákat veszünk figyelembe, ezért a kapott értéknek csak az egész részét kell megtartani. Vagyis a koordináták kiszámítása:
X0=INT(66*RND)
Y0=INT(66*RND)
A helymeghatározás további műveletet nem igényel. A (8.1) a hajó helyzete modul funkciója eléggé zárt és egyszerű ahhoz, hogy a további bontástól eltekintsünk.
A (8.2) mozgás modul kérdést tesz fel a játékosnak, hogy mozogjon-e az ellenséges hajó. A játékos 1 (igen) vagy 0 (nem) begépeléssel dönt. Egyszerűsége miatt ezt a modult sem kell felbontani.
A (8.2.1) irány és sebesség modul végrehajtása csak akkor szükséges, ha a játékos mozgó hajóra kíván vadászni. A modul funkciója, hogy véletlenszerűen meghatározza a hajó mozgásának irányát és sebességét. Mindkettő elvégezhető véletlenszám-generálással. Az irány meghatározásánál azt kell figyelembe venni, hogy a hajó mozgási iránya az x tengellyel 0<=D<=PI tartományba eső D szöget zárhat be. Tehát egy olyan véletlenszámot kell generálni az irányszögre, amely a fenti intervallumba esik. Ezt a helyzetmeghatározással analóg módon kaphatjuk meg:
D=PI*RND
A sebesség értékét hasonlóan lehet generálni a kívánt intervallumban:
V=3*RND+0.5
Ez biztosítja, hogy a sebesség értéke véletlenszerű legyen, és értéke a 0.5<=V<=3.5 intervallumba essen.
Ez az érték azonban még nem használható, csak akkor, ha x és y komponensekre felbontjuk. A komponensekre bontást az alábbi elv segítségével lehet elvégezni:
X9=V*COS(D)
Y9=V*SIN(D)
ahol X9 a sebesség x irányú, Y9 a sebesség y irányú összetevője.
A hajót minden lövés után az X tengely mentén X9, az Y tengely mentén Y9 távolságra kell továbbvinni, de ez már nem ennek a modulnak a feladata.
A (8.2.1) modul két funkciót teljesít, de ezek önmagukban elég kis terjedelműek, és kapcsolódnak is egymáshoz, ezért a modul szétbontása nem indokolt.
Térjünk vissza a (9) lövéssorozat modul elemzéséhez. Ebben a modulban kell végrehajtani a legfeljebb 20 lövésből álló vadászatot. Minden lövésnél először fogadni kell a játékos lövését. A lövéseket számlálni kell. Ezután ki kell értékelni a lövést, vagyis meg kell állapítani a becsapódás helyének és a hajónak a távolságát (R). Ha R>0 akkor ezt a játékos számára ki kell írni, hogy tudja, milyen távolságra közelítette meg a hajót. Ezután a lövéssorozat folytatódik. Ha R=0, akkor a játékos a hajót eltalálta, és ezt is ki kell írni. Ekkor az eltalált hajókat számláló változó (E) értékét eggyel meg kell növelni, és a hajó vadászata befejeződött.
Ha a játékos mind a húsz lövést leadta egy hajóra, és nem találta el, akkor a vadászat sikertelenül fejeződött be; ezt a sikertelen csaták számlálójának (S) növelésével kell nyugtázni.
Ha a lövés nem talált, és a játékos mozgó hajóra vadászik, akkor R>0 esetén a hajót a sebességnek megfelelően el kell mozdítani. Jelöljük a hajó mindenkori koordinátáit X1, Y1-gyel. Ez a jelölés álló hajóknál is használható. Mivel lehet, hogy a hajó kilépett a csatamezőből, el kell végezni az erre vonatkozó vizsgálatot. Ha a hajó valóban kilépett a csatamezőből, akkor az elmenekült hajók számát (M) eggyel növelni kell. Ekkor is befejeződött az aktuális hajó vadászata.
Akárhogy végződik a lövéssorozat, a hajók számlálóját (T) is növelni kell eggyel. Összefoglalva, a (9) lövéssorozat modul az alábbi funkciókat látja el:
Mielőtt a (9) modult tovább bontanánk, vizsgáljuk meg, hogyan végezhetők el a modul egyes műveletei. A játékos lövése a csatamező valamelyik pontjára vonatkozik. Ezt a pontot a játékos a koordinátáival (X2, Y2) definiálja. Mivel csak egész számú koordinátákat értelmezünk a játékban, biztosítani kell, hogy a játékos esetleges vegyes számú koordinátáiból a program csak az egész részt vegye figyelembe:
X2=INT(X2)
Y2=INT(Y2)
A becsapódás és a lövés távolságát a koordináták segítségével lehet kiszámítani:
Az R-nek is csak az egész részét szabad a játékossal közölni, mivel azonos egész részű R-ek esetében a törtrész értékéről az irányra lehet következtetni. Ha a törtrész 0, akkor vagy X1=X2 , vagy Y1=Y2. Tehát valamelyik koordinátát eltalálta a játékos. Minél nagyobb a törtrész, annál biztosabb, hogy a két koordináta eltérése megegyezik.
Példaként tekintsük azt az esetet, amikor a hajó az X1=35, Y1=8 koordinátájú pontban van. Ha a játékos az X2=35, Y2=18 pontra lő, akkor R=10. Ezzel szemben az X2=43, Y2=15 lövésnél a távolság R=10.63.
Az első esetben a játékos tudja, hogy az egyik koordinátát 10-zel kell megváltoztatnia, és eltalálja a hajót. A második esetben pedig tudja, hogy a találat érdekében mindkét koordinátát meg kell változtatnia, hozzávetőlegesen egyenlő mértékben.
Hogy a törtrész ne könnyítse meg a játékot, válasszuk le. Így a játékos az irányra vonatkozóan nem kap tájékoztatást.
Megjegyezzük, hogy a fenti állítások nem általános érvényűek, csupán az esetek többségében teljesülnek. Például, ha a fenti kifejezés valamelyik egész szám négyzetével egyenlő (6^2 + 8^2 = 100), akkor R is egész lesz anélkül, hogy bármelyik koordinátát eltaláltuk volna. A lövések számlálása az ismert módon elvégezhető.
A hajó mozgatásakor a jelenlegi koordinátákat a sebességkoordinátákkal módosítjuk:
X1=X1+X9,
Y1=Y1+Y9.
Ha a hajó áll, akkor
X9=0,
Y9=0,
és a hajó koordinátái nem módosulnak a "mozgatás" során.
Nem biztos, hogy a V sebesség egész szám, ezért az új koordinátákat egész számra kell kerekíteni.
Minden esemény után (találat, menekülés, sikertelenség) számlálni kell az adott eseményt és az összes vadászott hajó számát is. Ezt célszerű egy helyen végezni a programban.
Most már felbonthatjuk a (9) lövéssorozat modult. A következőket kapjuk:
Külön felhívjuk a figyelmet arra, hogy a (11), (12) és (13) modulok akkor hívják a (14) modult, ha az adott hajó vadászata befejeződik.
A (7) játék értékelése modult még nem elemeztük. A modul egyetlen funkciót lát el, vagyis a T, E, M, S értékek alapján értékeli a játékost a specifikációkban meghatározott formában és szempontok szerint.
Ezzel a feladat modulokra bontása befejeződött. A teljes bontást az alábbi ábra mutatja.
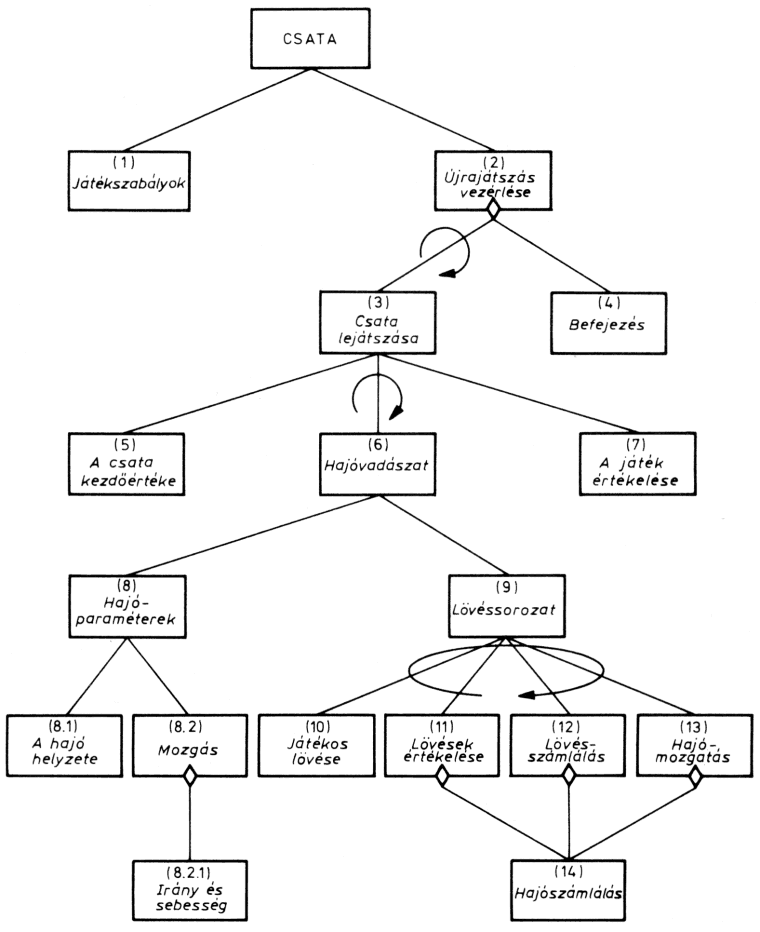
A feladat meglehetősen bonyolult, a programnak sok funkciót kell ellátnia. Bonyolult a feladat szerkezete is. A modulokra bontást 6 szinten végeztük el, vagyis a vezérlési szerkezet összetett.
Meg kell azonban jegyezni, hogy nem minden vezérlési ponton levő modult kell a programban kódolni. Így a (3), (6), (8) és (9) modulok a kódolásból kihagyhatok, mivel az alájuk tartozó modulok hívása nem igényel külső vezérlést. Az ábrából azonban nem érdemes kihagyni őket, hogy a szerkezetet pontosabban lehessen látni.
A feladat vezérlési szerkezetét vizsgálva megállapítható, hogy a program három egymásba ágyazott ciklust tartalmaz. A külső ciklus egy játék, ezen belül van a hajóvadászat, majd a legbelső a lövés végrehajtása. Ez a három ciklus egy kivételével valamennyi modult magában foglalja. Éppen ezért célszerű a szerkezetet mélyebben megvizsgálni.
A JÁTÉK ciklus
A ciklusmag művelete egy teljes játék lejátszás. A ciklusváltozó értékét (U) a játékos határozza meg, vagyis nem a program számítja ki. A ciklust mindaddig ismételni kell, amíg a játékos abba nem akarja hagyni.
A ciklust hátul tesztelő szerkezettel célszerű kialakítani, mivel a folytatásra vonatkozó kérdést a játék legvégén kell feltenni. Ha a játékos be akarja fejezni a játékot, akkor a ciklus befejeződik.
A ciklusban előkészítés nem szükséges, mivel a ciklusváltozó INPUT utasítással kap értéket. A többi változó kezdőértékének beállítását a további két ciklusban kell megvizsgálni.
A HAJÓVADÁSZAT ciklus
A JÁTÉK cikluson belül helyezkedik el. A ciklusmag művelete egy hajó vadászata.
A ciklusváltozó a vadászott hajók száma. Minden ciklusmag (egy vadászat) végrehajtása után a változó értékét eggyel növelni kell. A ciklusmag műveleteit addig kell ismételni, amíg a vadászott hajók száma meg nem egyezik a játékos által igényelt flotta hajóinak számával: T=N. Ekkor a ciklus befejeződik.
A ciklus befejezésének feltételét a ciklusmag végrehajtása után kell ellenőrizni, ezért ezt a ciklust is hátul tesztelő szerkezettel érdemes kialakítani.
A ciklus előkészítő részében a ciklusváltozót (T) és valamennyi komponensét (E, M, S) nullázni kell. Ezt a műveletet az (5) a csata kezdőértéke modulba be kell építeni.
A ciklus befejezése után egy utóműveletben ki kell értékelni a csatát. Ezt a feladatot a (7) a játék értékelése modul végzi el.
A LÖVÉS ciklus
Ez a HAJÓVADÁSZAT ciklusba beágyazott ciklus. A ciklusmag művelete egy lövés leadása és hatásának kiértékelése, beleértve a hajó mozgatását és helyének vizsgálatát is.
Ciklusváltozója a hajóvadászat végét jelző esemény. A ciklusmag műveletét mindaddig végre kell hajtani, amíg valamilyen esemény be nem következik (találat vagy menekülés, vagy sikertelen vadászat a 20. eredménytelen lövés leadása után).
Az események bekövetkezéséhez külön nem rendeltünk változót (ne tévesszük össze az események számát tartalmazó E, M, S változókkal). Ezért a ciklusváltozó valójában nem létezik. Az események bekövetkeztét a (11), (12) és (13) modulok valamelyike jelzi megfelelő logikai vizsgálattal.
Ezt a ciklust is hátul tesztelő szerkezettel célszerű megvalósítani, mivel az eseményvizsgálatot a lövés után kell elvégezni.
Mivel nincs formális ciklusváltozó, így az előkészítésben sem kell beállítani a kezdőértékét. Az előkészítő részben a hajó induló paramétereit kell beállítani [(8) modul] és a lövésszámlálót kezdőértékre (I=1) állítani.
Egy esemény bekövetkezése után a vadászott hajók számlálóját (T) eggyel kell növelni. Ez a lépés azonban már nem a lövés ciklus, hanem a hajóvadászat ciklus része.
Nem kell kódolni [(3), (6), (8) és (9)]. Látható, hogy ez a kódolt szerkezetet úgy módosítja, hogy a hiányzó modulokat a hozzájuk tartozó kódolt modulok helyettesítik balról jobbra haladva. Például az (5) modul után a (8.1) modul hajtódik végre. A (7) modul pedig a (14) modul után következik.
A programon belüli adatáramlás nem igényel magyarázatot, mivel az a vezérlési szerkezetben jól végigkövethető. Az (1)-(5), az (5)-(8.1), a (8.2)-(8.2.1), a (8.2)-(10), a (11)-(14), a (12)-(14), a (13)-(14), a (2)-(7) és a (2)-(4) kapcsolat vezérlés jellegű, a többi modulkapcsolat adat jellegű.
3. A modulok tervezése
(1) Játékszabályok
A modul eljárás típusú. Adatot kívülről nem kap, kimenete a játékszabályok megjelenítése. A program első modulja, ezért a programnév ennek az elején helyezkedik el. A modul egyetlen művelete a játékszabályok kiírása úgy, hogy a képcsöves terminálon is jól elférjen, és legyen még tartalék sor a folytatólagos szöveg kiírására.(2) Újrajátszás vezérlése
A modul vezérlő típusú. Adatot a játékostól kap, amely arra utal, hogy a (3) vagy (4) modult kell végrehajtani. A modul kimenete a vezérlés átadása a kiválasztott modulnak.
A program terve szerint a vezérlésátadás ciklus formájában szerveződött meg. A ciklus belsejében (a ciklusmagban) helyezkedik el az egyik hívható modul [elvileg a (3), de valójában az (5) modul], amely a játék kezdetét és ezen keresztül az egész játék lejátszását jelenti. A másik hívható modul a (4) befejezés modul. Ez a ciklus után helyezkedik el.
A ciklus hátul tesztelő, ezért a döntés alapjául szolgáló adatot is a tesztelés előtt, a játék végén kell bekérni a játékostól.
A ciklus viszont az (1) modul után kezdődik, így gyakorlatilag az egész programot magában foglalja. A modul leglényegesebb művelete egy kérdés a játékoshoz, hogy óhajt-e még egy játékot. Ha a játékos akar játszani, akkor 1-et ír le, és 0-t, ha nem. Ha a bemeneti adat 1, akkor a ciklus ismétlődik, ha nem, akkor a ciklus befejeződik, és a vezérlés a (4) modulra kerül.(3) Csata lejátszása
Nem kódolt modul.(4) Befejezés
A modul eljárás típusú. Kívülről nem kap adatot. Kimenete a játékot megköszönő üzenet. Kiírja a köszönő üzenetet, és a program befejeződik.(5) A csata kezdőértéke
A modul adat típusú, bár elég sok műveletet is végrehajt. Bemeneti adata a hajók száma, amelyet a játékos ír be. Kimeneti adata is az N, valamint az E, M, S és T változó nulla értéke.
A modul az első lépésben nulla értéket ad az E, M, S és T változónak. Ezután kérdést ír ki a játékosnak, hogy hány hajóra akar vadászni. A játékos az N érték begépelésével válaszol. Az N csak természetes lehet, ezért ha a játékos N<=0 értéket gépel be, akkor üzenetet kell kiírni, hogy az adat helytelen, és fel kell szólítani a játékost helyes adat megadására.
Az egészértékűséget úgy lehet biztosítani, hogy az N-nek eleve csak az egész részét vesszük figyelembe: N=INT(N).A (6) hajóvadászat és a (8) hajóparaméterek modulok nem kódolt modulok.
(8.1) A hajó helyzete
A modul eljárás típusú. Bemeneti adata két véletlenszám, amely a hajó koordinátáinak meghatározásához szükséges. Kimeneti adatai a hajó helyzetének koordinátái (X0, Y0).
A modul kezdetén ki kell írni a soron következő hajó sorszámát. A harcban már szerepelt hajók számát a T változó értéke rögzíti minden hajó vadászat végén. Ezért a következő hajó sorszáma: T+1 .
Ez az első olyan modul, amely véletlenszám-generálást végez, ezért még ezelőtt kell elhelyezni a RANDOMIZE utasítást, amely a játékmenetek különbözőségét biztosítja. Vigyázzunk, hogy ezt az utasítást csak kipróbált és jól működő programba tegyük bele. Ezután véletlenszám segítségével meg kell határozni a hajó induló X0 és Y0 koordinátáit:X0=INT (66*RND)
Y0=INT (66*RND)Mivel mozgó hajó esetén az induló koordináták értékét meg kell őrizni, az aktuális koordinátákat az X1, Y1 változókba másoljuk át.
Ebben a modulban kell a lövésszámlálót indulóértékre állítani: I=1.(8.2) Mozgás
A modul vezérlő típusú. Bemeneti adata a játékos kívánságát kifejező adat (A), amely arra utal, hogy a hajó mozogjon-e. Kimenete vagy a vezérlésátadás a (8.2.1) modulnak mozgó hajó esetén, vagy a V=0 sebesség beállítása és a vezérlésátadás a (10) modulra.
A modul kezdetén ki kell írni azt a kérdést, hogy mozogjon-e a hajó. Ha a játékos igent akar mondani, akkor 1-et gépel be, ellenkező esetben 0-t. Álló hajó esetén a sebesség és a komponensei nullák lesznek:V=0
X9=0
Y9=0és a vezérlést át kell adni a (10) modulnak.
Mozgó hajó esetén a (8.2.1) modult kell hívni a sebesség kiszámításához.(8.2.1) Irány és sebesség
A modul eljárás típusú. Bemeneti adatait két véletlenszám alkotja, amelyek alapján ki lehet számítani a mozgás irányát és sebességét. Kimeneti adatai a mozgó hajó két lövés között megtett útjának X9 és Y9 összetevői.
Ki kell számolni a mozgás irányát és a két lövés közötti elmozdulás hosszát (így definiáltuk a sebességet) a már bemutatott módon:D=PI*RND
V=3*RND+0.5A D ismeretében meg lehet határozni a V sebesség X és Y irányú komponenseit:
X9=V*COS(D)
Y9=V*SIN(D)Ezután innen is a (10) modulnak kell átadni a vezérlést.
(9) Lövéssorozat
Nem kódolt modul.(10) Játékos lövése
A modul típusa: adat. Bemeneti adata a játékos lövésének két koordinátája, amelyet a játékos gépel be. A modul kimenete: a lövés "kozmetikázott" koordinátái.
A modul kezdetén ki kell írni a játékos számára, hogy hányadik lövés következik. Ezt az I aktuális értéke tartalmazza. Ezután a program bekéri a soron következő lövés koordinátáit (X2, Y2). A specifikáció szerint mindkét koordinátának csak az egész részét vesszük figyelembe.(11) Lövések értékelése
A modul eljárás típusú. Bemeneti adatai a hajó aktuális koordinátái (X1, Y1) a (13) modulból és a becsapódás koordinátái (X2, Y2) a (10) modulból. A modul kimenete a találat jelzése vagy a hajó és a becsapódás helye távolságának kiírása.
A távolságot a program terve szerint azR=INT(SQR((X2-X1)^2+(Y2-Y1)^2))
illetve Spectrum BASIC-ben
R=INT (SQR (ABS (X2-X1)^2+ABS (Y2-Y1)^2))
kifejezéssel kell kiszámítani.
Ezután R értékétől függően két műveletsorozat valamelyikét kell végrehajtani (IF THEN ELSE szerkezet).
Ha R=0, akkor ki kell írni a találatot, és hogy hányadik hajót süllyesztette el a játékos. Ez itt is a T+1 érték lesz, mint a vadászat elején [(8.1) modul]. Mivel ez "esemény", az eltalált hajók számát növelni kell eggyel: E=E+1. Ezután a vezérlést a hajókat számláló (14) modulnak kell átadni.
Ha R>0, akkor ezt a játékos részére ki kell írni, és a vezérlést a (12) lövésszámlálás modulnak kell átadni.(12) Lövésszámlálás
A modul eljárás típusú. Bemeneti adata a leadott lövések száma, és ennek növelt értéke a modul egyik kimenete. A modul másik kimenete a sikertelen vadászat jelzése a 20. sikertelen lövés után.
A modul első műveleteként a leadott lövések számát eggyel növeli: I=I+1. Ezzel a lépéssel a program a következő lövés sorszámát állítja be.
Amíg I<21, addig a vezérlést a (13) modulnak kell átadni, hogy a hajó mozgatását elvégezze. Ellenkező esetben a játékos már 20 lövést leadott, és a hajót nem találta el. Ez egy sikertelen vadászat végét jelzi. Ilyenkor a sikertelen vadászatok számát növelni kell: S=S+1, és a vezérlést a (14) modulnak kell átadni a hajók számlálására. Jól érzékelhető, hogy ez a két utóbbi műveletsor IF THEN ELSE szerkezetet alkot.(13) Hajómozgatás
A modul eljárás típusú. Bemeneti adata álló hajónál a hajó jelenlegi helye (X1, Y1), amelyet induláskor a (8.1) modulból kap; a továbbiakban ezt az adatot a modul saját maga állítja elő. Mozgó hajó esetén pedig a két lövés között megtett út koordinátáinak hossza (X9, Y9) a (8.2.1) modulból. Kimeneti adatai egyrészt a hajó új helye, másrészt annak a pontnak a koordinátái (X1, Y1), amelyet a csatamező elhagyására utalnak.
A modulban a hajó helyzetét X9, Y9 távolsággal módosítani kell. Elvileg meg kellene vizsgálni, hogy mozgó hajóról van-e szó (A vizsgálata). Ettől el lehet tekinteni, ha az aktuális koordinátákat az alábbi kifejezésekkel számítjuk ki:X1=X1+X9
Y1=Y1+Y9Álló hajó esetében X9=0 és Y9=0, tehát a koordináták változatlanok maradnak.
Nem biztos, hogy az új koordináta egész szám lesz, mivel X9 és Y9 vegyes szám is lehet. Ezért a kapott koordinátákat a szokásos szabályok szerint kerekíteni kell. Megjegyezzük, hogy a törtrész egyszerű leválasztása (integerképzés) kevésbé pontos, mert a félnél nagyobb törtrész esetén is lefelé kerekítene.
A kerekítést egy egyszerű módszerrel fogjuk most elvégezni:X1=INT (X1+X9+.5)
Y1=INT (Y1+Y9+.5)Ha ugyanis az X1+X9 törtrésze kisebb, mint 0.5, akkor int (X1+X9+0.5) = int (X1+X9). Ekkor tehát a lefelé kerekítés helyes eredményt ad.
Ha az X1+X9 törtrésze nagyobb, mint 0.5, akkor int (X1+X9+0.5) = 1+int (X1+X9), mivel az X1+X9+0.5 összeg egész része már eggyel nagyobb, mint az X1+X9 egész része. Látható, hogy a 0.5 hozzáadásával az egészrész-függvény már eredményesen alkalmazható kerekítésre.
Ezután meg kell vizsgálni, hogy a hajó nem hagyta-e el a csatamezőt. Egy hajó akkor van a csatamezőben, ha az1<=X1<=66
1<=Y1<=66feltételek teljesülnek. Ebből következik, hogy ha az alábbi feltételek közül valamelyik teljesül, akkor a hajó elhagyta a csatamezőt:
X1<1
X1>66
Y1<1
Y1>66Ha a hajó elhagyta a csatamezőt, akkor elmenekült. Ezt a játékossal közölni kell, és ki kell írni az induló és az aktuális koordinátákat. A menekült hajók számlálóját meg kell növelni: M=M+1 , és a vezérlést a (14) modulnak kell átadni.
Ha a hajó nem menekült el, akkor a lövéssorozatot folytatni kell, és a vezérlést a (10) modulnak kell visszaadni.(14) Hajó számlálás
A modul eljárás típusú. Bemeneti adata a harcban már részt vett hajók száma (T). Kimeneti adata az aktualizált hajószám.
A modul valamilyen esemény után hajtódik végre. Ekkor a vadászott hajók számát növelni kell: T=T+1.
Ezután meg kell vizsgálni, folytatódik-e a játék. Ha T<N, akkor a játék folytatódik, és újabb hajóvadászat [(8.1) modul] következik. Ellenkező esetben a játék befejeződik, és a vezérlést a (7) játék értékelése modulnak kell átadni.(7) A játék értékelése
A modul típusa: eljárás. Bemeneti adatai az egyes események előfordulási száma (E, M, S) a (11), (12), (13) és az összes vadászott hajó száma a (14) modulból. Kimenete a játék eredményeinek kiírása. A modulban a játékos értékelése egy CASE szerkezetben megy végbe. Az első három lépésben az E (találatszám) és a T viszonyától függően választjuk ki a CASE szerkezet ágait. Ezek csökkenő sorrendben:E=T
E>=T/2 (E<T)
E<T/2Az utóbbit az E>0 feltétel vizsgálattal helyettesítjük.
A negyedik és az ötödik esetben E=0 . Ezt azonban már nem kell külön vizsgálni, mert ha a program a fenti feltételsort a megadott sorrendben megvizsgálja, akkor nem teljesülésük esetén E=0.
A negyedik esetben T=M, és az ötödikben S>0 , amit már nem is kell vizsgálni, mert ha az említett feltételek egyike sem teljesül, akkor az utóbbi eset áll fenn. Ezzel valamennyi lehetséges eseménykombinációt figyelembe vettünk.
4. A kódolás
(1) Játékszabályok
Ez a program első modulja, ezért ennek az elején helyezzük el a programnevet és a RANDOMIZE utasítást.10 REM *** Csata ***
20 RANDOMIZE
30 REM * Jatekszabalyok *
40 PRINT "Egy 66x66-os csatamezoben kell"
50 PRINT "egy ismeretlen helyen levo"
60 PRINT "hajot eltalalni a celpont"
70 PRINT "koordinatainak megadasaval."
80 PRINT "A program a becsapodas es a"
90 PRINT "hajo tavolsagat kozli."
100 PRINT "Tobb hajobol allo flottara"
110 PRINT "is vadaszhat, de a hajokra"
120 PRINT "egyenkent kell vadaszni."
130 PRINT "Minden ellenseges hajora"
140 PRINT "20 lovest adhat le. A hajok"
150 PRINT "allhatnak, vagy kerheti, hogy"
160 PRINT "mozogjanak. Csak akkor mozgassa"
170 PRINT "az ellenseg hajoit, ha mar sok"
180 PRINT "csatat megnyert, mert mozgo"
190 PRINT "celpontot nehezebb eltalalni!"(2) Újrajátszás vezérlése
A modul a hátul tesztelő JÁTÉK ciklust foglalja magában. Ennek megfelelő formában kell kódolni. A ciklusmagban helyezkedik el az első és az utolsó modul kivételével valamennyi, ezért a (2) modul eleje (cikluskezdet) a program elején, a tesztelés a program végén kap helyet:200 REM * Ujrajatszas vezerlese *
210 REM * Jatek ciklus kezdet *
...
1420 PRINT
1430 PRINT "Ohajt meg jatszani? (1/0)"
1440 INPUT U
1450 IF U=0 THEN GO TO 1470
1460 GO TO 200
1470 REM * Jatek ciklus vege *(5) A csata kezdőértéke
A modulban levő kérdés előtt egy üres sort írunk ki, hogy a kérdés elkülönüljön a megelőző kiírásoktól. Ezt az elvet a továbbiakban is alkalmazzuk. A modulban levő IF THEN ELSE szerkezetet az ismert formában kódoljuk. A modul kódja:220 REM * A csata kezdoerteke *
230 LET E=0
240 LET M=0
250 LET S=0
260 LET T=0
270 PRINT
280 PRINT "Hany hajobol allo flottaval"
290 PRINT "ohajt megkuzdeni?"
300 INPUT N
310 IF N<=0 THEN GO TO 330
320 GO TO 370
330 REM * THEN ag *
340 PRINT "Csak pozitiv szamod adhat meg!"
350 PRINT "Kerem, valaszoljon ujra!"
360 GO TO 270
370 REM ELSE ag
380 LET N=INT (N)
390 REM * IF veg *(8.1) A hajó helyzete
Ebben a modulban kezdődik a HAJÓVADÁSZAT ciklus, amelyet a kódolás megismert szabályai szerint ki kell fejezni. A modulban levő kiírást a (8.2) modulban levő adatkérés állítja le. A modul kódja:400 REM * A hajo helyzete *
410 REM * Hajovadaszat ciklus kezdet *
420 PRINT : PRINT
430 PRINT "A(z) ";T+1;". hajo kovetkezik!"
440 LET X0=INT (66*RND)
450 LET Y0=INT (66*RND)
460 LET X1=X0
470 LET Y1=Y0
480 LET I=1(8.2) Mozgás
A modul egy IF THEN ELSE szerkezetet is tartalmaz. A kódolást egyszerűsíteni lehet azzal, ha az IF utasítás sorában a THEN-ágban levő elágazást kódoljuk (GO TO 590). A modul kódja:490 REM * Mozgas *
500 PRINT
510 PRINT "Mozogjon az ellenseges hajo? 1/0"
520 INPUT A
530 IF A=1 THEN GO TO 590
540 REM * ELSE ag *
550 LET X9=0
560 LET Y9=0
570 GO TO 640
580 REM * IF veg *(8.2.1) Irány és sebesség
A modul kódja:590 REM * Irany es sebesseg *
600 LET D=PI*RND
610 LET V=3*RND+0.5
620 LET X9=V*COS (D)
630 LET Y9=V*SIN (D)(10) Játékos lövés
Ebben a modulban helyezkedik el a LÖVÉS ciklus kezdete. A modul kódja:640 REM * Jatekos lovese *
650 REM * Loves ciklus kezdet *
660 PRINT : PRINT
670 PRINT "A(z) ";I;". loves koordinatai: "
680 INPUT X2,Y2
690 LET X2=INT (X2)
700 LET Y2=INT (Y2)(11) Lövések értékelése
A modul egy IF THEN ELSE szerkezetet tartalmaz. A találat közlését tartalmazó szöveg kiíratását két sorra bontottuk, mivel egy sorban nem fért volna el.710 REM * Lovese ertekelese *
720 LET R=INT (SQR (ABS (X2-X1)^2+ABS (Y2-Y1)^2))
730 IF R=0 THEN GO TO 750
740 GO TO 810
750 REM * THEN ag *
760 PRINT
770 PRINT "On elsullysztette az ellenseg"
780 PRINT T+1;". hajojat."
790 LET E=E+1
800 GO TO 1100
810 REM * ELSE ag *
820 PRINT "A becsapodas tavolsaga: ";R
830 REM * IF veg *(12) Lövésszámlálás
A modul kódja:840 REM * Lovesszamlalas *
850 LET I=I+1
860 IF I>20 THEN GO TO 880
870 GO TO 950
880 REM * THEN ag *
890 PRINT
900 PRINT "Ez nem sikerult!"
910 PRINT "A Hajo a(z) ";X0;",";Y0
920 PRINT "Koordinatakrol indult"
930 LET S=S+1
940 GO TO 1100
950 REM * IF veg *(13) Hajómozgatás
Ebben a modulban helyezkedik el a LÖVÉS ciklus vége. A ciklus befejezését négy IF utasítás vizsgálja vagylagosan összekapcsolva. Az IF utasítások nem IF THEN vagy IF THEN ELSE szerkezetbeli funkciót látnak el, hanem ciklusbefejezést tesztelnek.960 REM * Hajomozgatas *
970 LET X1=INT (X1+X9+.5)
980 LET Y1=INT (Y1+Y9+.5)
990 IF X1<1 THEN GO TO 1040
1000 IF X1>66 THEN GO TO 1040
1010 IF Y1<1 THEN GO TO 1040
1020 IF Y1>66 THEN GO TO 1040
1030 GO TO 640
1040 REM * Loves ciklus veg *
1050 PRINT
1060 PRINT "A hajo a(z) ";X0;",";Y0
1070 PRINT "koordinatakrol indult es"
1080 PRINT "Az ellenseg elmenekult!"
1090 LET M=M+1(14) Hajószámlálás
A számlálás után ebben a modulban kap helyet a HAJÓVADÁSZAT ciklus befejezése. A modul kódja:1100 REM * Hajoszamlalas *
1110 LET T=T+1
1120 IF T>=N THEN GO TO 1140
1130 GO TO 400
1140 REM * Hajovadaszat ciklus veg *(7) A játék értékelése
A modul egy CASE szerkezetet tartalmaz. A végén fejeződik be a JÁTÉK ciklus.1150 REM * A jatek ertekelese *
1160 PRINT : PRINT
1170 PRINT "Az elsullyesztett hajok szama: ";E
1180 PRINT "Az elmenekult hajok szama: ";M
1190 PRINT "A sikertelen vadaszatok szama: ";S
1200 REM * CASE kezdet *
1210 IF E=T THEN GO TO 1260
1220 IF E>=T THEN GO TO 1300
1230 IF E=0 THEN GO TO 1330
1240 IF T=M THEN GO TO 1360
1250 GO TO 1400
1260 REM * 1. eset *
1270 PRINT "On egy zsenialis admiralis!"
1280 PRINT "Tokeletes gyozelmnet aratott!"
1290 GO TO 1410
1300 REM * 2. eset *
1310 PRINT "On jol harcolt, csak kisse meg rutintalan!"
1320 GO TO 1410
1330 REM * 3. eset *
1340 PRINT "On egy atlagos kepessegu hadvezer!"
1350 GO TO 1410
1360 REM * 4. eset *
1370 PRINT "Tanuljon meg celozni!"
1380 GO TO 1410
1390 REM * 5. eset *
1400 PRINT "On tehetsegtelen!"
1410 REM * CASE veg *(4) Befejezés
A modul kódja:1480 REM * Befejezes *
1490 PRINT
1500 PRINT "Koszonom a jatekot!"
1510 PRINT "Viszontlatasra!"
1520 STOP
5. Az eredmény értékelése
Az elkészült programot tesztelés után használatba vehetjük. A program elindítása után kiírja a játékszabályokat, és rögtön utána megkérdezi, hogy hány hajóból álló flottával óhajtunk játszani. A válasz begépelése után az 1. hajó vadászata kezdődik, azt kell eldönteni, hogy mozogjon-e a hajó.
Ezután következnek a lövések. A becsapódás távolsága támpontot ad a lövés koordinátáinak meghatározásához. Találat esetén a program közli az örvendetes eseményt, és a 2. hajó vadászata kezdődik el.
A menekülési pont megjelölésének szépséghibája, hogy nem a csatamező határpontjainak valamelyikét közli a program, hanem azt a pontot, ahová a hajó a legutolsó mozgatás eredményeként eljutott. Ez azonban nem nagyon zavaró.
Ha a játékos a 20. lövéssel sem találja el a hajót, a hajó vadászata sikertelenül fejeződik be.
Ezután a játékos újabb játékba kezdhet, vagy abbahagyhatja a játékot. Befejezés esetén a program elbúcsúzik a játékostól.
Látható, hogy a program a specifikáció szerint működik, és bárki meggyőződhet róla, hogy kellemes szórakozást nyújt. Hibájául róható fel, hogy az értékelésnél nem veszi figyelembe, hány lövéssel találja el a játékos az ellenséges hajót, holott ez elég lényeges.
4. Feladatok megoldása összetartozó adatokkal
Az előző fejezetben egyedi adatok feldolgozását ismertük meg. A felmerült problémákban szereplő kevés adatot többnyire egymástól függetlenül kezeltük, hiszen csak annyi összefüggés volt közöttük, hogy egy jelenség különböző jellemzőit jelölték. Az adatok kezelésével kapcsolatosan bonyolult helyzetek nem merültek fel, mivel a bemeneti adatokat többnyire egy néhány soros adat típusú modulban sikerült definiálni.
Ebben a fejezetben olyan feladatok megoldását tekintjük át, amelyekben több, valamilyen szempontból összetartozó adatot kell feldolgozni. Tekintsük át a IV. problémában szereplő számítógépes feladatot. Ha egy vállalat több dolgozójának havi bérelszámolását kellene számítógéppel elvégezni. A bemeneti adatok minden dolgozónál a név, az alapbér és a letiltás lennének. Egy-egy dolgozóra nézve ezek egyedi adatoknak számítanak, mivel különnemű adatok, és a számuk is kevés. De ha egy vállalat valamennyi dolgozóját tekintjük, akkor már más a helyzet. Ha a vállalatnál n fő dolgozik, akkor a feldolgozás során n nevet, n dolgozó alapbérét, letiltását kell megadni a feldolgozáshoz, fel kell dolgozni, az eredményeket ki kell írni, és összesítéseket kell végezni. A műveletek többségét annyiszor kell megismételni, ahány egyedhez tartozó adat vesz részt a feldolgozásban. Tudjuk, hogy ezt ciklikusan lehet elvégezni, és a feladatmegoldás szempontjából nem jelent nagyobb problémát (az idézett esetben). Ennél lényegesen komolyabb feladat a bemeneti adatok meghatározása. A IV. feladatban a gép egyszerre csak egy dolgozó adataival foglalkozott, és ezeket minden egyes feldolgozás elején kellett megadni a programnak. De mi lenne, ha ehhez a programhoz is a többi probléma során megismert módon adnánk meg a bemeneti adatokat: értékadási utasítással. Ezt 500 főnél 1500 utasításból álló "modul" végezné el. Ez már tárolási problémákat is felvetne (80 x 1500 = 120 000 bájt helyigényt kis számítógépek nem tudnak kielégíteni). Nehéz lenne az adatok elnevezése is, hiszen az egyszerűbb BASIC-változatok esetén 26 X 11= 286 különböző változónevet lehet képezni a megismert módon, tehát 1500 változót emiatt sem lehet kezelni.
Látható, hogy a sok adat olyan gondokat vet fel, amelyeket az eddig megismert módokon nem tudunk megoldani. Ezért a sok adat feldolgozásához más programozási eljárások szükségesek.
Felhasználjuk azt a tényt, hogy n nevet, alapbért, letiltást kell kezelni, azaz hasonló jellegű, valamilyen szempontból összetartozó adatokat. Ezt nemcsak az adatkezelés (adatok létrehozása, -válogatása, -módosítása stb.), hanem a feldolgozás során is figyelembe vesszük, ugyanis az adatokat valamilyen csoportokba osztva dolgozza fel a program (egyszerre 1 fő adatait).
Az összetartozó adatállományok jellemzői, hogy olyan adatokból állnak, amelyek hasonló egyedek tulajdonságainak értékei. Az említett példában az egyedek egy vállalat dolgozói. A hasonlóság az bennük, hogy ugyanattól a vállalattól kapják a bérüket azonos algoritmus szerint kiszámítva. Tulajdonságaik a nevük, az alapbérük és a letiltás. Az értékek a konkrét nevek, az alapbér és a letiltás összege.
Más problémánál az egyed lehet késztermék, nyersanyag, munkagép, családi ház stb. Tulajdonságaik pedig a feladattól függően és értelemszerűen a súlyuk, színük, méretük, nyersanyaguk, összetevőik stb., az adatok pedig ezek konkrét értékei.
Az adatokat mindig az egyedek szerint határoljuk el. Az egy egyedhez tartozó adatokat logikai rekordoknak tekintjük. Az adatállomány pedig logikai rekordok összessége. Egy adatállományon belül a logikai rekordok felépítése azonos (ugyanazok a tulajdonságok ugyanabban a sorrendben): a dolgozó neve, alapbére, letiltása. Ez az azonosság teszi lehetővé az adatkezelés és a feldolgozás egyszerűsítését. Ha például tudjuk, hogy egy logikai rekord egy állományon belül 3 adatból áll, és a logikai rekordok első adata egy név, akkor az adatokat elég csupán felsorolni a kötött sorrendben, és a definícióból minden adatról tudni lehet, hogy milyen tulajdonságnak az értéke, és melyik egyedre vonatkozik.
Az adatállományok logikai felépítése után azt kell megvizsgálni, hogy az adatállományokat hogyan lehet fizikailag tárolni, vagyis olyan módon, hogy egy program is tudja kezelni.
Az adatállományok tárolása fizikailag kétféleképpen valósítható meg:
Az első megoldás a kisebb adatállományok, a második a nagy adatállományok tárolására alkalmas.
A belső tárban további két tárolási mód alkalmazható:
A vektor egyedenként egyetlen tulajdonság értékeit (adatot) tartalmazza. Ez lehet vagy az egyed azonosítója, vagy ha ez nem fontos, akkor csak valamelyik tulajdonságának az értéke. Például olyan méréseknél, amikor mérésenként csupán egyetlen jellemzőt kell mérni, az adatokat tárolhatjuk egy vektorban. Ekkor a mérések azonosítóját külön nem lehet tárolni (mert nincs rá hely), de a tárolás sorrendje erre is utalhat. Tegyük fel, hogy a mérési eredmények az alábbiak:
t(1) = 22.3
t(2) = 20.8
t(3) = 15.6
t(4) = 9.2
t(5) = 12.7
t(6) = 19.8
Ha t indexei a mérés sorszámára utalnak, akkor az adatokat a megadott sorrendben tárolva az azonosítókat is közvetve tároljuk. A vektorban csak az értékek szerepelnek:
t = [22.3, 20.8, 15.6, 9.2, 12.7, 19.8, ...]
A vektor (méréssorozat) egyetlen név alatt szerepel (t). A vektor valamelyik adott elemére az elem indexével hivatkozunk:
t(5)=12.7
Egy vektor kötött számú (n) adatot tartalmaz.
A tömb egyedenként több, elvileg kötetlen számú tulajdonságértéket tartalmaz. A tömbben mindig van lehetőség az egyedi azonosító tárolására, ha szükséges. Tömbben lehet tárolni a fenti méréssorozat adatait, ha mérésenként több jellemző értéket kell mérni. Megállapodás szerint egy egyed adatai egy sorba, az azonos tulajdonságra vonatkozó adatok pedig egy oszlopba kerülnek.
t(1,1) = 22.3 t(1,2) = 20.8 t(1,3) = 19.2 t(2,1) = 20.8 t(2,2) = 18.2 t(2,3) = 17.6 t(3,1) = 15.6 t(3,2) = 14.1 t(3,3) = 13.1 ... ... ...
Az együvé tartozást az indexek is kifejezik. A kéttagú index első tagja az egyedre, a második a tulajdonságra utal. Ha az egyedek száma m, a tulajdonságok száma n, akkor m sorból és n oszlopból álló m x n méretű tömb szükséges az adatok tárolására.
A tömb egy konkrét elemére indexével lehet hivatkozni:
t(2,3) = 17.6
A BASIC csak kétdimenziós tömböket tud kezelni.
Külső tárolóeszközön azokat az adatállományokat kell tárolni, amelyek méretük miatt a belső tárban nem férnének el. Az ilyen adatállomány is tömbnek tekinthető. Egy tömbbeli sornak itt rekord a neve.
Mivel az ilyen állomány nem a belső tárban helyezkedik el, elemeire nem lehet közvetlenül hivatkozni, hanem rekordonként dolgozható fel. Vagyis egy konkrét adat csak úgy érhető el, ha az adatot tartalmazó rekordot a program behívja, és ebből a szükséges adatot kiolvassa. A külső tárolóeszközön tárolt adatállomány elvileg korlátlan méretű, de a gyakorlatban a nagyságát a tárolóeszközök fizikai méretei korlátozzák.
Az összetartozó adatok feldolgozását jellemzi, hogy
A tömbös szerkezetből adódik, hogy általában a kiírás is bonyolultabb, mivel sok oszlopos, sok soros táblázatok kiírása szükséges.
4.1 Vektorok és tömbök kezelése
A sok összetartozó adatot tartalmazó problémánál az adatok szervezése, az adatállomány definiálása, értékének meghatározása külön tervezési lépést igényel. Először azt kell eldönteni, hogy milyen egyedek vannak, és ezek milyen tulajdonságai vesznek részt a feldolgozásban. Egy programban több vektor és tömb is szerepelhet. Mindegyik méretét, felépítését pontosan meg kell tervezni.
A vektorok és a tömbök ugyanazokkal a jelekkel jelölhetők, mint a változók. Az eltérés az, hogy a vektor-, illetve a tömbnév után a zárójellel mutatjuk, hogy nem egyszerű változóról van szó.
A program elején - vagy legalábbis a vektor vagy a tömb használata előtt - a DIM utasítással kell helyet foglalni a felhasználandó vektor, illetve tömb részére:
x DIM V(egész szám)
Ennek hatására a fordító az egész szám által meghatározottnál eggyel nagyobb méretű V vektor számára foglal helyet, amelynek elemei közé tartozik a 0 indexű is. (Egyes BASIC változatokban a tömb első elemének indexe nem 0, hanem egy, tehát a tömb elemeinek száma a megadott számmal lesz egyenlő.)
Tömb számára hasonlóan lehet helyet fenntartani. Például:
20 DIM T(15,3)
Ebben az esetben a sorok indexe 0-tól 15-ig, az oszlopoké 0-tól 3-ig van megengedve.
Egy DIM utasításban - a BASIC implementációk többségében - több vektor és/vagy tömb is megadható vesszővel elválasztva:
20 DIM V(15),T(15,3)
Egyes BASIC implementációkban, ha a programban egy olyan vektorelemmel vagy tömbelemmel akarunk műveletet végezni, amelynek vektorát, illetve tömbjét nem definiáljuk, akkor a program a vektor számára 10 (illetve 11), a tömb számára 10 X 10 (illetve 11 X 11) elemű tömböt foglal le. Ha ilyen esetben 10-nél magasabb indexű elemmel akarunk műveletet végezni, a fordító hibát jelez és a program futása leáll. Ugyanez történik akkor is, ha definiált vektor, illetve tömb esetén a definiáltnál magasabb indexű elemmel akarunk műveletet végezni. (Tömb esetén elegendő az egyik indexet túllépni, hogy a hiba bekövetkezzék.)
A vektor, illetve a tömb elemeire a vektor, illetve a tömb jelével és az elem sorszámával, illetve koordinátáival (zárójelben) hivatkozunk:
V(11)
A V vektor 11-es indexű elemét jelöli. A
T(3,2)
A T tömb harmadik sorának második elemét ábrázolja, ha a 0 indexű elemeket nem vesszük tekintetbe.
IX. probléma
Maximum 100, de esetenként változó számú mérési sorozat eredményeit (hőmérséklet) kell kiértékelni. Meg kell határozni a mérések átlagát és szórását. Az értékeket növekvő sorba kell rendezni, és ki kell írni, hogy a szélsőséges értékeket külön is látni lehessen. Ezek kiírásakor az egyes értékeknél a mérés sorszámát is fel kell tüntetni, hogy a sorrendből adódó szélsőséges értékek felderíthetők legyenek. Az eredményeket a következő formában kell kiírni:
A MÉRÉS EREDMÉNYEI
A MÉRÉSEK SZÁMA: X
AZ ÁTLAGOS HŐMÉRSÉKLET: X C
A MÉRÉSEK SZÓRÁSA X.XA SORBA RENDEZETT MÉRÉSI EREDMÉNYEK
SORSZÁMA ÉRTÉK
(max 100 sor)
1. A probléma elemzése
A mérést - a probléma leírása alapján - nem a számítógép vezérli, ezért a mért értékeket a mérést végző olvassa le és adja a számítógépnek akár közvetlenül minden mérés végén, akár az adatok összegyűjtésével a mérés sorozat befejezésekor. A mérési sorozat maximum 100 mérésből állhat. Hogy a mérést végző ezt ne lépje túl, a mérések számát előre el kell kérni. Ezek alapján az adatbevitel programozható.
Az adatbevitel után az átlagot és a szórást a jól ismert kifejezések segítségével lehet meghatározni:
ahol
A = átlag,
ti = az i-edik mérés értéke,
m = a mérések száma.
Ezután a mérési eredményeket növekvő sorrendbe kell rendezni, és az eredményt ki kell írni. Minden eredmény mellé fel kell tüntetni a mérés sorszámát. Ez a feladat is elvégezhető számítógéppel.
A program adatait egy vektorban lehet tárolni. Mivel a vektor hőmérsékletadatokat tartalmaz, legyen a jele T. A vektor elemeit a felhasználó gépeli be. Minden esetben csak annyi adatot tartalmaz a feladat, ahány mérést végez a felhasználó. Az adatokból előbb átlagot, majd szórást kell számítani. Az utolsó lépésben az adatokat nagyság szerint kell sorba rendezni. Ehhez elég lenne egy másik vektor, amely az adatokat átrendezve tárolná, de a mért értékek mellett a mérés sorszámát is meg kell jegyezni, ezért a sorszámot is tárolni kell a mért érték mellett. Kétféle adat (sorszám, érték) vektorban nem tárolható, ezért erre egy tömböt kell felvenni. Legyen ennek a jele R (rendezett adatok). A T vektor 100 elemű, az R tömb pedig 100 sor x 2 oszlop méretű lesz.
A sorbarendezés csak akkor végezhető el helyesen, ha a felhasználó sorrendben adja be a mérési adatokat [T(1) = az első mérés eredménye, T(2)= második mérés eredménye, ...]. Ha ez nem biztosítható, akkor az adatbevitelnél is meg kellene jelölni, hogy melyik mérési adatbevitel következik. Feltételezzük azonban, hogy a felhasználó sorrendben tudja begépelni az adatokat.
A számítógépes programban szükség van egy adatrögzítő modulra, mely rögzíti a bemeneti adatokat. Ezekből kell átlagot, majd szórást számítani, végül az adatokat át kell rendezni. Az első modult kivéve mindegyik modulhoz tartozik kiírás is. Megoldásunkat úgy készítjük el, hogy a modulfunkciókhoz a kiírást is hozzávesszük. Ennek eredményeként a kiírás nem alkot önálló modult.
2. A program tervezése
A program első modulja végzi az adatok bevitelét. Mérésenként legfeljebb 100 adat lehetséges. A felhasználó minden konkrét esetben megtervezi, hogy hány mérést végez, ezért az adatbevitel elején tudni lehet, hány adatot kell a modulnak beolvasni terminálról. Ezt a felhasználó közli. Az adatbevitelt ciklikusan kell elvégezni, mivel így a legegyszerűbb. A modul további bontása felesleges.
A következő modul funkciója az átlagszámítás. Ehhez a mért értékeket összegezni kell, majd el kell osztani a mérések számával, a végén az eredményt ki kell írni. Célszerű a modult két modulra bontani; az egyik végzi a feldolgozást, a másik pedig a kiírást.
A szórásszámítás a következő funkció, amely felhasználja az átlagszámítás eredményét. Ezt a modult is célszerű kettévágni; az egyik modul végzi a számítást, a másik pedig a kiírást.
Az utolsó feladat a mérési eredmények sorbarendezése és kiírása. Ezt is célszerű két modulban elvégezni.
A programban vezérlőmodulokra nincs szükség. Elegendő, ha az egyes modulok továbbadják a vezérlést a megjelölt sorrendben. Ebből következik, hogy a modulok között adatkapcsolat van. Az (1) adatbevitel modul a (2.1) átlagszámítás, a (3.1) szórásszámítás és a (4.1) rendezés modul számára biztosít bemeneti adatokat. A (3.1) szórásszámításhoz a (2.1) átlagszámítás modul is ad adatot (az átlagot). A kiírási modulokhoz az adatokat az őket megelőző modulok szolgáltatják.
3. A modulok tervezése
(1) Az adatbevitel
A modul adat típusú, mivel fő funkciója a mérési adatok beolvasása. Bemeneti adatai a mérési adatok, amelyeket a felhasználó ad be. Kimenete szintén ez az adathalmaz, valamint a mérések száma, amelyet a többi modulnak ad át.
Ebben a modulban kap helyet a programnév, majd le kell kötni a mérési adatokat tároló 100 elemű T nevű vektor helyét a megismert DIM utasítással. Ezután kezdődhet a modul "érdemi" feladatának ellátása, az adatok beolvasása. Első lépésként az adott mérési folyamat méréseinek számát kell bekérni a felhasználótól a már ismert adatbeolvasási eljárás segítségével. A felhasználó számára ki kell írni: "A MÉRÉSEK SZÁMA:", erre a felhasználó begépeli az M változó értékét.
A mérési adatok beolvasásakor minden egyes adat begépelése előtt tanácsos kiírni, hogy hányadik adat következik. Ezzel segíthetjük a felhasználót, hogy mindig helyes adatot írjon be. Az adatbevitelt ciklusban kell végezni, hiszen hasonló műveletet kell M-szer ismételni.
A ciklusmagban két művelet kap helyet: a következő adat sorszáma és az adatbeolvasás. A ciklust addig kell folytatni, amíg a beolvasott adatok száma eléri M-et. Ekkor a ciklusból ki kell lépni, és az adatbeolvasás befejeződött.
Az adatbeolvasási ciklusban fontos követelmény, hogy a beolvasott adatok a megfelelő indexű vektorelembe kerüljenek, ami azt jelenti, hogy az első beolvasott adat a T(l) értéke, a második adat pedig a T(2) értéke stb. legyen. Ez elérhető, ha az indexek értékét minden beolvasás előtt eggyel növeljük. Ez úgy oldható meg, hogy az indexet I változónak tekintjük, és értékét minden adatbevitel előtt eggyel növeljük. Ezzel biztosítjuk, hogy az adott sorszámú mérési adat az ugyanolyan sorszámú vektorelembe kerüljön.
A ciklust egyszerűen meg lehet szervezni a FOR, NEXT utasításokból álló ciklussal, így ugyanis az I növelése és a befejezési feltétel kódolása kiesik. A ciklusváltozó itt az I index lesz, amelynek értéke 1-től M-ig változik az egyes lépésekben. Ez az algoritmus jellemző a vektorok kezelésére. A vektorok elemeit ugyanígy ciklusban kell feldolgozni. Mivel adott számú elemről van szó, a FOR, NEXT típusú ciklusok alkalmazása a legcélszerűbb. Ciklusváltozóként az 1-t vezetjük be, és ez 1-től M-ig minden egész értéken végigfut a feldolgozáskor. Hogy mindig a ciklusváltozónak megfelelő vektorelem kerüljön feldolgozásra, a vektorelem indexét az I jelöli: T(I).
Ennek eredményeként mindig az aktuális I értéknek megfelelő sorszámú vektorelemet dolgozza fel a program. Ezzel a modul algoritmusát meghatároztuk.(2.1) Átlagszámítás
A modul típusa: eljárás. Bemeneti adatai a T(I) mérési adatok és a mérések száma az (1) modulból. Kimeneti adata a mérési adatok átlaga. Az átlagot a már ismert kifejezés alapján kell kiszámítani. Először a T(I) adatok értékeit kell összegezni. Ezt az összeget az S változó tartalmazza. Az összegezést ciklusban érdemes elvégezni az (1) modulnál ismertetett módon. A ciklusmagban az S=S+T(I) összegezést kell elvégezni. Ebben az esetben is FOR, NEXT típusú feldolgozó ciklust alkalmazunk, amely biztosítja, hogy mindig a soron következő T(I) értéket adja hozzá a program az S-hez. A ciklus előkészítő műveletében az S gyűjtőt nullázzuk. Az összeget M-mel el kell osztani, és megkapjuk az átlagot.(2.2) Átlagkiírás
A modul eljárás típusú. Bemeneti adata az A átlagérték, amely egyúttal a kimenete is. A modul egyetlen művelete az átlag kiírása a specifikáció szerint.(3.1) Szórásszámítás
A modul eljárás típusú. Bemeneti adatai a mérési adatok és az adatok száma az (1) modulból, valamint a szórás számításához szükséges A átlagérték a (2.1) modulból. A modul kimenete a szórás (D2).
A szórást a már ismert kifejezés szerint kell kiszámolni. Először az (A-T(I))^2 különbségek négyzetét kell képezni a K változóban:K = K+(A-T(I))^2
Ezt a műveletet is egy M-szer végrehajtott ciklusban célszerű elvégezni FOR, NEXT szervezéssel. A kapott eredményt el kell osztani M-mel, és négyzetgyökvonás után a szórás értéke ren-delkezésre áll:
D2 = SQR(K/M)
(3.2) Szóráskiírás
A modul eljárás típusú. Bemeneti adata a D2 jelű szórásnégyzetet tartalmazó változó a (3.1) modulból, amely egyúttal a modul kimeneti adata is.(4.1) Rendezés
A modul eljárás típusú. Bemeneti adatai a T(I) mérési eredmények az (1) modulból. A modul kimeneti adatait ugyanezek az adatok alkotják, de növekvő sorrendbe rendezve.
A modul fő feladata a T(I) mérési adatok rendezése növekvő sorba. Vizsgáljuk meg, hogy a sorbarendezés milyen algoritmussal valósítható meg egy vektoron belül. Tartsuk szem előtt, hogy általános érvényű algoritmust kell megfogalmazni. A sorbarendezést többféleképpen el lehet végezni. A lehetséges megoldások közül bemutatunk egyet.
A megoldás lényege a páronkénti vizsgálat és csere. Vizsgáljuk meg, hogy növekvő sorrendben vannak-e. Ha igen, akkor mindkettő maradhat a helyén, mivel ez a két elem egymáshoz viszonyítva sorban van. Ha ez nem állna fenn, akkor a két elem értékét ki kellene cserélni. Ezután térjünk át a következő elempárosra. Ezekkel a lépésekkel végig kell menni a vektoron. Észrevehető, hogy az első végigjárás eredményeként a vektor legnagyobb eleme a helyére került, a többi még nem. Ezután a páronkénti vizsgálatokat elölről kell kezdeni, és addig kell ezt ismételni, amíg már nem kell cseréket végrehajtani. Ezzel a folyamat befejeződött. Az eljárás bizonyíthatóan rendezett vektort eredményez véges számú lépésen belül.Most fogalmazzuk meg az alkalmazott algoritmust általános formában! Adva van egy M elemű vektor, ennek két szomszédos elemét nézzük minden lépésben (az I-edik és az I+1-edik elemet). A két elemet összehasonlítjuk. Ha V(I)<=V(I+1), akkor át lehet térni a következő vizsgálatra, vagyis az I+1 és I+2 indexű elemekre. Másként fogalmazva az I indexet kell eggyel növelni, és az új érték mellett kell összehasonlítani az I-edik és az I+1-edik elemet.
Ha viszont V(I)>V(I+1), akkor a két elem értékét ki kell cserélni. Ez egy lépésben nem végezhető el, mivel valamelyik érték elveszne. Ennek elkerülésére például a V(I) értéket átmásoljuk az X kisegítő változóba: X=V(I). Ekkor a csere egyik része elvégezhető: V(I)=V(I+1), majd az X segítségével a másik is: V(I+1)=X.
Tudjuk, hogy a sorbarendezés akkor ér véget, ha ilyen cserét már nem kell végrehajtani. Ezért szükség van egy F figyelőváltozóra, melynek értékét a vizsgálatsorozat előtt 0-ra állítjuk, és csere esetén 1-re változtatjuk. Ha tehát végigmegyünk a vektoron, és egyetlen cserét sem kell elvégezni, akkor az F értéke 0 marad, ami azt jelöli, hogy a vektor elemei sorban vannak. Ha viszont csak egyetlen csere is történik a vektor végigpásztázása során, akkor F=1 lesz, vagyis szükség van még további műveletsorozatra. Az F csak akkor tájékoztat helyesen, ha minden vizsgálatsorozat előtt nullázzuk.
A vizsgálatot egy M elemű vektorban M-1-szer kell elvégezni, mivel minden vizsgálat magában foglalja az I+1 indexű elemet is. Tehát az M-1-edik vizsgálat a vektor utolsó - M-edik - elemére is kiterjed. Láthatjuk, hogy a vizsgálat elvégezhető ciklikusan. A ciklusváltozó itt is az I lehet.
Tudjuk, hogy a vizsgálatsorozatot addig kell folytatni, amíg csere már nem történik. Tehát a vizsgálatsorozatot is ciklikusan ismételni kell, amíg az F értéke 0 nem marad. Ezért minden vizsgálatsorozat előtt, mint ezt korábban kifejtettük, F=0 beállítás szükséges. Ha a vizsgálatsorozat végén F=1, akkor volt csere, tehát a vizsgálatsorozatot folytatni kell.
Ha F=0 marad, akkor a művelet befejeződik, a ciklust abba kell hagyni.
A külső ciklus (a vizsgálatsorozat) hátul tesztelő lesz, ciklusváltozója az F.A T vektor elemeinek sorbarendezését a bemutatott elv alapján végezhetjük el. A sorbarendezés az eredeti vektort megváltoztatja, ezért a rendezés előtt a T vektort át kell másolni egy V vektorba. Ezt elemenként ciklikusan kell elvégezni: V(I)=T(I) a vektor első M elemére.
A feladat szerint azonban nem elegendő a sorbarendezés. Meg kell őrizni az egyes elemek sorrendiségét őrző indexet is. Ez csak úgy lehetséges, ha a T(I) elemek mellett az eredeti I indexet is tároljuk, tehát két adat (index és érték) tárolása szükséges. Ezért nem vektorba, hanem egy tömbbe kell átmásolni az indexeket és az értékeket. A tömb (100 sor) x (2 oszlop) méretű lesz. Legyen ez a V(I,J) tömb, ahol max I = 100, max J = 2 .
A T (I) elemhez tartozó értékeket a V(I,1) elembe másoljuk: V(I,1)=T(I), és az indexeket a V(I,2) elembe: V(I,2)=I.
Tehát egy T(I) elem adatai a V tömb egy sorában helyezkednek el. Ez a tény annyiban módosítja a vizsgálat algoritmusát, hogy a T(I) és T(I+1) értékekkel azonos V(I,1) és V(I+1,1) elemeket kell összehasonlítani. Csere esetén viszont a V(I,2) és V (I+1,2) értékeket (méréssorszám) is ki kell cserélni. Látható, hogy J=1 (érték) és J=2 (index) esetén ugyanazt a cserét kell végrehajtani, ezért ezt szintén le lehet bonyolítani a vizsgálat ciklusban J=1-től J=2-ig.
A V(I,J) tömböt a modul elején kell definiálni.
A modul folyamatábrája:
(4.2) Rendezett adatok kiírása
A modul eljárás típusú. Bemeneti adatai részben az (1) modulból (M), részben a (4.1) modulból származnak (a V(I,J) tömb adatai). Ezek alkotják a modul kimenetét is.
A modul feladata, hogy a T(I) sorba rendezett értékeit és az értékekhez tartozó sorszámokat kiírja. Az előbbi adatokat a V tömb V(I,1), az utóbbiakat pedig a V(I,2) elemei tartalmazzák. A fejléc kiírása után ezt a két adatot kell kiírni minden lépéshez. Ezután a program befejeződik.
4. A program kódolása
(1) Adatbevitel
A modul elejére a program nevét írjuk. Ide be szúrtuk a T vektor helyfoglalását. Ezután beolvassuk a mérések számát. A mérési adatok bevitelét ciklusban kódoltuk. A modul kódja:10 REM * MERES *
20 REM ADATBEVITEL
20 DIM T(100)
30 PRINT "A MERESEK SZAMA: ";
40 INPUT M
50 FOR I=1 TO M
60 PRINT "AZ ";I;". ADAT KOVETKEZIK: ";
70 INPUT T(I)
80 NEXT ISpectrum BASIC-ben az INPUT eltérő működése miatt a programot célszerű kiegészíteni:
45 PRINT M
75 PRINT T(I)(2.1) Átlagszámítás
A modul kódja a tervek alapján a következő:100 REM ATLAGSZAMITAS
110 LET S=0
120 FOR I=1 TO M
130 LET S=S+T(I)
140 NEXT I
150 LET A=S/M(2.2) Átlagkiírás
A modul kódja az átlag kiírása előtt a fejléckiírásokat is magában foglalja. A modul kódja:160 REM ATLAGKIIRAS
170 PRINT: PRINT "A MERES EREDMENYEI:"
180 PRINT: PRINT "A MERESEK SZAMA: ";M
190 PRINT "AZ ATLAGOS HOMERSEKLET: ";A;"C"(3.1) Szórásszámítás
A modul a tervek szerint kódolva:200 REM SORASSZAMITAS
205 LET K=0
210 FOR I=1 TO M
220 LET K=K+(A-T(I))^2
230 NEXT I
240 LET D2=SQR(K/M)(3.2) Szóráskiíras
A modul két utasításból áll, mivel csak a szórást írja ki:250 REM SZORAS KIIRAS
260 PRINT "A MERESEK SZORASA: ";D2(4.1) Rendezés
Ez a modul a kód szempontjából is a legbonyolultabb. Az átmásolás alkotja az első ciklust, majd ezután 3 egymásba ágyazott ciklus következik. A külső ciklust a vektor, illetve a tömb átvizsgálás sorozat alkotja. Ezen belül helyezkedik el a páronkénti vizsgálat ciklusa, majd ebben működik egy IF szerkezet és a helycserét végrehajtó ciklus.270 REM RENDEZES
280 DIM V(100,2)
290 FOR I=1 TO M
300 LET V(I,1)=T(I): LET V(I,2)=I
310 NEXT I
320 REM KULSO CIKLUS KEZDET
330 LET F=0
340 FOR I=1 TO M-1
350 IF V(I+1,1)>=V(I,1) THEN GO TO 420
360 FOR J=1 TO 2
370 LET X=V(I,J)
380 LET V(I,J)=V(I+1,J)
390 LET V(I+1,J)=X
400 NEXT J
410 LET F=1
420 NEXT I
430 IF F=1 THEN GO TO 320(4.2) Rendezett adatok kiírása
A modul kódját a tervek alapján készítettük el. A modul kódja:440 REM RENDEZETT ADATOK KIIRASA
450 PRINT: PRINT "SORBARENDEZETT MERESI EREDMENYEK"
460 PRINT "MERT ERTEK","MERES SORSZAMA"
470 FOR I=1 TO M
480 PRINT V(I,1),V(I,2)
490 NEXT I
5. Az eredmények értékelése
A program tesztelés és esetleges javítás után használható. Mintaképpen bemutatjuk egy futáseredményét 5 bemeneti adat esetén:
A program helyesen működik, és az eredményeket jól áttekinthető formában közli.
A kiírás felszabdalása logikusnak tűnik, de azzal a hátránnyal jár, hogy a három kiírási modulon keresztül nehezebb a kiírási képet kézben tartani. Ha módosítani kell, akkor át kell nézni az egész programot, hogy melyik modulban kell változtatni.
A program bármilyen egydimenziós mérési eredménysorozat kiértékelésére alkalmas, csak a szöveget kell módosítani.
4.2. Sok oszlopos, sok soros táblázatok készítése
A bonyolult, sok tulajdonságot tároló adatállományok jellemzésére készülő táblázatok általában több oszlopot és több sort tartalmaznak, mint az eddig bemutatottak. Ennek az a magyarázata, hogy egy sok egyedből álló adatállomány sok tulajdonság szerinti megoszlását egy olyan táblázatban lehet ábrázolni, amely m X n méretű, ahol m az egyedek vagy egyedcsoportok száma, n pedig a tulajdonság száma.
Nagyméretű táblázat kiíratása a BASIC eddig megismert lehetőségeivel nem lesz formailag szép, áttekinthető. Tudjuk, hogy mind a vesszővel jelzett oszlopkiíratás, mind a szövegmezők kiszámolásával készített, vagy akár a TAB függvény segítségével beosztott táblázatok legnagyobb hibája, hogy a táblázat oszlopaiban nem biztosítható, hogy a tizedespont egymás alá essen.
Ha két egymás alá írandó számjegy nagyságrendje (számjegyeinek száma) nem változik a feldolgozások folyamán, akkor a számjegyeket megelőző szövegmező hosszával beállítható, hogy a két szám tizedespontja egymás alatt legyen. Ha viszont egy szám nagyságrendje változhat, akkor az egymás alá kerülés nem oldható meg, mivel a számok kiírása a szövegmezőt követi, függetlenül a hosszától.
Ez a probléma a formátumkiírást megvalósító PRINT USING utasítással szüntethető meg, mely a legtöbb BASIC implementációban megtalálható (de a Spectrum BASIC-ben nincs). A PRINT USING utasítással pontosan meg lehet határozni, hogy melyik változót melyik pozícióra írja ki a program - a változó nagyságrendjétől függetlenül.
Az utasítás formája:
PRING USING "formátum",változó-lista
A formátumban kell definiálni a kiírás képét, vagyis azt, hogy hány mezőt, egymástól milyen távolságra kell kiírni. A változólista pedig azokat a változókat tartalmazza sorrendben, amelyek értékét a kiírási mezőkben ki kell nyomtatni. A változókat vesszővel kell elválasztani.
A formátumban az, üres helyeket szóközökkel kell jelölni. Azokat a nyomtatási pozíciókat, ahová valamelyik változó értékét kell kiírni, a # jellel kell megjelölni. Szövegkonstanst változatlan formában kell beírni. Minden # jel egy helyértéket jelöl. Egy változó kiírására annyi pozíciót kell fenntartani, ahány maximális és minimális esetben is megfelelő. Ha az adat értéke negatív is lehet, akkor a mező elé mínuszjelet kell tenni, amelyet negatív értéknél kiír a program. A tizedespont helyét ponttal kell jelölni a mezőn belül. Kiíráskor az egész értékek a ponttól balra, a törtrészek a ponttól jobbra helyezkednek el. Ha kevesebb pozíciót hagyunk az egész rész kiírására, mint a változó tényleges értéke, akkor a program - BASIC implementációtól függően - a változó teljes értékét kiírja ugyan, de eléír egy % jelet, mutatván, hogy az íráskép nem jó vagy hibaüzenettel leáll a program futása. A törtrészből csak annyit ír ki a program, amennyire helyet hagyunk. Adott esetben a törtrész teljesen elhagyható. Ha tizedespontot nem tartalmaz a mező, akkor csak egész számot ír ki a program a fenntartott nyomtatási pozíciókban jobbra illesztve.
Szöveges változó is kiírható a formátum mezőibe. Ilyenkor is megfelelő hosszúságú mezőt kell biztosítani a változó kiírásához. Szöveges változót balra illesztve ír ki a program.
Példaként definiáljuk egy olyan sor kiírási formátumát, amelybe ki kell nyomtatni:
A megjelenítendő formátum:

Ezt utasításban az alábbiak szerint kell megfogalmazni:
100 PRINT USING "<#################### #### ###.#",N$,E1,H
Hatására az N$ értékét az első mezőbe balra illesztve (a < jel írja ezt elő), az E1 értékét a második és a H értékét a harmadik mezőbe írja ki a program.
A formátumot szöveges változóként is lehet definiálni, ekkor a formátumot a kiírási utasítás előtt kell meghatározni:
110 LET F1$="<#################### #### ###.#"
...
200 PRINT USING F1$,N$,E1,H
A kiírás a formátumban előjelhelyesen történik. Negatív számnál az előjelnek is hagyni kell 1 pozíciót.
A PRINT USING utasítással könnyen áttekinthető, világos táblázatok készíthetők.
Szövegek pozícionálása
Gyakran kell valamilyen kiírandó szöveget (amely változó hosszúságú is lehet) kiíráskor pozícionálni egy másik szöveghez. Ennek sok fajtája lehet, de csak egy jellegzetes esetet vizsgálunk meg, amely támpontot ad további feladatok megoldásához.
Például egy, a program futása közben beolvasott, változó hosszúságú szöveget kell az oldal közepére kiírni. Tegyük fel, hogy az adott terminálon egy sorban 70 pozíción lehet kiírni. A feladat csak akkor értelmezhető, ha a szöveg 70-nél kevesebb pozíciót foglal le, vagy ha két sorban kell kiírni. Maradjunk az első esetnél.
Egyszerűen belátható, hogy a középre helyezést úgy kell elvégezni, hogy 70-ből kivonjuk a szöveg karaktereinek számát, és elosztjuk kettővel. A kapott szám mutatja meg, hogy hányadik pozíción kell kezdeni a nyomtatást. A feladat megoldásához a LEN(szöveges változó) függvényt lehet felhasználni. A LEN függvény értéke a változóként szereplő szöveges változó karaktereinek száma a szövegközi szóközökkel együtt.
Például:
O változó tartalmazza, hány oszlop jeleníthető meg az adott képernyős terminálon, ekkor
10 LET O=32
20 LET C$="HAVI MEGOSZLAS"
30 LET H=LEN(C$)
esetén H=14 lesz. A LEN függvény segítségével meg lehet határozni, hogy középre állításhoz hányadik pozíción kell kezdeni a nyomtatást.
A PRINT utasítás és a TAB függvény együttes alkalmazásával kiírható a megfelelő számú szóköz a szöveg elé:
40 PRINT TAB(O-H)/2;C$
A szóközök után nyilvánvalóan a kiírni kívánt szöveget kell nyomtatni.
5. Programtesztelés és hibajavítás
Még gyakorlott programozóknál is a legritkábban fordul elő, hogy az elkészült program az első futáskor hibátlan, és helyesen működik. A programozás bonyolult tevékenység, a programkészítés menet közben nehezen - csak elvont gondolkodással - ellenőrizhető. A program hibáinak felderítése, kijavítása külön figyelmet érdemel.
E fejezetben bemutatjuk a gyakoribb hibákat, a program kipróbálását, a hiba feltárási módjait és kijavítását.
5.1. Hibalehetőségek a programban
Egy program futását nemcsak a programban levő hibák, hanem a környezet hibái is megakadályozhatják. Ezek közül két hibatípust említünk meg:
Mint említettük, a program hibái magában a felhasználói programban vannak. Hibákat a program készítésének minden szakaszában lehet okozni. A hibák jelentősége vagy súlya attól függően változik, hogy melyik szakaszban követtük el őket. Ha a program elemzési fázisában vétünk el valamit (pl. egy funkciót kifelejtünk), akkor az sokkal súlyosabb problémákat vet fel, mint pl. az értékadó utasításból kifelejtett egyenlőségjel. Az előző miatt esetleg az egész programot újra kell készíteni, az utóbbi pedig másodpercek alatt kijavítható. A programkészítés kezdeti szakaszában elkövetett hiba kijavítása sokkal több időt igényel, mint egy, a későbbi fázisok valamelyikében elkövetett hiba. A tapasztalat azt mutatja, hogy a programkészítés utolsó részében követik el a programozók a legtöbb hibát, vagyis a hibaszám a készítés kezdetétől a végéig valamilyen formában növekszik.
A következőkben tekintsük át, hogy a programkészítés egyes szakaszaiban milyen jellegzetes hibák fordulnak elő.
Feladatelemzés
A probléma félreértése vagy nem teljes megértése okozhat hibát. Ennek eredményeként a program valamilyen funkciót hibásan vagy egyáltalán nem fog ellátni. Ehhez közelálló jelenség, hogy valamilyen elemet, tényezőt kifelejtünk az elemzésnél. Végül meg lehet említeni hibaforrásként a nem teljes körű vizsgálatokat is.
Egy állóeszköz-nyilvántartó rendszer (amortizációszámítás) esetén ilyen jellegű hibát követünk el, ha nem vesszük figyelembe, hogy különböző hosszúságú leírási kulcsok vannak, vagy nem vesszük figyelembe az állóeszközök számát, és emiatt alkalmatlan adathordozót választunk.
Az elemzés során elkövetett hibák sokba kerülnek, ezért az elemzést nagyon körültekintően, átgondoltan kell elvégezni a bemutatott problémák megoldásához hasonlóan.
Programtervezés
A program tervezésekor hibát okozhat a modulok funkciójának hiányos megfogalmazása. Ez fakadhat abból, hogy a program valamely funkcióját nem rendeljük hozzá egyik modulhoz sem, vagy valamelyiket két modulba is beépítjük (redundancia). Lehet az is, hogy a modulok közötti kapcsolatból (hívás, adatátadás, -átvitel) kihagyunk valamit. Előfordulhat például, hogy egy modulnak másik három modult kell vagylagosan hívnia, de a vezérlési feltételeket csak két modul hívására tervezzük meg.
Problémát okozhat az adathordozó helytelen megválasztása is. Ha például olyan táblázatot kell kiírni, amely egy sorban több pozíciót igényel mint amennyi a képernyős terminálon megjeleníthető, akkor az eredmény nem íratható ki terminálra, csupán sornyomtatóra vagy nyomtatós terminálra, de sornyomtatóként használva (nyomtatási adatállományok).
Végül meg kell említeni azt az esetet, amikor túl nagy programot tervezünk. BASIC nyelvi változatonként és gépenként változik a programok maximális mérete. Ha ezt túllépjük, akkor az adott operációs rendszer és a fordító nem tudja futtatni a programot. Ezt a hibát a fordító hibaüzenettel jelzi. Ez a hiba a megoldó program alkalmas méretű programokra darabolásával küszöbölhető ki.
Modultervezés
A modul tervezésénél általában akkor követünk el hibát, ha nem a modulra specifikált funkciókat valósítjuk meg (valamit kifelejtünk vagy feleslegesen hozzáteszünk).
A modul algoritmusának kialakításakor az alábbi hibák fordulnak elő leggyakrabban:
A feltételek felcserélése. Ha például egy A műveletet akkor kell végrehajtani, ha C<B, akkor tévedésből a B<C esetben hajtódik végre az A művelet.
Nem teljes adattartomány figyelembevétele. Főleg a felhasználó által begépelt adatok esetén fordul elő a hiba. Azt jelenti, hogy a program nincs felkészülve arra, ha pl. negatív bemeneti adat érkezik.
Változónév többszöri használata. Egy korábbi modulban használt változónevet újra használunk. Ez a változó számára helytelen indulóértéket eredményezhet.
A megengedettnél nagyobb indexek használata. Főleg olyankor fordul elő, ha egy vektor vagy tömb elemeinek az indexeit aritmetikai művelettel számítjuk ki. Ha a számított index nagyobb, mint a megengedett, akkor az elemre való hivatkozásnál hibajelzés történik. Mivel ez is a fordító által felismerhető hiba, a fordító üzenetet ad ki, és a futás leáll.
Nem elegendően nagy tömb definiálása. A tömböt (vagy vektort) csak az elemek számának megfelelő méretűre választjuk, és nem vesszük figyelembe az összeg sor(ok) és/vagy összeg- oszlop(ok) helyigényét. Ebben az esetben az index értéke meghaladja a DIM utasításban megjelölt értéket, így ekkor is hibaüzenet jelenik meg, és a futás leáll.
Osztás 0-val. Rendszerint tömbön vagy vektoron belüli műveleteknél fordul elő, ha valamelyik, osztónak használt elem értéke zérus. A fordító - implementációtól függően - jelzi a hibát, de ettől függetlenül a futás megy tovább (a hányados 0 értéket kap), vagy a programfutás hibaüzenettel leáll.
Túlcsordulás, alulcsordulás. Előfordulhat, hogy egy változó értéke túllépi a lehetséges felső vagy az alsó határt valamilyen művelet hibás meghatározásánál.
A ciklusváltozó kezdeti vagy végértékének helytelen megválasztása. Ha például egy elöl tesztelő ciklust 100-szor kell végrehajtani, és közben a C ciklusváltozó 1-től egyesével növekszik, akkor a befejezés feltétele helytelenül:
X IF C<100 THEN (újabb ciklus).
Ekkor ugyanis a ciklust csak 99-szer hajtja végre a program.
Helyesen:
X IF C=<100 THEN (újabb ciklus).
Végtelen ciklus. Viszonylag gyakori hiba. Egymást keresztező IF szerkezetek, ciklusok tervezésénél fordul elő.
Kódolási hibák
Kódoláskor úgy lehet hibát elkövetni, hogy a kód nem a modul folyamatábráját követve készül, vagy a kódoló nem tartja be a BASIC nyelvtani szabályait.
Néhány jellegzetes hiba:
Hibás vezérlésátadás. A GO TO utasításban helytelen utasítás-sorszám szerepel, így a vezérlés is máshová kerül. Kedvezőtlen esetben ez a hiba végtelen ciklust is okozhat.
Meg nem engedett változónév használata. Olyan változónevet használunk, amelyet a BASIC nyelvtana nem enged meg. Ezt a hibát a fordító a futás megkísérlésekor hibaüzenettel jelzi és a programfutás leáll.
Írásjelek kifelejtése. A leggyakrabban előforduló hibák közé tartozik. Ilyen például a zárójelek elhagyása, idézőjel, vessző elfelejtése.
Betűcserék. Az írásjelek rossz használatához hasonlóan ezek is szintaktikai hibák. Gyakori eset, hogy - különösen a kezdők, akiknek egyébként gépírási gyakorlatuk már van - 0 helyett 0 betűt, 1 helyett L betűt írnak be vagy egyszerű gépelisi hibát vét.
A két utóbbi hibatípust szintaktikai hibáknak nevezzük, a BASIC fordítók ezek felderítésében kétféle eljárást követhetnek: A sor értelmezése adatbevitelkor nem, csak a program futása közben történik meg, így programfutáskor okoznak hibát, ami a programfutás leállását eredményezi. Más implementációk már a sor bevitelekor értelmezik azt, így rögtön képesek jelezni az ilyen jellegű hibákat.
Sorszámismétlés. Módosításoknál fordul elő. Nagyon nehezen észrevehető hiba. Jellemzője, hogy a fordító a két (vagy több) azonos sorszámú utasítás közül az utolsóként előfordulót jegyzi meg.
Túl hosszú sor. Implementációtól függően a sor vége elvész, vagy bevitelkor hibajelzést kapunk.
Futás közbeni hibák
Hibázás még a futás közben is előfordulhat. Két jellegzetes hibát említünk meg:
Helytelen típusú adat megadása. Numerikus adat helyett szöveges adatot adunk meg. Egyes implementációkban a programfutást megszakítását okozó hibát eredményez, a többi figyelmeztető üzenet kiírása új adat bevitelére vár.
Kevesebb adat megadása. DATA sorok alkalmazásakor fordulhat elő, hogy a felhasználó kevesebb adatot ad meg, mint amennyit a program vár.
5.2. A program tesztelése
A tesztelés az a folyamat, amelynek segítségével megállapítható, hogy a program a specifikációban rögzített elvárásoknak megfelelően működik-e, azaz hogy van-e hiba a programban.
A tesztelés a program elkészülése utáni munkafázis, célja nem egyéb, mint hogy megállapítsa, helyesen működik-e a program. Ha kiderül, hogy nem, akkor a program hibás. Ekkor a hibát meg kell keresni és ki kell javítani.
A tesztelés általánosan elfogadott elve, hogy
kell elvégezni. A modulonkénti tesztelés azért kedvező, mert egy viszonylag kicsi, jól áttekinthető részt fog át. Valamennyi modul ellenőrzése után az egész programot egyben is tesztelni kell. A megtervezett próbaadatok jelentősége abban áll, hogy minél kevesebb próbaadattal minél teljesebb ellenőrzést lehessen elvégezni.
A tesztelés lényege, hogy különböző bemeneti adatokkal próbájuk ki a programot (illetve a modulokat), és közben figyeljük, hogy a specifikáció szerint működik-e a program.
A tesztelés módjai:
A tesztelés folyamata
Teszteléskor mindegyik - fent leírt - módot alkalmazni kell. Az asztali tesztet modulonként végezzük el. Ennek során a kódolás helyességét lehet ellenőrizni és a feltárt hibákat javítani.
Ezután át kell térni a száraztesztre. Ezt a változók leggyakrabban előforduló értékeivel legalább egyszer el kell végezni. Olyan bemenetiadat-értékeket kell felvenni, amelyekkel a modul nagy valószínűség szerint működik, és jól működik. A szélsőséges adatokkal való tesztelést a számítógépre kell bízni.
A kézi tesztelések lefolytatása után következhet a gépi modulteszt. Ehhez a programot kismértékben át kell alakítani. Először a tesztelésnek alávetett modulokat le kell szigetelni. Ez azt jelenti, hogy a tesztelt modul előtti modulokat kihagyjuk a végrehajtásból, hogy ne zavarjanak. Ezt GO TO utasítással éljük el, amely a modul kezdetére adja a vezérlést. A modul végére STOP utasítást írunk, amely a futást a további beavatkozásig leállítja. Így csak a kiszemelt modul hajtódik végre.
A modulteszt első kísérletekor a száraztesztnél használt "könnyű" adatokat alkalmazzuk. A kihagyott modulokból származó adatok indulóértékeit értékadó utasításokkal határozzuk meg, amelyeket a modul elején helyezünk el.
Az első futások eredménye a szintaktikai hibák gépi kimutatása lesz, amennyiben az alkalmazott BASIC implementáció a sorok bevitelekor nem végzi el a szintaktikai ellenőrzést. Ez már tulajdonképpen - a következő két lépés - a hibafelderítés és -javítás része. A szintaktikai hibák kijavítása után olyan tesztadatokat kell megadni, amelyek lehetőleg minden ágat (IF-THEN és IF-THEN-ELSE szerkezetek ágai) kipróbálnak, eközben figyelni kell a működés helyességét. Ebbe a fázisba tartoznak a szélsőséges adatok is, amelyek a legszigorúbb követelményeket jelentik (pl. mit csinál a modul akkor, ha a felhasználó tévesen negatív számot ad meg egy dolgozó bérének). Ha a modul nem a specifikáció szerint működik, akkor a hibakeresésre térünk át.
A program valamennyi moduljának tesztelése után a teszteléshez használt utasításokat töröljük a programból, és az egész program tesztelése következik. Itt is előbb egyszerű adatokkal próbáljuk ki a programot, majd az esetleges szintaktikai hibák kijavítása után a szisztematikus próbákra kell áttérni. Működési hibánál meg kell keresni a hiba okát. Ez lehet egy modulban, de akár több modulra is kiterjedhet a kapcsolatok révén. Ha a program a specifikációnak megfelelően működik, akkor használható.
5.3. A hibakeresés eszközei
A program elkészítésének következő lépése az esetleges hibák kiderítése. A tesztelés során kiderülhet, hogy a programban hiba van, de a tesztelés közvetlenül nem mutatja ki, hogy hol. A hiba megtalálása (debugging) külön tevékenység eredménye.
A hibakeresés egyik módja a nyomkövetés. Ez lényegében hasonló tevékenység, mint a szárazteszt, azzal a csekély különbséggel, hogy a száraztesztnél a működés felderítésére törekszünk, a nyomkövetés hibakeresési céllal folyik. A nyomkövetés eredménye is egy táblázat, amely mutatja, hogy a változók milyen értéket vesznek fel az utasítások végrehajtása után. A nyomkövetés folyamán már azt is vizsgálni kell, hogy ha a változó értéke hibás, mi ennek az oka, vagyis hol a hiba. Tehát nem elég csupán a táblázatot elkészíteni, hanem alaposan kell elemezni is.
Egyes BASIC-változatoknak van nyomkövetési képességük. A TRACE utasítást be kell iktatni a programba, hatására a fordító futás közben kiírja a végrehajtás alatt álló sor sorszámát, esetleg a változó értékváltoztatását, feltüntetve, hogy milyen sorszámú utasításban történt az értékváltoztatás, és mennyi lett.
Az eredmény megfelel a szárazteszt eredményének, csak éppen sokkal gyorsabb és megbízhatóbb. Sajnos csak kevés BASIC-változatban található ilyen lehetőség.
A hibakeresés nehezen formalizálható, sok intuíciót követelő tevékenység. Még könyörtelenebb logikát kíván a program készítőjétől, mint a program tervezése vagy írása. Egy program elkészítése során a hibakeresés szokta okozni a legnehezebb perceket, órákat. Gyakran előfordul, hogy maga a program készítője is "ciklusba esik", és nem tud megszabadulni attól a gondolattól, hogy a program biztosan jó, valami rejtélyes dolog okozza a hibát. Ilyenkor logikusan végig kell gondolni, hogy mi a jelenség, mi az oka, mi idézi elő, és hogyan javítható ki.
A hiba kiderítésére fordított sok szellemi munka mellett néhány esetben a gép segítségét is igénybe lehet venni. A legegyszerűbb számítógépes eszköz a programkódlista. Ez csak kevés igényt elégít ki, hiszen enélkül sem asztali, sem szárazteszt nem végezhető el. Bármilyen hibakeresés alapja, hogy a felhasználó a programlista alapján tájékozódjék, mi lehet a hiba. A programlista képernyős terminálon kilistázható (LIST parancs). Ilyenkor általában egy billentyű lenyomásával leállítható a listázás, majd tovább indítható. A BASIC-ben mód van arra is, hogy egy- egy sort ki lehessen listázni. Ez különösen akkor előnyös, ha a fordító valamelyik sorban hibát jelez. Ilyenkor a hibát tartalmazó sort ki lehet listázni a
LIST x
paranccsal, (x a programsor sorszáma) és meg lehet keresni a hibát.
A hibakeresést és a program olvashatóságát segítik a REM utasításokban elhelyezett megjegyzések és a strukturált kódolás is.
A hibakeresést azok az eszközök segítik legjobban, amelyek kiírják a változók értékeit a program valamelyik pontján, vagy amelyek lehetővé teszik a változók értékeinek kiíratását. A legegyszerűbb ilyen eszköz a PRINT utasítás (ha nincs TRACE utasítás, vagy nem annyira bő szolgáltatással).
Ha kíváncsiak vagyunk arra, hogy egy változó a program egy adott pontján milyen értéket vesz fel, akkor erre a pontra be kell iktatni egy PRINT utasítást, hogy a változó értékét kiírja. Ha például az alábbi programponton ismerni kívánjuk az F változó értékét, akkor egy PRINT utasítást kell beiktatni:
Eredeti kód:
...
210 LET F=D/N
220 IF F=2 THEN GO TO 240
...
Hibakereső kód:
...
210 LET F=D/N
215 PRINT "F=";F
220 IF F=2 THEN GO TO 240
...
Ennél van rugalmasabb, hatékonyabb módszer is. Ez a STOP utasítás és az ún. közvetlen mód együttes használata. Először ismerkedjünk meg mindkettővel.
A STOP utasítás BASIC programokban használható utasítás. Hatására a program leáll, és a kijelzi az utoljára végrehajtott programsor sorszámát. Ez azért fontos, mert egy programban több STOP utasítás is lehet, s a program készítőjének tudnia kell, hogy melyik STOP utasításnál állt le a program.
A STOP utasítás hatására leállt program a közvetlen módban indítható el újra. A közvetlen mód azt jelenti, hogy a READY üzenet megjelenése után lehet egy egysoros parancsot írni, amelyet a fordító a RETURN billentyű lenyomása után azonnal végrehajt. Hogy a közvetlen módú parancsokat meg lehessen különböztetni a programutasításoktól, nem kell utasítássorszámot írni eléjük. Például:
PRINT 15*40
Egy sorba több utasítást is lehet írni, akár változógenerálást is lehet végezni:
FOR I=1 TO 5: LET V=I^2: PRINT V: NEXT I
Azért lehet csak egysoros parancsot írni, mert a fordító a RETURN / ENTER billentyű lenyomása után lefuttatja a sorszám nélkül írt sort. Így a "második sort" ismét "elsőnek" fogja érzékelni.
A közvetlen módot két területen érdemes alkalmazni:
Az első alkalmazási terület világos az olvasó számára. Hogyan használható hibakeresésre? Egy program lefutása után - függetlenül attól, hogy normálisan fejeződött-e be (akár STOP utasítással) vagy hibaüzenettel - a program változói legutóbbi értékükkel a belső tárban megtalálhatók, és ezeket az értékeket közvetlen módban ki lehet íratni. Nézzünk meg egy olyan esetet, amikor egy program befejezése után tudni akarjuk, hogy a Z1 változó milyen értéket vett fel. Ezt a
PRINT Z1
parancs kiadásával megtudhatjuk. De egész tömb értékeit is ki lehet íratni:
FOR I=1 TO 5: FOR J=1 TO 3 PRINT A(I,J): NEXT J: NEXT I
Ezt a szolgáltatást nemcsak a program végén lehet igénybe venni, hanem program közben tetszés szerinti ponton, ha a programot STOP utasítással előzőleg leállítottuk. Ekkor meg lehet vizsgálni a változóknak a megállítás helyén fennálló értékeit.
A közvetlen mód lehetőséget ad arra, hogy a programot
GO TO x
közvetlen utasítással tovább futtassuk. Az x helyébe a STOP utasítás utáni sor sorszámát - vagy bármilyen más sorszámot - kell beírni. Ezután a vezérlés a megjelölt sorra kerül, és a program normálisan folytatódik. Néhány BASIC implementáció ismeri a CONTINUE (vagy CONT) parancsot, amely a megszakított programot a megszakítás helyétől folytatja tovább.
Természetesen normális továbbfutásról csak akkor lehet beszélni, ha nem változtattuk meg a változók értékeit.
Jegyezzük meg, hogy ha a program STOP utasítás hatására állt le, nem ajánlatos RUN parancsot kiadni, mert ekkor a program futása elölről kezdődik (persze lehet ez is a cél).
A bemutatott eszközökkel és józan gondolkodással a hibát előbb-utóbb megtaláljuk. A következő lépés a hiba kijavítása.
A program kijavítása
A felfedett hiba kijavítása a jellegétől függően megy végbe. Ha elemzési hiányosság okozta, akkor vissza kell térni az elemzésre, és a programot újra kell tervezni, illetve a tervet módosítani. Ugyanez érvényes a modulokra és a kódra is. Ha a hibát a tervezésben követtük el, akkor csak ide kell visszatérni. A legegyszerűbb esetben pedig csak a kódot kell kijavítani.