A BASIC
nyelvű programozás ábécéje

1985 - Dusza Árpád, Varga Antal
Lektorok: Garádi János, dr. Ratkó István

Tartalom

A számítógépek kialakulása, a számítástechnika fejlődése

A számítástechnika születését és fejlődését különböző nézőpontból közelíthetjük meg. Tisztelettel adózva elődeinknek, felsorolhatnánk jeles tudósoknak, matematikusoknak a számítások meggyorsítására, automatizálására tett kísérleteit és eredményeit. Ez azonban inkább egy tudománytörténeti munka feladata lenne. Így ezekre az izgalmas előzményekre most nem térünk ki.
A próbálkozások után az első igazi "számítógépet" a 19. sz. közepén, 1822-ben korát messze megelőzve, Charles Babbage a cambridge-i egyetem tanára tervezte. A számítógép mechanikus működésű volt, a számok reprezentálására fogaskerekek bizonyos fordulatai szolgáltak.
Boole 1847-ben dolgozta ki a kétállapotú kifejezések algebráját - részletesebben lásd később -, hangoztatva, hogy felhasználásával logikai problémákat lehetne automatizálva elemezni és megoldani. A nagyszerű gondolat gyakorlati megvalósítása azonban csaknem 100 évet váratott magára. Ekkor még anyagi megvalósítás nem tudta követni a szellemi terméket.
A XX. század társadalmi és gazdasági tekintetben egyaránt hallatlan nagy fejlődést hozott. Mindez éreztette hatását a műszaki és tudományos életben, így a számítástechnika kifejlődésében is. 1911-ben alakult meg az első számítógépeket felhasználó társaság, a CTR (Computer Tabulator Recording), amely 1924-ben alakult át a világ számítástechnikai iparában a mai napig is vezető szerepet játszó IBM-mé (International Business Machines).
1939-ben, Atanasoff tervei alapján, építettek egy gépet elektroncsövek felhasználásával, amely többismeretlenes egyenletrendszerek megoldására volt alkalmas.
1941-ben Konrad Zuse irányítása mellett készül el az első elektromechanikus működésű, de általános jellegű feladatok megoldásához is használható számítógép, a Z3. Az IBM is kialakított egy ilyen eszközt 1944-ben, amely a Harward egyetemen 1950-ig dolgozott. Hagyományos elemekből készült, és 6 s alatt tudott egy szorzást elvégezni.
1945-ben, a világon először, a magyar származású, világhírű matematikus, Neumann János tervei alapján kezdik el az USA-ban egy belső programvezérlésű számítógép kifejlesztését. Igaz, hogy csak 1952-ben készült el, EDSAC néven, de a "Neumann elv"" meghatározóan fontos szerepet kapott a számítástechnika fejlődésében.
1946-ban készült el szintén az USA-ban az első elektronikus működésű, de még külső vezérlésű számítógép, amely ugyan gigantikus méretű, de az adott körülményekhez képest gyors és megbízható volt.
A számítógépek sorozatgyártását 1951-ben kezdték el az USA-ban, ennek a "gépcsaládnak" az UNIVAC nevet adták. A következő nagy ugrás a gépek korszerűsítésében a félvezetők elterjedése. Alkalmazásával a méret és a teljesítményfelvétel csökkenése mellett a gépek üzembiztonsága és műveleti sebessége nőtt meg. Ezeknek az ún. második generációs gépeknek a fő alkotó része a tranzisztorokból épített logikai áramkör volt.
A harmadik generációhoz tartozó gépek integrált áramköri elemeket tartalmaznak ('60-as évek). Ezek az egységek minimális helyfoglalással összetett logikai és aritmetikai feladatok ellátására alkalmasak. Így a fejlődés iránya a komplex számítástechnikai munkák megoldására alkalmas, nagy kapacitású óriásgépek mellett egyre inkább a felhasználóval közvetlen kapcsolatot teremtő mikrogépek fejlesztése felé is mutat. Ezeknek a személyi számítógépeknek a felhasználási területe rendkívül széles, népszerűségük a hozzáférhetőséget, árat, egyszerűséget tekintve érthető. Központi feldolgozó egységük - Central Processor Unit, CPU - egy mikroprocesszor. Ez egy olyan eszköz, amely több logikai áramkört tud egy időben helyettesíteni a legáltalánosabb feladatok végrehajtásában: elektronikus háztartási eszközök, számológépek, számítógépek stb. Az első mikroprocesszort 1971-ben készítették el. Alkalmazásával és széleskörű elterjedésével a fejlődés a kívülállók számára már szinte követhetetlenül felgyorsult. A tankönyv nagyságú személyi számítógépek használata, amelyek ráadásul nagyon könnyen elsajátítható és jól használható nyelven "értenek" (BASIC), valóban bűvészkedésnek tűnhet a laikusoknak! Hogy nem az, azt feltehetően a könyvünk tanulmányozása után mindenki beláthatja.

A számítógépek működése és felépítése

Ahhoz, hogy egy számítógépet "jó ismerősként", optimálisan kihasználva működtessünk, nem elég, ha csak értve a közös nyelvet, azon "utasítgatjuk" különböző feladatok végrehajtására, valamilyen szinten a "lelkébe" is be kell tekintetni. Ezért ismerkedjünk meg általánosságban a felépítésével, működésének alapvető logikájával és a hozzá-tartozó jelölésrendszerrel.
Talán még ma is sokan vannak, akikben valamilyen irányban irreális kép alakult ki a számítógépekről. Vagy leegyszerűsítve csak egy nagyon gyorsan számoló automatának képzelik, vagy pedig egy fel nem fogható, teljesen elvont elvek alapján működő eszköznek. Az ugyan tény, hogy az alapműveletek elvégzésében hihetetlenül gyorsak. A "hőskorban", az elektroncsöves gépek 1000-5000 műveletet, a tranzisztoros elemek felhasználásával 10 000-50 000 műveletet, az integrált áramköri egységekből épített gépek pedig 100 000-nél is több műveletet képesek elvégezni 1 másodperc alatt. De ez nem minden! Többek között persze a nagy műveleti sebesség az, ami olyan feladatok elvégzésére is alkalmassá teszi a számítógépet, amelyek a gyakorlatban előforduló "gépies" feladatoknál lényegesen magasabb rendűek. A gyorsaság, a logikai döntések lehetősége, az igen nagy számú adat tárolása lehetővé teszi, hogy - természetesen a programozó által kidolgozott eljárás alapján - matematikai, műszaki, gazdasági stb. problémákban, a lehetséges kimeneteleket szimulálva mérlegeljen, és a legkedvezőbb megoldásokat megkeresse, a várható következmények elemzésével együtt.
A gondolatmenet érzékeltetésére talán alkalmas példa a személyi számítógépekkel is játszható sakkprogram, amelynek a futása során valóban az az érzésünk, mintha "gondolkozna" a gép, pedig csak az előre megírt és beolvasott program lépéseit járja végig.
Összefoglalva tehát, a számítógépek felhasználásával olyan feladatok is megoldhatók, amelyek megoldása nélkülük vagy csak nagyon rossz hatásfokkal lenne elvégezhető, vagy a megoldhatatlan feladatok közé tartozna. Gondoljunk pl. egy űrhajó adatainak meghatározására, pályájának módosítására az előző adatok alapján 10 km/s sebesség mellett, számítógép nélkül! Nézzük tehát meg egy kicsit közelebbről, hogyan is épül fel, működik egy ilyen, bonyolultságában is egyszerű eszköz, mint a számítógép.
A számítógép fő részei:

1. Központi egység (Central Processor Unit CPU)
2. Be- és kiviteli egységek (Input-Output).

Minden számítógépben a következő funkciók határozhatók meg egy adott feladat végrehajtásakor: adatbevitel, vezérlés, műveletvégzés, eredménykiíratás.
Az adatok beolvasása, az eredmények kiíratása a be- és kimeneti egységeken keresztül történik, a géptől függően kényelmesebb vagy nehézkesebb eszközökkel: lyukszalag, lyukkártya, mágnesszalag, mágneslemez stb. így történik a végrehajtó program betöltése is.
A program feldolgozása és végrehajtása a központi egységben történik. Ennek részei, a feladataik szempontjából osztályozva:

1. aritmetikai (logikai) egység,
2. memória,
3. vezérlőegység.

Az aritmetikai egység
Az aritmetikai egységet számolóegységnek vagy műveleti egységnek is nevezik a szakirodalomban. Ez a gép legkisebb egysége. Alapvető feladata az összeadás elvégzése, mivel látni foguk, hogy a kivonás, a szorzás és az osztás egyaránt visszavezethető az összeadásra. A műveletre váró mennyiségeket - amelyek nem okvetlenül számok, és a továbbiakban operandusoknak nevezzük őket - ideiglenes tárolókba, a regiszterekbe helyezi el a gép, és tulajdonképpen a következő egyszerű eljárást hajtja végre:

R1 regiszter R2 regiszter

Műveletvégző

R3 regiszter

Azaz a műveletvégző elvégzi az R1 és az R2 regiszterek tartalma között az adott műveletet, és az eredményt az R3 regiszterben elhelyezni.
Az esetek többségében a műveletben résztvevő operandusok eredeti értékére nincs szükségünk, így az eredmény tárolható pl. az egyik eredeti helyén is. Ezzel kevesebb regisztert foglal egy-egy elemi művelet. A "főregisztert" akkumulátornak nevezzük, amelynek az a különleges szerepe, hogy itt történik meg az összeadás, és az eredmény is tárolódhat itt.
A gép aritmetikai egysége válaszolni tud arra is, hogy az akkumulátor tartalma egyenlő vagy nem egyenlő nullával. Ez pedig a program írásnál nagyon lényeges és jól használható, a programok elágaztatásánál van fontos szerepe.
Maga a számolómű olyan egységekből áll, amelyek a beérkező jeleket - az operandusok kódjait - átmenetileg elraktározzák, a műveletet elvégzik, és az eredményt ismét tárolják. Az első generációs gépeknél mindezt jelfogókból fölépített billenőkörökkel oldották meg. Ezért nevezzük ezeket az eszközöket elektromechanikus gépeknek. Később az ilyen áramköröket tranzisztorok felhasználásával alakították ki úgy, hogy bizonyos összetartozó egységeket (pl. összeadó áramkörök) előre összeszerelt állapotban helyeztek be, így szükség esetén a javítás, csere egyszerű volt. Természetesen a műveleti sebesség és a megbízhatóság megnőtt, hiszen az áramkörök működése nem járt együtt mechanikai mozgással. Az integrált áramkörök alkalmazásával több olyan funkcionális áramkört zsúfoltak össze működés szempontjából olyan parányi egységekbe, amelyeken belül az elemek már nem választhatók szét sem elhelyezés, sem működés szerint. 1971-től kezdődően, a mikroprocesszorok széleskörű elterjedésével és alkalmazásával, lehetőség nyílt a további miniatürizálásra, az elemi feladatok további összevonására, és arra, hogy bizonyos belső mikroprogram beültetésével ezek az egységek szinte tetszőleges feladatokhoz igazodhassanak.

A memória
A központi memória (Operatív tár)
A nagy adathalmazok kezeléséhez, raktározásához az átmeneti tároló regisztereken kívül természetesen szükség van nagy kapacitású tárra is. Ez az operatív tár. Szemléletesen úgy képzelhetjük, mint egy négyzethálós papírt, amelynek minden egyes négyzetébe csak nullát vagy egyet írhatunk, és így minden sorba egy kettes számrendszerbeli számot helyezünk el. Erre a számábrázolásra később még részletesen visszatérünk.
Ahhoz, hogy a memóriában elhelyezett adatok között tájékozódni lehessen, a tárat kisebb egységekre, ún. rekeszekre osztják. Ezeket a rekeszeket megszámozzák, így kapjuk meg a címüket. Egy-egy rekesz azzal jellemezhető, hogy hány darab kétállapotú jel - bit (a bit szócska a "binary digit" - kettes számrendszerbeli számjegy - kifejezésből származik), amelynek értéke nulla vagy egy - befogadására alkalmas. A rekeszek hossza nem egységes a különböző gépeknél. Eleinte a 6-bites, majd egyre inkább a 8-bites, azaz 1-bájtos (az angol byte-ból) rekeszhossz, ill. ennek a többszöröse terjedt el. Ezeket a gépeket nevezzük "szószervezésű"-nek, ahol a "szó" hossza lehet: 16,18, 24. 32, 60, 64 bit is.
A nagyobb szóhossz a pontosabb számábrázolást teszi lehetővé. A központi tár kapacitását a memóriában levő rekeszek száma adja meg. Ezeket 0-tól kezdve sorszámozzák, és ezek lesznek a rekeszek címei. 2^10 = 1024 rekeszt 1k-val jelölünk, ahol: k (olvasd kilo), és az 1024-nek a 10^3-ra való kerekítését jelenti. A központi tár általában modulszerűen építhető, bővíthető és fejleszthető. Létezik egy minimális tárméret, amely a működéshez alapvetően szükséges. Általában 8k nagyságú egységekkel bővíthető a memória, de a maximális méretnek is határt szab a gazdaságosság, a feladat-orientáltság stb. A "bájt" szervezésű gépek között pl. kisgépnek számít az, amelynek a tárkapacitása 4-32 kbájt között van, azaz ennyiszer 1024x8 bit fér el benne. A személyi számítógépek között szinte minden igényt kielégít a 64 kbájt memóriájú gép. Ma már nem ritka a több ezer kbájt feletti óriásgép sem. De a személyi számítógépek családjában is készült már 3 millió bájt kapacitású gép (1984. szeptember, IBM AT).

A központi memóriával szemben kettős követelményt kell támasztanunk. Egyrészt nagy legyen a tárolási kapacitás, másrészt rövid a hozzáférési idő, azaz időtartam, amely alatt egy tetszőleges információ kiolvasható, ill. bevihető.
Évekkel ezelőtt a legelterjedtebb, és még ma is használatos változat a ferritgyűrűs memória volt. Ebben néhány mm átmérőjű mágnesezhető fémgyűrűk kétféle mágnesezésű állapota felel meg a két lehetséges (1 és 0) bit-értéknek. A gyűrűk négyzetrács pontokban helyezkednek el. Ennél a tártípusnál a hozzáférési idő kb. 0,5 és 1 µs között van. Nagy előnye, hogy az adatmozgatás nem jár együtt mechanikai mozgással, az információ be- és kivitelét a gyűrűkön átvezetett író- és olvasóvezetékek segítségével végezzük. Egyik fő hátránya - amely korlátot szab az alkalmazásának is - a nagy méret.
Az adattárolás optikai úton is történhet. így lehetőség van arra, hogy egy 10x10 négyzetcentiméteres tárolólemezen akár százmillió információ is helyet kapjon. Ennek a módszernek a továbbfejlesztésével alakították ki a holografikus adatábrázolást, amely elsősorban a hozzáférési időt csökkentette tovább.
Még modernebb eljárással készül az ún. MOS tároló (Metál Oxid Semiconductor, azaz fémoxid félvezető típus), amelynél egy-egy parányi egység-chip több ezer információ befogadására alkalmas. Ez a fejlődés a gyorsaság, az árak csökkenése mellett a miniatürizálás irányába mutat, de bonyolultságában és sokféleségében (RAM, ROM, EPROM stb.) az amatőr érdeklődők számára szinte elérhetetlen területet jelent. Kizárólag nagy fejlesztőrendszerekben építhetők be, ott viszont igen változatos feladatokra, és olcsó előállítási költségek mellett.
Az integrált áramkörök további integrálódásával, a mikroszámítógépek kifejlesztése és elterjedése óriási lendületet kapott. Az LSI technológia (Large Scale Integration, azaz nagyfokú integráltság) elterjedésével újabb típusú és még előnyösebb tulajdonságú tárakat lehetett létrehozni.
A mikroelektronikában sokáig, egészen a '70-es évekig hiányoztak azok a tárolóegységek, amelyek a gyors és nem "felejtő" memóriák, valamint a lassúbb periférikus memóriák közötti tartományba eső, 10-^3 - 10^-4 s közötti elérési időt biztosítanak. Egy lehetséges megoldást 1967-ben, az amerikai "Bell Telephone Laboratory"-ban találtak meg, a mágneses buborékmemóriában. Ez az eljárás időközben széles körben elterjedt, többek között hazánkban, a KFKI-ben fejlesztettek ki ilyen eszközöket. Működésük azon az elven alapul, hogy mágneses tulajdonságú kristályrétegben mágneses tartományokat - ún. "doméneket" - lehet létrehozni, megszűntetni és mozgatni, mikroelektronikai technológiával.
Azt hiszen mindannyian érezzük, hogy ezzel még korántsem merült ki minden lehetőség. Például az egyik legújabb ('80-as évek) félvezető technikával kidolgozott tároló chip a NVRAM, amely ugyanolyan hozzáférési sebességgel rendelkezik, mint akármelyik RAM egység, de a tárolt információt kikapcsolás után is megtartja.

Eddig csak a számítógép központi egységében levő tárakról volt szó. Közös tulajdonságuk, hogy gyors hozzáférésűek, és szemben az átmeneti tároló regiszterekkel, a rekeszek tartalmát megőrzik. A központi tár mellett, ill. azzal együtt szükség van még nagyobb kapacitású és nem okvetlenül gyors hozzáférésű külső tárakra is. A további munka során még felhasználásra kerülő információkat ui. nem érdemes egy viszonylag lassú működésű egységgel, pl. sornyomtatóval vagy képernyős megjelenítővel "kimenteni" az operatív tárból. Ez az eljárás lassú és költséges.
Ilyenkor szokás - ha rendelkezésre áll - az információkat átvinni az ún. háttértárba, ahol azok hosszabb ideig tárolhatók, az elérésük is gyors és egyszerű.
A háttértár feladata tehát az, hogy a pillanatnyi működéshez nem szükséges, általában nagy mennyiségű információt tárolja. Az adatok be- és kivitelére szolgáló egységekkel együtt szokás ezeket "perifériáknak" is nevezni, utalva így elhelyezésükre is.

A vezérlőegység
A ma használatban levő gépek nagy részénél olyan szorosan összekapcsolódik a számoló- és a vezérlőegység vagy vezérlőmű feladata, hogy nem is szokás mindig különválasztani ezeket. A CPU, a központi feldolgozó egység mindkettőt magában foglalja.
Ez az egység irányítja a számítógép munkájának a menetét, biztosítja a kapcsolatot a gép egyes részei között. Értelmezi a betöltött program utasításait, amelyek általában két részből állnak, természetesen a gép számára érthető jelekkel kifejezve:

• műveleti rész, amely meghatározza, hogy milyen típusú műveletet kell elvégezni;
• címrész, amely azokat a regisztereket jelöli ki, amelyek tartalmával az adott műveletet végre kell hajtani.

A vezérlőmű tehát a memória megfelelő rekeszéből az operandus címét a címregiszterbe, a végrehajtandó utasítás kódját pedig az utasításregiszterbe tárolja. Ezután megtörténik a műveletvégrehajtás, és az eredmény megjelenik a megfelelő regiszterben. Az éppen végrehajtás alatt álló utasítás címét az utasításszámláló-regiszter tárolja, amelynek tartalma a végrehajtás után 1-gyel nő.
A következő rajz szemlélteti a számítógép által elvégzett egyetlen elemi műveletet:

"C" Címregiszter Tár "R" regiszter

Vezérlőmű Műveletvégző Akkumulátor

Az eljárás tehát a következő:
A "C" címregiszter tartalma szerinti címen levő operandus a memóriából átkerül az "R" regiszterbe.
A vezérlőmű az utasításregiszter tartalmának megfelelő műveletet elvégezteti a műveletvégző egységgel az "R" regiszter és az akkumulátor aktuális tartalma között. Az így kapott eredményt az akkumulátorban (főregiszter) tárolja.
Összefoglalva, a CPU akkor képes ellátni a feladatát, ha a következő kritériumoknak eleget tesz:

• adott címről kiolvas, ill. oda adatot ír be;
• adatokon matematikai és logikai műveleteket végez;
• utasításokat adott sorrendben végrehajt.

A működés legfontosabb feltétele egy olyan utasításnyelv, amely a számítógép számára közvetlenül érthető módon rögzíti a program egyes lépéseit.

Az adatok, információk megjelenítése
Minden információt, amelyet meg akarunk "értetni" a géppel, és szeretnénk, ha a bevitt adatokkal műveleteket végezne, le kell fordítani - kódolni - a gép mint műszaki eszköz által értelmezhető nyelvre. A használt kódrendszer akkor éri el a célját, ha a kívánt információ úgy alakítható át valamilyen jellé, hogy abból az eredeti információ egyértelműen visszaalakítható legyen. Az emberi beszéd írásban való rögzítése is egyfajta kódolás. Gondoljunk csak pl. az egyiptomi, az arab vagy a japán írásjelek "rajz-képeire"!
A kódrendszer annál könnyebben használható, minél kevesebb jelből áll a jelkészlete és ezek a jelek minél egyszerűbbek. A számítógépekkel való információ ábrázolására a legalkalmasabb, ha mindössze két lehetséges jelet engedünk meg. Az elektronikai elemek ui. a két állapotot egyszerűen képesek tárolni és feldolgozni, mégpedig az esetek többségében egy bizonyos feszültségjel-megjelenésével, ill. a jel hiányával. Később részleteiben is megismerjük az ilyen kétállapotú jelekkel kialakított kódrendszert (EBCDIC-kód).
Az ábrázolandó információ minden egyes jelét - a karaktereket - nyolc pozíción, ill. nyolc biten jelenítjük meg. Ez az ábrázolásmód szoros összefüggésben áll a kettes számrendszerrel.
Bár eddigi tanulmányaink során már használtunk a tízes számrendszertől különböző számrendszert is, emlékeztetőül tekintsük röviden át a legfontosabb fogalmakat!

A számrendszerek
A tízes vagy decimális számrendszert nap mint nap használjuk valamennyien, de szinte csak mechanikusan. Senki nem gondol pl. a 225 leírásakor arra, hogy tulajdonképpen egy összeggel, a 2*10^2 + 2*10^1 + 5*10^0 kifejezéssel dolgozik!
A 10 a számrendszer alapszáma (alapszám=radix, jelölése: R), az adott helyen előforduló különböző lehetséges számjegyek, az együtthatók, amelyek csak 0 és (R-1) közötti egész értékeket vehetnek föl.
Általánosságban, az R alapszámú számrendszerben egy N természetes számot, amely n számjegyből áll, a következőképpen írhatunk fel:

Megjegyzés: az ai együtthatók nem okvetlenül különbözőek, és lehet közöttük nulla is.
A választott számrendszer alapszáma tehát az R, ami bármely 1-nél nagyobb természetes szám lehet, azaz tetszőlegesen sok alapszám alkalmas számrendszer képzéséhez, így pl. a százas számrendszerben 100 különböző számjegy, a tizenhatos számrendszerben 16, a kettes számrendszerben 2 számjegy szerepelhet minden egyes pozíción.
Nézzük meg, melyik az a legnagyobb szám, amely egy R alapszámú számrendszerben, n pozíción megjeleníthető! Ez lesz ui. az adott n pozíciót kifejezhető legnagyobb szám, a számolás felső határa. Decimális számrendszerben, R=10, pl. három pozíción, n=3, a legnagyobb szám: 999, azaz 10^3-1. Ez az egyszerű szabály - gondoljuk meg! - általánosan is érvényes! Nmax=R^n-1. Rn értéket modulusnak (M) nevezzük. M megadja az összes egymástól különböző állapotok számát. Az előbbi példánál maradva, három decimális pozíción kifejezhetjük 0 és 10^3-1 között az egész számokat, összesen 10^3 decimális számot. Például a gépkocsik kilométerszámlálóján, öt helyen, a maximális kilométerállás 99999, a lehetséges kilométer állások száma 100 000.
A digitális számítógépek működése szempontjából számunkra a legfontosabb a kettes (bináris) számrendszer!
R=2 esetén az egyes biteken használható együtthatók, azaz a bináris számrendszer számjegyei: 0 vagy 1. Egy tetszőleges kettes számrendszerbeli szám értéke a decimális számrendszerben a következő egyszerű "számolgatással" határozható meg:

10011b = 1*2^4 + 0*2^3 + 0*2^2 + 1*2^1 + 1*2^0 = 16 + 2 + 1 = 19

Természetesen nemcsak egész, hanem törtszámok is szerepelhetnek munkánk során. Például:

1011.01b = 1*2^3 + 0*2^2 + 1*2^1 + 1*2^0 + 0*2^-1 + 1*2^-2 = 8 + 2 + 1 + 1/4 = 11.25

A számrendszer alapszámát szokás a legkisebb helyértékű számjegy után zárójelben jelölni vagy pl. a kettes számrendszerbeli számot 'B' betűvel jelölni. Mi ettől a továbbiakban az egyértelmű esetekben eltekintünk vagy a 'B' jelölést használjuk.
A kettes számrendszer használatának nagy előnye abból adódik, hogy minden biten vagy csak 0, vagy csak 1 állhat. Ha 0 szerepel, akkor ez a bit nulla értéket képvisel, ha pedig 1, akkor a kettő megfelelő hatványát. Bináris számrendszerben dolgozva, pl. 8 biten, a modulus M = 2^8 = 256. Az ábrázolható legnagyobb szám pedig: Nmax = 2^8 - 1 = 255. Ennek megjelenítése a nyolc biten:

11111111

Az előbbi átalakítás alapján, amelyet a számrendszerek közötti konverziónak neveznek, az is látható, hogy a decimálisán két helyértéken fölírt szám - példánkban a 19 - binárisan öt bitet igényel, tehát lényegesen hosszabban fejezhető ki ugyanaz az érték. Ezért a számítástechnikában két másik, a 8-as (oktális), és a 16-os (hexadecimális) számrendszer is használatos, elsősorban az eredmények kiértékelésére, megjelenítésére. Az aritmetikai és logikai műveletek elvégzése, az eredmények tárolása binárisan történik.

Nyolcas (oktális) számrendszer
Egy oktális szám decimális értékét, az általános érvényű szabályok alapján így határozhatjuk meg:

6574(8) = 6*8^3 + 5*8^2 + 7*8^1 + 4*8^0 =
= 6*512 + 5*64 + 7*8 + 4 = 3072 + 320 + 56 + 4 = 3452

Látható, hogy az oktális és a decimális szám hossza és nagyságrendje között nincs lényeges különbség.

Tizenhatos (hexadecimális) számrendszer
Jelölése: 'H'. R = 16 miatt minden pozíción 16 különböző jelet kell megjeleníteni. Erre nem elegendő a decimális számrendszer tíz számjegye. Ezért a hiányzókat betűvel jelölik, mégpedig a következő módon:

A már megismert "helyértékes" kifejezést használva, nézzük a következő egyszerű konverziót:

32D9h = 3*16^3 + 2*16^2 + 13*16 + 9 = 12288 + 512 + 208 + 9 = 13017

Ha összehasonlítjuk a bináris, oktális és a hexadecimális számrendszer sajátosságait, észre kell vennünk, hogy az oktálisan egy helyértéken kifejezhető számok, azaz az oktális számjegyek binárisan három biten írhatók föl, a hexadecimális számjegyek pedig négy biten. Általában is igaz, hogy ha egy számrendszer alapszáma egy másik számrendszer alapszámának az egész kitevőjű hatványa - 16 = 2^4, 8 = 2^3 -, akkor a számrendszerek közötti konverzió egyszerűen elvégezhető. Ha bináris számot írunk át oktálisba, ill. hexadecimálisba, a bináris ponttól - így nevezik a tizedesvessző bináris megfelelőjét - kiindulva három bites (triéd), ill. négy bites (tetrád) csoportokra osztjuk a számot. Ezután minden egyes csoportból egy oktális, ill. egy hexadecimális számjegyet képezünk, és ezeket egymás mellé írva kapjuk az átalakított számot.
Gyakorlásképpen nézzünk néhány egyszerű konverziót!

Bináris oktális:

1 110 101.1011 = ?
1  6   5 .5 4
Tehát: 1110101.1011B = 165,54(8)

Hexadecimális bináris:

111 0101.1011 = ?
 7    5 .  B
Tehát: 1110101.1011B = 75.Bh

Vegyük észre, hogy a hiányos triádokat, ill. tetrádokat gondolatban nullákkal töltjük fel!
Ha nyolcas számrendszerből kettesbe alakítunk, az elv ugyanaz, de az egyes számjegyeket úgy kell hármas bitekkel helyettesíteni, hogy minden bit fel legyen töltve!

Oktális bináris:

 6  7  2 . 4  3(8) = ?
110111010.100001

Tizenhatos számrendszerből kettesbe alakításkor az egyes számjegyeket négyes bitekkel helyettesítjük.

Hexadecimális bináris:

  8   A   5   D .  1   Ch = ?
1000101001011101.00011100

Mindezt figyelembe véve, elegendő ha a bináris-decimális átalakításban megbízható gyakorlatot szerzünk (számítógépeink is ezt teszik!), így a decimális-oktális, decimálishexadecimális konverzió nehézkes és számolásigényes műveleteit kikerülhetjük.
Nézzük meg tehát részletesen, milyen nehézségek adódhatnak, ha egy tetszőleges decimális szám bináris megfelelőjét keressük! Az egész és törtrészt is tartalmazó számok átírásakor a legegyszerűbb, ha külön számoljuk ki az egész és külön a törtrész bináris megfelelőjét, majd ezeket a bináris ponttal egyesítjük.
Az egész rész átalakításához a következő módszer ajánlható:

1. A számot osztjuk kettővel, leírjuk a hányadost és a maradékot. A maradék lehetséges értéke 0 vagy 1.
2. Az előző osztásnál kapott hányadossal megismételjük a kettővel való osztást, mindaddig, amíg el nem érünk a nulla hányadosig. Véges sok lépésen belül ez megtörténik, mivel minden lépésnél "legalább" a felére csökken az osztandó.
3. A maradékok az utolsótól kiindulva adják a bináris szám egész részét. Tehát az utolsó hányadoshoz (amelynek értéke mindig 0) tartozó utolsó maradék (amelynek értéke mindig 1) adja a bináris szám legnagyobb helyértékű bitjét.

Írjuk át a 121.79-et binárisba. Az egész résszel kezdve:

121/2
a hányadosok:	60 30 15 7 3 1 0		a maradékok:	1 0 0 1 1 1 1

A maradékok kiolvasásának iránya alulról fölfelé! Tehát a szám:

121 = 1111001b

A törtrész átalakítása a következő szabály szerint történhet:

1. Szorozzuk kettővel a szám törtrészét, és leírjuk külön a szorzat egész részét is és törtrészét is.
2. Az előző szorzásnál kapott törtrészt ismét szorozzuk kettővel, egészen addig, amíg a szorzandó szám törtrésze nulla nem lesz. Természetesen az esetek többségében ezt a nullát nem érjük el, hiszen nem biztos, hogy 1/2 hatványaival pontosan kifejezhető a deci-mális szám törtrésze, de tetszőleges pontossággal megközelíthető.
3. A szorzásnál kapott egész részek (amelyek értéke 0 vagy 1) adják a decimális szám törtrészének bináris alakját, a legmagasabb helyértékű bittől kezdődően.

0,79*2
eglsz részek:	1 1 0 0 1 0 1 0		a maradékok:	58 16 32 64 28 56 122 24

Az egész részek kiolvasási iránya fölülről lefelé, tehát a szám 0,79 = 0,11001010b - 8 bit pontossággal.
A teljes átalakítás tehát, 8-8 biten ábrázolva az egész és a törtrészt: 121,79 = 111001.11001010. Ugyanezen szám átírása oktális, ill. hexadecimális számrendszerbe:

121,79 = 1 111 001.110 010 10 = 171,624(8)
121,79= 111 1001.1100 1010 = 79,CAh

Gyakorlásképpen végezzük el a következő átalakításokat:

Hexadecimális decimális: 5A3.05h = ?
(1443.0507812)

Oktális decimális: 3025.17(8) = ?
(1557.2657812)

Decimális bináris: 53,625 = ?
(110101.101b)

Aritmetikai műveletek bináris számrendszerben
Számítógépünk alapvető feladatai közé tartozik a bevitt és a tárolt adatokkal operandusokkal - való művelet végzése. Ezen a területen mutatkozik meg igazán a bináris számrendszer előnye. A négy alapművelet közül ui. elegendő csak az összeadásra és a kivonásra megtanítani a gépet, mivel ebben a számrendszerben - mint ahogy ezt később látni fogjuk - a szorzás adott számú összeadásra, az osztás pedig ismételt kivonásra vezethető vissza. Sőt, a kivonás művelete is helyettesíthető összeadással, tovább egyszerűsítve ezzel a számítógép műszaki kialakítását.
Mielőtt rátérnénk a bináris műveletek tanulmányozására, alapvetően fontos, hogy megismerkedjünk a Boole-algebrával, a kétállapotú mennyiségek algebrájával. Alapjait George Boole dolgozta ki a múlt században, de a számítógépek működésében ma is nélkülözhetetlen. Általános tételeket és szabályokat tartalmaz, függetlenül attól, hogy a kétféle jel - állapot - milyen jelentéssel rendelkezik. Ha a két lehetséges érték az 1 és a 0, a kettes számrendszerre ad jól használható és egyértelmű információkat.
A két értéknek tulajdoníthatunk olyan jelentést, amely egy esemény bekövetkezését vagy be nem következését jelenti. Ilyenkor azt mondjuk, hogy az adott eseményhez rendelünk egy logikai változót - logikai, mert ezekkel az eseményekkel aritmetikai műveletek nem végezhetők, de amint ezt hamarosan látjuk, logikai műveletek igen -, amelynek logikai értéke bekövetkezéskor "igaz", ellenkező esetben "hamis". Az igaz, ill. a hamis értéknek megfeleltethetjük az "l"-et, ill. a "0"-át. Például:

1. Megírom egy feladat számítógépes programját, tehát az eseményhez rendelt logikai változó értéke 1, ha;
2. Van az iskolában számítógép - ha van 1, ha nincs 0, és ha
3. Tudok programozni. Ennek a változónak a lehetséges értékei 1 vagy 0.
   Tehát az (1) változó értéke 1, ha a (2) és a (3) változók értéke is 1.

Így ha nem is jelentésben, de jelölésben, műveletekben szoros analógia figyelhető meg a "bináris" algebra és a "logikai" algebra között. Lényeges különbség az, hogy a bináris algebrában a változóknak numerikus jelentésük van, és lehetséges értéküket egy csupa 0-ból és 1-ből álló jelsorozat képviseli, a Boole-algebrában pedig a változóknak csak logikai jelentése van, és két lehetséges értéke, amelyeket csak jelölünk 0-val vagy 1-gyel.
A logikai algebra tulajdonképpen az események, azaz a logikai változók között végezhető műveletekkel foglalkozik. Az eredmény szintén csak kétértékű lehet.

Logikai műveletek:
Ezek végeredményét, azaz az adott művelet "bemenő" és "kimenő" adatai között az összefüggést ún. igazságtáblázatokkal szemléltetjük.

"NEM" (NOT) művelet, logikai tagadás. Egy "A" esemény tagadását, a következő egyszerű igazságtáblázat tartalmazza:

A = 1 NOT A = 0
A = 0 NOT A = 1

Tehát az eredeti logikai értéket minden esetben az ellentettjére kell változtatni. Ezt nevezik invertálásnak.

"ÉS" (AND) művelet, logikai szorzás. Itt két vagy több bemenő esemény és egy kimenő szerepel. A műveletet a szorzás jelével is jelöljük: X = A*B. Az egymással ÉS kapcsolatban levő bemenő változók mindegyikének "1" értéket kell felvenni, csak akkor lesz "1" az eredmény. Így az igazságtáblázat:

A = 1, B = 1 A AND B = 1
A = 1, B = 0 A AND B = 0
A = 0, B = 1 A AND B = 0
A = 0, B = 0 A AND B = 0

"VAGY" (OR) művelet, logikai összeadás. Szintén kétváltozós művelet, amelynek jelölése: X = A+B. Azt tartalmazza, hogy valamelyik esemény bekövetkezése már maga után vonja az eredmény igaz értékét. Az igazságtáblázata:

A = 1, B = 1 A OR B = 1
A = 1, B = 0 A OR B = 1
A = 0, B = 1 A OR B = 1
A = 0, B = 0 A OR B = 0

Nem tartozik szorosan a logikai alapműveletek közé, de gyakran használatos a "kizáró VAGY" (XOR) művelet, amely annyiban tér el a VAGY-tól, hogy a bemenő események egyidejű bekövetkezésekor 0 értéket vesz föl. Tehát ha A = 1 és B = 1 egyszerre teljesül, akkor X = 0.

A = 1, B = 1 A XOR B = 0
A = 1, B = 0 A XOR B = 1
A = 0, B = 1 A XOR B = 1
A = 0, B = 0 A XOR B = 0

A három logikai alapművelettel tetszőleges további logikai összefüggés fölépíthető. Pl:

A+B = (NOT A)*B + A*(NOT B)

Ez az állítás könnyen belátható, akár az igazságtáblázatok összevetésével, akár a matematikában ismert halmazelméleti megfontolással, ahol a logikai változóknak egy-egy síkbeli ponthalmazt feleltetünk meg.
Az összetett logikai kifejezések átalakítása az ún. de Morgan azonosságok alapján végezhetők el:

(NOT A) + (NOT B) = NOT (A*B)	(nem a) vagy (nem b) = nem (a és b)
(NOT A) * (NOT B) = NOT (A+B)	(nem a) és (nem b) = nem (a vagy b)

Ezek igazolását az olvasóra bízva, megjegyezzük, hogy a logikai áramkörök tervezésénél jól használhatók ezek az "egyszerűsítő" átalakítások.
Logikai műveleteket nemcsak logikai változókkal végezhetünk, hanem tetszőleges kétállapotú adatokkal is. Ilyenkor az operandus egyes bitjeivel egymástól függetlenül kell elvégezni az adott műveletet. Végezzünk pl. logikai VAGY-ot a következő két hexadecimális szám, ill. bináris megfelelőik között:

"A" = B2Fh, "B"=685h
"A" + "B"= ?

1011 0010 1111
+ 0110 1000 0101	=
1111 1010 1111

Tehát az eredmény: FAFh. Ahogy azt majd hamarosan látni fogjuk, ez az eredmény majdŹnem megegyezik a bináris összeadással kapott eredménnyel.
ÉS műveletet végezve az előbbi két operandussal, szintén bitenként:

B2Fh * 685h = ?

1011 0010 1111
* 0110 1000 0101	=
0010 0000 0101

Az eredmény hexadecimálisan fölírva: 205.
Az említett logikai azonosságok és az alapműveletek tulajdonságainak felhasználásával összetett logikai kifejezések egyszerűbb alakra hozhatók. Például:

(NOT A)*(A+B) = (NOT A)*B
A + (A*B) + ((NOT A)*B) = A+B
A + (NOT A) = 1
A * (NOT A) = 0

Meg kell végezetül említeni még a relációkat, mivel ezekkel gyakran találkozunk a programozás során. Ilyenkor két, nem okvetlenül algebrai kifejezés viszonyát vizsgáljuk, amelyek lehetnek: kisebb, nagyobb vagy egyenlő.
Nézzük tehát hogyan végez számítógépünk aritmetikai műveleteket!

Bináris összeadás
Mivel a gép összeadó egysége is, még több összeadandó esetében is egyszerre csak két operandus között végzi el a műveletet, mi is ezt az egyszerű esetet tanulmányozzuk. Minden helyértéken - biten - a következő lehetséges esetek fordulhatnak elő:

• 0 + 0 = 0
• 1 + 0 = 1
• 0 + 1 = 1
• 1 + 1 = 0 (átvitel: 1)

Az "átvitel" 1-es átvitelt jelent a következő, 1-gyel magasabb helyértékű bitre, és ezt ott természetesen összeadandónak kell tekinteni. Az átvitellel keletkezett 1-es megfelel a decimális számrendszerben a tízes átlépésnek. Több számjegyű számok összeadásánál tehát ügyelni kell az egyes biteken kialakuló részeredményre és az alacsonyabb helyértékről esetleg átkerülő átvitelre is.
Nézzünk erre is példát úgy, hogy eredményeinket "ellenőrizzük" decimálisán!

101110			46
+ 10111	=		+ 23	=
1000101			69

Az előbbi példából látható, hogy előfordulhat, hogy az összeg nem fér el annyi biten, mint az összeadandók. Ebben az esetben keletkezhet az ún. "túlcsordulás", amelyre később még visszatérünk.

Bináris kivonás
A tízes számrendszerben megszokott és tetszőleges számrendszerben alkalmazható módszer kényelmesen használható ugyan kettes számrendszerben is, azonban a számítógépek belső kiépítése szükségessé tette egy másik eljárás kialakítását. Az alapvető elv az volt, hogy az alapműveleteket egymásra visszavezethetően lehessen elvégezni! Ezért használják a kivonás elvégzésére az ún. "komplemens aritmetikát", amely lehetővé teszi, hogy a kivonást is az összeadó egység végezze el. A komplemens szó két egymást kölcsönösen kiegészítő dolog egyikét jelenti. Mit kell kivonáskor kiegészíteni, és mire?!
A kivonandót, azaz a negatív számot, az adott pozíciószámhoz tartozó modulusra, és így már végezhető is az összeadás. Nézzük ezt meg részletesen! Például 8 biten (1 bájt) a -5 megjelenítése a következő módon történik komplemens képzéssel: -5 = ?

1. 5 = 101 = 00000101
2. Invertálás, azaz az 1 értékű biteket 0-ra, a 0 értékűeket 1-re cseréljük: 00000101 11111010
3. Az így nyert számhoz 1-et hozzáadunk, mivel a modulus 1-gyel nagyobb mint a legnagyobb ábrázolható szám. Tehát: -5 = 11111011

Ezek alapján a számítógép 8 biten a 22-5 = 22+(-5) = 17 egyszerű műveletet így végzi el:

22:	00010110
-5:	11111011	=
17:	1 00010001	(átvitel: 1)

A 8 biten keletkező eredmény a helyes értéket adja meg. Az első pozíción, azaz a kilencedik biten keletkező 1-es értéket nem kell figyelembe venni. Ezt a gép is "elfelejti", hiszen csak nyolc biten számol! Ez természetesen nem azonos a túlcsorduláskor keletkező 1-gyel, hiszen a nyolcadik pozíción álló 0 azt is jelenti, hogy az eredmény pozitív előjelű, nem kell "visszaalakítani".
Vizsgáljuk meg azt az esetet is, amikor az eredmény is negatív lesz.

75 - 96 = 75 + (-96) = -21

75:	01001011
96:	01100000
invertálás	10011111
+1 -96	10100000
eredmény	11101011

A legmagasabb helyértékű biten - ez az előjel bit - álló 1-es a negatív előjelre utal, így az eredményt még vissza kell alakítani, rekomplementálni:

11101011 00010100 + 1 00010101 = 21

Tehát a helyes eredmény az előjellel együtt: -21.
Lehetséges, hogy ez az eljárás első olvasásra nehézkesnek tűnik, de ha meggondoljuk, felhasználásával a számítógépben csak összeadó és invertáló egység szükséges a négy alapművelet - hamarosan látjuk, hogy a szorzás és az osztás is elvégezhető ilyen egységgel - elvégzéséhez. Belátható, hogy ez már megéri a fáradságot.
Természetesen a komplemens aritmetika használható decimális számrendszerben is előjeles számok összevonására, de ott az invertálás a számjegyek 9-re történő kiegészítését jelenti. Kipróbálni lehet, sőt érdemes, de használni jobb a "hagyományos" kivonást!

Mivel a számítógépek nagy része az adatokat 32 biten, azaz 4 bájton tárolja (ezek a "szószervezésű" gépek), nézzünk még egy feladatot előjeles számok összeadására, 32 biten, hexadecimális alakban, amelynél 32 bit = 1 szó áll rendelkezésünkre egy- egy szám ábrázolásához. (Általában lehetőség van félszó és duplaszó használatára is.)

179:	00000000 00000000 00000000 10110011	= 000000B3
108:	00000000 00000000 00000000 01101100	= 0000006C
-108:	11111111 11111111 11111111 10010100	= FFFFFF94
179-108:	00000000 00000000 00000000 10110011
	11111111 11111111 11111111 10010100
=	1 00000000 00000000 00000000 01000111	= 00000047

A kapott szám pontosan +71-nek a hexadecimális alakja.

Amennyiben az eljárás érthető, ellenőrizzük tudásunkat a következő feladat megoldásán!

1. Egy művelet során, 32 biten, előjelesen a következő eredményt kaptuk: FFFFF3C8h. Értelmezzük az eredményt, milyen decimális számnak felel meg?

Megoldás:

• FFFFF3C8h = 11111111 11111111 11110011 11001000
• Az "előjelbit" 1-es, tehát negatív számról van szó, invertálni kell:
  00000000 00000000 00001100 00110111
• 1-egy hozzá kell adni:
  00000000 00000000 00001100 00111000
• Ez a szám hexadecimális számrendszerben: C38h = 3128
• Tehát a végeredmény az előjelet is figyelembe véve:
  FFFFF3C8h = -3128

Szorzás és osztás elvégzése kettes számrendszerben
Amint már jeleztük, ez a két művelet is visszavezethető összevonásra. Az eljárás teljesen megegyezik a decimális számrendszerben használttal, ezért csak egy-egy példán keresztül vizsgáljuk meg!

Szorzás: pl. 11*13 = 143
binárisan:

   1011 * 1101
  1011
 1011
10001111 = 143

Osztás: pl. 117/22 = 5.3181
Előbb számítsuk ki az egész részt:

1110100 / 10110
10110
 011101
  10110

Elvégezve az utolsó kivonást, folytathatjuk a törtrész kiszámításával:

11100 / 10110 = .01010001
10110
  11000
  10110
     100000
      10110
       1010

Ez az utolsó maradék, a számolást tovább folytathatjuk, tetszőleges pontosságig. Tehát az eredmény: 101.01010001 = 5.318.

Feltehetően a két előbbi példából látható, hogy a szorzás valóban visszavezethető egymáshoz képest sorozatosan eltolt összeadásokra, az osztás pedig annak az eldöntése, hogy egy adott szám a másikból hányszor vonható ki. így a négy alapművelet elvégzésére alkalmas egységnek, az aritmetikai egységnek nem kell mást "tudnia", mint az előjel bitet is beleértve, bitenként összeadni, jobbra, ill. balra eltolni (ez a siftelés) és invertálni. A gépi szintű programozásnál még visszatérünk erre a kérdésre. Hogy az ilyen egységeket hogyan valósítják meg ma a gyakorlatban, annak tárgyalására ebben a könyvben nincs mód.

Adathordozók
A számrendszerekben végzett barangolásunk után kanyarodjunk most vissza kiindulási kérdésünkhöz, a számítógépben megjelenítendő adatok ábrázolásához.
A számítógépek többsége, különösen a személyi számítógépek olyan műszaki adottsággal - hardver (angolul: hardware) - rendelkeznek, amely minden információt kétállapotú jelek sorozatával tárol. Ezért is foglalkoztunk, bár a teljesség igénye nélkül, de részletesen a bináris számrendszerrel és a Boole-algebrával. A személyi számítógépek közül sokban a nemzetközi szabvány szerint a nullának a +12V,az egynek a -12V felel meg. A belső karakter ábrázolás legelterjedtebb módja az EBCDIC-kód. Ez a rövidítés egy angol kifejezés kezdőbetűit tartalmazza: Extended Binary Coded Decimal Interchange Code. Magyarul: A binárisan kódolt decimális számok kiterjesztett átalakító kódja. 8 biten (1 bájt) kerül minden karakter ábrázolásra, azaz a modulus: M=256. Tehát ez a kód alkalmas 256 féle jel kifejezésére! Ez olyan nagy szám, hogy ennyi karakter fölösleges a számítógépek egyszerű nyelvén. Ezért lehetőség van bizonyos egyszerűsítő, a megjegyzést megkönnyítő összevonásokra is. A 8 bit fel van osztva két 4-bites tetrádra, két félbájtra:

zóna bitek / numerikus bitek

Az így létrejövő 1-1 félbájt tartalma éppen 1-1 hexadecimális számjeggyel reprezentálható. Ennek alapján a nagybetűk (alfabetikus jelek) EBCDIC kódjai hexadecimális alakban a következők:

"A": C1, "B": C2, ... "I": C9
"J": D1, "K": D2, ... "R": D9
"S": E2, "T": E3, ... "Z": E9

Az "egyéb" karakterek kódjai, amelyek általában az adott gép leírásában megtalálhatók, szintén "beleférnek" a 256 lehetőségbe. Például a szóköz kódja: 40, a "+": 4E, a "-": 60.
A decimális számjegyek kódjai:

"0": F0, "1": F1, ..., "9": F9

Ilyen alakban azonban a zónabitek miatt a gép nem tud aritmetikai műveleteket végezni ezekkel a számokkal. Csak a „szövegszerű” információk kezelésénél használható ez a kódolás, ahol a "szöveg", amely tartalmazhat betűket, számokat és egyéb karaktereket, annyi bájtot foglal el, ahány karakterből áll.
Például a "VW GOLF" kifejezés EBCDIC formája a következő: E5 E6 40 C7 D6 D3 C6.

Az aritmetikai műveletekhez is használható numerikus adatok ábrázolásának egyik közismert módja a BCD kód. A BCD (Binary Coded Decimal) jelentése: binárisan kódolt decimális szám. Ez az ábrázolási forma azt tartalmazza, hogy decimális számrendszerben marad az adott szám, de minden egyes számjegyét bináris számrendszerben írjuk fel. A tíz decimális számjegy kódolásához négy bit szükséges, így 1 bájton két BCD számjegy fér el. Ez a forma az ún. tömörített alak. A szám előjele a legkisebb helyértékű félbájton kerül kifejezésre, és mivel félbájt nem maradhat üresen, a páros számú számjegyből álló számok esetében a legnagyobb helyértékű félbájtot 0000-vel kell feltölteni.

Az előjel kódja:
"+": 1100 = C
"-":  1101 = D

Így pl. 1984 kódja:
0000 0001 1001 1000 0100 1100 = 0 1984C.

A tömörített alakban kódolt operandusokkal bizonyos típusú számítógépek képesek aritmetikai műveleteket végezni, de csak azok, amelyek rendelkeznek "decimális aritmetikai egységgel". Ebben az esetben a számok előjelét, azaz az utolsó félbájtot külön kell választani, és az eredmény előjelét megállapítani. A másik nehézség, hogy ebben a formában nincs lehetőség a tizedestörtek használatára, tehát csak egész típusú adatoknál használható. Éppen ezért a BCD kód elsősorban olyan gépeknél használatos, amelyek alkalmazási területe az adatfeldolgozás, az ügyvitelszervezés, ahol többnyire elegendő a négy alapművelet elvégzése egész típusú változókkal.
A művelet befejezése után az eredmény tárolása, ill. kiíratása is úgy lenne könnyen kezelhető, ha egy-egy bájt tartalma egy-egy karakter EBCDIC kódjaként jelentkezne. Ehhez azonban a tömörített alakot szét kell húzni, hiszen ott egy bájton két számjegy jelenik meg. Ez az ábrázolás a zónás alak. Minden decimális számjegyet egy teljes bájton ábrázolunk, kivéve a legalacsonyabb helyértéken állót, mivel ott az egyik félbájton továbbra is az előjel kap helyet. A számjegyeket tartalmazó bájtok első fele, a zónarész 1111-gyel van kitöltve. Így a zónás alakban kódolt decimális szám alakja a következő:

(zónarész) (BCD számjegy) (zónarész) (BCD számjegy) ... (előjel) (számjegy)

Az előjel kódja itt is a már megismert: "+": 1100 = C és "-": 1101 = D.

Példaként nézzük meg 1080 BCD kódját, zónás alakban:

11110001 11110000 11111000 11000000 = F1 F0 F8 C0.

Látható, hogy ez az alak már csak az utolsó bájt tartalmában különbözik az adott szám EBCDIC alakjától. A mai gépeknél automatikusan végbemegy az átalakítás, amelynél az előjel kikerül a szám elé, az utolsó előtti félbájt pedig 111 = F-fel töltődik fel.
Eddigi ismereteink alapján valamennyi, a programozás során felhasználásra kerülő karakter, numerikus, alfabetikus és egyéb karakterek, felírhatok és felismerhetők egységes formában, EBCDIC kódban. A betű- és egyéb karakterek ábrázolására elterjedt és használatos ez a forma. A numerikus adatokhoz azonban sokkal inkább a bináris számrendszerbeli ábrázolást használják. Ekkor nem csupán a decimális számjegyek átírását jelenti a kódolás, hanem a teljes szám konvertálását bináris rendszerbe. Valamennyi ma használatban levő gép ilyen alakban ábrázolja és dolgozza fel az adatokat, mégpedig kétféle módon: fixpontos és lebegőpontos formában.

Fixpontos számábrázolás
Ez a számábrázolás csak egész számok esetén használható. A gép általában az utolsó számjegy után helyezi el a képzeletbeli bináris pontot. A rendelkezésre álló terület minden gépnél adott.
Maradjunk jelenleg a 32 pozíción történő megjelenítésnél. A legnagyobb helyértékű bit az előjelbit. A már korábban tárgyalt komplemens-aritmetika használata miatt a pozitív előjelet a nulla, a negatívat az 1 jelenti. Kötelező szabály a "jobbra tömörítés", tehát az előjelbit és a bináris szám közötti pozíciókon csupa nulla áll.
Például a 39-es szám ábrázolása fixpontosán, 32 biten:

00000000 00000000 00000000 0100111 = 00 00 00 27h

Az egy "szó"-ban kifejezhető legnagyobb pozitív szám:

Nmax = 2^31-1 = 2 147 483 647 = 7F FF FF FFh

A negatív számok ábrázolása a korábban megismert komplemens aritmetika alapján történik, azaz invertálunk, majd 1-et hozzáadunk. Például -100 = ?

+100 = 1100100
-100 = 0011011+1 = 0011100

Mindez 32 biten; az invertálást minden biten végrehajtva:

FF FF FF FCh

A fixpontos számábrázolás nagy előnye, hogy az alapműveletek így már mind visszavezethetők az előjellel együtt végrehajtandó összeadásra. Az előjelbitet csak az eredmény előjelének értelmezésénél kell külön kezelni.
Abban az esetben, ha két olyan nagy azonos előjelű számot vonunk össze, hogy az eredmény nem ábrázolható az adott számú pozíción, a végeredmény hibás lesz. Ez a jelenség a túlcsordulás, amelyet az előjelbit indokolatlan megváltozása jelez. Általában a számítógép programfutás közben "figyeli" a túlcsordulást, és jelzi.

Lebegőpontos számábrázolás
Mivel a fixpontosán ábrázolt számoknál az értékhatár meghatározott, és csak egész számok ábrázolhatok így; azok amelyeknek abszolút értéke 2^(n-1)-1-nél kisebb, ha "n" bites eszközzel dolgozunk, nem minden esetben megfelelő. Ennél általánosabb és rugalmasabb a lebegőpontos ábrázolás. Főleg a számításos feladatoknál elkerülhetetlen a törtszámok használata. Ezek kódolásánál a matematikában jól ismert normálalakból indulunk ki. Minden A valós szám fölírható a következő alakban: A = X * R^Y. Ezt az átírást nevezzük normalizálásnak, ahol A az eredeti szám; X az együttható vagy mantissza; R a számrendszer alapszáma; Y a kitevő vagy karakterisztika.
A számítástechnikában a normálalak annyiban különbözik a matematikában megszokott normálalaktól, hogy itt a mantissza nem 1 és 10 közé esik, hanem mindig 0 és 1 közé. Ennek az az előnye, hogy a mantisszában nem kell tizedes vesszőt vagy bináris pontot stb. használni, az automatikusan a szám elé kerül. A karakterisztika, amely mindig egész szám, tulajdonképpen a tizedesvessző (bináris pont stb.) eredeti helyéhez képest az eltolás lépéseinek a számát jelenti. A karakterisztika előjele pedig megadja az eltolás irányát. Tekintsünk egy-két példát normál alakra!

10-es számrendszerben:

+1948 =	+0,1948*10^4;	X = 1948, Y = 4
+0,001948 =	+0,1948-10^-2;	X = 1948, Y =-2

Kettes számrendszerben:

+1010.001 =	+0.1010001*2^4	X = 1010001, Y = 4
-0.101 =	-101*2^0	X = 101, Y = 0

Tizenhatos számrendszerben:

+9C.3FA =

+0.9C3FA*16^2

X = 9C3FA, Y = 2

Amennyiben az alapszámot előre meghatározzuk, mint ahogy a ma használatos számítógépeknél 16-osra normalizálnak, akkor az eredeti A számot egyértelműen megadhatjuk az előjelével, a mantisszával és az előjeles karakterisztikával. Az ábrázolás hossza most is megegyezik a gép által használt szó hosszával. Így pl. 32 biten a szokásos ábrázolás forma:

1 bit előjel, 7 bit előjeles karakterisztika, 24 bit mantissza.

Az előjel - ami a matissza és egyben a szám előjele is - megjelenítése a már megismert módon történik:
A pozitívat jelenti a 0, a negatívat pedig az 1. A karakterisztika, az előjeles kitevő kódolására egy különleges módszer, az alapértékes ábrázolás használatos. 7 pozíció áll rendelkezésre, ezen 128 különböző állapot fejezhető ki. Ennek az értéknek a fele, 64, jelenti a kitevőt, ez az "alapérték". A pozitív kitevőt ehhez hozzáadjuk, a negatív kitevő értékét pedig ebből levonjuk. Mivel a hét biten megjeleníthető maximális szám: 1111111b = 127, és ez a 1000000b alapértéknél 0111111b = 63-mal nagyobb, így a maximális kitevő: 63. A legkisebb kitevő - azaz a legnagyobb abszolút értékű negatív szám nagyságrendje - amely még ábrázolható, úgy kapható meg, ha az alapértékből a lehetséges legnagyobb számot: 1000000b = 64-et vonunk le. Tehát az ábrázolható legnagyobb negatív kitevő: -64.
A mantisszát mindig binárisan ábrázoljuk. Ha rövid vagy egyszeres pontosságú lebegőpontos alakot használunk, akkor egy szóhosszon (32 bit) a mantissza számára 24 bit jut. Dupla pontosságú számábrázolásnál - erre a számítógépek többségénél általá-ban van lehetőség - a karakterisztika változatlan, a mantissza viszont 64-8 = 56 bitre kerülhet.

Ezek után nézzük meg pl. -75 rövid lebegőpontos ábrázolását 16-osra normalizálva:

-75 = -1001011b = -4Bh = -0,4B -16^2

• negatív előjelbit: 1;
• a karakterisztika +2, tehát az alapértékhez hozzáadjuk: 1000010b;
• a mantissza: 01001011b = 4Bh.

Tehát a teljes szám 32 biten:

1 1000010 01001011 0000000 00000000

Mivel kiíratáskor a gép is így jár el, írjuk át mi is hexadecimális alakra: (balról kiindulva képezünk tetrádokat)

-75 = C2 4B 00 00

Bevezetés a programozásba

Az eddig elmondottakból feltételezhetően mindenki számára kiderült, hogy a számítógép akkor képes a felhasználó által kitűzött feladatot "automatikusan" megoldani - azaz a bemenő adatok alapján az eredményt meghatározni -, ha ismeri a feladat hibátlan programját. Azaz, ha mi elkészítjük az adott probléma megoldásához elvezető algoritmust.
Az algoritmus tehát egy olyan eljárás, amely egy nem okvetlenül matematikai feladat véges sok elemi lépésben való optimális megoldására irányul, amennyiben van megoldás! A valamennyire is összetett feladatokat elemi lépésekre kell bontani, amely lépések során vagy megfelelő értékeket rendelünk változókhoz, vagy a változók aktuális értékétől függően a feladat további lépéseinek lehetséges menetét határozzuk meg. Az ilyen elágaztatási pontoknál felmerülő döntések értelmezéséhez bizonyos logikai ítéletek igazságát kell megvizsgálni, és annak értelmében továbblépni.
Ha egy algoritmus már a számítógép által értelmezhető lépésekből, utasításokból áll, akkor nevezzük programnak. (Ennek különböző szintjei: gépi nyelven, assembly szinten és magas szintű programnyelven írt.)
Ahhoz, hogy programunk "fusson" a gépen, azaz, hogy a gép helyesen felismerje az általunk közölt utasításokat, valamint, hogy azok önmagukban és a feladat egészét tekintve is helyesek legyenek, lényeges tulajdonságokkal kell rendelkeznie:

1. Pontos és részletes leírását tartalmazza azoknak a műveleteknek, amelyek a bemenő adatokból a kimenő adatokat előállítják, beleértve a műveletek végrehajtási sorrendjét is.
2. A program a számítógép által értelmezhető nyelven megfogalmazva tartalmazza ezeket az utasításokat.

Egyelőre válasszuk külön a két szempontot, és csak az elsővel foglalkozzunk. A programnyelvre a későbbi fejezetekben teljes részletességgel kitérünk.
A program megtervezéséhez, az algoritmus egyes lépéseinek a rögzítéséhez általánosan és jól használható módszer a blokkdiagram készítése. Ez egy jelölésrendszer, amely bizonyos egyszerű geometriai jelekből, és az ezekben elhelyezett matematikai és logikai leírásokból áll. A blokkdiagramban levő egyes lépések a soron következő elemi lépést definiálják. Azok az elemi lépések, amelyek már a gép által végrehajthatók, döntően kétféle típusúak lehetnek:

1. Az értékadó vagy általános művelet, amelynek egy téglalap a jele. Ebbe írjuk a végrehajtandó műveletet ill. tevékenységet, matematikai kifejezéssel vagy szövegesen.
2. A döntési művelet, amelyet rombusszal jelölünk, és ez tartalmazza az eldöntendő kérdést. Ha a kérdés logikai jellegű, akkor kétféle irányban léphet tovább a feladat, a lehetséges válasz ui. a kérdésre "igen" vagy "nem". Ha a kérdés matematikai jellegű, a továbblépés három irányban is lehetséges, pl. az adott kifejezés kisebb mint nulla, nulla, vagy nagyobb mint nulla esetén. A lépések egymásutánját az összekötő nyilazott vonalak jelzik.

Szokás még az egész eljárás kezdő- és végpontját "START"-tal, ill. "STOP"-pal jelölni.
Természetesen ugyanazon feladat megoldásához többféle algoritmus is készíthető, a helyes eredményhez többféle úton is eljuthatunk. Most néhány közismert feladat algoritmusát és blokkdiagramját készítjük el. Amikor már megismertünk egy programnyelvet is, visszatérhetünk ezekhez a feladatokhoz, és megírhatjuk a kész, futtatható programot is.
Hasznos lenne, ha először mindenki önállóan próbálná elkészíteni a feladatot, és csak ezek után vetné össze az itt közölt megoldással. Remélhetőleg ezeknél ötletesebb, szebb megoldás is születik!

1. feladat
Készítsünk blokkdiagramot ahhoz a programhoz, amely kiszámolja az első n természetes szám összegét. Legyen n olyan bemenő adat, amelyet tetszőlegesen változtathatunk. Az összeget a következő képlet alapján számoltassuk ki:

Sn = N*(N+1)/2

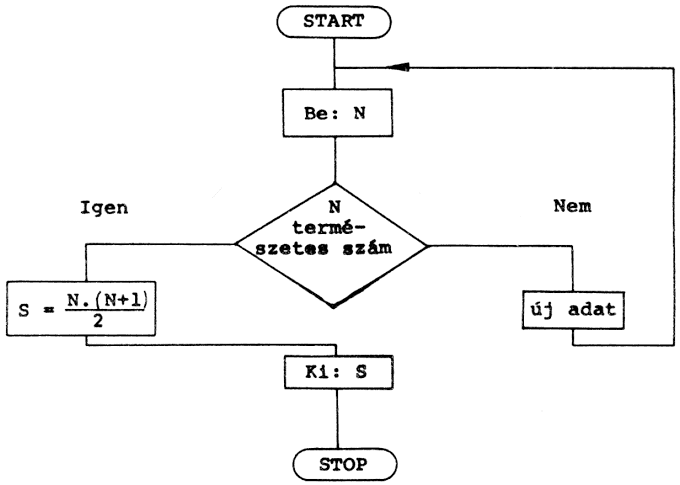
2. feladat
Az A*x^2+B*x+C = 0 másodfokú egyenlet megoldóképletének a blokkdiagramját készítsük el, feltételezve, hogy valóban másodfokú az egyenlet, tehát A<>0.

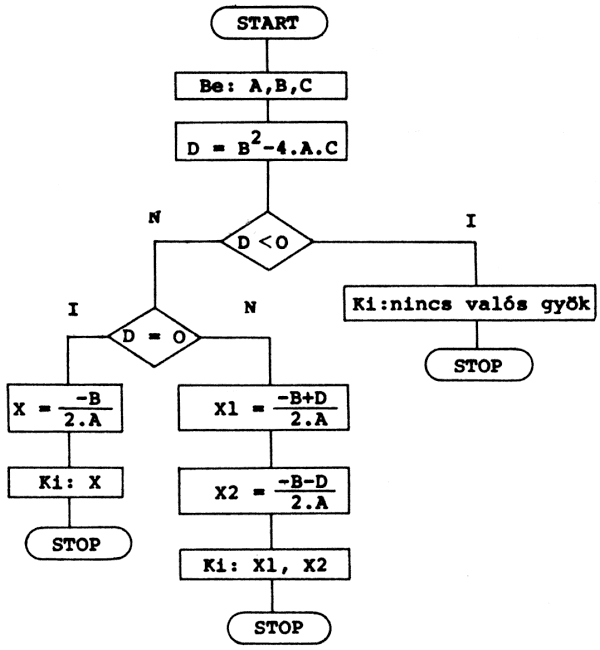
3. feladat
Három különböző szám közül, amelyeket bemenő adatnak tekintünk, válassza ki program a legkisebbet, és azt írassuk ki!

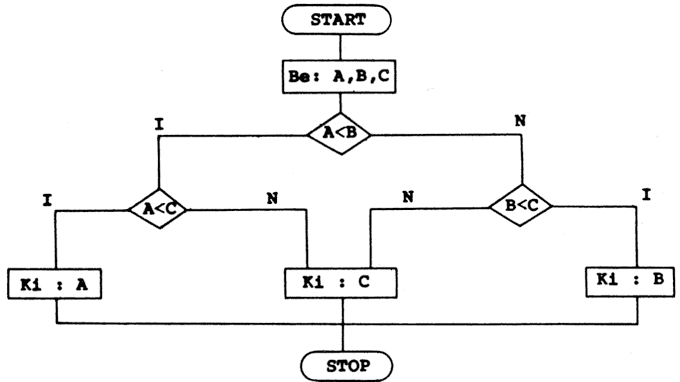
Megjegyzés: A döntési műveletek vizsgálatánál (szokás ezeket feltételes ugró utasításnak nevezni) a fő nehézség abból adódik, hogy meg kell vizsgálni minden lehetséges utat a továbblépéshez. Ezt figyelembe véve, a közölt algoritmus akkor működik igazán helyesen, ha az A, B, C értékek különbözőek. Finomítható a feladat, ha az esetleges egyenlőség esetét is tartalmazza.
Próbáljuk meg ezzel a kiegészítéssel is megoldani, esetleg úgy, hogy a három számot a program növekvő sorrendben rendezze!

Ciklusszervezés
A számítógépek széles körben és nagyon kényelmesen használható képessége, hogy ugyanazt a műveletet vagy utasítás-sorozatot tetszőlegesen sokszor elvégeztethetjük, akár állandó, akár az eljárás során változó értéket fölvevő bemenő adatokkal. Ezt a módszert nevezzük ciklusképzésnek vagy ismétlődő (iterációs) cselekvésnek.
Az általános ciklusutasítás blokkdiagramja:

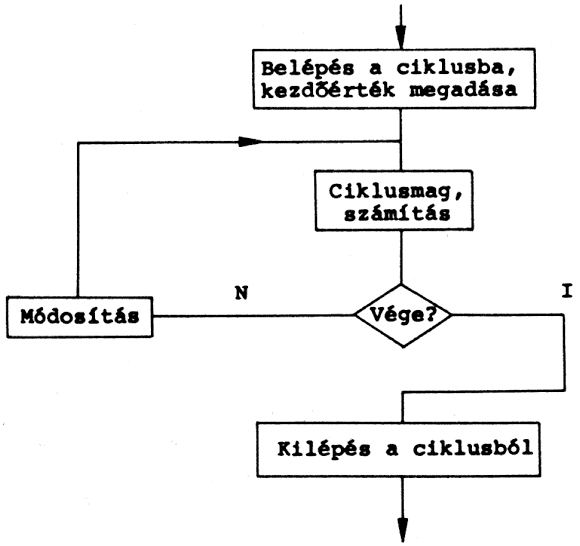
A "számítás" részt, amely során a ciklikusan elvégzett művelet zajlik, ciklusmagnak nevezzük. Ebben az esetben a "döntés-utasítás"-nak különleges szerepe van. Amennyiben hibásan vizsgáljuk meg továbblépés lehetőségeit, a számítógép végtelen ciklusba kerülhet, azaz a számításokat vég nélkül végzi, és az eredményt nem tudja felhasználni a további lépésekben.
Nagyon egyszerű példa a következő utasítás: 100 GOTO 100 , amely hatására a program tetszőlegesen sokáig "várakozik", és csak a futás megszakításával (BREAK) lehet kilépni a ciklusból.
Az ilyen döntés-vizsgálatoknak általában két fő típusa van:

1. Számlálás, amelynél előre megadott számú ismétlés után történik meg a kilépés.
2. Egy olyan változó értékének a vizsgálata, amelyet a számítás során kapunk (pl. bizonyos pontosság vizsgálata stb.).

Természetesen a két lehetőség együtt is használható.

4. feladat
Az első n pozitív egész szám összegének kiszámolása, az összegképlet felhasználása nélkül!

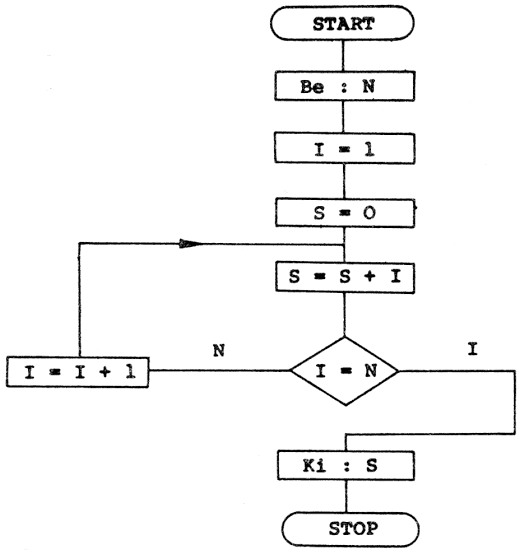
Akik először látnak olyan egyenlőséget, mint: I=I+1, bizonyára furcsának találják. A számítástechnikában az elfogadott és gyakran használatos jelölés, és nem azt a matematikai egyenletet takarja, amelynek nincs gyöke. Ez a szimbólum azt tartalmazza, hogy az I változó aktuális értéke legyen 1-gyel nagyobb, mint I előző értéke volt.

5. feladat
Készítsük el annak a programnak az algoritmusát, amely kiszámolja egy tetszőleges N természetes számig az összes természetes szám szorzatát. A matematikában ezt a szorzatot N!-sal jelölik, és N faktoriálisnak mondjuk. Tehát N! = 1*2*…*(N-1)*N. Csak olyan számokkal dolgozzunk, amelyekre N! elfér a memóriában.

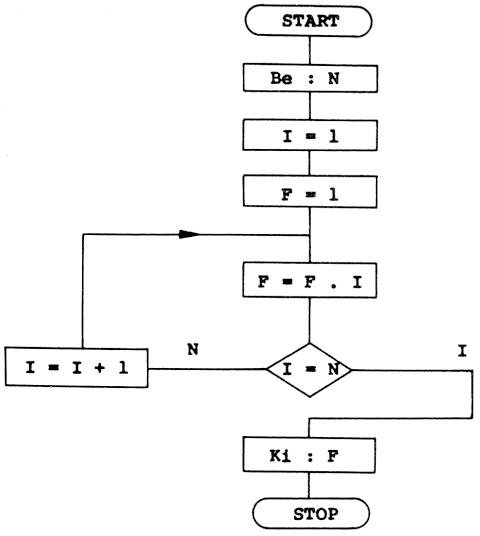
Nézzünk meg még egy érdekes matematika feladat talán nem egészen közismert megoldását!

6. feladat
Írjunk algoritmust két pozitív egész szám legnagyobb közös osztójának a meghatározására. A matematikában több módszer ismeretes erre a problémára, és ezek az eljárások többnyire nagyon jól algoritmizálhatok.
A bemutatott megoldás előnye az, hogy a gép aritmetikai egységét alig-alig "dolgoztatja". Az alapgondolat az, hogy ha egy S szám osztója A-nak és B-nek is, akkor osztója a két szám különbségének is. Ez a különbség mindig kisebb, mint A és B közül a nagyobbik, legyen ez pl. A. Ezután B-t és A-B-t vesszük az eredeti két szám helyett, és ismételjük az előbbi eljárást mindaddig, amíg a két szám egyenlő nem lesz. Belátható és bizonyítható, hogy ez a végső érték lesz az eredeti két szám legnagyobb közös osztója.
Az algoritmus véges sok lépésen belül eredményre vezet. Ezt nem bizonyítjuk, de gondoljuk végig! A programot elkészíthetjük pl. a következő eljárás segítségével:

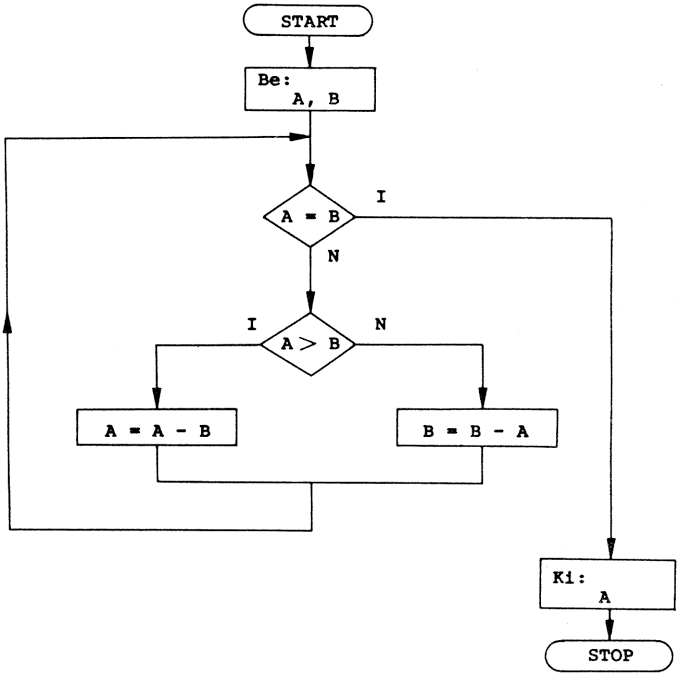
7. feladat
Végül nézzünk egy olyan problémát, amely nem közvetlenül matematikai jellegű, azaz megoldásához a matematikai modellt kell először kitalálnunk. Ez a feladat az adattömbök kezeléséhez lesz jó példa! Tulajdonképpen ezért is érdemes hasonló jellegű "játékokkal" foglalkozni már a számítástechnikai ismereteink kezdetén, hogy nehogy valaki abba a hibába essen, hogy "programozni" csak matematikusok tudnak, és csak matematikai feladatokat!
Ez a feladat arra szolgál, hogy pl. idegen szavak magyar megfelelőit visszakérdezzük. Nevezhetjük akár "szódolgozatnak" is! A két csoportban beírt adatokat, azaz az egyikben az idegen szavak, A(N), a másikban a magyar jelentésük, B(N), - "a másik játékos" ezt nem ismeri.
Az egyik csoport elemeit egyesével kiíratjuk: A(I), a "felelő" pedig beírja a szavak megfelelőit, ha ismeri: C(I). Amennyiben a C(N) tömb elemei rendre megegyeznek a B(N) tömb megfelelő elemeivel, akkor "helyes" a "felelő" megoldása, ha pedig nem, akkor "hibás".
A program természetesen nem kizárólag idegen szavak "kikérdezésére" szolgál, használható bármilyen két halmaz elemeinek az összehasonlítására.

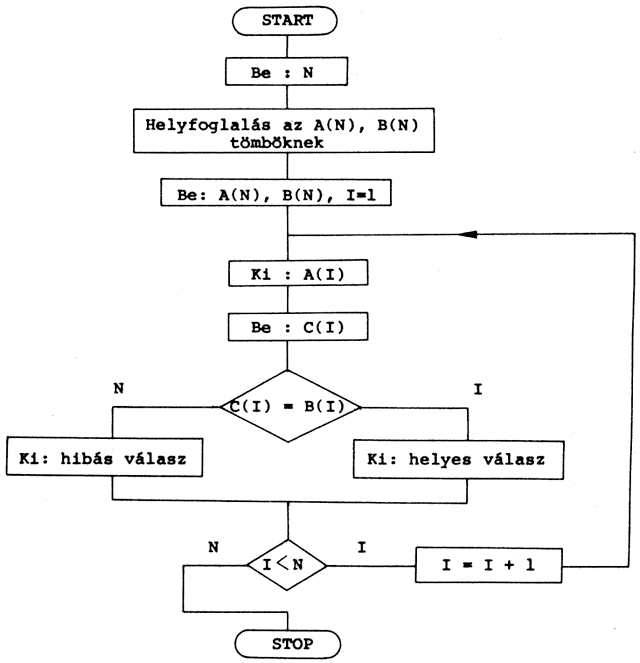
Különösen hasznos, amíg nem rendelkezik valaki nagy programozási gyakorlattal, hogy a program megírása előtt elkészítse a feladat folyamatábráját. Így sokkal nagyobb eséllyel találja meg az optimális utat, és amennyiben a program hibás, annak okát is könnyebb lesz kinyomozni!

A személyi számítógépek kialakulása és működése
Az egész világon, így hazánkban is, akik programozni akarnak, függetlenül a feladattól - matematikai, gazdasági jellegű vagy játék -, a legkönnyebben a személyi számítógépekhez tudnak hozzájutni. Ezek felhasználási területe rendkívül széleskörű, népszerűségük oka összetett: emberközelség, ár, hozzáférhetőség, egyszerűség. Meg kell azonban jegyezni, hogy memóriakapacitásban nem veszik föl a versenyt a nagyobb számítógépekkel.
A személyi számítógép egy "kicsi, olcsó, általános célú digitális számítórendszer", amely központi egységként egy LSI (Large Scale Integrated - nagymértékben integrált) mikroprocesszor-elemet tartalmaz, és valamilyen magasszintű programozási nyelven írt (BASIC, PASCAL) programok tárolására és végrehajtására alkalmas. Az információk általában írógépszerű billentyűzetről írhatók be, a kimeneti jel pedig a géphez csatlakozó televízió képernyőjén jelenik meg. Szabályos hangfrekvenciás mágnesszalagos kazetta használatával a billentyűzettel bevitt programok és adatok rögzíthetők és tárolhatók, így nem szükséges minden használatkor begépelni azokat. A nálunk forgalomban levő számítógépek nagy részénél Z80-as típusú, 8 bites mikroprocesszort használnak központi egységként. A felhasználó részére géptípustól függően különböző pl. 16 kbájt, 48 kbájt vagy 64 kbájt szabad tárterület áll a programok és az adatok rendelkezésére. A memóriának van olyan területe, amelynek tartalmát a programozás során nem szabad elveszíteni vagy megváltoztatni. Itt kap helyet pl. a BASIC nyelv értelmező programja, amelyet már a gyártás során építenek be a tárba. Erre a gazdasági megfontolásokon kívül azért is szükség van, mert ha minden programot kazettáról töltenénk be, lényegesen lassúbb és instabilabb lenne a rendszer. Hátránya viszont az, hogy ha már egyszer tartalmazza a BASIC értelmezőprogramot, akkor ezen már változtatni nem lehet, más programozási nyelv alkalmazása szinte megoldhatatlan. Igaz ugyan, hogy pl. egy egyszerűbb PASCAL nyelvet értelmező program 10-12 kbájton elfér, és így maradhat a program számára is elegendő memória.
A BASIC nyelv jelen pillanatban egyértelműen a személyi számítógépek "sikernyelve"! Az egyszerűség, a könnyen tanulhatóság mellett hallatlan nagy előnye, hogy gyakorlatilag az összes matematikai és adatkezelési függvényt tartalmazza, amelyre a programozás során szükségünk lehet. Bizonyos esetekben korlátozza a használhatóságát a lassú futás. A programot ui. nem a futtatásra kész, a gép számára érthető utasítások alkotják, hanem egy olyan karaktersorozat, az ún. ASCII (American Standard Code for Information Exchange) karakterek, amelyet az értelmező programnak soronként meg kell vizsgálnia és a megfelelő kódú gépi rutint aktivizálnia.
Persze ez a lassúság nem behozhatatlan hátrány, a BASIC nyelv egyéb előnyei bőven kárpótolják érte a programozót. Így pl. a hibakeresés, a hibajavítás sokkal egyszerűbb és gyorsabb, mintha egy másik, magas szintű nyelven bevitt programban kellene, a fordítás után megtalálni a hibát. Ennél komolyabb problémát jelent az a tény, hogy a BASIC nyelven megírt programnak és a BASIC-et értelmező programnak egyszerre kell a tár megfelelő helyén lenni, és ez a felhasználó számára nagyon lecsökkenti a szabad tárterületet. Például az a "rutinprogram", amely a billentyűzet használatát biztosítja, minimum 100 programsort vesz igénybe. Az is igaz ugyan, hogy ma, amikor a viszonylag drága ferritgyűrűs memóriákat a sokkal modernebb és olcsóbb félvezetőtárak váltják fel, a nagy tár-igény sem jelent megoldhatatlan gondot a tervezőknek. A szükséges tárterület egyrészt a használt mikroprocesszortól, másrészt a felhasznált BASIC-től függ. A legkisebb tárigénye az ún. TINY-BASIC-nek van, mindössze 2 kbájt. Ez a BASIC változat csak a -32768 és +32767 közé eső egész számokkal tud dolgozni. Egy "átlagos" igényt kielégítő BASIC kb. 8 kbájton fér el, 16 kbájton pedig már speciális problémák is programozhatok: grafikus funkciók, hanggenerátor.
Ha a számítógépünkhöz egyéb periférikus egységek is csatlakoznak, mint pl. sornyomtató, mágneslemez stb., akkor ezek használatához a kiterjesztett BASIC értelmező program szükséges, amely akár 45 kbájtot is igényel. (Megjegyzés: számítógép vásárlás esetén érdemes ügyelni ezekre a szempontokra.)
Az eddig elmondott funkciókat a mikroszámítógépek meglehetősen bonyolult rendszerként képesek megoldani, pedig tulajdonképpen csak néhány integrált áramköri elemet tartalmaznak. Ha kiindulunk egy kicsit leegyszerűsített "számítógép-modellből", akkor ennek az összetett rendszernek a működése minden bizonnyal érthetőbb lesz. Márpedig olvasóink közül valószínűleg többnek is előbb vagy utóbb megfordul a fejében az a gondolat, hogy akár "építeni" is lehetne egy mikroszámítógépet. A technológia hallatlanul gyors fejlődését figyelembe véve, erre nálunk is lehetősége van az érdeklődőknek.
Ez a bizonyos "alapgép" csak két nagy egységet tartalmaz: a központi tárat és a központi egységet.

Központi tár
Itt található valamennyi felhasznált és feldolgozandó információ, egységes formában kódolva, 1 bájt hosszúságú rekeszekben. (Megjegyzés: a jelenleg legelterjedtebb mikroprocesszort, a 8 bitest vesszük alapul.) A központi tár rekeszei és a központi egység átmeneti tároló regiszterei között történik a programfutás alatt az információk és az adatok áramlása, cseréje.
A tár rekeszei címezhetők, és a megfelelő című rekesz kijelölése a címregiszterben történik. A címregiszter általában két bájt hosszúságú, mivel így a rendelkezésre álló 16 biten 2^16 = 65536 tárrekesz címezhető. Ez a 64 kbájt már elegendő a forgalomban levő személyi számítógépek tárcímzéséhez.
A központi - vagy operatív tár - kétféle tártípusból állhat, mindkettő korszerű, magas integráltságú félvezető típusú tár:

1. Program tárolásra használt tár
Az itt tárolt információk a tápfeszültségtől függetlenül mindig bent vannak a számítógépben, bekapcsoláskor azonnal aktivizálhatók. Az ilyen típusú tárnak is több változata ismeretes.

• ROM (Read Only Memory): csak olvasható tár. A feltöltése a számítógép kialakítása során történik, az állandóan használt programokat, rutinprogramokat tartalmazza (pl. BASIC értelmező program), a programozó által nem módosítható és hozzáférhető.
• PROM (Programmable Read Only Memory): programozható, de csak olvasható tár. Bizonyos eljárással utólag is programozható, de a beírt program már nem módosítható, hibás beírás esetén a tár használhatatlanná válik.
• REPROM (Re-Programmable Rom): újraprogramozható, de csak olvasható tár. Az itt tárolt információk hibás beírás esetén vagy módosításkor ultraibolya fénnyel törölhetők vagy újra írhatók, mindez azonban igen lassú és költséges eljárás.
• Léteznek még az ún. EAROM (Electrically Alterable ROM) tárak, amelyek annyiban egyszerűbbek, hogy a törlés és az újraírás is elektromos jellel történik.

2. Adatok tárolására használt tár
Egyaránt alkalmas az információk gyors kiolvasására, ill. a beírásra, de tartalma "elveszik" a tápfeszültség kikapcsolásakor. Sőt még üzem közben is, kb. 10 ms-onként egy külön "felfrissítő" áramkör felhasználásával stabilizálni kell a tartalmat. Ezek az ún. dinamikus-RAM tárak: (Random Access Memory) tetszőleges hozzáférésű vagy írható-olvasható tár. A csekély előállítási és szerelési költségek és egyéb előnyös tulajdonságok miatt a mikroszámítógépekben elterjedten használják. Egy adat "hozzáférési ideje" 100...400 ms.
A statikus RAM tárakat tulajdonképpen a mikroszámítógépekhez fejlesztették ki, a legkorszerűbb CMOS (olyan félvezető technológia, amelynek a teljesítmény felvétele egészen minimális) technológia felhasználásával. A közös tulajdonságok mellett annyiból jobb, hogy nincs szükség felfrissítésre.

Központi egység
Közismert elnevezése a CPU (Central Processing Unit). A számítógép "magja", itt történik a vezérlés, a műveletvégzés. Itt kapnak helyet a regiszterek, amelyeknek a száma és funkciója meglehetősen típusfüggő. Az általános célú regiszterek a következők:

• Utasításszámláló (PC: Program Counter) regiszter. Ez tartalmazza a soron következő utasítás - amely a tár egy adott rekeszében van elhelyezve - címét. Tekintettel arra, hogy az operatív tár címregisztere 16 bites, így az utasításszámlálóban is 16 bit hosszúságú információkat kell elhelyezni. A regiszter tartalma minden végrehajtott lépés után 1-gyel nő, ha pedig ugró utasításhoz ér a program, a továbbszámlálás helyett új értéket vesz föl.
• Akkumulátor (AC) regiszter. Ha egyáltalán létezik fontossági sorrend, akkor abban ez az első! Az elvégzendő művelet egyik operandusát tartalmazza, és átmenetileg az eredményt. Tárolja a műveletvégzés során esetleg keletkező túlcsordulást is, és az átvitel bitet. E regiszter által tárolt bitek számát mindig az alkalmazott mikroprocesszor szóhossza határozza meg. Tehát a 8 bites mikroprocesszorok esetében ez a regiszter is 8 bites.
• Utasítás regiszter (IR: Instruction Register). Ez is 8 bites, itt kap helyet az éppen végrehajtás alatt levő utasítás kódja.
• Vezérlőegység: Azokat a jeleket állítja elő, amelyek nyitják, ill. zárják az információk útját az operatív tár és a központi egység regiszterei között.
• Aritmetikai Logikai Egység (ALU: Aritmetic Logic Unit). Egy olyan kombinációs hálózat, amely az adatokból a kívánt eredményt képezi, amelynek eredménye az akkumulátorba kerül, törölve annak előző tartalmát. Működése, felépítése függ a gép kialakításától.

A központi egység és a központi tár együttes, összehangolt működése előfeltétele a hatékony munkának. Még a legelemibb művelet, egy összeadás elvégzése is többszörös oda-vissza kapcsolatot - gépi ciklust - jelent ezek között az egységek között.
Szólni kell még röviden a személyi számítógépek periférikus egységeiről, amelyek itt sokkal jobban összefonódnak elhelyezés és működés szempontjából egyaránt a központi géppel, mint a nagy számítógépeknél. Ezek a következők:

• Billentyűzet. Ez a minimálisan szükséges beviteli eszköz ahhoz, hogy valamilyen magas szintű programnyelven kommunikálni tudjunk a számítógéppel. A használatos karakterkészlet az ún. ASCII kód alapján van kódolva.
• Kazettás mágnesszalagos tároló. Ez egy közönséges hangfrekvenciás magnetofon, amely a programot és az adatokat mágneses jelekként képes tárolni.
• Képernyős megjelenítő, amely a bevitt utasításokat, adatokat és a kiírt eredményeket megjeleníti a felhasználó előtt. Lehet egyszerűen egy TV készülék, vagy a legegyszerűbb esetben egy folyadékkristályos kijelző.

Nyomtató. Vannak, amelyek a hagyományos távírógéphez hasonló sornyomtatók, és léteznek saját mikroprocesszort tartalmazó gyorsnyomtatók is. A kiírandó információkat általában egy elektromos jelre érzékeny, alumíniummal bevont papírra viszik föl.
Hajlékony mágneslemezes rendszer, amely minden szempontból a legjobb periférikus gyorstároló. A hajlékony mágneslemez vagy más néven floppy, egy vékony rugalmas plasztiktárcsa, amely mágneses réteggel van bevonva. A mágnesszalaggal szemben nem "soros hozzáférésű", tehát nem kell végigpörgetni az egész lemezt ahhoz, hogy egy adott helyen levő információt betöltsük a gépbe. A tartalom betöltése rendkívül gyors, a tárolás megbízható, és egy-egy lemez akár 200 kbájt adatot is képes tárolni.

Természetesen a személyi számítógépek az "extra" egységek nélkül, alapkiépítésben is jól használhatók a legkülönbözőbb feladatokhoz. Azonban a fejlődés tendenciáját tekintve, a közeljövőben ezek az elemek is ugyanolyan elterjedtek és hozzáférhetőek lesznek, mint maga a gép.
Nálunk az 1980-as évek kezdetétől terjednek mind szélesebb körben és nagyobb számban a személyi számítógépek. A "nagy ugrás" az 1983-as év volt, amikor egységesen, valamennyi középiskolában hozzáférhetővé vált a hazai gyártmányú és szervizelésű "Iskolai számítógép". Álljanak itt felsorolásszerűen, figyelembe véve a "kínálat" szinte napi változását, a jelenleg forgalomban levő és legelterjedtebb személyi számítógépek típusai: ABC 80, HT-1080, HT-2080, ZX-81, ZX SPECTRUM, AIRCOMP, COMMODORE, PRIMO.

A programozás különböző szintjei
Programozási nyelvnek azt a jelölésrendszert nevezzük, amely felhasználásával a feladat végrehajtásához szükséges utasítások sorozatát, azaz magát a programot leírtuk. A legegyszerűbb esetben mindez tulajdonképpen egy bináris számsorozat, amely a gép kiépítése alapján a gépi utasítások kódjait tartalmazza. Ha ezen számkódok betűképeit vihetjük be, a mi dolgunk egyszerűbb, a gép munkája viszont lényegesen komplikáltabb.
A programnyelveknek három fajtáját szokás megkülönböztetni:

1. Gépi kód.
2. Szimbolikus nyelv vagy Assembly.
3. Magas szintű programnyelv.

Nézzük meg közelebbről az "idegen nyelveket" általánosan, és azután a lehetőségekhez képest teljes részletességgel egyet. Nem azért választottuk ki a BASIC nyelvet, az a "legjobb"! Nincs legjobb programnyelv! Azért döntöttünk így, mert jelenleg, 1984-ben, és még minden bizonnyal egy ideig ez lesz az a programnyelv, amelyen keresztül nálunk a legtöbben meg tudnak ismerkedni ezzel a tudománnyal.

A gépi kód
A számítógép csak ilyen utasításokat képes értelmezni, és végrehajtás után válaszolni azokra. Ez a számítógép "anyanyelve". A kezdeti időszakban, az egyetlen lehetőség ez volt a programozásra. Ma viszont a számítógépek többségénél a felhasználó alig tud gépi nyelven dolgozni, helyette "emberi nyelven" beszélget a géppel. A számítógép működése viszont sokkal érthetőbb, sokkal inkább közel kerül hozzánk, ha ezt a lehetőséget is megismerjük, megjegyezve, hogy a gépi nyelven történő programozás nehézkes, hosszú munka, és nem is vezet okvetlenül rövidebb futási időhöz!
A gépi kódú programozás főbb elvei és egyben nehézségei is a következők:

• A műveleti kódokat numerikus formában kell megadni, általában hexadecimális alakban.
• Az egyes műveleteket "abszolút" elemi szintre kell lebontani.
• Ismerni kell a központi tár pontos felosztását, és csak adott tárterületre történhet a program betöltése.

A gépi kódú programozás nagy hátránya az, hogy az esetleges hibáról futás közben semmiféle információt sem szerezhetünk, még csak a hiba jellegéről sem. Ezt nekünk kell kideríteni. Természetesen bizonyos feladatokhoz megéri vállalni ezeket a nehézségeket, pl. a rövidebb futási idő vagy a memória ideális kihasználása érdekében.
Az elmondottak illusztrálására nézzük meg egy nagyon egyszerű feladat gépi nyelven írt programját a HT-1080 iskolai számítógépre, amelyben a központi feldolgozó egység egy Z80-as mikroprocesszor, amely eléggé elterjedt ahhoz, hogy a program hasonló legyen több más személyi számítógépben is (pl. ZX Spectrum-on, ZX 81-en). Két egész szám összeadásáról van szó. Legyen az A regiszterben 15, a B regiszterben pedig 30, a két szám összegét pedig kérjük az A regiszterben:
A program az adatokkal együtt:

binárisan:	hexadecimálisan:
0011111000001111 0000011000011110 1000000000101101	3E 0F 06 1E 80 2D

Az első lépésben az A regiszterbe betesszük az egyik számot, a második lépésben a B regiszterbe a másikat, a harmadik lépésben pedig az A regiszterbe a két regiszter tartalmát. A programozónak meg kellett, és ma is meg kell tanulnia a gépi szintű utasítások kódjait, ha így akar kommunikálni a géppel.
A nehézségek áthidalását próbálták megoldani a gépi nyelvhez még közelálló, de a gépi műveletek számkódjait különböző kulcsszavakkal helyettesítő, szimbolikus nyelvekkel. Ez az Assembly nyelv.

A szimbolikus nyelv
Az Assembly még mindig gépfüggő, tehát egy program csak egy gépen futhat, és ehhez is szükséges a gépi nyelvre lefordító fordítóprogram (assembler editor). Az assembly szintű utasítások a tényleges gépi utasításoknak felelnek meg, de nem egy "száraz" számhalmazként, hanem szemléletesebb, könnyebben felismerhető és áttekinthető formában.
Az assembler utasításai három részre tagozódnak, három mezőben írhatók le:

cím utasításkód operandus

A cím részbe tetszőleges betűsorozat írható, de maradhat akár üresen is. Akkor van jelentősége, ha a program során - pl. feltételes ugrás - hivatkozni akarunk egy adott utasításra.
Az utasításkód helyén tulajdonképpen az adott assembly nyelv alapszavai állhatnak. Ezek az adott utasítást leíró angol szó rövidítései, amely megfelel az adott gépi kódú utasításnak. Például:

LD ADD SUB JP

- töltsd - összead - szorzás - ugrás

Az operandus határozza meg azt a címet, amely címen levő adattal az adott utasítást végre kell hajtani. Ez lehet ún. "direkt" operandus is, amikor nem a memória egy címét, hanem közvetlenül annak tartalmát adjuk meg. Természetesen hivatkozhatunk más a programban szereplő címre is.
Például:

LD A,10 LD A,B LD A,(32000)	- az A regiszterbe elhelyezzük a 10 számot. - az A regiszterbe tároljuk a B regiszter tartalmát. - az A regiszterbe tároljuk a memória 32000-es című rekeszének tartalmát.
ADD A,B	az A regiszterbe elhelyezzük a B és az A regiszterek tartalmának összegét.

Ezek alapján az előzőekben említett egyszerű összeadási példa Z80-as assembler programja a következő lesz:

LD A,15 LD B,30 ADD A,B

(A-ba 15) (B-be 30) (A-ba az összeg)

A gépi nyelv és a szimbolikus nyelv összehasonlításakor látható a szimbolikus nyelv előnye. Azonban még ez is magán viseli a gépi kód jellegzetességeit. Például minden gépi utasításnak megfelel egy-egy assembler utasítás. Ebből következik, hogy ez a nyelv is erősen géphez kötött. Ezen kívül hosszú és bonyolult szerkezetű programok megírása hosszadalmas és nehézkes. A programozói munka megkönnyítését, hatékonyabbá tételét szolgálják az ún. ROM-rutinok, amelyek felhasználásával bizonyos gyakran használatos feladatok megtervezését nem kell assembly szinten elvégezni. Ilyen pl. az aritmetikai rutin, a grafikus rutin stb.
Megjegyzés: a HT-1080 gépen a gépi kódban írt programok (pl. a játék-programok többsége) betöltése különbözik a BASIC programokétól. A LOAD helyett a SYSTEM paranccsal indíthatjuk a beolvasást, majd a képernyőn megjelenő "?"-re az adott program nevét kell megadni. Ezután indítható a magnetofonról a beolvasás.
Ismeretes több olyan programnyelv, amelyek az assembly nyelvekből fejlődtek ki, és bizonyos géptípusra ill. felhasználási területre dolgozták ki. Ezek az "Autokód"-ok. Mivel nem nyújtottak a programozók számára hatásos új eszközöket, nem terjedtek el széles körben, de ma is használatosak.

Magas szintű programnyelv
A gépfüggetlen, univerzális nyelvek kialakítása egyszerűsítette le lényegesen a felhasználói munkát. Az így megírt program minden olyan számítógépen lefuttatható, amely rendelkezik az adott nyelv fordítóprogramjával (ez a compiler). Így nem szükséges minden feladatot minden gépen újra programozni, használhatók a "programkönyvtárak" is.
A legelterjedtebb, a lehetőségekhez képest gépfüggetlen, feladatorientált, de általános jellegű programnyelvek a következők:

Fortran
A Formula Translation szavak rövidítése. Különösen a tudományos, matematikai jellegű feladatok programozására alkalmas. A FORTRAN az assembly utasításokhoz képest két fontos új elemet tartalmaz:

• Az utasításokban tetszőleges aritmetikai formulákat használhatunk. Például az X = B^2-4*AC képlet FORTRAN utasítása a következő:
  X = SORT(B2-4AC)
• Lehetőség van a többször használt programrészek hívására (szubrutin használat).

A FORTRAN nyelv nagy előnye, hogy könnyen és gyorsan elsajátítható. Hátránya, hogy nem rendelkezik azokkal az eszközökkel, amelyek a jól tagolt, világosan átlátható szerkezetű programok írását lehetővé teszik.

Algol
Az Algorithmic Language szavakból szármáik. Az összetett műszaki és tudományos feladatok megoldására dolgozták ki, a lokalitás elve jelenti az újdonságot az előző programnyelvekhez képest. A programrészek vagy "blokkok" tetszés szerint egymásba skatulyázhatok, és egy-egy blokkon belül saját programváltozók használható, anélkül, hogy ez zavarná a program többi részét. Ez a koncepció olyan sikeresnek bizonyult, hogy azóta is szinte minden magas szintű programozási nyelv alapját jelenti. Ma is az ALGOL nyelv továbbfejlesztett változatai adják a programnyelvek zömét (pl. PASCAL)

Cobol
A Common Business Oriented Language angol kifejezés kezdőbetűiből származik a programnyelv elnevezése. Az olyan problémák megoldásához használható gazdaságosan, ahol nem a matematikai műveletek dominálnak, hanem a nagy tömegű adatfeldolgozási tevékenység. Ezért elsősorban a gazdasági életben, a közgazdasági jellegű feladatok programozására alkalmas.

PL 1 (Programme Language 1)
Az egész nyelv struktúrája azzal a céllal készült, hogy mint egy univerzális programnyelv egyaránt jól felhasználható legyen a tudományos, műszaki és adatfeldolgozási munkában.
Használatos még számos más, különböző mértékben elterjedt programnyelv, mint pl.: Pascal, Elan, Forth, APL stb. Ezek a nyelvek, bár közismert a széleskörű felhasználásuk, nem tartoznak könyvünk témájához.

A további részekben a BASIC nyelvről igyekszünk a lehetőségekhez képest részletes és teljes képet adni, mivel jelenleg hazánkban, középiskolai szinten ez a legelterjedtebb, legismertebb programnyelv.

BASIC
Ez is egy magas szintű programnyelv, a Beginner's All-Purpose Symbolic Instruction Code - magyarul: "Kezdők általános célú szimbolikus utasításkódja" -, kifejezés rövidítése. 1964-ben, egy magyar származású tudós, John Kemény és kollégái fejlesztették ki Amerikában, kezdő programozók számára, de általános feladatok megoldására. Az alap a FORTRAN nyelv volt, és elsősorban a személyi számítógépek programozására tervezték. A programozó közvetlen kapcsolatban áll a géppel, billentyűzeten keresztül írhatók be az utasítások, és így akár futás közben is javítható, kiegészíthető a program. Az ismertebb személyi számítógépek mind "értik" a BASIC nyelvet, azaz rendelkeznek BASIC értelmező programmal, de a "beszélt" nyelvekhez hasonlóan mind csak a saját "tájszólásában". Nem valószínű, hogy pl. egy Sinclair Spectrum-ra írt program működőképes a HT típusú iskolaszámítógépen is! Mivel a számítógépeket gyártó cégeknek nagyon kényelmes, hogy a BASIC elég jól "igazítható" a különböző műszaki megoldású gépekhez, ezért nem várható hogy egyhamar egységesen programozhatnánk minden típuson! gy kénytelenek vagyunk mi, a felhasználók megtanulni a különböző nyelvi változatokat.
A helyzet azért nem teljesen kilátástalan, hiszen az alapvető utasításokat valamennyi BASIC ugyanolyan formában tartalmazza (PRINT, LIST, RUN stb.), és ha egy adott gépet már ismerünk, akkor könnyű átállni egy másik programozására is.
Az eltérések az egyes gépek különböző kiépítéséből is adódnak, mint pl. mágnes-lemez, sornyomtató, kazettás adattároló stb. így nagyon fontos, hogy használat előtt alaposan tanulmányozzuk a gépkönyvet, és csak így, a lehetőségeket ismerve és figyelembe véve kezdjük el a munkát!

A BASIC programok kezelése

A BASIC programozási nyelv egyik jellemzője az interaktív programozási mód, amit párbeszédes üzemmódnak is neveznek. A programozó vagy felhasználó közvetlen kapcsolatban van a számítógéppel. A kapcsolatteremtés egyik nyelve a BASIC. A kapcsolatot biztosító hardver eszközök: a billentyűzet és a képernyős megjelenítő, ami legtöbb esetben egy közönséges TV.
A billentyűzeten begépelt karakterek, amikkel a számítógép működését szándékozunk befolyásolni, éppúgy megjelennek a képernyőn, mint a számítógép üzenetei, amik a felhasználó számára adnak információt. A BASIC rendszer ezt a folyamatot teremti meg. Ezzel segíti a programozást, és megkönnyíti a BASIC nyelv tanulását is.
A legelső lépés, ha a számítógépet használni szeretnénk, hogy megismerkedünk a számítógép billentyűzetével. A billentyűzeten begépelt karaktersorozatot a BASIC rendszer csak akkor kezdi értelmezni, ha a NEW LINE (Spectrum-on ENTER) billentyűt benyomjuk. Ezzel kell zárni a parancsokat és a programok utasítássorait is.
Nem megfelelő, a BASIC rendszer számára érthetetlen karaktersorozat begépelésekor a BASIC rendszer hibát jelez. A hibajelzésben szereplő betűkód a hiba jellegére utal.
A billentyűzetet ismerve, felhasználóként már használni is tudjuk a számítógépet, ha a kész programok kezelésére vonatkozó BASIC parancsokat megtanuljuk:

Kész programokat mágneskazettán tárolhatunk. A számítógépekhez beszerezhető programkazetták olyan programokat tartalmaznak, amelyek a legkülönbözőbb feladat megoldására teszik alkalmassá a számítógépet. A felhasználónak csak annyit kell tudni, hogy a mágnesszalagon rögzített programot hogyan kell beolvasni a számítógép központi memóriájába, és azt hogyan kell elindítani.

HZ-1080Z-n a BASIC rendszerünk a

READY
>_

kiírással jelzi, hogy parancsra vár.
A _ jel a kurzor pillanatnyi állását mutatja, azaz azt a karakterpozíciót, ahol megjelenik az a karakter, amit begépelünk.
Állítsuk a mágnesszalagot oda, ahol a BASIC program kezdődik, és kapcsoljuk lejátszásra a magnetofont. (Az F1 nyomógomb legyen olyan állásban, hogy a magnetofon ne induljon el.) Gépeljük be a CLOAD parancsot! Arról természetesen ne feledkezzünk meg, hogy a CLOAD szó begépelése után a NEW LINE billentyűt kell lenyomnunk. A parancs végrehajtása csak akkor kezdődik.
Helyes beolvasáskor a képernyő jobb felső sarkában megjelenő két csillag közül a jobb oldali villog. Miután a program betöltése sikeresen befejeződik, a READY kiírás jelenik meg a képernyőn. A programot a RUN paranccsal indíthatjuk.
A begépelt vagy a kazettáról beolvasott és módosított programot kazettán tárolhatjuk. Az F1 nyomógombot úgy állítsuk be, hogy a magnetofon ne induljon el! Adjuk ki a CSAVE "A" parancsot! A parancs hatására a felvétel elindul és a mágnesszalag rögzíti a programot. A program neve A lesz. Ez lenne a neve akkor is, ha az idézőjelek közé az ALMA szót írjuk, mert csak az első betűt veszi figyelembe a rendszer.
A felvételt úgy ellenőrizhetjük, hogy a szalagot visszacsévéljük a felvett program elejére, a magnetofont lejátszásra állítjuk, és kiadjuk a CLOAD? parancsot. Amennyiben a felvétel sikerült, az ellenőrzés közben a képernyő sarkában az egyik csillag villog, és a beolvasás végén kiíródik a READY szó.
Hiba esetén a felvételt megismételhetjük, mivel a program még a memóriában van.

A Sinclair ZX Spectrum bevezetés c. könyv részletes ismertetőt ad a magnó használatáról.

A billentyűzet megismerésének legjobb módja, ha kész programot gépelünk be. A tankönyv mintaprogramjai megfelelnek erre a célra, de találunk programokat a szakfolyóiratokban is. Akkor, ha még nem tudunk programozni, csak olyan programok begépelésével próbálkozzunk, amit kifejezetten az adott számítógépre írtak. Más géptípusra írt BASIC programok átírásához ismernünk kell mindkét számítógép BASIC nyelvét, tudnunk kell az eltérésekről.
A tankönyvben szereplő mintaprogramokat a HT-1080Z és Sinclair Spectrum számítógépek BASIC nyelvén írtuk.
Mielőtt elkezdenénk a begépelést, a NEW paranccsal töröljük ki a memóriából az előző BASIC programot. A programok begépelésekor arra kell ügyelni, hogy a program utasítássorai mindig valamilyen pozitív egész számmal kezdődnek. Ezek az utasítássorok sorszámai. Miután begépeltünk egy utasítássort, nyomjuk le a NEW LINE / ENTER billentyűt. Ezzel zárjuk a sort, amit a számítógép tárol. Arról, hogy mit sikerült begépelnünk, úgy győződhetünk meg, hogy a LIST paranccsal kiíratjuk a programot.
A program indítása a RUN paranccsal történik.

Az elkerülhetetlen, hogy a program begépelésekor ne tévedjünk. Meg kell tanulnunk, hogy hogyan javíthatjuk a hibákat.
Mielőtt még lezárnánk a sort, a tévesen beütött karaktereket visszatörölhetjük.
A tárolt utasítássorokat

• törölhetjük,
• felülírhatjuk és
• az utasítássorok közé, eddig nem használt sorszámmal, utólag is beírhatunk utasítássorokat.

Egy programsort úgy törölhetünk, hogy begépeljük a törlendő sor sorszámát.
A felülírás azt jelenti, hogy a hibás utasítássor helyett begépeljük a helyeset. Azonos sorszámmal begépelt utasítássorok közül a számítógép az utolsóként begépelt utasítássort őrzi meg.

Kérdések és feladatok

1. Hogyan történik a mágnesszalagon tárolt program beolvasása?
2. Milyen paranccsal indíthatjuk el a BASIC programokat?
3. Hogyan rögzíthetjük mágnesszalagra a programot, és azt hogyan ellenőrizhetjük?
4. Melyik billentyűvel zárjuk a parancsokat és az utasítássorokat?
5. Ismertessük a program kezelésére vonatkozó parancsokat!
6. Milyen javítási lehetőségeket ismerünk?

Programozás BASIC nyelven

Adatbeolvasás és -kiírás

Feladat:
Írjunk olyan programot, amivel kiírathatjuk a számítógéppel a nevünket, és azt, hogy hány évesek vagyunk!
Nagyon egyszerű a feladat, ha mi számoljuk ki az életkorát annak, aki a programot használni szeretné. Ekkor a programunk csak egy utasításból áll, amivel kiíratjuk a megfelelő szöveget.

10 PRINT "EMESE 16 EVES"

Általánosabb megoldásnak tekinthetjük, ha a felhasználó gépeli be azt, amit látni szeretne a képernyőn.
Kérjük a programmal a szöveget, és írassuk ki!

10 INPUT A$
20 PRINT A$

Az INPUT utasítás végrehajtásakor a képernyőn megjelenik egy kérdőjel, ami azt jelzi, hogy a program valamilyen adatot vár. Programunk kéri azt a szöveget, amit ki szeretnénk íratni a képernyőn. Miután begépeljük a karaktersorozatot és lenyomjuk a NEW LINE / ENTER billentyűt, a számítógép tárolja azt az A$ (olvasd A dollár) változóban. Ezzel az INPUT utasítás végrehajtása befejeződött. Következik a PRINT utasítás, amivel kiíratjuk az A$ változó értékét, azaz azt a szöveget, amit begépeltünk. A karaktersorozatot karakterláncnak nevezzük.
Az A$ értéke a program minden futtatásánál más és más lehet, tehát változhat. Innen az elnevezés: változó.
Az előzőekből a következőket tanulhattuk meg:

• a program végrehajtása a sorszámok növekvő sorrendjében történik;
• INPUT utasítással adatokat kérhetünk;
• az A$ változó bármilyen karaktersorozatot jelenthet;
• PRINT utasítással kiírathatjuk az A$ változó értékét.

Feladat:
Írjunk olyan programot, amelyikkel kiírhatjuk a nevünket és azt, hogy hány évesek vagyunk, ha megadjuk mikor születtünk!
Az előző megfogalmazásból az hiányzott, hogy nem adtuk meg, milyen bemenő (input) adatokkal dolgozzon a számítógép. A programban tehát kérni kell a születési évet, és ebből kell meghatároznunk az életkort.

7 INPUT A$
12 INPUT X
23 PRINT A$;1984-X;"EVES"

Spectrum-on a számok kiírása kicsit másképp működik:

23 PRINT A$;" ";1984-X;" EVES"

Értelmezzük a programot!

• 7-es sor: Kéri a nevet, az A$ karakterlánc-változó értékét.
• 12-es sor: Kéri a születési évet, az X numerikus-változó értékét.
• 23-as sor: Kiírja a nevet, az életkort - miután azt kiszámította - és azt, hogy EVES.

Mit kell észrevennünk?

• Kétféle változót használunk a programban:
  • A$ karakterlánc-változó értékének tetszőleges karaktersorozatot megadhatunk.
  • X értéke csak numerikus adat lehet.
• A PRINT utasítással kiírathatjuk:
  • a változók értékét,
  • az aritmetikai műveletek eredményét és
  • tetszőleges karaktersorozatot.

A PRINT utasításban vesszővel vagy pontosvesszővel választhatjuk el a kiírandó elemeket.
Amikor a program az INPUT utasítással az adatokat kéri, csak a kérdőjel jelenik meg, és így a felhasználó nem tudhatja, hogy milyen adatot kér a program. Adjunk tájékoztatást a felhasználónak, és írassuk ki a programmal, hogy milyen adatot kell begépelni. Ezt többféleképpen oldhatjuk meg.

3 PRINT "KEREM A NEVET: ";
5 INPUT A$
12 INPUT "SZULETESI EVE: ";X

A 3-as sorban a PRINT utasítással íratjuk ki a tájékoztató szöveget, de elhelyezhetjük azt az INPUT utasításban is (12-es sor). Az INPUT utasításban a kiírandó szöveg után pontosvesszőt (Spectrum-on vesszőt is lehet, mely ugyanúgy működik, mint a PRINT utasításban) kell tenni, és ezután következhetnek azok a változók, amelyeknek az értékét kérjük.
Egy INPUT utasítással több változó értékét is kérhetjük. A változókat vesszővel választjuk el egymástól:

10 REM ELETKOR
20 PRINT "NEV, SZULETESI EV: ";
30 INPUT N$,E
40 PRINT N$;1984-E;"EVES"

Az első adat begépelése után, ha azt a NEW LINE / ENTER billentyűvel zárjuk le, a rendszer két kérdőjel (Spectrum-on egy kérdőjel) kiírásával jelzi, hogy még nem adtunk minden változónak értéket. Akkor, ha az INPUT utasításban több változó értékét kérjük, az adatokat úgy is megadhatjuk, hogy azokat vesszővel választjuk el, és csak az utolsó begépelése után nyomjuk le a NEW LINE / ENTER billentyűt.

A kiírás formája a PRINT utasításban használt elválasztójeleknek (pontosvessző, vessző) megfelelően különböző lesz:

• Pontosvessző esetén a kiírás folyamatos.
• Vessző után a következő zóna elején folytatódik a kiírás.
  • HT-1080Z: A képernyő 64 karakterpozíciója négy zónából áll, ezek kezdőpontjai: a 0., 16., 32. és a 48. karakterpozíció.
  • Spectrum: A képernyő 32 karakterpozíciója négy zónából áll, ezek kezdőpontjai: 0., 15. karakterpozíció.

A program elején álló REM utasítás az értelmező program számára azt jelenti, hogy az utána következő karaktersorozatot ne vegye figyelembe. Mi most a program nevét írtuk ide.

A beolvasó utasítás:

INPUT változólista
jelentése: "Olvasd be a listában szereplő változók értékeit!"
A változólista elemeit vesszővel választjuk el egymástól.

INPUT "karakterlánc";változólista
jelentése: "Írd ki a karakterláncot és kérd a változólista elemeinek értékeit!"

A kiíró utasítás:

PRINT kiíratási-lista
jelentése: "Írd ki a kiíratási-lista elemeinek értékeit!"
HT-1080Z-n a PRINT utasítás helyett elég a ?-et begépelni.

A listaelem lehet:

• konstans: programban adott állandó.
• aritmetikai kifejezés: konstansokon, változókon és függvényeken kijelölt műveletsor (pl.: 2*R*3.1415)
• TAB függvény: adott helyközzel léptetjük a kurzort.

Az utóbbi két listaelemről a következőkben lesz bővebben szó.

A konstans lehet:

• numerikus: valamilyen szám (pl: 1984   2.34E15)
• karakterlánc: karaktersorozat, amit a PRINT utasításban idézőjel közé teszünk,
• változó: adatok tárolására, azok azonosítására szolgáló szimbólum.

A változó lehet:

• numerikus,
  • HT-1080Z: a neve egy betű vagy egy betű és egy alfanumerikus karakter lehet (pl.: X, A5, IK)
  • Spectrum: a neve bármilyen hosszú lehet és bármilyen betűt vagy számot tartalmazhat, az egyetlen megkötés az, hogy az első helyen egy betű szerepeljen
• karakterlánc,
  • HT-1080Z: a nevét ugyanúgy képezhetjük, mint a numerikus változókét, végén $-jel áll (pl.: A$, K3$, KP$)
  • Spectrum: neve egyetlen betű és az azt követő $ jel lehet (pl.: A$)

Feladat:
Írjunk programot, amivel kiszámíthatjuk egy téglatest alakú tárgy felszínét, térfogatát és tömegét, ha adott az oldalélek hossza és a sűrűsége!
Az oldaléleket jelöljük a -val, b-vel és c-vel, a sűrűséget d-vel. Ekkor a test felszíne:

F = 2*a*b + 2*a*c + 2*b*c

térfogata:

V = a*b*c

tömege:

m = a*b*c*d

A program:

10 REM TEGLATEST
20 INPUT "OLDALELEK ";A,B,C
30 INPUT "SURUSEG: ";D
40 PRINT "FELSZIN  = ";2*A*B+2*A*C+2*B*C
50 PRINT "TERFOGAT = ";A*B*C
60 PRINT "TOMEG    = ";A*B*C*D

A programból is látszik, hogy az aritmetikai kifejezések házalóképpen írandók a programban, mint ahogyan a matematikában a paraméteres kifejezéseket leírjuk. A műveletek végrehajtása, a kifejezés értelmének kiszámítása azonos a matematikai sorrendiségi szabállyal.
Az osztás (jele: /) a szorzással, a kivonás az összeadással azonos sorrendiségű művelet. Legelőször a hatványozást végzi el a számítógép (jele: ^). A műveletek sorrendje tehát a következő:

1.	^	hatványozás
2.	*	szorzás
2.	/	osztás
3.	+	összeadás
3	-	kivonás

A műveletek végrehajtásának sorrendjét zárójelek alkalmazásával tudjuk megváltoztatni. A test felszínét kiszámíthatjuk a

40 PRINT "FELSZIN  = ";2*(A*B+A*C+B*C)

Feladat:
Írunk programot, amivel kiszámíthatjuk egy adott sugarú gömb felszínét és térfogatát!
Legyen a sugár r, akkor a gömb felszíne:

F =4*r^2*Pi

térfogata:

V = 4*r^3*Pi/3

A program:

10 REM GOMB
20 INPUT "SUGAR: ";R
30 PRINT "FELSZINE:  ";4*R^2*3.1415
40 PRINT "TERFOGATA: ";4*R^3*3.1415/3

Spectrum-on használhatjuk az előre definiált PI függvényt:

30 PRINT "FELSZINE:  ";4*R^2*PI
40 PRINT "TERFOGATA: ";4*R^3*PI/3

A kifejezésekben háromféle számtípust használhatunk, és ilyen alakban adhatjuk meg a numerikus adatokat is:

• egész (pl. 1984)
• tizedespontos (pl. 3.1415)
• lebegőpontos alak (pl. 31415E-4)

Ezt az alakot általában nagyon nagy, vagy nagyon kis abszolútértékű számok esetén használjuk.

6*10^23 =	6E23
6.67*10^-11 =	6.67E-11

Az E betű a 10 kitevőjét választja el az értékes jegyektől.

10 REM HATVANYOZAS
20 INPUT "ALAP:  ";A
30 INPUT "KITEVO ";K
40 PRINT "HATVANY ERTEKE: ";A^K

Feladat:
Írjunk programot, amivel kitapasztalhatjuk, hogy milyen értéke lehet a hatványalapnak, és milyen a kitevőnek!

10 REM HATVANYOZAS
20 INPUT "ALAP:  ";A
30 INPUT "KITEVO ";K
40 PRINT "HATVANY ERTEKE: ";A^K

A program segítségével meggyőződhetünk arról, hogy a számítógép pozitív hatványalap esetén a 0, negatív és törtkitevőjű hatványozást is végrehajtja. Amennyiben a kitevő egész, negatív alap esetén is kiszámítja a hatvány értékét.

Feladat:
Számítsuk ki a 14,36 cm sugarú kör kerületét és területét!
Ilyen egyszeri felhasználásra programot írni felesleges. A PRINT utasítást parancsként használva a következőképpen oldhatjuk meg a feladatot:

PRINT 2*14.36*3.1415,14.36^2*3.1415

Spectrum-on az alábbi alak is helyes:

PRINT 2*14.36*PI,14.36^2*PI

Sorszám nélkül begépelt utasítást, a parancsot a számítógép azonnal végrehajtja. Ezt a használati módot kalkulátor üzemmódnak is nevezik. Számítások gyors elvégzésére és az utasítások hatásának a vizsgálatára használjuk.

Kérdések és feladatok

1. Miért nem egyesével növeljük a programutasítás sorainak sorszámait?
2. Hogyan jelölhetjük a numerikus-változókat, és hogyan a karakterlánc-változókat?
3. Miben különbözik a numerikus-változó a karakterlánc-változótól?
4. Írjunk programot az egyenes körhenger felszínének és térfogatának a kiszámítására, ha adott az alapkör sugara és a henger magassága!
5. Adjuk meg különböző alakban a következő numerikus adatokat!
   14,37
   44,3*10^-4
   -0,0001
   30000
   248,7
   123456789

Megoldásuk helyességét a következő programmal ellenőrizhetjük:

10 INPUT X
20 PRINT X

Értékadás

Feladat:
Írjunk programot, amivel meghatározhatjuk az egyenes körhenger alakú test felszínét, térfogatát és sűrűségét, ha adott az alapkör sugara, a magasság és a test tömege! A körhenger

• felszíne: 2*r^2*Pi + 2*r*Pi*h = 2*r*Pi*(r+h)
• térfogata: r^2*Pi*h, ha

a henger alapkörének sugara r, magassága h. Jelöljük a test térfogatát V-vel, a test tömegét m-mel. Ekkor a

• sűrűség: m/V

Oldjuk meg a feladatot eddigi ismereteink alapján!

10 REM KORHENGER-1
20 INPUT "ALAPKOR SUGARA, MAGASSAG? ";R,H
30 INPUT "TOMEG? ";M
40 PRINT "FELSZIN: ";2*R*3.1415*(R+H)
50 PRINT "TERFOGAT: ";H*R^2*3.1415
60 PRINT "SURUSEG: ";M/(H*R^2*3.1415)

Az 50-es sorban a PRINT utasítás kiszámítja és kiírja a test térfogatának mérőszámát. Mivel ezt az értéket nem tárolta a számítógép, ezért a sűrűség meghatározását ismét ki kell számítania, nekünk pedig még egyszer le kellett írnunk a test térfogatát kiszámító kifejezést, amikor a programot írtuk.
Járjunk el hasonlóan, mint ahogyan azt a feladat matematikai leírásában tettük. Számíttassuk ki a térfogat értékét, és helyezzük el azt a V változóban! Ezt oldja meg a LET utasítás, amit értékadó utasításnak neveznek.
A PI értékére is többször szükség van. Adjuk a P változónak a PI értékét, és akkor csak a P változóra kell hivatkoznunk a kifejezésekben. (Erre Spectrumon nincs szükség, ott használjuk a PI függvényt.)

10 REM KORHENGER-2
20 INPUT "ALAPKOR SUGARA, MAGASSAG? ";R,H
30 INPUT "TOMEG? ";M
40 LET P=3.14159
50 PRINT "FELSZIN: ";2*R*P*(R+H)
60 LET V=H*R^2*P
70 PRINT "TERFOGAT: ";V
80 PRINT "SURUSEG: ";M/V

Az értékadó utasítás

LET változó = aritmetikai kifejezés
jelentése: "Legyen a változó értéke a jobb oldalon álló aritmetikai kifejezés kiszámított értékével egyenlő!" vagy másképpen fogalmazva:
"Vegye fel az egyenlőségjel bal oldalán álló változó a jobb oldali kifejezés kiszámított értékét!"
A LET utasításszó - mit a legtöbb BASIC változatban - HT-1080Z-n elhagyható, Spectrumon azonban ki kell írni.

A változók értékadása többféleképpen történhet. Az INPUT utasítással a program futtatásakor kérjük a bemenő adatokat, akkor adunk értékeket a változóknak, a LET utasítással a programban adjuk meg a változók értékeit.
HT-1080Z-n, ha egy változóra úgy hivatkozunk, hogy korábban nem kapott értéket - amit úgy is mondunk, hogy nem definiáltuk a változót -, akkor a változó értéke 0 lesz. Spectrum-on azonban nem kap 0 kezdőértéket a változó, ezért ilyen esetben hibaüzenetet kapunk.

Értelmezzük a következő programot!

10 REM ERTEKADAS
20 PRINT I
30 INPUT I
40 PRINT I
50 LET I=I+1
60 PRINT I

HT-1080Z-n futtatva a programot, három számot ír ki: nullát, azt amit I-nek adtunk az INPUT utasítássál és ennél 1-gyel nagyobbat (a Spectrum a 20. sornál hibaüzenettel leáll).
A 20-as sorban az I értékre úgy hivatkoztunk, hogy az I-nek még nem adtunk értéket. Ezért írja ki a nullát. Az 50-es sorban az I értékét 1-gyel megnöveltük. Ez az utasítás jól mutatja, hogy az egyenlőségjel a LET utasításban nem egyenlőséget jelöl, hanem az értékadás jele. Adjuk meg szóban ezt az utasítást: "Legyen I értéke I+1-gyel egyenlő!" A végrehajtás során az történik, hogy az I+1 kifejezést kiszámítja a számítógép, és azt az I változóban elhelyezi. Ezzel I értéke módosul.

Feladat:
Írassuk ki a hosszúság alapmértékegységének tized-, század- és ezredrészének megnevezését!

10 REM MERTEKEGYSEGEK
20 LET A$="METER"
30 LET K$="CENTI"
40 LET L$="MILLI"
50 LET X$="DECI"+A$
60 LET Y$=K$+A$
70 LET L$=L$+A$
80 PRINT X$,Y$,L$

A programban karakterlánc-változóknak adunk értéket a LET utasítással. A + jellel a karakterláncok összefűzésének műveletét jelöljük. Két karakterláncból előállítunk egy újabbat, amit egy karakterlánc-változóban helyezünk el. Vegyük észre, hogy az L$ változó értéke az LET L$=L$+A$ utasítás hatására módosul.

Feladat:
Határozzuk meg egy adott sugarú kör kerületét és területét a lehető legnagyobb pontossággal (HT-1080Z-n)!

10 REM PONTOSSAG
20 INPUT "SUGAR";R
30 P=3.14159
40 KE=2*R*P
50 TE=R*R*P
60 PRINT "KERULET: ";KE,"TERULET";TE

A PI értékét hiába adjuk meg pontosabban, csak 7 értékes számjegyet tudunk a P változóba elhelyezni, és ennyi értékes számjegye lesz a KE és a TE változók értékeinek is.
Írjuk a programba az

15 DEFDBL R,P,K,T
30 P=3.141592653589793

utasításokat. A DEFDBL utasításban felsorolt betűkkel kezdődő változókat az utasítás hatására kétszeres pontosságú változóként kezeli a rendszer. A kétszeres pontosságú változók értékes számjegyeinek száma maximálisan 16. A DEFDBL utasítás helyett, a kétszeres pontosságú változók megjelölésére használhatjuk a # karaktert is. Ekkor a programban az R#, P#, KE# és TE# változókat használjuk.
Megkülönböztetésül az eddig használt változókat egyszeres pontosságú változóknak is nevezzük. Az egyszeres pontosságú változók kijelölése DEFSNG utasítással vagy a !-lel történik: A!, X2!, MN!. Alaphelyzetben a változók egyszeres pontosságúak.

Feladat:
Írjunk programot egy 8 bites bináris szám (bájt) tízes számrendszerbeli értékének kiszámítására!
Jelöljük a bináris szám számjegyeit az ABC első nyolc betűjével! A szám decimális értékét az

a*2^7+b*2^6+c*2^5+d*2^4+e*2^3+f*2^2+g*2+h

kifejezés vagy más formában felírva a

((((((a*2+b)*2+c)*2+d)*2+e)*2+f)*2+g)*2+h

kifejezés értéke adja. Ez utóbbi formát Homer elrendezésnek nevezik.

10 REM BYTE DECIMALIS ERTEKE1
20 INPUT "8 BITES BINARIS SZAM SZAMJEGYEI: ";A;B;C;D;E;F;G;H
30 LET X=A*2^7+B*2^6+C*2^5+D*2^4+E*2^3+F*2^2+H*2+H
40 PRINT "A DECIMALIS ERTEKE: ";X

10 REM BYTE DECIMALIS ERTEKE2
20 INPUT "8 BITES BINARIS SZAM SZAMJEGYEI: ";A;B;C;D;E;F;G;H
30 LET X=((((((A*2+B)*2+C)*2+D)*2+E)*2+F)*2+G)*2+H
40 PRINT "A DECIMALIS ERTEKE: ";X

A feladatot a két összetett kifejezés értékének a kiszámításával külön-külön megoldottuk.

A programban a változók értéke csak egész szám lehet, ezért HT-1080Z-n használhatunk egész változókat is. Az egész változókat a DEFINT utasítással vagy a változók neve után írt %-jellel jelölhetjük ki: A%, X%. Az egész változók -32768 és 32767 közötti értékeket vehetnek fel.

HT-1080Z-n a változók típusától függ, hogy hány memóriarekeszt használ fel a rendszer a változók értékének tárolására:

• Egész változó esetén 6-ot,
• egyszeres pontosságú változó értékéhez 7,
• kétszeres pontosságú változó tárolásához 11 rekesz szükséges.

Egy rekeszbe 8 bit írható, azaz 1 bájt.

Feladat:
Írjunk programot két pozitív egész szám maradékos osztásának a végrehajtására!
Tudnunk kell, hogy HT-1080Z-n az egész változók a tört értékének csak az egész részét tárolják. A két adott szám hányadosának egész része megadja a maradékos osztás hányadosát. A hányados ismeretében kiszámíthatjuk a maradékot is.

10 REM MARADEKOS OSZTAS
20 INPUT "A KET SZAM (A>=B): ";A,B
30 DEFINT H
40 H=A/B
50 M=A-B*H
60 PRINT "HANYADOS: ";H
70 PRINT "MARADEK:  ";M

Spectrum-on is ugyanezzel az elvvel megoldhatjuk a feladatot. Ott ugyan nincs egész változó, de az INT függvénnyel vehetjük egy kifejezés értékét:

10 REM MARADEKOS OSZTAS
20 INPUT "A KET SZAM (A>=B): ";A,B
40 LET H=INT(A/B)
50 LET M=A-B*H
60 PRINT "HANYADOS: ";H
70 PRINT "MARADEK:  ";M

Kérdések és feladatok

1. Milyen utasításokkal adhatunk értékeket a változóknak?
2. Milyen típusú változókat ismerünk?
3. Hasonlítsuk össze az INPUT és a LET utasítást!
4. Mi lesz az értéke a definiálatlan karakteriánc-változónak?
5. Hogyan történhet az egész, az egyszeres pontosságú, a kétszeres pontosságú és a karakterlánctípusú változók kijelölése HT-1080Z-n?
6. Készítsünk programot az ax+b=cx+d alakú egyenlet megoldására!
7. Íjunk programot, ami, ha megadjuk az időtartamot órában, percben, másodpercben, akkor kiírja másodpercben!

A program vezérlése
Eddigi mintaprogramjaink ún. soros programok voltak, amelyekben az utasítások végrehajtásának sorrendjét a sorszámok egyértelműen meghatározták. A soros programok végrehajtása a legkisebb sorszámú utasítással kezdődik, és a sorszámok növekvő sorrendjében folytatódik.
Akkor, ha ezen a sorrenden változtatni akarunk, ha azt szeretnénk elérni, hogy ne a sorszám szerint következő utasítás végrehajtására kerüljön sor, hanem attól nagyobb vagy kisebb sorszámú utasítás következzen, akkor vezérlő utasításokat kell használnunk. Ezekkel az utasításokkal befolyásolhatjuk az utasítások végrehajtásának sorrendjét, azaz "vezérelhetjük" a programot.

Feltétel nélküli vezérlés
A feltétel nélküli vezérlés utasításszava a GOTO (Spectrum-on az írásmód GO TO). Magyar jelentése: menj, ugorj. Az utasításszó után írt sorszámmal azt adjuk meg, hogy hová ugorjon", azaz hogy melyik utasítássor végrehajtása következzen. A következő mintaprogramban a GOTO 10 utasítással a program végéről ugrunk a 10-es sorra, a program elejére, és így nem kell mindig újraindítani a programot.

Feltétel nélküli vezérlő utasítás:

GOTO sorszám
jelentése: "Az adott sorszámú utasítássor végrehajtásával folytatódjon a program!"

Feladat:
Írjunk programot, amivel kiszámíthatjuk a négyzetes egyenes csonkagúla felszínét és térfogatát, az alap és a fedőnégyzet élhosszából (a és b) és a csonkagúla magasságából (m)!
A csonkagúla térfogata:

felszíne:

A program:

1 REM CSONKAGULA
10 INPUT "ELHOSSZ (A,B): ";A;B
20 INPUT "MAGASSAG: ";M
30 LET V=M*(A^2+A*B+B^2)/3
40 LET F=A^2+B^2+(A+B)*SQR(4*M^2+(A-B)^2)
50 PRINT "TERFOGAT: ";V
60 PRINT "FELSZIN: ";F
70 GOTO 10

A GOTO 10 utasítással a programunkat "végtelenítettük", azaz egy végtelen ciklust, ismétlődést hoztunk létre. Ez a program csak akkor áll le, ha lenyomjuk a BREAK billentyűt. Ezt nevezzük külső programmegszakításnak.

Feladat:
Írassuk ki programmal a páratlan természetes számokat!
A megoldás lényege, hogy egy változó értékét kell mindig növelni 2-vel, és azt kell kiíratni. Ezeknek az utasításoknak az ismételt végrehajtását a GOTO utasítással éljük el. Az első szám, amit ki kell írnia a programnak az 1. Ez lesz a változó kezdőértéke, és erről nekünk kell gondoskodnunk egy értékadó utasítással.

10 LET I=1
20 PRINT I,
30 LET I=I+2
40 GOTO 20

Vegyük észre, hogy most nem ismétlődik mindegyik utasítás a végrehajtás során, mint az előző programban. Az ismételten végrehajtott utasítások (20-as és 30-as sorok) alkotják a ciklusmagot. A GOTO utasítás végrehajtása is ismétlődik, de ezt nem tekintjük a ciklusmag részének. Ez az utasítás az ismétlődést biztosítja.
A következő részben arról is szó lesz, hogy milyen utasítást kell beírnunk a programba, ha csak egy adott számig akarjuk kiíratni a páros számokat, tehát véges számszorzattal akarjuk végrehajtani a ciklusmagot.

Feltételes vezérlő utasítás
A matematikai relációjeleket a BASIC programozási nyelv is használja. Jelentésük azonos, csak a leírásuk különböző. Alkalmazkodni kell a gépelés kötöttségéhez. Összetett relációjeleket két karakterrel adunk meg.

=	egyenlő
<	kisebb
>	nagyobb
<=	kisebb vagy egyenlő
>=	nagyobb vagy egyenlő
<>	nem egyenlő

A relációjelekkel konstansok, változók és aritmetikai kifejezések értékeit hasonlítjuk össze. Azok viszonyáról állítunk valamit. Ilyen relációkkal kifejezett állítások:

A>B	A nagyobb B-nél,
I<=100	I kisebb, mint 100 vagy egyenlő 100-zal,
B^2-4*A*C>0	a relációjei bal oldalán álló kifejezés értéke nagyobb mint 0.

Miután a változóknak minden alkalommal más-más értéket adhatunk, és változhat értékük a program futása közben is, ezért ezek az állítások vagy igazak, vagy hamisak. A relációk logikai értéke, a relációkban szereplő kifejezések értékétől függ.
A BASIC rendszer a relációk logikai értékeit numerikus értékekkel azonosítja: -1 az IGAZ (Spectrumon: 1), 0 a HAMIS állításnak felel meg.
Próbáljuk ki ezt a következő programmal!

10 INPUT A,B
20 PRINT A<B

A logikai értékektől függő vezérlésátadó utasítást feltételes vezérlésátadó utasításnak nevezzük.
Ezzel az utasítással fogalmazhatjuk meg a számítógép számára azt, hogy egy feltétel, egy állítás a logikai értékétől függően mit csináljon, milyen utasításokat hajtson végre.

Feladat:
Írassuk ki 100-ig a páratlan természetes számokat!
Most oldjuk meg azt a problémát, hogy a páratlan számok kiírása csak egy adott határig történjen. Addig, ameddig az I < 100 egyenlőtlenség teljesül. Ezt a feltételünket az IF-THEN utasítással adjuk meg.

10 LET I=1
20 PRINT I
30 LET I=I+2
40 IF I<=100 THEN GOTO 20
50 PRINT "VEGE"

Az IF és a THEN utasításszavak magyar jelentését ismerve, az utasítást így olvashatjuk: "HA I kisebb mint 100, AKKOR ugorj a 20-as utasítássorra!"
Ez azt jelenti, hogy amennyiben a reláció logikai értéke IGAZ, akkor az I értékét írja ki a program, ha HAMIS, akkor az 50-es utasítássort hajtja végre a számítógép és kiírja a VEGE szót.
Az IF ... THEN GOGO ... szerkezet olyan gyakori, hogy sok BASIC-ben nem is kell ilyenkor kiírni a GOTO kulcsszót. HT-1080Z-n ezért a 40-es sort így is írhatjuk:

40 IF I<=100 THEN 20

Feladat:
Írassuk ki N-szer a BASIC szót!
Az előző program alapján könnyen megoldható a feladat, ha átfogalmazzuk: írassuk ki 1-től N-ig a természetes számokat! Ez azt jelenti, hogy N darab számot kell kiíratnunk, azaz N-szer kell a ciklusmagot végrehajtania a programnak. A ciklusmagban elhelyezzük a PRINT "BASIC" utasítást és ezzel megoldottuk a feladatot:

10 INPUT N
20 LET I=1
30 PRINT I,"BASIC"
40 LET I=I+1
50 IF I<=N THEN GOTO 30

Az előző két mintaprogramban ciklust szerveztünk, azaz előállítottunk egy olyan programrészletet, amellyel utasítások ismételt végrehajtását írtuk elő. Az IF-THEN utasítás hatására vagy visszaugrunk egy kisebb sorszámú utasítássorra, és így újból végrehajtja a számítógép ettől kezdődően az utasításokat, vagy folytatódik a program az IF-THEN utasítást követő utasítással. Az utóbbi esetben azt mondjuk, hogy kiléptünk a ciklusból. A IF-THEN utasítással tehát megoldható, hogy valamilyen feltételtől függően különböző utasításokat hajtson végre a számítógép. Az IF-THEN utasítás a feltételt megvizsgálja és ennek megfelelően történik a döntés.
A következő programokban a vizsgálaton lesz a hangsúly. A vizsgálat eredményétől függően elágaztatjuk a programot, és így különböző utasítássorozatok végrehajtását írhatjuk elő.

Feladat:
Készítsünk programot, amivel két tetszőleges számot növekvő sorrendben írathatunk ki!

10 INPUT A,B
20 IF A>B THEN LET T=A:LET A=B:LET B=T
30 PRINT A,B

Akkor, ha az A változónak nagyobb értéket adunk, kicseréljük a két változó értékét, és így a kiíráskor mindig az A változó értéke lesz kisebb.
Az IF-THEN utasításban a sorszám helyett bármilyen utasítássorozatot írhatunk a THEN szó után. Amennyiben a reláció logikai értéke IGAZ, ezeket az utasításokat végre-hajtja a számítógép. Amikor HT-1080Z-n sorszámot írunk a THEN után, akkor az is egy utasítás, csak nem írjuk ki a GOTO szót.
A két változó értékének a cseréjéhez felhasználtunk egy munkaváltozót, amiben megőriztük az egyik értéket.

Feladat:
Írassuk ki programmal egy szám abszolút értékét!

Megoldás HT-1080Z-n:

10 INPUT X
20 IF X<0 THEN PRINT -X ELSE PRINT X

A 20-as sorban a következő utasítást adtuk: "HA X értéke kisebb, mint nulla, AKKOR írjuk ki a szám negatívját, EGYÉBKÉNT magát a számot!"
Az ELSE <utasítás> szó után azokat az utasításokat írhatjuk, amiket a reláció HAMIS értékénél kell végrehajtania a programnak.
Az ELSE használatát nem mindegyik BASIC rendszer engedélyezi - így a Spectrum BASIC-je sem. Használata akkor előnyös, amikor két különböző műveletsort kell végrehajtanunk a feltételtől függően. A folyamatábra ebben az esetben a következő:

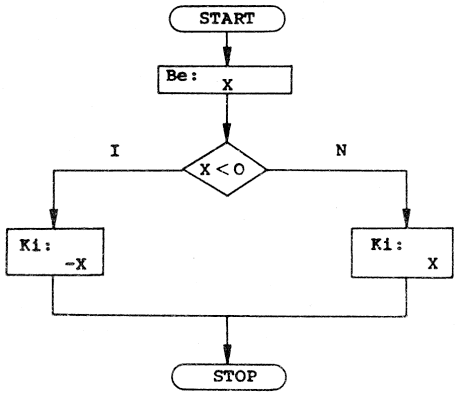
A feladat megoldható az ELSE használata nélkül is. A program folyamatábrája a következő:

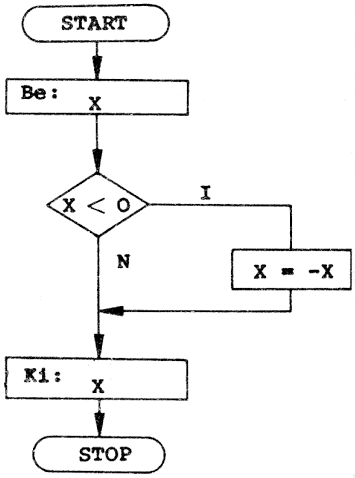
10 INPUT X
20 IF X<0 THEN LET X=-X
30 PRINT X

A feltételes vezérlésátadó utasítás:

HT-1080Z:
IF állítás THEN utasítások ELSE utasítások
jelentése: "Ha az állítás igaz, akkor a THEN szó utáni utasításokat, ha hamis, akkor az ELSE szó utáni utasításokat kell végrehajtani!"
az ELSE szót nem kötelező használni.
Amennyiben csak a GOTO utasítás szerepelne a THEN vagy az ELSE szavak után, elég csak a sorszámot megadni, a GOTO szó elhagyható.

Spectrum:
IF állítás THEN utasítások
jelentése: "Ha az állítás igaz, akkor a THEN szó utáni utasításokat kell végrehajtani!"

Feladat:
Írjunk programot, amivel kiírhatjuk szavakkal az osztályzatot, ha azokat számokkal adjuk meg!

10 REM OSZTALYZATOK-1
20 INPUT "OSZTALYZAT: ";X
30 IF X=1 THEN PRINT "ELEGTELEN": GOTO 70
40 IF X=2 THEN PRINT "ELEGSEGES": GOTO 70
50 IF X=3 THEN PRINT "KOZEPES": STOP
60 IF X=4 THEN PRINT "JO": STOP
65 PRINT "JELES"
70 REM EZ LESZ AZ UTOLSO SOR

A program befejezését többféleképpen oldottuk meg. A GOTO 70 utasítással a program utolsó sorára ugrunk és így fejeződik be a program. Az utolsó sort csak azért írtuk a mintaprogramunkba, hogy legyen hova ugrani. Amennyiben folytatódna a program, minden esetben ezt a megoldást kellene választanunk.
Az 50-es, 60-as sorban a STOP a utasításnak (A HT-1080Z az END szót is ismeri) azonos a szerepe. Megállítják a program futását. A STOP utasítás hatására a számítógép azt is kiírja, hogy a program melyik soron állt meg.
A programozásban megkülönböztetjük a program fizikai végétől, a logikai végét. A legnagyobb sorszámú utasítássor lesz a program fizikai vége. A program logikai végén értjük azt, ahol a program futása befejeződik.

Feladat:
Értelmezzük a következő HT-1080Z-n futó programot!
A programban egy utasítás dönti el, hogy X értékétől függően mi történjen. Ez az utasítás az ON-GOTO.

10 REM OSZTALYZAT-2
20 INPUT "OSZTALYZAT: ";X
30 ON X GOTO 50,60,70,80
40 X$="JELES": GOTO 90
50 X$="ELEGTELEN": GOTO 90
60 X$="ELEGSEGES": GOTO 90
70 X$="KOZEPES": GOTO 90
80 X$="JO"
90 PRINT X$

Az ON-GOTO utasítással megadjuk, hogy X értékétől függően, hol folytatódjon a program. Akkor, ha az X értéke nagyobb, mint amennyi sorszámot megadtunk az utasításban, vagy 0, akkor a következő utasítássorral folytatódik a program. Ezt használtuk ki a JELES kiírásánál. X < 0 esetén hibát jelez a rendszer.

Feladat:
Írassuk ki a tanulmányi átlagot betűvel (HT-1080Z-n), ha a rendűségi határok: 1.75; 2.75; 3.75 és 4.75!
Elég az előző program 30-as sorát átírni:

30 ON X+0.25 GOTO 50,60,70,80

Az ON-GOTO utasításban tetszőleges aritmetikai kifejezés szerepelhet. Ennek egészértéke határozza meg, hogy hol folytatódjon a program. A kifejezés értéke nem lehet negatív, mert akkor hibát jelez a rendszer.
Az IF utasítást tekinthetjük logikai, az ON utasítást aritmetikai feltételes vezérlő utasításnak. Az ON utasítást többirányú elágaztató utasításnak is nevezik.

Az ON-GOTO alakja (HT-1080Z):

ON aritmetikai kifejezés GOTO sorszámlista
jelentése: az aritmetikai kifejezés egész értéke megmutatja, hogy a sorszámlista hányadik elemét tekintsük a következő végrehajtandó utasítássornak.
Akkor, ha a kifejezés egész értéke 0 vagy nagyobb, mint amennyi elemből áll a sorszámlista, akkor a következő utasítássorral folytatódik a program.
Negatív érték esetén hibajelzéssel megáll a program.

Feladat:
Készítsünk programot, amivel a képernyőn egy karaktert mozgathatunk a J, B, L, F billentyűk segítségével! Akkor, ha a J billentyűt nyomjuk le, a karakter az előző karakter mellett jobbra, ha a B-t nyomjuk le, balra jelenjen meg. Az F és az L billentyű lenyomására felette, ill. alatta jelenjen meg!

HT-1080Z:
A PRINT@ (olvasd PRINT egységár v. "kukac") utasítással a képernyő tetszőleges karakterpozíciójába állíthatjuk a kurzort, és ettől a pozíciótól kezdődően történik a kiírás.
A képernyő karakterpozícióinak sorszámozása a képernyő bal felső sarkától -val kezdődően, sorfolytonosan történik. Ez azt jelenti, hogy az első sor utolsó karakterpozíciója a 63., mivel egy sorba 64 karaktert írhatunk, így a második sor első karakterpozíciója lesz a 64. A képernyőn 16 sor jeleníthető meg, tehát összesen 16-64 = 1024 karakter írható a képernyőre. Az utolsó karakterpozíció az, amelyik a képernyő jobb alsó sarkában van. Ez a 1023. lesz.
A következő programmal a képernyő minden pontjába elhelyezzük a * karaktert. Mielőtt a csillagok kiíratását elkezdenénk, töröljük a képernyőt a CLS utasítással:

10 REM CSILLAGOK
20 CLS: REM KEPERNYO TORLES
30 I=0
40 PRINT @I,"*";
50 I=I+1: IF I<=1023 THEN 40

A PRINT @I,"*" utasítással a kurzort a képernyő I. karakterpozíciójába állítjuk, ahová kiíratjuk a karaktert. Az I értékét ciklussal változtatjuk.
A PRINT @ utasításban a képernyő karakterpozícióját kijelölő aritmetikai kifejezés után vesszőt írunk, és ezután következik a kiíratási lista. Ezzel az utasítással a képernyő bármely pozíciójába tudunk írni.
A lenyomott billentyűt az INKEY$ függvény érzékeli. Az INKEY$ függvény értéke az a karakter lesz, amelyik billentyűt lenyomva tartjuk a függvény kihívásakor. Amennyiben nincs lenyomott billentyű, a függvény értéke "üres karakter" lesz. Az INKEY$ függvénnyel beolvasott karakter nem jelenik meg a képernyőn.
Az eredeti feladat programja tehát a következő lesz:

10 REM KARAKTER MOZGATASA
20 CLS: I=7: J=32
30 IT=I: JT=J: PRINT @I*64+J,"*";
40 X$=INKEY$: IF X$="" THEN 40
50 IF X$="J" THEN J=J+1: GOTO 90
60 IF X$="B" THEN J=J-1: GOTO 90
70 IF X$="F" THEN I=I-1: GOTO 90
80 IF X$="L" THEN I=I+1
90 PRINT @IT*64+JT," ";
100 IF I*64+J<0 THEN END
110 IF I*64+J<1024 THEN 30

Spectrum:
Egyszerűbb dolgunk van: nem kell karakterpozíciót számolni. A PRINT AT sorszám,oszlopszám utasítással a kurzort a képernyő tetszőleges pozíciójába állíthatjuk. A sorokat 0-tól (a képernyő teteje) 21-ig, az oszlopokat 0-tól (a képernyő bal oldala) 31-ig számozzuk.

10 REM KARAKTER MOZGATASA
15 LET I=11: LET J=16
20 LET IT=I: LET JT=J
30 PRINT AT I,J;"*";
40 LET X$=INKEY$: IF X$="" THEN GO TO 40
50 IF X$="j" AND J<31 THEN LET J=J+1: GOTO 90
60 IF X$="b" AND J>0 THEN LET J=J-1: GOTO 90
70 IF X$="f" AND I>0 THEN LET I=I-1: GOTO 90
80 IF X$="l" AND I<21 THEN LET I=I+1
90 PRINT AT IT,JT," ";: GO TO 20

(Az AND szóról a Vizsgálat c. alfejezetben lesz szó.)
Az INKEY$ függvénnyel beolvassuk a karaktert, és a karaktertől függően változtatjuk az I, ill. a J változók értékeit, amivel a képernyő sorát, ill. oszlopát adjuk meg, ahová a következő csillagot íratjuk ki. Az IT és JT változókkal adott karakterpozícióba szóköz karaktert írunk, amivel töröljük a csillag karaktert.

Feladat:
Készítsünk programot HT-1080Z-n, amivel úgy jeleníthetjük meg a BASIC szót a képernyő legfelső sorában, hogy a BASIC szóból mindig eggyel több betűt lássunk a képernyő jobb oldalán, és az így kialakított szó fusson végig a képernyőn, a képernyő bal oldalára!
Karakterláncokat kell kiíratnunk, ami először egy karakterből áll, legvégül ötből. A karakterek összefűzését karakterenként végezzük. Ezeket a műveleteket egymás utáni utasítássorokban hajtjuk végre. Az ON-GOTO utasítással megoldhatjuk azt, hogy mindig annyi karakter alkossa a karakterláncot, amennyit ki akarunk írni. Akkor, amikor már minden karaktert kiírtunk, csak a "lemaradó" karakterek törléséről kell gondoskodni (60-as sor). A karakterláncokról és a karakterláncokkal végezhető műveletekről később még részletesen szó lesz. Az ott leírtak ismeretében a feladat egyszerűbben is megoldható.

10 REM KEPUJSAG
20 I=1
30 CLS
40 X$=""
50 ON I GOTO 110,100,90,80,70
60 X$=" "+X$
70 X$="C"+X$
80 X$="I"+X$
90 X$="S"+X$
100 X$="A"+X$
110 X$="B"+X$
120 PRINT @64-I,X$
130 I=I+1: IF I<=64 THEN 40

Kérdések és feladatok

1. Milyen vezérlő utasításokat ismerünk? Hogyan csoportosíthatjuk azokat?
2. Írassuk ki programmal a 200-nál kisebb pozitív páratlan számokat csökkenő sorrendben!
3. Írjunk programot, amivel kiírathatjuk a 2^n+1 alakú egész számokat! Csak pontos értékek jelenjenek meg a képernyőn!
4. Írjunk programot:
   1. az elsőfokú kétismeretlenes egyenletrendszer megoldására;
   2. a másodfokú egyenlet megoldására;
   3. a háromszög területének és kerületének kiszámítására, ha adottak az oldalak;
   4. számtani és mértani sorozatok első n elemének az előállítására;
   5. n szám összegének és szorzatának meghatározásához.
5. Mit csinál a következő program? Magyarázd meg!

10 INPUT A
20 IF A THEN PRINT 1/A

Vizsgálat
Egyszerű példán, a szám abszolút értékét előállító program néhány változatával mutatjuk be, hogy ugyanazt az eredményt hányféleképpen kaphatjuk meg, ha különböző relációjeleket használunk az IF utasításban.

10 INPUT X
20 IF X<0 THEN LET X=-X
30 PRINT X

10 INPUT X
20 IF X>0 THEN GOTO 40
30 LET X=-X
40 PRINT X

HT-1080Z-n:

10 INPUT X
20 IF X>0 THEN 30 ELSE X=-X
30 PRINT X

A vizsgálat ügyes megválasztásával rövidebbé és áttekinthetőbbé tehetjük programjainkat.

Feladat:
Írjunk programot N darab szám összegének és szorzatának meghatározására!
A ciklusmag N-szeres ismétlését az előző fejezetben bemutatott formában oldjuk meg.

• A ciklusmagban helyezzük el a számok beolvasását végző, összegüket és szorzatukat képző utasításokat.
• A ciklusmag része lesz a ciklusváltozó értékének módosítása is, az LET I=I+1 utasítás.
• A ciklusba lépés előtt gondoskodnunk kell az összeg és a szorzat értékét tartalmazó változók kezdőértékéről.

A számok összegét az S változó értéke adja, ennek kezdőértéke 0. A P változóban a számok szorzatát tároljuk, amelyiknek 1 kezdőértéket kell adni.

10 REM SZORZAT, OSSZEG
20 INPUT "N: ";N
30 LET S=0: LET P=1: LET I=1
40 INPUT X
50 LET S=S+X: LET P=P*X
60 LET I=I+1: IF I<=N THEN GOTO 40
70 PRINT "OSSZEG: ";S,"SZORZAT: ";P

A ciklusváltozó értékét más relációval is vizsgálhatjuk, de ekkor más helyre kell írnunk a ciklusváltozó értékét módosító utasítást, és meg kell változtatnunk az IF utasítás szerkezetét is. Néhány változatot mutatunk be. Csak a program végét írjuk le, ahol módosítottuk az eredeti programot.

60 IF I<N THEN LET I=I+1: GOTO 40
70 PRINT "OSSZEG: ";S,"SZORZAT: ",P

60 IF I=N THEN 80
70 LET I=I+1: GOTO 40
80 PRINT "OSSZEG: ";S,"SZORZAT: ",P

HT-1080Z-n:

60 IF I>=N THEN 70 ELSE I=I+1: G0T0 40
70 PRINT "OSSZEG: ";S,"SZORZAT: ",P

Általában egyszerűbben megtervezhető egy program, ha az összetett állításokat logikai műveletekkel fogalmazzuk meg. Háromféle logikai műveletet alkalmazhatunk:

NOT	a tagadás
AND	az ÉS
OR	a VAGY logikai műveletet jelent

Az összetett logikai kifejezésekben szereplő logikai műveletek kiértékelése is ebben a sorrendben történik.

Feladat:
Írjunk programot az elsőfokú kétismeretlenes egyenletrendszer megoldására! A feladat megoldását azzal kell kezdeni, hogy megoldjuk az

ax+by = c
dy+ey = f

elsőfokú egyenletrendszert!
Az egyenletrendszer gyökei:

X = (ce-bf) / (ae-bd)
Y = (af-dc) / (ae-bd)

ha ae-bd <> 0.
Akkor, ha ae-bd = 0 és

• af-cd <> 0 vagy ce-bf <> 0, nincs megoldása az egyenletrendszernek;
• végtelen sok megoldás van, ha af-cd = 0 és ce-bf = 0.

Az algoritmusunk az előzőek szerint a következő:

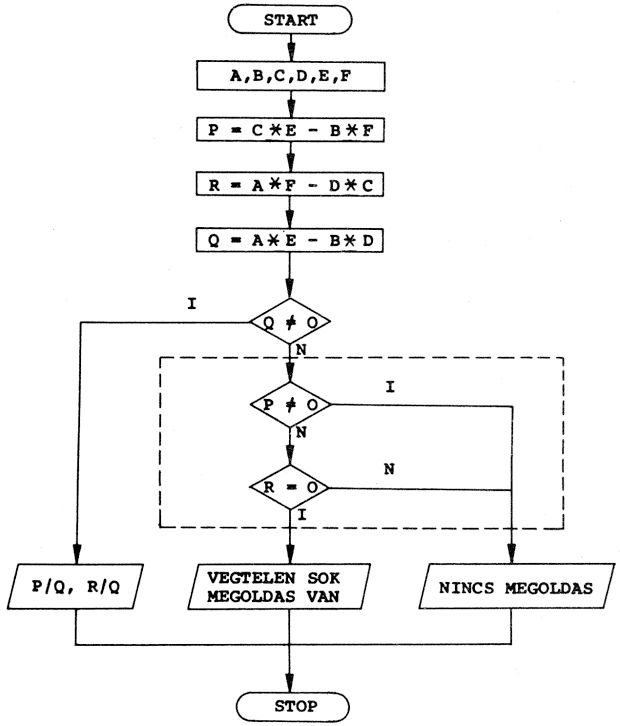
A program:

10 REM ELSOFOKU EGYENETRENDSZER
20 INPUT "EGYUTTHATOK, KONSTANSOK ",A,B,C,D,E,F
30 LET P=C*E-B*F: LET R=A*F-D*C:LET Q=A*E-B*D
40 IF Q<>0 THEN PRINT P/Q,R/Q: STOP
50 IF P<>0 THEN GOTO 70
60 IF R=0 THEN PRINT "VEGTELEN SOK MEGOLDAS VAN": STOP
70 PRINT "NINCS MEGOLDAS"

A folyamatábrán szaggatott vonallal jelzett részét egy vizsgálattal a következőképpen oldhatjuk meg:

50 IF P^2+R^2<>0 THEN PRINT "NINCS MEGOLDAS": STOP
60 PRINT "VEGTELEN SOK MEGOLDAS VAN": STOP

A feladat diszkussziójának leírásában a szereplő kifejezéseket a következőképen fogalmazzuk meg a BASIC nyelv szabályai szerint.
Logikai műveletekkel a vizsgálat:

50 IF A<>0 OR B<>0 THEN PRINT "NINCS MEGOLDAS": STOP
60 PRINT "VEGTELEN SOK MEGOLDAS VAN"

Itt a VAGY logikai műveletet használtuk. Az ES művelettel a megoldásunk a következő:

50 IF A=0 AND B=0 THEN PRINT "VEGTELEN SOK MEGOLDAS VAN": STOP
60 PRINT "NINCS MEGOLDAS "

Kérdések és feladatok

1. Egészítsük ki az ÖSSZEG, SZORZAT programot! Csak a 100-nál kisebb pozitív számokat összegezzük!
2. Írjunk programot az (x-a)*(x+b) = 0 alakú egyenlet megoldására!
3. Hogyan oldanánk meg a programban a KIZÁRÓ VAGY logikai műveletet?
4. Ellenőrizzük programmal a de Morgan-féle azonosságot!
5. Írjunk programot, amivel meghatározhatjuk:
   1. két pont kölcsönös helyzetét a számegyenesen;
   2. egy pont és egy egyenes;
   3. egy pont és egy kör kölcsönös helyzetét a síkban!
      Amennyiben két pont távolsága kisebb, mint 0.0001, a két pontot tekintsük illeszkedőnek.
6. Írjunk programot, amivel kiírhatjuk a hét napjainak nevét, ha megadjuk a napok sorszámát!

Adatok a programban

Feladat:
Írassuk ki programmal a hét napjainak nevét, ha megadjuk, hogy hányadik napra gondoltunk!

10 REM HET NAPJAI
20 INPUT "HANYADIK NAP? ";N
30 IF N=1 THEN PRINT "HETFO": STOP
40 IF N=2 THEN PRINT "KEDD": STOP
50 IF N=3 THEN PRINT "SZERDA": STOP
60 IF N=4 THEN PRINT "CSUTORTOK": STOP
70 IF N=5 THEN PRINT "PENTEK": STOP
80 IF N=6 THEN PRINT "SZOMBAT": STOP
90 PRINT "VASARNAP"

A hét napjainak nevét tekinthetjük adatoknak. Ezek közül kell kikeresnünk a megfelelő sorszámút. A kikereséshez csaknem annyi IF utasítást használtunk, amennyi adat van. Ez a megoldás már ennyi adatnál is kényelmetlen.
Helyezzük el a hét napjainak nevét mint adatokat a DATA utasítással a programba. Az így megadott adatokhoz a READ utasítással tudunk hozzáférni. A programban a READ X$ utasítással olvassuk be, a legkisebb sorszámú DATA utasítással kezdődően az adatokat. Amennyiben egy DATA utasítás után nincs több adat, akkor a beolvasás a következő DATA utasítás adatainak beolvasásával folytatódik. A DATA utasításban az adatokat vesszővel választjuk el egymástól. Egy DATA utasításban szereplő adatok alkotják az adatlistát.
A READ X$ utasítást annyiszor hajtja végre a program, ahányadik nap nevét kérjük. A beolvasás elkezdődik a legkisebb sorszámú adatlistából és sorba beolvassa a program az adatokat, míg a kérdéses nap nevéhez nem ér. Amikor kilépünk a ciklusból az X$ értéke a keresett nap neve lesz.

10 REM KIKERESES DATA-BOL
20 INPUT "HANYADIK NAP? ";N
30 LET I=1
40 READ X$
50 LET I=I+1: IF I<=N THEN GOTO 40
60 PRINT "EZ A NAP ";X$
70 DATA "HETFO","KEDD","SZERDA"
80 DATA "CSUTORTOK","PENTEK"
90 DATA "SZOMBAT","VASARNAP"

HT-1080Z-n a DATA utasítás után a szövegeket nem szükséges idézőjelbe tenni.

Ezzel a programmal tulajdonképpen bármilyen adatsorból kikereshetjük az N. elemet. A DATA adatlistát kell csak átírni.
Egy adatsor adott elemének sorszámát is hasonlóképpen határozhatjuk meg. Nézzünk erre egy példát!

Feladat:
Egy atlétikai verseny résztvevőinek nevét, a rajtszámuk növekvő sorrendjében a DATA adatmezőbe beírjuk.
A DATA adatmezőn a DATA adatlistákban szereplő adatok összességét értjük.
Írjunk programot, amivel a versenyzők neve alapján meghatározhatjuk a versenyző rajtszámát! Az adatmezőből egymás után beolvassuk a versenyzők neveit, és számláljuk, hogy a megadott név az adatmező hányadik eleme lesz. Ez lesz a versenyző rajtszáma, ha a rajtszámok egyesével növekednek.
A ki nem osztott rajtszámoknak megfelelő helyre csillag karaktereket írunk.

10 REM RAJTSZAMOK
20 INPUT "A VERSENYZO NEVE: ";X$
30 LET I=1
40 READ Y$
50 IF X$=Y$ THEN PRINT "A RAJTSZAM: ";I: STOP
60 LET I=I+1: IF I<8 THEN GOTO 40
70 PRINT "NEM TALALOM"
80 DATA "KISS","KOVACS","VARGA"
90 DATA "*","NAGY","*","SZABO"

A programban hét adatot adtunk meg. Gondoskodtunk arról, hogy csak ennyi adatot olvashasson be a program. Akkor, ha olyan nevet adunk meg, ami nem szerepel az adatok között, kiírja, hogy NEM TALALOM.
A vizsgálatra azért van szükség, mert ha a READ utasítással akkor is akarunk adatot beolvasni, amikor már az adatmező végére értünk, akkor a számítógép hibát jelez.

Feladat:
Készítsünk "szótár" programot! A program adja meg a BASIC utasításszavak magyar jelentését! Az utasításszavakat és azok jelentését beírjuk a DATA adatlistákba. Innen kell kikeresnünk a megfelelőt.
Most is gondolnunk kell arra, hogy a READ utasítással a beolvasást csak annyiszor kíséreljük meg, amennyi adatunk van. Előfordulhat, hogy olyan utasításszót adunk meg, amelyik nem szerepel a megadott adatok között. Ez természetesen csak akkor derül ki, ha az adatmező adatait végigvizsgáltuk. Azt, hogy mikor értünk az adatmező végére, többféleképpen megadhatjuk.
Ha ismerjük az adatok számát, akkor a beolvasást és a vizsgálatot egy olyan ciklusban helyezzük el, amivel csak annyi adatot olvashatunk be, amennyi van.

1 REM SZOTAR
10 LET N=9: LET I=1
20 INPUT "AZ UTASITASSZO: ";X$
30 READ U$,J$
40 IF U$=X$ THEN GOTO 70
50 LET I=I+1: IF I<N THEN GOTO 30
60 PRINT "NEM TALALOM": STOP
70 PRINT U$;" JELENTESE: ";J$
100 DATA "READ","OLVASS","DATA","ADATOK"
110 DATA "IF","HA","STOP","ALLJ","THEN","AKKOR"
120 DATA "PRINT","NYOMTAT","LET","LEGYEN"
130 DATA "INPUT","BEVITEL"

Az előző megoldás annyiból nem a legszerencsésebb, hogy új adatok beírásakor, a szókészlet bővítése esetén, változtatnunk kell az N értékét is.
Jelöljük az adatmező végét valamilyen jellel, ami nem fordulhat elő az adatok között. Ennek típusában meg kell egyeznie a többi adattal.
Programunkban egy utasítással két adatot olvasunk be, ezért két karakterlánccal jelezzük az adatmező végét.

1 REM SZOTAR
10 INPUT "AZ UTASITASSZO: ";X$
20 READ U$,J$
30 IF U$="***" THEN GOTO 60
40 IF U$<>X$ THEN GOTO 20
50 PRINT U$;" JELENTESE: ";J$: STOP
60 PRINT "NEM TALALOM"
100 DATA "READ","OLVASS","DATA","ADATOK"
110 DATA "IF","HA","STOP","ALLJ","THEN","AKKOR"
120 DATA "PRINT","NYOMTAT","LET","LEGYEN"
130 DATA "INPUT","BEVITEL"
140 DATA "***","***"

Feladat:
Számítsuk ki, hogy egy adott munkabér esetén mennyi nyugdíjjárulékot kell fizetni!
A nyugdíjjárulék a bér egy bizonyos százaléka, ami a bértől függ. Ismernünk kell a bérhatárokat, és a bérhatárokhoz tartozó százalékokat, hogy a számítást elvégezhessük:

• 1800 Ft-ig 3 %,
• 2300 Ft-ig 4%,
• 3000 Ft-ig 5 % stb.

Az adatokat DATA-ban helyezzük el, ahonnan sorban kiolvassuk, és összehasonlít?juk a megadott bérrel. Célszerű a vizsgálatot a legmagasabb bérhatártól kezdeni. Ekkori program egyszerűbb.

10 REM NYUGDIJJARULEK
20 INPUT "A BER: ";B
30 READ H,S: REM HATAR, SZAZALEK
40 IF B<H THEN GOTO 30
50 PRINT "NYUGDIJJARULEK: ";B*S/100
60 DATA 24000,15,12000,12,10000,13,8000,12,7000,11
70 DATA 6000,9,5000,8,4000,7,3000,6,2300,5,1800,4
80 DATA 1000,3

A DATA adatlista a programban bárhol elhelyezhető. Általában a programtól elkülönítve, az elejére vagy a végére írjuk.

Feladat:
Adott N darab számjegy. Írassuk ki azokat betűvel HT-1080Z-n!
A számjegyek nevének kikeresésekor valameddig eljutunk az olvasással az adatmező-ben, mire megtaláljuk a megfelelő adatot. A következő számjegy kikeresését ismét az adatmező elejéről kell kezdenünk, ezért használnunk kell a RESTORE utasítást. A RESTORE utasítás hatására, a következő READ utasítás az adatmező elejéről, tehát a legkisebb sorszámú adatlista elejéről olvassa be az adatot.

10 REM SZAMJEGYEK BETUVEL
20 INPUT "SZAMJEGYEK SZAMA: ";N
30 I=1: ON ERROR GOTO 200
40 INPUT "A SZAMJEGY: ";Y: RESTORE
50 J=0
60 READ Z$
70 J=J+1: IF J<=Y THEN 60
80 PRINT Y;"- ";Z$
90 I=I+1: IF I<=N THEN 40
100 END
110 DATA NULLA,EGY,KETTO,HAROM,NEGY,OT
120 DATA HAT,HET,NYOLC,KILENC
200 PRINT "ILYEN SZAMJEGY NINCS"
210 RESUME 40

Ebben a programban két ciklust ágyaztunk egymásba. A külső ciklus a betűket számolja, a belső a keresést végzi.
A RESTORE utasítást akkor adjuk ki, amikor elkezdődik a keresés, amikor belépünk a belső ciklusba. A kikeresés tehát az adatmező elejéről kezdődik.

Kérdések és feladatok

1. Gondoljuk végig, hogy hogyan oldanánk meg a fejezetben található programokat a READ és a DATA utasítások ismerete nélkül!
2. Mi a RESTORE utasítás hatása?
3. Keressük ki, hogy az előző fejezet feladatai közül melyiket lehet megoldani a READ és a DATA utasításokkal!
4. Írjunk programot
   1. Vasúti jegyek árának meghatározásához;
   2. Bérek címletezéséhez!

Ciklus
A ciklusszervezéssel kapcsolatos legfontosabb fogalmakkal már megismerkedtünk. Fontosságukra való tekintettel rendszerezzük azokat:

• Ciklus: programrészlet és annak ismételt végrehajtását biztosító utasítások.
• Ciklusmag: az a programrészlet, aminek végrehajtása ismétlődik.
• Vizsgálat: annak eldöntése, hogy az ismétlődés folytatódjon-e.
• Ciklusváltozó: az a változó, amelyiknek az értékétől függ a program futása során a ciklus befejezése.
• Előkészítés: azok az utasítások, amelyekkel a ciklusbalépés előtt a változók kezdő?értékeit megadjuk.

A ciklusszervezés a ciklus megtervezését jelenti. Mit kell végiggondolnunk, ha a programban ciklust akarunk létrehozni?

Mi ismétlődik?
Akkor, amikor egy műveletsort többször végre akarunk hajtatni a számítógéppel, gondoljunk arra, hogy ciklust szervezzünk. Az ismétlődő programrészletet fogalmazzuk meg általánosan, változók segítségével. Ez lesz a ciklusmag.

Mi változik?
A ciklusmag végrehajtása során legalább egy változó legyen, aminek az értéke változik. Amennyiben ilyen nincs, nekünk kell gondoskodnunk a ciklusváltozóról. A ciklusváltozó értékétől függ, hogy mikor fejeződik be a ciklus.

Mit vizsgálunk?
Az ismétlődést valamilyen feltételtől tesszük függővé. Ez lehet egy vagy több változó értékének függvénye. Azok a változók, amelyeknek értékei szerepet játszanának annak eldöntésében, hogy befejeződik-e a ciklus, azokat ciklusváltozókként kezeljük.

Milyen kezdőértékei lesznek a változóknak?
Mielőtt belépnénk a ciklusba, értéket kell adnunk a ciklusmagban található változóknak.

Feladat:
Pozitív számokból álló számhalmazból válasszuk ki a legkisebbet!
Az adatokat a DATA adatlistából egymás után be kell olvasni, és mindegyiket össze kell hasonlítani a korábban beolvasott adatok közül kiválasztott legkisebbel. Ez ismétlődik.
Az adatsor végét kell felismernie a programnak, hogy a ciklus befejeződjön. Az előző fejezetben láttuk, hogy erre két lehetőségünk van:

1. A beolvasott adatok változnak. Használjuk ezt ki. írjunk olyan adatot az adatsor végére, ami biztosan nem szerepel az adatok között. Feladatunkban lehet az a feltétel, hogy akkor fejeződjön be a ciklus, ha a beolvasott érték 0.
Hogyan lépünk a ciklusba? Mihez hasonlítjuk az első elemet? Az M változóba helyezzük el mindig a kisebb értéket. Legyen az M kezdőértéke egy olyan nagy szám, aminél biztos, hogy a számhalmaz elemei kisebbek.

10 REM LEGKISEBB-1
20 LET M=1E38
30 READ X
40 IF X=0 THEN GOTO 70
50 IF X<M THEN LET M=X
60 GOTO 30
70 PRINT "A LEGKISEBB: ";M
80 DATA 123,47,58,3,9,0

2. Akkor, ha ismerjük az adatok számát, a ciklusváltozóról nekünk kell gondoskodnunk. Legyen ez az I változó. Az I változó értékét egyesével növeljük a ciklusmagon belül. Ez a beolvasott adatok számlálását jelenti. A vizsgálatot I változó értékével végezzük.
Az előző megoldásban észrevehetjük, hogy az M értéke már az első adat beolvasása után megváltozik. Legyen most az M kezdőértéke az első adat.

10 REM LEGKISEBB-2
20 LET N=5
30 READ M
40 LET I=2
50 READ X
60 IF X<M THEN LET M=X
70 LET I=I+1
80 IF I<=N THEN GOTO 50
90 PRINT "A LEGKISEBB: ";M
100 DATA 123,47,58,3,9

Vegyük észre, hogy a két program között a leglényegesebb különbség az, hogy az elsőnél nem tudjuk előre megmondani, hogy a ciklusváltozó hogyan változik, a másodiknál a változás ismert. Ismerjük a ciklusváltozó kezdő és végértékét is.
A második programban szereplő ciklushoz hasonló ciklusok létrehozására szolgál a FOR / NEXT utasításpár, amit ciklusképző utasításpárnak neveznek. Ezzel az utasítással a feladat megoldása:

10 REM LEGKISEBB-3
20 LET N=5
30 READ M
40 FOR I=2 TO N
50 READ X
60 IF X<M THEN LET M=X
70 NEXT I
80 PRINT "A LEGKISEBB: ";M
100 DATA 123,47,58,3,9

A FOR / NEXT utasításpár gondoskodik a ciklusváltozó kezdőértékének megadásáról, a ciklusváltozó értékének változtatásáról és a vizsgálatról is. A FOR és a NEXT utasítások között kell elhelyeznünk a ciklusmagot.
A FOR és a NEXT utasítások mindig csak párban szerepelhetnek a programban. Az összetartozást azzal jelezzük, hogy a NEXT utasításban is szerepel az a ciklusváltozó, amelyikre vonatkozik.
A ciklusváltozó értéke a programunkban 1-gyel nő minden ismétlésnél mindaddig, ameddig nagyobb nem lesz, mint a végérték. A programunkban a ciklusváltozó kezdőértéke 2, a végértéke N.
A FOR utasítást megadhatjuk a következő alakban is:

40 FOR I=2 T0 N STEP 1

Az utasítás teljes alakját csak akkor kell használni, ha a lépésköz 1-től különböző.

A ciklusképző utasítás:

FOR ciklusváltozó = kezdőérték TO végérték STEP lépésköz
<a ciklusmag utasításai>
NEXT ciklusváltozó

A ciklusváltozó kezdő és végértékét, valamint a lépésközt megadhatjuk tetszőleges aritmetikai kifejezéssel, de HT-1080Z-n az nem lehet kétszeres pontosságú.
Az utasítás leírása:

1. Vegye fel a ciklusváltozó a kezdőértéket!
2. Fusson az azonos ciklusváltozójú NEXT utasításig a program!
3. Növelje a ciklusváltozó értékét az adott lépésközzel!
4. Vizsgálja meg, hogy a ciklusváltozó a kezdő és a végérték közé esik-e, és ha igen: 2. ponton folytassa!
   ha nem: folytatódjon a program végrehajtása a NEXT utáni utasítással!

A következő kis programmal kitapasztalhatjuk a FOR / NEXT utasítás működését.

10 INPUT "KEZDOERTEK: ";K
20 INPUT "VEGERTEK: ";V
30 INPUT "LEPESKOZ: ";L
40 FOR X=K TO V STEP L
50 PRINT "CIKLUSMAG ";X
60 NEXT X
70 PRINT "KILEPTUNK A CIKLUSBOL ";X

Akkor, ha a lépésköz pozitív, a ciklusváltozó értéke növekszik, ha negatív, csökken.
Ábrázoljuk a számegyenesen a kezdő és végértékeket, valamint a ciklusváltozó értékeit:

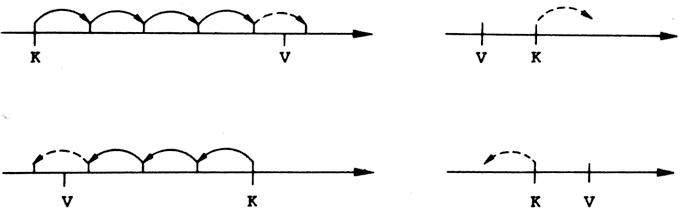
A kezdő értékkel minden esetben végrehajtódik a ciklus, kivéve, ha a kezdőérték máris teljesíti a kilépés feltételét. A módosított értékű ciklusváltozóval csak akkor, ha az értéke a kezdő és a végérték közé esik vagy a végértékkel egyenlő. Szemléletesen ezt úgy értelmezhetjük, hogy ha a ciklusváltozó értékeivel a végérték felé haladunk, és ha azon még nem léptünk túl, akkor a ciklusmag végrehajtódik.
Szaggatott vonallal jeleztük annak az értéknek a felvételét, amivel már kilépünk a ciklusból. A program 70. sorában ezt az értéket íratjuk ki.

Feladat:
Képezzük az ai =1/(2^i) sorozat első n elemének összegét, ahol i = 0, 1, 2, ..., n!
Ciklusszervezéskor arra ügyeljünk ebben a feladatban, hogy az első szám kitevője 0, ezért a ciklusváltozóval vagy számlálunk, vagy a kitevőket jelöljük. Az utóbbi esetben az n-edik elem kitevője n-1.

10 REM SOROZAT ELEMEINEK OSSZEGE-1
20 LET S=0: INPUT "ELEMEK SZAMA: ";N
30 FOR I=0 TO N-1
40 LET S=S+1/2^I
50 NEXT I
60 PRINT N;" ELEM OSSZEGE: ";S

A ciklusutasítás először változtatja a ciklusváltozó értékét, és csak ezután történik a vizsgálat. A következő program jobban szemlélteti az ilyen szerkezetű ciklust.

10 REM SOROZAT ELEMEINEK OSSZEGE-2
20 LET S=0: INPUT "ELEMEK SZAMA: ";N
30 LET I=0
40 LET S=S+1/2^I
50 LET I=I+1
60 IF I<=N-1 THEN GOTO 40
70 PRINT N;" ELEM OSSZEGE: ";S

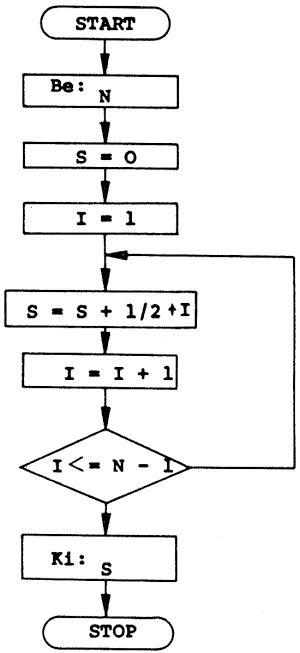
Utólagos vizsgálattal szervezett ciklus
Az utólagos vizsgálattal szervezett ciklusok általános sémáját mutatjuk be a következő ábrán:

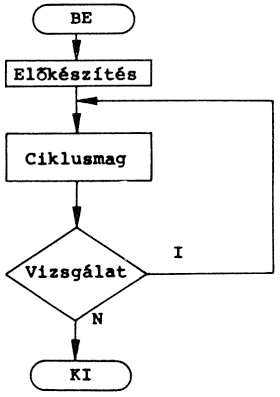
Feladat:
Összegezzük HT1080Z-n az ai = 1/(2^i) sorozat elemeit mindaddig, ameddig ai nagyobb mint 1E-15 (i = 0; 1; 2; ...)!
A sorozat elemeit osztással állítjuk elő, az előző elem ismeretében:

ai = ai-1/2

A programunk ezzel gyorsabb lesz, és kétszeres pontossággal számolhatunk, mivel nem használjuk a hatványozást.
Nem tudjuk előre, hogy hányadik elemnél lépjük át a határt, ezért az összegezés előtt kell a vizsgálatot elvégeznünk:

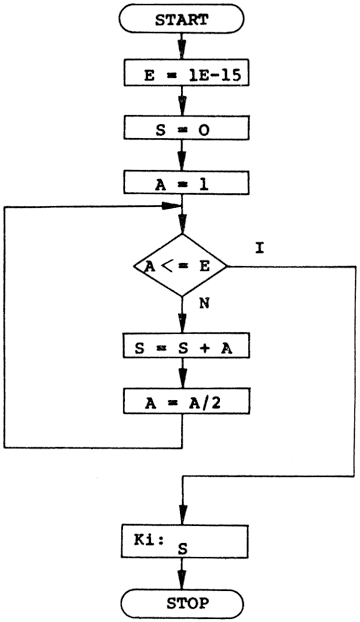
A program:

10 REM SOROZAT ELEMEINEK OSSZEGE-3
20 DEFDBLA-Z: CLS
30 E=1E-15
40 S=0: A=1
50 IF A<=E THEN 90
60 S=S+A: PRINT @0,S,A
70 A=A/2
80 GOTO 50
90 PRINT "OSSZEG: ",S

A 60-as sorban a PRINT @0,S,A utasítással kiíratjuk a részösszegeket és az elemeket, így a közelítést követni tudjuk.
A változók értékeinek változását figyelemmel tudjuk kísérni, ha beírjuk a következő utasítássort:

75 IF INKEY$ =" " THEN 75

A program mindaddig várakozik ennél a sornál, ameddig le nem nyomunk egy billentyűt.

Előzetes vizsgálattal szervezett ciklus
Az előzetes vizsgálattal szervezett ciklusok általános sémáját mutatja a következő ábra:

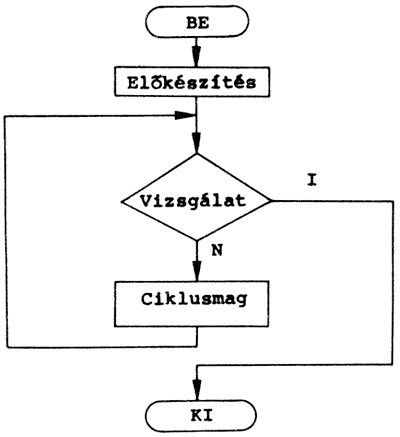
Feladat:
Összegezzük egy n elemű számhalmaz 100-nál kisebb elemeit az első negatív számig!
A feltételek szerint meg kell vizsgálnunk a beolvasott elemeket, és csak a 100-nál kisebb pozitív számokat kell összegeznünk. Negatív szám esetén ki kell ugranunk a ciklusból.
A feladat szerint N számot kell összegeznünk, tehát az N elem beolvasásához a FOR / NEXT ciklusképző utasítást használhatjuk. Akkor, ha negatív számot találunk a be-olvasott adatok között, korábban kilépünk a ciklusból.

10 REM KIKERESES OSSZEGZES
20 LET N=13
30 LET S=0
40 FOR I=1 TO N
50 READ X
60 IF X<0 THEN GOTO 100
70 IF X>100 THEN GOTO 90
80 LET S=S+X
90 NEXT I
100 PRINT "AZ OSSZEG: ";S
110 DATA 123,41,2,3,56,0,36
120 DATA 77,-13,56,47,-46,32

A 100-nál kisebb számok kiválasztása a 70-es sorral történik. Akkor, ha nem összegezzük a beolvasott számot, a NEXT utasításra ugrunk. A ciklusmag befejezése, a ciklusváltozó egy adott értékénél csak így történhet, a NEXT utasítás végrehajtásával.

Feladat:
Határozzuk meg két szám legnagyobb közös osztóját!
A bemutatásra kerülő algoritmust szóban már ismertettük a Bevezetés a programozásba c. fejezet 6. feladatában: Meg kell keresnünk azt a legnagyobb számot, amelyik mindkét számnak osztója. Legyen a két szám a és b, a legnagyobb közös osztó k, akkor felírható, hogy

a = k*a' és b = k*b'

k osztója lesz a két szám különbségének is: a-b = k*a'-k*b' = k*(a'-b'), ami biztosan kisebb, mint a két szám közül a nagyobb.
A nagyobb szám helyett mindig vesszük a két szám különbségét, és ezt ismételjük mindaddig, míg a különbség nem nulla, azaz a két szám nem egyenlő. Egyenlőség esetén a számok a legnagyobb közös osztót adják! A két vizsgált szám értékének a csökkenése miatt biztos, hogy véges lépésben meghatározhatjuk az eredeti számok legnagyobb közös osztóját.
Az algoritmusunk lépésenként leírva:

1. Adott két szám.
2. A két szám egyenlő?
      igen: 5. ponttal folytasd!
      nem: 3. ponttal folytasd!
3. A nagyobb szám helyett vegyük a két szám különbségét!
4. 2. ponttal folytasd!
5. Ez lesz a legnagyobb közös osztó!

A program HT-1080Z-n:

10 REM LEGNAGYOBB KOZOS OSZTO
20 INPUT "A KET SZAM: ";A,B
30 IF A=B THEN 60
40 IF A>B THEN A=A-B ELSE B=B-A
50 GOTO 30
60 PRINT "LNKO: ";A

Kérdések és feladatok

1. Ismertessük a ciklusszervezéssel kapcsolatos fogalmakat!
2. Ismertessük a ciklus szerkezetét! Ábrázoljuk folyamatábrával!
3. Írjunk programot, amelyikkel az INPUT utasítással beolvasott adatok közül
   1. legkisebbet,
   2. a legnagyobbat,
   3. a legkisebbet és a legnagyobbat is kiválasztjuk!
4. Milyen ciklus létrehozásakor alkalmazhatjuk a FOR/NEXT ciklusképző utasítást? Keressük ki az előző mintaprogramok közül ezeket, és oldjuk meg a feladatokat a FOR/NEXT utasításpárral is!
5. Készítsünk folyamatábrát a ciklusképző utasítás működésének leírásához!
6. Hogyan fejeződik be a ciklusmag a FOR/NEXT utasításban?
7. Írjunk programot, amivel meghatározhatjuk egy numerikus adathalmaz 3-mal osztható páros számait!
8. Hogyan határozható meg két szám legkisebb közös többszöröse, ha a két szám legnagyobb közös osztóját ismerjük?
9. Hogyan oldjuk meg a kettes számrendszerben adott számok tízes számrendszerbe történő átírását ciklus segítségével?
10. Mire kell ügyelni két ciklus egymásba ágyazásakor?
11. Írjunk programot, amivel függvények értéktáblázata készíthető!
12. Írjunk programot, amivel előállíthatjuk egy szó betűiből a szó morze kódját! A betűket és azok kódjait a DATA adatlistában helyezzük el.
13. Írjunk programot, amivel PI közelítő értékét kiszámíthatjuk!

    PI/2 = 2/1 * 2/3 * 4/3 * 4/5 * 6/5 * 6/7 ...

(Wallis, 1659)

PI/4 = 1 - 1/3 + 1/5 - 1/7 + 1/9 ...

(Leibnitz, 1673)

Aritmetikai függvények
Az aritmetikai kifejezésekben közvetlenül hivatkozhatunk a BASIC által ismert elemi függvényekre. Ezeket a függvényeket, amint azt látni fogjuk, nemcsak függvényeket tartalmazó kifejezések értékének meghatározására használhatjuk, hanem programozási feladatok megoldásában is segítségünkre lehetnek. A függvények gyakorlati alkalmazására látunk példákat programjainkban.
A függvények három v. négybetűs azonosító neve a matematikai jelölésükkel azonos vagy arra utal.
A függvény független változójának értékét a függvény neve után a zárójelben megadott kifejezés értéke adja. Ez a függvény argumentuma. Spectrumon - a többi BASIC változattól eltérően - a függvény argumentumát nem kell zárózelbe tenni, csak ha az összetett aritmetikai kifejezés!

SQR(A*A+B*B)
ABS(Y-(A*X+B))
SIN(A*3.1415/180)

Az argumentumnak a függvény értelmezési tartományába kell esni. Az értelmezési tartományt a függvény matematikai értelmezése és az argumentumban szereplő kifejezés lehetséges pontossága, annak számtartománya együtt határozza meg.
Az SQR(X) függvény negatív számokra nincs értelmezve, és HT-1080Z-n az argumentum egyszeres pontosságú lehet, ezért az értelmezési tartomány: 0 <= X <= 1.701411E38.

Feladat:
Adott három szakasz. Határozzuk meg a szakaszokból szerkeszthető háromszög kerületét és területét!
Mielőtt a számításokhoz hozzákezdenénk, a háromszögek oldalaira vonatkozó egyenlőtlenségek felhasználásával megvizsgáljuk, hogy a három szakasz háromszöget alkot-e. Ha igen, kiszámítjuk kerületét és a Heron-képlet alkalmazásával a területét.

K = a+b+c

ahol s = k/2

10 REM HAROMSZOG KERULETE ES TERULETE
20 INPUT "OLDALAK: ";A,B,C
30 IF A+B<=C OR A+C<=B OR B+C<=A THEN PRINT "NEM LEHET HAROMSZOG!": STOP
40 LET K=A+B+C: LET S=K/2
50 LET T=SQR(S*(S-A)*(S-B)*(S-C))
60 PRINT "KERULETE: ";K
70 PRINT "TERULETE: ";T

A négyzetgyök függvény helyett alkalmazhatjuk a törtkitevőjű hatványozást is:

50 LET T=(S*(S-A)*(S-B)*(S-C))^0.5

Páros gyökkitevő esetén a négyzetgyök függvényeket egymásba építhetjük, ami azt jelenti, hogy a függvény argumentumát meghatározó kifejezés is tartalmazhat függvényt. X változó értékének negyedik gyöke:

SQR(SQR(X))

Spectrumon:

SQR (SQR X)

Ehelyett célszerűbb itt is a törtkitevő használata:

X^0.25

Páratlan kitevőjű gyökök kiszámítását is a törtkitevőjű hatványozással oldhatjuk meg, pl:

X^(1/5)

A logaritmus azonosságait felhasználva, a LOG és EXP függvények segítségével is meghatározhatjuk a gyököket.

Feladat:
Írjunk programot, amivel HT-1080Z-n kétszeres pontossággal kiszámíthatjuk egy szám négyzetgyökét!
Alkalmazzuk a Newton-féle iterációt. Lépésenként közelítjük a szám négyzetgyökét. Az eljárás lényege, hogy ha xi < SQR(x), akkor x/xi > SQR(x), és ekkor xi és x/xi számtani közepe

x négyzetgyökének egy pontosabb megközelítését adja. Ugyanez érvényes, ha xi > SQR(x), mert akkor x/xi < SQR(x). xi az iteráció i. képzésében a közelítő érték.

Az első közelítő érték x1 =x/2

Az i. közelítő érték ismeretében meghatározzuk az i+1. közelítő értéket, ami a következő lépésben az i. szerepét tölti be.
Az i. közelítő értéket nevezzük "régi", az i+1.-et "új" közelítő értéknek. Ez jobban kifejezi azt, hogy az iterációval egy olyan értéket állítunk elő, amit a következő lépésben már mint kiindulási értéket veszünk figyelembe.
Az E értéke jelentse a közelítés pontosságát. Amikor az "új" és a "régi" közelítő érték közelebb van egymáshoz, mint E (E > Q), akkor az iterálást befejezzük:

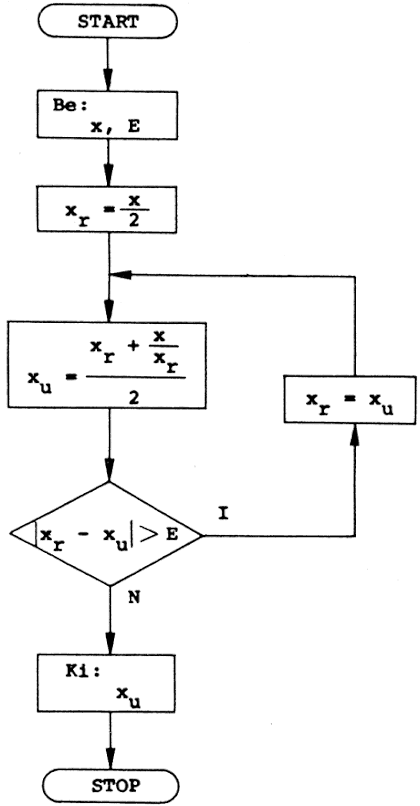
A változókat kétszeres pontosságúaknak deklaráltuk a DEFDBL utasítással.
A függvények között van olyan, aminek az argumentuma HT-1080Z-n kétszeres pontosságú érték is lehet. Ilyen az abszolútérték függvény is, amivel az XR és az XU változó értékével adott intervallum hosszát határozzuk meg. Az abszolútérték függvény függvényértéke is kétszeres pontosságú lesz.
Ezzel a programmal bemutattuk azt is, hogy a függvényértékek kiszámítására vannak olyan matematikai eljárások, amelyekben csak a négy alapműveletet használjuk.

10 REM NEWTON-FELE ITERACIO
20 DEFDBL X,E: CLS
30 INPUT "A SZAM: ";X
40 INPUT "PONTOSSAG: ";E
50 XR=X/2
60 XU=.5*(XR+X/XR)
70 IF ABS(XU-XR)>E THEN XR=XU: GOTO 60
80 PRINT X;" NEGYZETGYOKE: ";XU

Feladat:
Adott két pozitív szám. Osszuk el maradékosan a nagyobb számot a kisebbel! HT1080-Z-n a FIX(X) egészrész függvény értéke az az egész szám lesz, amit úgy kapunk, hogy elhagyjuk X értékének tizedes részét. "Levágjuk" a tizedes számjegyeket.
A két pozitív szám hányadosának egész része tehát megadja, hogy hányszor van meg a nagyobb számban a kisebb. A maradékot ebből már meg tudjuk határozni!

10 REM MARADEKOS OSZTAS
20 INPUT "A KET SZAM: ";A,B
30 IF A<B THEN T=A:A=B:B=T
40 H=FIX(A/B):M=A-B*H
50 PRINT A;"=";H;"*";B;"+";M

Spectrumon a feladat ugyanígy megoldható, ott az INT egészrész függvényt tudjuk használni:

10 REM MARADEKOS OSZTAS
20 INPUT "A KET SZAM: ";A;B
30 IF A<B THEN LET T=A: LET A=B: LET B=T
40 LET H=INT(A/B): LET M=A-B*H
50 PRINT A;"=";H;"*";B;"+";M

Feladat:
Kerekítsük egész számra A változó értékét!
Az INT(X) egészérték függvény azt a legnagyobb számot adja, amelyik nem nagyobb, mint X értéke. Szemléletesen ez azt jelenti, hogy egy számhoz azt az egész számot rendeljük, amelyik tőle balra a legközelebb van a számegyenesen, ha a számot a számegyenesen ábrázoljuk.
HT-1080Z-n a negatív számtartományban nem egyezik a FIX és az INT függvények értéke. Egy szám kerekítésekor azt az egész számot kell kapnunk, amelyik A értékéhez a legközelebb van. Egy egység annak az intervallumnak a hossza, amelyből választva a kerekítendő számot, ugyanazt az értéket kapjuk.
Az INT függvénnyel két egész szám közötti intervallum pontjaihoz rendeljük ugyanazt a számot. Helyezzük ide a kerekítendő számot. Adjunk a számhoz 0.5-öt!

10 REM KEREKITES
20 INPUT "KEREKITENDO SZAM: ";A
30 LET A=INT(A+0.5)
40 PRINT "EGESZ RESZRE KEREKITVE: ";A

Amennyiben két tizedesre akarjuk kerekíteni a számot, a 30-as sor a következő lesz:

30 LET A=INT(A*100+0.5)/100

HT-1080Z-n az eredményeket kerekítve a PRINT USING utasítással is kiírathatjuk. A # jelekkel, és a tizedesponttal meghatározhatjuk, hogy hány tizedes pontossággal írja ki a változó értékét. Az utolsó számjegyet kerekítve kapjuk meg.
A következő program két tizedes pontossággal és ahogyan a K$ változó értékével kijelöljük, úgy írja ki A értékét.

10 REM PRINT USING
20 INPUT "A SZAM";A
30 INPUT "FORMATUM";K$
40 PRINT USING"####.##";A
50 PRINT USING K$;A

Kerekített értékek kiíratását a PRINTUSING utasítással egyszerűen megoldhatjuk, de ha kerekített értékkel szeretnénk számolni, akkor az INT függvénnyel kell a kerekítést elvégezni.

Feladat:
Állítsunk elő program segítségével 5 db LOTTÓ számot!
Az, hogy milyen LOTTÓ számokat sorsolnak ki, a véletlenen múlik. Ilyen véletlen események szimulálását tudjuk programozni a RND függvény segítségével: Véletlen számot állít elő az argumentumtól függően egy adott számtartományból.

HT-1080Z-n a függvény működését paraméterekkel vezérelhetjük:

• RND (0) - a függvény értéke egy egyszeres pontosságú szám a (0; 1) intervallumból;
• RND (N) - értéke egy egész szám az [1; N] intervallumból.

Az RND függvény első értékét a RANDOM utasítással állítjuk elő (hogy a sorozat valóban véletlenszerű legyen a program minden lefuttatásakor).

Spectrumon az RND függvénynek nincs oaramétere: 0 és 1 közé eső véletlenszámot ad (a 0 értéket felveheti, az 1-et nem).
RANDOM helyett RANNDOMIZE használható a véletlenszám-generátor inicializálására.

A program HT-1080Z-n:

10 REM LOTTO SZAMOK
20 RANDOM
30 FOR I=1 TO 5
40 PRINT RND(90)
50 NEXT I

Másik lehetséges megoldás:

40 PRINT INT(90*RND(0)+1)

Spectrumon:

40 PRINT INT (90*RND+1)

A TAB függvény nem aritmetikai függvény. Az argumentummal a képernyő egy sorának karakterpozícióját jelöljük ki. A TAB függvénnyel a kiíratás helyét jelölhetjük ki, amiből következik, hogy csak a PRINT utasításban használhatjuk.

Feladat:
Adott az ax+b egyenes és a P(p1; p2) pont. Írjunk programot, amivel meghatározhatjuk a pont és az egyenes kölcsönös helyzetét! A program íja ki, hogy ALATTA VAN vagy FELETTE VAN, vagy, hogy ILLESZKEDIK!

Az IF utasítás helyett alkalmazzuk az SGN előjel függvényt (értéke -1 negatív, 0 a zérus és +1 pozitív paraméter esetében), amivel ugyancsak megoldható a feladat.
Az ábra a pont és az egyenes egy lehetséges elhelyezkedését mutatja:

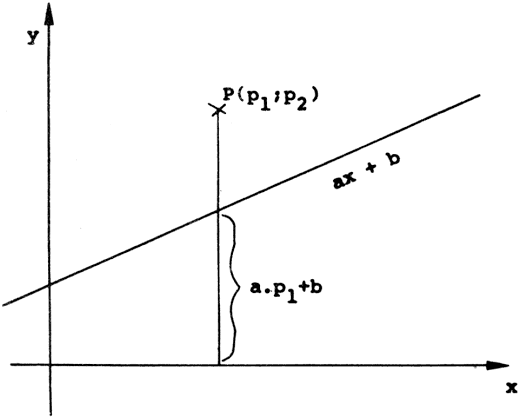
A pont ordinátáját (p2) kell összehasonlítanunk az egyenes p1 abcisszájú pontjának ordinátájával ap1+b. A p2 - (ap1+b) kifejezés értéke, a pont és az egyenes elhelyezkedésétől függően lehet negatív, 0 vagy pozitív. Az IF utasítással ezt kellene vizsgálni.
A p2-(ap1+b) kifejezés SGN függvénye -1, 0 vagy 1 értékek közül valamelyiket veszi fel. 2-vel növelve ezt az értéket, 1-et, 2-t vagy 3-at kapunk.
Oldjuk meg a feladatot HT-1080Z-n az ON-GOTO utasítással!

10 REM PONT-EGYENES-1
20 CLS: INPUT "PONT KOORDONATAI: ";P1,P2
30 INPUT "A*X+B PARAMETEREI: ";A,B
40 Y=A*P1
50 ON SGN(P2-Y)+2 GOTO 70,80
60 PRINT "FELETTE VAN.": STOP
70 PRINT "ALATTA VAN.": STOP
80 PRINT "ILLESZKEDIK."

Ez a program azon kívül, hogy az SGN függvény alkalmazására látunk példát, arra is jó, hogy meggyőződjünk arról, hogy a számítógép csak egy megadott pontossággal számol. A programunk nem működik úgy, ahogyan azt várjuk. Az illeszkedést nem jelzi minden esetben, holott mi esetleg úgy adtuk meg az adatokat. Írassuk ki a P2-Y kifejezés értékét, és akkor látni fogjuk, hogy ilyenkor az eredmény nem mindig 0.
Az egyenlőséget nem lehet 0-ra vizsgálni. Meg kell adnunk azt az értéket, aminél ha kisebb az eltérés, már azt mondjuk, hogy a pont illeszkedik az egyenesre. Legyen ez a határ 10^-6. A gyakorlatban ilyen eltérés már nem tekinthető számottevőnek.

10 REM PONT-EGYENES-2
20 INPUT "PONT KOORDINATAI: ";P1,P2
30 INPUT "A*X+B PARAMETEREI: ";A,B
40 LET Y=A*P1: LET D=Y-P2
60 IF ABS(D)<1E-6 THEN PRINT "ILLESZKEDIK.": STOP
70 IF D<0 THEN PRINT "FELETTE VAN.": STOP
80 PRINT "ALATTA VAN."

Feladat:
Adott egy egész szám. írassuk ki a számjegyeket fordított sorrendben!
A szám felbontását számjegyekre az INT függvénnyel oldjuk meg. 10-zel osztva a számot és képezve az így kapott számnak a törtrészét, megkapjuk az utolsó számjegyből álló szám tizedrészét.
Azt, hogy a szám hány számjegyből áll, a szám tízes alapú logaritmusából határozható meg. A LOG függvény (Spectrumon: LN) az argumentum természetes alapú logaritmusát adja, aminek az alapszáma e = 2.71828... A függvény matematikai jelölése lnx. Egy szám tízes alapú logaritmusának kiszámításához használjuk fel a lgx = lnx / ln10 összefüggést.

A program HT-1080Z-n :

10 REM SZAM FORDITVA
20 INPUT "A SZAM: ";X
30 N=LOG(X)/LOG(10)+1
40 FOR I=1 TO N
50 Y=INT(X/10):T=10*(X/10-Y)
60 PRINT INT(T+0.5);
70 X=Y
80 NEXT I

Spectrumon:

10 REM SZAM FORDITVA
20 INPUT "A SZAM: ";X
30 LET N=LN X /LN 10+1
40 FOR I=1 TO N
50 LET Y=INT(X/10): LET T=10*(X/10-Y)
60 PRINT INT(T+0.5);
70 LET X=Y
80 NEXT I

Feladat:
Adott három szakasz. Határozzuk meg a szakaszokból szerkesztett háromszög szögeit!
A három szakaszt nagyság szerint sorbarendezzük. Erre azért van szükség, hogy a legnagyobb oldallal szemközti szöget meg tudjuk határozni koszinusztétel segítségével. A következő szög, amit szinusztétellel számítunk ki, így biztos, hogy hegyesszög lesz. Mielőtt a számításokat elkezdenénk, megvizsgáljuk, hogy a három szakaszból szerkeszthető-e háromszög. Miután sorbarendeztük a szakaszokat, elég azt megnézni, hogy a legnagyobb szakasz nagyobb-e, mint a két rövidebb szakasz összege.
A rendezést a következő algoritmussal oldjuk meg:

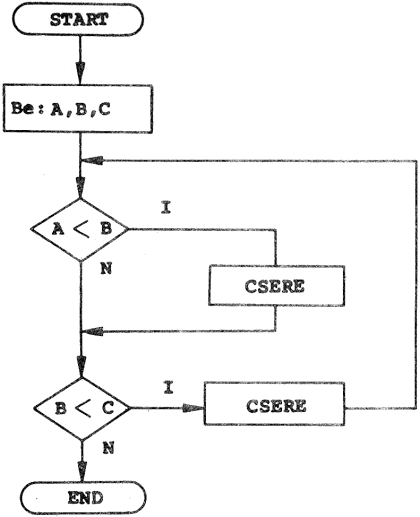
A trigonometrikus függvényekről tudnunk kell, hogy az argumentumokat radiánban kell megadni és radiánban kapjuk a szöget is az ATN függvénnyel. Ez az arkusztangens függvény, aminek az értéke az a szög lesz, amelyiknek a tangense az argumentummal egyenlő.
Egy szög szinuszát vagy koszinuszát ismerve, a szög kiszámításához a következő azonosságokat kell alkalmaznunk:

A program HT-1080Z-re:

10 REM HAROMSZOG SZOGEI
20 INPUT "A HAROM OLDAL: ";A,B,C
30 IF A<B THEN T=A: A=B: B=T
40 IF B<C THEN T=B: B=C: C=T: GOTO 30
50 IF B+C<=A THEN PRINT "NEM SZERKESZTHETO HAROMSZOG!":GOTO 20
60 X=(B*B+C*C-A*A)/(2*B*C)
70 X=SQR(1-X*X)/X
80 X=ATN(X)
90 IF X<0 THEN X=4*ATN(1)+X
100 P=X*45/ATN(1)
110 Y=SIN(X)*B/A: Y=ATN(Y/SQR(1-Y*Y))
120 Q=Y*45/ATN(1)
130 Z=4*ATN(1)-X-Y: R=180-P-Q
140 R$="FOK": F$="RADIAN"
150 PRINT " ALFA = ";X;F$: PRINT TAB(8);P;R$
160 PRINT " BETA = ";Y;F$: PRINT TAB(8);Q;R$
170 PRINT "GAMMA = ";Z;F$: PRINT TAB(8);R;R$

Spectrum-ra:

10 REM HAROMSZOG SZOGEI
20 INPUT "A HAROM OLDAL: ";A;B;C
30 IF A<B THEN LET T=A: LET A=B: LET B=T
40 IF B<C THEN LET T=B: LET B=C: LET C=T: GOTO 30
50 IF B+C<=A THEN PRINT "NEM SZERKESZTHETO HAROMSZOG!":GOTO 20
60 LET X=(B*B+C*C-A*A)/(2*B*C)
70 LET X=SQR(1-X*X)/X
80 LET X=ATN X
90 IF X<0 THEN LET X=4*ATN 1 +X
100 LET P=X*45/ATN 1
110 LET Y=SIN X *B/A: LET Y=ATN(Y/SQR(1-Y*Y))
120 LET Q=Y*45/ATN 1
130 LET Z=4*ATN 1 -X-Y: LET R=180-P-Q
140 LET R$=" FOK": LET F$=" RADIAN"
150 PRINT " ALFA = ";X;F$: PRINT TAB 8;P;R$
160 PRINT " BETA = ";Y;F$: PRINT TAB 8;Q;R$
170 PRINT "GAMMA = ";Z;F$: PRINT TAB 8;R;R$

Feladat:
Igaz az, hogy

Készítsünk programot HT-1080Z-n, amivel meghatározhatjuk egy szög szinuszát adott pontossággal! Az összeg első tagja x. Az i. tag ismeretében az i+1. tag:

Az így képzett tagokat összegezzük mindaddig, ameddig valamelyik tag abszolútértéke kisebb nem lesz, mint a megadott pontosság, azaz nem befolyásolja az összeg értékét a pontosságnál nagyobb mértékben.

10 REM SZOG SZINUSZA
20 DEFDBL A-Z: CLS: INPUT "A SZOG RADIANBAN: ";X
30 INPUT "PONTOSSAG: ";E
40 Y=X: A=X: I=1
50 I=I+1
60 A=-A*X*X/(2*I-2)/(2*I-1)
70 Y=Y+A
80 PRINT @580,"SIN ";X;" = ";Y
90 IF ABS(A)>E THEN 50

Kérdések és feladatok

1. Ábrázoljuk és elemezzük az aritmetikai függvényeknek megfelelő elemi függvényeket! Határozzuk meg értelmezési tartományukat és az értékkészletüket!
2. Milyen közelítő eljárást ismerünk még a számok négyzetgyökének meghatározására?
3. Írassuk ki a négyzetgyök közelítő értékét a megadott pontossággal!
4. Készítsünk "kockadobó" programot!
5. Írjunk programot, amivel az összeadást lehet gyakorolni az egész számok körében!
6. Határozzuk meg egy szám n. gyökét a LOG és EXP függvények segítségével!
7. Ellenőrizzük a HAROMSZOG SZÖGEI programot! Vizsgáljuk meg, hogy speciális vagy elfajuló esetekben helyesen működik-e a program! Nézzük meg az összes lehetséges esetet!
8. Határozzuk meg a csúcspontjainak koordinátáival adott háromszög kerületét, területét, szögeit és nevezetes pontjainak koordinátáit program segítségével!
9. Készítsünk programot a kör és a pont kölcsönös helyzetének vizsgálatára!
10. Készítsünk TOTO tippeket előállító programot!

Grafika (HT-1080Z)
A képernyőt tekintsük egy olyan koordináta-rendszernek, amelyen az első negyed egy részének rácspontjait BASIC utasítással megjeleníthetjük, törölhetjük. A képernyő koordinátarendszerének Y tengelye lefelé mutat:

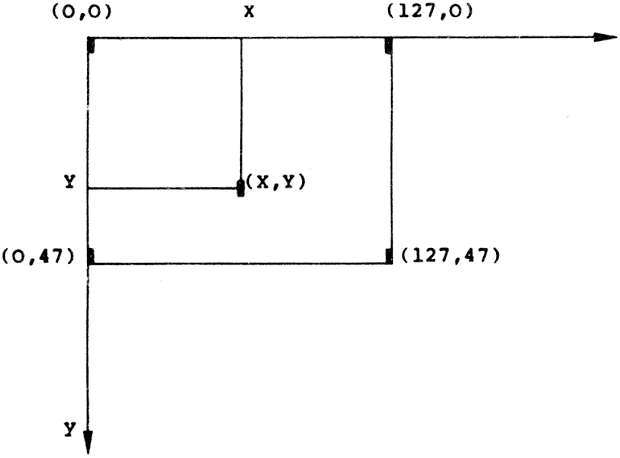
A SET (X,Y) utasítással megjelenítjük, a RESET(X, Y) utasítással töröljük a képernyő (X,Y) koordinátájú pontját.
Az előző ábrán a képernyő sarokpontjainak koordinátáit adtuk meg, amiből arra következtethetünk, hogy a

0 <= X <= 127
0 <= Y <= 47

relációknak teljesülniük kell.
A pont koordinátáit tetszőleges aritmetikai kifejezéssel megadhatjuk, ezért szintaktikailag helyesek a következő utasítások:

SET(A+1,15)
RESET(I,2*J)
SET(X,20*SIN(X) +24)

Ezeknek a kifejezéseknek az egészértéke lesz a pont koordinátája.
A POINT(X,Y) függvénnyel vizsgálhatjuk egy pont,állapotát. Logikai függvényként értelmezve a POINT függvény értéke IGAZ, ha világít a pont, HAMIS, ha a képernyő X,Y koordinátájú pontja sötét. Ennek megfelelően a függvény aritmetikai értéke -1, illetve 0.

Feladat:
Pattogjon egy golyó négy fal között!
A falakat a képernyőre rajzolt egyenesekkel jelezzük. A golyót a képernyő egy világító pontjának mozgásával szimuláljuk. A falak kirajzolásakor csak az egyik koordinátát kell változtatni, a másik állandó.
Meg kell oldanunk, hogy az (X,Y) koordinátájú pont megjelenítése után valamelyik szomszédos pontot világítsuk ki, és az előző pontot töröljük. A mozgó pont pályáját úgy rajzolhatjuk meg, ha az ütközés 45 fokos, hogy a vízszintes koordináták egységnyi változtatásával a függőleges koordinátát is egységnyivel változtatjuk.
A változást V és F változók értékeivel adjuk meg. Kezdőértéküket az RND függvénnyel állítjuk elő (80-as sor). Értékük 1 vagy -1 lehet. Ezek az értékek két ütközés között nem változnak. Vizsgáljuk meg a programban, hogy melyik falnak ütközött a pont, ebből meghatározható, hogy a koordináták értékei hogyan változnak az ütközés után:

• Ütközés az oldalsó falba: X értékének a változása ellentétes lesz: V = -V.
• Ütközés az alsó vagy felső falba: Y értéke változik ellentétesen F=-F.

10 REM PATTOGO GOLYO
20 CLS: RANDOM
30 REM BAL-JOBB FAL
40 FOR I=0 TO 47: SET(0,I): SET(127,I): NEXT
50 REM ALSO-FELSO FAL
60 FOR I=0 TO 127: SET(I,0): SET(I,47): NEXT
70 REM A PONT
80 X1=RND(126): Y1=RND(46)
90 REM MOZGAS IRANY
100 V=SGN(RND(0)-0.5): F=SGN(RND(0)-0.5)
110 X=X1+V: Y=Y1+F
120 IF X=1 OR X=126 THEN V=-V
130 IF Y=1 OR Y=46 THEN F=-F
140 SET(X,Y): RESET(X1,Y1)
150 X1=X: Y1=Y: GOTO 110

Feladat:
Írjunk programot, amivel nagyobb formátumban jeleníthetjük meg a betűket! A betűket 7 soros és 5 oszlopos pontmátrixszal adjuk meg.
A programban a DATA utasítással valamilyen módon meg kell adnunk, hogy az egyes betűknél a pontmátrix melyik pontját kell megjeleníteni. A pontmátrix pontjainak megadása többféleképpen történhet. Az a mód, ahogyan az adatok adottak, meghatározza a megjelenítő eljárást is.
A programok írása adatszerkezetek kialakítását, és algoritmusok megalkotását jelenti. A két tevékenység elválaszthatatlan egymástól.

a) Jelöljük a pontmátrix pontjainak állapotát az 1 és a 0 számjegyekkel, attól függően, hogy a pont világít vagy nem!
Minden programban csak az A betűt kódoljuk. A program kiegészítése a többi betűvel már nem okozhat gondot.

10 REM BETUK-1
20 CLS: INPUT "BETU: ";B$
30 CLS: U=50: V=20
40 REM KIKERESES
50 READ X$: IF B$<>X$ THEN 50
60 REM DEKODOLAS-MEGJELENITES
70 FOR I=1 TO 7: FOR J=1 TO 5
80 READ X
90 IF X=1 THEN SET(U+J,V+I)
100 NEXT J: NEXT I
200 DATA A,0,0,1,0,0
210 DATA 0,1,0,1,0
220 DATA 1,0,0,0,1
230 DATA 1,0,0,0,1
240 DATA 1,1,1,1,1
250 DATA 1,0,0,0,1
260 DATA 1,0,0,0,1

b) A pontmátrix sorait bináris számokkal adjuk meg. A számjegyek jelzik a pontok állapotát. A szám számjegyekre történő felbontását programmal oldjuk meg. A megjelenítendő betű kérése és kikeresése az előző program szerint történik.

10 REM BETUK-2
20 CLS: INPUT "BETU: ";B$
30 CLS: U=50: V=20
40 REM KIKERESES
50 READ X$: IF B$<>X$ THEN 50
60 REM DEKODOLAS-MEGJELENITES
70 FOR I=1 TO 7
80 READ X
90 FOR J=1 TO INT(LOG(X)/LOG(10))+1
100 P=X-10*INT(X/10)
110 IF P=1 THEN SET(U+5-J,V+I)
120 X=(X-P)/10
130 NEXT J: NEXT I
140 DATA A,100,1010,10001,10001
150 DATA 11111,10001,10001

Az előző programokban mindig adott számú adatot kellett beolvasni egy betű megjelenítéséhez. Ez lehetővé tette, hogy a betűket karakterrel adhattuk meg. A következő programokban a betűk kódját kérjük. Kódjuk alapján keressük ki az adatokat. (Az "A" betű kódja: 65.)

c) Adjuk meg a DATA adatmezőben a pontmátrix azon pontjainak sor- és oszlopszámát, amelyek világítanak!
A kódszámokat úgy különböztetjük meg a világító pontok helyzetét meghatározó adatoktól, hogy azokat negatív számokkal adtuk meg. Ez jelzi a következő betűhöz tartozó adatok kezdetét.

10 REM BETUK-3
20 CLS: INPUT "KARAKTER KODJA: ";K
30 REM HELYKIJELOLES
40 CLS: U=50: V=20
50 REM KIKERESES
60 READ X: IF -X<>K THEN 60
70 REM DEKODOLAS
80 READ I: IF I<0 THEN END
85 READ J
90 SET(U+J,V+I): GOTO 80
100 DATA -65,1,3,2,2,2,4,3,1,3,5,4,1
110 DATA 4,5,5,1,5,2,5,3,5,4,5,5,6,1
120 DATA 6,5,7,1,7,5
130 DATA -66

d) A világító pontok két koordinátáját megadhatjuk egy kétszámjegyű számmal is. A számjegyek a sort és az oszlopot jelölik. A szétválasztást a program végzi.

10 REM BETUK-4
20 CLS: INPUT "KARAKTER KODJA: ";K
30 REM HELYKIJELOLES
40 CLS: U=50: V=20
50 REM KIKERESES
60 READ X: IF -X<>K THEN 60
70 REM DEKODOLAS
80 READ P: IF P<0 THEN END
90 I=INT(P/10): J=P-10*I
100 SET(U+J,V+I): GOTO 80
200 DATA -65,13,22,24,31,35,41
210 DATA 45,51,52,53,54,55,61
220 DATA 65,71,75
230 DATA -66

A karakterlánc-függvények ismeretében megírhatjuk az előző két programot úgy is, hogy a betű kódja helyett a betűket íjuk.

e) Adjuk meg soronként egy-egy decimális számmal a világító pontokat. A szám számjegyei jelezzék, hogy hányadik pont világít a sorban.

10 REM BETUK-4
20 CLS: INPUT "KARAKTER: ";B$
30 REM HELYKIJELOLES
40 CLS: U=50: V=20
50 REM KIKERESES
60 READ X$: IF X$<>B$ THEN 60
70 REM DEKODOLAS
80 FOR I=1 TO 7
90 READ S
100 T=INT(S/10): J=S-10*T
110 IF J=0 THEN 130
120 SET(U+J,V+I): S=(S-J)/10: GOTO 100
130 NEXT
140 END
150 DATA A,3,24,15,15,12345,15,15

Feladat:
Rajzoljuk ki programmal a képernyőre a SIN(2*X)/X függvényt!
A feltételek legyenek a következők:

• legyen adott annak az intervallumnak a kezdőpontja, amelyben ábrázoljuk a függvényt (X értéke);
• adjuk meg azt, hogy milyen lépésközönként ábrázoljuk a függvényt (D értéke);
• a tengelyeken két pont távolsága D értékével legyen egyenlő;
• két szomszédos pont távolsága a tengelyen azonos.

10 REM FUGGVENY
20 CLS: INPUT "KEZDOERTEK: ";X
30 INPUT "LEPESKOZ: ";D: CLS
40 REM KOORDINATA TENGELYEK
50 FOR I=0 TO 127: SET(I,24): NEXT
60 IF X>0 OR -X/D>127 THEN 90
70 FOR I=0 TO 47: SET(-X/D,I): NEXT
80 REM FUGGVENY RAJZOLAS
90 FOR I=0 TO 127
100 IF X=0 THEN 140
110 Y=SIN(2*X)/X
120 Y=-Y/D+24: Y=INT(Y+0.5)
130 IF Y>=0 AND Y<48 THEN SET(I,Y)
140 X=X+D
150 NEXT
160 IF INKEY$="" THEN 160 ELSE END

Először kirajzoljuk az X tengelyt (50-es sor) a képernyő közepére. A 60-as sorban azt vizsgáljuk, hogy ki kell-e rajzolni az Y tengelyt.
A függvény kirajzolása úgy történik, hogy X kezdőértékétől kiindulva, D lépésközönként kiszámítjuk a függvény értékét 128 helyen. Az így kapott (X,Y) koordinátájú pontokat jelenítjük meg azután a képernyő koordinátarendszerében úgy, ahogyan azt a feltételek előírják. A függvény értékét egy adott X értéknél a 100-as és a 110-es sorokban határozzuk meg. Az értelmezési tartomány vizsgálatát is ide kell számítanunk (100-as sor).
Az Y = Y/D+24 utasítással transzformáljuk a függvényt a képernyő koordinátarendszerébe, amelynek a tengelyeit X'; Y'-vel jelöltük a következő ábrán. Az Y/D transzformációval elértük azt, hogy két pont távolsága függőlegesen is az az érték legyen, mint vízszintesen.

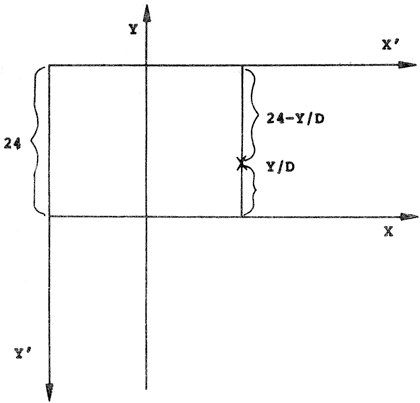
Az Y értékének kerekítésével kisebb lesz az ábrázolás hibája. A kerekítést természetesen megoldhatjuk a SET(I,Y+0.5) utasítással is.

Feladat:
Ábrázoljuk a függvényt olyan koordinátarendszerben, amelyiknek X tengelye függőlegesen helyezkedik el a képernyőn!
A PRINT utasítással rajzoljuk ki a függvényt. A függvényértéknek megfelelő karakterpozícióba egy *-ot írunk. Írógépen vagy nyomtatón történő függvényrajzolás legtöbbször ezzel a módszerrel történik.

10 K=-10: V=10: D=0.2: A=20: CLS
20 FOR X=K TO V STEP D
30 PRINT @15*64+32,".";
40 PRINT @15*64+32+SIN(2*X)*X,"*"
50 NEXT

Futtatva a programot, azt tapasztaljuk, hogy a függvényrajzolás folyamatos lesz. Az utolsó sorba íjuk a *-ot (nincs utána pontosvessző), ezután soremelés történik. A képernyő tartalma egy sorral feljebb kerül, és az utolsó sor üres marad (ide írhatjuk a következő *-ot).

Ismerkedjünk meg a grafikus karakterekkel!
Egy karakterpozíció hat (2*3) grafikus pontnak felel meg, amik egy grafikus karaktert alkotnak. A képernyő tartalma tehát három képponttal kerül feljebb, ha az utolsó sorba írunk egy karaktert, ami után soremelést hajtunk végre.

10 REM GRAFIKUS KARAKTER
20 INPUT "SOR,OSZLOP";K,L
30 V=3*K: U=2*L: CLS
40 FOR I=0 TO 2: FOR J=0 TO 1
50 READ P
60 IF P=1 THEN SET(U+J,V+I)
70 NEXT: NEXT
90 DATA 1,1,0,1,1,0

Kérdések és feladatok

1. Ismertessük a grafikus utasításokat!
2. Oldjuk meg az AND művelettel annak vizsgálatát, hogy az (X,Y) koordinátájú pont a képernyőn van-e!
3. Jelenítsünk meg a képernyőn egy ábrát, majd annak negatív képét!
4. A "pattogó golyó" ütközési szöge ne 45 fokos legyen!
5. Írjunk programot a cirill betűk megjelenítésére!
6. Ábrázoljunk más függvényeket is a tankönyv programjaival!
7. Készítsünk függvénygörbe rajzoló programokat!
   1. Ábrázoljuk a függvényt egy adott intervallumban azonos beosztású tengelyekkel!
   2. Adott értékhatárok között jelenítsük meg a függvényértékeket (A<=Y<=B)!
   3. Legyen A a legkisebb, B a legnagyobb függvényértékkel egyenlő!
8. Miért kell kerekítést végezni a megjelenítés előtt?
9. Módosítsuk a következő programot úgy, hogy kör jelenjen meg a képernyőn!

10 CLS: INPUT "HANY PONT: ";B
20 FOR X=0 TO 8*ATN(1) STEP 0.1
30 SET(64+20*COS(X)+0.5,24+B*SIN(X)+0.5)
40 NEXT
50 IF INKEY$="" THEN 50

Indexes változók

Feladat:
Tízes alapú számrendszerben adott számot alakítsunk át nyolcas alapú számrendszerbe!
Végezzünk el egy ilyen átalakítást! Legyen az átalakítandó szám 1984.

A maradékos osztás maradékai adják a nyolcas számrendszerben a szám számjegyeit. Ezeket fordított sorrendben kellene kiíratnunk, hogy megkapjuk a szám nyolcas számrendszerbeli alakját: 1984 = 3700(8)
A számjegyeket tehát tárolnunk kell, hogy a kiírást az utoljára kapott számjeggyel kezdhessük.
A maradékokat a B indexes változók értékeként őrizzük meg a B(I) = X-8*H utasítással. Az I változó értékét a programban változtatjuk, és így 1984 átszámítása a következő utasítássorozatnak felel meg:

B(0)=0: B(1)=0: B(2)=7: B(3)=3

A változó neve után zárójelben adjuk meg, hogy hányadik számjegyről van szó. Ez lesz a változó indexe.

A HT-1080Z program:

10 REM KONVERTALAS NYOLCAS SZAMRENDSZERBE
20 INPUT "SZAM: ";X
30 I=0
40 H=INT(X/8)
50 B(I)=X-8*H
60 X=H: I=I+1
70 IF X<>0 THEN GOTO 40
80 PRINT "NYOLCAS SZAMRENDSZEBEN:"
90 FOR J=I-1 TO 0 STEP -1
100 PRINT B(J);
110 NEXT

A program elején azért nem használtuk a DIM utasítást, mert 10 elem részére a rendszer mindenképpen biztosít helyet.

A Spectrum program:

10 REM KONVERTALAS NYOLCAS SZAMRENDSZERBE
15 DIM B(11)
20 INPUT "SZAM: ";X
30 LET I=1
40 LET H=INT(X/8)
50 LET B(I)=X-8*H
60 LET X=H: LET I=I+1
70 IF X<>0 THEN GOTO 40
80 PRINT "NYOLCAS SZAMRENDSZEBEN:"
90 FOR J=I-1 TO 1 STEP -1
100 PRINT B(J);
110 NEXT J

A B indexes változók értékét a program végén íratjuk ki. A változókra indexükkel hivatkozunk, tehát számokkal. A kiíró ciklus visszafelé számlál, és ezzel megadjuk az indexes változó indexeinek értékét.
Az indexek természetes számok, ezért az indexes változók értékadását tekinthetjük olyan megfeleltetésnek, amikor a természetes számokhoz rendeljük egy számsorozat elemeit. Matematikai jelöléssel a számsorozatunk:

B0=0; B1=0; B2=7; B3=3

A számsorozat elemei rendezettek, mivel a természetes számok rendezett halmazt alkotnak. Ez indokolja, hogy a B indexes változót nevezhetjük B vektornak is.

Feladat:
Adott egy N elemű számsorozat. Válasszuk ki a számsorozat legnagyobb és legkisebb elemét!
Az N darab számot beolvassuk az A vektorba. A vektor elemeire indexükkel hivatkozhatunk, amit egy változó értékeként adunk meg.
Feladatunkban egy vektor elemeit össze kell hasonlítanunk a korábban kiválasztott legnagyobb, ill. legkisebb elemmel. Ezt megoldhatjuk egy ciklussal, amivel az indexet változtatjuk.
A K és az L változó a legnagyobb, ill. a legkisebb elem indexét jelenti. Az összehasonlítás a második elemtől kezdődik, mivel a legnagyobbnak, ill. a legkisebbnek az első elemet adjuk meg. K és L változó értéke a ciklusba lépés előtt 1 lesz.
Az indexes változók értékei a memóriában egymás után helyezkednek el. A tároláshoz szükséges memóriaterületet a DIM utasítással határozzuk meg. Így adjuk meg, hogy hány elemből áll a vektor.

10 REM LEGISEBB-LEGNAGYOBB
20 INPUT "ELEMEK SZAMA: ";N
30 DIM A(N)
40 FOR I=1 TO N: INPUT A(I): NEXT I
50 LET K=1: LET L=1
60 FOR I=2 TO N
70 IF A(I)<A(K) THEN LET K=I
80 IF A(I)>A(L) THEN LET L=I
90 NEXT I
100 PRINT "LEGKISEBB: ";A(K)
110 PRINT "LEGNAGYOBB: ";A(L)

Feladat:
Írjunk programot, amivel abc sorrendbe rendezhetünk angol szavakat!
A szavak számát előre nem ismerjük. A szavak bevitelét a üres szövegfüzér bevitelével zárjuk. Feltesszük, hogy 100-nál nincs több szó. A DIM utasítással az indexhatárt 100-nak vesszük. Ezzel megadjuk az elemek maximális számát.
Karakterláncok esetében a karakterláncot alkotó karakterek számától függ, hogy mennyi hely szükséges a memóriából. Nagy pazarlás lenne, ha elemenként 255 karakter számára biztosítanánk helyet (ennyi karakterből állhat maximálisan egy karakterlánc). Egy karakter elhelyezéséhez egy memóriarekeszre van szükség. Átlagban számoljunk a programunkban 8 betűs szavakkal. Ekkor 800 rekeszre van szükségünk a szavak elhelyezésére. HT1080Z-n ezt a memóriaterületet a CLEAR 800 utasítással foglaljuk le. Ez az utasítás törli a változók értékeit is, ezért általában a program elejére írjuk.

A sorbarendezéshez a legkisebb elem kiválasztásának algoritmusát használjuk fel. Kiválasztjuk az elemek közül a legkisebbet, és azt a helyre tesszük. A külső ciklussal nem csak azt adjuk meg, hogy a legkisebb keresése hányadik indextől kezdődjön, hanem azt is, hogy hová helyezzük el a legkisebb elemet. A legkisebb elem kikeresése mindig 1-gyel nagyobb indexszel kezdődik. A korábban kiválasztott elemeket így nem vizsgáljuk:

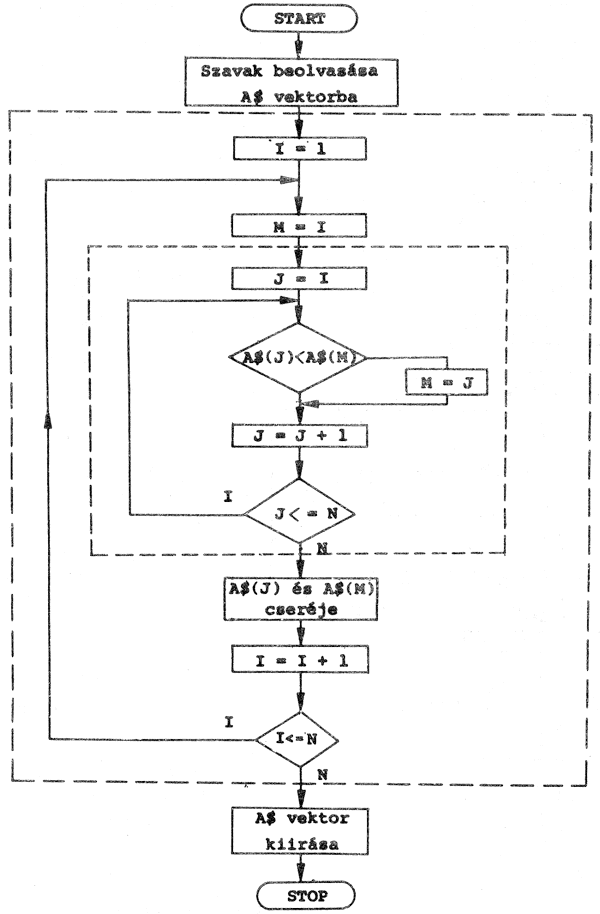
Vegyük észre, hogy a folyamatábrában szereplő két egymásba ágyazott ciklus FOR/NEXT ciklusképző utasításokkal is megoldható. Az indexeket, azaz egymás után következő természetes számokat, kell előállítanunk a ciklusokkal.

A HT-1080z program:

10 REM SORBARENDEZES
20 CLEAR 800: DIM A$(100)
30 CLS: I=1
40 REM BEOLVASAS
50 PRINT I;". NEV";:INPUT A$(I)
60 IF A$(I)<>"" THEN I=I+1: GOTO 50
70 REM RENDEZES
80 N=I-1: FOR I=1 TO N-1
90 M=I
100 FOR J=I TO N
110 IF A$(J)<A$(M) THEN M=J
120 NEXT J
130 T$=A$(M): A$(M)=A$(I): A$(I)=T$
140 NEXT I
150 REM KIIRATAS
160 FOR I=1 TO N: PRINT A$(I): NEXT

A Spectrum program:

10 REM SORBARENDEZES
20 DIM A$(100,20)
30 LET I=1
40 REM BEOLVASAS
50 PRINT I;". NEV: ";:INPUT A$(I)
60 IF A$(I,1)<>" " THEN PRINT A$(I): LET I=I+1: GOTO 50
65 PRINT
70 REM RENDEZES
80 LET N=I-1: FOR I=1 TO N-1
90 LET M=I
100 FOR J=I TO N
110 IF A$(J)<A$(M) THEN LET M=J
120 NEXT J
130 LET T$=A$(M): LET A$(M)=A$(I): LET A$(I)=T$
140 NEXT I
150 REM KIIRATAS
160 FOR I=1 TO N: PRINT A$(I): NEXT I

Feladat:
Írjunk "kockadobó" programot! Számoljuk meg a különböző értékű dobásokat! Hatféle dobás lehetséges, tehát hat változó szükséges a számláláshoz. Ezek a változók legyenek egy vektor elemei. Azt, hogy melyik változónak az értékét kell növelni, a dobás értéke adja meg. Ez lesz az index.

A HT-1080z program:

10 REM KOCKADOBAS
20 INPUT "KOCKADOBASOK SZAMA: ";N
30 RANDOM
40 FOR I=1 TO N
50 K=RND(6): A(K)=A(K)+1
60 NEXT
70 FOR I=1 TO 6: PRINT I,A(I); " DB": NEXT

A Spectrum program:

10 REM KOCKADOBAS
15 DIM A(6)
20 INPUT "KOCKADOBASOK SZAMA: ";N
30 RANDOMIZE
40 FOR I=1 TO N
50 LET K=INT(RND*6)+1: LET A(K)=A(K)+1
60 NEXT I
70 FOR I=1 TO 6: PRINT I,A(I); " db": NEXT I

Feladat:
Írjunk programot, amivel az ezernél kisebb számokat betűkkel íratjuk ki!
Olyan programot már készítettünk, amellyel a számjegyek neveit írattuk ki. Ekkor a DATA adatlistából kerestük ki a számjegyekhez tartozó karakterláncot, a számjegyek nevét.
A szavakat most is a DATA adatlistában helyezzük el, de már nem onnan történik a kikeresés. A karakterláncokat beolvassuk egy vektorba, és az index segítségével választjuk ki a megfelelő elemet. Ez az eljárás nemcsak gyorsabb, mint a kikeresés, de a program szerkezete is egyszerűbb lesz.

HT-1080Z program:

10 REM SZAMOK KIIRATASA BETUVEL
20 DIM A$(22): DIM P(3)
30 INPUT "A SZAM (<1000): ";X
40 IF X>999 THEN 30
50 FOR I=1 TO 22: READ A$(I): NEXT
60 X=1000+X
70 FOR I=1 TO 3
80 P(I)=X-10*INT (X/10)
90 X=INT(X/10)
100 NEXT
110 IF P(3)=0 THEN Z$="" ELSE Z$="SZAZ"
120 IF P(2)=0 THEN 140
130 IF P(1)=0 AND P(2)<=2 THEN P(2)=P(2)+20 ELSE P(2)=P(2)+10
140 PRINT A$(P(3));Z$;A$(P(2));A$(P(1))
150 DATA EGY,KETTO,HAROM,NEGY,OT
160 DATA HAT,HET,NYOLC,KILENC,***
170 DATA TIZEN,HUSZON,HARMINC,NEGYVEN
180 DATA OTVEN,HATVAN,HETVEN,NYOLCVAN
190 DATA KILENCVEN,***,TIZ,HUSZ

Spectrum program:

10 REM Szamok kiiratasa betuvel
20 DIM a$(22,9): DIM p(3)
30 INPUT "A szam (<1000): ",x
40 IF x>999 THEN GO TO 30
50 FOR i=1 TO 22: READ a$(i): NEXT i
60 LET x=1000+x
70 FOR i=1 TO 3
80 LET p(i)=x-10*INT (X/10)
90 LET x=INT (x/10)
100 NEXT i
110 IF p(2)<>0 AND p(1)=0 AND p(2)<=2 THEN LET p(2)=p(2)+20: GO TO 130
120 LET p(2)=p(2)+10
130 IF p(3)<>0 THEN PRINT a$(p(3));"szaz";
140 IF p(2)<>0 THEN PRINT a$(p(2));
150 PRINT a$(p(1))
160 DATA "egy","ketto","harom","negy","ot"
170 DATA "hat","het","nyolc","kilenc",""
180 DATA "tizen","huszon","harminc","negyven"
190 DATA "otven","hatvan","hetven","nyolcvan"
200 DATA "kilencven","","tiz","husz"

A számjegyeket a P vektorba helyezzük el. Az X=1000+X utasítással megoldottuk azt, hogy mindig három számjegyű számmal dolgozhatunk. Nem kell vizsgálnunk a számjegyek számát.
Az egyesek és tízesek nevein kívül gondolni kell arra is, hogy a TÍZ és HÚSZ szavakra is szükségünk van, ha az egyesek helyén 0 áll és a tízesek száma 1 vagy 2.
Mivel a HT-változatban az A$(0) változónak nem adtunk értéket, ezért 0 számjegy esetén is helyesen működik a programunk. Definiálatlan karakterlánc-változó értéke az "üres karakter".

Feladat:
Készítsünk programot, amivel meghatározhatjuk egy N tagú brigád tagjainak heti, és a brigád napi teljesítményét!
A brigád tagjainak napi teljesítményét táblázatba foglaltuk:

A tagokat sorszámukkal azonosítjuk, ugyanúgy a napokat is. A táblázat egy adatát így a sor és az oszlop sorszámával egyértelműen megadhatjuk.
A táblázat adatait a programunkban kétindexes változókban tároljuk. Ezek a kétindexes változók egy mátrixnak lesznek az elemei. A vektort egy-, a mátrixot kétdimenziós tömbnek is szokás nevezni. A táblázat adatai tehát: A(1,1), A(1,2), A(1,3) ..., kétindexes változók értékei lesznek. Az első index a sort, a második az oszlopot mutatja.
Az adatok beírása több időt vesz igénybe, mint a program futtatása, és számolnunk kell a tévedéssel is, ezért az adatokat a DATA adatlistában helyezzük el. A könnyebb áttekinthetőség céljából egy sorba csak egy munkás teljesítményét írjuk.
A beolvasás soronként történik, amit úgy is mondunk, hogy a beolvasás sorfolytonos.
A munkások heti teljesítményét a B vektorba, a brigád napi teljesítményét a C vektorba összesítjük. A sorokat, ill. az oszlopokat összegezzük.

10 REM MUNKA KIERTEKELES
20 CLS: INPUT "BRIGADLETSZAM: ";N
30 DIM A(N,5): DIM B(N): DIM C(5)
40 REM ADATBEOLVASAS
50 FOR I=1 TO N: FOR J=1 TO 5
60 READ A(I,J)
70 NEXT J: NEXT I
80 PRINT "TAGOK TELJESITMENYE"
90 FOR I=1 TO N: FOR J=1 TO 5
100 LET B(I)=B(I)+A(I,J)
110 NEXT J: PRINT I,B(I): NEXT I
120 PRINT "NAPI TELJESITMENY"
130 FOR J=1 TO 5: FOR I=1 TO N
140 LET C(J)=C(J)+A(I,J)
150 NEXT I: PRINT J,C(J): NEXT J
500 REM ADATOK
510 DATA 23,47,18,28,37
520 DATA 25,18,23,24,23

HT-1080Z-n egy DIM utasítással több tömböt is definiálhatunk, a 30-as sort így rövidíthetjük:

30 DIM A(N,5),B(N),C(5)

Feladat:
A brigád teljesítményét több héten keresztül értékeljük, és az adatokat mágnesszalagon tároljuk (HT-1080Z-n).
Állapítsuk meg a teljesítmények ismeretében, hogy a hét munkanapjain mennyire egyenletes a tagok és a brigád teljesítménye!
Ehhez a programhoz össze kell gyűjteni több hét teljesítményadatait, hogy ne kelljen újból begépelni azokat. A programot kiegészítjük egy olyan programrészlettel, amivel az adatokat mágnesszalagra íratjuk ki. A kiírás a PRINT#-1, A(I,J) utasítással történik. A # (számjel) karakter utáni számmal a perifériát jelöljük, ahová karunk: 1 - beépített magnetofon, 2 - csatlakoztatott magnetofon.

200 REM ADATOK MAGNESSZALAGRA
210 PRINT "KAPCSOLD FELVETELRE A MAGNOT"
220 PRINT "ES NYOMJ LE EGY BILLENTYUT"
230 IF INKEY$="" THEN 230
240 FOR I=1 TO N: FOR J=1 TO 5
250 PRINT #-1,A(I,J)
260 NEXT J: NEXT I

Spectrumon egy tömbváltozó kazettára mentése egyetlen utasítással megoldható:

240 SAVE "adatok" DATA a()

Gondoljunk az adatkivitel ellenőrzésére is. Olvassuk be azokat még azzal a programmal, amelyben rendelkezésünkre állnak az adatok, és így hiba esetén megismételhetjük a kiíratást.

300 REM ELLENORZES
310 PRINT "CSEVELD VISSZA A SZALAGOT ES ALLITSD LEJATSZASRA A MAGNOT!": PRINT "NYOMJ LE EGY BILLENTYUT!"
320 ON ERROR GOTO 400
330 IF INKEY$="" THEN 330
340 FOR I=1 TO N: FOR J=1 TO 5
350 INPUT #-1,X: PRINT X
360 IF INKEY$<>"" THEN ERROR 1
370 NEXT J: NEXT I
380 V$=INKEY$: IF V$="" THEN 380 ELSE IF V$="N" THEN 200 ELSE END
400 REM HIBAKEZELES
410 PRINT "KIIRATAS VAGY ELLENORZES (K-E)"
420 T$=INKEY$: IF T$="" THEN 420 ELSE IF T$="K" THEN RESUME 200 ELSE RESUME 300

A hibafigyelést a 320-as sorban az ON ERROR GOTO 400 utasítással indítjuk. A 350-es sorban az INPUT #-1,X utasítással olvassuk be az adatokat a szalagról, amiket azután a képernyőre is kiírunk, hogy ellenőrizhessük, mit olvasott be a program. Hibás adat esetén, ami adódhat a mágnesszalag hibájából, a 400-as utasítássorral folytatódik a program. Itt kezdődik a hibakezelő programrészlet. A beütött billentyűtől függően a programunk a 200-as, vagy a 300-as utasítássoron folytatódik, és az adatokat újból ellenőrizhetjük, vagy megismételhetjük a kiíratást.
A 360-as sorban hibát szimulálunk az ERROR 1 utasítással, ha lenyomunk beolvasás közben egy billentyűt. Előfordulhat, hogy a beolvasást nem elölről kezdtük, ilyenkor megszakíthatjuk a beolvasást, és beállíthatjuk újból a szalagot.

Készítsük el ezek után azt a programot, amivel a heti teljesítmények összehasonlítását végezzük!
A heti teljesítményadatokat egy háromdimenziós tömbbe olvassuk be, amelynek elemei háromindexes változók lesznek. A harmadik indexszel a heteket jelöljük. Az A(3,4,2) indexes változó értéke ezek szerint azt jelenti, hogy a 3. munkás a 2. hét 4. napján mennyit teljesített.
A mágnesszalagról az adatokat az INPUT #-1,A(I,J,K) utasítással olvassuk be. A # karakter utáni számmal azt a perifériát jelöljük, ahonnan az adatokat beolvassuk.
A tagok teljesítményét a B mátrixban, a brigád teljesítményét a C vektorban összegezzük.

10 REM TELJESITMENY A HET NAPJAIN
20 INPUT "DOLGOZOK SZAMA: ";M
30 INPUT "HETEK SZAMA: ";N
40 DIM A(N,5,M),B(N,5),C(5)
50 PRINT "ALLITSD A SZALAGOT AZ ADATO ELEJERE"
60 PRINT "ES INDITSD EL A MAGNOT!"
70 FOR K=1 TO M: FOR I=1 TO N
80 FOR J=1 TO 5
90 INPUT #-1,A(I,J,K)
100 NEXT J: NEXT I: NEXT K
110 REM OSSZEGZES
120 FOR J=1 TO 5: FOR I=1 TO N
130 FOR K=1 TO M
140 B(I,J)=B(I,J)+A(I,J,K)
150 C(J)=C(J)+A(I,J,K)
160 NEXT K: NEXT I: NEXT J
170 REM KIIRAS
180 PRINT "TAGOK TELJESITMENYE"
190 FOR I=1 TO N: FOR J=1 TO 5
200 PRINT B(I,J),
210 NEXT J: PRINT: NEXT I
220 PRINT "BRIGAD TELJESITMENYE"
230 FOR I=1 TO 5: PRINT C(I): NEXT I

Feladat:
Készítsünk programot a tíznél kisebb pozitív egész számok hatványainak kiszámítására!
A hatványok értékét a kétszeres pontosságú változókkal 16 számjegyig tudjuk meghatározni. Nagyobb számok meghatározása csak úgy lehetséges, ha a számjegyeket egy vektorban helyezzük el.
HT-1080Z-n a MEM függvény a szabad memóriarekeszek számát adja. Egy egész változó 6 memóriarekeszt foglal el. Ezt felhasználva a DIM A(MEM/6) utasítással az A vektor számára lefoglaljuk a teljes szabad memóriaterületet.
A programmal azt az algoritmust követjük, ahogyan egy többszámjegyű számot egy egyjegyű számmal szorzunk. Az AT változó tartalmazza az átvitelt, a részszorzatok tízes értékét.

A HT-1080Z program:

10 REM HATVANYOK
20 DIM A(255)
30 INPUT "AZ ALAP (<10): ";A
40 LET N=1: REM A SZAMJEGYEK SZAMA
50 LET K=0: REM A HATVANYKITEVO
60 LET A(1)=1
70 REM SZORZAS
80 LET AN=0
90 FOR I=1 TO N
100 LET A(I)=A(I)*A+AN
110 LET AN=INT (A(I)/10): LET A(I)=A(I)-10*AN
120 NEXT I
130 IF AN>0 THEN LET N=N+1: LET A(N)=AN
140 REM KIIRATAS
150 LET K=K+1: PRINT A;"^";K;" = ";
160 FOR L=N TO 1 STEP -1: PRINT A(L);: NEXT L
170 PRINT
180 IF N<255 THEN GO TO 70

Spectrum program:

10 REM HATVANYOK
20 DIM A(255)
30 INPUT "AZ ALAP (<10): ";A
40 LET N=1: REM A SZAMJEGYEK SZAMA
50 LET K=0: REM A HATVANYKITEVO
60 LET A(1)=1
70 REM SZORZAS
80 LET AN=0
90 FOR I=1 TO N
100 LET A(I)=A(I)*A+AN
110 LET AN=INT (A(I)/10): LET A(I)=A(I)-10*AN
120 NEXT I
130 IF AN>0 THEN LET N=N+1: LET A(N)=AN
140 REM KIIRATAS
150 LET K=K+1: PRINT A;"^";K;" = ";
160 IF N=1 THEN GO TO 180
170 FOR L=N TO 2 STEP -1: PRINT A(L);: NEXT L
180 PRINT A(1)
190 IF N<255 THEN GO TO 70

Az alap az A változó értéke lesz. Megkülönböztetésül, a nem indexes változókat egyszerű változóknak nevezzük. Egy programban ugyanazzal a névvel jelölhetünk egyszerű változót és különböző dimenziójű tömböket is.

Kérdések és feladatok

1. Hogyan csoportosíthatjuk a változókat?
2. Hogyan nevezzük az azonos nevű egy-, ill. kétindexes változókat?
3. Mi a DIM utasítás szerepe?
4. Készítsünk programot, amivel megszámlálhatjuk az azonos osztályzatú dolgozatok számát, és kiszámíthatjuk az osztályátlagot!
5. Határozzuk meg a primszámokat az eratosztheneszi-szita módszerével!
6. Írjunk programot, amivel egy vektor elemeit egy hellyel körbeforgathatjuk!
7. Egészítsük ki a SZAMOK KIIRASA BETŰVEL programot úgy, hogy 1000-nél nagyobb számokat is lehessen betűvel kiíratni!
8. Írjunk programot, amivel kiszámíthatjuk egy osztály tanulóinak és a tantárgyaknak az átlagát!
9. Kíséreljük meg "lóugrással" bejárni a sakktáblát! Csak oda léphetünk, ahol még nem voltunk! A lépések lehetnek véletlenszerűek, de követhetünk valamely szabályt is!
10. Készítsünk "torpedó" játékot! Véletlenszerűen elhelyezett "hajók" helyzetét kell eltalálnunk!
11. Írjunk lottószámokat előállító programot! A számokat növekvő sorrendben írassuk ki, és gondoskodjunk arról, hogy az öt szám között ne szerepeljen két egyforma!
12. Írjunk programot két 20 számjegyű, tetszőleges számrendszerbeli szám összegezésére!

Karakterláncok
A BASIC nyelvben az adatokat két csoportba soroljuk: számok és karakterláncok. A számokat numerikus adatoknak, a karakterláncokat stringeknek is nevezik.
Numerikus adatok kezelésével, az azokkal végezhető műveletekkel az aritmetikai kifejezések és az aritmetikai függvények tárgyalásakor már megismerkedtünk.
A karakterláncok olyan karaktersorozatok, amiket a képernyőn megjeleníthetünk; betűk, számjegyek, írásjelek. Az ilyen típusú adatokat karakterlánc-változókban tároljuk, amiket HT 0180Z-n a DEFSTR utasítással jelölünk ki vagy a $-jellel különböztetjük meg a numerikus változóktól.
Értelmezzük a következő programot!

10 REM KARAKTERLANCOK-1
20 LET A$="METER"
30 INPUT "MEROSZAM: ";M
40 INPUT "ELOTAG :";E$
50 PRINT M;" ";E$;A$

A mértékegység megfelelő előtagja pl. KILO, DECI vagy MIKRO, az E$, a mértékegység az A$ karakterlánc-változó értéke lesz. A hosszúságot így egy adott egységben írathatjuk ki.
A következő program ugyanezt a feladatot oldja meg HT-1080Z-n, csak a karakterlánc-változókat most a DEFSTR utasítással adjuk meg.

10 REM KARAKTERLANCOK-2
20 DEFSTR A,E
30 A="METER"
40 INPUT "MEROSZAM: ";M
50 INPUT "ELOTAG :";E
60 PRINT M;E;A

Az értékadó utasításban a karakterláncot idézőjelek közé tesszük. Idézőjelek köze írjuk a PRINT vagy az INPUT utasítással kiírandó karakterláncot is.

A karakterláncokkal műveletet is végezhetünk: kettő vagy több karakterláncot összefűzhetünk eggyé. A hosszúság egységét az első programunkban a B$ változóba írhatjuk a következő értékadó utasítással: LET B$=E$+A$.
HT1080Z-n egy karakterláncban legfeljebb 255 karakter lehet. Hosszabb karakterláncok esetén azonban már gondolnunk kell arra, hogy rendelkezésünkre álljon a tárolásához szükséges memóriaterület, amit a CLEAR utasítással biztosíthatunk.
Egy karakter egy memóriarekeszt foglal le.

Feladat:
Írjunk programot, ami tízes számrendszerben adott számokat kettes számrendszerbe ír át!
Ezt a programot indexes változókkal egyszer már megoldottuk. Az algoritmust ott írtuk le. Most a karakterláncok összefűzésével oldjuk meg azt, hogy a bináris számjegyek megfelelő sorrendben legyenek.

HT-1080Z program:

10 REM KONVERTALAS KETTES SZAMRENDSZERBE
20 INPUT "A SZAM: ";X
30 I=0: X$=""
40 H=INT(X/2): B=X-2*H
50 IF B=1 THEN B$="1" ELSE B$="0"
60 X$=B$+X$
70 X=H: IF X<>0 THEN 40
80 PRINT X$

Az X$ változóba - amelyik kezdetben "üres" volt - írjuk a biteket. A legkisebb helyértékű bitet kapjuk meg először, ezért a következőket a már meglevő számjegyek elé helyezzük (60-as sor).
Az 50-es utasítássorban a B értékéből karakterláncot állítunk elő, hogy az "összefűzést" el tudjuk végezni.
Ezt valósítja meg a STR$ karakterlánc függvény is. Ekkor az utasítássor:

50 B$=STR$(B)

Ez a függvény a B változó numerikus értékét karakterlánccá alakítja. Argumentumként kifejezés is szerepelhet, ezért a következő utasítássorok is ugyanazt az eredményt adják:

40 H=INT(X/2)
50 B$=STR$(X-2*H)

Spectrum program (az STR$ fügvény használatával):

10 REM KONVERTALAS KETTES SZAMRENDSZERBE
20 INPUT "A SZAM: ";X
30 LET I=0: LET X$=""
40 LET H=INT (X/2)
60 LET X$=STR$(X-2*H)+X$
70 LET X=H: IF X<>0 THEN GO TO 40
80 PRINT X$

A STR$ függvény inverze a VAL függvény, amivel numerikus karakterláncot tudunk numerikus adattá alakítani.

Feladat:
Állapítsuk meg program segítségével, hogy hány éves és hány hónapos az illető, ha ismerjük a személyi számát!

Megoldás HT1080Z-n: A személyi szám 2. és 3. karaktere a születési év utolsó két számjegye. Ezt a karaktert a MID$ függvénnyel "vesszük ki" a személyi számból, és átalakítjuk numerikus adattá a VAL függvénnyel, hogy számolni tudjunk vele.
A MID$ függvény argumentumában azt kell megadnunk, hogy melyik karakterláncból, és a karakterlánc hányadik karakterétől kezdődően, mennyi karaktert "veszünk ki". A "kivételt" úgy kell értelmeznünk, hogy az argumentumban szereplő karakterlánc változatlan marad:

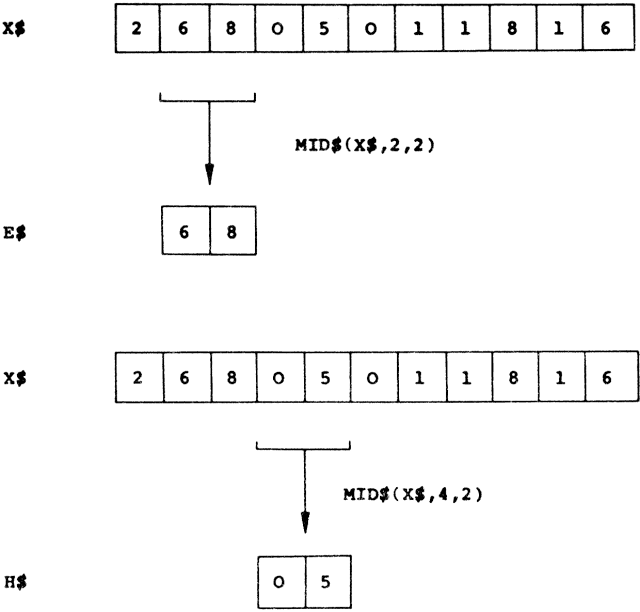
Az E$ változóba a születési év utolsó két számjegyét, a H$ változóba a születés hónapját helyezzük el.

10 REM ELETKOR
20 INPUT "FOLYO EV ES HONAP: ";A,B
30 INPUT "SZEMELYI SZAM: ";X$
40 F=A-1900
50 E=VAL(MID$(X$,2,2)): H=VAL(MID$(X$,4,2))
60 E=F-E: H=B-H
70 IF E<=0 AND H<=0 THEN PRINT "EZ NEM LEHETSEGES!": GOTO 20
80 IF H<0 THEN E=E-1: H=12+H
90 PRINT "A ";X$;" SZEMELYI SZAM TULAJDONOSA:"
100 PRINT E;"EVES ES";H;"HONAPOS."

A "kivételt" megoldhatjuk a LEFT$ és a RIGHT$ függvényekkel is. Ezekkel a függvényekkel egy karakterlánc elejéről, ill. végéről választhatunk le adott számú karaktert:

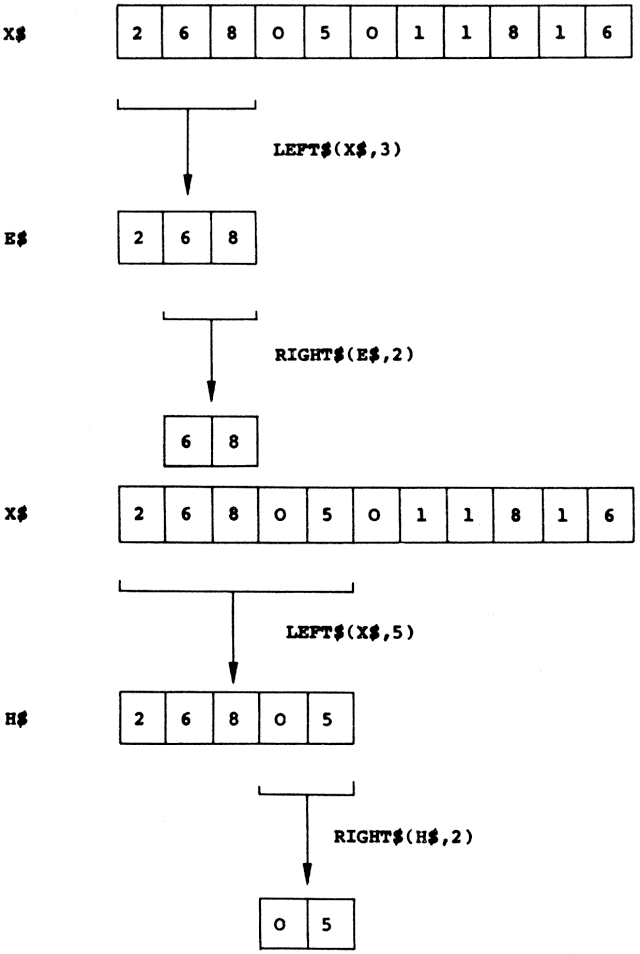
A függvények argumentumában függvények is szerepelhetnek, tehát az 50-es utasítássor helyett írhatjuk a következőket is:

50 E=VAL(RIGHT$(LEFT$(X$,3),2)): H=VAL(RIGHT$(LEFT$(X$,5),2))

vagy

45 Y$=MID$(X$,2,4)
50 E=VAL(LEFT$(Y$,2)): H=VAL(RIGHT$(Y$,2))

Megoldás Spectrumon:
Spectrumon a részstring-képzés, azaz a "kivétel" sokkal egyszerűbb, nincs szükség MID$, LEFT$, RIGHT$ függvényekre. A részstring-képzés alakja:

string-kifejezés (kezdet TO vég)

A program:

10 REM ELETKOR
20 INPUT "FOLYO EV ES HONAP: ";A;B
30 INPUT "SZEMELYI SZAM: ";X$
40 LET F=A-1900
50 LET E=VAL X$(2 TO 3): LET H=VAL X$(4 TO 5)
60 LET E=F-E: LET H=B-H
70 IF E<=0 AND H<=0 THEN PRINT "EZ NEM LEHETSEGES!": GO TO 20
80 IF H<0 THEN LET E=E-1: LET H=12+H
90 PRINT "A ";X$;" SZEMELYI SZAM": PRINT "TULAJDONOSA:"
100 PRINT E;" EVES ES ";H;" HONAPOS."

Feladat:
Írjunk programot, amivel meghatározhatjuk, hogy egy karakterláncban egy-egy betű hányszor fordul elő!

HT-1080Z program:

10 REM BETUK ELOFORDULASA
20 DIM T(26)
30 INPUT "SZOVEG: ";X$
40 FOR I=1 TO LEN(X$)
50 L=ASC(MID$(X$,I,1))-64
60 IF L>0 AND L<27 THEN T(L)=T(L)+1
70 NEXT
80 REM KIIRATAS
90 FOR I=1 TO 26
100 PRINT CHR$(64+I);" - ";T(I);" DB",
110 NEXT

Az ASC függvénnyel előállítjuk a karakterlánc karaktereinek kódját, amiből kiszámíthatjuk, hogy a karakter az abc-ben hányadik helyen áll. Ezt mutatja az L változó értéke. A T vektor L-edik elemének az értékét 1-gyel növelve, a T vektorban megkapjuk, hogy az abc betűi hányszor fordulnak elő a karakterláncban.
A LEN függvénnyel egy karakterlánc karaktereinek számát határozhatjuk meg, azaz egy karakterlánc hosszát. A LEN(X$) függvény értéke megadja, hogy hány karaktert kell kiválasztanunk a vizsgálathoz az X$ karakterláncból. A karakterek kiválasztását a MID$ függvénnyel végezzük.
A betűk előfordulásának száma mellé a CHR$ függvénnyel kiíratjuk az abc betűit is. A CHR$ függvény argumentumában szereplő 64+I kifejezés értékével az abc betűinek kódját állítjuk elő az I értékének változtatásával.
Az ASC függvény a karakterlánc első karakterének kódját adja meg, ezért az 50-es utasítássor helyett írhatjuk az

50 L=ASC(RIGHT$(X$,LEN(X$)-I+1))-64

utasítássort is.

Spectrumon az ASC függvény helyett a CODE használható ugyanarra a célra, és a programot érdemes felkészíteni a kisbetűk-nagybetűk kezelésére:

10 REM BETUK ELOFORDULASA
20 DIM T(26)
30 INPUT "SZOVEG: ";X$
40 FOR I=1 TO LEN (X$)
50 LET L=CODE X$(I TO I)-64
60 IF L>32 AND L<59 THEN LET L=L-32
70 IF L>0 AND L<27 THEN LET T(L)=T(L)+1
80 NEXT I
90 REM KIIRATAS
100 FOR I=1 TO 26
110 PRINT CHR$ (64+I);" - ";T(I);" DB",
120 NEXT I

Feladat:
Íjunk programot, amivel kiírathatjuk a karakterek kódját és a karaktereket!

10 REM KARAKTERKESZLET
20 FOR I=32 TO 255
30 PRINT I;" - ";CHR$(I),
40 NEXT I

A karaktereket kódszámaik szerint a következő csoportokra oszthatjuk:

A vezérlő karakterek ún. nem megjelenő karakterek. Kiírásukkal a képernyő állapotát, a kiíratás módját határozhatjuk meg.
A karaktereket olyan gyorsan úja ki a program, hogy nem tudjuk követni. A Spectrum minden "teleírt" oldal után megáll a "SCROLL?" kérdéssel. HT-1080Z-n a SHIFT és @ billentyűk egyszerre történő lenyomásával is megszakítható a program futása. A program végrehajtása ebben az esetben bármelyi billentyű lenyomásával folytatódik.

Feladat:
Csillag karakterekből rajzoljunk ki a képernyőre egy téglalapot HT-1080Z-n!

10 REM TEGLALAP
20 INPUT "OLDALAK: ";N,M: CLS
30 PRINT STRING$(M+2,"*")
40 FOR I=1 TO N
50 PRINT "*";CHR$(192+M);"*"
60 NEXT
70 PRINT STRING$(M+2,"*")

A STRING$ függvénnyel azonos karakterekből álló karakterláncot tudunk előállítani. Argumentumként meg kell adni a karakterlánc hosszát és a karakterek kódját. A függvény argumentumban a karakter kódja helyett írhatjuk magát a karaktert is.
A CHR$(192+M) kiírásával M darab szóköz karaktert állítunk elő.

Feladat:
Véletlenszerűen imbolyog egy tengerész a hídon? Grafikus karakterekből rajzoljuk meg a hidat és a tengerészt HT-1080Z-n!

10 REM IMBOLYGO TENGERESZ
20 CLS
30 FOR I=0 TO 63: PRINT @9*64+I,CHR$(191);: NEXT
40 RANDOM: P=32
50 Q=P+SGN(RND(0)-0.5)
60 IF Q<0 OR Q>61 THEN PRINT @11*64,"LEESETT": END
70 PRINT @7*64,TAB(Q);CHR$(178);CHR$(177);" "
80 PRINT @8*64,TAB(Q);CHR$(150);CHR$(169);" ";
90 PRINT @7*64,TAB(P);" "
100 PRINT @8*64,TAB(P);" ";
110 P=Q: GOTO 50

Kérdések és feladatok

1. Hogyan kell megadni egy karakterláncot
   a) az értékadó utasításban,
   b) az INPUT utasításnál,
   c) a DATA adatlistában?
2. Hogyan különböztetjük meg a numerikus változóktól a karakterlánc-változókat?
3. Milyen hosszú lehet egy karakterlánc?
4. Csoportosítsuk a karakterlánc-függvényeket!
   - a karakterláncról ad információt,
   - a karakterláncból új karakterláncot állít elő,
   - numerikus karakterláncokkal kapcsolatosak,
   - a karakterek és kódjaik között teremtenek kapcsolatot.
5. Hogyan lehet eldönteni egy helyesen felírt függvényről, hogy a függvényérték karakterlánc vagy numerikus adat lesz-e?
6. Milyen karakterek szerepelhetnek az STR$ függvényértékeként kapott numerikus karakterláncban a számjegyeken kívül?
7. Írjunk programot, amivel egy mondatot szavakra bonthatunk!
8. Keressük ki a háromjegyű számok közül azokat, amelyek egyenlők számjegyeik köbeinek összegével!
9. Írjunk programokat, amikkel az oszthatóságot vizsgáljuk, az oszthatósági szabályok alkalmazásával!
10. Írjunk programot annak eldöntésére, hogy egy karakterláncban megtalálható-e egy másik karakterlánc?
11. Rajzoljunk a képernyőre grafikus karakterek kiíratásával vízszintes és függőleges egyeneseket!
12. Mire használhatjuk az
    40 IF INKEY$="" THEN GOTO 40
    utasítást?
13. Állítsuk abc sorrendbe egy szó betűit!
14. Írjunk programot, amivel meghatározhatjuk, hogy egy betű hányszor szerepel egy adott szóban!
15. Rajzoljunk sakktáblát a képernyőre!

Szubrutin

Feladat:
Írunk függvénytáblázatot készítő programot! Írassuk ki a trigonometrikus függvények értékeit 0.05-os lépésközönként a 0 <= x <= PI intervallumban!
Feltételek az output-ra:

• Készítsünk fejlécet, amelyben kiírjuk a függvények neveit!
• Az X értékét és a hozzá tartozó függvényértékeket egy sorban jelentessük meg. A képernyőn egyszerre legfeljebb tíz sor legyen látható.
• A függvényértéket négy tizedesjegy pontossággal írassuk ki! A negyedik tízes legyen kerekített érték.

A program folyamatábrájában két helyen is szerepel a fejléc kiírása. Először a ciklusba lépés előtt, majd a cikluson belül, minden tizedik sor kiírása után.
A fejléc kiírása a programon belül egy részfeladat. Ezt egy szubrutinnal oldjuk meg. A szubrutin olyan részprogram, amelynek végrehajtása a GOSUB utasítás hatására kezdődik, és egy RETURN utasítás végrehajtásával fejeződik be.

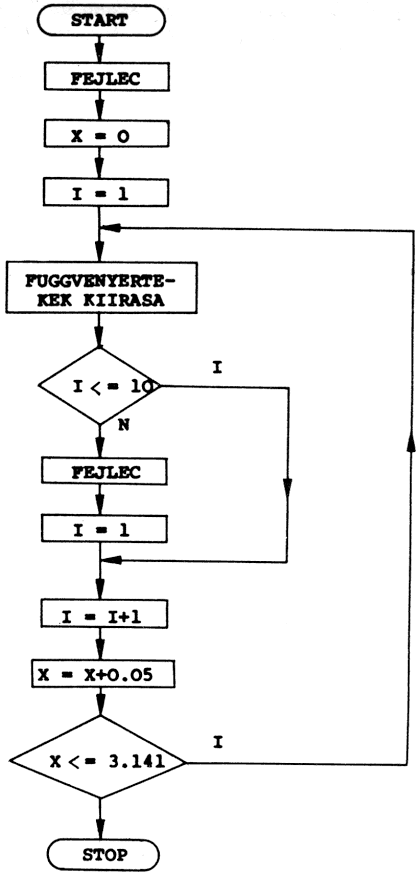
HT-1080Z program:

10 REM FUGGVENYTABLAZAT
20 GOSUB 100: REM FEJLEC
30 X=0: I=1
40 GOSUB 140: REM KIIRATAS
50 X=X+0.05: X=INT(100*X+0.5)/100: I=I+1
60 IF I<=10 THEN 80
70 IF INKEY$="" THEN 70 ELSE GOSUB 100: I=1
80 IF X<4*ATN(1) THEN 40 ELSE END
100 REM FEJLEC
110 CLS: PRINT TAB(24);"FUGGVENYTABLAZAT": PRINT
120 PRINT TAB(15);"SIN(X)";TAB(28);"COS(X)";TAB(41);"TAN(X)";TAB(53);"COSTAN(X)"
130 RETURN
140 REM FUGGVENYERTEKEK
150 PRINT "X=";X;TAB(8);
160 Y=SIN(X): GOSUB 210
170 Y=COS(X): GOSUB 210
180 IF X=2*ATN(1) THEN PRINT STRING$(7,32)+"--"; ELSE Y=TAN(X): GOSUB 210
190 Y=TAN(X): IF Y<>0 THEN Y=1/Y: GOSUB 210: PRINT ELSE PRINT STRING$(7,32)+"--"
200 RETURN
210 REM KIIRATAS
220 F$=STRING$(10-LEN(STR$(INT(ABS(Y)))),35)+".####": PRINT USING F$;Y;
230 RETURN

A fejléckiíró szubrutinunk a 140-es utasítássorral kezdődik, ezért a GOSUB 140 utasítással "hívhatjuk" a szubrutint. A szubrutin hívó utasítás hatására a 140-es utasítássoron folytatódik a program. A szubrutinban maradunk mindaddig, ameddig egy RETURN utasítás végrehajtására nem kerül sor. A RETURN utasítás után a program futása a szubrutin hívó utasítást követő utasítással folytatódik.
Összetettebb feladatokat részfeladatokra bonthatunk, és megoldásukra szubrutinokat írhatunk. A programnak azt a részét, ahonnan ezeket a részfeladatokat megoldó szubrutinokat hívjuk, főprogramnak nevezzük.
Mintaprogramunkban a főprogramból még egy szubrutint hívunk. Ez a szubrutin a függvényértékeket számítja ki, és a megadott formátumban kiírja.
A kiíratást is egy szubrutin végzi. Ennek kezdő sorszáma 210. Hívása a szubrutinból történik. Szubrutinok egymásba skatulyázásának nevezzük azt, amikor szubrutinból hívunk egy másik szubrutint. A RETURN utasítás hatására mindig az utoljára végrehajtott GOSUB utasításhoz tér vissza a program, és az azt követő utasítás végrehajtásával folytatódik.

Spectrumon a kisebb képernyőméret miatt át kell alakítani a programot:

10 REM FUGGVENYTABLAZAT
20 GO SUB 100: REM FEJLEC
30 LET X=0: LET I=1
40 GO SUB 140: REM KIIRATAS
50 LET X=X+.05: LET X=INT (100*X+0.5)/100: LET I=I+1
60 IF I<=18 THEN GO TO 80
70 IF INKEY$="" THEN GO TO 70
75 GO SUB 100: LET I=1
80 IF X<4*ATN 1 THEN GO TO 40
85 STOP
100 REM FEJLEC
110 CLS : PRINT TAB 6;"FUGGVENYTABLAZAT": PRINT
120 PRINT TAB 8;"SIN(X)";TAB 16;"COS(X)";TAB 24;"TAN(X)"
130 RETURN
140 REM FUGGVENYERTEKEK
150 PRINT "X=";X;TAB (8);
160 LET Y=SIN X: GO SUB 210: PRINT TAB 16;
170 LET Y=COS X: GO SUB 210: PRINT TAB 24;
180 IF X=2*ATN 1 THEN PRINT " --";: GO TO 190
185 LET Y=TAN X: GO SUB 210
190 PRINT
200 RETURN
210 REM KIIRATAS
220 PRINT INT (Y*10000+0.5)/10000;
230 RETURN

A szubrutin hívó utasítás alakja:

GOSUB sorszám
Jelentése: "Menj az adott sorszámmal kezdődő szubrutinra!"
Hatása: a GOSUB utasításban szereplő sorszámmal folytatódik a program egy RETURN utasítás végrehajtásáig.

Visszatérés a szubrutinból:

RETURN
Jelentése: "Térj vissza az utoljára végrehajtott GOSUB utasításhoz és a GOSUB utasítást követő utasítást hajtsd végre!"

Kész szubrutinok alkalmazásához nem elegendő az, hogy ismeijük a kezdő sorszámot. Meg kell adni, hogy milyen változókat használ a szubrutin, és azok közül melyeknek kell értéket adnunk, mielőtt kérnénk a szubrutint. Ezek lesznek a szubrutin bemenő paraméterei, amiket a főprogramban adunk meg. A szubrutin által használt változók ismerete azért szükséges, hogy ilyeneket a főprogramban ne használjunk. Ezért jelöltük ezeket ritkán használt nevekkel.
Az eddigiek alapján a szubrutinok alkalmazása a következő előnyökkel jár:

• összetett feladatot részfeladatokra lehet bontani;
• nem kell többször leírni a programban ugyanazt az utasítássorozatot, az ilyen programrészlet lehet egy szubrutin;
• kész szubrutinokat, amik valamilyen részfeladatok megoldására szolgálnak, beépíthetünk a programunkba.

Feladat:
Írjunk programot, ami N darab LOTTO szelvény kitöltéséhez ad tippet!
A program tervezését "felülről" kezdjük (felülről történő tervezés, azaz először a főprogramot írjuk meg, utána a szubrutinokat). Először a főprogramot gondoljuk át. A LOTTO számok előállítását, a számok egyezőségének vizsgálatát, és a sorba rendezett kiíratást szubrutinokkal oldjuk meg:

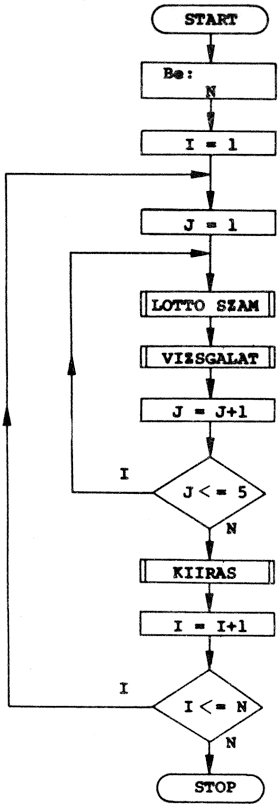
Mielőtt megírnánk a főprogramot, megtervezzük a szubrutinokat, és így alulról közelítjük meg a megoldást.
A lottószámokat az öt elemű A vektorban helyezzük el. Miután megállapítottuk, hogy ilyen szám nincs a korábban előállított számok között. A W változó értékével jelezzük, ha találtunk ugyanilyen számot:

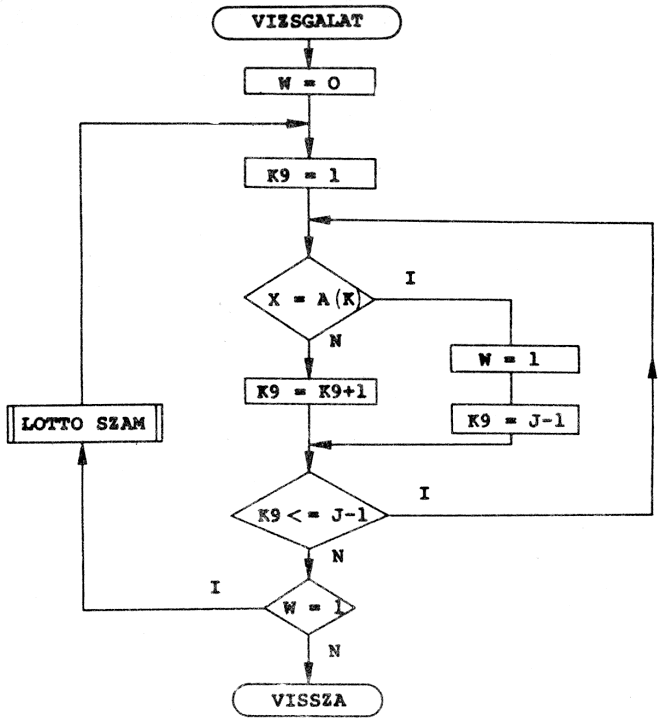
HT-1080Z program:

10 REM LOTTO SZELVENYEK
20 CLS: RANDOM
30 INPUT "SZELVENYEK SZAMA: ";N
40 FOR I=1 TO N
50 FOR J=1 TO 5
60 GOSUB 180
70 IF J<>1 THEN GOSUB 120
80 A(J)=X
90 NEXT
100 GOSUB 210: NEXT
110 END
120 REM VIZSGALAT
130 W=0: FOR K9=1 TO J-1
140 IF X=A(K9) THEN W=1: K9=J-1
150 NEXT
160 IF W=1 THEN GOSUB 180: GOTO 130
170 RETURN
180 REM LOTTOSZAM
190 X=RND(90)
200 RETURN
210 REM KIIRAS
220 V=0: FOR L=1 TO 4
230 IF A(L)>A(L+1) THEN T=A(L): A(L)=A(L+1): A(L+1)=T: V=1
240 NEXT
250 IF V=1 THEN 220
260 FOR L=1 TO 5: PRINT A(L);: NEXT
270 PRINT
280 RETURN

Spectrum program:

10 REM LOTTO SZELVENYEK
20 RANDOMIZE : DIM A(5)
30 INPUT "SZELVENYEK SZAMA: ";N
40 FOR I=1 TO N
50 FOR J=1 TO 5
60 GO SUB 180
70 IF J<>1 THEN GO SUB 120
80 LET A(J)=X
90 NEXT J
100 GO SUB 210: NEXT I
110 STOP
120 REM VIZSGALAT
130 LET W=0: FOR K=1 TO J-1
140 IF X=A(K) THEN LET W=1: LET K=J-1
150 NEXT K
160 IF W=1 THEN GO SUB 180: GO TO 130
170 RETURN
180 REM LOTTOSZAM
190 LET X=INT (RND*90)+1
200 RETURN
210 REM KIIRAS
220 LET V=0: FOR L=1 TO 4
230 IF A(L)>A(L+1) THEN LET T=A(L): LET A(L)=A(L+1): LET A(L+1)=T: LET V=1
240 NEXT L
250 IF V=1 THEN GO TO 220
260 FOR L=1 TO 5: PRINT A(L);" ";: NEXT L
270 PRINT
280 RETURN

Azonos szám előfordulása esetén előállítunk egy másik lottószámot, és a vizsgálatot kezdjük elölről.

A VIZSGALAT szubrutin kezdő sorszáma: 120

• bemenő paraméterei:
     A vektor - a lottószámok értékei,
     J - az előállított lottószámok száma;
• használt változók
     K9 - ciklusváltozó (Spectrumon: K),
     W - azonos szám előfordulásának jelzése;
• kimenő paramétere:
     X - új lottószám, amelyik a korábbiak közül egyikkel sem azonos.

A KIÍRÁS szubrutinban a lottószámokat, azaz az A vektor elemeit növekvő sorrendbe állítjuk és kiírjuk.
A sorbarendezést az ún. buborék módszerrel végezzük. (A szubrutin a 210-es sorszámmal kezdődik.) A módszer lényege az, hogy a vektor szomszédos elemeit összehasonlítjuk, és értéküket kicseréljük, ha nem megfelelő a sorrend. Kövessünk végig egy ilyen rendezést! Azt látjuk, hogy a nagyobb lottószámok a magasabb indexű változók felé "mozognak", úgy mint a buborékok.

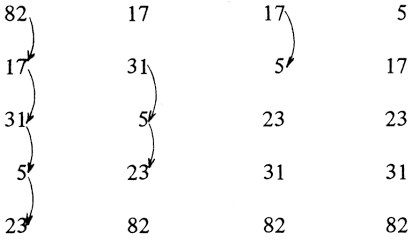
A V értéke jelzi, hogy az összehasonlítások során mikor nem történt csere. Akkor, ha nincs csere, a sorbarendezés kész.
Vegyük észre, hogy a vizsgált sorozat végén legalább egy szám biztosan a megfelelő helyre kerül. A vizsgálatot erre már nem végezzük.

A KIÍRÁS szubrutin

• bemenő paraméterei:
     A vektor - lottószámok;
• kimenő paramétere nincs;
• használt változók:
     V - csere jelzése,
     L - ciklusváltozó,
     T - átmeneti tároló.

Feladat:
Készítsünk "kockadobó" programot. A kocka oldallapjának kirajzolásával jelezzük a dobás értékét!
Az első ötlet az, hogy írunk, hat szubrutint, a hat különböző oldal kirajzolására, és a "dobás" értékének megfelelő szubrutint HT-1080Z-n az ON-GOSUB utasítással választjuk ki. Vegyük észre, hogy az oldalak rajzában azonos karakterláncok ismétlődnek. Az összes esetet figyelembe véve az oldalak kirajzolásához elegendő a következő hat rövid szubrutin:

200 PRINT "-----": RETURN
210 PRINT "!*  !": RETURN
220 PRINT "!  *!": RETURN
230 PRINT "!* *!": RETURN
240 PRINT "! * !": RETURN
250 PRINT "!   !": RETURN

A program:

10 REM DOBOKOCKA
20 RANDOM: X=RND(6)
30 GOSUB 200
40 ON X GOSUB 250,220,220,230,230,230
50 ON X GOSUB 240,250,240,250,240,230
60 ON X GOSUB 250,210,210,230,230,230
70 GOSUB 200
80 END
200 PRINT "-----": RETURN
210 PRINT "!*  !": RETURN
220 PRINT "!  *!": RETURN
230 PRINT "!* *!": RETURN
240 PRINT "! * !": RETURN
250 PRINT "!   !": RETURN

Spectrumon IF utasításokkal kell kiválasztanunk a megrajzolandó kockát:

10 REM DOBOKOCKA
20 RANDOMIZE : LET X=INT (RND*6)+1
30 GO SUB 200
40 IF X=1 THEN GO SUB 250: GO SUB 240: GO SUB 250
50 IF X=2 THEN GO SUB 220: GO SUB 250: GO SUB 210
60 IF X=3 THEN GO SUB 220: GO SUB 240: GO SUB 210
70 IF X=4 THEN GO SUB 230: GO SUB 250: GO SUB 230
80 IF X=5 THEN GO SUB 230: GO SUB 240: GO SUB 230
90 IF X=6 THEN GO SUB 230: GO SUB 230: GO SUB 230
100 GO SUB 200
110 STOP
200 PRINT "-----": RETURN
210 PRINT "!*  !": RETURN
220 PRINT "!  *!": RETURN
230 PRINT "!* *!": RETURN
240 PRINT "! * !": RETURN
250 PRINT "!   !": RETURN

Kérdések és feladatok

1. Mit nevezünk szubrutinnak?
2. Mikor ajánlott a szubrutinok használata?
3. Mit kell tudni egy kész szubrutinról, ha azt használni akarjuk a programban?
4. Általánosítsuk a sorbarendező szubrutint!
5. Miért kellett END (STOP) utasítást írnunk a főprogramok végére a szubrutinok alkalmazása esetén?
6. Írjuk meg a DOBOKOCKA programokat indexes változók alkalmazásával!
7. Írjunk szubrutint, ami meghatározza, hogy egy karakterlánc előfordul-e egy adott karakterláncban!
   bemenő paraméterek:
      O$ - az a karaktersorozat, aminek az előfordulását vizsgáljuk;
      W$ - az, amiben vizsgáljuk;
   Kimenő paraméter:
      L9 - hányadik karaktertől található W$-ben O$, L9 értéke 0, ha nem található.
8. Készítsünk programot, ami a lottószelvények kiértékelését végzi! A találatok számlálásához íjunk szubrutint!

Alkalmazási feladatok

Egy összetettebb feladat (HT-1080Z-re)
Vállalatok, üzemek gazdasági, termelési, értékesítési, ügyviteli és műszaki tevékenysége együtt jár nagy mennyiségű adat tárolásával és feldolgozásával. Ilyen jellegű feladatok megoldására kiválóan alkalmas a számítógép. Meggyorsíthatja az ügyintézést, segítheti a vállalati folyamatok irányítását és gyors információval szolgálhat a vállalati vezetés számára.

Feladat:
Használt személygépkocsik vásárlásával és eladásával foglalkozó vállalat a következő feladatokat szeretné megoldani számítógéppel:

• a forgalom időbeni alakulásáról, személygépkocsi típusonként és összesítve készítsen kimutatást;
• adott személygépkocsi típus vásárlóinak címlistáját állítsa össze;
• adott értékhatárok közé eső személygépkocsik rendszámát úja ki;
• egy adott időpontnál régebben vásárolt gépkocsikról, a vásárlások időpontjának sorrendjében adjon listát!

Mintafeladatunkkal, - az alkalmazási lehetőség bemutatásán kívül - az összetettebb programok, programrendszerek készítését megelőző, ahhoz szorosan kapcsolódó feladatokra is szeretnénk felhívni a figyelmet. Az adatok kódolása, rekordok, adatállományok kialakítása éppúgy meghatározója a készítendő programnak, mint az alkalmazott algoritmus. Mindezek megtervezéséhez, a megfelelő módszerek kiválasztásához viszont az szükséges, hogy ismerjük azt a programozási nyelvet és számítógépet, amin meg akarjuk írni a programot és amin azt futtatni szeretnénk. Ismernünk kell lehetőségeinket.
A feladat megoldása során a következő kérdésekre kell választ adnunk:

1. Milyen kimenő adatokat szeretnénk kapni?
2. Ehhez milyen bemenő adatok szükségesek?
3. Milyen számítógéppel kell megoldani a feladatot?
4. Hogyan kódoljuk az adatokat?
5. Hogyan alakítsuk ki a rekordokat, adatállományokat?
6. Hol tároljuk az adatokat?
7. Milyen műveleteket kell végezni az adatokon, rekordokon, adatállományokon?
8. Milyen algoritmust alkalmazzunk?

Az első kérdésre a feladat megfogalmazásával adtuk meg a választ. Ez egyben meghatározza azt is, hogy milyen bemenő adatokra van szükség.
A hardver feltételek ilyen feladatoknál döntőek lehetnek. Megfelelő nagyságú memória és háttértároló szükséges az adatok tárolásához. A HT-1080Z számítógép mágneslemezt és mágnesszalagot is használhat adattárolásra. Az iskolák csak az utóbbival rendelkeznek, ezért a mintafeladatban is csak ezt használjuk.

Az adatok mágnesszalagra történő kiírása és onnét azok beolvasása nagyon lassú. (A gyakorlatban csak mágneslemezzel érdemes megoldani ezt a feladatot.) Ezért az adatok elhelyezésével, a file-szerkezetek kialakításával próbálunk javítani a helyzeten.
Mágnesszalagon adatállomány csak soros szervezésű lehet. Ez azt jelenti, hogy az adatállomány i. rekordját csak úgy tudjuk beolvasni, ha előzőleg beolvastuk az előző i-1 rekordot. Célszerűnek látszik, hogy az adatállomány a gépkocsik rendszáma szerint rendezett legyen, azaz a rekordok a rendszámok növekvő sorrendjében helyezkedjenek el a szalagon.
A feladatok megoldásához szükséges adatok a következő elrendezésben alkotnak egy rekordot:

Adat	Karakterszám
Vétel    rendszám    típus kódszáma	6 2
vétel időpontja    évszám utolsó két jegye    hónap    nap	2 2 2
vételi ár eladási ár	6 6
Előző tulajdonos    neve    címe       irányítószám       helység, utca, házszám	változó + $ 4 változó + &
Eladás    eladás időpontja       évszám utolsó két jegye       hónap       nap	2 2 2
új tulajdonos       neve       címe irányítószám helység, utca, házszám	változó + * 4 változó

Az adatokat egy karakterlánccá összefűzzük, és úgy írjuk ki a szalagra. Feldolgozáskor fordított műveletet kell végeznünk: a karakterláncot fel kell bontani adatokra.
Amennyiben az adatok hosszát ismerjük, könnyű meghatározni, hogy hol helyezkedik el az, amelyiket keressük. Helytakarékosság szempontjából azonban nem érdemes minden adat hosszát rögzíteni. A változó hosszúságú adatok kezdetét vagy a végét, vagy mindkettőt valamilyen (máshol elő nem forduló) karakterrel jelöljük ($, &, * stb.). Pozíciójukat egy szubrutinnal határozzuk meg.
A rendszer alapja az a program, amivel a napi forgalom adatait rögzítjük és napra kész állapotba hozzuk a törzsadatokat tartalmazó adatállományt.
A napi adatokat, azok rendszám szerinti rendezése után, "összefésüljük" a törzsadatokkal. Ezzel az eljárással két rendezett adathalmazból egy rendezett halmazt állítunk elő.
Az adatrögzítés és a törzsadatok felújításának rendszer folyamatábrája a végrehajtandó tevékenységeket, azok sorrendjét, és az adatok mozgását írja le:

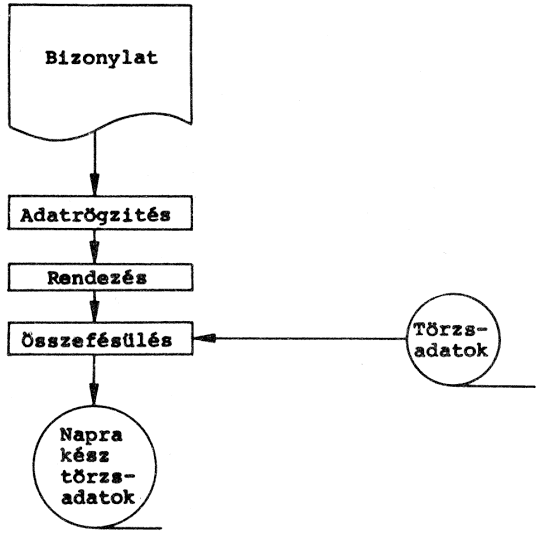
Írjuk meg az adatrögzítő programrészletet!
Az adatokat az adás-vételi szerződés alapján gépeljük be. Ez lesz a bizonylatunk. A programot úgy íjuk meg, hogy az adatok hosszára az adatrögzítőnek nem kell ügyelnie.

10 REM *** ADATROGZITES ***
20 CLS: CLEAR 5000: I=1
30 PRINT "VETEL - ELADAS - ZARAS (V, E, Z)"
40 V$=INKEY$: IF V$="E" THEN 170
50 IF V$="Z" THEN 240 ELSE IF V$<>"V" THEN 40
60 INPUT "RENDSZAM: ";R$
70 PRINT "VASARLAS IDOPONTJA"
80 GOSUB 1000: D$=X$
90 INPUT "VETELI AR: ";A: Y=A
100 GOSUB 2000: A$=Y$
110 INPUT "ELADASI AR: ";E: Y=E
120 GOSUB 2000: E$=Y$
130 GOSUB 3000: GOSUB 4000
140 IF V$="I" THEN 60
150 A$(I)="V"+R$+T$+D$+A$+E$+N$+"$"+C$+V$+"&"
160 I=I+1: GOTO 30
170 INPUT "RENDSZAM: ";R$
180 PRINT "ELADAS IDOPONTJA"
190 GOSUB 1000: D$=X$
200 PRINT "UJ TULAJDONOS": GOSUB 3000
210 GOSUB 4000: IF V$="I" THEN 60
220 A$(I)="E"+R$+D$+N$+"*"+C$+U$
230 I=I+1: GOTO 30
1000 REM *** DATUM ***
1010 INPUT "EV: 19";P: IF P>99 THEN 1010
1020 INPUT "HO: ";Q: IF Q>12 THEN 1020
1030 INPUT "NAP: ";R: IF R>31 THEN 1030
1040 X=P*1E4+Q*1E2+R: X$=STR$(X)
1050 X$=RIGHT$(X$,6)
1060 RETURN
2000 REM *** KIEGESZITES ***
2010 Y$=STR$(1E6+Y): Y$=RIGHT$(Y$,6)
2020 RETURN
3000 REM *** NEV-LAKHELY ***
3010 INPUT "TULAJDONOS NEVE"; N$
3020 INPUT "CIM - IRANYITOSZAM: ";C$
3030 INPUT "HELYSEG, UTCA, HAZSZAM: ";U$
3040 RETURN
4000 REM *** JAVITAS ***
4010 PRINT "AKAR JAVITANI (I/N)? ";
4020 V$=INKEY$: IF V$<>"I" AND V$<>"N" THEN 4020
4025 PRINT V$
4030 RETURN

Numerikus adatok karakterlánccá való átalakításakor gondolnunk kell az előjel leválasztására (1050-es és 2010-es sorok). A numerikus adatokat numerikus változók értékeként kérjük, hogy csak numerikus adatot fogadjon el a program. Ezt vizsgálja a rendszerünk.

Egészítsük ki a programot!
Rendezzük az adatokat a gépkocsik rendszáma szerint növekvő sorrendbe!

240 REM *** RENDEZES ***
250 N=I-1
260 FOR I=1 TO N-1
270 M=I: FOR J=I+1 TO N
280 IF MID$(A$(J),2,6)<MID$(A$(M),2,6) THEN M=J
290 NEXT
300 W$=A$(I): A$(I)=A$(M): A$(M)=W$
310 NEXT

Egészítsük ki a programot!
Az A$ vektor elemekből és a mágnesszalagon tárolt törzsadatokból hozzuk létre a napra kész rendezett adatállományt!
Az "összefésülés" módszerét akkor alkalmazhatjuk, ha az adathalmazok rendezettek. Ezt a feltételt elégítettük ki az adatok rendezésével.
A törzsadatokat az 1-es számú magnetofonról olvassuk be. Mindig csak egyet, és azt összehasonlítjuk az A$ vektor soron következő elemével. Azt a rekordot íratjuk ki, amelyben a rendszám kisebb. A következő rekordot onnan választjuk ezután, ahonnan a kiírt rekordot vettük. Ezt folytatjuk mindaddig, ameddig valamelyik adathalmaz végére nem érünk. Ezek után már csak azokat a rekordokat kell kiíratnunk, amelyek a másik adathalmazból megmaradtak.
Az "összefésülés" algoritmusát írja le a következő ábra:

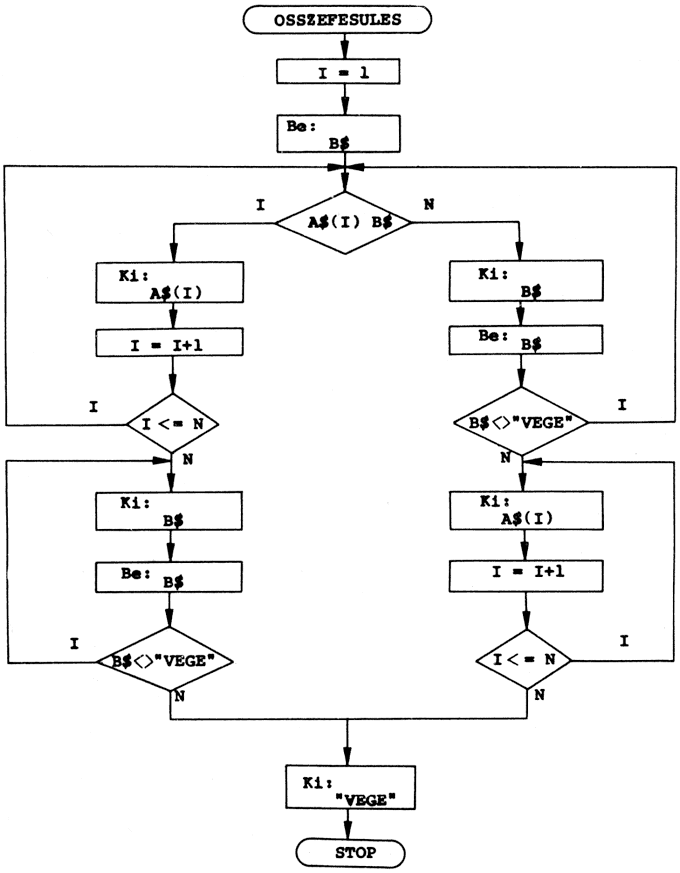
A folyamatábrában nem jelöltük a két rendszám egyenlőségének vizsgálatát. Ezt az esetet is meg kell vizsgálni, mert a gépkocsi eladásakor ez áll fenn. Mindkét adathalmazból be kell olvasni egy-egy rekordot és a két rekordot összefűzve kell kiíratnunk.
Az A$ elemének első karaktere jelzi, hogy "eladás" vagy a "vétel" rekordról van szó. Amennyiben "vétel" rekord rendszámával van egyezőség, akkor az utalhat valamilyen hibára (ismételt bevitel), de jelentheti a törzsadat módosítását is. Mi az utóbbira használjuk fel.
Egyenlőség esetén gondoljunk arra, hogy a két adatállomány végére egyszerre is érhetünk.

320 REM *** OSSZEFESULES ***
330 I=1: INPUT #-1,B$
340 IF MID$(A$(I),2,6)<>MID$(B$,1,6) THEN 410
350 Z$=RIGHT$(A$(I),LEN(A$(I))-1)
360 IF LEFT$(A$(I),1)="E" THEN PRINT #-2,B$+Z$ ELSE PRINT #-2,Z$
370 I=I+1: INPUT #-1,B$
380 IF I>N AND B$="VEGE" THN 500
390 IF I>N THEN 480
400 IF B$="VEGE" THEN 440
410 IF MID$(A$(I),2,6)<MID$(B$,1,6) THEN 460
420 PRINT #-2,B$: INPUT #-1,B$
430 IF B$<>"VEGE" THEN 340
440 PRINT #-2,A$(I)
450 I=I+1: IF I<=N THEN 440 ELSE 500
460 PRINT #-2,RIGHT$(A$(I),LEN(A$)-1)
470 I=I+1: IF I<=N THEN 340
480 PRINT #-2,B$: INPUT #-1,B$
490 IF B$<>"VEGE" THEN 480
500 PRINT #-2,"VEGE"
510 END

Miután a törzsadatok napra készen rendelkezésünkre állnak, elkészíthetjük azokat a programokat, amelyek a törzsadatok feldolgozásával bizonyos információt szolgáltatnak.

Írjunk programot, amivel adott rendszámú gépkocsi előző és jelenlegi tulajdonosainak nevét és címét kikereshetjük!
Amennyiben nem tudunk minden adatot beolvasni a memóriába, csak az a lehetőség marad, hogy sorba minden rekordot beolvasunk és mindegyiket megvizsgáljuk. Ez a megoldás nehézkes, lassú.
Tételezzük fel, hogy a törzsadatok elférnek a memóriában. Azokat a B$ vektorban helyezzük el. Legyen a vektor elemeinek száma N, akkor a megfelelő elem kikeresése a következő algoritmus szerint történhet:

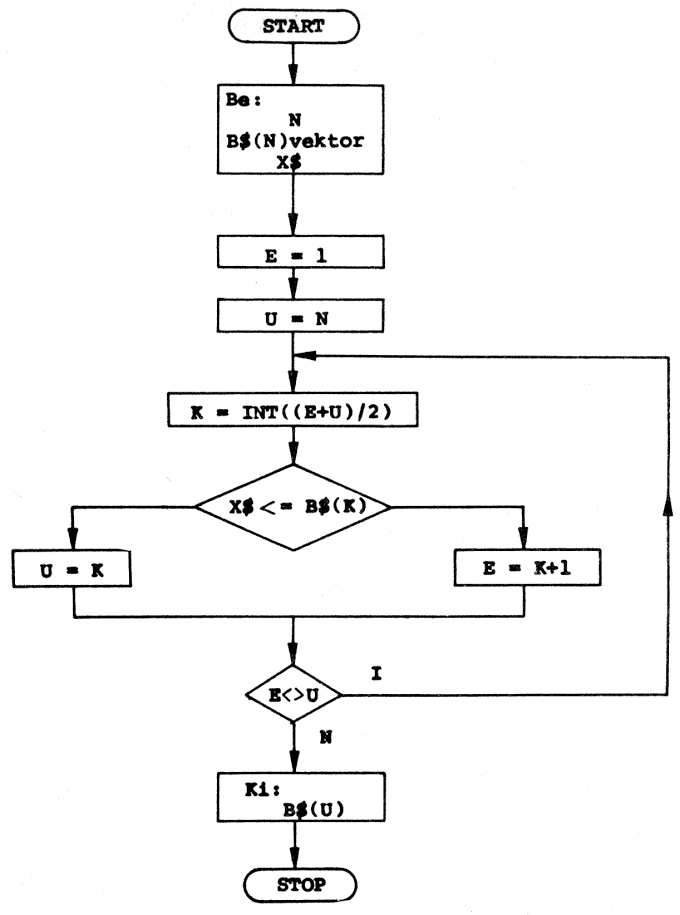
Ezt a módszert "felezéses keresésnek" nevezik. Csak rendezett adathalmazok esetén tudjuk használni ezt az eljárást.
Az algoritmus lényege: egy rendezett adathalmaz középső elemét kiválasztjuk és összehasonlítjuk a keresett értékkel. Amennyiben a középső elem kisebb vagy azzal egyenlő, akkor a keresett értéket az adathalmaz első felében, ha nagyobb, akkor a második felében kell a továbbiakban keresni. A vizsgált adathalmaz elemeinek száma minden lépésben feleződik. Amikor a halmaznak már csak egy eleme van, a keresés véget ér. Ez lesz a keresett elem.
Ezzel az eljárással mágneslemezről is kikereshetünk adatokat.

Mintafeladatunk megoldását ezzel még nem fejeztük be. Írjuk meg a többi programot is, de ezt már önállóan. A számítógépet ebben a példában egy üzlet, vállalat információs rendszerébe építettük be. A bemenő adatokat az üzlet, vállalat információs rendszerétől kapjuk és a kimenő adatokat is ott használják fel. Egészítsük ki a számítógépes információs rendszerünket további programokkal, amikkel a meglevő adatokból újabb információkhoz juthatunk!

Numerikus módszerek
A számítógépek nagy műveleti sebessége olyan matematikai módszerek alkalmazást is lehetővé teszik a gyakorlatban, amelyek nagyon sok számolást igényelnek. Azokat a matematikai eljárásokat, amelyekkel véges sok lépésben, véges sok szám meghatározásával megkapjuk az eredményt, numerikus módszereknek nevezzük.
Ebben a fejezetben olyan feladatokat oldunk meg, melyek megoldására a számítási műveletek nagy száma a jellemző. A megoldáshoz szükséges idő a számítógép műveleti sebességén kívül az algoritmustól is függ. Egy feladat megoldására általában több algoritmust ismerünk. Ezek a gyorsaságon kívül pontosságukban is különböznek egymástól. Kiválasztásukkor ezt is figyelembe kell venni.

Feladat:
Határozzuk meg az x^4 - 0.8*x^3 - 5.3*x^2 + 3.8*x + 4.8=0 egyenlet valós gyökeit 0.00001-nél kisebb hibával!
Ezt a feladatot középiskolai ismeretek alapján csak grafikusan tudnánk megoldani. Ezt a pontosságot azonban nem tudnánk elérni.
Az egyenlet valós gyökeinek adott pontosságú meghatározásához ismernünk kell azokat az intervallumokat, amelyekben az y = x^4 - 0.8*x^3 - 5.3*x^2 + 3.8*x + 4.8 függvény zérushelyei elhelyezkednek. Az intervallumok végpontjainak meghatározásához ábrázoljuk a függvényt, vagy alkalmazzuk a gyökelkülönítő programot.
A programban azt a tételt használjuk fel, ha f(a) előjele f(b) előjelével ellentétes, akkor az f(x) folytonos függvénynek biztosan van legalább egy zérushelye az (a,b) intervallumban. Lehet, hogy több zérushely is van, ezért a függvényt alaposan meg kell vizsgálni.

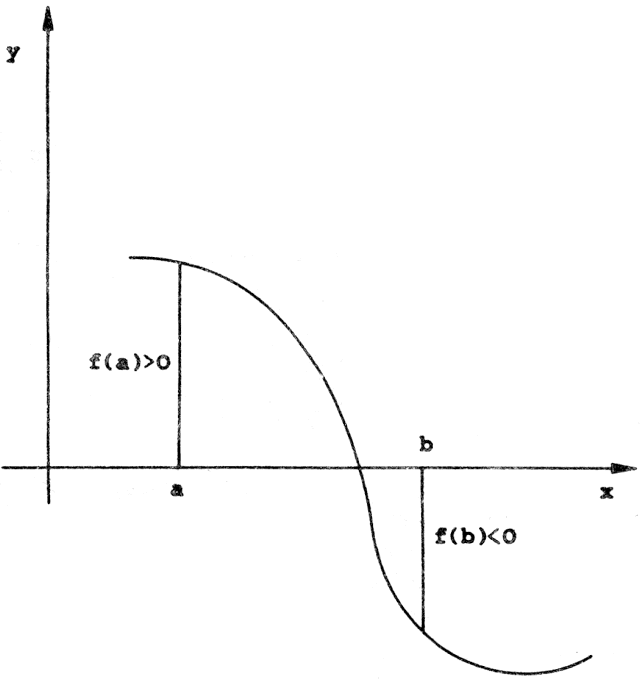
A gyökelkülönítést végző program csak segít a zérushelyeket tartalmazó intervallumok kikeresésében, de nem biztos, hogy minden zérushelyet meg tudunk így határozni.
A programmal a függvény értelmezési tartományának egy intervallumában, adott lépésközönként kiszámíthatjuk a függvényértékeket, és megvizsgáljuk, hogy két szomszédos x értékhez tartozó függvényérték szorzata milyen előjelű. Amennyiben a szorzat negatív, akkor a két x érték között biztosan létezik legalább egy zérushely.

10 REM GYOKELKULONITES
20 CLS: INPUT "KEZDOPONT: ";K
30 INPUT "VEGPONT: ";V
40 INPUT "LEPESKOZ: ";L
50 X=K: GOSUB 1000: YA=Y
60 FOR X=K+L TO V STEP L
70 GOSUB 1000: YB=Y
80 IF YA*YB<0 THEN PRINT "A=";X-L,"B=";X
90 PRINT "YA=";YA,"YB=";YB
100 YA=YB
110 NEXT
120 END
1000 REM FUGGVENY
1010 LET Y=X^4-0.8*X^3-5.3*X^2+3.8*X+4.8
1020 RETURN

A feladatban szereplő egyenlet gyökei közül kettőt találtunk meg a programmal. Ezeket a (-3, -2) és a (-1, 0) intervallumokban kell keresnünk. Azt, hogy az egyenletnek nincs több valós gyöke, csak a függvény viselkedésének ismeretében dönthetjük El. A gyökök adott pontosságú meghatározására, a gyökfinomításra, több közelítő eljárást ismerünk. Ezek közül a legegyszerűbb az ún. felezési módszer.
Legyen a függvénynek az (a, b) intervallumban egy zérushelyre. Határozzuk meg az intervallum c felezéspontját, és számítsuk ki a hozzá tartozó függvényértéket! Akkor, ha a c pont nem zérushely (ezt külön vizsgáljuk), a zérushely az (a, b) intervallum valamelyik felében van.

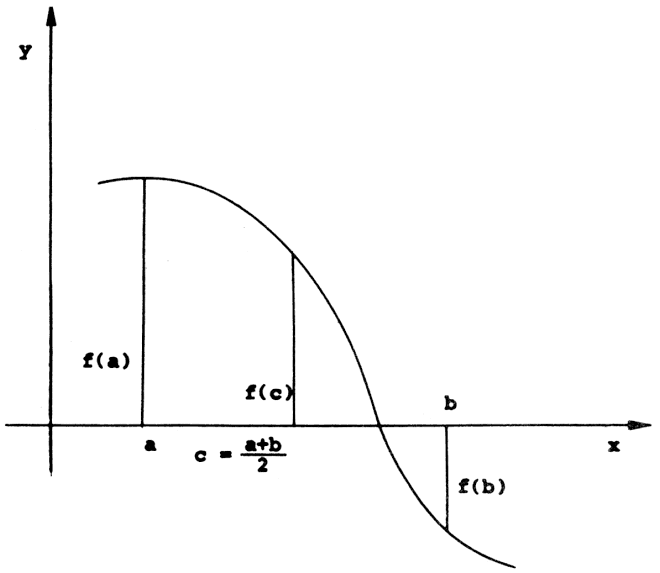
Mi azt vizsgáljuk, hogy f(a), f(c) különböző előjelűek-e, azaz f(a)*f(c) < 0 egyenlőtlenség teljesül-e. Amennyiben igen, a zérushely az (a, c) intervallumban, ha nem, akkor a (c, b) intervallumban van. A vizsgálat eredményétől függően c az új intervallum végpontja vagy kezdőpontja lesz. Kaptunk egy új, az előzőnél kisebb intervallumot, amelyiknek egyik pontja a zérushely.
Ezt az eljárást ismételjük mindaddig, ameddig az (a, b) intervallum kisebb nem lesz egy adott értéknél, a közelítés pontosságánál.
A felezési módszer folyamatábrája:

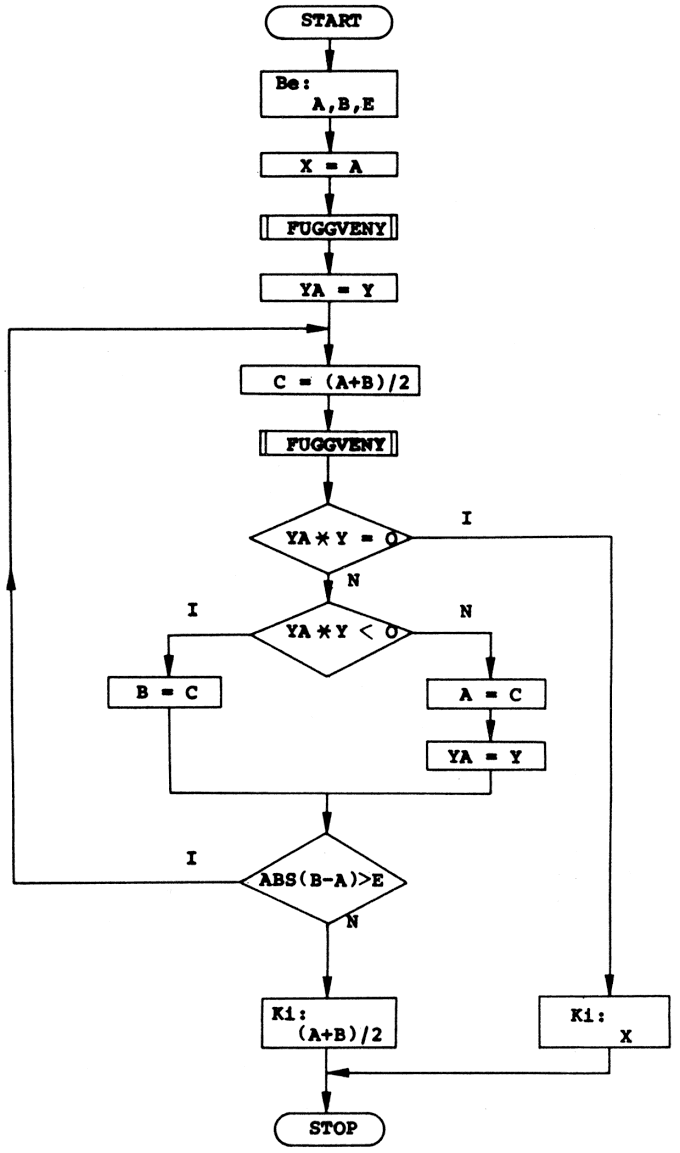
és HT-1080Z programja:

10 REM *** GYOKFINOMITAS-FELEZES ***
20 CLS: INPUT "AZ INTERVALLUM VEGPONTJAI (A<B)";A,B
30 INPUT "PONTOSSAG: ";E
40 X=A: GOSUB 1000: YA=Y
50 C=(A+B)/2: X=C: GOSUB 1000
60 IF YA*Y=0 THEN PRINT "ZERUSHELY= ";C: END
70 IF YA*Y<0 THEN B=C ELSE A=C: YA=Y
80 PRINT "A=";A,"B=";B
90 IF ABS(B-A)>E THEN GOTO 50
100 PRINT "ZERUSHELY = ";FIX((A+B)/2/E)*E: END
1000 REM *** FUGGVENY ***
1010 LET Y=X^4-0.8*X^3-5.3*X^2+3.8*X+4.8
1020 RETURN

Határozzuk meg az f(x) > 0 függvény görbéje alatti területet az [a, b] intervallum felett adott pontossággal!
Osszuk fel az [a, b] intervallumot n részre, és jelöljük az osztópontokhoz tartozó függvényértékeket. Két szomszédos osztópont xi és xi+1, valamint az A(xi,f(xi)), B(xi+1,f(xi+1)) pontok egy trapézt alkotnak. Az így megrajzolt trapézok területének összege közelítőleg a függvény görbe alatti területét adja. Ott követünk el pontatlanságot, hogy a függvény görbéje helyett egyenessel kötjük össze a függvény két pontját. Az eltérés egyre kisebb lesz, ha az n értékét növeljük.

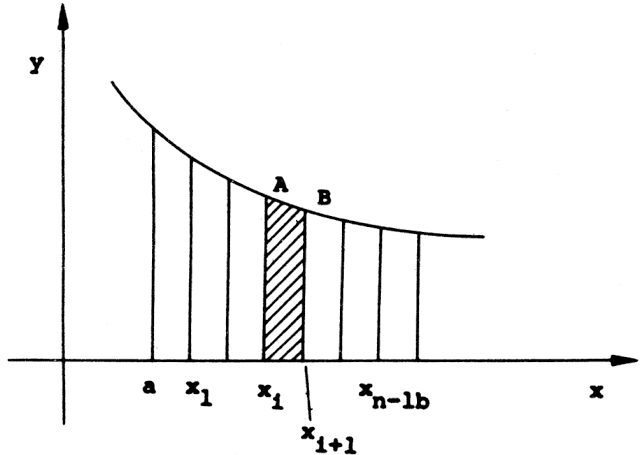
Az i. részintervallum fölé emelt trapéz területe tehát:

ahol Xi-Xi-1 a trapéz magassága.
Az [a,b] intervallumot n részre osztottuk, ezért a kis trapézokmagassága m =(b-a)/n
A trapézok területének összege tehát:

A lehetséges összevonások végrehajtása után:

Ebből már látszik, hogyan kell megírnunk a programot. A belső osztópontokhoz tartozó függvényértékek összegét kell képeznünk T értékének kiszámításához.
A beosztások számát mindig a kétszeresére növeljük, és a két egymás után kiszámított területértéket összehasonlítjuk. Amennyiben az eltérés kisebb, mint a kívánt pontosság, akkor az utolsó összeget elfogadjuk. Ez lesz a kérdéses terület adott pontosságú mérőszáma.

10 REM *** FUGGVENY GORBEJE ALATTI TERULET ***
20 INPUT "INTERVALLUM KEZDOPONTJA: ";A
30 INPUT "VEGPONTJA: ";B
40 INPUT "PONTOSSAG: ";E
50 INPUT "BEOSZTASOK SZAMA: ";N
60 LET S=0
70 LET T=0: LET D=(B-A)/N
80 LET X=A: GOSUB 160: LET T=T+Y/2
90 FOR X=A+D TO B-D STEP D
100 GOSUB 160: LET T=T+Y
110 NEXT X
120 GOSUB 160: LET T=T+Y/2: LET T=T*D
130 PRINT "N = ";N,"T = ";T
140 IF ABS(S-T)>E THEN LET S=T: LET N=2*N: GOTO 70
150 STOP
160 REM *** FUGGVENY ***
170 LET Y=1/X
180 RETURN

Kombinatorikus feladatok
Az előző fejezetben tárgyalt módszerekhez hasonlóan a kombinatorikus feladatok megoldásában is döntő az algoritmus.
Egy optimumszámítási feladatot az összes lehetséges eset előállításával oldunk meg. Az esetek száma még kis számú adat esetén is nagy. Ilyen módszerre csak számítógép alkalmazásával gondolhatunk.
A kombinatorika témakörébe tartozik ugyan ez a feladat, de annak matematikai megfogalmazásához, a rendszer matematikai modelljének megalkotásához, a programtervezéshez gráfokat és mátrixokat is alkalmazunk.

• N várost szeretnénk a legrövidebb időn belül körbejárni. A városokat összekötő utak megtételéhez szükséges időket ismerjük. Az oda és a vissza út időtartama általában nem egyenlő. Határozzuk meg a körbejárás sorrendjét!
• Helyezzük el egy NXN-es sakktáblán N bástyát úgy, hogy minden sorban csak egy bástya legyen! Írassuk ki az összes lehetséges állást!

Két, látszólag egymástól távol álló problémáról van szó. Az első feladat gyakorlati jelentősége egyértelmű. Megoldásához a második feladat algoritmusát használjuk fel, egy-két kiegészítéssel.
Legyen a sakktáblánk 3x3-as. Az első 8 állás a következő:

Vegyük észre az előállítási szabályt! A táblák mellé négyzetekbe írjuk, hogy a bástya hányadik oszlopon áll. Alulról felfelé olvasva a számokat azt látjuk, hogy mindig három egymást követő számot alkotnak a számjegyek.
Algoritmusunk tehát az, hogy a legfelső sorban elhelyezett bástyát mindig egy pozícióval jobbra toljuk. Abban az esetben, ha lekerülünk a tábláról, a bástyát az első oszlopra helyezzük, és a következő sorban lépünk eggyel jobbra. Amikor valamelyik sorban lelépünk a tábláról, mindig meg kell vizsgálnunk, hogy a következő sorban hová került a bástya. Akkor, ha a bástya a táblán van, megkaptuk a bástyák elhelyezésének egy esetét.
A táblák melletti számokkal a bástyák helyzetét egyértelműen meghatározhatjuk. Azt jelölik, hogy hányadik oszlopban állnak. Legyenek ezek az A vektor elemeinek értékei.
A(l) értékét kell növelnünk, és meg kell vizsgálnunk az A vektor elemeit, hogy az értékük nagyobb-e N-nél, ha a "sakktábla" NXN-es.
A kezdőértékek beállítása után a bástyák lehetséges elhelyezését követhetjük nyomon a következő folyamatábrán:

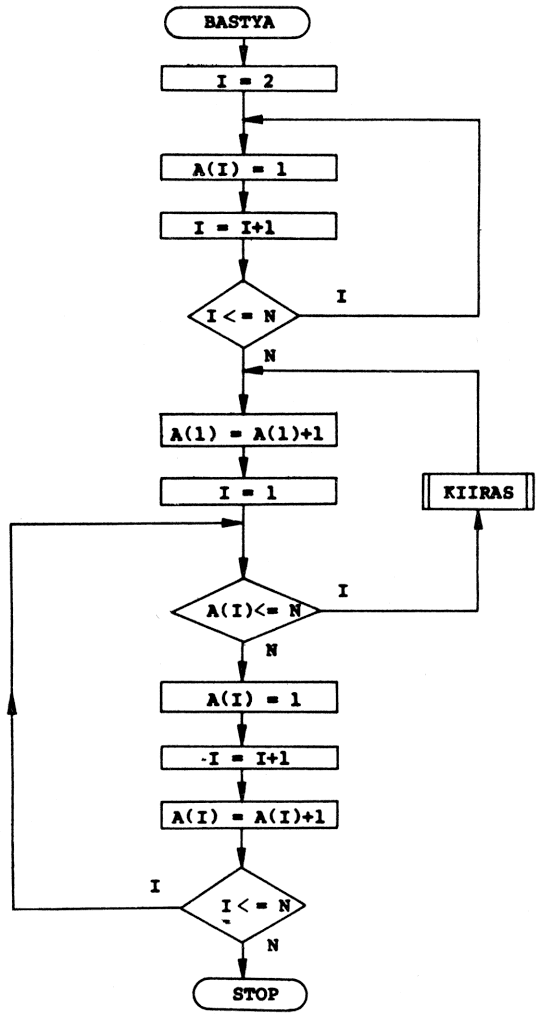
A bástyák elhelyezése akkor fejeződik be, ha I>N reláció teljesül. Az A(I)=A(I)+1 utasítás végrehajtására I=N+1 esetében is sor kerül. Ez indokolja a DIM A(N+1) utasítás használatát.

10 REM *** BASTYA ***
20 LET N=3: DIM A(N+1)
30 FOR I=2 TO N: LET A(I)=1: NEXT I
40 LET A(1)=A(1)+1
50 LET I=1
60 IF A(I)<=N THEN GOSUB 200: GOTO 40
70 LET A(I)=1: LET I=I+1: LET A(I)=A(I)+1
80 IF I<=N THEN GOTO 60
90 STOP
200 REM KIIRATAS
210 FOR L=1 TO N: PRINT A(L);: NEXT L
220 PRINT
230 RETURN

Feladat:
Helyezzük el a bástyákat úgy, hogy egyik se üsse a másikat!
Ez azt jelenti, hogy egy sorban és egy oszlopban két bástya nem lehet. Ki kell szűrnünk ezeket az állásokat, összehasonlítjuk az A vektor elemeit, és ha két elem értéke megegyezik, akkor azt az esetet nem írjuk ki. Az előbbi program kiíró szubrutinját kell módosítanunk:

200 REM KIIRATAS
210 FOR J=1 TO N-1: FOR K=J+1 TO N
220 IF A(J)=A(K) THEN RETURN
230 NEXT K: NEXT J
240 FOR L=1 TO N: PRINT A(L);: NEXT L
250 PRINT
260 RETURN

Feladat:
Négy várost és a városokat összekötő utak megtételéhez szükséges időket adjuk meg a következő ábrán:

1 2 3 4 1 0 3 2 1E3 2 6 0 3 4 3 2 4 0 5 4 1E3 3 6 0

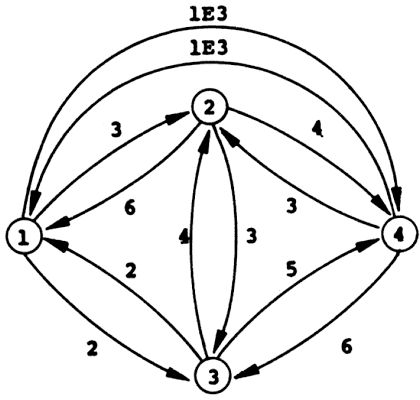Nagy időértékkel jelöljük, ha a két város között nincs út.
Határozzuk meg azt az utat, ahogyan a négy várost a legrövidebb idő alatt körbejárhatjuk!
Az időértékeket helyezzük el egy mátrixba (ld. előző kép jobb oldali táblázat).
A körutazás során minden városon egyszer haladunk át. Ezt azt jelenti, hogy egyszer megyünk be a városba, tehát minden oszlopból egyet, és egyszer jövünk ki a városból, tehát minden sorból ugyancsak egy elemet kell kiválasztanunk. Ez megfelel a bástyák olyan elrendezésének, amikor azok nem ütik egymást: A(J)=A(K).
A körutak kikeresésekor azokat az eseteket is ki kell hagynunk, amikor valamelyik elem a mátrixnak abban az átlópontjában van, amelyiknek a sor- és oszlopindexe megegyezik: A(J)=J. Ilyen elemet azért nem választhatunk, mert minden városból ki kell jönnünk.
Ugyanerre az átlóra nem lehet két kiválasztott elem szimmetrikus: A(J)=K AND A(K)=J, mert a két várost összekötő utat csak egyszer tehetjük meg.

10 REM *** KORUT ***
20 LET N=4: DIM A(N+1): DIM B(N,N)
30 REM BEOLVASAS
40 FOR I=1 TO N: FOR J=1 TO N
50 READ B(I,J)
60 NEXT J: NEXT I
70 REM KIVALASZAS
80 FOR I=2 TO N: LET A(I)=1: NEXT I
90 LET A(1)=A(1)+1
100 LET I=1
110 IF A(I)<=N THEN GOSUB 200: GOTO 90
120 LET A(I)=1: LET I=I+1: LET A(I)=A(I)+1
130 IF I<=N THEN GOTO 110
140 STOP
200 REM ELLENORZES
210 FOR J=1 TO N-1: FOR K=J+1 TO N
220 IF A(J)=J OR A(J)=A(K) OR A(J)=K AND A(K)=J THEN RETURN
230 NEXT K: NEXT J
240 REM OSSZEGZES
245 PRINT A(1);" ";
250 LET S=0: FOR L=2 TO N: LET S=S+B(A(L-1),A(L)): PRINT A(L);" ";: NEXT L
260 PRINT S
270 RETURN
300 REM ADADTOK
310 DATA 0,3,2,1E3,6,0,3,4
320 DATA 2,4,0,5,1E3,3,6,0

A feltételek teljesülését a 220-as sorban vizsgáljuk.
Az utak megtételéhez szükséges időadatokat a DATA adatlistából olvassuk be a 4x4 méretű B tömbbe, és a körutak megtételéhez szükséges időt ebből határozzuk meg.
A program kiírja az összes körutat. A legkisebb időérték kiválasztását a program kiegészítésével oldhatjuk meg.

Szimulálás
Az előző fejezetben egy "kirándulás" matematikai modelljét adtuk meg. A számítógép segítségével minden lehetséges útvonalat kipróbáltunk. Egy-egy úthossz kiírását tekinthetjük úgy is, mintha az útvonalat végigjárnánk és megmérnénk a megtett utat. A matematikai modell segítségével a bemenő adatokból kiszámítjuk az úthosszakat. Ilyenkor a modellen tesszük meg a "kirándulást", nem a valóságban. Kísérletet végzünk a modellen, hogy megfigyelhessük az eredményt, azaz az útvonalhosszakat. Ezt nevezzük szimulálásnak.
Rendszerek, jelenségek szimulálására a számítógépet igen széles körben alkalmazzák. A holdraszállás számítógépes lejátszása, kikísérletezése éppúgy szimuláció, mint a játékok.

Feladat:
v kezdősebességgel függőlegesen feldobunk egy testet. Mennyi idő múlva lesz h magasságban?
A gravitációs erőtér hatására a test egyenletesen változó mozgást végez. Az idő függvényében a test pillanatnyi helyzetét a

h=-g/2*t^2 + v*t

képlet segítségével határozhatjuk meg.
Ez lesz a függőleges hajítás matematikai modellje homogén gravitációs térben, és ha nem vesszük figyelembe a közegellenállást.
Akkor, amikor különböző magasság (h) és kezdősebesség (v) értékekhez meghatározzuk - a modell alapján - az időértékeket, tulajdonképpen egy-egy hajítást hajtunk végre. Kísérleteket végzünk a modellel. Lejátsszuk a jelenséget, azaz szimuláljuk azt!

10 REM FUGGOLEGES HAJITAS-1
20 INPUT "KEZDOSEBESSEG (M/S): ";V
30 INPUT "MAGASSAG (M): ";H
40 LET A=-9.81/2: LET B=V: LET C=-H
50 LET D=B*B-4*A*C
60 IF D<0 THEN PRINT "NEM ERI EL EZT A MAGASSAGOT.": STOP
70 LET U=-B/2/A: LET V=SQR(D)/2/A
80 PRINT "A TEST ";H;"M MAGASSAGBAN"
90 PRINT U+V; " ES ";U-V;" SEC MULVA LESZ."

Szimulációs programunkkal egy másodfokú egyenletet oldunk meg és az eredményeket, a feladatnak megfelelően értelmezzük.
A függőleges hajítást írja le a következő algoritmus is:

A test helyzetét delta t időközönként meghatározzuk. Ezalatt az idő alatt a test sebessége vk-ról vv-re változik, ha a gyorsulása a

A delta t idő alatt megtett út:

A delta t idő alatt megtett utak összege adja a test helyzetét.
A nyíllal az értékadást jeleztük.

Feladat:
Rajzoltassuk ki az előző programmal a függőlegesen feldobott test hely-idő grafikonját! (HT-1080Z-n)
A test helyzetét a program delta t időközönként kiszámítja, majd megjeleníti.

10 REM FUGGOLEGES HAJITAS-2
20 CLS
30 INPUT "KEZDOSEBESSEG (M/S): ";V
40 INPUT "IDOKOZ (S): ";DT
50 CLS: S=0: VK=V: A=-9.81: T=0
60 VV=VK+A*DT
70 DS=(VK+VV)/2*DT
80 S=S+DS: T=T+DT: VK=VV
90 IF S<0 THEN 110
100 L=L+1: IF S<47 THEN SET(L,47-S)
110 IF L<127 AND S>=0 THEN 60
120 IF INKEY$="" THEN 120 ELSE CLS

Rajzoltassuk ki a test pályáját!
A függőlegesen feldobott test egy egyenes mentén mozog, ezért csak akkor tudjuk követni a test mozgását, ha csak egy pont látható a képernyőn.

10 REM FUGGOLEGES HAJITAS-3
20 CLS
30 INPUT "KEZDOSEBESSEG (M/S): ";V
40 INPUT "IDOKOZ (S): ";DT
50 CLS: S=0: VK=V: A=-9.81: T=0
60 VV=VK+A*DT
70 DS=(VK+VV)/2*DT
80 S=S+DS: T=T+DT: VK=VV
85 IF H<47 THEN SET(60,47-H)
90 IF S<0 THEN 130
100 IF S<47 THEN SET(60,47-S)
110 IF S-DS<47 THEN RESET(60,47-S+DS)
120 GOTO 60
130 IF INKEY$="" THEN 130 ELSE CLS

Feladat:
Egy egér össze-vissza szaladgál egy labirintusban. Írjunk HT-1080Z-n programot, amivel az egér mozgását szimuláljuk!
A programmal be lehet mutatni, hogy az "egér", még ha sok lépésben is, de végül megtalálja a kijáratot.
A képernyő egy pontjának véletlenszerű mozgását, amivel az "egér" mozgását szimuláljuk, úgy valósítjuk meg, hogy mindig más szomszédos pont vizsgálatával kezdjük az útkeresést (a 130-as sortól a 180-as sorig).

10 REM BOLYONGAS A LABIRINTUSBAN
20 CLS: RANDOM: FOR I=10 TO 20
30 SET(I,10): SET(10,I): SET(I,20): SET(20,I)
40 NEXT
50 FOR I=1 TO 9
60 READ X$
70 FOR J=1 TO LEN(X$)
80 SET(10+VAL(MID$(X$,J,1)),I+10)
90 NEXT: NEXT
100 RESET(10,11)
110 X=12:Y=15
120 SET(X,Y):RESET(X1,Y1)
130 ON RND(4) GOTO 140,150,160,170
140 IF POINT(X-1,Y)=0 THEN X=X-1: GOTO 190
150 IF POINT(X,Y-1)=0 THEN Y=Y-1: GOTO 190
160 IF POINT(X+1,Y)=0 THEN X=X+1: GOTO 190
170 IF POINT(X,Y+1)=0 THEN Y=Y+1: GOTO 190
180 GOTO 140
190 RESET(X1,Y1): SET(X,Y): X1=X: Y1=Y
200 IF X<>10 THEN 120
210 DATA 4,24578,27,4578,12,4568,248,2468,6

Feladat:
Ne legyen a labirintusnak olyan elválasztható fala, amelyiket körbe lehet járni. Ilyen labirintusból úgy tudunk kijutni, hogy az egyik kezünkkel (legyen ez a bal kezünk), mindig érintjük a labirintus falát, miközben előre haladunk. "Tanítsuk meg" erre az "egeret"!
A programmal azt az algoritmust kell megfogalmaznunk, ami az egér, azaz a képernyőn megjelenő pont mozgását vezérli. Tekinthetjük az egeret egy automatának, aminek a mozgását egy programmal irányítjuk.
A szomszédos pontok vizsgálatát mindig a mozgás irányához képest balra elhelyezkedő ponttal kezdjük. K változó értéke jelzi, hogy milyen irányba indult el az "egér" K értékei: balra k = 0, fel k = 1, jobbra k = 2, le k = 3. K értéke jelzi, hogy hol kezdjük a vizsgálatot (180-as sor). A megfelelő vizsgálat kiválasztása a 110-es sorban történik, és az óramutató járásával megegyező irányban folytatódik, ha az adott irányban fal van, azaz a képernyőn a grafikus pont világít.
A program HT-1080Z-re:

10 REM KIUT A LABIRINTUSBOL
20 CLS: PRINT @2*64+7," ";: FOR I=1 TO 5: PRINT CHR$(176);: NEXT
30 PRINT CHR$(13);: FOR I=1 TO 3: PRINT STRING$(8,32);CHR$(149);CHR$(192+3);CHR$(170): NEXT
40 PRINT TAB(8);: FOR I=1 TO 5: PRINT CHR$(131);: NEXT
50 FOR J=1 TO 9
60 READ X$
70 FOR I=1 TO LEN(X$)
80 IF MID$(X$,I,1)="1" THEN SET(16+I,8+J)
90 NEXT: NEXT
100 RESET(16,9): X=22: Y=15: X1=X: Y1=X
110 SET(X,Y): ON K GOTO 130,140,150
120 IF POINT(X-1,Y)=0 THEN K=0: X=X1-1: GOTO 170
130 IF POINT(X,Y-1)=0 THEN K=1: Y=Y1-1: GOTO 170
140 IF POINT(X+1,Y)=0 THEN K=2: X=X1+1: GOTO 170
150 IF POINT(X,Y+1)=0 THEN K=3: Y=Y1+1: GOTO 170
160 GOTO 120
170 RESET(X1,Y1): X1=X: Y1=Y
180 IF K=0 THEN K=3 ELSE K=K-1
190 IF X=15 THEN PRINT @13*64,: END ELSE 110
200 DATA 01001001,010111,00000101
210 DATA 10110101,1011,0001011
220 DATA 010101,01110101,000101

Vissza