Hanoi King

1983 - Contrast Software

logikai

Spectrum (48k)

Bizonyára mindenki ismeri a Hanoi tornyai logikai- vagy pontosabban matematikai játékot. A feladat lényege, hogy a réz rúdra (1. rúd) 64 darab lyukas korong van feltéve, ezek mindegyike valamivel kisebb az alatta lévőnél. A 64 korongot át kell tenni az arany rúdra (3. rúd), de egyszerre csak egy korong mozgatható, és bármelyik korong mindig csak nála kisebb korongra tehető rá. Segítségképpen (egy mai szakember azt mondaná, pufferként) igénybe vehető az ezüstrúd (2. rúd).
A játékot 1883-ban Édouard Lucas francia matematikus "találta fel." Az ötletet egy legendából kapta, ami szerint a világ megteremtésekor egy 64 korongból álló hanoi torony feladványt kezdtek el "játszani" Brahma szerzetesei. A legenda szerint, amikor a szerzetesek végeznek majd a korongok átjuttatásával a harmadik rúdra, a kolostor összeomlik, és a világunk megszűnik létezni. A feladvány így szól a hanoi torony játékokban: Mennyi a legkevesebb szükséges lépés, amivel az első rúdról a harmadik rúdra lehet juttatni a korongokat, úgy, hogy nagyobb korongot kisebb korongra tilos mozgatni? Ma már tudjuk, hogy a szerzetesek "túl optimisták voltak", mert a feladat megoldásához 2^64-1 lépés szükséges, másodpercenként 1 áthelyezést végezve éjjel-nappal, megállás nélkül, kb. 584 milliárd év alatt végeznénk, azonban a nap várhatóan "mindössze" 5 milliárd év múlva vörös óriássá duzzad, ami mindenképen a ma ismert világunk megszűnését eredményezi.

Eme kiábrándító tény nem tántorítottal el az amúgy különösebben nívósnak nevezhető programmal nem büszkélkedhető Contrast Software-t (1983-ban adtak ki pár egyszerűbb játékot), hogy kiadjon egy amúgy praktikusan használható "korongrakosgatós" programot. A realitások talaján maradva persze csak 3-9 korongot kérhetünk. Mivel általánosan megfogalmazva n korong átrakásához 2^n-1 lépés szükséges, már a 9 korong átrakása is 511 lépést igényel, hacsak előbb bele nem zavarodunk (ami szinte bizonyos...)

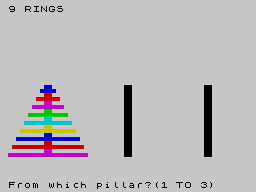A menüben válaszható lehetőségek:

  • I - INSTRUCTIONS: a játékszabályokat ismerteti.
  • P - Az előző, vagy a megszakított játékban eddig megtett lépések listázása nyomtatóra vagy képernyőre.
  • Z - AUTOMATIC REPLAY - az előző, vagy betöltött játék lépéseinek visszajátszása.
  • L - LOAD PREVIOUSLY TAPED GAME - korábban kimentett játékállás betöltése. A letölthető .TAP file "gyárilag" tartalmaz egy játékállás mentést, mely 9 korongra mutatja be a megoldást.
  • S - SAVE CURRENT POSITION - a jelenlegi játékállás kimentése.
  • E - START NEW GAME - új játék indítása.
  • ENTER - aktuális (vagy betöltött) játékállás folytatása.

A játék kezelése nagyon praktikus, csak a honnan-hova oszlopok számait kell sorban megnyomnunk (ENTER sem kell). Az R megnyomásával pedig visszaléphetünk a menübe. A feladat megoldásához itt találhatunk segítséget. A program számolja a megtett lépéseket, a játék végén, pedig külön gratulál, ha a minimális lépésszámmal sikerül megoldani a feladványt. Érdekes, bár haszontalannak tűnő funkció a pontszámtábla, melybe beírhatjuk a nevünket.