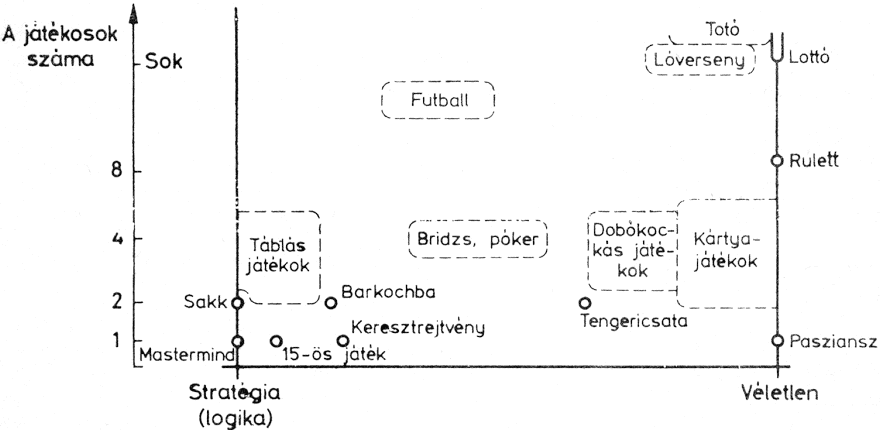
1.1. ábra: A közismert klasszikus játékok egy lehetséges csoportosítása
Játékok számítógéppel
Csákány Antal - Dr. Vajda Ferenc - 1980
Műszaki Könyvkiadó
Lektorálta: Kovács Győző, okl. villamosmérnök
E sorozat létrehozásáról a szocialista országok műszaki könyvkiadóinak VII., 1975. évi moszkvai konferenciája határozott.
A nemzetközi sorozatban részt vevő kiadók:
Műszaki Könyvkiadó, Budapest
SNTL, Nakladatelstvi Technické Literatury, Prága
Szovjetszkoje Ragyió, Moszkva
VEB Verlag Technik, Berlin
Tartalom
Előszó
Hamlethez - végzetes párviadala előtt - így szól egy udvaronc: "A király, fenség, arra fogadott, fenség, hogy ő és fenséged közötti tizenkét vímenetből ő háromnál többször nem talál, mint fenséged; ő pedig tizenkettő ellen kilencre fogadott..." - Élet és halál kérdése, ugyanakkor játék is. Tiszta szerencsejáték, vagyis az ember ősi küzdelme a mai valószínűségszámításnak, játékelméletnek, lineáris programozásnak és ki tudja még milyen tudománynak a tételeivel. Shakespeare, a szellem egyik óriása világosan utalt arra, hogy az ember még számára veszélyes helyzetekben is képes egy különleges absztrakcióra, a játékra.
Mindannyian, mindig játszunk. Néha csak egy szerep meghatározta lehetőségek között, mely szerepet például kedvelt és kevésbé szeretett rokonaink számára találunk ki, máskor azonban szinte teljesen elszakadva mindenféle realitástól színezett figurák önkényesen kitalált lépései között keresünk menedéket, új erőt.
Vannak klasszikus menedékeink - kártya, sakk, malom, dominó, rulett, lóverseny és ezernyi társuk - és vannak új eszközeink. Az autó és az atombomba mellett megjelent egy újnál is újabb, érdekesnél is érdekesebb, a számítógép. A számítógép néhány vonásában hasonlít ránk, legalábbis szeretnénk, ha hasonlítana. A számítógép is tanítható, nem meglepő tehát, ha kialakításának kezdete óta sokan fáradoznak azon, hogy a talán legemberibb időtöltésre, a játékok játszására is megtanítsák.
Nekünk is meg kell tanulnunk a számítógép minden csínját-bínját. Mindenkiben ki kell alakítani a korlátok és lehetőségek olyan érzését, hogy felszabadultan, hasznos célokra maximális hatékonysággal tudja alkalmazni. Azonban senki sem lesz hangszere mesterévé, ha a tanulás folyamata alatt csupán skálázik, vagy ha csak merev, feszes versenyműveket gyakorol. Néha kellemes melódiákat, fülbemászó dallamokat, magunkcsinálta daltöredékeket is kell gyakorolni ahhoz, hogy a hangszeren való játékban a szinte öntudatlan készség szintjét elérjük. A számítógép esetében ezeket a tudat alatti folyamatokból kialakuló kedvelt melódiákat a játékok helyettesíthetik.
Egyre több ember kerül közvetlen kapcsolatba a számítógéppel, de sokan csak a fehér köpenyt, a magas technikai és szellemi színvonalat, a társadalom megkülönböztetett figyelmét veszik észre benne. Pedig a világ jó nagyot fordult az elmúlt években: megjelentek az olcsó, személyi számítógépek is. Ezekkel majd odahaza fogunk személyi problémákat megoldani, de ami ennél fontosabb: fokozatosan megtanuljuk a számítógépek személyre szólóan "emberi" és "békés""felhasználását is. Ennek a hosszú folyamatnak válik jelentős részévé az, amint az ember a gépet valamely játékra tanítja, és ahogy ennek következtében az ember is egyre jobban "játszik".
A könyv írása során a választott téma és a szerzők kölcsönösen alakították egymást. E kölcsönhatás következtében a szerzők elálltak eredeti szándékuktól, hogy egyfajta, a játékokra vonatkozó szakácskönyvet - bevált receptgyűjteményt - adjanak az Olvasó kezébe. Világossá vált, hogy a számítógépes játékok ennél sokkal többet jelentenek. Az előző hasonlatot folytatva: feltételezzük, hogy az Olvasó az alapvető élelemfeldolgozási technológia folyamatait már ismeri, és mi különlegességeket, furcsa ízeket, szokatlan formákat próbálunk leírni számára, hogy további gasztronómiai örömök kitalálására serkentsük.
Meggyőződésünk, hogy a számítógépes játékok nem csupán játékok. Érdekes utat jelentenek mind a számítástechnika alapjainak megismeréséhez, mind pedig az alapvető emberi gondolkodási folyamatok, a helyzetfelismerés, a kombinálás, a döntés tanulmányozásához. Még egy fontos dolog (talán a legfontosabb): a játékok révén az ember nemcsak megismeri a számítógépeket, hanem meg is szereti.
A könyv megírásában sokat segítettek azok a kollégák, akik maguk is - egy vagy több - számítógépes játék jó értelemben vett megszállottjai. Köszönjük a velük lefolytatott "veszekedéseket", a játékprogramok hibáit árgus szemekkel figyelő magatartásukat. Köszönet illeti Egri Bélát szellemes karikatúráiért. Különösen sokat köszönhetünk lektorunknak, Kovács Győzőnek nem pusztán a kézirat hibáinak lelkiismeretes gyomlálásáért, hanem értő, konstruktív megjegyzéseiért.
A szerzők
"...
jó szóval oktasd, játszani is engedd szép,
komoly fiadat!"
József A.
A játék szót sokszor ellentmondó értelemben, változó hangulati töltéssel használjuk a mindennapi beszédben. Utalunk vele sporteseményekre (olimpiai játékok), használjuk lekicsinylő értelemben ("ez csak játék"), máskor pedig önfeledt csodálkozással, elismeréssel kiáltunk fel: de jó játék! Más nyelvekben is hasonló a helyzet: a játék szó tartalma nehezen körülhatárolható, jelentése eléggé változatos.
Nem lehet célunk a játékkal kapcsolatos kultúrtörténeti, pszichológiai, nyelvészeti kérdéseket taglalni. Néhány olyan megállapítást azonban nem nélkülözhetünk, amelyek az általunk használt játékfogalmat megkísérlik körülírni. Pontos definíciót nem tudunk adni azért, mert a játék klasszikus értelemben is eléggé nyitott fogalom, a számítógépekkel kombinált játék lényege, értelme, célja pedig csak most van kialakulóban. Az alábbi megállapításokat azonban nagyon lényegesnek érezzük:
A felsorolt jellemzőkön túlmenően a játékokról még nagyon sok igaz és mély dolgot lehet elmondani. Szélsőséges példának Schillert idézzük: "...a játék, és csak a játék az, amit az ember egyedül csinált". Természetesen ebben az értelemben tudatosan végzett emberi tevékenységre gondolunk, tehát elsősorban a felnőttek játékaira. A gyermekek játékai fejlődésük szempontjából igen lényegesek, indítékaik, szabályrendszerük stb. azonban a felnőttek játékától sokszor különbözik.
Az emberi játékok nagy részéhez eszközök is kellenek, dobókockák, színes kavicsok, különleges lapok stb. Ezek régmúlt idők múzeumi leletei között is fellelhetők: a fáraósírok és egyéb régészeti leletek egyértelműen utalnak arra, hogy a játékeszközök történetének szinte nincs kezdete. Napjainkban - az előző történelmi korszakokhoz képest igen hatékonyan gondolkodó és termelő ember korszakában - érdekes módon szaporodnak a játékok is. Egy-egy játékból világsiker is lehet. Jó példa erre a Monopoly (Capitaly), amelynek egy változata hazánkban is kapható "Gazdálkodj okosan" néven. A játék értékét és hasznát ne firtassuk, de csodálkozzunk el azon, hogy a játék kitalálásának 100. évfordulójára könyvek és folyóiratcikkek egész sora jelent meg, amelyek a játék igen sokrétű elemzését végzik. (Pl.: A Monopoly marxista értékelése; a Monopoly mint Markov-folyamat; A Monopoly stratégiája; A számítógépes Monopoly-játék stb.) Hasonlóképpen alig néhány év alatt az egész világon mindenhova eljutott a Mastermind nevű játék. Ha ehhez még hozzávesszük azt, hogy soha annyi sakk-készletet, kártyát stb. nem készítettek és hoztak forgalomba, mint manapság, akkor világosan láthatjuk: a játékkedv - talán részben a növekvő szabadidő következtében - ugyancsak növekszik.
A játéknak tervezett igazi játékok mellett azonban van még egy olyan motívum, mely a játékok számát állandóan növeli. Ezt röviden úgy fogalmazhatjuk meg, hogy az ember még eddig mindenből, amit előállított, játékot is csinált. Néhány példa: a kardból olimpiai versenyszám lett; a puskaporból agyaggalamblövő verseny; a velocipédből versenykerékpározás; a szuperszonikus repülőgépekből modellépítés; az autóból autóverseny és távirányítású modellek küzdelme, s így tovább szinte vég nélküli sorban. Nem kell tehát meglepődni azon, hogy a huszadik század második felének talán legnagyszerűbb termékét: a számítógépet ma már szintén a játékeszközök közé sorolhatjuk.
A számítógép azonban lényegesen eltér a technika által létrehozott elődeitől. Ennek oka univerzalitásában rejlik, vagyis abban a tényben, hogy a számítógép "számolni" és logikai műveleteket végezni azonos sebességgel, azonos feltételek mellett képes. Úgy is mondhatnánk: a számítógépben végbemenő folyamatok nagyon hasonlítanak egy, eddig kizárólag emberben létezőnek tartott készséghez, a gondolkodáshoz. A számítógép tévedéseket nem tűrő, gyors logikai képessége néha szinte "emberfelettinek" is tűnik. Nem meglepő tehát az, hogy a számítógépek létrejöttével egyidejűleg maguk a számítógépek is játékeszközökké váltak. A sokszor fáradt, de ennek ellenére lelkes szakemberek - matematikusok, mérnökök - saját szabad idejüket és persze a gépek szabad idejét sem kímélve kezdték a számítógépeket megtanítani játszani. Első lépésként meglevő, ismert, többé-kevésbé egyszerű játékokra tanították a gépeket, azzal a határozott indítékkal, hogy a gépek előbb-utóbb mindenfajta játék "mesterszintű játékosaivá" válnak. Bár ez néhány egyszerűbb játéknál már be is következett, az "igazi nagy játékok" (sakk, bridzs, póker, go stb.) még állják az ostromot; ezeket jelenleg még az emberek sikeresebben játsszák, mint a számítógépek.
Mi indítja a számítógépekhez hozzáférő szakembereket számítógépesjáték-programok írására? Elsősorban talán az a szinte kísérteties gondolat: hátha sikerül valami olyat létrehozni, ami - legalább egy szűk területen, a játék szabályrendszerében - okosabb, mint az alkotója. Persze ezt a kijelentést nem lehet egészen szó szerint értelmezni: a gép nem "tud" többet, mint az, aki programozta, de amit tud, azt tévedhetetlenül tudja, és rutinszerű műveleteket, számításokat fáradhatatlanul, nagy sebességgel végez. Számos klasszikus játék számítógépes változata már ma is olyan jó, hogy élő játékosoknak szinte nem is érdemes többé ezeket játszaniuk.
A számítógépes játékok egy csoportja azonban túlnő a közvetlen érdek nélküli szellemi tevékenység kategóriáján. A számítógépek alkalmazásának, felhasználásának nagy figyelmet vonzó területe az ún. mesterséges intelligencia kutatása. E kutatás célja az, hogy megismerjék és leírják az emberi intelligencia azon jellegzetes vonásait, amelyeket a számítógép utánozni képes. Ezek közé tartoznak a játékok is, itt tehát a játékok elemzése során az emberi gondolkodás alapvető jellegzetességeit kutatják. Ennek pedig már nagyon sok gyakorlati haszna, következménye lehet. Megérthetjük, megismerhetjük önmagunkat, miközben gondolkodásmódunk részleteit vizsgáljuk. Kis túlzással azt mondhatnánk, hogy a mesterséges intelligencia kutatása nem más, mint analitikus eszközökből építkező pszichológia. A játékok pontosan körülhatárolt volta remek lehetőséget nyújt konfliktushelyzetek vizsgálatára, a nyereséges vagy veszteséges állapotok stratégiamódosító hatásának tanulmányozására stb. (Id. a 3.3.4 pontot). A mesterséges intelligencia kutatása nagyon alapos és széles matematikai ismeretet igényel, hatalmas számítógépet, terjedelmes programokkal. Így azután nem meglepő, hogy a konferencia kiadványoknak, szakkönyveknek pl. a póker játékról írott részei nem feltétlenül jelentenek könnyen felfogható és hasznosítható információt még egy nagyon jó pókerjátékos számára sem.
1.1. A játékok csoportosítása
A játékokat nagyon sokféleképpen lehet csoportosítani. A csoportosítás során általában lényegi ismertetőjegyek alapján sorolnak különböző osztályokba dolgokat, az ismertetőjegyek választása pedig mindig valamilyen alapvető tulajdonság felismerését jelenti. Az 1.1. ábra szerint a játékok megkülönböztethetők a bennük részt vevő játékosok száma szerint, valamint aszerint, hogy milyen szerephez jut a játékban a véletlen, ill. a stratégia. A teljesen véletlenen alapuló játékok egyszemélyes változatát a fordítva lerakott kártyák előírt szabályok szerinti felemelése (pasziánsz), a sok résztvevős változatot pedig a rulett és a lottó jelenti. A lóverseny, a toto már tartalmaz (vagy tartalmazhat) bizonyos stratégiai elemeket is. A kártyajátékok többségét a véletlen uralja, a bridzs és póker azonban kivételek: itt a játékosok ügyessége is beleszól az eredménybe. Egyszemélyes - tisztán stratégiai - játék a mastermind, ehhez hasonló a 15-ös játék. A sakk kétszemélyes stratégiai játék, amelyben a véletlennek egyáltalán nincs szerepe. A táblás játékok többségén - amelyekben a játéktér geometriáját valamilyen módon kijelölik - a stratégia uralkodik. A dobókockás játékok jelentős része is táblához kötött (pl.: a ki nevet a végén), azonban ezeknél már a véletlen is szerephez jut. Az ábrán természetszerűleg nem tudtunk minden népszerű játékot feltüntetni, sőt még azt sem tudtuk jelölni, hogy bizonyos játékoknál az érdekek száma nem egyezik meg a játékosok számával. (A bridzs pl. négyszemélyes játék, de csak két érdekeltségű; a futballt 22 személy játssza és szintén két érdekeltségű stb.).

1.1. ábra: A közismert klasszikus játékok egy lehetséges csoportosítása
Míg az 1.1. ábra a klasszikus játékok csoportosítását mutatja, addig az 1.2. ábrán a számítógépes játékok nagyvonalú osztályozását láthatjuk.
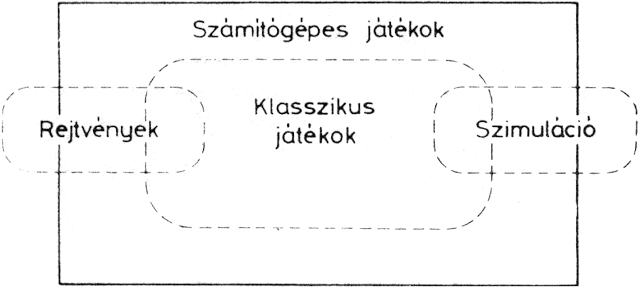
1.2. ábra: Szinte kimerírhetetlen lelőhelyek a számítógépes játékokhoz
Eszerint a számítógépes játékok fogalmába beletartoznak a klasszikus, ill. az azokhoz hasonló, számítógéppel játszható játékok, a rejtvények, valamint a számítógép különleges lehetőségein nyugvó szimulációs játékok. A rejtvények általában egyszemélyes időtöltések és az esetek többségében egyértelmű megoldásúak. Ha a megoldást a játékos megkeresi vagy megtudja, akkor érdeklődése általában megszűnik. Persze kivételek is vannak: egy-egy jól sikerült rejtvény hosszan élhet. Pl. az 1.3. ábrán látható feladvány: a fehér és fekete lovak helyzetét kell a lehető legkevesebb lépéssel megkeresni. A lovak a sakkjáték szabályai szerint léphetnek. Egy kockán csak egy ló lehet. A feladvány megjelenésekor (1974-ben) triviálisnak és 26 lépésben megoldhatónak tűnt. Azóta találtak rá megoldást 18, sőt újabban 16 lépésben is, és nincs bizonyítva, hogy ennél kevesebb lépés nem elegendő.
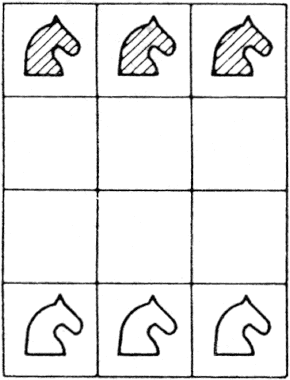
1.3. ábra: Hány lóugrással lehet a fekete és fehér lovak helyét felcserélni?
A számítógépek egyik igen fontos alkalmazási területe a szimuláció. Ha egy folyamat elemei, valamint a közöttük levő kapcsolatok ismertek, akkor szinte mindig készíthető felhasználásukkal számítógépes szimulációs modell (program), vagyis a számítógép "úgy viselkedik", mintha benne a kérdéses folyamat zajlana le. Ez sok játékra nyújt módot: autóversenyt, űrhajóleszállást, ökológiai rendszert, pilótafülkét stb. modellezve élő játékosok versenyezhetnek egymással, megismerve egy-egy bonyolult rendszer nehezen áttekinthető viszonyait (ld. a 4. és az 5. fejezetet).
Meg kell vizsgálnunk a számítógépeknek a különböző játékokban betöltött szerepét is. A legalacsonyabb szintű számítógép-alkalmazásban a számítógép ügyel a játék szabályainak betartására; felszólítja az egyes játékosokat a lépések megtételére; elvégzi a könyvelést, vagyis rögzíti a téteket, nyereményeket, veszteségeket; kiértékeli a végeredményt, megállapítja a helyezési sorrendet, tehát röviden: elvégzi a játékkal kapcsolatos adminisztratív munkát. A következő szintet az jelenti, amikor a számítógép a játék szabályainak és a játék helyzetének ismeretében meghatározza a következő lépést, és ezt közli az élő játékossal, aki ezt elemzi, elfogadja vagy elveti. Itt a számítógép amolyan tanácsadó szerepet tölt be. A számítógép legmagasabb szintű tevékenysége az, amikor egy (vagy több) élő játékost teljes mértékben helyettesít, vagyis aktívan játszik. Természetesen itt is lehetnek fokozatok: a kezdőtől a mesterszintű játékosig minden előfordulhat.
Az előzőek összefoglalását az 1.4. ábrán találjuk meg. A játéktípustól és a számítógép szerepétől függően megkülönböztethető esetekre közlünk itt olyan példákat, amelyeket a könyvben részletesen ismertetünk.
A számítógép |
|||
adminisztrál |
tanácsadó |
aktív játékos |
|
| Rejtvény | Életjáték |
15-ös játék |
Bűvös négyzet |
| Játék | Rulett |
Go |
Sakk |
| Szimuláció | Gazdasági játékok |
Holdraszállás |
Star-Trek |
Röviden le kell írnunk azt is, hogy az egyes játékok elemzése során milyen fogalmakat használunk, ill. a játékokról milyen általános képet tételezünk fel. Ezek a fogalmak, képek részben maguktól értetődőek, részben azonban magyarázatot igényelnek. Magyarázatukat a játékelmélet igen bőséges irodalmában találjuk meg.
A játék lépések sorozatából áll. A játékosok lépéseiket általában valamilyen stratégia alapján választják. A stratégia azon szabályok együttese, amelyek alapján a játékos a rendelkezésére álló lehetőségek között úgy választ, hogy a játékot megnyerje, vagy nagy (az elérhető legnagyobb) nyereségre tegyen szert. Ha a játék szabályai pontosan ismertek, a játék megoldásának a játékelmélet szempontjából azt tekintjük, ha matematikailag pontosan megfogalmazható az egyes játékosok által követendő stratégia.
A nyereségmátrix ismeretében ez egyszerű feladat. Az 1.5. ábrán az A és B játékosok választanak egymástól függetlenül tetszőlegesen 1...3, ill. 1...4 közötti számot. Amikor e számok ismertté válnak, a nyereségmátrix megfelelő sorában és oszlopában levő összeget fizeti B játékos az A játékosnak. Az ábrán megadott mátrix alapján B mindig veszít, de gondolkodhat azon, hogy veszteségét minimalizálja. Ha végignéztük, hogy a B által választható lépések (oszlopok) maximumértékei közül melyiknek az értéke minimális, akkor kitűnik, hogy B-nek a 2. értéket kell választania. A játékos szempontjából - aki nyereségének maximalizálására törekszik - célszerű a sorminimumok maximumát választani. Ennek a butácska alig-játéknak a stratégiája tehát viszonylag könnyen megfogalmazható. Természetesen vannak olyan kifizető mátrixok, amelyeknél a stratégia már jóval összetettebb. Példaképpen a "snóbli" játékra utalunk (ld. 3.2.1. pontot).
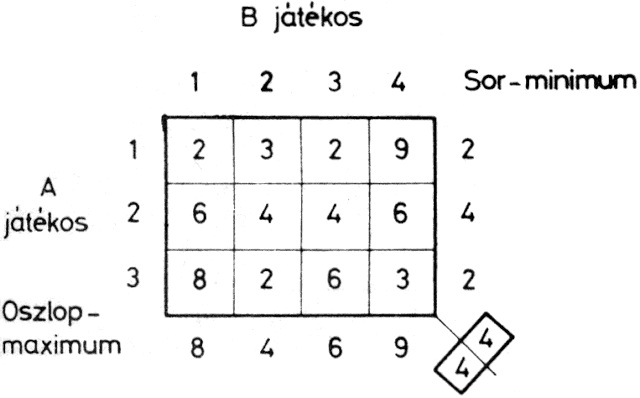
1.5. ábra: Nyereségmátrix
ha a B játékos hármat választ, az A játékos pedig kettőt, akkor B két egységnyi összeget fizet A-nak
A diszkrét helyzetek sorozatából álló játékok reprezentációjára állapot-diagramot készíthetünk. Ily módon ábrázolható játék nagyon sok van: a táblás játékok szinte kivétel nélkül, továbbá a nim, Hanoi tornyai stb. Az 1.6. ábrán egy fiktív játék menetét ábrázoltuk, amelyben az A és a B játékos lehetséges helyzeteit körökkel, ill. négyzetekkel jelöltük. A játék végállapotait téglalapok jelzik, bennük a kifizetésre kerülő összeggel. Próbáljuk ezt a játékot "megoldani". Az a helyzetben a B játékosnak két lehetséges lépése van (-2, 0), ha az ő célja a kifizetés maximálása, akkor részére előnyösebb a 0 értékű téglalap elérése. Az a négyzetbe tehát beírhatjuk a 0 értéket, mert B számára ez az állapot "ennyit ér". A b-vel jelzett kör vizsgálata az A játékos szempontjából -2 értékű, a c-vel jelölt négyzet 0 értékű stb., vagyis az egész állapotdiagram ellátható számokkal, természetesen a kezdőhelyzet is. E számok követése jelenti a stratégiát mindkét játékos számára.
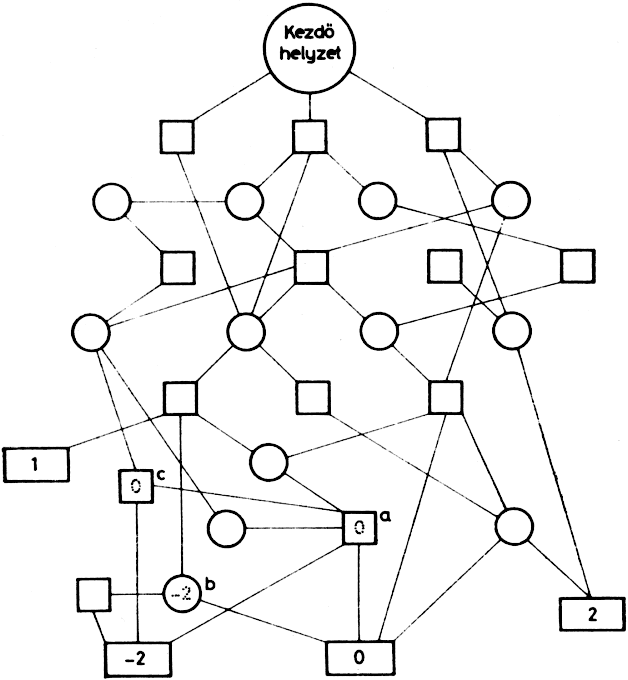
1.6. ábra: Egy játék állapotdiagramja
A játék végállapotait téglalapok jelzik, a beléjük írt számok pedig a játék "értékét" tüntetik fel
A játékok jelentős részénél az állapotdiagram a kezdőhelyzetből indulva egyre jobban terebélyesedik, szélesedik. Az ilyen állapotdiagramokat a játék fájának szokták nevezni. Ezek alkalmazhatóságára részletes példákat találunk a 2. és 8. fejezetben.
A játékoknál - különösen a számítógépes játékok egy részénél - a játék állapotai nem diszkrét, egymástól jól elhatárolható állapotokból állnak, hanem a játék állapotai folytonosan változhatnak. Jó példa lehet erre a számítógépes szimulációk köréből (ld. a 4. fejezetet) választott autóverseny vagy holdraszállás, amelyeknél a játékos folyamatos beavatkozásának hatását folyamatosan megfigyelheti.
A differenciáljátékok egyik legkönnyebben áttekinthető változatát, az ún. üldözéses játékokat az 1.7. ábrán vázoljuk. Képzeljük el, hogy egy gyilkos szándékú autóvezető v2 sebességgel haladó autót irányít. Bármely pillanatban irányt változtathat, azonban a pálya görbületi sugara egy adott értéknél kisebb nem lehet. Az autóvezető egy gyalogost akar elütni, ill. azt egy adott, kicsiny távolságnyira megközelíteni. A gyalogos v1<v2 sebességgel mozog, és irányváltoztatására semmiféle megkötés nincs. A játékkal kapcsolatban több kérdés tehető fel: ha az autóvezető és a gyalogos egyaránt látják egymást, v1, v2, R ismeretében eldönthető-e az, hogy az autó egyáltalán képes-e megközelíteni a gyalogost; az előző kérdésre adott igenlő válasz esetén hogyan kell manővereznie az autóvezetőnek, hogy célját minimális idő alatt érje el?
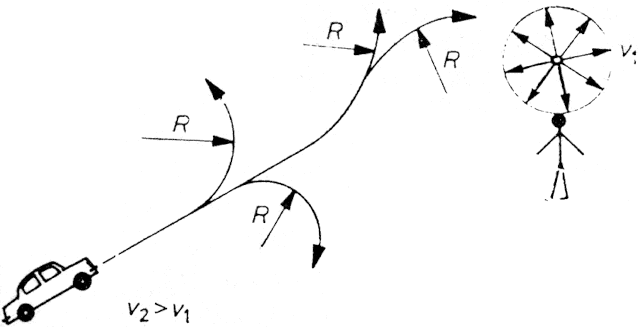
1.7. ábra: Egy gyorsabb, de irányváltozásait tekintve kötöttebb jármű üldöz egy lassúbb, de kötetlenebbül mozgó gyalogost
Láthatjuk tehát, hogy ez a játék elég sok nyitott kérdést tartalmaz. Ha arra gondolunk, hogy e játéknak egy lehetséges "változata" pl. az, amikor egy gyors vadászgép üldöz egy helikoptert, akkor azt is megértjük, hogy ennek és az ehhez hasonló feladatoknak a megoldásával miért foglalkoznak olyan sokan, olyan nagy igyekezettel.
A felsorolt három játéktípus (nyereségmátrixszal leírható, játékfával ábrázolható és a differenciáljáték) valamint a játékos viszonya az 1.8. ábra alapján egy visszacsatolt rendszernek is tekinthető. A játékos úgy választja lépéseit, hogy a kimenet minél inkább megközelítsen valamely általa várt értéket. A kimenetet azonban a többi játékos hasonló célja vagy valamely véletlen folyamat módosítja. A játékos a játék pillanatnyi kimenetelétől függően módosítja a bemenetet, ez újabb kimenőhelyzetet hoz létre stb.
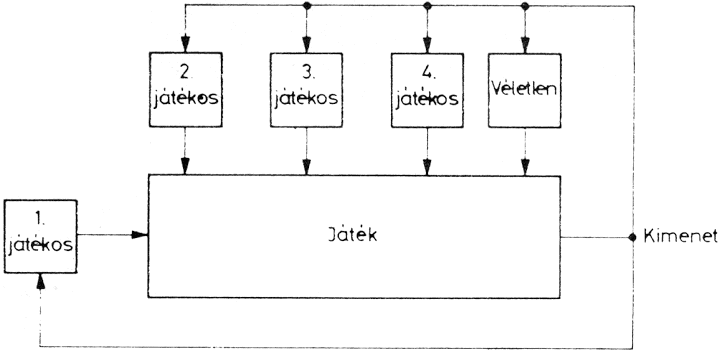
1.8. ábra: A játék-játékos(ok)ból álló rendszer lényeges eleme a visszacsatolás. A játékos játékmódját a kimenet függvényében változtatja.
A játék - mint már láttuk - alapulhat a mindenkori helyzet pontos ismeretén, vagyis a teljes mértékű informáltságon (pl. sakk), lehet stratégiája, amelyet azonban véletlen események befolyásolhatnak (pl. bridzs, póker), és lehet olyan, amelynél a játék következő állapotára a játékosnak semmiféle befolyása sincs (pl. rulett). De nemcsak a játékok, hanem a játékosok is különbözőek lehetnek. Játékos az is, aki csupán a szabályokat ismeri; játszik az is, akinek csak rövid távú stratégiája (taktikája) van; a játékos ismerheti a játék stratégiáját, és ennek szellemében választhat lépést; a játékos tanulhat: nyert és vesztett játékok tanulságait levonva módosíthatja stratégiáját.
Nyilván ez a legutóbbi játékostípus a legérdekesebb, ennek képességei folyamatosan javulhatnak. Ezért olyan nagy jelentőségűek a mesterséges intelligencia kutatásokban azok a játékprogramok, amelyek tanulni is képesek. Könyvünk 2.2.3. pontjában és a 6.1. szakaszban erre is közlünk két egyszerű példát.
A játékok és a játékosok lehetséges stratégiái ugyancsak változatosak; a számítógépes játékok ezt a változatosságot még tovább fokozzák. Szinte lehetetlen valamifajta optimális csoportosítást kitalálni a lehetséges rendező elvek nagy száma miatt. A könyv fejezeteinek csoportosítása is e feladat megoldhatatlanságára, ill. a közel egyenértékű megoldások nagy számára utal.
1.2. A számítógépes játékok eszközei
Valószínűleg mindenki számára nyilvánvaló, hogy a számítógépes játékokhoz a számítógépek nélkülözhetetlenek. Nem úgy, mint pl. a sakkjáték esetében a tábla és a figurák, hiszen sakktáblát a földre is lehet rajzolni, a figurákat pedig akár jól összeválogatott kavicsdarabok is helyettesíthetik, sőt esetleg - némi gyakorlással - fejben is lehet sakkozni. A klasszikus játékok eszközei általában helyettesíthetők egyszerűbb megoldásokkal, a számítógépes játékokkal azonban egészen más a helyzet.
A számítógépes játékok számítógép nélkül nem életképesek. Még akkor sem, ha ezt az állítást látszólag könnyű megcáfolni. Amikor ugyanis egy sakkozógép elromlik, szerepét nehézség nélkül tudja átvenni egy jól sakkozó játékos. Nincsen azonban olyan ember, aki úgy gondolkozna sakkozás közben, mint a gép, amely logikai tévedések nélkül nézi végig olyan lépéslehetőségek százait, amelyeket egy kezdő sakkozó azonnal elvet. Ha pedig a számítógép nem klasszikus, hanem kifejezetten számítógépre készített játékot játszik, akkor szinte semmi esély sincs arra, hogy az élő játékos azt a teljesítményt tudja nyújtani, mint a számítógép.
1.2.1. Számítógép-terminálok
Számítógépes játékot tulajdonképpen minden általános célra készített digitális számítógépen lehet játszani. Nem közömbös azonban az, hogy a gépet milyen nyelven lehet programozni. A számítógépes játékok ugyanis szinte kivétel nélkül valamifajta interaktív terminált, ill. programnyelvet igényelnek, vagyis olyat, amely módot nyújt a géppel való "beszélgetésre". E programnyelvek kérdéseit később részletesebben taglaljuk, először a számítógépes játékok hardware-eszközeit ismertetjük.
Bár az egyes gépkategóriák közötti határok csak pontatlanul jelölhetők meg, a számítógépes játékok szempontjából beszélhetünk nagyszámítógépekről, miniszámítógépekről, mikroszámítógépekről és különleges, célorientált eszközökről (1.1. táblázat):
| Számítógépkategóriák: | |
| Nagyszámítógép | >64 K szó operatív tár, háttértárak, sokfajta periféria, több programnyelv, operációs rendszer, időosztásos üzemmód |
| Miniszámítógép | 8...64 K szó operatív, tár, háttértár, egyszerű perifériák, több programnyelv |
| Mikroszámítógép | 4...16 K szó operatív tár, egyszerű háttértár, kevés periféria, legalább BASIC |
A nagy-, a mini- és a mikroszámítógépeken számítógépes játékot általában akkor játszhatunk, ha a játék céljára elérhető
A számítógépes játékok többsége teletype-ot vagy alfanumerikus képernyős megjelenítést igényel, ill. erre a két igen elterjedt perifériatípusra készült. Mindkét eszköz alkalmas ki- és bemenő adatok kezelésére, ez a játékok alapfeltétele. A teletype előnye, hogy a játék minden fázisáról dokumentum készül, ez különösen a játékok tervezése, életrekeltése esetén előnyös. Hátrányos tulajdonsága viszont az, hogy használatával a kiíratás lassú és zajos, továbbá ábrák, vázlatok, koordináta-rendszerek stb. csak nagyon gyatra minőségben állíthatók elő. Az alfanumerikus képernyős megjelenítés csendes, jóval gyorsabb, bizonyos típusain jobban lehet egyszerű ábrákat szerkeszteni. Természetesen a játéknak nem marad nyoma; nem keletkezik róla "bizonylat".
A játékok egy részéhez nélkülözhetetlen a grafikus képernyős megjelenítés valamilyen változata. Ezek igen változatos képességűek lehetnek. Sok esetben a néhány száz pontnyi vízszintes és függőleges felbontású letapogató típusú (raszter rendszerű) képernyős megjelenítés egészen remek játéklehetőséget teremt. Mind az alfa-numerikus, mind a grafikus képernyős megjelenítésnek van egy előnye: a képernyőn kialakuló ábrát - általában - tv-készülékeken meg lehet ismételni. Ez pl. sakkjátéknál növelheti meg az érdeklődők, ill. játékosok számát. A számítógéppel szerkesztett ábrák rögzítésére rajzgépet vagy módosított karakterkészletű nyomtatót lehet használni (Id. a 7. fejezetet).
Az előző felsorolásból eléggé határozottan kitűnik, hogy a játékok meglevő rendszerek adottságaira épülnek. Ezért végeredményben közömbös, hogy az ismertetett terminálok egy nagy gép köré telepített számítógépes hálózat elemei-e, vagy a helyszínen, néhány méternyi vezetékkel csatlakoznak egy miniszámítógéphez. A lényeg: a bemenő és kimenő adatok, ill. eredmények gyors közlése, a terminál kezelője és a gép közötti interaktív kapcsolat.
1.2.2. Személyi számítógépek
Az elmúlt esztendőkben az integrált áramkörök gyártása hatalmasat fejlődött; egyre bonyolultabb áramköröket sikerült egyre olcsóbban előállítani. Egyetlen áramköri tokban ma már nem csupán egy eléggé bonyolult és gyors központi egység kaphat helyet, hanem kisebb memóriaegységek, perifériakezelés stb. is. Az olcsó perifériális eszközök megjelenése következtében kialakult a számítógépek egy új kategóriája, az ún. személyi számítógép.
A személyi számítógép olyan univerzális digitális számítógép, amelynek ára az elektronikában fejlett országokban 1...3 tv-készülék árával egyezik meg, ezért lehetővé válik, hogy valaki saját, házi használatra számítógépet vásároljon. Némileg önkényesen a személyi számítógépeket három csoportba sorolhatjuk.
Az első csoportba tartozó eszközök hasonlítanak leginkább a hagyományos értelemben vett számítógéphez. A központi egység külön mechanikai egységben helyezkedik el, ehhez csatlakoznak a megszokott perifériák: lyukszalagolvasó, lyukszalaglyukasztó, írógép, olcsó nyomtató, háttértár. Ez utóbbiként főleg a floppy-diszkek terjedtek el, mérsékelt áruk, egyszerű kezelésük miatt. A felsorolt elemekből létrejövő konfiguráció (1.9. ábra) igen sokfajta feladat megoldására használható. Itt egyet említünk: ki lehet alakítani a személyi számítógépekkel pl. ún. szövegfeldolgozó rendszert. Ezzel írott szöveget lehet módosítani különböző céloknak megfelelően, pl.:
Kicsit túlozva: egy ügyes, fáradhatatlan és hihetetlenül jó memóriájú gépírónőt helyettesíthet ez a rendszer. Publikációk, jelentések írása és szerkesztése esetén, valamint levelezéshez nyilván igen jól használható.
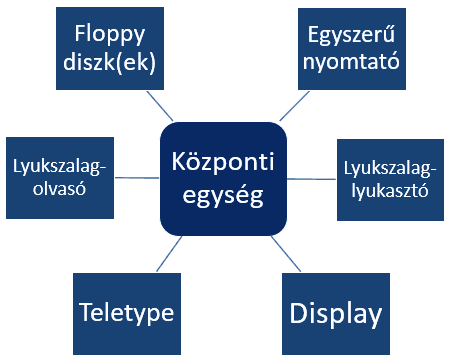
1.9. ábra: Változatos feladatok megoldására alkalmas mikroszámítógép-konfiguráció
A személyi számítógépek második csoportjához az 1.10. ábrán látható készülék tartozik:
1.10. ábra: A személyi számítógépek egyik gyakori megjelenési formája
Ezek tipikus képviselője a PET (Personal Electronic Transactor), amely billentyűzetből, képernyőből, kazettás magnetofonból és egy mikroszámítógépből áll. A mikroszámítógép tárának egy részébe kitörölhetetlenül beírják általában egy magasszintű programnyelv fordítóprogramját (BASIC). A felhasználó 4...8 Kbyte szabad operatív tár felett rendelkezik. A programok a kazettára is rögzíthetők, szükség esetén innen lehet őket újra a gép tárába behívni. Ez az írógépnél alig nagyobb készülék igen sokféleképpen használható:
A felsorolt lehetőségek végén - talán legjelentősebb alkalmazásként - ott találhatók a számítógépes játékok. A PET erre különösen alkalmas, mivel billentyűzetén nem csupán betűk, hanem ábraelemek, kártyajelek stb. is találhatók, így a képernyőn változatos ábrákat (pl. sakktáblát és figurákat) lehet kelteni.
Harmadik csoporthoz a legegyszerűbb és legolcsóbb személyi számítógép tartozik, mely látszólag csak egy billentyűzetből áll (1.11. ábra). A billentyűzet dobozában azonban a PET-hez hasonló képességű mikroszámítógép rejtőzködik. A számítógéphez műsorvételre alkalmas tv-készüléket kapcsolhatunk, ill. kommerciális kazettás magnetofont. Ez az összeállítás azon alapul, hogy a háztartások legnagyobb részében e két utóbbi készülék már amúgy is megtalálható.
1.11. ábra: A legolcsóbb számítógép, amihez a perifériális eszközök a háztartási készülékek sorából választhatók
A személyi számítógépek számával együtt növekszik a használatukra vonatkozó kiadványok száma is. Leginkább az Interface Age, Personal Computing, BYTE, Creative Computing folyóiratokra hívjuk fel a figyelmet: az alig egy-két esztendős múlttal rendelkező nagyszámú kiadvány arra utal, hogy a személy számítógépek megjelenése a rádióamatőr mozgalomhoz hasonlóan egy új, népszerű hobby-t indított útjára. Klubok, szervezetek alakulnak, ahol találékony számítógép tulajdonosok közkinccsé teszik hardware és software ötleteiket. Kiállításokat, gyűléseket rendeznek, ezzel is hatékonyan terjesztik a számítástechnikai módszereket fokozzák a számítástechnikai kultúrát.
1.2.3. Céleszközök
Az elmúlt esztendőkben egyre több olyan játék jelent meg a piacon, amely valahol, belül, elrejtve számítógépet is tartalmaz. Ezeknél a számítógép kívülről nem hozzáférhető, a számítógépbe egyetlen program van kitörölhetetlenül beleírva. Többségükben valamilyen ismert játékhoz jelentenek játékpartnert.
Elsőnek a sakkozó játékokat kell említenünk. Ezek könyv méretű eszközök, sakktábla és a figurák csak az élő játékosnak szükségesek a játék menetének követéséhez. A gép nem "lép", vagyis nem mozgatja a figurákat, ezt a játékos teszi meg helyette. A gép a figurák helyzetét sem érzékeli; ha a játékos nem a gép által kijelzett vagy az általa bebillentyűzött lépést hajtja végre, nem veszi észre a tévedést. A számítógép-program különböző játékerősségű fokozatra kapcsolható. Az élő játékos számára ez a gép gondolkodási idejének változását jelenti (Id. a 8.3. szakaszt). A sakkozó játékokban a program nem tanul, ha tehát egyszer sikerült valahogy megverni, akkor ugyanúgy játszva a gép mindig veszíteni fog. Ennek ellenére azt állítják, hogy a gép kiváló gyakorlási lehetőséget nyújt kezdő és közepes játékosoknak.
Létezik számítógéppel ellenőrzött "tengeri csata" játék is. Itt a számítógép feladata alig megy túl a játék adminisztrációján, továbbá a csata különböző helyzeteihez illő hanghatások keltésén.
Készítettek számítógéppel egybeépített malomjátékot is. Itt is a játékos kezeli a "bab vagy kukoricaszemeket"; azonban ha a játékos nem arra a pontra helyezi a gép figuráját, amelyet az villogó fénnyel jelez, a hiba kijavításáig a játék megáll. A gép tehát bizonyos mértékig érzékeli a játékmezőt is. A beírt program igen jó, a számítógép szinte mindig nyer.
Forgalomba került olyan eszköz is, amely a bridzs játékhoz nyújt valamelyes segítséget. Az eszköz eléggé szerény teljesítőképességű, tulajdonképpen csupán a kártyalapok nélküli bridzsezés lehetőségét biztosítja.
Néhány szóval meg kell emlékeznünk az egyre olcsóbbá váló és egyre "többet tudó" tv-játékokról is. Ezek első generációja külön erre a célra kifejlesztett digitális áramkörön alapult. A játékok többsége a rugalmas ütközés képernyőn történő utánzásán alapult. Az újabb tv-játékok már mikroprocesszort is tartalmaznak, belső felépítésük egyre jobban megközelíti a számítógépek architektúráját. Programjaik változtathatók, cserélhetők, ehhez csak a programot tartalmazó mágnesszalagos kazettát kell megvásárolni. Az így felépíthető játékok már nagyon összetettek: színes képernyőn különböző figurák képesek mozogni és egymásra lövöldözni. A tv-játékok belsejében elhelyezkedő univerzális digitális számítógép azonban kívülről, a felhasználó oldaláról nem érhető el.

Nekem olyat vegyél, amelyik néha megpróbál csalni, de én mindig rájövök!
1.3. Tanácsok a könyv olvasásához, használatához
A szerzők véleménye szerint a számítógépes játékokról szóló könyv két embercsoport érdeklődését keltheti fel: azokét, akik hívei valamilyen vagy mindenfajta játéknak, és azokét, akik a számítógépek lelkes megszállottjai. Leginkább persze azokhoz szól, akik mindkét csoporthoz tartoznak, vagyis ismerik a számítógépeket, és szívesen töltik idejüket játékkal.
Számítógépes játékokat nem lehet fejben játszani, a számítógépes játékok megismeréséhez személyes tapasztalat, személyes számítógépes gyakorlat szükséges. Szerencsére örvendetesen növekszik környezetünkben a számítógépek száma; üzemek-munkahelyek, iskolák jutnak önálló kisgéphez vagy nagygéphez csatlakozó terminálokhoz. Így nő a személyes tapasztalatszerzés lehetősége is.
A számítógépes játékok igazában csak akkor szereznek örömet, ha magunk készítjük őket, vagy pedig a játék programját alaposan ismerjük. Így a számítógépes játékok jóval túlnőnek a közvetlen cél nélküli időtöltésen és az ismeretszerzés, a számítógépes gyakorlat elsajátításának válnak vonzó eszközeivé. A számítógépek felépítését, programozását oktató tanfolyamok sokszor csak azért nehezek, unalmasak, mert hiányzik belőlük az emberi - közvetlen motiváció. Túlságosan absztrakt gondolkodást igényel egy programnyelv megtanulása, ha nem serkentik apró személyes indítékok. Úgy véljük, hogy a számítógépes játékok erre a célra nagyszerűen megfelelnek.
Könyvünket olyan olvasóknak írtuk, akik a számítógépeket, számítástechnikát legalább középfokú szinten ismerik. Ezért a számítástechnikai alapfogalmakat, kifejezéseket sehol sem magyarázzuk meg külön. A játékok alapötletét bemutató fejezetrészektől (2...8 fejezet) azonban a konkrét játékprogramokat szétválasztottuk azért, hogy a különböző számítástechnikai ismerettel rendelkező Olvasók is folyamatosan olvashassák a könyvet. A programok megértéséhez szükséges alapelveket, jelöléseket stb. a leíró részben közöljük.
A könyv egyes fejezetei többé-kevésbé önállóak. Így a könyv látszólag tetszőleges sorrendben is olvasható. Valójában azonban a 2. fejezet nagyon sok alapfogalmat, eljárást tartalmaz, így ennek elolvasása után fogjon hozzá csak az Olvasó más részekhez.
A 3. fejezet több olyan szerencsejáték leírását is tartalmazza, amelyek a "tiltott" jelzőt is magukon viselik. A szerzők ettől szeretnék elhatárolni magukat: ezek a játékok számítógépes gyakorlatoknak tekintendők, amelyek célja valószínűségszámítási és játékelméleti összefüggések demonstrálása, nem pedig a számítógéppel segített nyerészkedésre való buzdítás.
A 4. és 5. fejezetben szimulációs játékokról írunk, ill. pontosabban fogalmazva: olyan számítógépes szimulációkról, melyek játéklehetőséget is rejtenek magukban.
A 6. fejezet arra akarja felhívni a figyelmet, hogy némi számítógép ismerettel és fantáziával szinte megszámlálhatatlanul sokfajta játékötletet realizálhatunk.
A 7. fejezetben a számítógép grafikus eszközként szerepel, a "számítógép-művészet" és a számítógépes animáció (alakmegelevenítés) egyszerű, játékos módozatait írtuk le.
A 8. fejezet önálló; a legnépszerűbb, legnehezebb játékról, a sakkról szól. A számítógépes játékok csúcsteljesítményüket ebben érik el.
1.3.1. A programokról
A könyvben található programok mindegyike valamelyik fejezetben részletesen is említett játék programja, program listája. A programnyelv mindenütt BASIC.
A BASIC a számítógépes játékoknak szinte egyeduralkodó nyelve. Ennek számos oka van: könnyen megtanulható, "beszélgetést" tesz lehetővé, számítások végzésére és szövegmanipulációkra egyaránt alkalmas. A legfontosabb azonban: nagyon elterjedt, szinte kivétel nélkül minden gép "megérti", a személyi számítógépek többsége is. (Kicsit számítástechnikai eszperantó jellege van. Aki bármilyen más számítógépnyelvet ismer, annak számára a BASIC megtanulása szinte semmi fáradsággal sem jár.)
Annak az Olvasónak, aki valamelyik programot felhasználni kívánja, a következőket tanácsoljuk:
A BASIC nyelv nem jelent egységes szintaktikai és szemantikai szabályrendszert. Az egyes implementációk közötti néhány eltérésre fel kell hívnunk a figyelmet:
A programok felhasználása tehát biztos programozási ismereteket igényel.
A számítógépes programok nyomtatott-leírt formáról számítógépek adathordozóra való átmásolása kellemetlen feladat. Éppen ezért a személyi számítógépek programellátására több megoldás született. Mutatóba néhány közülük:
Befejezésül pedig megismételjük: az egyéni vonásokat tükröző, "testreszabott" játékprogramok általában többet érnek, mint egy nagy, bonyolult játékprogram, amit valaki más készített.
A játékok e kategóriájában olyan "problémákkal" állunk szemben, amiket egy megadott - pontosan definiált - kezdőállapot és egy ugyancsak pontosan megadott végső cél jellemez. A végső célt közbeeső célok (állapotok) sorozatán keresztül érhetjük el. Egyik állapotból a másikba műveletek alkalmazásával juthatunk, amelyeket lépéseknek szoktunk nevezni. (Ezeket a játék szabályai pontosan megadják.) Egy-egy adott állapotban, amelyet a játékoknál állásnak nevezünk, a játékosnak lehetősége van választani alternatív lépések közül. A lehetőségek közötti választásban segítséget nyújt a játék stratégiája (ha van ilyen, ill. ha a játékos ismeri azt), amely valamilyen - közbeeső vagy végső - cél érdekében megteendő lépésre (lépéssorozatra) vonatkozik. A játékos képzettsége (tehát a játék elméletének, stratégiájának ismerete) valamint gyakorlottsága a siker, vagyis a győzelem forrása. A véletlennek tehát ezekben a játékokban semmiféle szerepe nincs a lehetséges folytatások közötti választásban.
Ezeket a játékokat - egy kissé erőltetetten - a következő csoportra osztottuk:
2.1.1. A minimax és az alfa-béta eljárás - tik-tak-to
Ezt a játékot, amely nagyon népszerű nálunk is (minden iskolában játsszák!) különösebben nem kell ismertetni. Röviden összefoglaljuk azonban a szabályokat.
A számítógépes változatot kilenc (3x3) négyzetből álló elrendezésben fogjuk bemutatni. (A papíron játszott változatot mi "amőba" néven ismerjük és négyzethálós papíron játszhatjuk.) A két játékos, esetünkben a játékos és a számítógép egy-egy négyzetbe felváltva rajzolja a saját jelét (az egyiké: 'o',a másiké 'x'). Az nyer, aki három jelét (vízszintesen, függőlegesen vagy diagonálisan) egymás mellé be tudja rajzolni.
Ez a játék érdekes és szórakoztató, és egyben lehetőséget ad számunkra, hogy segítségével bemutassuk az ún. játékfák kiértékelésének egy nagyon jól ismert módszerét is.
Az alábbi gondolatmenet végigkövetése nagyon hasznos, - számos játék optimális stratégiája határozható meg az itt leírt módszerrel. Könyvünkben sok helyütt használjuk is ezt az eljárást, ezért ismertetjük kissé részletesebben.
Becsüljük meg először a tik-tak-to játékfa méretét. Mivel először kilenc, majd nyolc stb. lehetséges választás van, 9! = 362 880 csomópont lesz a fa alján! A sok szimmetrikus elrendezés miatt gyakorlatilag körülbelül 5000 különböző tik-tak-to játék van. Az egész fa vizsgálata helyett célunk mindig az adott pozícióhoz tartozó jó lépés kiválasztása - a vizsgálatot adott mélységig (lépésszámig) végezve. Az ennek megfelelő részfán vagy "szélesség" vagy "mélység" szerint (vagy a kettő kombinációját jelentő ún. irányított módon) haladunk végig. A fa legalsó csomópontjaihoz a játék szabályaihoz igazodó számértékeket rendelünk, amely az illető csomópont értékének mérőszáma. A hozzárendelést az adott állásnak megfelelő helyzetet értékelő ún. statikus értékelőfüggvény segítségével végezzük (ld. később).
A legjobb lépést a minimax eljárás segítségével választjuk ki. Az eljárás lényege, hogy az egymást követő csomópont "szinteken" (amelyek az egyes játékosok lehetséges lépéseit felváltva jelentik) a játékosok mindig a számukra legkedvezőbb kombinációt választják. Ha ezt a legalsó szinten az egyik számára a legnagyobb számmal jelzett csomópontot (maximum) jelenti, a következő szinten a másik számára a legkedvezőbb a legkisebb (minimum). Így a fán alulról felfelé haladva mindig az ilyen módon kiválasztott értéket visszük "feljebb". Eképpen elérve szintről szintre a kezdőpontot, a lépés kiválasztása a legnagyobb értékű ág szerint történik.
Az eljárás alkalmazása azon a helyes feltételezésen alapszik, hogy előrehaladva a játékfáján és felhasználva a statikus értékelő függvényt a pozíció értékelésére, a játék végéhez közelebb levő helyzetet vesszük tekintetbe, így lehetőségük van egy adott lépés következményeinek valamilyen "mélységű" értékelésére.
Lássuk most már a minimax eljárás alkalmazását a tik-tak-to játék esetén. Lépjen először a keresztet használó játékos és azután a kört használó. A lehetséges kombinációkat szélesség szerint képezzük, majd a második szinten levő csomópontokra alkalmazzuk a statikus értékelő függvényt.
Ezt a statikus kiértékelő függvényt úgy kell "kitalálnunk", előállítására nincsenek matematikai módszerek. Sok-sok játszmából származó tapasztalatainkat kell egyszerű, könnyen kezelhető formulába öntenünk, e formulában fogalmazva meg a játék lényegét. Példaként a bridzsben szokásos játékerő értékelési módszereket említhetjük, ahol a különböző kártyáknak különböző értéket tulajdonítunk és ezen értékek összegezésével állapítjuk meg a kézbentartott lap játékerejét. A többfajta kiértékelő módszer létezése arra utal, hogy a statikus kiértékelő függvény korántsem egyértelmű. Különösen nehéz jó kiértékelő függvényt alkotni a sakkjátékhoz.
A tik-tak-to esetén helyzetünk könnyebb és már egy viszonylag egyszerű kiértékelő függvény is megfelel. Legyen az e(p) kiértékelő függvény a játék egy p pozíciójában a következőképpen definiálva:
e(p) = px-p0
ahol
px = a szabad teljes sorok, oszlopok és diagonálisok száma x számára
p0 = a szabad teljes sorok, oszlopok és diagonálisok száma o számára.x győzelmi esélye tehát annál nagyobb, minél nagyobb pozitív szám az e(p) függvény értéke, míg o esélyét a negatív előjelű szám abszolút értéke jelzi.
Ha p győzelmet jelent x számára, akkor e(p)=végtelen.
Így pl., ha p pozícióban az elrendezés:
akkor e(p)=6-4=2
A szimmetriát kihasználva ezzel egyenlő értékűnek fogjuk tekinteni a következő összes elrendezést:
A tik-tak-to fa ágainak száma így a játék elején a szimmetria felhasználásával kis értéken tartható, míg azt a későbbiekben a szabad négyzetek csökkenő száma fogja korlátozni.
A 2.1. ábrán a két lépés mélységnek megfelelő fát mutatjuk be. A fenti helyzet statikus értékelésének megfelelő becsült értékeket a legalsó csomópontok alatt tüntettük fel, míg az ezek közül minimax eljárással kiválasztott és "felvitt" értékeket bekereteztük.
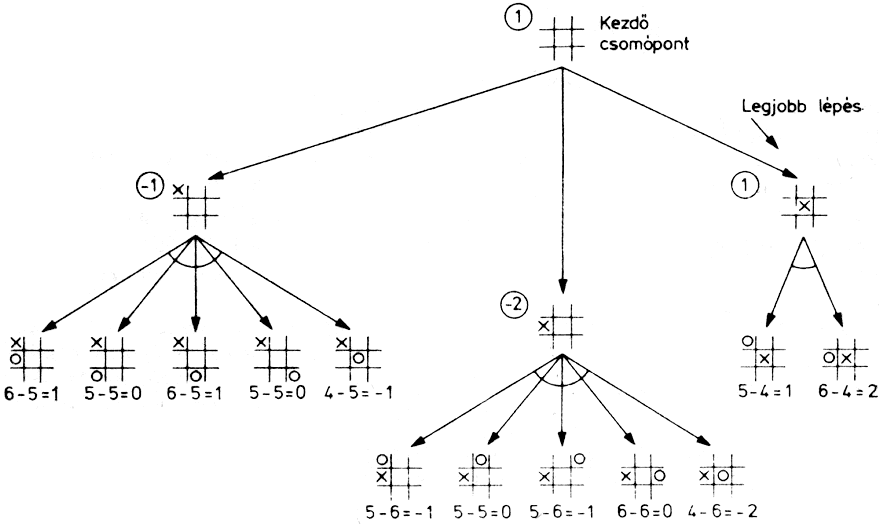
2.1. ábra: Minimax eljárás alkalmazása a tik-tak-to játékra (1. fázis)
A játékfában az ÉS és VAGY típusú csomópontok szintjei felváltva szerepelnek. (Ábránkon a VAGY típusú csomópontokat olyan módon különböztettük meg, hogy az azokból induló ágakat egy körívvel összekötöttük). VAGY csomópontok a feladat megoldásánál alternatívan megoldandó részfeladatokat jelölnek, míg az ÉS csomópontok a megoldásban feltétlenül kell, hogy szerepeljenek.
Mivel
értéke a legnagyobb, ezt választjuk első lépésként. Tételezzük fel, hogy az erre adott válasz:
(Ez egy elég rossz lépés szegény o számára, mivel ennek hatására e(p)=6-4=2, míg pl.
lépés esetén e(p)=5-4=1, tehát nem valami jó játékstratégiát választott!
Ezután ismét előállítjuk a két lépés mélységű fát kiindulva a
kezdőállásból (2.2. ábra).
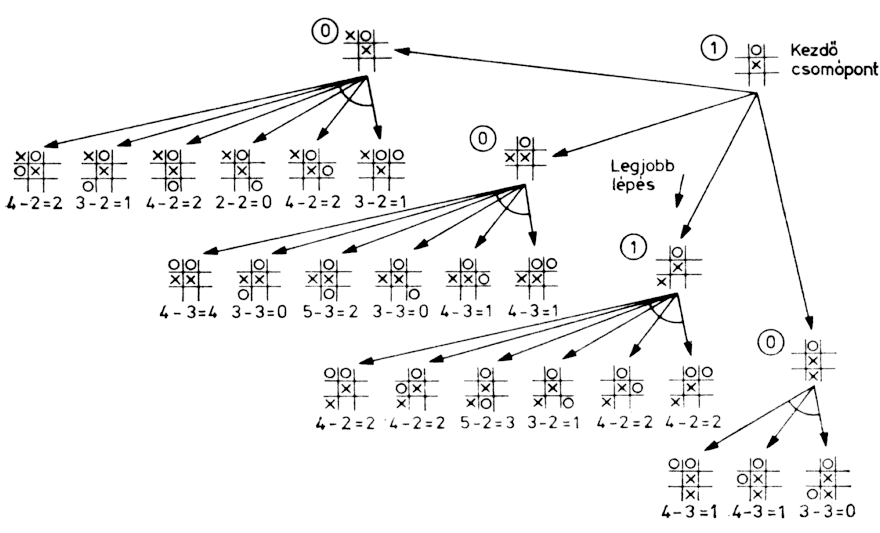
2.2. ábra: Minimax eljárás alkalmazása a tik-tak-to játékra (2. fázis)
x legjobb lépése az ábrán jelzett, amelyre o olyan választ ad, amellyel elkerülheti az azonnali vereséget. Ennek eredményeként a következő állás alakul ki:
Ebből kiindulva újra előállítjuk a fát a 2.3. ábra szerint.
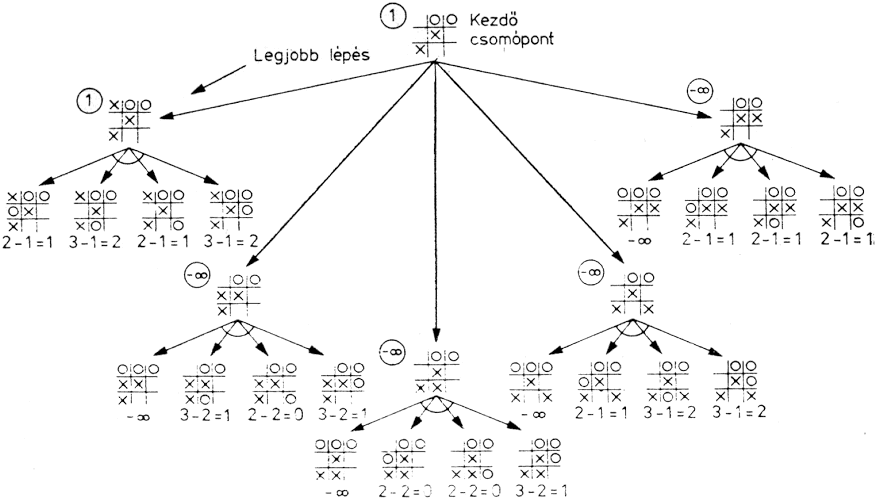
2.3. ábra: Minimax eljárás alkalmazása a tik-tak-to játékra (3. fázis)
Itt több végső pozíció is o nyerési lehetőségét mutatja, így ezeket -végtelen értékkel jelöltük. Ha az értékelést elvégezzük, azt találjuk, hogy x legjobb lépése egyben az egyetlen olyan is, amellyel a közvetlen vereséget elkerülheti. Most azonban már x látja, hogy a következő lépésnél o mindenképpen győz, így feladja a játékot.
Eddigiekben a fa generálását és kiértékelését (a legjobb lépés kiválasztását) egymás után külön végeztük. így csak a fa (farészlet) előállításának teljes befejezése után kezdtük el a kiértékelést. Ez a különválasztás azonban rossz hatásfokú stratégiát eredményez, mivel ha a kiértékelést és a generálást egyidejűleg végeznénk, jelentős megtakarítást érhetnénk el a fa egyes ágainak és az ezeket követő ágaknak az elhagyásával. (Ez a csökkenés bizonyos esetekben sok nagyságrendet is jelenthet!)
Tekintsük ismét a 2.3. ábra szerinti fát. Tételezzük fel azt, hogy egy végpontot elérve, a generálással egyidejűleg azt azonnal értékeljük is. így pl. az ábránkon, miután a -végtelen értékű pontot generáltuk és kiértékeltük, nincs értelme az 1, 0, 1 értékűekkel foglalkoznunk, mivel o számára ennél a folytatásnál (ez -végtelen értékű!) jobb lépés nem képzelhető el. Persze, ha a vizsgálatot nagyobb mélységnek megfelelően végeztük volna, még további megtakarítást értünk volna el azáltal, hogy ezen csomópontok "utódait" sem kellene létrehoznunk.
Példánkban a fa egyszerűsítésénél azt használtuk ki, hogy az adott csomópontban o számára nyerési lehetőség volt. Hasonló megtakarítást érhetünk el azonban abban az esetben is, ha a fa csomópontjaiban nincs közvetlen nyerési lehetőség egyik fél számára sem.
Tekintsük most a tik-tak-to játék fájának első fázisát (ld. a 2.1. ábrát), amelynek egy részét a 2.4. ábrán újra kirajzoltuk.
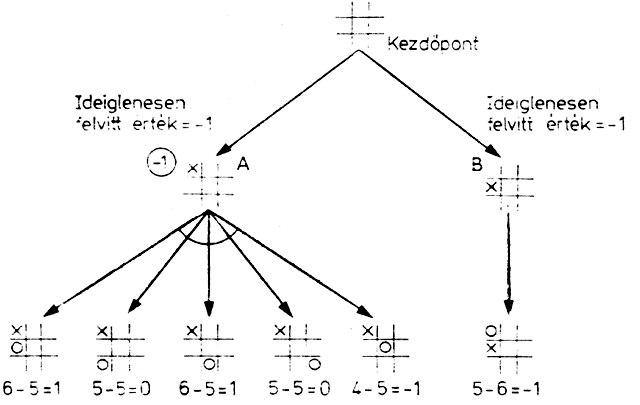
2.4. ábra: A 2.1. ábra részlete
Mélység szerint előrehaladva, ha egy végponthoz érünk, a statikus értékelést rögtön elvégezzük, és az ismertetett szabály szerint a kiválasztott értéket is rögtön felvisszük a következő szintre. E szerint pl. az A csomópont VAGY ágaihoz tartozó végpontok kiszámolt értékei közül -1 kerül fel az A csomópontba. Ideiglenes értékként vigyük ezt az értéket még feljebb a kezdőpontba. Az értéket ideiglenesnek nevezzük, mivel a kezdőpont további ágai azt még módosíthatják. Ez a módosítás növelheti ezt az értéket, de kisebb értékek figyelembevétele szükségtelen.
A vizsgálatot most már B csomópont és az őt követő csomópont generálásával folytatjuk, amelynek statikus értékelésből kapott értéke -1. Mivel a további vizsgálatból kiderül, hogy B-től származó értékek nem haladhatják meg a -1 értéket, így B csomópont alatt a vizsgálat szükségtelen, mivel 8 nem szolgáltathat A-nál kedvezőbb folytatást.
Szabályainkat most már általánosítva, a fában ideiglenesen felvitt értékek segítségével való egyszerűsítést a következő formában fogalmazhatjuk meg:
Az ÉS csomópontok ideiglenesen felvitt értékeit szokásosan alfa értékeknek, míg a VAGY csomópontok ilyen értékeit béta értékeknek szokták nevezni. Így ha a keresést az 1. szabály szerint nem kell folytatni alfa levágásról, ha pedig a 2. szabály szerint, akkor béta levágásról beszélhetünk. Az egész eljárást, amikor tehát az ideiglenesen felvitt értékeket figyelemmel kísérjük - és ahol csak lehetséges a fa "szükségtelen ágait levágjuk" - alfa-béta eljárásnak hívják.
Az eljárás lényegét - mivel a játékok programozásakor nagy fontosságú - általánosabb formában a 2.5. ábra segítségével még egyszer összefoglaljuk. A hat szint mélységű fa végpontjainak statikus értékeit a 2.5. ábrán feltüntettük. A mélység szerinti vizsgálatot (ill. fa generálást) a bal oldali ágnál kezdjük. Az alfa-béta eljárás segítségével lecsökkent ("megvágott") fát az ábrán a vastagabban kihúzott ágak jelzik. A könnyebb áttekinthetőség kedvéért négyzet jelenti az ÉS, míg kör jelzi a VAGY csomópontokat. A "kivágott" csomópontokat áthúztuk (X). Az eredeti 41 végpont közül csak 18 értékelését kellett elvégezni. (Az Olvasó a példa eredményének a nyomonkövetésével ellenőrizheti, hogy mennyire tette magáévá az alfa-béta eljárást.)
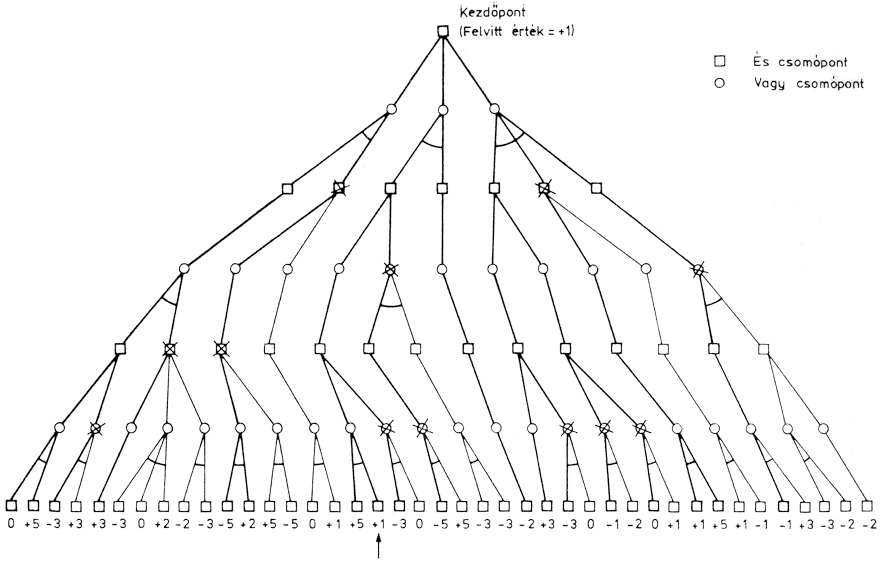
2.5. ábra: Alfa-béta eljárás alkalmazását bemutató példa
A játék programját a ZX Spectrum BASIC-ben adjuk meg. A program a következő módon számozott elrendezésnek megfelelően kívánja a lépés megadását:
1 2 3
4 5 6
7 8 9
A játékos és a számítógép felváltva lépnek. A program a táblán minden lépés után kirajzolja az állásnak megfelelő elrendezést is.
2 PRINT TAB (10);"Tik-Tak-to"
4 PRINT TAB (6);"CREATIVE COMPUTING": PRINT TAB (4);"MORRISTOWN, NEW JERSEY"
8 PRINT : PRINT "A tabla szamozasa:"
10 PRINT " 1 2 3"
12 PRINT " 4 5 6"
14 PRINT " 7 8 9": PRINT
20 DIM S(9)
50 INPUT "'x'-t vagy 'o'-t valasztja? ";C$
55 IF C$="X" THEN GO TO 475
60 LET P$="O": LET Q$="X"
100 LET G=-1: LET H=1: IF S(5)<>0 THEN GO TO 103
102 LET S(5)=-1: GO TO 195
103 IF S(5)<>1 THEN GO TO 106
104 IF S(1)<>0 THEN GO TO 110
105 LET S(1)=-1: GO TO 195
106 IF S(2)=1 AND S(1)=0 THEN GO TO 181
107 IF S(4)=1 AND S(1)=0 THEN GO TO 181
108 IF S(6)=1 AND S(9)=0 THEN GO TO 189
109 IF S(8)=1 AND S(9)=0 THEN GO TO 189
110 IF G=1 THEN GO TO 112
111 GO TO 118
112 LET J=3*INT ((M-1)/3)+1
113 IF 3*INT ((M-1)/3)+1=M THEN LET K=1
114 IF 3*INT ((M-1)/3)+2=M THEN LET K=2
115 IF 3*INT ((M-1)/3)+3=M THEN LET K=3
116 GO TO 120
118 FOR J=1 TO 7 STEP 3: FOR K=1 TO 3
120 IF S(J)<>G THEN GO TO 130
122 IF S(J+2)<>G THEN GO TO 135
126 IF S(J+1)<>0 THEN GO TO 150
128 LET S(J+1)=-1: GO TO 195
130 IF S(J)=H THEN GO TO 150
131 IF S(J+2)<>G OR S(J+1)<>G THEN GO TO 150
133 LET S(J)=-1: GO TO 195
135 IF S(J+2)<>0 OR S(J+1)<>G THEN GO TO 150
138 LET S(J+2)=-1: GO TO 195
150 IF S(K)<>G THEN GO TO 160
152 IF S(K+6)<>G THEN GO TO 165
156 IF S(K+3)<>0 THEN GO TO 170
158 LET S(K+3)=-1: GO TO 195
160 IF S(K)=H THEN GO TO 170
161 IF S(K+6)<>G OR S(K+3)<>G THEN GO TO 170
163 LET S(K)=-1: GO TO 195
165 IF S(K+6)<>0 THEN GO TO 170
166 IF S(K+3)<>G THEN GO TO 170
168 LET S(K+6)=-1: GO TO 195
170 GO TO 450
171 IF S(3)=G AND S(7)=0 THEN GO TO 187
172 IF S(9)=G AND S(1)=0 THEN GO TO 181
173 IF S(7)=G AND S(3)=0 THEN GO TO 183
174 IF S(9)=0 AND S(1)=G THEN GO TO 189
175 IF G=-1 THEN LET G=1: LET H=-1: GO TO 110
176 IF S(9)=1 AND S(3)=0 THEN GO TO 182
177 FOR I=2 TO 9: IF S(I)<>0 THEN GO TO 179
178 LET S(I)=-1: GO TO 195
179 NEXT I
181 LET S(1)=-1: GO TO 195
182 IF S(1)=1 THEN GO TO 177
183 LET S(3)=-1: GO TO 195
187 LET S(7)=-1: GO TO 195
189 LET S(9)=-1
195 PRINT : PRINT "A szamitogep lepese..."
202 GO SUB 1000
205 GO TO 500
450 IF G=1 THEN GO TO 465
455 IF J=7 AND K=3 THEN GO TO 465
460 NEXT K: NEXT J
465 IF S(5)=G THEN GO TO 171
467 GO TO 175
475 LET P$="X": LET Q$="O"
500 PRINT : INPUT "Hova lep? ";M
502 IF M=0 THEN PRINT "Koszonom a jatekot.": GO TO 2000
503 IF M>9 THEN GO TO 506
505 IF S(M)=0 THEN GO TO 510
506 PRINT "Ez a mezo foglalt!": PRINT : PRINT : GO TO 500
510 LET G=1: LET S(M)=1
520 GO SUB 1000
530 GO TO 100
1000 PRINT : FOR I=1 TO 9: PRINT " ";: IF S(I)<>-1 THEN GO TO 1014
1012 PRINT Q$;" ";: GO TO 1020
1014 IF S(I)<>0 THEN GO TO 1018
1016 PRINT " ";: GO TO 1020
1018 PRINT P$;" ";
1020 IF I<>3 AND I<>6 THEN GO TO 1050
1030 PRINT : PRINT "---+---+---"
1040 GO TO 1080
1050 IF I=9 THEN GO TO 1080
1060 PRINT "!";
1080 NEXT I: PRINT : PRINT
1095 FOR I=1 TO 7 STEP 3
1100 IF S(I)<>S(I+1) OR S(I)<>S(I+2) THEN GO TO 1115
1110 IF S(I)=-1 THEN GO TO 1350
1112 IF S(I)=1 THEN GO TO 1200
1115 NEXT I: FOR I=1 TO 3: IF S(I)<>S(I+3) THEN GO TO 1150
1130 IF S(I)<>S(I+6) THEN GO TO 1150
1135 IF S(I)=-1 THEN GO TO 1350
1137 IF S(I)=1 THEN GO TO 1200
1150 NEXT I: FOR I=1 TO 9: IF S(I)=0 THEN GO TO 1155
1152 NEXT I: GO TO 1400
1155 IF S(5)<>G THEN GO TO 1170
1160 IF S(1)=G AND S(9)=G THEN GO TO 1180
1165 IF S(3)=G AND S(7)=G THEN GO TO 1180
1170 RETURN
1180 IF G=-1 THEN GO TO 1350
1200 PRINT "Megvert! Jo jatek!": GO TO 2000
1350 PRINT "En gyoztem!!!": GO TO 2000
1400 PRINT "Dontetlen! Koszonom a jatekot."
2000 STOP
Tulajdonképpen egy nagy csoport tik-tak-to-hoz hasonló játék létezik. Ezek alapvető szabályai megegyeznek a tik-tak-to-éval, vagyis két játékos felváltva tesz egy x és o jelet a táblára. Az egyik különbség a "tábla" elrendezésben van. Az alapjáték "kétdimenziós" táblájához képest ez lehet háromdimenziós is, sőt elvileg akárhány dimenziós. (Ezzel persze már nehéz a gyakorlatban is játszani.) A másik különbség a nyerő pozícióban van, vagyis, hogy hány egyforma "jel" jelenti a nyert állást. Így beszélhetünk n^k tik-tak-to játékokról, pl. a mi korábbi 3x3 négyzetből álló kétdimenziós alapjátékunknál n=3 az oszlop- és a sorszám k=2 pedig a dimenziószám. Egy egyszerű háromdimenziós változat, amelyre szintén készültek számítógépprogramok, a QUBIC (4x4x4). Ennél n=4 és k=3.
Játékelméleti alapon kimutatható, hogy a tik-tak-to egy tipikus "döntetlen" típusú játék, tehát mindkét játékos számára a döntetlenhez vezető stratégia adott.

Te a minimax eljárás szerint játszol, vagy az alfa-béta eljárást szereted?
2.1.2. Feladatredukálás - Hanoi tornyai
A feladatmegoldás jól ismert módszere a feladatredukció. Ennek a lényege, hogy a megoldandó feladatból kiindulva "visszafelé" haladunk, részfeladatokra és újabb rész-rész-feladatokra bontva azokat addig, ameddig az eredeti feladatot triviális megoldású primitív feladatra nem vezettük vissza.
Ennek a feladatmegoldási módszernek az illusztrálására egy jól ismert rejtvényjátékot mutatunk be. Ez a logikai játék a Közel-Keletről származik. Néha szokták fáraó tűinek is nevezni, de a leggyakrabban használt neve Hanoi tornyai. A legenda szerint Hanoi városa közelében élt egy titkos szerzetesrend. Volt nekik három nagy tornyuk, melyek tűre fűzött korongokból álltak. Egyszerre csak egy korongot mozgatva és sohasem téve nagyobbat a kisebb korongra, a szerzetesek megpróbálták átrakni a korongtornyot a bal oldali tűről a jobb oldalira. A legenda szerint akkor lesz vége a világnak, amikor befejezik a 64 korongból álló torony áthelyezését.
Ebben a játékban a feladatot a számítógéppel fogjuk szimulálni. Célunk, hogy minél kevesebb lépéssel oldjuk meg a feladatot. A feladatmegoldás menetének bemutatására tekintsünk előbb egy egyszerűbb esetet, amikor három különböző nagyságú korongunk van. A 2.6. ábrán a korongokat A, B és C betűkkel jelöltük. A feladat az, hogy a kezdeti állapotból a korongokat - a megadott - végső állapotba juttassuk.

2.6. ábra: A Hanoi tornya fejtörő
A feladat megoldható az ún. állapottér-módszer segítségével. Ennek megfelelően a 2.7. ábra gráfja a teljes állapotteret adja meg.
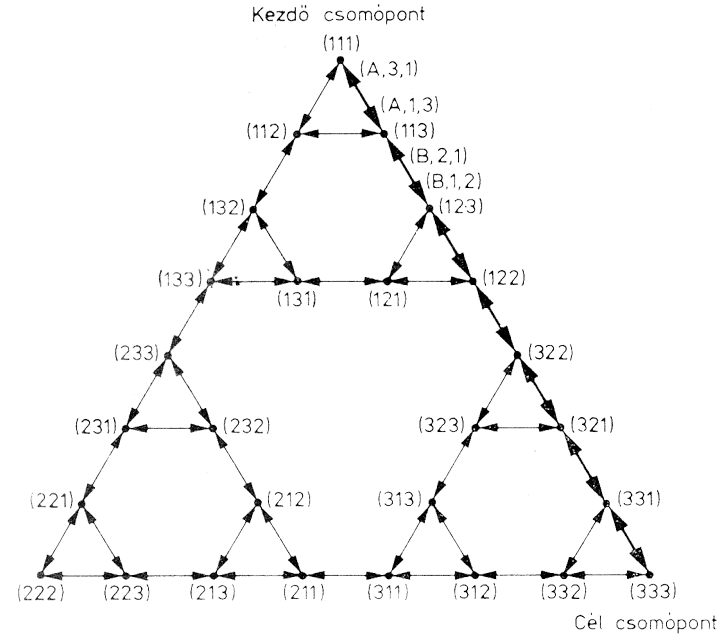
2.7. ábra: A Hanoi tornyai fejtörő gráfja
A gráfnak 27 csomópontja van, amelyek mindegyike egy legális korong elrendezésnek felel meg. A csomópontokban jelöljük, hogy a C, B és A korong éppen melyik helyzetben van. A csomópontok jelölési módjára példákat láthatunk a 2.8. ábrán, ahol az egyes elrendezés alatti zárójelben levő három szám az illető korongelrendezésnek felel meg. A 2.7. gráf csomópontjait ennek megfelelően jelöltük. Természetesen, ha egynél több korong van ugyanazon a tűn, a játék szabályai szerint a legnagyobbnak kell legalul lennie, a kisebbnek felette stb. A csomópontpárokat összekötő él azt jelenti, hogy ha egy korongot az egyik tűről a másikra áthelyezünk, akkor az egyik csomópontnak megfelelő konfiguráció a másiknak megfelelővé változik. Például a (113)-ból (123)-ba mutató él azt jelenti, hogy (113) átalakítható (123)-má azon a módon, hogy a 8 korongot az 1-es tűről a 2-es tűre tesszük át. Ezt a műveletet az élhez írt (8, 1, 2) felirat jelenti. A gráfban vastagabb vonallal kihúzott út adja a legkevesebb lépést tartalmazó megoldást.
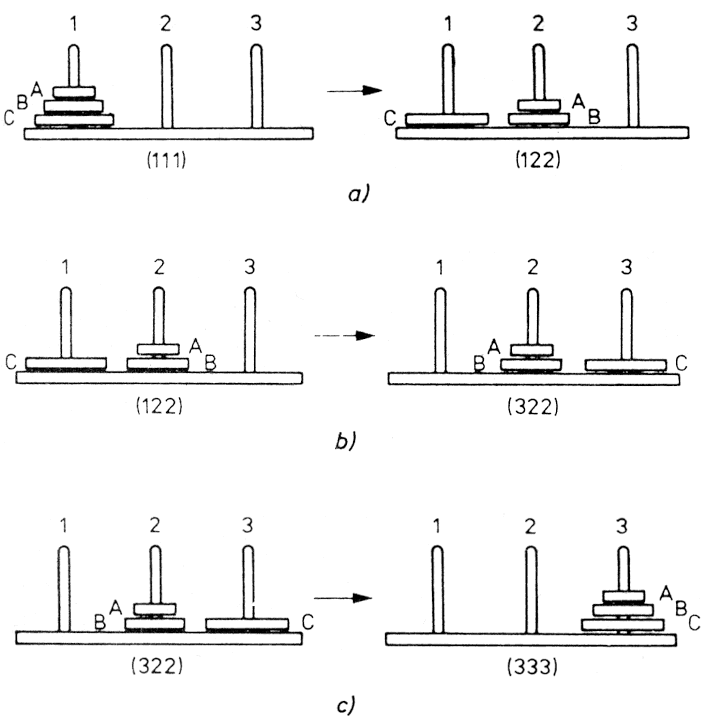
2.8. ábra: A részfeladatra bontás eredménye
A Hanoi tornyai fejtörő megoldható egyszerű feladatredukció módszerével is. Az eredeti, 2.6. ábra szerinti feladat egyszerű (triviális) feladatokra vezethető vissza a következő okoskodási lépések alapján:
Ennek alapján az eredeti feladatot a 2.8. ábra szerinti három egyszerűbb feladatra redukáltuk:
Mivel mindhárom feladat egyszerűbb az eredetinél, tehát könnyebben megoldhatók is.
Tulajdonképpen a 2. feladatot egy igen egyszerű - primitív - feladatnak tekinthetjük, mivel megoldásában csak egy korongmozgatás szerepel. Hasonló okoskodás alapján az 1. és 3. feladat is egy korongossá egyszerűsíthető, ahogy azt vázlatosan a 2.9. ábrán is láthatjuk. Természetesen azonos felépítésű vázlat alapján tetszőleges számú korongot tartalmazó kiinduló konfigurációt is megoldhatunk.
A 2.9. ábrán látható elrendezés a Hanoi tornyai játék ÉS-VAGY gráfja. Ez a feladat olyan részfeladatokra való bontását mutatja be, ahol a "primitív" feladatok már csak egyetlen korong áthelyezését kívánják. Ennél az eljárásnál olyan operátorokat alkalmazunk, amelyek a feladat leírását részfeladat-leírássá transzformálják. A leíráshoz természetesen különböző eszközöket használhatunk fel, pl. listákat, fákat, karakter-sorozatokat, vektorokat, mátrixokat stb. A Hanoi tornyai fejtörő esetén a részfeladatot kételemű listák írják le. A leírásban [(113), (333)] például azt jelenti: "Változtasd meg a (113) konfigurációt (333) konfigurációvá".
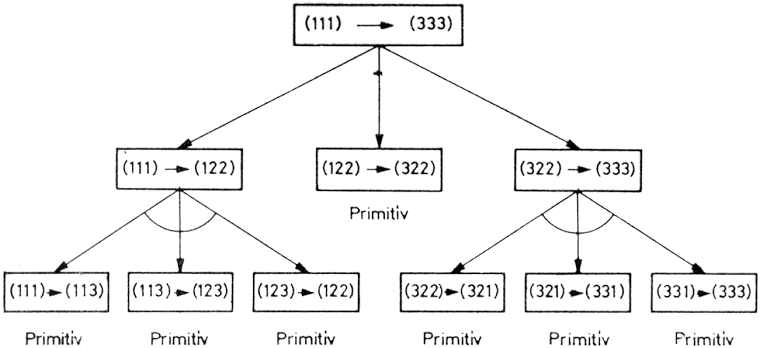
2.9. ábra: A Hanoi tornyai fejtörő részprobléma gráfja
2.1.3. Fokozatos megközelítés - Mastermind
Ez a játék ebben a formájában a legutóbbi években született és terjedt el az egész világon rendkívül gyorsan. ('Logikai játék' néven nálunk is kapható.) A "feltaláló" Mordechai Meirovich amatőr matematikus 1971-ben mutatta be Nürnbergben a játékkiállításon, de csak 1975 karácsonyától indult el "világhódító" útjára. Legismertebb formájában a Mastermind egy műanyag játékdobozból áll, amelynek a tetején lyukak vannak a 2.10. ábrának megfelelően.
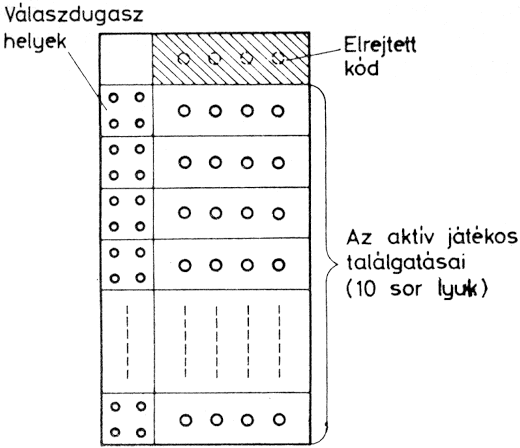
2.10. ábra: A Mastermind-játék alapelrendezése
A játékot ketten játsszák, akik közül az egyik passzív szerepet játszik. Az ő feladata egy kód elkészítése a rendelkezésre bocsátott hatféle színű dugaszok kombinációjából és a másik játékos által nem látható négy lyukba való elhelyezése. (Lehet azonos színű dugaszokat többször is szerepeltetni.) A másik, aktív játékos feladata a kód "kitalálása". Ez a játékos olyan módon találgat, hogy először az első négy lyukat tartalmazó sorban - majd egymás után maximum tíz sorban - különböző színű dugaszkombinációkat dug be. Minden egyes találgatás után a kódkészítőtől "választ" kap, hogy a találgatás milyen "közel" volt az elrejtett kódhoz. A válasz céljára szolgál a bal oldalon levő négy lyuk. Ide annyi fekete dugaszt helyez a kódkészítő, ahány színes dugasz a találgatásnál a kóddal megegyező színű volt abban az esetben, ha ezek a helyes pozícióban is voltak. Minden olyan dugaszra, amely megfelelő színű, de nincs helyes pozícióban, fehér dugasszal válaszol. E válaszok pozíciói csak azt jelzik, hogy valamit kitalált az aktív játékos, de azt nem, hogy a válasz melyik dugaszra vonatkozik. A játék célja, hogy maximálisan tíz találgatással kitaláljuk az elrejtett kódot a válaszok értelmezésével, ill. azok birtokában az egyre "céltudatosabb" találgatással.
2.1.4. Definit játékok - Nim, Batnum, Harapás
A nim egyike a legrégebben ismert kétrésztvevős játékoknak. Állítólag ez is az ősi Kínából származik, amit egyszerű felépítése és ügyes lépésstratégiája is valószínűsít. Európában és Amerikában a XIX. század végén Fan-Tan néven is ismerik. Maga a nim név Charles Leonard Boutontól, a Harvard Egyetem matematika professzorától származik, aki a játék első elemzését 1901-ben publikálta. A név valószínű eredete a niman régies angolszász szó, amelynek a jelentése elvenni vagy ellopni.
A nim játék legegyszerűbb és legismertebb változatában tetszőleges számú tárgy (a manuális változatban pénz, gyufaszál, babszem stb.) tetszőleges számú halomba vagy sorba csoportosítható bármilyen megosztás szerint. A játékosok felváltva vesznek el tetszőleges számú tárgyat (minimum egyet, maximum a választott halomban levő valamennyit) bármelyik, de csak egyetlen halomból.
A játékot az egyik változat szerint az nyeri, aki az utolsó tárgyat leveszi, a másik szerint aki nem az utolsót veszi el.
A nyerés stratégiáját az első változatra Bouton professzor matematikai formában a következőképpen definiálta: Egy elrendezést biztonságos vagy veszélyes kombinációnak nevezett az egyes csoportokban levő elemek számának bináris jelölése segítségével. Eszerint, ha az elemek kettes számrendszerbeli számának a mod 2 összege (független oszloponkénti összeadás, átvitel nélkül) zérus, az elrendezés biztonságos, míg ha ez nem teljesül, veszélyes.
Pl. ha három csoport van, amelyek 8, 7 és 15 elemet tartalmaznak, ezek az előbbi módon a következőképpen ábrázolhatok:
Így ez egy ún. "biztonságos" kombináció. Most nézzük meg a 4, 7 és 2 elemet tartalmazó három csoportot. Ez veszélyes kombinációnak tekinthető:
Tehát könnyen belátható, hogy ha az első játékos olyan módon vesz el valahány elemet egy csoportból, hogy biztonságos kombináció maradjon, a második játékos nem tudja ugyanezt megtenni. (Valamelyik sorból legalább egy 1-et el kell vennie, aminek következtében nulla összeg nem jöhet létre.) Ezzel szemben az első játékos mindig vissza tudja állítani a biztonságos kombinációt. Eszerint, ha a kezdeti elrendezés biztonságos, a második (tehát nem kezdő!!!) játékos nyer, mivel minden lépésével vissza tudja állítani a biztonságos kombinációt.
Pl. ha kezdetben három csoportban, egyenként 4, 5 és 6 elem van, az első játékos lényegében paritásvizsgálatot végez az egyes oszlopokra:
Ennek alapján a 4-es csoportból egy, vagy az 5-ös csoportból három, vagy a 6-os csoportból öt elemet elvéve minden oszlopban páros paritást, vagyis zérus mód 2 összeget, azaz biztonságos elrendezést kapunk, amely a győzelem feltétele.
Eszerint egy adott veszélyes kombinációból többféle módon is kaphatunk biztonságos elrendezést.
A nim játék másik változatában az a játékos veszít, aki az utolsó elemet elveszi. Ebben az esetben az alapvető stratégia nem változik, csupán a biztonságos és veszélyes elrendezések definíciói megcserélődnek.
Ha az egyes csoportokban az elemek számát kezdetben véletlenszerűen választjuk meg, és maximálisan csoportonként 2^m-1 elemet engedünk meg, (ahol m tetszőleges egész szám), k csoport esetén a különböző elrendezések lehetséges száma:
Ha pl. a csoportok száma: k=3
Ebben az esetben a biztonságos kombinációk száma:
Így annak a valószínűsége, hogy kezdetben egy biztonságos kombinációt hozunk létre:
ami egyben annak is valószínűsége, hogy a második játékos nyeri a játékot, feltételezve természetesen, hogy hibátlan stratégiával játszik.
5 RANDOMIZE
10 DEF FN r(x)=INT (RND*x+1)
40 LET n=FN r(4)+2
50 DIM p(n)
60 FOR i=1 TO n: LET p(i)=FN r(7)
70 NEXT i: GO SUB 400
80 PRINT : PRINT "Akar kezdeni (i / n)?"
90 LET i$=INKEY$: IF i$="" THEN GO TO 90
100 IF i$="i" OR i$="I" THEN GO TO 210
110 LET c=0
120 FOR a=1 TO n
125 IF p(a)=0 THEN GO TO 160
130 FOR b=1 TO p(a): GO SUB 500
140 IF c=1 THEN GO TO 190
150 NEXT b
160 NEXT a
170 LET a=FN r(n)
175 IF p(a)=0 THEN GO TO 170
180 LET b=FN r(p(a))
190 LET p(a)=p(a)-b: GO SUB 400
200 IF t=0 THEN PRINT : PRINT "En gyoztem....": GO TO 900
210 INPUT "Melyik halom? ";a
230 IF a<1 OR a>n THEN GO TO 210
240 IF p(a)=0 THEN GO TO 210
250 INPUT "Hany szalat huz? ";b
270 IF b<1 OR b>p(a) THEN GO TO 250
280 LET p(a)=p(a)-b: GO SUB 400
290 IF t=0 THEN PRINT : PRINT "On gyozott!": GO TO 900
300 GO TO 110
400 CLS : PRINT TAB (4);"Nim - 1983, Sparrow Books": PRINT : PRINT "Halom","Gyufaszal"
410 LET t=0
415 FOR i=1 TO n
420 PRINT i,p(i): LET t=t+p(i)
425 NEXT i
430 RETURN
500 LET p(a)=p(a)-b
510 LET q=0: LET r=0: LET s=0
520 FOR i=1 TO n
525 IF p(i)=0 THEN GO TO 550
530 RESTORE : FOR j=1 TO p(i): READ x,y,z: NEXT j
540 LET q=q+x: LET r=r+y: LET s=s+z
550 NEXT i
560 LET p(a)=p(a)+b
570 IF q/2=INT (q/2) AND r/2=INT (r/2) AND s/2=INT (s/2) THEN LET c=1
580 RETURN
600 DATA 0,0,1,0,1,0,0,1,1,1,0,0,1,0,1,1,1,0,1,1,1
900 PRINT : PRINT "Ujra jatszik? (i / n)"
910 LET i$=INKEY$: IF i$="" THEN GO TO 910
920 IF i$="i" OR i$="I" THEN GO TO 40
930 STOP
A nim játéknak nagyszámú változata létezik. Az egyik ezek közül a mátrix elrendezésű nim, amelyet tak-tix-nek is neveznek. Ebben az elemek egy m x n mátrix elemei és a játékosok akár oszlop szerint, akár sor szerint elvehetnek egymással "összefüggő" elemcsoportokat. Az érdeklődők figyelmét felhívjuk arra, hogy az irodalomban sok nim játékváltozat van leírva, amelyek optimális nyerési stratégiája még nincs kidolgozva.
A nim-hez hasonló játékot kaphatunk, ha az elemeket nem csoportosítjuk, de az egyes játékosok által egy lépésben elvehető elemszámot valamilyen szabály szerint megszabjuk. Legegyszerűbb esetben ez a korlátozás így fogalmazható:
1 <= n <= a
ahol n az egyszerre elvehető elemek száma, a pedig ennek maximális értéke. Ebben az esetben a biztonságos elrendezések feltétele, hogy az elemek száma zérus legyen, mód (1+a) szerint végezve az összeadást.
További változatokat kapunk, ha adott egész számok sorozata formájában szabjuk meg ezt az elvételi szabályt, amik lehetnek pl. a prímszámok, négyzetszámok stb. Ilyen játék a Batnum, amelynek programját a ZX Spectrum BASIC-ben adjuk meg, ahol a korlátozás nem csupán az a felső, hanem a b alsó határ megadását is jelenti, vagyis az előbbi jelöléssel: b <= n <= a
10 PRINT TAB (12);"BATNUM"
20 PRINT TAB (6);"CREATIVE COMPUTING": PRINT TAB (4);"MORRISTOWN, NEW JERSEY"
30 PRINT
110 PRINT "A jatekot tetszoleges szamu"
120 PRINT "koronggal jatszuk. A jatekosok"
130 PRINT "(a gep es on) felvaltva vesznek"
140 PRINT "el a megadott min. es max. "
150 PRINT "ertekek kozotti darabszamu"
155 PRINT "korongot."
160 PRINT "A jatekot egyik valtozatban az"
170 PRINT "nyeri, aki az utolso korongot"
180 PRINT "elveszi, a masikban aki az"
190 PRINT "utolsot elkeruli."
192 PRINT "A korongok szamat, az elveheto"
193 PRINT "min es max korongok szamat, hogy"
194 PRINT "ki kezdjen, es ki nyerjen, a"
196 PRINT "program jatek elott megkerdezi."
200 PRINT
210 GO TO 330
220 FOR I=1 TO 10
230 PRINT
240 NEXT I
330 INPUT "Hany korong? ";N
340 IF N=0 THEN GO TO 1080
350 IF N>=1 THEN GO TO 370
360 GO TO 330
370 IF N<>INT (N) OR N<1 THEN GO TO 220
390 PRINT "Ki nyer?"
395 PRINT "1 - aki az utolsot huzza,": PRINT "2 - aki elkeruli ": INPUT M
410 IF M=1 THEN GO TO 430
420 IF M<>2 THEN GO TO 390
430 INPUT "Minimum, maxmimum ";A,B
450 IF A>B OR A<1 THEN GO TO 430
470 IF A<>INT (A) OR B<>INT (B) THEN GO TO 430
490 PRINT "Ki kezd?": INPUT "1 - a gep, 2 - a jatekos ";S
500 PRINT : PRINT
510 IF S=1 THEN GO TO 530
520 IF S<>2 THEN GO TO 490
530 LET C=A+B
540 IF S=2 THEN GO TO 570
550 GO SUB 600
560 IF W=1 THEN GO TO 220
570 GO SUB 810
580 IF W=1 THEN GO TO 220
590 GO TO 550
600 LET Q=N
610 IF M=1 THEN GO TO 630
620 LET Q=Q-1
630 IF M=1 THEN GO TO 680
640 IF N>A THEN GO TO 720
650 LET W=1
660 PRINT "A gep elvesz ";N;"-t es veszit."
670 RETURN
680 IF N>B THEN GO TO 720
690 LET W=1
700 PRINT "A gep elvesz ";N;"-t es nyer."
710 RETURN
720 LET P=Q-C*INT (Q/C)
730 IF P>=A THEN GO TO 750
740 LET P=A
750 IF P<=B THEN GO TO 770
760 LET P=B
770 LET N=N-P
780 PRINT "A gep elvesz ";P;"-t es marad ";N
790 LET W=0
800 RETURN
810 PRINT : PRINT "On jon"
820 INPUT "Hany korongot vesz el? ";P
830 IF P<>0 THEN GO TO 870
840 PRINT "Nulla nem lehet! A gep nyert!"
850 LET W=1
860 RETURN
870 IF P<>INT (P) THEN GO TO 920
880 IF P>=A THEN GO TO 910
890 IF P=N THEN GO TO 960
900 GO TO 920
910 IF P<=B THEN GO TO 940
920 PRINT "Szabalytalan lepes! Ujra!"
930 GO TO 820
940 LET N=N-P
950 IF N<>0 THEN GO TO 1030
960 IF M=1 THEN GO TO 1000
970 PRINT "On vesztett!"
980 LET W=1
990 RETURN
1000 PRINT "Gratulalok, on nyert!"
1010 LET W=1
1020 RETURN
1030 IF N>=0 THEN GO TO 1060
1040 LET N=N+P
1050 GO TO 920
1060 LET W=0
1070 RETURN
1080 STOP
A program először kérdést tesz fel a nyerés feltételére vonatkozóan, majd a két határérték az a és b megadását kéri.
A harapás (eredeti nevén Chomp) is egy nim típusú játék, amelyet David Gale, a kaliforniai Berkeley Egyetem matematikusa talált ki.
A játék alapformája kétdimenziós, és két játékos játssza, de többdimenziós változatai is léteznek és kettőnél több játékos is részt vehet benne.
A harapás-t "manuális" formában zsetonokkal játsszák vagy papírra írt - a zsetonokat jelképező - jelekkel. Kezdetben a zsetonokat egy téglalapnak megfelelően kell kirakni (r sorban, soronként s darab zsetont elhelyezve). A játékosok felváltva általuk kijelölt mennyiségű zsetont vesznek el. Az veszít, akinek az utolsó (bal felső sarokban levő) zseton jut. A szabály a következő: ki kell jelölni egy ri sor- és egy si oszlopszámmal egy zsetont, és e lépés következményeként minden ez alatt levő és ettől jobbra levő zseton (beleértve a kijelöltet is), a lépés következményeként fog "eltűnni". (A játék neve is ebből az elvételi szabályból származik. Tekintsük az eredeti elrendezést pl. egy darab csokoládénak vagy keksznek, amelyből derékszögű darabokat harapunk ki. Az utolsó "kocka" - amely, ha benne van a "falatban" vesztést jelent - "mérgezett".)
A játék célja tehát az, hogy arra kényszerítsük az ellenfelet, hogy neki jusson a bal felső sarokban levő zseton.
Általános érvényű nyerési stratégia a két következő triviális esettől eltekintve nem ismert a játékra:

2.11. ábra: Triviális elrendezések harapásjátéknál
A játék külön érdekessége, hogy bár az bizonyítható, hogy minden esetben létezik egy olyan lépés a kezdő fél számára, amely a győzelmet jelenti, azonban erre vonatkozó általános stratégiát (formulát) eddig létrehozni nem sikerült. A 2.12. ábrán bemutatunk néhány 3 x n méretű elrendezéshez (n = 2, 3, 4, 5, 6, 7, 8, 9) tartozó győzelmet jelentő kezdőlépést. Minden elrendezéshez csak egyetlen ilyen kezdőlépés létezik.

2.12. ábra: Győztes első lépések az n x 3 méretű elrendezés esetén
10 PRINT TAB (12);"CHOMP"
20 PRINT "Creative Computing Morristown,": PRINT TAB (10);"New Jersey"
30 PRINT : PRINT : PRINT
40 DIM A(10,10)
100 REM *** The game of Chomp *** Copyright PCC 1973 ***
120 PRINT "This is the Game of Chomp": PRINT " (Scientific American, Jan 1973)"
130 PRINT : PRINT "Do you want the rules?": PRINT " (1 = YES, 0 = NO!)"
140 INPUT R
150 IF R=0 THEN GO TO 340
160 LET F=1: LET R=5: LET C=7
190 PRINT : PRINT "Chomp is for 1 or more players (humans only)."
200 PRINT
210 PRINT "Here's how a board looks (this one is 5 by 7):"
220 GO SUB 540
230 PRINT
240 PRINT "The board is a big cookie":
250 PRINT "r rows high and c columns wide. You input r and c at the start. In the upper left corner of the cookie is a poison square (p)."
270 PRINT "The one who chomps the poison square loses. To take a chomp, type the row and column of one of the squares on the cookie."
290 PRINT "All of the squares below and to the right of that square": PRINT "(including that square, too) disappear -- chomp!!"
310 PRINT "No fair chomping squares that have already been chomped, or that are outside the original dimensions of the cookie."
330 PRINT
340 PRINT "Here we go..."
360 LET F=0
370 FOR I=1 TO 10
372 FOR J=1 TO 10
375 LET A(I,J)=0
377 NEXT J
379 NEXT I
380 PRINT
390 INPUT "How many players?",P
395 IF P<1 THEN PRINT "Nobody wants to play?": GO TO 390
400 PRINT P;" players."
410 LET I1=0
420 INPUT "How many rows?",R
440 IF R<=9 THEN PRINT r;" rows.": GO TO 470
450 PRINT "Too many rows (9 is maximum)."
460 GO TO 420
470 INPUT "How many columns?",C
490 IF C<=9 THEN PRINT C;" columns.": GO TO 530
500 PRINT "Too many columns (9 is maximum)."
510 GO TO 470
530 PRINT
540 FOR I=1 TO R
550 FOR J=1 TO C
560 LET A(I,J)=1
570 NEXT J
580 NEXT I
590 LET A(1,1)=-1
600 REM PRINT THE BOARD
610 PRINT
620 PRINT TAB (7);"1 2 3 4 5 6 7 8 9"
630 FOR I=1 TO R
640 PRINT I;TAB (7);
650 FOR J=1 TO C
660 IF A(I,J)=-1 THEN GO TO 700
670 IF A(I,J)=0 THEN GO TO 720
680 PRINT "* ";
690 GO TO 710
700 PRINT "P ";
710 NEXT J
720 PRINT
730 NEXT I
740 PRINT
750 IF F=0 THEN GO TO 770
760 RETURN
770 REM GET CHOMPS FOR EACH PLAYER IN TURN
780 LET I1=I1+1
790 LET P1=I1-INT (I1/P)*P
800 IF P1<>0 THEN GO TO 820
810 LET P1=P
820 PRINT "PLAYER";P1
830 PRINT "Coordinates of Chomp?"
835 INPUT "Row?",R1
840 PRINT " Row: ";R1
845 INPUT "Column?",C1
846 PRINT " Column: ";C1
850 IF R1<1 THEN GO TO 920
860 IF R1>R THEN GO TO 920
870 IF C1<1 THEN GO TO 920
880 IF C1>C THEN GO TO 920
890 IF A(R1,C1)=0 THEN GO TO 920
900 IF A(R1,C1)=-1 THEN GO TO 1010
910 GO TO 940
920 PRINT "No fair. You're trying to chomp on empty space!": PRINT
930 GO TO 820
940 FOR I=R1 TO R
950 FOR J=C1 TO C
960 LET A(I,J)=0
970 NEXT J
980 NEXT I
990 GO TO 610
1000 REM END OF GAME DETECTED IN LINE 900
1010 PRINT "You lose, PLAYER";P1
1020 PRINT
1030 INPUT "Again? (1=YES, 0=NO!)",R$
1050 IF R$="1" THEN GO TO 340
Az alapjáték egy érdekes, továbbfejlesztett változata is ismert. A játékosok megállapodnak egy N pozitív egész számban és előállítják ennek az összes osztóját (beleértve N-t és 1-t is). Legyen pl. ez a szám: N=432. Ennek prim tényezői 24x33. Rajzoljunk most egy 5x4 méretű mezőt (az exponensek nagysága +1 alapján). Számozzuk meg az oszlopokat 2 hatványai, a sorokat pedig 3 hatványai szerint. Az egyes zsetonok "értéke" legyen ezen sor- és oszlopszám szorzata. Írjuk be ezt a megfelelő mezőbe (2.13. ábra). A játékosoknak most a választott N szám egy osztóját és annak az összes osztóját kell felváltva elvenniük. Az veszít, aki arra kényszerül, hogy a sarokban levő N számot elvegye. Ha az N számnak két prim osztója van, kapjuk az ismertetett síkbeli játékot, ha három a játéktér háromdimenziós stb. A térbeli elrendezés nyerő lépésének meghatározása már elég nehéz feladat. Erre a változatra számítógép-program még nem készült.
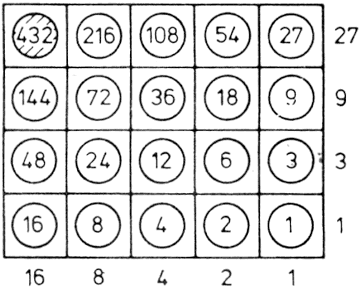
2.13. ábra: A harapásjáték osztó változata
2.2. Táblás játékok
Ezeknél a játékoknál, mint már említettük, a véletlennek nincs semmiféle szerepe, és a játék kimenetelét lényegében a játékosok ügyessége és a játékkal kapcsolatos jártassága, tapasztalata szabja meg. Ezek valamilyen adott elrendezésű játéktéren, a játékra jellemző táblán játszhatók, és a játékban szereplő figurák lépései is ezen a táblán vannak definiálva.
A játék célját tekintve ezek lehetnek:
2.2.1. Elfogó játékok - Halma
A Halmajátékot eredetileg sakktáblán játszották; a tábla átlósan elhelyezkedő sarkaiba helyeztek el négy-nyolc világos, ill. sötét gyalogot. A játék során a figurák léphetnek és ugorhatnak. Lépéseik a sakk király figurája lépéseinek felelnek meg, tehát minden irányban egy kockát mozoghatnak. A saját és az ellenfél figuráit átugorhatják - egymás után többet is - ha a figurák egy vonalban (pl. átlósan) helyezkednek el. A játék célja: a saját figurákat az ellenfél kezdő figuráinak helyébe eljuttatni, minél kevesebb lépéssel, az ellenfél hasonló célú mozgásának megakadályozásával.
A játék általában kétszemélyes (bár van olyan változata, amelynél mind a négy sarokból indulhatnak figurák, ez esetben négyen játszhatják); két - egymással ellentétes - érdekeltségű; a játék során a véletlennek külön szerep nem jut, tehát stratégia készíthető. A lépések viszonylag egyszerűen megfogalmazhatók a számítógépek nyelvén, így ez a játék számítógépesítésre különösen alkalmas.
A 2.14. ábrán egy játszma leírását és néhány részletábráját találjuk meg. A sötét figurákat egy számítógép mozgatta egy csökkentett méretű sakktáblán, amelynek kockái helyett koordináta-rendszer hálóvonalait rajzoltuk. Ezeket a 2.14. ábra részletén jelölt módon 11-től 66-ig számoztuk.
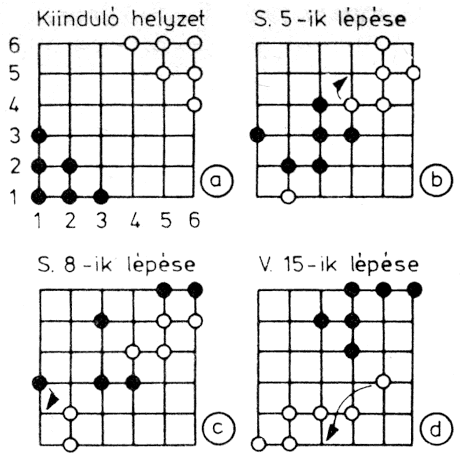 |
|
2.14 ábra:A Káin és Ábel elnevezésű számítógépprogram Halmát játszik
A halmajáték számítógépes programozása a sakkjáték programozásával számos rokonvonást mutat, természetesen lényegesen egyszerűbb körülmények között. A számítógépes program lényege; a helyzet kiértékelése, majd ennek alapján a lehetséges lépések közötti választás. Ha egy figura az A helyről a B-re léphet, és a két hely koordinátái x, y és X, Y továbbá B közelebb van a játék végcéljához, akkor az ún. Manhattan-távolság:
D = (X+Y)-(x+y)
A halmajátékok különböző játékerősségű szinteken írhatók meg. A legegyszerűbb esetben a program kiértékeli az egyes lépésekhez tartozó Manhattan-távolság értékét, és azt a lépést választja, amelynél D a legnagyobb, feltéve, hogy D>2. Ha D=2, a program azt a lépést választja, amelynél a céltól legmesszebb elhelyezkedő figura mozog. D<2 esetén oldallépést választ a számítógép, esetleg véletlenszerűen válogatva a lehetőségek között.
A következő játékerősségszinten a számítógép kiszámítja a saját lépését követő ellenféllépéseket (ezek Manhattan-távolságát C-vel jelöljük) és az E=D-C különbség maximumát választja. Ha több azonos E érték adódik, akkor a legnagyobb C értékű lépést teszi a számítógép. A metódus tovább folytatható, így pl. magasabb játékszintet nyerhetünk, ha az ellenfél lehetséges válaszlépéseinek sorához a saját következő lépésünket is figyelembe vesszük, vagyis a játék fájának elemzését legalább három szintet magába foglaló mélységben végezzük el. Természetesen a lépések meghatározására szolgáló gépi "gondolkodási idő" így tetemesen megnőhet.
2.2.2. Területszerző játékok - Go, Gomoko
A go ősi keleti játék, amit Kínában már sok ezer évvel ezelőtt ismertek. Innen Japánba valamikor az időszámításunk előtti nyolcadik században került és azóta is az egyik legnépszerűbb játék. Bár Európában és így nálunk is alig ismert, érdekességét és a játékok között betöltött szerepét tekintve vetekedik a sakkal. Vannak ugyan olyan, talán elfogult vélemények is, hogy ez a világ legérdekesebb játéka, azt azonban nyugodtan elhihetjük, hogy nehéz elképzelni ma harmadik olyan játékot, ami ezzel a kettővel egyenértékű.
Az általunk is használt go elnevezés Japánban használatos, Kínában wei-ki-nek (vagy wei-chi-nek), Koreában patok-nak ismerik.
A játék alapszabályai nagyon egyszerűek és egyértelműen rögzítettek. Az egyszerű szabályok mellett nagyon bonyolult és főleg sokféle álláselrendezés és szituáció alakulhat ki a játék folyamán. A használatos tábla 18x 18 négyzetet tartalmazó háló, ahol a 19x19=361 csúcspontra helyezhet a két játékos felváltva fekete, ill. fehér korongokat. (Az eredeti játéknál gömbölyű kavicsokat használnak.) A játék összetettségéről már a lehetséges táblaelrendezések száma alapján is fogalmat alkothatunk. A táblán 361 pozíció lehet, ezért a háromféle betöltöttség (azaz fehér, fekete vagy üres) figyelembevételével az összetettségre jellemző szám: 3^361 = 10^172.
Talán egy fokkal jobban megfogható elképzelést alkothatunk a gojátékról, ha összehasonlítjuk olyan jól ismert játékokkal, mint a sakk vagy a dámajáték. Becsüljük ezek lépésszámát egy átlagos játék esetén 50-nek, ill. 20-nak. Vegyük úgy, hogy átlagosan a sakk esetén 5, a dámajáték esetén 3 lépés közül választ a játékos. Így a különböző játékok száma a sakk esetében 5^50 és a dáma esetében 3^20. Ezzel szemben egy tipikus gojáték 300 lépésig tart, és legalább 100 lépésen keresztül 10 lehetséges folytatás közül választhat a játékos. Így legalább 10^100 különböző lefolyású gojáték fordulhat elő a fenti megkötések figyelembevételével. E számok már önmagukban is figyelemre méltóak, de különösen érdekesek akkor, ha a játék számítógépes változata kidolgozásának problémája lebeg a szemünk előtt. Ebben az esetben a variációk nagy száma mellett még azt is figyelembe kell vennünk, hogy a gojátéknak ma nem ismert matematikai formában megfogalmazott elmélete, és rövidesen - a játék szabályainak vázlatos ismertetése után - magunk is be fogjuk látni, hogy nem is várható ennek kidolgozása belátható időn belül.
Lássuk akkor röviden a szabályokat. A go a sakkhoz hasonlóan a "hadijáték", de célját tekintve talán még sokkal közelebb is áll egy valóságos szárazföldi hadjárathoz. A játék célja és egyben a győzelem feltétele ui. a tábla minél nagyobb területének elfoglalása és az ellenfél minél több korongjának körülfogása és ezáltal elfogása. (Az elfogottak a tábláról levehetők.) Egyik játékos 181 fekete, a másik 180 fehér korongot kap. A fekete korongokkal játszó kezd a korongot az általa elfoglalni kívánt szabad táblakereszteződésre (csúcspontra) helyezve, majd a fehér és így tovább felváltva. Az egyszer letett korong nem mozdítható el. A játék egészen addig tart, amíg a teljes tábla megtelik, vagy amíg mindkét játékos egymás után nem "passzol" (vagyis nem tesz), amit a játék folyamán bármelyik, bármikor megtehet, de ekkor egy "elfogott" korongot át kell adnia az ellenfélnek. A játék végén a pontszámot a saját korongjai által körülfogott (elfoglalt) terület és a birtokában levő (elfogott) ellenséges korongok száma alapján számítjuk ki.
A játék szabályai csak vízszintes és függőleges korongelrendezésekre vonatkoznak. Azonos színű vízszintes vagy függőleges elrendezésű korongok láncot képeznek. A láncot (vagy egyetlen korongot) körülvevő szabad (üres) pontok száma az adott elrendezés szabadságfoka. Ha ez zérus, az illető elrendezés fogságba esett. "Öngyilkosság" nem megengedett, vagyis egy játékos nem tehet le úgy egy korongot, hogy azzal saját lánca szabadságfokát zérusra csökkentse. A 2.15. ábrán egy tipikus goelrendezést tüntettünk fel, ahol a fekete korongok egy négytagú fehér láncot már "elfoglaltak".
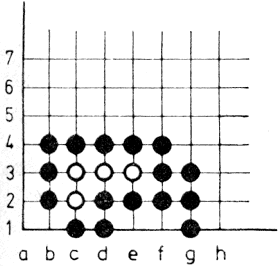
2.15. ábra: Tipikus goelrendezés. 4 fehér korong zérus szabadságfokkal, 16 fekete korong 15 szabadságfokkal
Lehetnek olyan területek, amelyeket már valamelyik fél körülvett, de a belül levő szabad helyeket (ún. szemeket) nem foglalhatja el, mert akkor hátrányba kerül. Egy ilyen, ún. Seki helyzetet mutat a 2.16. ábra, ahol az egyik játékos sem meri a d1 pozíciót elfoglalni, mert akkor a másik körülzárja. Az ilyen Seki területek a végső elszámolásnál nem számítanak.
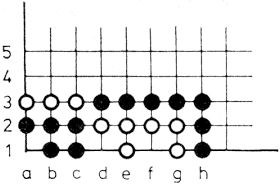
2.16. ábra: Tipikus Seki helyzet. A d1 szemet egyik fél se "töltheti be"
A sakkhoz hasonlóan itt is speciális szabály akadályozza meg a sorozatos lépésismétlést. A Ko szabály szerint ui. tilos elfoglalni egy olyan pozíciót, amely az előző lépésben egyetlen korong elfogása miatt felszabadult. A 2.17. ábrán mutatunk be egy ilyen tipikus "Ko elrendezést". Ha a fehér koronggal játszó játékos d3-t lép és elfog egy fekete korongot, a feketével játszó közvetlenül ezután nem léphet e3-t, ezzel elfogva egy fehéret és visszaállítva az eredeti elrendezést. Ehelyett ha a fekete feltétlenül itt akar "válaszolni" (vagyis megnyerni a Ko-t) először máshol kell fenyegetnie, megfelelő válaszlépésre kényszerítve a fehéret és csak azután foglalhatja el e3-at.
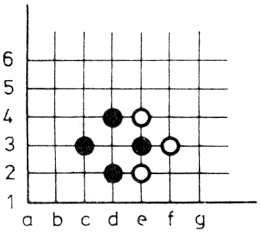
2.17. ábra: Tipikus Ko elrendezés
Lássunk ezen "kvázistatikus" helyzetek után egy valóságos "dinamikus" támadást. A 2.18. ábrán láthatjuk fehér előkészített támadó állását. Fekete hiába akarja megvédeni "hadseregét", ez nem sikerül neki. Fehér a "létra hadművelet" segítségével elfogja a fekete korongjait (2.19. ábra). Ezzel szemben, ha fekete egy további koronggal rendelkezik már kezdetben b4 pozícióban, fehér a nyolcadik lépésben kénytelen c5-t, majd f3-at lépni, hogy megvédje c4 és e5 korongjait. Ezzel a helyzet teljesen másképp alakul (2.20. ábra). Ez a példa is bizonyítja azt a fontos goalapelvet, hogy támadás indításánál óvatosnak kell lenni. Azt is láthatjuk a fenti példából, hogy a kezdőhelyzettől távol levő egyetlen korong is jelentős szerepet játszhat a játszma végső kimenetelében, vagyis a tábla távoli helyein levő korongokat is figyelembe kell venni a stratégia kialakításánál.
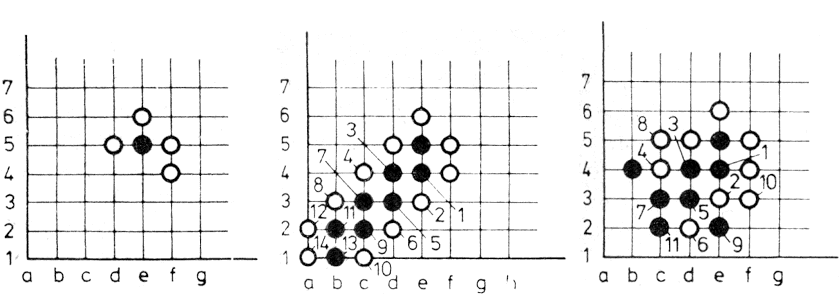 |
||
2.18. ábra: Fehér támadó kezdő elrendezése |
2.19. ábra: A "létra hadművelet" |
2.20. ábra: Sikertelen "létra hadművelet" |
Olyan számítógépprogramot készíteni, amely elfogadható szinten játssza ezt a játékot, még sokkal nehezebb, mint egy sakkozóprogram készítése. A játék természetéből következik, hogy itt is két lehetséges út közül választhatunk. Az egyikhez arra volna szükség, hogy formális alapelvekben rögzítsük le a jó stratégia kívánalmait. Ezek az alapelvek a go esetében azonban még a sakkénál is sokkal inkább kvalitatívek és misztikusan megfoghatatlanok. A következőkben vázlatosan bemutatunk példaként egy olyan programot is, ahol "ismerős" (előre megadott) elrendezések felismerésével és ennek alapján végzett kalkulációval értékeli a gép a lehetséges lépéseket.
A másik követhető út egy "tanuló program" készítése, amely a játékos és a számítógép előző játékainak összegyűjtött tapasztalatai alapján dönt és választja ki a következő legalkalmasabb lépést.
Ahhoz, hogy adott alakzatokat megkülönböztethessünk, nem csupán az egyes korongokat, hanem a környezetüket is figyelembe kell vennünk. Egy lehetséges heurisztikus eljárás a következő: Tételezzük fel, hogy a játék már folyik, és az aktuális táblaelrendezést rögzítettük. Ezt az elrendezést most transzponáljuk át egy olyan 19x19 egész számból álló tömbbé, ahol pl. minden fekete korong +50-et, minden fehér korong -50-et ér és 0-ák vannak az üres helyeken. Ezek után minden olyan pozíció (tömbelem), amely pozitív, +1-et ad át a négy szomszédjának, minden negatív pedig -1-et. E számok összegződnek, az egész eljárást pedig ismételjük meg négyszer. Az ilyen módon kialakított "potenciálok" szerint végezhetjük az egyes táblaterületek szegmentálását. A számértékek az egyes érdekszférákon belüli fehér vagy fekete befolyás mértékére is jellemzők lesznek. A program e tömbön kívül még hat továbbit definiál. Ezek a következők:
A 2.21. ábrán egy olyan elrendezést láthatunk (nevezzük ezt hármas elrendezésnek), amelyet a program képes felismerni. Az A pontban olyan fekete korong van, amelynek szabadságfoka egy. A B pont egy üres hely. C pontban olyan fekete korong van, amely egy biztonságban levő csoport része. A kategorizálás az állásnak megfelelő tömbök numerikus értékelésével történik. A program képes ezen elrendezést a táblán bárhol - bármilyen elforgatott vagy tükrözött formában - felismerni, és az összetettebb elrendezéseket is ilyen elemi elrendezések (ennél a programnál 85-öt definiáltak) segítségével ismeri fel. A program az értékelést szükség esetén 100 lépés mélységnek megfelelően előretekintve is elvégzi, ameddig a tényleges bekerítés befejeződik.
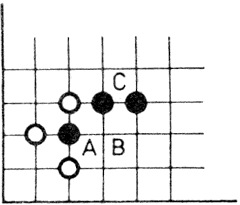
2.21. ábra: Hármas elrendezés
A gojátékot játszó program készíthető olyan módon is, hogy csak a minimálisan szükséges játékszabályokat adjuk meg és a lépéseket - lehetőség szerint - egy összegyűjtött lépéstár segítségével választjuk ki. Ezt a programot ki kell még egészítenünk a tanuláshoz (adatgyűjtéshez) szükséges döntések kiértékelő függvényeivel (sikeres és sikertelen lépések osztályozása), valamint valamiféle pótmegoldással, ha a lépéstárban való keresés nem vezet eredményre. Egy ilyen program alapvető felépítését láthatjuk a 2.22. ábrán.
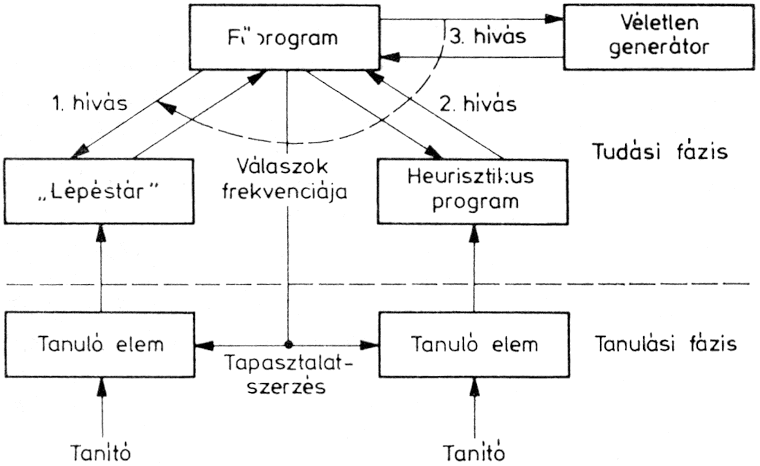
2.22. ábra: Tanuló goprogram felépítése
Először a főprogram meghatározza a játékszabályok szerint megengedett lépéseket. Ezután keresni kezd a lépéstárban egy, az adott elrendezésnek megfelelő, sikeres lépést. Ha több, mint egy ilyet talál heurisztikus alapon, az egyes lépésekhez súlyfüggvényeket rendel. Ehhez a számításhoz figyelembe vett tényezők a következők: a lánc lehetséges és aktuális szabadságfok, az ejtett foglyok száma, az ellenfél által letett legutolsó korongtól való távolság, az adott területen levő saját és ellenséges korongok száma stb. Ezen tényezők lineáris kombinációja a döntési kritérium. Ezt a számítást a program hat féllépés mélységig végzi el a minimax eljárást alkalmazva.
Hasonlóan a tényleges tanulás folyamatához, kezdetben a lépéseket főleg a véletlenszám-generátor (ld. 2.22. ábra) fogja kiválasztani, ezt követően egyre nagyobb szerepet kap a program heurisztikus része és végül a lépéstár, a memória.
Magának a programnak a futása két részből áll egy ún. tudási fázisból, amikor játszik és egy külön tanulási fázisból, amikor a tapasztalatokat feldolgozza. Ez a tanulás a sikeres lépések megkülönböztetésén és rendezett összegyűjtésén túlmenően a lépések súlyozási tényezőinek módosítására is kiterjed. Természetesen a program nem csupán saját lépéseiből tanul, hanem az ellenfél lépéseiből is.
A go tábla ugyanakkor alkalmas arra is, hogy rajta - hasonlóan a sakktábla ilyen másodlagos felhasználásához - alapvetően eltérő célú és alapelvű játékokat játsszanak. Egy ilyen ugyancsak keleti játék a gomoko vagy gomoku. Alapelvét tekintve lényegében megegyezik a tik-tak-to-val, csupán itt öt azonos színű egymás melletti korong (vízszintesen, függőlegesen vagy ferdén) jelenti a nyerő pozíciót.
2.2.3. Akadályozó játékok - Dáma, Hatgyalog
A Dámajáték sakktáblán játszható úgy, hogy a világos és sötét figurákat a sakktábla szembenálló oldalának két-három sorában helyezzük el. A figurák csak átlós irányban mozoghatnak, mozgás közben figurákat (az ellenfélét vagy a sajátot is) átugorhatnak. Ugrás közben - ha arra lehetőség van - irányt is változtathatnak. A játék célja a figuráknak az ellenkező oldalra való átvitele.
A 2.23. ábrán a figurák kezdőhelyzetét mutatjuk be, továbbá a kockák számozását, hogy ezzel a közölt játszma egyértelművé váljék. A leírt játék két ellenfele: az A. L. Samuel által készített számítógépprogram és R.W. Nealey - a dámajátékot mesteri szinten játszó - játékos. A játszmát a számítógép nyerte meg, bizonyítva, hogy a számítógépesjáték- programok igen magas játékerőt képviselhetnek.
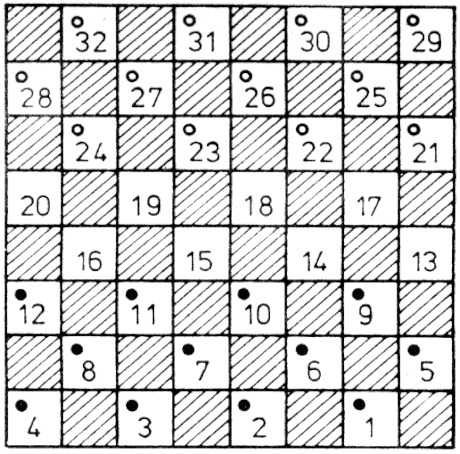 |
|
2.23. ábra: A dámajáték kiinduló állása és egy játszma R. Nealey (világos) és egy számítógép között
Sámuel programja eléggé összetett, készítéséhez a mesterséges intelligenciakutatások számos részeredményét felhasználta. Így pl. a helyzetek kiértékeléséhez ún. parametrikus függvényeket használt, amelyek lehetővé tették, hogy a számítógép a játékok során saját maga javítson taktikáján. Hasonlóképpen módosított a játék fájának kiértékelésén az, hogy az ún. előremetszés technikáját alkalmazta a fa egyes csomópontjainak rendezésénél. Ezzel azt a - játék során triviálisnak tűnő - képességet biztosította programjának, hogy csupán a leginkább kézenfekvő és sikerrel kecsegtető változatok elemzésére fordít időt, a kevéssé magától értetődő megoldások vizsgálata helyett.
Mind a dáma-, mind pedig a halmajáték számítógépes programjai eléggé fejlettek ahhoz, hogy segítségükkel az emberi intelligencia, a döntési szabályok stb. vizsgálatát is végezni lehessen. Csupán szélsőséges példaképpen említjük, hogy a játékok eleven játékosairól a számítógép által készített feljegyzések és elemzések alapján meglehetősen nagy megbízhatósággal vonhatók le következtetések az ún. IQ (intelligenciahányados) nagyságáról, vagy még az esetleges neurotikus tulajdonságok meglétéről is.
A dáma- és a halmajátékhoz hasonló játékot tervezett M. Gardner, amelyet "hat-gyalog"-nak (hexapawn) nevezett el. A játék nagyon egyszerű, mondhatnánk triviálisnak is. Egy 3x3 mezőből álló sakktáblán 6 gyalog helyezkedik el (2.24. ábra). Ezek a következő szabályok szerint léphetnek: egyenesen előre egy üres mezőre; átlósan előre, ha ott ellenséges figura van, ezt le kell venni. (Hasonlít a valódi sakkhoz, itt azonban az en passant lépés hiányzik.) A játék háromféleképpen nyerhető meg:
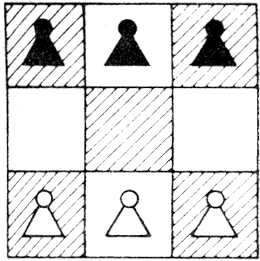
2.24. ábra: a hatgyalog játék kezdő helyzete
Ez az egyszerű játék alkalmas arra, hogy vele egy nagyon érdekes elvi lehetőséget - a tanulást - demonstráljuk. Ezért az alábbiakban bemutatjuk, hogyan tanul meg játszani egy számítógép.
Képzeljük el, hogy a sötét játékos (a számítógép) teszi a második, negyedik, hatodik lépést. A játék elemzéséből kiderül, hogy a gép szempontjából mindössze 24 megkülönböztethető helyzet létezik (2.25. ábra). Az ábrán feltüntettük az egyes helyzetekhez tartozó lehetséges lépéseket is, a megkülönböztethetőség érdekében eltérő módon jelölve őket (egyszerű, kettős, pontozott nyilak).
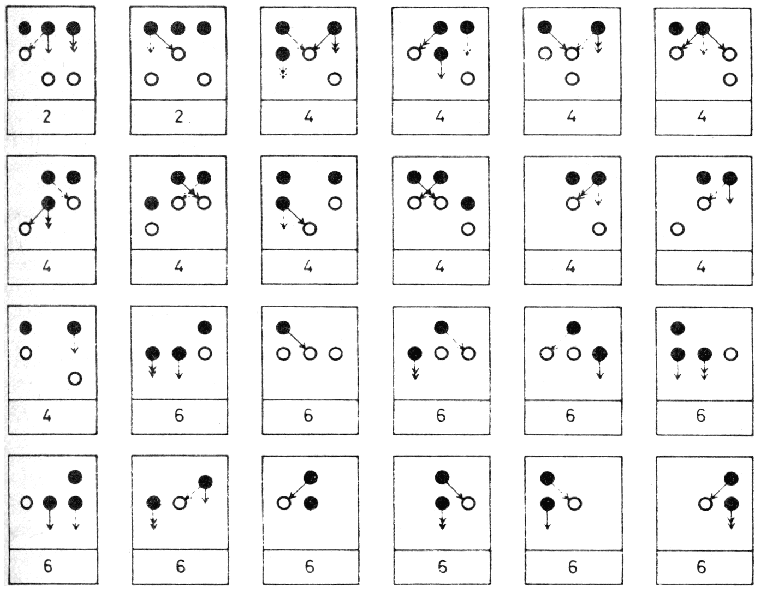
2.25. ábra: A hatgyalog játék lehetséges állapotai
Most képzeljük el, hogy a 24 helyzetnek megfelelően 24 gyufásdobozba a nyilak számától függően két vagy három színes golyót teszünk. A golyók színe egyértelműen utal a lépésre: pl. a piros golyó a pontozott nyílnak felel meg. A játék a következőképpen zajlik: amikor a számítógép kerül sorra, először megkeresi azt a dobozt, amelyik a táblán található helyzetnek felel meg. A dobozban található golyókat összerázza, majd "behunyt szemmel" kiemel egyet közülük. A golyó színének megfelelően lép, ezzel azt is biztosítja, hogy csak legális lépéseket tesz.
A számítógép tehát véletlenszerűen lép, semmiféle stratégiája vagy taktikája sincs. Véletlenül nyer vagy veszít - nagyon "buta" játékot folytat. Mód van azonban arra, hogy a számítógépet tanítsuk. Ha veszít, akkor pl. a golyóknak a következő játékhoz való visszarakásánál a vesztes lépést eredményező golyót "elkobozzuk", nem tesszük vissza. Így a számítógép nem fogja tudni ezt a hibát még egyszer elkövetni. Ezt az eljárást több játszmán keresztül ismételve egyes dobozok teljesen kiürülnek, a többiben pedig csak a nyerő játszmához szükséges golyók maradnak benn. A 2.26. ábrán azt láthatjuk, hogyan lett a számítógépből 11 vesztett játszma árán tökéletes játékos.
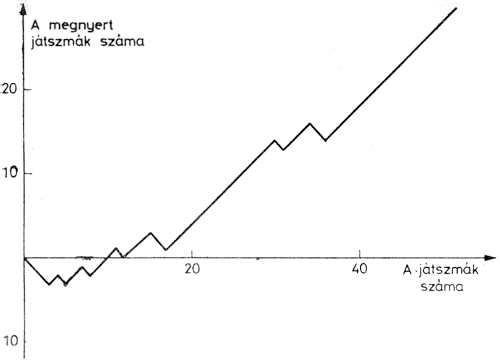
2.26. ábra: A gépi tanulás folyamata a hatgyalog játéknál
A gép az első három játszmát elvesztette, majd egyet megnyert, újra egyet vesztett, kettőt nyert stb.
Nagyon érdekes, hogy a számítógépet nem csak "büntetéssel" lehet oktatni, hanem "jutalmazással" is. Ilyenkor nyertes játszmák esetén a játszma során kihúzott golyókkal azonos színű golyókból kettőt helyezünk vissza, ezzel növeljük a gép nyerési esélyeit. Persze előfordulhat, hogy a számítógép egy-egy játszmát elveszít, ennek valószínűsége azonban a megnyert játszmák számával arányosan csökken.
Természetesen az első lépést tevő játékos számára is kidolgozhatunk egy teljesen hasonló rendszert. Nincs akadálya annak, hogy e két tanuló rendszert egymással szembeni játékra késztessük. Ilyenkor a játék igazi öröme helyett a pártatlan "kibic" érzelemmentes pozíciójából élvezhetjük a tőlünk függetlenné vált küzdelmet.
A szakirodalomban megtalálható olyan program leírása, amely a vázolt elvek szerint tanul. A program induláskor nagyon buta, az ismételt játékok során azonban egyre jobban játszik. Érdekes, hogy jól játszó ellenféltől a program gyorsabban tanul. Bár a program BASIC nyelven íródott, mégsem közöljük, mert utasításai a szabványosnak tekinthető BASIC-től ugyancsak eltérnek. Az utasítások átírása sok vesződséggel jár, - egyszerűbb, ha az Olvasó gyakorlásként a fent vázolt elvek alapján maga készíti el,a programot olyan utasításokat használva, amelyek gépi értelmezése nem okoz nehézséget.
Ebben a fejezetben két témakörről lesz szó részletesebben. Az első témakörbe tartozókat "fejtörőknek, rejtvényeknek, érdekességeknek" nevezhetjük. Ezek egyszemélyes időtöltések, ahol a játékos "küzd" a rejtvény megfejtéséért, a feladat megoldásáért.
A rejtvények igen tág spektrumából olyanokat választottunk ki, amelyek megoldásaira a "számítógépszerű gondolkodás" jellemző. Ilyen eljárásokat az ember a saját fejével gondolkodva csak ritkán választana. Talán meglepőnek tűnik, hogy a rejtvények között geometriai alapokon nyugvó feladatok nem szerepelnek. Ennek oka az, hogy eltolható, elforgatható stb. geometriai elemekkel igen nehézkesen boldogulnak a számítógépek. Az általunk választott gépkonfigurációk lehetőségeit ezek a feladatok meghaladják.
A fejezet második részében olyan játékokat ismertetünk, ahol a játékosoknak a játék menetére semmiféle befolyásuk sincs. Ezeket a játékokat a nyereség vagy veszteség izgalma teszi érdekessé, no meg az a matematikailag téves, de pszichológiailag igazolható feltételezés, hogy van valami szabályosság mégis pl.: "négy piros után most már biztosan feketének kell következnie"
A kártyajátékok különböző változataiban különbözőképpen keveredik a véletlen és a jó játékstratégia jelentősége. A huszonegyesben még a véletlen dominál, a verseny-bridzsben pedig ennek a szerepe szinte zérusra csökken.
3.1. Játék a számokkal
A játékok, fejtörők nagyon jelentékeny részében számok szerepelnek. Ezeken belül találjuk az ún. matematikai fejtörők csoportját. Ezek megoldása olyan ismert algoritmusok valamelyikén alapul, amelyek precíz matematikai formában megadhatók. Most ezek közül mutatunk be röviden néhány olyat, amely egyszerű módon számítógépesíthető, vagyis számítógépprogram formájában is megfogalmazható.
3.1.1. A 15-ös fejtörő
A játékot, amelyet bizonyára mindenki ismer, mivel "manuális" változata mindenhol kapható, 1878-ban Sam Loyd találta ki sok hasonló fejtörővel együtt. A 15-ös fejtörőt, amelyet valamilyen okból Amerikában a Boss Puzzle (Főnök fejtörője) néven is emlegetnek, azóta is szinte mindenki kipróbálta vagy még az iskolaévek alatt (egy-egy unalmas órán) vagy később az életben valamilyen adandó alkalomból.
A játék célja egy - 15 különböző számból álló - konfigurációt átrendezni valamilyen más megadott sorrendnek megfelelően (ld. pl. a 3.1. ábrát.)
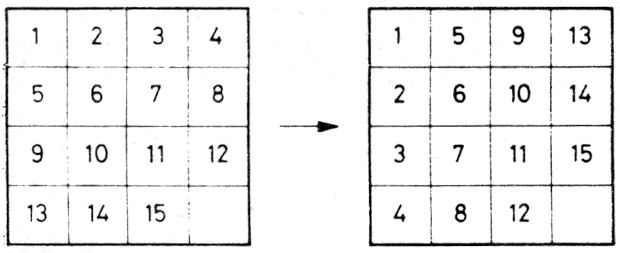
3.1. ábra: Két 15-ös elrendezés
A bal oldali elrendezést kell a jobb oldalon megadott sorrendbe átrendezni
A játék 15 számozott négyzet alakú lemezkéből (amely készülhet például műanyagból, fából vagy fémből) áll, melyek szabadon csúszkálhatnak egy dobozban. Ebben a dobozban 4x4 = 16 hely van, ezért egy hely mindig szabad. Az eredetileg beállított elrendezésből a célul kitűzött elrendezést úgy kell elérni, hogy csak csúsztatni szabad a lemezeket, de a dobozból kiemelni nem. (A kereskedelemben kapható megoldásoknál a doboz kialakításával ezt biztosítják is.) Így pl. a 3.1. ábra szerinti alapelrendezésnél az első lehetséges lépést csak a 12. vagy 15. lemezke teheti.
Már a játék megjelenése után röviddel, amikor nagy díjat tűztek ki egy látszólag egyszerű elrendezés kialakítására, kiderült, amit később matematikailag is bizonyítottak, hogy csak a lehetséges
16! = 20 922 789 888 000
különféle elrendezés fele, azaz 10 461 394 944 000 valósítható meg. Itt most nem bizonyítjuk matematikailag az eljárás alapelvét, amelynek segítségével eldönthetjük, hogy egy adott számelrendezés megvalósítható-e vagy sem, csupán az algoritmust közöljük. Ez a következő:

3.2. ábra: A 15-ös fejtörő pozícióinak azonosítói
Példaként a 3.3. ábrán bemutatunk egy megvalósítható és egy nem megvalósítható számelrendezést.
 |
|
a. |
b. |
3.3 ábra: Példa egy megvalósítható és egy nem megvalósítható elrendezésre
A kiinduló állapot mind a két esetben a 3.1. ábra bal oldali sorrendjének felel meg
Az ismertetett eljárásnak megfelelő számítás menetét a 3.1. táblázat alapján kísérhetjük nyomon.
Betű pozíció |
M-nél kisebb szám |
|
3.3a. ábra elrendezése |
3.3b. ábra elrendezése |
|
A B C D E F G H I J K L M N O P |
6 6 6 6 5 0 0 3 2 1 0 0 3 2 1 0 |
14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 0 |
| Összeg | 41 |
105 |
| "üres pozíció" | +1 |
+0 |
| végösszeg | 42 (páros) |
105 (páratlan) |
3.1. táblázat: A 3.3. ábra szerinti számelrendezések kiértékelése
A fenti algoritmust számítógépprogram segítségével is előállíthatjuk. A program a 3.4. ábra szerinti folyamatábrát valósítja meg. Az elérendő elrendezés pozícióinak számértékét az INPUT művelet kérdőjele után sorfolytonosan kell beírni, az egyes értékeket vesszővel elválasztva egymástól. (Az üres pozíciót 16-os érték jellemezze ismét.)
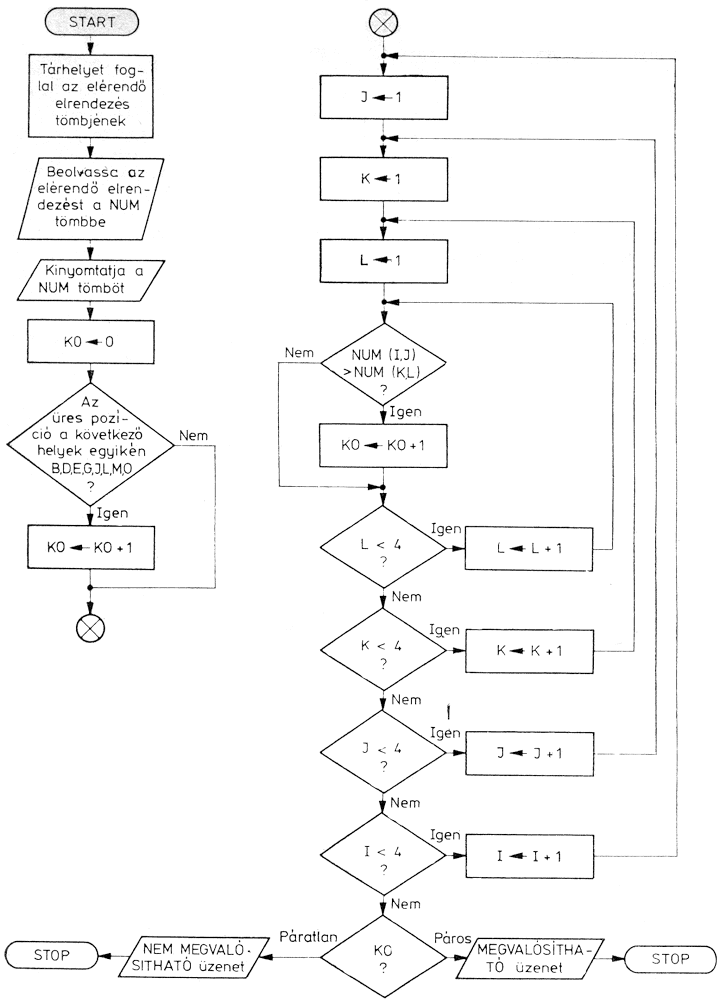
3.4. ábra: 15-ös fejtörő kiértékelő program folyamatábrája
Maga a 15-ös fejtörő ugyanakkor nagyon alkalmas arra is, hogy segítségével a feladatmegoldás módszereit általánosabban is illusztráljuk. Ez a játék ugyanis pontosan definiált kezdőállapottal, precízen meghatározott végső állapottal (céllal) jellemezhető, és azok a lépések is ("műveletkészlet"), amelyekkel egyik állapotból a másikba juthatunk pontosan adottak és ugyanakkor egyszerűek és kézenfekvőek is. A megoldási módszerek tárgyalásához vezessünk be két fogalmat, az állapotot és az operátort.
Esetünkben az állapot nem más, mint egy adott számelrendezés a játékban. Ennek megfelelően beszélhetünk kezdeti és célállapotról is. Az állapottér pedig tartalmazza mindazokat a számelrendezéseket, amelyeket a kezdeti állapotból elindulva létrehozhatunk olyan módon, hogy a számokat a megengedett módon elmozdítjuk helyzetükből. A 15-ös fejtörő esetében ez az állapottér rendkívül nagy lesz, mivel már láttuk, hogy a lehetséges 16! különböző konfiguráció fele (kb. 10,5x10^12) megvalósítható egy adott kezdeti elrendezésből kiindulva.
Az operátor transzformálja át egyik állapotot egy másik állapotba. A 15-ös fejtörő legtermészetesebb módon úgy értelmezhető, hogy négy operátorunk van a lehetséges elmozdulásoknak megfelelően. Vagyis az üres pozíciót mozgathatjuk jobbra, balra, fel és le. (Természetesen lesznek olyan szélső helyzeteink is, amikor egy vagy két operátort nem alkalmazhatunk.)
Így most már az állapotok és operátorok "nyelvén" fogalmazhatjuk meg feladatainkat: a 15-ös fejtörő adott elrendezéspárjának megfelelő megoldását. E szerint a kezdő-állapotból a célállapotba az operátorok sorozata viszi a rendszert.
Szokásos és hasznos a kezdeti állapotból elérhető állapotok terét egy gráfnak elképzelni. A gráfban a csomópontok az állapotoknak felelnek meg, az őket összekötő élek pedig az operátorokat jelentik. A 15-ös fejtörő ilyen módon értelmezett gráfjának egy kis részletét láthatjuk a 3.5. ábrán, ahol a gráf csomópontjait magukkal a megfelelő számelrendezésekkel jellemeztük. A 15-ös fejtörő most már olyan módon oldható meg, hogy először a kezdeti állapotokra alkalmazzuk az operátorokat új állapotokat létrehozva, majd ezekre vonatkoztatjuk az operátorokat egészen addig, amíg a célállapotot létre nem hoztuk. A végső állapot keresésének szervezésére és az ehhez kapcsolódó módszerek kialakítására általában a gráfábrázolás nagyon alkalmas. Az adott feladat megoldásánál a már megismert állapottér módszert alkalmazzuk.
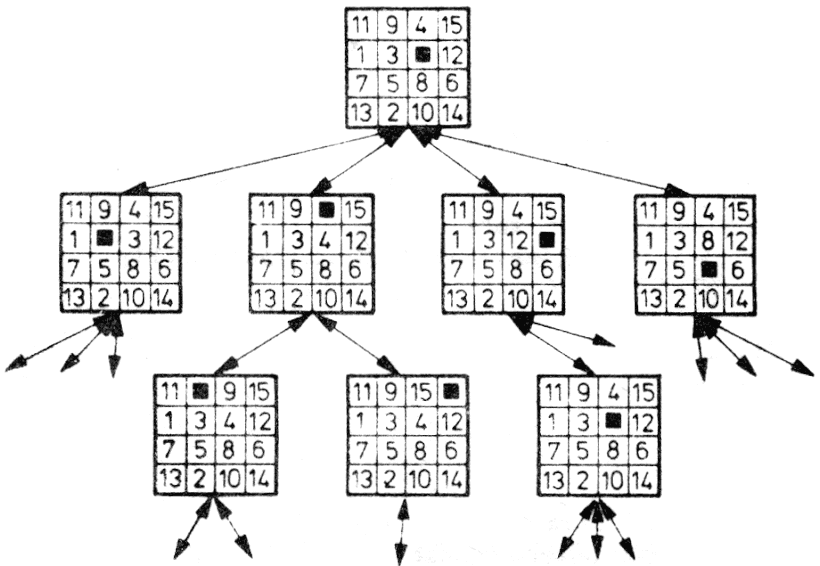
3.5. ábra: A 15-ös fejtörő gráfjának egy részlete
Az operátorok alkalmazásával a kezdőállapotból fokozatosan létrehozzuk az állapotteret. A tér kialakítását először szélesség szerint haladva végezhetjük, de az éppen létrehozott csomópontból továbbhaladva először a mélységet is növelhetjük. Mindkét módszert a "vakon való keresés" eljárásának is szokták nevezni, mivel a célállapot helye nem befolyásolja az állapottér kialakításának sorrendjét.
A továbbiakban a módszerek világosabb bemutatása kedvéért vizsgálatainkat gráfok helyett az ún. fákra korlátozzuk. (A fák ebben a leegyszerűsített formában tehát olyan gráfok, amelyekben minden csomópontnak - a kezdőpont vagy "gyökérpont" kivételével - egyetlen meghatározott megelőző csomópontja, más szóval "szülője" van.)
A fák segítségével való végállapot-keresés ezért lesz egyszerűbb, mert ebben az esetben, ha egy új csomópontot generálunk, biztosak lehetünk abban, hogy az előzőleg még nem szerepelt és később sem fog újból szerepelni. (Ez az egyszerűsítés a 15-ös játéknál azt fogja jelenteni, hogy egy számelrendezésnek megfelelő állapotot csak egyetlen módon hozunk létre a vizsgálat során.)
A módszer bemutatásakor további egyszerűsítésként nem a 15-ös fejtörővel, hanem az azzal elvileg azonos, de egyszerűbb felépítésű 8-as fejtörővel fogunk foglalkozni. (Az egyes állapotokat egy másik állapotba átvivő operátorok a 3.6. ábra szerint definiált ún. átírási szabályok szerint működnek.)
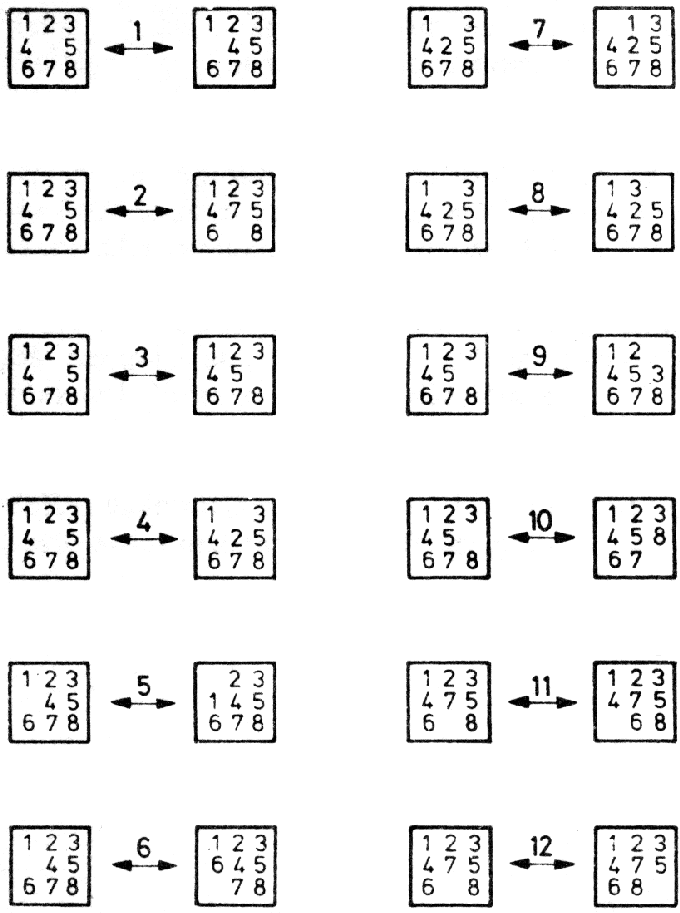
3.6. ábra: a 8-as fejtörő átírási szabályai
Legyen a feladat a 3.7. ábra szerinti kezdő-állapot átalakítása az adott végállapotra.
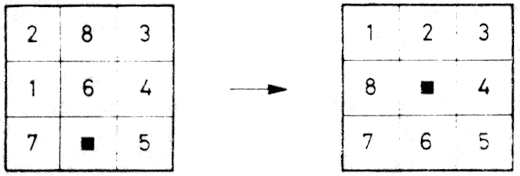
3.7. ábra: 8-as fejtörő feladat
A szélesség szerinti fagenerálás alapján haladva a 3.8a ábrán a számok sorrendjében hozzuk létre az egyes csomópontoknak megfelelő állapotokat. Az ábrán látható módon a megoldáskor 46 csomópontot generáltunk és a célt 26 lépés után értük el.
Lássuk most ugyanezt a feladatot a mélység szerint haladva először a fa generálásánál. Ekkor a 3.8b ábra szerinti fát kapjuk ahol a számok ismét a csomópontok létrehozási sorrendjét jelzik.
Bár a megoldást megadja, mindkét "vakon való keresés" módszere nagyon fárasztó, mivel az eredmény eléréséhez igen sok csomópont generálása szükséges. A számítógépes megoldásnál ez azt fogja jelenteni, hogy a számolási idő túl hosszú, a tárkapacitásigény pedig túl nagy lesz, ami azt jelenti, hogy idő és hely hiányában a program gyakorlatilag nem is lesz futtatható.
Ezért hatásosabb keresési algoritmusra van szükségünk. A sok ismert eljárás közül most ismét csak egyet mutatunk be, az ún. irányított keresés módszerét (3.8c ábra).
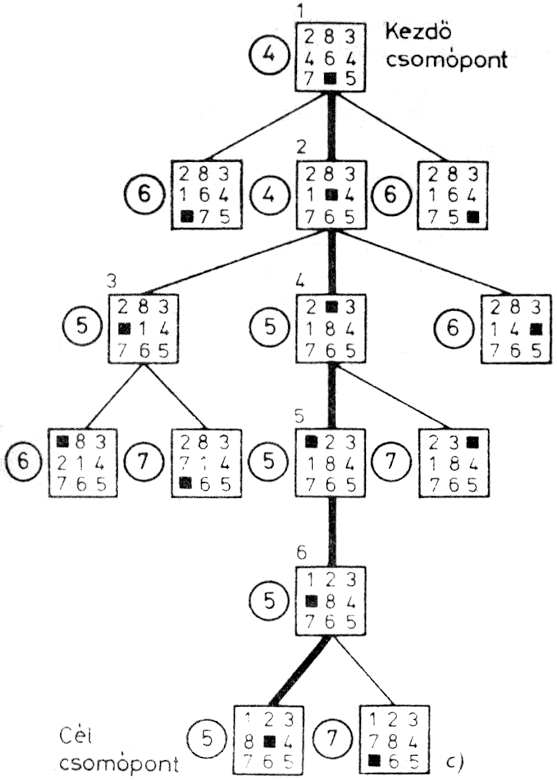
3.8c. ábra: A 8-as fejtörő irányított keresés segítségével generált fája
A módszer lényege abban van, hogy mielőtt egy adott csomópontban továbbhaladnánk, valamilyen módon értékelnünk kell a lehetséges utakat és választani közülük. Eszerint tehát valamilyen mérőszámot kell rendelnünk a lehetséges folytatásokhoz és ennek alapján a "legígéretesebb" irányba továbbhaladni. Ezt a mérőszám-hozzárendelést az ún. értékelőfüggvények segítségével végezhetjük el. Természetesen az értékelőfüggvény "jósága" (objektivitása!) egyértelműen meg fogja szabni a keresés eredményességét. Mivel az optimális értékelőfüggvény meghatározásának módszerei túl messzire vezetnének, a módszert ismét csak példákkal illusztráljuk.
Legyen a feladat még mindig a 3.7. ábrán megadott kezdeti elrendezésből az ugyancsak ott szereplő végállapot elérése. Használjuk a következő egyszerű értékelőfüggvényt:
f(n) = g(n) + h(n)
ahol g(n) az n csomópontban a fa úthossza (szakaszainak száma) a kezdőponttól, h0(n)=W(n) pedig az n-edik csomóponthoz tartozó állapotban még nem a végső állapotnak megfelelő helyen levő számlemezkék száma.
Így pl. a kezdőpontban, ahol g(1)=0, a W(1)=4, mivel a 2, 8,1 és 6 nincs még jó helyen. Így
f(1) = g(1) + W(1) = 0+4 = 4
Irányított keresésnek nevezzük azt, amikor olyan csomópontokat kell keresni, ahol f(n+1)<f(n). Ezek a csomópontok ugyanis "közelebb" vannak a célcsomóponthoz, mint a megelőzőek.
Az irányított keresés algoritmusa - fenti értékelőfüggvény alkalmazásával a 3.8c ábra szerinti fát eredményezte. Az ábrán a csomópontok létrehozásának sorrendjét az állapotokat bemutató táblák feletti számok jelzik, míg az egyes csomópontok melletti bekeretezett számok a megfelelő f(n) értékek. Láthatjuk, hogy ez a megoldás lényegesen kevesebb csomópont létrehozását tette szükségessé, így számítógépes változata is lényegesen kevesebb számolási időt és tárkapacitást igényel. Azonban h0(n) értékének a fenti - a még nem a helyükön levő W(n) lemezkék számával való jellemzése - nem ad jó eredményt, ha bonyolultabb feladatot oldunk meg, mivel nem nyújt felvilágosítást az elrendezés bonyolultságáról vagyis a végállapot eléréséhez szükséges lépések számáról.
Ebből a szempontból jobb becslést jelent
h1(n)=P(n)
szerinti értékelés, ahol P(n) minden lemezke, a célállapotban elfoglalt helyétől vett távolságának összege. Azonban még ez a függvény sem veszi figyelembe két szomszédos lemezkepozíció szükséges megcserélésének nehézségét.
Ezen utóbbi problémát is figyelembe vevő, jó hatásfokú értékelést a következő összefüggés ad:
h2(n) = P(n) + 3S(n)
ahol az S(n) mennyiség a sorrendre vonatkozó "pontérték", amelyet olyan módon kapunk, hogy minden olyan lemezkének, amelyet nem a megfelelő számú lemez követ, 2 pontértéket, a többieknek 0 pontértéket, a középen levőnek 1 pontértéket adunk.
Az f(n) = g(n) + h(n) összefüggés szerint kiszámított értékeket tüntettük fel bekeretezett formában a 3.9b ábrán, ahol a 3.9a ábra szerinti feladatot megoldó, irányított keresés segítségével létrehozott fát láthatjuk.
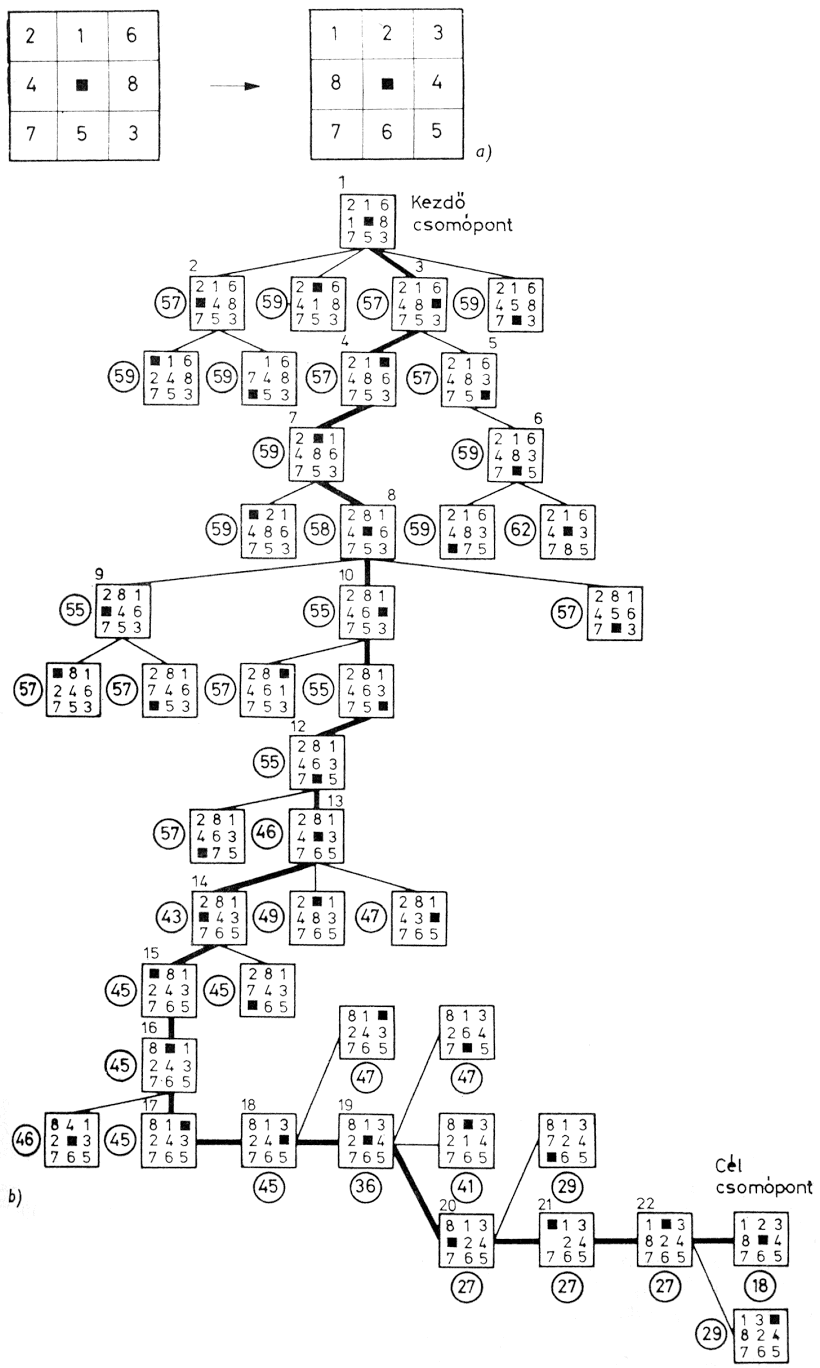
3.9. ábra: 8-as fejtörő feladat
a) elrendezése; b)irányított keresése
Végezetül meg kell még jegyeznünk, hogy az értékelőfüggvény kiválasztásánál fontos szempont az is, hogy mennyi számolási munkával jár a h(n) szerinti értékelés, mivel ez a futási idők értékét jelentősen befolyásolja.
3.1.2. Bűvös négyzetek
A bűvös négyzetek talán a számokkal való játékok közül a legrégebbiek és ugyanakkor legjobban ismertek is. Maga a bűvös négyzet egy olyan számelrendezés, ahol négyzet alakban számokat ábrázolunk úgy, hogy minden sorban és oszlopban azonos darabszámú szám van. A bűvös négyzet n-edrendű, ha egy-egy oldalán n darab számot tartalmazó cella van.
Egyik csoportban a bűvös négyzetekben a számok úgy vannak elrendezve, hogy minden egyes sorban, oszlopban és a két fő átlóban szereplő számok összege megegyezik. Ezt a különös számot (vagyis az előbbi módon definiált összeget) szokták bűvös számnak (B) hívni.
Ha a bűvös négyzetben szereplő számok az 1 és az n^2 közötti számok, akkor a B bűvös szám a következő formulával számítható:
ahol n a négyzet mérete.
Tehát pl. 5x5 méretű négyzet esetén
B5 = 5x26/2 = 65
Ha a számtartomány p-től (n^2+p-1)-ig terjed, akkor a bűvös szám
ahol p a kezdőérték és n a négyzet mérete.
Adott rendű bűvös négyzet előállításának számos egyszerű módszere van, ezek közül egy-kettőt bemutatunk.
Harmadrendű bűvös négyzet csak egy van, de ez nyolc különböző formában jelenhet meg, ha a tükrözéseket és a 90 fokos, a 180 fokos és a 270 fokos elforgatásokat is figyelembe vesszük. Ezzel szemben negyedrendű 880 van (itt, ha a tükrözéseket és elforgatásokat is figyelembe vesszük 7040) és az ötödrendű bűvös négyzetek száma már több, mint tizenhárom millió!
A páros rendű és páratlan rendű négyzetek előállítása különböző. (Itt a "rendűség" tulajdonképpen a négyzet "méretét" jelenti.)
Páratlan rendű bűvös négyzetet pl. az Agrippa-módszer segítségével generálhatunk. Az eljárást egy 5x5-ös négyzet előállítása kapcsán mutatjuk be (3.10. ábra).
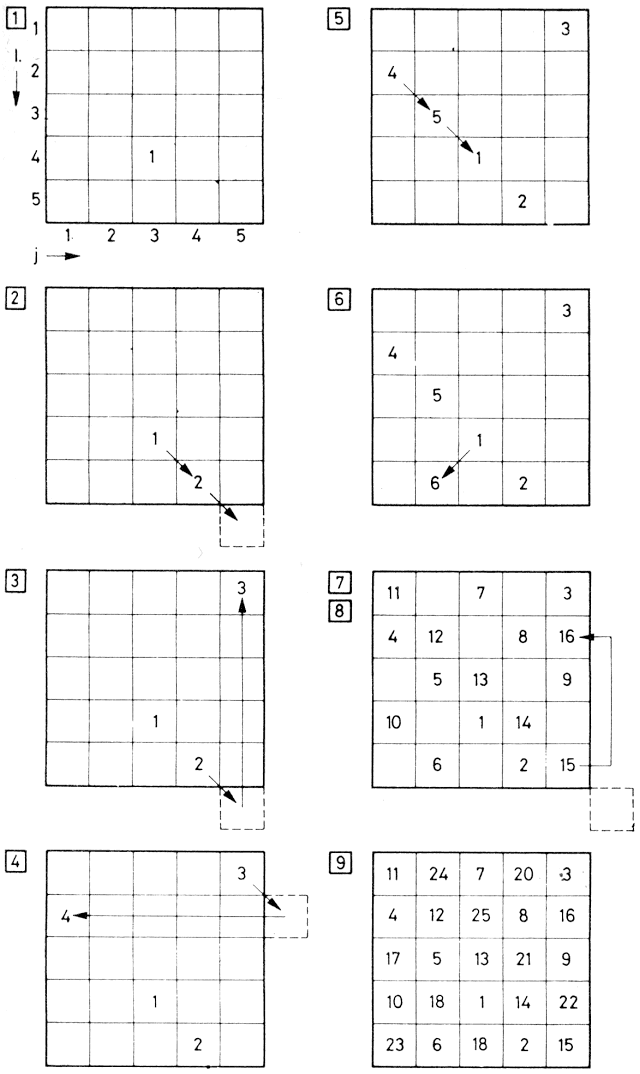
3.10. ábra: 5x5 méretű bűvös négyzet előállításának menete az Agrippa-módszer alkalmazásával
Az Agrippa-módszer segítségével adott (maximálisan 21x21) méretű bűvös négyzetet generáló program folyamatábráját a 3.11. ábrán láthatjuk.
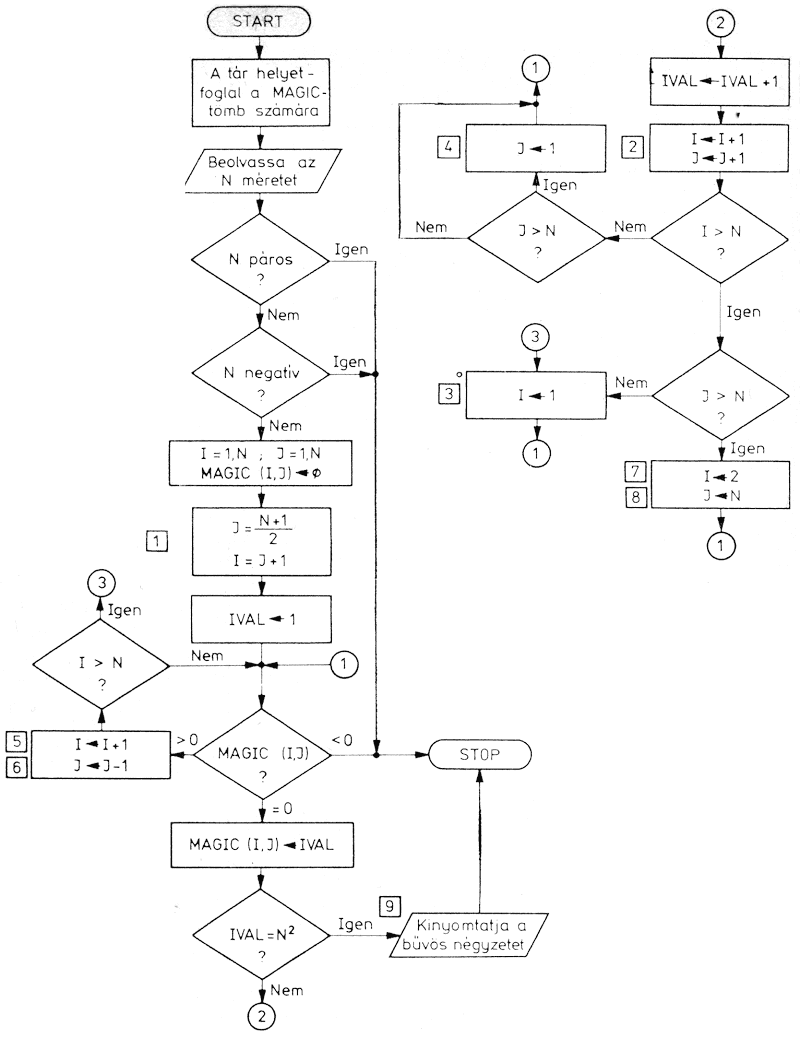
3.11. ábra: Az Agrippa-eljárást felhasználó bűvösnégyzet-generáló program blokkvázlata
A program először beolvassa a négyzet méretét (N) és ellenőrzi, hogy az megfelelő szám-e. Ezután a bűvös négyzet számára fenntartott MAGIC tömb minden elemét (tárhelyét) nullára állítja. Az I (sor) és J (oszlop) indexek jelölik ki a cella helyét a tömbben. Az indexek beállított kezdőértéke:
J = (N+1)/2 és I = J+1
A program egy változóban (IVAL) tárolja a következő betöltendő számértéket amely 1-től N^2-ig fog változni.
Az Agrippa-módszer szerint haladva megvizsgálja a MAGIC tömb minden egyes celláját és, ha MAGIC (l,J)=0, beírja a cellába az IVAL változó aktuális értékét.
Ha az indexek meghaladják a négyzet méretét, vagy már nem üres elemet talál a program, az Agrippa-eljárás szerint jár el. Végezetül kinyomtatja a teljes NxN méretű bűvös négyzetet.
Ha a 15-ös fejtörőben az üres mező "értékét" 16-nak tekintjük, tulajdonképpen egy 4x4 méretű bűvös négyzethez jutunk. Itt a bűvös szám értéke:
Ennek alapján szokták ezt a játékot 34-es fejtörőnek is nevezni. A feladat tehát olyan számelrendezés előállítása, amely egyrészt megfelel a bűvös négyzet szabályainak (minden sorban, oszlopban és a főátlókban szereplő számok összege 34) kiegészítve azzal, hogy itt minden egymás mellett levő négy számból álló (összesen kilenc féle) csoport összege is 34 kell, hogy legyen. A 3.12. ábrán bemutatunk néhány az előbb ismertetett szabályoknak megfelelő "megoldott" 34-es fejtörő elrendezést is.
|
|
||||||||||||||||||||||||||||||||
|
|
3.12. ábra: Megoldott 34-es fejtörő elrendezések
Bűvös négyzetek másik csoportjánál bármely sorban, oszlopban és a főátlókban levő számok szorzata adja a bűvös számot.
Egy lehetséges szerkesztési módszert az ún. De la Loubere eljárás alapján az 5x5-ös négyzet előállításával mutatjuk be (3.13. ábra).
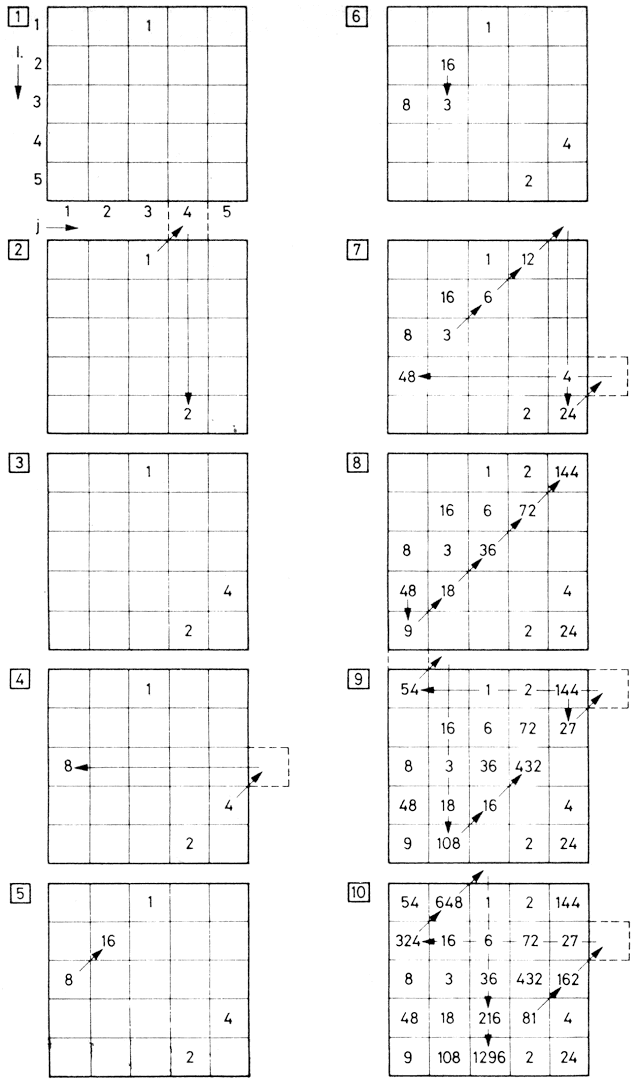
3.13. ábra: 5x5 méretű "szorzat típusú" bűvös négyzet előállítása a De la Loubere-módszer alapján
Az egyes lépéseket és az előálló bűvös négyzetet is feltüntettük a 3.13. ábrán. Az ismertetett eljárást megvalósító program folyamatábráját a 3.14. ábrán mutatjuk be.
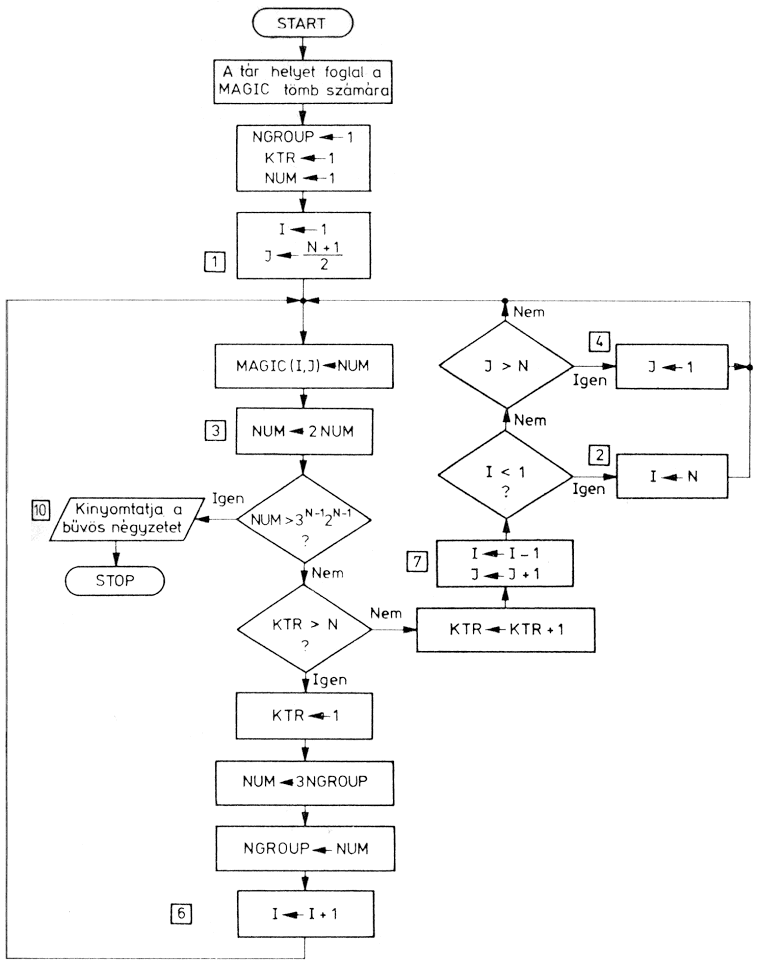
3.14. ábra: De la Loubere eljárást felhasználó bűvösnégyzet-generáló program folyamatábrája
A ZX Spectrum BASIC program először tárhelyeket köt le a bűvös négyzet számára a MAGIC tömbben. Az NGROUP változó az, amely minden öt számból álló csoport kezdőértékét tartalmazza. A számlálót a KTR nevű változó tartalmazza, míg a NUM változó a MAGIC tömbbe kerülő következő kiszámított bűvös négyzetmező tartalmát fogja időlegesen tárolni. Mindhárom változó kezdőértéke: 1.
A MAGIC tömb I és J indexét az éppen kiszámítandó értéknek megfelelően állítjuk be, a kezdőérték tehát az első sor közepének felel meg. Az új értékek előállítását addig folytatjuk, amíg a NUM változó nem lépi túl a 25. számnak megfelelő 1296 értéket. A KTR számláló mutatja, hogy mikor kell az új csoport számítását elkezdeni; ilyenkor ezt vissza kell állítani 1-re. Az új index értékeket mindig a következő sor és oszlop értéknek megfelelően számítjuk ki. Ha I< 1, akkor "felül" léptünk ki, így az utolsó sornak megfelelően kell l-t beállítani, míg J>N azt jelenti, hogy "jobbra" léptünk ki, így ezt az indexet az első oszlopnak megfelelően kell beállítanunk.
Bűvös négyzetet játékos formában is létrehozhatunk. Ilyen játékra mutatunk most be egy. A játék célja, hogy a játékos és a számítógép felváltva írja be a megfelelő számot a megfelelő cellába, a bűvös négyzet képzése szabályainak a betartásával. A program egy 3x3-as bűvös négyzet létrehozását teszi lehetővé oly módon, hogy a beírandó számok 1 és 9 közé esnek és a bűvös szám 15 (azaz a számok összege minden sorban, oszlopban és átlóban ezzel a számmal kell, hogy egyenlő legyen). A cellák számozása a következő:
1 2 3
4 5 6
7 8 9
A számítógép felszólítására:
AZ ÖN LÉPÉSE: CELLA, SZÁM
a válasz, ha pl. a 7-es számot kívánjuk a 3 számú cellába helyezni: 3, 7. Ha hibázunk, elvesztettük a játékot, ha nem, a számítógép segítségével létrehozunk egy bűvös négyzetet.
10 PRINT "Buvosnegyzetjatek"
15 DIM A(9): DIM B(9)
20 PRINT : PRINT "A cellak szamozasa a kovetkezo:"
30 PRINT
90 PRINT "1 2 3"
91 PRINT "4 5 6"
92 PRINT "7 8 9"
95 FOR I=1 TO 9
96 LET A(I)=0: LET B(I)=0
97 NEXT I
98 LET M=0: LET W=0
100 INPUT "Az on lepese (cella,szam): ";I,N
105 IF I<1 OR I>9 OR N<1 OR N>9 THEN GO TO 130
110 IF A(I)=0 AND B(N)=0 THEN GO TO 150
130 PRINT "Szabalytalan lepes!": GO TO 100
150 LET A(I)=N: LET B(N)=1: LET M=M+1
170 GO SUB 960
180 GO SUB 800
200 IF W=0 THEN GO TO 230
210 PRINT "Sajnalom? vesztett!": GO TO 560
230 IF M<5 THEN GO TO 400
240 PRINT "Dontetlen? De kirajzoltunk egy buvos negyzetet.": GO TO 560
400 FOR Q=1 TO 9
410 IF A(Q)>0 THEN GO TO 480
420 FOR R=1 TO 9
430 IF B(R)>0 THEN GO TO 470
435 LET A(Q)=R
440 GO SUB 800
450 IF W=0 THEN GO TO 500
460 LET Q1=Q: LET R1=R: LET W=0: LET A(Q)=0
470 NEXT R
480 NEXT Q
490 LET W=1: LET R=R1: LET Q=Q1: LET A(Q)=R
500 LET B(R)=1
520 PRINT "A ";Q;" cellaba lepek a ";R;" szammal."
530 GO SUB 960
540 IF W=0 THEN GO TO 100
550 PRINT "Vesztettem, on nyert!"'
570 PRINT "Jatszunk ismet?": GO TO 20
800 FOR X=1 TO 8
820 IF X=1 THEN LET J=1: LET K=2: LET L=3: GO TO 900
830 IF X=2 THEN LET K=4: LET L=7: GO TO 900
840 IF X=3 THEN LET K=5: LET L=9: GO TO 900
850 IF X=4 THEN LET J=4: LET L=6: GO TO 900
860 IF X=5 THEN LET J=2: LET L=8: GO TO 900
870 IF X=6 THEN LET J=3: LET L=7: GO TO 900
880 IF X=7 THEN LET K=6: LET L=9: GO TO 900
890 IF X=8 THEN LET J=7: LET K=8
900 IF A(J)=0 OR A(K)=0 OR A(L)=0 THEN GO TO 930
920 IF A(J)+A(K)+A(L)<>15 THEN GO TO 940
930 NEXT X
935 GO TO 950
940 LET W=1
950 RETURN
960 PRINT
965 PRINT A(1);" ";A(2);" ";A(3)
970 PRINT A(4);" ";A(5);" ";A(6)
975 PRINT A(7);" ";A(8);" ";A(9)
977 PRINT
978 RETURN
3.1.3. Naptár
A számokon alapuló játékok között meg kell említenünk azokat a játéknak a szó szoros értelmében csak némi túlzással nevezhető, azonban időtöltésre alkalmas eljárásokat, amelyeknek az alapja a naptár. Az alább közölt programrészlet azt számítja ki, hogy egy megadott dátum (amely az E évszámból, H hónapból, és N napból áll), a hét hányadik napja (1 = hétfő . 7 = vasárnap)
10 INPUT "Ev, ho, nap ";e,h,n
20 IF H<3 THEN LET E=E-1:LET H=H+12
30 LET E=INT(365.25*E)-INT(E/100)+INT(E/400)+31*(H-1)-INT(.4*H+2.3)+N+1721060
40 LET W=E-INT(E/7)*7+1
50 PRINT "A het ";W;". napja.
A megadott eljárás igen változatos feladatok megoldására használható. Ennek segítségével megállapítjuk, hogy ünnepeink milyen napokra esnek.
E programrészlet alapján készíthetünk ismerőseinknek személyre szóló naptárakat, amelyeken a kérdéses személyhez kötött bizonyos dátumok, napok, időszakok feltűnően kiemelhetők.
Természetesen egyszerű mód nyílik a napjainkban divatos (áltudományos?) játéknak, a személyre szóló bioritmusgörbének az előállítására is. A dátumból, valamint a születési időpontból bárki életkora meghatározható napokban, - ezután már csak a 23, 28, 33-mal történő osztás maradékát kell meghatároznunk és az érzelmi, értelmi, fizikai görbéinek állapota ismertté lesz. Az eredmény látványos kinyomtatását, esetleges tanácsadással az Olvasó is megszerkesztheti: minden bizonnyal az eközben szerzett programozási ismeretek és gyakorlatok adják a játék egyedüli hasznos vonását, eredményét.
Az is kedvelt változata a dátumokkal végzett játéknak, ha a számítógép statisztikai-adatokra támaszkodva kiszámolja a születési dátumból, hogy az illető személy eddig hány napot aludt, töltött evéssel, tisztálkodott stb. Az eredmények egy része - első alkalommal látva őket - meghökkentő hatású is lehet.
3.1.4. Számsorrend
A számok nagysága szerinti sorba állításával is készíthetünk játékot. Egy ilyen játék - a Fordíts - programját közöljük. A program 1 és 9 közötti számokat véletlenszerű sorrendben írja fel, és a játékos feladata ezeket olyan módon átrendezni, hogy balról jobbra nagyság szerinti sorrendben kövessék egymást. A játékos a módosítást olyan módon végezheti, hogy - balról kezdve - megadott "darabszámú" szám sorrendjét megfordítja.
Például, ha a számok éppen aktuális sorrendje a következő:
2 3 4 5 1 6 7 8 9
és ha az első négy szám sorrendjét megváltoztatjuk, akkor a következő számsort kapjuk:
5 4 3 2 1 6 7 8 9
Ha most már az első öt szám sorrendjét változtatjuk meg, megkapjuk a kívánt végső sorrendet:
1 2 3 4 5 6 7 8 9
A játéknál akár algoritmikus, akár heurisztikus stratégiát választhatunk. Algoritmikus eljárásunk a következő lehet: kezdjük a rendezést a legnagyobb számmal (esetünkben a 9-cel). Módosítsuk a sorrendet akkora számcsoporttal, hogy a 9-es szám először a bal szélre (első pozícióba) jusson, majd mind a kilenc szám sorrendváltoztatásával a 9-es szám a "helyére" vagyis a 9-ik (jobbszélső) pozícióba jut. Ezt követően a 8-as számot először a balszélső, majd a 8. pozícióba visszük. A játékot a 7., 6. stb. számmal folytatva a módszer segítségével maximum 2N-3, vagyis esetünkben, ahol N=9, 15 lépésben megoldhatjuk a feladatot.
Heurisztikus módszerként lehet pl. a lista "részeinek" a sorrendjét felhasználni. Így a következő lépést mindig az adott listaelrendezés fogja megszabni. Ennek a módszernek az alkalmazása nem szolgáltat megoldást előre megadható számú lépésben, de ha a játékos szerencsés és főleg ügyes, feltétlenül gyorsabban eredményre vezet, mint az algoritmikus eljárás. Gyakorlatban a játékos természetesen mindkét módszert "keverten" is felhasználhatja. Ügyes stratégiával kilenc elemből álló listát 10-nél kevesebb lépésben is sorba rendezhetünk.
10 PRINT TAB 11;"FORDITS": PRINT
20 PRINT "A program az 1 es 9 kozotti"
30 PRINT "szamokat veletlenszeru"
40 PRINT "sorrendben irja fel, es a"
50 PRINT "jatekos feladata ezeket olyan"
60 PRINT "modon atrendezni, hogy balrol"
70 PRINT "jobbra nagysag szerinti"
80 PRINT "sorrendben kovessek egymast."
90 PRINT "A jatekos a modositast olyan"
100 PRINT "modon vegezheti, hogy - balrol"
110 PRINT "kezdve - megadott darabszamu"
120 PRINT "szam sorrendjet megforditja."
130 RANDOMIZE
140 DIM A(20)
150 LET N=9
160 LET A(1)=INT ((N-1)*RND+2)
170 FOR K=2 TO N
180 LET A(K)=INT (N*RND+1)
190 FOR J=1 TO K-1
200 IF A(K)=A(J) THEN GO TO 180
210 NEXT J: NEXT K
220 PRINT : PRINT "A lista a kovetkezo:"
230 LET T=0
240 GO SUB 450
250 PRINT "Hanyat forditsak meg?"
260 INPUT R
270 IF R=0 THEN GO TO 410
280 IF R<=N THEN GO TO 300
290 PRINT "Tul sok! Maximalisan ";N;"-t tudok megforditani": GO TO 250
300 LET T=T+1
310 FOR K=1 TO INT (R/2)
320 LET Z=A(K)
330 LET A(K)=A(R-K+1)
340 LET A(R-K+1)=Z
350 NEXT K
360 GO SUB 450
370 FOR K=1 TO N
380 IF A(K)<>K THEN GO TO 250
390 NEXT K
400 PRINT "Megnyerte ";T;" lepesben"
410 PRINT "Megprobalja ujra? (I/N)";
420 INPUT A$
430 IF A$="I" OR A$="i" THEN PRINT : GO TO 160
440 PRINT : PRINT "Remelem tetszett!": GO TO 470
450 FOR K=1 TO N: PRINT A(K);" ";: NEXT K
460 PRINT : PRINT : RETURN
470 STOP
3.2. Véletlenen alapuló játékok
A klasszikus szerencsejátékok érméi, kockái, forgó kerekei tulajdonképpen véletlenszám-generátorok, melyek csak több-kevesebb megszorítással tettek és tesznek eleget a követelményeknek. Érthető okokból - matematikusok és szerencsejátékosok - alaposan megvizsgálták már ezeket az eszközöket: sok-sok kísérlet eredményét gyűjtötték össze és vetették matematikai elemzés alá. Úgy találták, hogy a manapság gyártott érmékkel végrehajtott pénzfeldobások fej-írás eloszlása a várakozásoknak megfelelő. Sokkal rosszabb a helyzet a dobókockáknál: egy 100 000 dobásból (!) álló sorozat kiértékelése pl. azt mutatta, hogy az egyes számjegyek előfordulásának várható értéke korántsem azonos. így aztán nem nagyon meglepő, hogy a nagy játékkaszinók által használt dobókockák nem egyszerű tárgyak: a 10 mikrométer pontossággal megmunkált kemény, homogén anyagból készített kockákat puha posztófelületre ejtik és néhány száz dobás után kivonják azokat a forgalomból, újjal cserélik ki.
A rulett történetében is számos nyomot találunk arra, hogy a szerencsekerék nem egyenletes eloszlásban állította elő a számokat. Igen jelentős mennyiségű egymást követő szám gondos matematikai elemzése a kerekek apró fogyatékosságaira világíthat rá, amelyet a játékba bekapcsolódva természetesen gyümölcsöztetni is lehet. Hatalmas nyereségek, a szerencsekerekek sürgős cseréje és a bank részéről a fokozott ellenőrzés mutatja azt, hogy a valószínűségszámításnak közvetlen hatása lehet az élet eseményeire.
A számítógépes szerencsejátékok alapja valamilyen - rendszerint a számítógép alapszolgáltatásai között szereplő - véletlenszám-generátor. Az esetek többségében a (v) véletlenszámot a 0 <= v < 1 intervallumban állítják elő, leggyakrabban kongruencia módszerrel. Az így előálló véletlenszám-sorozatok rendszerint kielégítik a statisztikai eloszlásukra vonatkozó matematikai feltételeket. Kényesebb esetekben különböző véletlengenerátorok által keltett számok véletlenszerű keverésével igyekeznek az egymást követő számok egymástól való függését csökkenteni. Általában: a számítógép sokkal "becsületesebb", mint az ember az ő pénzfeldobásával, kockájával stb.
A számítógépes szerencsejátékok kapcsán néhány lehetőséget is meg kell említeni. Először arra hívjuk fel a figyelmet, hogy a számítógép véletlenszám-generátorának ellenőrzését célszerű valamely szerencsejáték kapcsán elvégezni. Ehhez természetesen rövidebb-hosszabb programot is kell írni, és valamelyest el kell mélyedni a valószínűségszámításban is. A játék melléktermékeként így értékes, sokszor felhasználható ismerethez juthatunk.
Arról sem szabad megfeledkeznünk, hogy a számítógépprogram megírásánál, módosításánál a csalásra (öncsalásra) is lehetőség nyílik. Csak példaképpen: kihasználhatjuk azt a tényt, hogy a rendszer bekapcsolásakor a véletlenszám-generátor kezdőhelyzete rendszerint egyértelműen megadott, így mód nyílhat az előzetesen már megismert és kipróbált számsorozatokkal játszani. A számítógép programozása során végzett "manipulációk" felderítése igen nehéz. Nem ok nélküli, hogy a játékkaszinók a bizalom fenntartása érdekében ragaszkodnak az egyszerű, hagyományos módszerekhez és eszközökhöz.

Az ember és a véletlen
3.2.1. Snóbli
A népszerű szerencsejáték legegyszerűbb változatánál a két játékos mindegyike egy-egy pénzdarabot helyez kezével lefedve az asztalra, majd kezüket felemelve megállapítják, hogy az érmék azonosak (1) vagy különbözőek (-1). Ez eldönti, hogy melyik játékos a nyertes. Ez az ún. kifizetőmátrix tehát:
fej írás
Mindkét játékos számára az optimális stratégiát a fej vagy írás 0,5 arányú véletlen-szerű választása jelenti. Ez esetben a játék várható értéke zérus. A játék így nem tűnik különösebben érdekesnek: ha pl. két különböző véletlenszám-generáló program játszik így egymással, az azt figyelő embert ez nem szórakoztatja. Az emberi játékosok azonban ezt a helyzetet alapvetően megváltoztatják. Ennek két okát említjük.
A játékot matematikai szempontból már alaposan megvizsgálták, és a játék lehetséges stratégiái is ismeretesek. Így pl. a játék egy adott pontján követendő taktikát a 3.15. ábra alapján állapíthatjuk meg. A játék eddigi menete alapján meghatározható, hogy a következő lépésként mit kell játszani. Ehhez a fej választások és a találatok eddigi arányát kell megállapítani. Az így meghatározott pont az ábrán látható négy háromszög valamelyikébe esik, amelyek közül három felirata közvetlenül utal a következő lépés megválasztására. A legalsó háromszögbe eső Q pont esetén a CQ pontokat összekötő egyenes kimetszi az X távolságot, vagyis a fej és írás előfordulási arányát x/(1-x) értékűre kell választani.
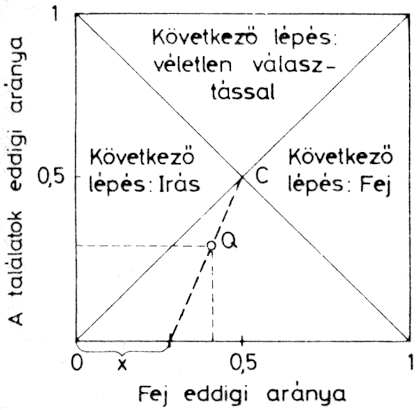
3.15. ábra: Így kell választani a játék eddigi tapasztalatai alapján
A 3.15. ábra alapján természetesen már szerkeszthetünk olyan számítógépprogramot, amely elég ügyesen játszik. A játéknak azonban van egy másikfajta - szellemesebb és sikeresebb - megoldása is. Ez azon alapul, hogy a számítógép figyeli az ellenfél játékát és szabályszerűségeket keres benne. A SEER (SEquence Extrapolating Robot: sorozat-extrapoláló automata) önálló gépként épült meg, amely felismert négy különböző sorozattípust:
FFFF...
IIII...
FIFIFI...
FFIIFFII...
Amint a gép felismert egy sorozattípust, eszerint játszott tovább addig, míg égy újabb típus felismerésére meg nem változtatta lépéseit. Ezt a folyamatot mutatja a 3.16. ábra. Itt feltüntettük a folyamatosan nyerő sorozatot, a gép által generált sorozatot, valamint azt, hogy a játék során a gép nyeresége fokozatosan növekvő tendenciájú lett.
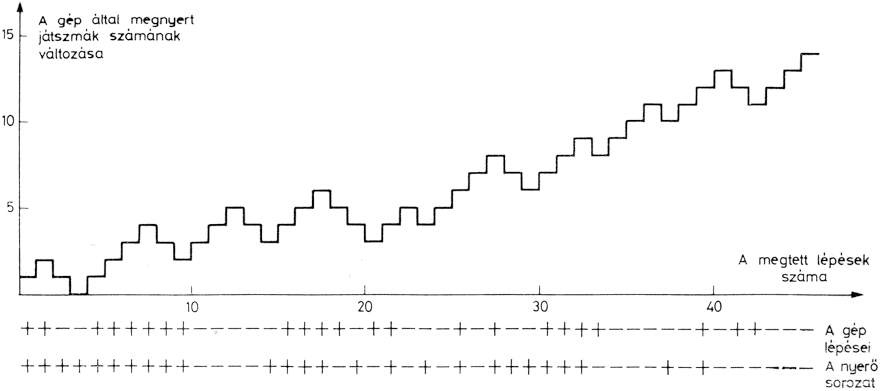
3.16. ábra: Így játszott a SEER, a sorozatot kitaláló robot
A SEER gép csak akkor játszik a felismert sorozat alapján, ha egyébként nyerésben van, vesztes állapotban véletlenszerűen választja lépéseit. A gép lépései a játék állapotától függenek. A játék állapotát az határozza meg, hogy az előző és az azt megelőző játékot megnyerte vagy elveszítette-e a gép, ill. az előző állapotban változtatott vagy nem változtatott játékot a gép. Ha pl. két játékot elvesztett már, akkor következő lépése véletlenszerű lesz. Ha két játékból egyet nyert, akkor nagyobb valószínűséggel (3:1) változatlanul folytatja a játékot. Ha két játékot nyert, akkor a felismert sorozat alapján játszik tovább.
A géppel a Bell Telephone Laboratories alkalmazottai és látogatói 9795 játszmát játszottak. Ebből a gép 5218 alkalommal nyert, 4577 esetben pedig veszített. Ilyen jelentős különbségű eredmény véletlenszerűen alig állhat elő, ugyanis ennek valószínűsége 10^-10-nél is kisebb. Érdekes azonban az, hogy a gép játékmódszerének ismeretében optimális nyerő stratégiát lehet a géppel szemben kidolgozni, amely a játékos számára 0,6 valószínűségű nyerési esélyt biztosít.
A SEER gép megmérkőzött Shannon által épített elődjével. Shannon gépe hasonló elven működött, de a változásokat gyorsabban detektálta és "nagyvonalúbban" játszott. Az eredmény 55:45 a gyorsabb gép javára.
A most ismertetett módszeren kívül még számos más is létezik, melyek segítségével jó képességű snóblizó programot készíthetünk. A számítógépek számítási sebessége és tárterületük nagysága módot nyújt matematikai szempontból alaposabb, de jóval nagyobb számítási igényű megoldások kipróbálására is. Így azután a Fourier-analízis, az egyedi és páros jelek korrelációja segítségével, valamint a mesterséges intelligencia alakfelismerési módszereinek alkalmazásával ezt a játékot számítógépek - emberekkel szemben - igen sikeresen játsszák. Mivel azonban egy nem különösebben érdekes játékot, főleg egy nagyon jó játékossal szemben senki sem játszik szívesen, ezért itt külön programot erre nem is közlünk.
3.2.2. Rulett
Egyike a legközismertebb szerencsejátékoknak. Felfedezését különböző személyeknek tulajdonítják, eredete tehát kétséges. Nem kétséges azonban az, hogy egy XVIII. századbeli párizsi rendőrtiszt igen sokat tett elterjesztéséért, ugyanis e játékkal kívánta kora cinkelt kockákon és hamiskártyákon alapuló szerencsejátékait "becsületesebbé" tenni.
Bankrobbantások és legendás mértékű veszteségek egyaránt szerepelnek a játék krónikájában, amely matematikai szempontból alig nevezhető játéknak. Ennek oka az, hogy a játék felépítése olyan, hogy hosszú távon a bank feltétlenül nyer. A játékosok számára tehát a cél nem a nyereség (bár egy-egy pillanatban ez vonzóan tetemes lehet), hanem az, hogy adott mennyiségű pénzzel minél tovább játékban tudjanak maradni, és ezzel "szórakozásuk" időegységre vonatkozó költségeinek mértékét csökkentsék.
A rulettjáték közismert voltára hivatkozva a játék szabályait nem ismertetjük. A játékosok tétjeikkel megkísérelnek "előre látni" egy adott intervallumba eső véletlenszámot. Még az az örömük sem marad meg, mint pl. az előzőekben tárgyalt snóblinál, hogy az ellenfél (vagyis ez esetben a bank) részéről bármiféle racionális vagy emocionális tevékenységet feltételezhessenek.
A számítógép viszonylag egyszerűen el tudja látni a játék adminisztrátorának, a krupié-nak a szerepét, és elfogulatlanul tud véletlenszámokat is generálni. Egy egyszerű rulettprogram a - az ebben a formában kicsit unalmas - játékon kívül módot teremt egy igen fontos kísérletsorozat elvégzésére: a különböző fogadási szisztémák kipróbálására és a tanulságok levonására. Mutatóban néhány rulett tétrendszer:
3.2.3. Lóverseny
A lovak tenyésztése versenyzés céljára sokezeréves múltra tekinthet vissza. A régi görög olimpiák versenyszabályai már részletesen intézkedtek e sport szabályairól. Persze a lóverseny csak a lovas és a ló számára jelent "sportot". A lóverseny szó hallatára nálunk mindenkinek egy olyan időtöltés jut eszébe, melynek kapcsán a fanatikus résztvevők elvesztik pénzüket, kisebb ingóságaikat, esetleg akár felsőruházatukat is.
A lóversenyt már az antik Rómában is összekötötték fogadásokkal. A verseny kimenetelét meghatározó nagyszámú komponens nem ismerhető előre teljes bizonyossággal (a pálya állapota, az időjárás, a lovak erőnléte, a hajtók képességei, egy új nyereg hatása stb.). Mivel ezekből nagyon nehéz az esélyeket egyértelműen "kiszámítani", sok ember érdeklődését kötik le ma is a lóversenyek.
A lóversenyfogadások számos változata ismeretes. A játékosok befizetett tétjeinek jelentős részét a fogadóirodák maguknál tartják, így a játék a játékosok összessége szempontjából mindig veszteséges. Helyes becsléssel és némi szerencsével azonban egy-egy játékos számára a lóverseny jelentős nyereséggel járhat.
A számítógépes lóversenyprogramok nem nagyon izgalmasak, mert nélkülözik a "környezetet", vagyis a lelátókon helyet foglaló zaklatott lelkű érdekeltekből kisugárzó pszichikai feszültséget.
3.3. Kártyajátékok
A kártyajátékok felfedezését tulajdonították már az indiaiaknak, araboknak, egyiptomiaknak. Kínai feljegyzések szerint már háromezer évvel ezelőtt ismerték ezt a játékot. Európába - a legvalószínűbb feltevés szerint - a keresztesháborúk nyomán került. Mindenesetre népszerűségére, terjedésére jellemző, hogy 1423-ban Sienában egy szószékről már az ördög találmányának minősítették. Az is igen érdekes, hogy a könyv-nyomtatás feltalálása a bibliát és az első nyomtatott kártyákat ugyanabban az évben tette sokak számára elérhetővé.
Különböző kártyatípusok hosszabb-rövidebb ideig uralkodtak, majd újaknak adták át a terepet. A kártyatípusokkal együtt változtak maguk a kártyajátékok is. A kártyák általában többszínű nyomással készülnek, részben számokat, részben pedig ábrákat - többnyire alakokat - ábrázolnak. Kialakításuk általában olyan, hogy az egyes lapok könnyen megkülönböztethetők, egy "szemvillanással" felismerhetők. A legtöbb kártya a hierarchikus felépítésű társadalmak nyomait viseli magán: király, dáma, nemesek, arcnélküliek (számozott kártyák) szerepelnek rajtuk. így azután a kártyajáték könnyen válik ütközet vagy egyéb összeütközés "modelljévé".
Ma nálunk leginkább két kártyatípus van forgalomban: az ún. magyar kártya (pontosabban: német vagy svájci kártya) 32 lapból áll, a francia kártya pedig 52-ből. Mindkettő négy "színű", vagyis az egyes számértékek és a figurák négyszer ismétlődnek.
A kártyajátékok népszerűségének alapja az, hogy különböző változatai különböző mértékben vegyítik magukba a
A kártyajátékok szempontjából a számítógépnek több előnyös tulajdonsága is van. "Memóriája" tévedhetetlen, így tehát az erre alapozott játékokban verhetetlen ellenfél. A véletlen folyamatok kezelésében, generálásában - ahol az a játék alapja - szintén igen jól megállja a helyét. Rosszabb a helyzet azoknál a kártyajátékoknál, ahol a számítógépnek "játszania" kell, vagyis valamilyen stratégia szerint kell lépéseit megválasztania. A kártyajátékok jelentős része összetett, vagyis a játék fája igen bonyolult. Éppen ezért viszonylag kevés kártyajátéknak van olyan számítógépre írt változata, amelyben a számítógép egy jó játékos szintjén, aktívan játszik. Érdekes, hogy a számítógépes kártyajátékok között milyen kiemelkedő szerepre tett szert a póker. Ennek okát a pókerjátékról írott fejezetrészben megkíséreljük részletezni, magyarázni.
A számítógépes kártyajátékok - "kártyapartnerek" - elterjedésének azonban nem csupán az az akadálya, hogy a jó játékos nagy memóriával rendelkező, gyors számítógépet kíván, amelynek a programját bonyolultsága miatt nehéz megírni. Az is akadály, hogy a kártyajáték sokat veszít érdekességéből, ha a megszokott lapok helyett kódszámok, kódjelek tájékoztatnak arról, hogy "milyen lapom van". A leggyakoribb számítógép-perifériákon - teletype, nyomtató, alfanumerikus képernyős megjelenítő - a lapok természetes érzést keltő megjelenítése nehézkes, költséges vagy sokszor lehetetlen. Gondoljuk csak meg, hogyan is kellene pl. a zöld ász képét tárolni - megjeleníteni -, mekkora tárat és gépidőt foglalna le mindez! Az sem előny a kártyajátékok számítógépesítése szempontjából, hogy általában annyi függetlenül kezelhető terminálra van szükség, ahány játékos van. Milyen lenne egy olyan játék, amelyben a képernyőn megjelenik a felirat: "Az #1 játékos most forduljon el, mert a #2 játékos lapját fogom mutatni"? Ha még hozzáfűzzük azt is, hogy a legnépszerűbb és legjobb kártyajátékok rendszerint négy játékost kötnek le, érzékelhetővé válik, hogy miért árusítanak viszonylag olcsón "sakkpartnert", és miért nem kerül forgalomba valamiben kártyajátékot játszó mini- vagy mikroszámítógép.
3.3.1. Kártyakeverés
A kártyajátékok legnagyobb része csak akkor igazán élvezetes, ha a csomag "jól meg van keverve", vagyis a kártyák egymásutánja kielégítő mértékben véletlenszerű. A kártyakeverésnek többfajta technikája van: két halomba osztott kártyák egymásba csúsztatása, sarkuknál egymásba pörgetése stb. Azt, hogy a kártyacsomag jól meg van-e keverve, elvben csak matematikai vizsgálatokkal lehet eldönteni, amelyek lefolytatására a számítógép különösen alkalmas.
A számítógépek véletlenszám-generátora segítségével a kártyakeverést általában igen egyszerűen el lehet végezni. A fontosabb - gyakoribb - változatokat a 3.17. ábrán tüntettük fel.
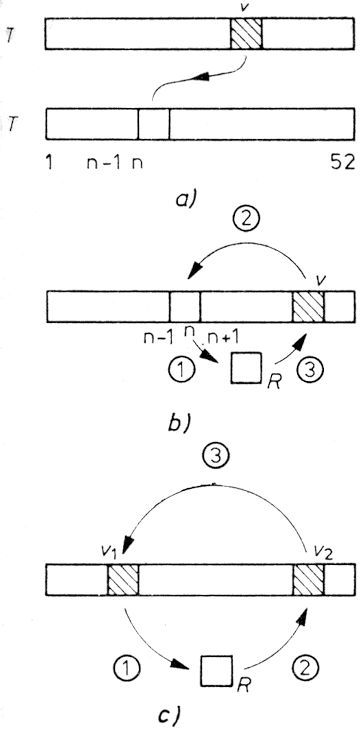
3.17. ábra: A gépi kártyakeverés elvi lehetőségei
A 3.17a ábra szerinti eljárásnál a T tár egymást követő rekeszeiben elhelyezzük a kártyákat, pl. úgy, hogy a tárat feltöltjük 1-től 32-ig (vagy 1-től 52-ig) terjedő számokkal és - valahol másutt - egy táblázatban megjegyezzük, hogy melyik számjegyhez melyik kártya tartozik. A kártyákat egyesével - véletlenszerűen - kivesszük a T tárból és a V tár egymást követő helyeire helyezzük. Az n-edik kártya áthelyezése előtt tehát a T' első n-1 helyén már a megkevert kártyák találhatók. Az n-edik lépés egy (1 és 32 közötti) véletlenszám generálásával kezdődik, ez jelöli ki a T tár azon rekeszét, ahonnan az új kártyát kivesszük. Mielőtt azonban ezt T' n-edik rekeszében elhelyezzük, meg kell néznünk, hogy ezt a kártyát nem helyeztük-e el már az n-1 előző rekesz valamelyikében. Ha igen, akkor új véletlenszámmal kell kísérleteznünk.
Jól látszik, hogy ez az eljárás - különösen az utolsóként maradó kártyák elhelyezésével - eléggé rossz hatásfokú. Gondoljuk csak meg: ha már csak két kártyát kell átraknunk, azért is meglehetősen sok véletlenszámot kell generálnunk, míg az megfelelő lesz. A keverés ilyen módon történő végrehajtásának egyszerű programját a Kártyacsata program 280...350 sorában megtalálhatjuk.
A 3.17b ábrán hatékonyabb eljárást találunk. Itt is az n-edik lépést vázoljuk. Tegyük fel, hogy az első n-1 helyen már megkevert kártyák vannak. Az n-edik helyen levő számot (kártyát) írjuk át az R közbülső tárba! Az n+1-től 32 vagy (52)-ig terjedő rekeszek közül válasszunk ki egyet véletlenszerűen! Ezt írjuk át az n-edik helyre, majd befejező lépésként R tár tartalmát töltsük az előbb véletlenszerűen kiválasztott rekeszbe!
A 3.17c ábra az előzőhöz hasonló eljárást mutat. Itt minden lépésnél két véletlenszámot generálunk, ezek két rekeszt jelölnek ki, amelyek tartalmát megcseréljük. (Persze, itt is szükség van az R átmeneti tárra.) Ha ezt a műveletet elegendően sokszor elvégezzük (kb. 32, ill. 52-szer), akkor a kártyacsomagot megkevertnek tekinthetjük.
A leírt eljárások közül a legtöbb gépidőt a 3.17a igényli. Ennél a gép sebességétől, valamint a véletlenszám-generáló szubrutin időigényétől függően 5...150s-ra is adódhat a kártyacsomag megkeverésének időtartama. A többi módszer ennél lényegesen gyorsabb.
3.3.2. Kártyacsata
Az alábbi kártyajáték nem nagyon bonyolult és nem is nagyon izgalmas, mivel semmiféle taktika nem tartozik hozzá. A hiányzó izgalmat pótolni lehet, ha a játékot nagyobb összegű tétekkel játsszák (ami viszont veszélyes...).
Egy csomag kártyát összekeverünk, és az osztónak és a játékosnak egyaránt egy-egy lapot kiosztunk. Az lesz a nyertes, akinek a lapja értékesebb. Ezt a műveletet folytatjuk, amíg a csomag el nem fogy. Alább közöljük a játék programját. A kártya keverése a 280...350 sorok között történik. Mivel az itt választott eljárás nagyon időigényes, ezért a 265. sorban megnyugtatjuk a játékost és türelemre intjük. A gép és a játékos közötti "csata" részeredményeit a gép pontosan közli, ill. tájékoztat arról, hogy a csomagban levő kártyák elfogytak.
Az egyes kártyákat 1...32 számok jelölik, és mindegyikhez egy A$ alfanumerikus karaktersorozat van hozzárendelve. Itt a T: tök, M: makk, Z: zöld, P: piros a számok és betűk pedig a lap minőségére utalnak (A: alsó, F: felső, K: király, ASZ: ász). Az A$ tömb feltöltésénél a heteseket a nyolcasok stb. követik, ezért a lapok "nagyságának" egybevetése eléggé könnyű. M1 és M2 jelöli a kiosztott lapokat, ezek számértékének negyedrészét véve (mivel a játékban a szín nem számít), majd ennek egész részét képezve eljutunk a győztes megállapításához szükséges N1 és N2 értékhez.
A ZX Spectrum BASIC-re írt program kipróbálása jól illusztrálja, hogy csupán alfanumerikus jelek ábrázolására alkalmas kiíró eszközökön a kártyajátékok eléggé "színtelenek", egysíkúak, nehezen áttekinthetők.
10 PRINT TAB (4);"KARTYACSATA (NASI-VASI)"
20 PRINT TAB (6);"CREATIVE COMPUTING": PRINT TAB (4);"MORRISTOWN, NEW JERSEY"
30 PRINT
100 PRINT "Egy csomag magyarkartyat ossze-"
110 PRINT "keverunk. Az osztonak es a"
120 PRINT "jatekosnak egy-egy lapot"
130 PRINT "kiosztunk. Az nyer, akinek a"
140 PRINT "lapja ertekesebb. Ha elfogy a"
150 PRINT "pakli, vege a jateknak."
160 PRINT
170 PRINT "A kartyak jelolesei:"
180 PRINT "T-tok, M-makk, Z-zold, P-piros"
190 PRINT "A-also, F-felso, K-kiraly, ASZ"
200 PRINT
220 RANDOMIZE
230 DIM A$(32,5): DIM L(32)
235 LET P=0: LET A1=0: LET B1=0
240 FOR I=1 TO 32
250 READ A$(I)
260 NEXT I
270 PRINT "Keverem a kartyakat..."
275 PRINT "Az alapos kevereshez ido kell!"
280 FOR J=1 TO 32
290 LET L(J)=INT (32*RND)+1
295 IF J=1 THEN GO TO 350
300 FOR K=1 TO J-1
310 IF L(K)<>L(J) THEN GO TO 340
330 GO TO 290
340 NEXT K
350 NEXT J
360 LET P=P+1
370 LET M1=L(P)
380 LET P=P+1
390 LET M2=L(P)
400 PRINT
420 PRINT "Onnek: ";A$(M1),"Nekem: ";A$(M2)
430 LET N1=INT ((M1-.5)/4)
440 LET N2=INT ((M2-.5)/4)
450 IF N1>=N2 THEN GO TO 490
460 LET A1=A1+1
470 PRINT "En nyertem!"
475 PRINT "Onnek ";B1;", nekem ";A1;" pontom van."
480 GO TO 540
490 IF N1=N2 THEN GO TO 530
500 LET B1=B1+1
510 PRINT "On nyert!"
515 PRINT "Onnek ";B1;", nekem ";A1;" pontom van."
520 GO TO 540
530 PRINT "Ez a huzas dontetlen."
540 IF P=32 THEN GO TO 620
550 PRINT "Folytatjuk (I/N)?"
560 INPUT V$
570 IF V$="I" OR V$="i" THEN GO TO 360
580 IF V$="N" OR V$="n" THEN GO TO 650
590 PRINT "'I' vagy 'N'! ";
600 GO TO 540
620 PRINT
630 PRINT "Elfogyott a pakli."
635 PRINT "Vegeredmeny:"
640 PRINT "Onnek: ";B1;", Szamitogep: ";A1: PRINT
650 PRINT "Koszonom jatekot!"
655 PRINT
660 DATA "T-7","M-7","Z-7","P-7","T-8","M-8","Z-8","P-8"
670 DATA "T-9","M-9","Z-9","P-9","T-10","M-10","Z-10","P-10"
680 DATA "T-A","M-A","Z-A","P-A","T-F","M-F","Z-F","P-F"
690 DATA "T-K","M-K","Z-K","P-K","T-ASZ","M-ASZ","Z-ASZ","P-ASZ"
999 STOP
3.3.3. Huszonegyes
E népszerű szerencsejáték eredete nem tisztázott; az első világháború alatt vagy után terjedt el. Számos játékkaszinó standard szerencse-lehetőségeihez tartozik. Ebben a játékban is dominál a véletlen, azonban kisebb mértékű taktikai lehetőségek is adódnak, sőt a játék megfigyelése és gondos valószínűségelemzések a játék bizonyos fajtájánál jócskán megnövelhetik a játékos nyerési esélyeit. Elég a híres történetre utalni: egy amerikai matematikus hatalmas vagyont nyert (mielőtt kitiltották a játék-kaszinókból) azzal, hogy a lejátszott lapokat nem keverték vissza azonnal abba a kártyacsomagba, amelyből tovább játszottak. (Gondoljunk csak utána: annak a valószínűsége, hogy egy 54 lapos kártyacsomagból két kártyát egymás után kihúzva két ászt tartunk a kezünkben:
P2Á = (4/54) x (3/53)
Ha azonban az elsőként kihúzott ászt visszatesszük és a csomagot megkeverve újra húzunk egy lapot, akkor
P2Á,K = (4/54) x (4/54)
A két módszerrel történő húzásnál tehát a két ász húzásának valószínűségei jócskán eltérnek egymástól:
P2Á,k / P2Á = (4/54) x (53/3) = 1,309
A két valószínűségérték több mint 30%-nyira különbözik egymástól.
A huszonegyes kártyajátékot matematikai szempontból már alaposan elemezték. Ennek indítóoka elsősorban az volt, hogy a huszonegyes játék során - eltérően a többi népszerű szerencsejátéktól (rulett, lóverseny, lottó stb.) - a játékos nem feltétlenül vesztes.
A játékot egyszerű szabályai miatt könnyű elektronikus eszközökkel modellezni: a digitális technikát oktató, a kibernetikába bevezető könyvek gyakran közölnek egyszerű számláló kapcsolásokat, amelyek a játékos első két lapja után közlik, hogy szükséges-e (célszerű-e) újabb lapot kérni, vagy sem.
Leggyakrabban az 52 lapos huszonegyes játéknak azon változatát játszák, amellyel a játékkaszinók (esetleg kisebb módosítással) szolgálnak a bátor, ill. gazdag játékosoknak. A kártyák értéke: a rájuk írt szám; figurák esetén 10; az ász 1-et vagy 11-et ér, a játékos ítéletétől függően. Egyidejűleg több játékos játszhat, az osztó ("bank") állja a téteket. A játék azzal kezdődik, hogy minden játékos és az osztó is kap két kártyát. Az osztó egyik kártyája azonban fedve marad, csak a játékosok manőverei után kerül nyilvánosságra ennek az értéke.
A játékos első új lapja alapján a következőket választhatja:
Az osztó lehetőségei már szűkreszabottabbak: ha 16-nál kevesebbje van, újabb lapot kell osztania magának, 17 és 21 között megáll. Ha lapjai között ász is van, akkor ezt 11-nek kell számolnia, ha ezzel lapjának értéke 17 és 21 közé esik, egyébként 1-nek.
Ha a játékos vagy a bank lapjainak összértéke a 21-et meghaladja, "befuccsolnak", vagyis elvesztik pénzüket. Ha senki sem fuccsol be, akkor az nyer, akinek lapja közelebb van a 21-hez. Értékegyezés esetén senki sem nyer. Ha a játékos nyer, a tétjével azonos összeget kap a bankártól.
Az "erős huszonegyes" egy ászból és egy tízesből áll, és minden mással szemben nyerést jelent. A játékos "erős huszonegyese" esetén tétjének 1,5-szeresét kapja. Ha az osztó felfedett kártyája ász, akkor lehetőség nyílik az ún. "biztonsági tétre", vagyis a játékos eredeti tétje felével fogadhat arra, hogy az osztó még nem ismert lapja tízes-e. Ha a játékos nyer, 2:1 arányban kap pénzt, de mivel eredeti tétje elveszik, éppen pénzénél marad. Ha veszít, tétje felét elviszi az osztó és a játék folytatódik.
A huszonegyes játék szabályai e formájukban tehát eléggé összetettek, így nem csodálkozhatunk, ha az ezt megvalósító programok terjedelmesebbek. A számítógép a játék során tulajdonképpen csak adminisztrál, regisztrál, a az osztó részéről semmiféle taktika nem megvalósítható.
3.3.4. Póker
A póker olyan kártyajáték, amely azzal büszkélkedhet, hogy a számítógép alkalmazásával foglalkozó szakemberek figyelmét különösen magára vonta. Nagyon sok pókert játszó program keletkezett és van keletkezőben ma is. A számítógéppel lejátszott játékok - esetleg számítógépes - kiértékelésével számos, sokfajta szakmát képviselő szakember foglalkozik, mivel a pókerjátszmában a mindennapi élet megszokott szituációi jelennek meg kicsiben, az élet "modelljeként". Az embernek ugyanis állandóan döntenie kell, lehetőségek között választani, még akkor is, amikor a döntéshez nincs elegendő információja. Persze valamelyest a helyzetét (saját lapját) ismeri, de társai lapját, törekvéseit csak nagyon átszűrten (licitből), pontatlanul. Ki van téve annak, hogy bizonyos információk csak blöffök, félrevezetési szándékkal adta őket egy másik játékos. Bizonyos információszerzési lehetősége persze van: a licitek erre szolgálnak, de ez pénzbe kerül. Mintegy kompenzációképpen ő is adhat helytelen információt, sőt ezt meg is kell tennie, mert ha valaki blöffölés nélkül játszik, hosszú távon biztosan ráfizet. A póker tehát nem csupán a szabályok adta keretek közötti taktikázás, hanem pszichológiai küzdelem is.
Így azután a póker felkeltette mindazok érdeklődését, akik az emberi gondolkodással, az emberi döntések kialakulásának folyamataival foglalkoznak. Pszichológusok, közgazdászok, tervezők, katonák stb. tanulmányoznak különböző problémákat azért, hogy kiderítsék, hogyan reagálnak az emberek egy-egy szituációra. Az sem érdektelen kérdés, hogyan változik az idők folyamán a helyzetek megítélése: hogyan befolyásolja a döntést a nyereséges vagy a veszteséges állapot; a legutóbbi néhány játszmának van-e döntő hatása; a régi sikerek idején játszott taktika dominál-e stb.
A póker sok érdekes összetevőből áll és - most szempontunkból ez a fontos - programja még "belefér" a mai számítógépekbe. Nem meglepő tehát, hogy a mesterséges intelligencia kutatásokkal foglalkozó intézmények szinte kivétel nélkül eljutnak a pókerjátékhoz, vagy ahhoz hasonló feladat vizsgálatához. A mesterséges intelligencia, a kibernetika tárgykörében rendezett konferenciák, kiadott könyvek szinte kivétel nélkül tartalmaznak pókerre vonatkozó előadásokat vagy fejezeteket.
A pókernek számos változata van, ezek közül az ún. húzós póker a legnépszerűbb (itt van lehetőség a lapcserére). Ez a játék kifejezetten szerencsejáték, amely igen nagy nyereségekre és veszteségekre ad lehetőséget. A játékszabályokat ismertnek tételezzük fel, mivel leírásuk számos helyen megtalálható, továbbá a Magyarországon játszott változatok a nyugati - elsősorban amerikai - játékfajta összes lényeges vonását tartalmazzák.
A pókerjátékot valószínűség számítási módszerekkel már alaposan kielemezték. A 3.2. táblázat pl. a lehetséges (ötösével kiosztott)
52! / (5!x47!) = 2 598 960
féle lapnak a pókerjáték szempontjából fontos valószínűségeit tünteti fel. Ebből kiderül, hogy az osztások több, mint felében a játékosnak csak "egy" lapja van, ill. kb. 8 % annak a valószínűsége, hogy egy párnál jobban indul.
| Lap | Valószínűség |
| Egyes Pár Két pár Hármas Straight Flush Full Négyes Straight-flush Royal flush Négyes flush Négyes straight (Közbülső lap hiány) |
0,5012 0,4226 0,0475 0,0211 0,0039 0,0020 0,0014 0,24x10^-3 0,14x10^-4 0,15x10^-5 0,043 0,123 |
3.2. táblázat: A lapok valószínűsége pókerban
Nagyon sokat tudhatunk meg a 3.3. táblázatból, ahol a kezdőlaphoz húzott kártyák számának függvényében megbecsülhetjük a javítások esélyeit.
| Kezdő lap | Lapcserék száma |
Javított lap | Valószínűség |
| Pár Két pár Hármas Négyes straight Négyes flush Hármas flush Kettes flush Négyes straight |
3 3 3 3 3 2 2 2 2 2 1 2 2 2 1 1 1 1 1 2 3 1 |
Két pár Hármas Full Négyes Bármi javulás Két pár Hármas Full Négyes Bármi javulás Full Full Négyes Bármi javulás Full Négyes Bármi javulás Straight Flush Flush Flush Straight flush |
0,160 0,114 0,0102 0,0028 0,287 0,172 0,078 0,0083 0,0009 0,260 0,085 0,061 0,043 0,104 0,064 0,021 0,085 0,085 0,191 0,042 0,0102 0,043 |
3.3. táblázat: A húzások valószínűségei pókerban
A pókerjátszma ismeretében azonban nyilvánvaló, hogy ezek az adatok - vagy tudja őket a játékos (a számítógép), vagy csak "érzi" - nem elegendők. A póker nem játszható heurisztikus részmegoldások, heurisztikus taktika nélkül. Éppen ezért volt nagy-jelentőségű egy pókert játszó programrendszer, amely nem csupán egy új számítógépes nyelvet teremtett a póker pillanatnyi helyzeteinek feldolgozásához, hanem ezen túlmenően a heurisztikus szabályok és heurisztikus definíciók fogalmát is alkalmazta. Egyszerű példa: "Ha a bank nagy, tromfolj" - heurisztikus szabálynak tekinthető. A "nagy" azonban magyarázatot igényel, pl.: "a bank nagy, ha értéke nagyobb, mint 100". Ez utóbbi állítás a heurisztikus definíció mintapéldája. (A heurisztikus definíciók és szabályok lehetséges halmazainak végigvizsgálása ugyancsak sok gépidőt igényel.) Úgy is értelmezhetjük a program gondolatmenetét, hogy a játék fáját ki kell bővítenünk a lehetséges lépéseken túlmenően a lehetséges heurisztikus definíciókkal és szabályokkal. Szerencse, hogy a pókernél a játék egy adott pontján a lehetséges lépések száma viszonylag kicsiny, így az alfa-béta eljárás hatékonyan alkalmazható.
Tételezzük fel, hogy az eddig felsoroltak alapján egy, az átlagosnál jobb pókerjátékost tudunk a számítógépben előállítani. Ez esetben azonban nyitva marad a kérdés: hogyan gyűjti össze a program a játszma (több egymást követő játék azonos játékosokkal) során szerzett tapasztalatait, és hogyan építi be ezeket taktikája, stratégiája kialakításába. A feladat eléggé nehéz, azonban ma már több megoldása is van. Egy amerikai egyetemen a szerencsejátékokat ellenőrző rendőri szervek és az egyetem etikai bizottságának engedélyével kísérletsorozat indult. Ezeken "profi" pókerjátékosok fizetést kapnak a játékban való részvételükért, fizetésükkel azonban játszaniuk kell. A játék nem a szokásos formában zajlik; a játékosok egy-egy képernyő előtt ülnek és játékostársaikat csupán azok sorszáma (pontosabban az asztal körül elfoglalt helye) alapján ismerik. A meglepő: a játékosok egy része nem más, mint különböző játékstratégiákat megvalósító számítógépprogram.
A színes képernyőn megjelenik a játékos kézben tartott kártyáinak képe, a játék pillanatnyi helyzetére vonatkozó információval együtt (pl. mekkora a bank, húzás előtti licit zajlik-e, mi az egyes játékosok pillanatnyi vagyoni helyzete stb.). Az emberi játékos semmiféle közvetlen emberi" kapcsolatban sincs társaival, így nem tudja, hogy melyik játékos sorszámhoz tartozik élő játékos és melyikhez számítógépprogram.
A számítógépprogramok egymástól lényegesen különböznek. Így pl. az egyik program (1) a játék folyamán megismert és fokozatosan pontosabbá váló valószínűségszámítási értékekből próbál élni, a másik (2) a játék kezdetén megbecsüli ellenfeleinek lapját és a becsült értékeket a játék során folyamatosan módosítja. A harmadik program (3) az ideális matematikus: sohasem blöfföl, tétjeit mindig saját lapja alapján teszi meg. Egy újabb program (4) egy különleges "játékérték" alapján játszik. Ez a játékérték azt fejezi ki, hogy mennyire érdemes egy adott pillanatban a játékban maradni. A játékérték meghatározását befolyásolja: ha a bank nagy, ha még sokan vannak a játékban, ha még a játékos után többen szólhatnak, ha nagy összeg kell a játékban maradáshoz stb. Az alkalmazkodva-igyekvő program (5) eléggé az emberi gondolkodáshoz áll közel: a kockázatot egybeveti pillanatnyi vagyoni helyzetével és a játékban szerzett múltbeli tapasztalataival. A hatodik program (6) szintén egy emberi alapállást szimulál: félrevezető információt közöl magáról, és pénzt áldoz azért, hogy ellenfeleiről valamit megtudjon.
Képzeljük most el, hogy élő játékosok és a fenti számítógépprogramok játszanak együtt sok-sok játékot. A játék során a számítógépes programok tanulnak, vagy legalábbis alkalmazkodnak környezetükhöz. Az egymást követő játszmák során azonban az "életrevalóbb" programok nagyobb nyereségre tesznek szert. A 3.18. ábrán egy ilyen, eléggé nagyszámú játék folyamatos kiértékelését mutatjuk be.
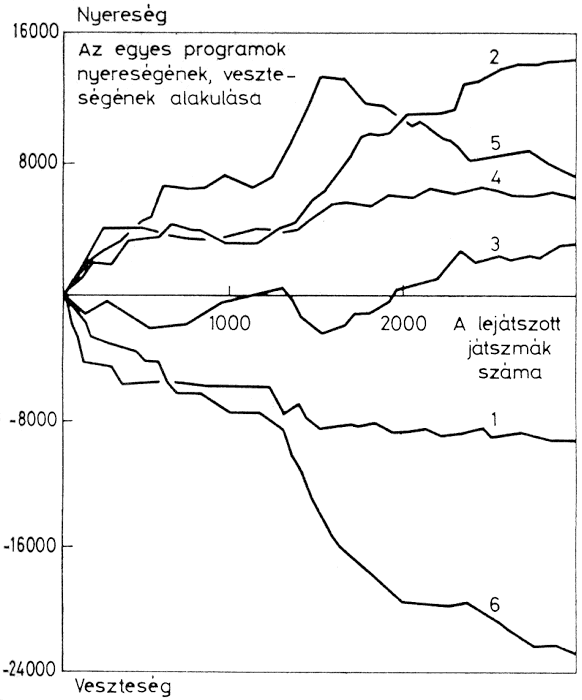
3.18. ábra: Különböző pókerprogramok hatékonysága
Még egy érdekesség: a számítógépprogramok és az élő játékosok közötti gondolkodási időt kiegyenlítve, az élő játékosok képtelenek voltak az élő és számítógépesprogram-játékost megkülönböztetni.
Az ilyen magas szintű játékot nyújtó programok terjedelmesek, futtatásuk csak nagy és gyors számítógépeken lehetséges. Mini- és mikrogépeken szerényebb programok tudnak csak futni: általában egyetlen játékos játszik húzós pókert a számítógéppel. Ezek a programok nem nagyon játszanak (kivéve a lap értékétől függő téteket), csupán a játék adminisztratív részét végzik. Ez azonban a póker szabályainak ismeretében nem kicsiny teljesítmény: a póker lapjainak azonosítása, értékelése eléggé összetett feladat.

Ha szépen megcsinálod a bérelszámolást és az anyagleltárt, egy kicsit majd pókerezünk!
3.3.5. Bridzs
A bridzs egyike a legnépszerűbb kártyajátékoknak nálunk és külföldön egyaránt. A társasági "beszélgetéspótló" szinttől kezdve az igen nagyfokú szellemi koncentrációt igénylő versenybridzsig sok fokozata létezik.
A játék szabályainak még rövid ismertetésére sem váltakozhatunk e könyv keretében, ezért feltesszük, az Olvasó tudja, hogy a bridzs 4 személyes, két érdekeltségű játék, két egymástól jól megkülönböztethető játékfázissal. A számítógépes bridzsprogramok szempontjából a bridzsjátéknak a következő fontosabb fázisai vannak:
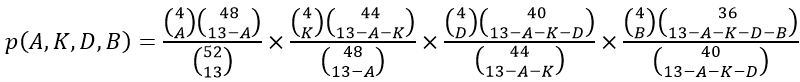
képletből könnyen meghatározható. A számítógép tehát értékelni tudja saját lapját abból a szempontból, hogy az mennyire szokványos vagy ritka. Persze ez még a játékhoz nem elég. A lapnak a játék szempontjából történő értékelésére számos módszert dolgoztak ki. A Goren-módszer szerint a figurák értéke 4-3-2-1, továbbá bizonyos kártyakombináció esetén ehhez még további pontok járulnak. A bridzsjáték története során több különböző kiértékelő rendszert használtak, ill. használnak ma is. Ez is arra utal, hogy a játék alaphelyzete sem határozható meg egyértelműen. A játékerő megítélésére használt két különböző rendszerhez tartozó valószínűségeloszlást a 3.19. ábrán láthatjuk.

3.19. ábra: Különböző lapértékelő módszerekhez tartozó valószínűségértékek
A nagy számítógépek programrendszerei mellett a mikroszámítógépek és személyi számítógépek megjelenésével egyre gyakrabban olvashatunk kisgépeken futtatható bridzsprogramokról. Ezek általában csak egy-egy lap lejátszására alkalmasak, tulajdonképpen csak a kezdő játékosok gyakorlataihoz nyújtanak némi segítséget. (Itt is hátrány - miként a pókernél -, hogy a játékhoz egyidejűleg több képernyőre lenne szükség.) A mini- és mikrogépek bridzsprogramjai korántsem olyan jók és ügyesek, mint ugyanezen gépek sakkozó programjai.
4. Természeti és technikai jelenségeket szimuláló játékok
Ebben és a következő fejezetben olyan játékokról írunk, amelyek alapja a számítógépes szimuláció, vagyis valamely jelenség vagy jelenségcsoport utánzása számítógép segítségével. A lehetőségek köre igen tág: az elemi mechanika legegyszerűbb mozgásaitól a tavak halállományának változásain keresztül a reklámpszichológiai műveletek hatásosságának becslésén át az emberiség életkörülményeinek előrebecsléséig terjedhet.
A számítógépes szimuláció igazi "szakma", specifikus fogásokkal, gyakorlattal, ismeretháttérrel. Szakmai szempontból meg szokták különböztetni a folytonos rendszerek szimulációját és a diszkrét rendszerek szimulációját. Mi itt nem ezt a felosztást követjük, hanem a játékok gondolatához jobban simuló megoldást választunk. E fejezetben a természeti és technikai, az 5. fejezetben pedig embercsoportokkal kapcsolatos jelenségek számítógépes utánzásáról lesz szó.
4.1. A számítógépes szimulációról általában
A számítógépek egyik igen fontos alkalmazási területe: összetett, bonyolult rendszerek vizsgálatának lefolytatása szimulációs módszerekkel. Ezen eljárás során elkészítik a vizsgálni kívánt jelenség matematikai modelljét, majd ennek számítógépes programját. A szimuláció során változtatják a bemenő adatokat - esetleg a modellrendszer felépítését is - és megfigyelik ezeknek a kimenő adatokra való hatását. A program változó körülmények közötti ismételt futtatása az eredeti rendszerről közöl ismereteket, néha eléggé meghökkentőeket.
Talán legjobb példa ennek illusztrálására az ún. Római Klub jelentése. E jelentés szerint, ha a Föld nyersanyagkészletének, élelmiszertermelésének, az ipari termelésnek, a népesség alakulásának és a környezetszennyezésnek az egymásra hatását - azok időtartománybeli viselkedését is figyelembe véve - megbecsülik, akkor a jelenlegi adatok alapján "jósolni lehet" a következő évtizedekre, évszázadokra vonatkozóan. E paraméterek közötti kapcsolat nagyon összetett, sok visszacsatolás is van a rendszerben; az időbeli változások hagyományos módszerrel alig követhetők. A Római Klub jelentése tehát egy rendkívül összetett rendszer számítógépes szimulációján alapult. A számítógép által előállított eredmények ugyanis azt mutatták (4.1. ábra), hogy mintegy 40...60 év múlva az emberiség lélekszáma hirtelen radikálisan csökken és alig van mód a "világ vége" elkerülésére.

4.1. ábra: A Föld legfontosabb jellemzőinek modellezése a Római Klub jelentése alapján
E jelentést azóta különböző ideológiai alapokból, szakmai oldalról stb. már alaposan megbírálták. Ennek hatására újabb - most már részletesebb és pontosabb - modellek keletkeztek. Hatalmas kutatóintézetek foglalkoznak ma is hasonló modellek létrehozásával, mögöttük matematikusok hadával és nagyteljesítményű számítógépekkel. Az eredeti ötlet pedig átköltözött a kisszámítógépek körébe; a Római Klub modellje több kisgép demonstratív programcsomagjának lett egy komponense, és így sok ember számára vált hozzáférhetővé egyfajta - nem mindennapi - játéklehetőségként.
A számítógépes szimuláció sok érdekes gyakorlati alkalmazási lehetősége közül még egy példát emelünk ki: a repülőgép-szimulátort. Ez a berendezés lehetővé teszi, hogy valaki az ugyancsak bonyolult felépítésű korszerű repülőgépeken "vezetni" tanuljon anélkül, hogy a levegőbe emelkedne. A tanuló "valódi" pilótafülkében ül, amelynek műszerei, kezelőszervei számítógéphez vannak kapcsolva. A számítógép programja a repülőgép viselkedését a legkülönbözőbb repülési helyzetekben hűen utánozza. Egy ilyen berendezés haszna nyilvánvaló, és nem csupán oktatási célra jó, hanem a megszerzett tudás állandó szinten tartására is. Ezen eszköz komoly értékei mellett azonban játékra is ingerli az embert, a felnőtteket is.
A kisgyerekek részére műanyagból előállított autó kormánykerék-duda-sebességváltó összeállítás közismert és igen népszerű játék. A gyermek pszichológiai-szellemi fejlettségi szintjén a játékhoz ez is elegendő, mivel nála még a saját mozgás, saját szerep dominál. A felnőttek is szeretik a mozgásokat szimuláló játékokat, de ők már űrhajósok, versenyautók vezetői szeretnek inkább lenni. Egy jól sikerült számítógépprogram könnyen nyújthatja ezt az illúziót vagy annak legalább egy részét.
E könyv keretében nem mélyedhetünk el a szimuláció alapkérdéseiben, mindössze arra vállalkozhatunk, hogy a közölt játékokhoz szükséges legegyszerűbb ismereteket vázlatszerűen összefoglaljuk.
A szimulációs játékokhoz két nagyobb témakör ismerete szükséges: a differenciálegyenletek numerikus megoldása és a különböző valószínűségeloszlások előállítása.
A differenciálegyenletek megoldására használatos módszerek közül kettőt kell megemlítenünk. Az
Y' = F(x,y)
típusú elsőrendű differenciálegyenlet megoldásának legegyszerűbb módja az ún. Euler-módszer módszer. Ha a független változó kezdeti értéke X0 és a h növekmény állandó, akkor
Ez a módszer, bár nagyon egyszerű, csak akkor ad megbízható eredményt nagy k értékeknél, ha h értékét megfelelően kicsinyre választjuk. Jóval pontosabb eredményt kaphatunk az ún. negyedrendű Runge-Kutta-eljárás valamelyik változatát alkalmazva, így pl.
Nyilvánvaló, hogy a részletesebb, pontosabb számolás, tehát a Runge-Kutta-módszer több gépidőt, nagyobb kapacitású számítógépet igényel, mint az egyszerűbb Euler-módszer.
A szimulációs játékok egy részénél az egyenletes eloszlástól eltérő véletlenszám-eloszlásra is szükség van. Ezek előállítására vonatkozó transzformációk megtalálhatók a standard matematika könyvekben. Sok esetben azonban egyszerűbben is célhoz juthatunk. Ha pl. normális eloszlású véletlenszámok sorozatára van szükségünk, akkor ezt előállíthatjuk egyenletes eloszlású véletlenszámok összegeként. Így pl. eléggé jól használható M átlagértékű és S szórású normális eloszláshoz jutunk, ha a (0,1) intervallumban keltett egyenletes eloszlású véletlenszámból (xi) 12-t egymás után összegezünk az alábbi képlet szerint:
A differenciálegyenletek megoldására és különböző valószínűségeloszlások előállítására külön példát nem adunk. A fejezet további részeiben szereplő játékok programjai ezeket a módszereket is használják.
4.2. Mozgást utánzó játékok
Az ember fejében a mozgások kiértékelésére, előrebecslésére számos kitűnő "szubrutin" található. Ennek köszönhetjük, hogy a városi forgalomban gyalogosként vagy gépkocsivezetőként egyaránt részt tudunk venni, labdajátékokat játszunk, síelünk, biliárdozunk, árkot ugrunk stb. Az az emberi képesség azonban, hogy pillanatnyi helyzetekből, sebességekből determinisztikus fizikai világkép alapján a mozgások eredményét előre megmondjuk, csak bizonyos környezetben, megszokott helyzetekben működőképes. Ha az ember egy tárgy elhajítását nem "érzi" izmaiban, nem szemével követi a röppályát, hanem azt egy számítógéphez kötött képernyős megjelenítő mutatja neki, akkor már sokszor és nagyot téved, itt az alkalom tehát a képességfejlesztésre, a játékra.
A legegyszerűbb mozgással kapcsolatos számítógépes játékok a ferde hajítások köréből származnak. A mozgásegyenletek itt még nagyon egyszerűek, megoldásuk is közismert. (A légellenállás vagy súrlódás hatását nem szokás ezekben az egyszerű feladványokban figyelembe venni.) A 4.2. ábrán ennek az alapfeladatnak két változatát látjuk.
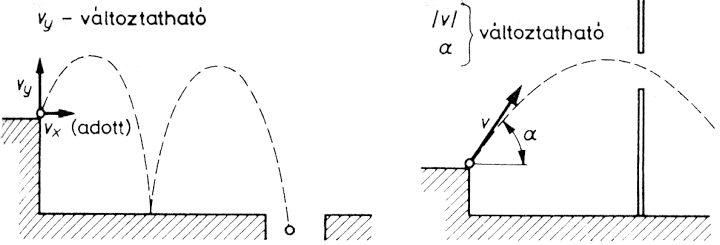
4.2. ábra: Egyszerű feladatok a ferde hajítások köréből
Az egyik esetben - rugalmas ütközéseket feltételezve - úgy kell a labdát a lyukba juttatni, hogy vízszintes sebességkomponense adott, állandó értékű; a függőleges komponens nagysága azonban szabályozható. A másik feladat kissé életszerűbb; a parittyázás számítógépes változata. Itt a kezdősebesség nagyságának és irányának megváltoztatásával kell a lövedéket a feltüntetett résen keresztüljuttatni. A könyvben külön programot nem közlünk róluk.
4.2.1. Rakéták, hajók, űrhajók
A mozgásegyenletekkel való játék kimeríthetetlen lehetőségeit jelentik a rakéta, ill. űrhajófeladatok. Ezeknél a mozgásegyenletek általános alakja
ahol m az objektum tömege, r helyzetvektor, Fv a gravitációs vonzásból adódó erő, F(t) a rakéta hajtóműve által szolgáltatott erő.
A differenciálegyenlet megoldását azonban nem csupán az nehezíti, hogy a játék során a játékosnak módja van különböző nagyságú rakétatoló, ill. fékező erőt beállítani, hanem sok feladatnál azt is figyelembe kell venni, hogy a mozgás inhomogén gravitációs térben történik, vagyis
akkor, ha az r vektort a mozdulatlannak tekintett Föld, Hold stb. középpontjától mérjük. Tovább bonyolítja a viszonyokat, hogy a rakéta hajtóművének üzeme a rakéta önsúlyát csökkenti. Ha m(t) tömegű v sebességgel mozgó testből delta m tömegű testet kilövünk az m tömegű testhez képest u sebességgel, az e hatásra bekövetkező sebesség-változás:
így az m0 induló tömegű rakéta sebessége t idő múlva
értékű lesz. Homogén gravitációs térben (g nehézségi gyorsulás) pl. függőlegesen felfelé haladó rakétánál, ha az időegység alatt kiáramló gáz tömege c:
Ezzel az összefüggéssel azt illusztráltuk, hogy a mozgásegyenletek megoldása menynyire eltérő lehet a szabadesésnél megszokott lineáris, ill. másodfokú kifejezésektől.
A játékok egy részénél a feladat egydimenziós: a rakéta az égitest felszínére merőlegesen emelkedik vagy süllyed. Ezen alapuló játék (ZX Spectrum) számítógépes változatának programját alább találjuk.
10 PRINT TAB (14);"LUNAR"
20 PRINT
30 PRINT "A jatek az Apollo Lunar Module"
40 PRINT "holdraszallasanak szimulacioja."
50 PRINT "A fedelzeti szamitogepet"
55 PRINT "manualisan kell iranyitania."
60 PRINT "A leszalloegyseg sulya: 15034 kg"
70 PRINT "rend. allo uzemanyag: 8165 kg"
80 PRINT "Beallithato uza. egetesi seb.:"
90 PRINT " 0 kg/sec = szabadeses,"
95 PRINT "100 kg/sec = max. teljesitmeny"
100 PRINT "(Tizedes ertek is megadhato.)"
105 PRINT "Beavatkozas 10 masodpercenket."
110 PRINT : PRINT "Sok sikert!"
120 LET L=0
130 PRINT : PRINT "SEC KM KM/H UZEMA. FELH."
135 FOR I=1 TO 32: PRINT "=";: NEXT I: PRINT
140 LET A=120: LET V=1: LET M=33075: LET N=15112: LET G=1E-03: LET Z=1.8
150 PRINT L;TAB (4);INT (A*160.9)/100;TAB (11);INT (3600*V*1.609);TAB (18);(M-N)/2.2;TAB (27);: INPUT K
152 IF K>100 THEN GO TO K=100
153 PRINT K
155 LET T=10: LET K=K*2.2
160 IF M-N<1E-03 THEN GO TO 240
170 IF T<1E-03 THEN GO TO 150
180 LET S=T: IF M>=N+S*K THEN GO TO 200
190 LET S=(M-N)/K
200 GO SUB 420: IF I<=0 THEN GO TO 340
210 IF V<=0 THEN GO TO 230
220 IF J<0 THEN GO TO 370
230 GO SUB 330: GO TO 160
240 PRINT "Az uzemanyag elfogyott a"
242 PRINT L;"-ik masodpercbem."
245 LET S=(-V+SQR (V*V+2*A*G))/G
250 LET V=V+G*S: LET L=L+S
260 LET W=3600*V: PRINT "Holdat ert a ";L;"-ik mp-ben"
265 PRINT : PRINT "Sebesseg talajerinteskor:"
270 PRINT W*1.609;" KM/H"
274 IF W<=3 THEN PRINT "Tokeletes leszallas!": GO TO 440
280 IF W<=8 THEN PRINT "Jo leszallas (lehetne jobb)!": GO TO 440
282 IF W>60 THEN GO TO 300
284 PRINT "A holdkomp megserult. Remeljuk"
286 PRINT "megerkezik a mentocsapat,"
287 PRINT "mielott elfogy az oxigen..."
288 GO TO 440
300 PRINT "Becsapodott a holdba, senki nem maradt eletben."
310 PRINT "Egy ";W*.227*.305;"m atmeroju"
315 PRINT "kratert hozott letre!"
320 GO TO 440
330 LET L=L+S: LET T=T-S: LET M=M-S*K: LET A=I: LET V=J: RETURN
340 IF S<5E-03 THEN GO TO 260
350 LET D=V+SQR (V*V+2*A*(G-Z*K/M)): LET S=2*A/D
360 GO SUB 420: GO SUB 330: GO TO 340
370 LET W=(1-M*G/(Z*K))/2: LET S=M*V/(Z*K*(W+SQR (W*W+V/Z)))+.05: GO SUB 420
380 IF I<=0 THEN GO TO 340
390 GO SUB 330: IF J>0 THEN GO TO 160
400 IF V>0 THEN GO TO 370
410 GO TO 160
420 LET Q=S*K/M: LET J=V+G*S+Z*(-Q-Q*Q/2-Q^3/3-Q^4/4-Q^5/5)
430 LET I=A-G*S*S/2-V*S+Z*S*(Q/2+Q^2/6+Q^3/12+Q^4/20+Q^5/30): RETURN
440 INPUT "Ujra probalja? ";V$
450 IF V$="i" OR V$="I" THEN PRINT : PRINT : GO TO 60
Itt kezdetben egy rakéta 193 km távolságban van a Holdtól és 5792 km/h sebességgel közeledik felé. A játékos az üzemanyag elégetésének mértékét és ezzel a fékezőerőt szabályozza. A program 10 másodpercenkénti állapotjellemzőket közöl (helyzet, sebesség) és adatot kér a fékezés mértékére. A program futása során keletkező nyomtatási kép:
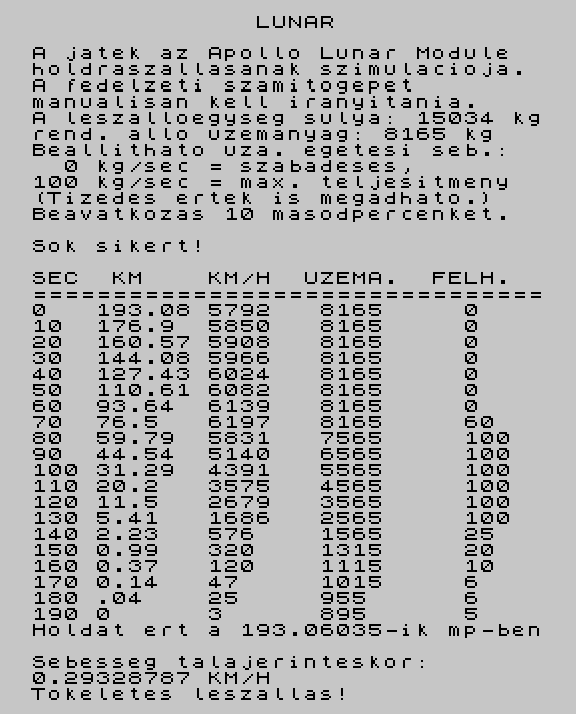
Az ilyen jellegű játékok programjai két változatban készülnek. Az egyik szerint az előzőkben már felírt differenciálegyenletet folyamatosan oldjuk meg. A másik - sokszor alkalmazott - eljárás során a differenciálegyenlet megoldása ismert, legalább is közelítő formában. Ilyenkor a számítógép a helyzetet, sebességet stb. hatványsorból számolja ki. (ld. programlista 420, 430 sor.)
A mozgásegyenleteken alapuló igazi érdeklődést is keltő játékoknak két fontos tulajdonságuknak kell lenniük. Meg kell szabadulniuk az egydimenziós feladatok szűk változtatási lehetőségeitől, és a mozgásegyenletek megoldását, kiértékelését legalább két dimenzióban - síkban - kell nyújtaniuk. Másrészt viszont mind a helyzet folyamatos kijelzését, mind pedig a szabályozott paraméter értékének folyamatos bevitelét biztosítani kell. Így tehát az egyébként igen jól hasznosítható teletype és alfanumerikus képernyős megjelenítő mint kimeneti perifériák, nem nagyon jönnek számításba lassúságuk és azon tulajdonságuk miatt, hogy csak "egyirányúak". A papírszalag és a képernyős megjelenítő sorai ugyanis meghatározott módon követik egymást, ezért visszafordulást, egy helyben tartózkodást stb. nem lehet velük ábrázolni.
Igazában jó rakéta-, vagy űrhajójátékot tehát csak grafikus vagy majdnem grafikus képernyős megjelenítő felhasználásával lehet játszani. Emellett gondoskodni kell arról is, hogy a játékos keze ügyében olyan eszköz is legyen, amelyről a számítógép folyamatosan tud adatot bevinni. A jó játéknak az is feltétele, hogy a számítógép sebessége legyen elegendő az ismétlődő számítások elegendően gyors elvégzéséhez.
Egy kétdimenziós űrhajós játék hardware-elemeit és alapgondolatát a 4.3. ábra mutatja.
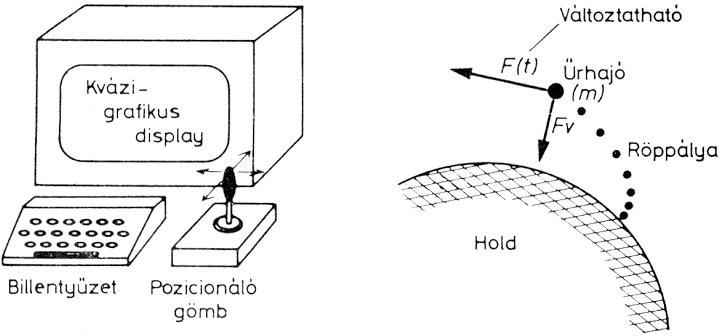
4.3. ábra: Űrhajójáték hardware-elemei és a játék vázlata
A képernyős megjelenítőnek korlátozott ábramegjelenítési lehetősége van: 240x180 pont ábrázolható rajta raszter-rendszerben. A pontok felvillantását a számítógép vezérli. A pozícionáló gömb (amolyan botkormány) mozgatásával egy fénylő pont helyzetét változtatjuk. Ennek egy referenciaponthoz viszonyított helyzetével folyamatosan megadhatjuk az űrhajóra ható F(t) erő irányát és nagyságát. A számítógépprogram az
differenciálegyenletet oldja meg lépésről lépésre Runge-Kutta-módszerrel. Mivel a számítógépben a számítások elvégzésének ideje nem függ a számítások eredményétől, a differenciálegyenlet egy-egy növekményéhez tartozó számítási idő állandó. Ez az idő a játékidő alapja: ilyen időközönként jelenik meg az űrhajó pályájának egy újabb pontja.
A játék során a rakéta a Hold meghatározott pontjáról, adott sebességgel és irányba elindul. Ettől kezdve mozgását a pozícionáló gömb által megszabott erőhatás irányítja. A feladat: minél rövidebb idő alatt megkerülni - egyszer körberepülni - a Holdat. Az elemi lépéshez tartozó időtartam kb. 2-3 s, így az irányítási feladat az emberi észlelések, mozgások által kezelhető tartományba esik. Az ismételt játékok során sok ismeretet lehet szerezni a newtoni mechanika alapvető jelenségeiről, a centrifugális erőről stb.
Ennek az űrhajós játéknak több változata létezik. A háromdimenziós játék igen nagy figyelmet kíván a játékostól, a játék alapfeltételeként grafikus képernyős megjelenítőre is szükség van.
Kétdimenziós mozgásegyenlet-megoldáson alapul néhány "autóverseny" elnevezésű játék. Itt bonyolult pályákon kell végigvezetni egy autót, miközben a ráható erő iránya és nagysága, vagyis a kormány állása és a gázpedál változtatható.
A mozgást utánzó-játékok sorában még egy érdekes változatot kell bemutatnunk. A játék alapjaként felhasznált ötlet: egy négyzet alakú területen valahol, ismeretlen helyen egy hajó tartózkodik. Ezt a hajót kell "eltalálni" a koordináta-rendszer kezdőpontjából leadott lövésekkel. A számítógép minden egyes lövés után közli, hogy a hajó és a lövedék becsapódási helye közötti távolság mekkora.
Ha a hajó nem mozog, akkor helyét két próbálkozás után pontosan megtudhatjuk (4.5. ábra).
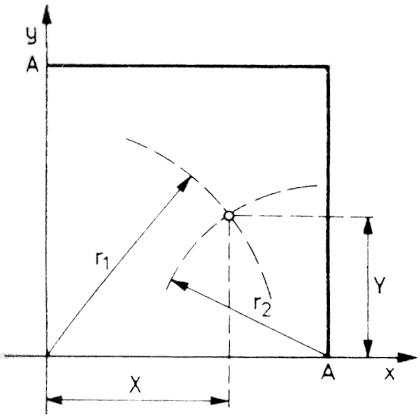
4.5. ábra: A célbalövésel vázlata
Elsőként pl. a (0,0) pontba célozva megkapjuk az
távolságot, majd az (A,0) pontra leadott lövésből az
mennyiséget. A két "mérésből" X és Y meghatározható:
Így tehát a feladat nagyon egyszerűen megoldható, és játékot csupán annak jelenthet, akinek elemi geometriai ismeretei hiányoznak. Igazi játékká válik azonban a feladat, ha a hajó nem áll egy helyben, hanem állandó - természetesen ismeretlen - sebességgel mozog. A közölt program tartalmazza ezt a lehetőséget is. A 15-16. sorban a hajó kezdőhelyzetét véletlenszerűen megválasztjuk, a 25...45. sorban pedig mozgásáról intézkedünk. A mozgás sebessége véletlenszerűen 0,5...3,5 egység/idő nagyságú lesz, iránya pedig olyan, hogy a hajó sohasem a négyzet szélei felé indul, hanem a játéktér belsejébe (persze az is előfordulhat, hogy valamelyik koordinátatengellyel párhuzamosan fog haladni).
A játék fontos feltétele, hogy az idő csak akkor "telik", amikor egy-egy lövést leadunk. Így "méréseink" eredményei azonos időtartamnyira levő helyzetekről tájékoztatnak. Kissé nehezíti a feladatot, hogy a távolságértékeket egész számok formájában kapjuk, így a négyzetszámok kiértékeléséből ravaszkodva nem tudjuk a feladatot megoldani.
1 REM Celloves
4 PRINT "Egy 66x66-os mezoben kell egy ismeretlen helyen levo"
6 PRINT "hajot eltalalni a celpont koordinatainak megadasaval."
8 PRINT "A program a becsapodas es a hajo tavolsagat kozli."
12 RANDOMIZE
15 LET X0=INT(66*RND)
16 LET Y0=INT(66*RND)
17 LET C1=X0:LET C2=Y0
21 LET A=0
22 PRINT "Mozogjon a hajo (I/N)";:INPUT V$
24 IF V$="N" OR V$="n" THEN LET N=0:LET S1=0:GOTO 40
25 LET S=ABS(ATN((32.5-Y0)/(32.5-X0)))
30 LET S1=S+PI*(.5-RND)/2
35 LET N=3*RND+.5
40 LET X1=N*COS(S1)*SGN(32.5-X0)
45 LET Y1=N*SIN(S1)*SGN(32.5-Y0)
46 LET A=A+1
47 PRINT A;". kiserlet"
50 PRINT "Koordinatak: ";:INPUT J,K
55 LET R=SQR((X0-J)^2+(Y0-K)^2)
58 IF R=0 THEN 95
60 PRINT "A becsapodas tavolsaga: ";INT(R+.5):PRINT
65 LET X0=INT(X0+X1+.5)
70 LET Y0=INT(Y0+Y1+.5)
75 IF X0*Y0<=0 THEN 100
80 IF X0>=66 OR Y0>=66 THEN 100
86 IF A=20 THEN 88
87 GOTO 46
88 PRINT "Ez nem megy. A hajo a ";C1;",";C2;"pontrol indult"
89 GOTO 105
90 GOTO 46
95 PRINT "Gratulalunk!":PRINT "A hajo elsullyedt."
98 GOTO 105
100 PRINT "A hajo kiert a veszelyes zonabol az ";X0;",";Y0;" pontokon."
103 PRINT "Indulasi helye: ";C1;",";C2;" volt."
105 PRINT "Akar ujra jatszani (I/N) ";:INPUT V$
107 IF V$="I" OR V$="i" THEN 12
A játéknak e változata nem játszható valamiféle taktika vagy stratégia nélkül. Az nagyon könnyen átlátható, hogy a statikus változat megoldásánál alkalmazott módszer csak nehézkesen járható, mert a feladat megoldása azt jelenti, hogy a hajó kezdőhelyzetén (X0,Y0) kívül a mozgásának sebességkomponenseit (Vx,Vy) is ismerni kell. Így a számítások meglehetősen összetett egyenletrendszerre vezetnek.
Ha a játék kezdetben túl nehéznek tűnik, és a hajó mindig "kiér a veszélyes zónából" találat nélkül, az 58. sorban a feltételt kissé lazíthatjuk: R^N választásával nem csupán a "pontos" találatot tekinthetjük sikeresnek, hanem azt is, ha a lövedék N=1, 2, 3 egységnyi távolságra csapódik be a hajó közelében.
4.2.2. Csillagutazás - Star-Trek
A következőkben vázlatosan ismertetünk egy olyan számítógépes játékot, amely eléggé elterjedtnek mondható. Mintegy 10 évvel ezelőtt keletkezett a játék első változata, és nagyon sok közismert géptípushoz készítették el a megfelelő programnyelv változatát. A program eléggé terjedelmes: legalább 32 K szó tárkapacitás szükséges a tárolásához, futtatásához. Éppen ezért a részletes programot nem közöljük, csak irodalmi forrásokra hivatkozunk.
"Mint minden iskolásgyerek tudja, a Tejút-rendszer legintelligensebb civilizációi már jóval a Harmadik Magellán Konferencia előtt (ezt az 1. számú Szövetségi Csillagbázison tartották a 1016-1021 csillagidőpontban) megállapodást kötöttek az ún. 2^6 Egyezményében a galaktika jelölésrendszeréről. E történelmi okmányban az aláíró kultúrák megegyeztek abban, hogy a galaktikát kétdimenziós ábrázolásban 64 részre osztják, egy 8x 8-as mátrix formájában. Ezt különösen a Föld kultúrája szorgalmazta (amelynek múlhatatlan érdemei vannak a Szövetség létrejöttében), mert így évszázados csillagtérképeinek a földi égbolt csillagképei szerinti felosztását követhették. A 16 régió mindegyikét négy kvadránsra osztották, régi Római Számokkal jelölve őket (ez utóbbiak eredete már teljes homályba merült)."
Így kezdődik a játék leírása, amiből azonnal érezhető, hogy a játékosok a csillagutazások jövőben esetleg megvalósuló feltételei között fognak játszani. A játék célja az, hogy az "Enterprise" nevű űrhajó kapitányaként a játékos megsemmisítse a 17 űrhajóból álló Klingon űrflottát, amely a Bolygók Egyesült Szövetségét veszélyezteti.
A játék kezdetekor a számítógép közli a csillagtérképet, vagyis a játékos és az ellenség űrhajóinak helyzetét, a csillagbázisok és a csillagok helyét. A csillagbázisok szerepe nagy: itt javítják az űrhajókat, ill. energiatartályaikat itt lehet feltölteni. A játékos az alábbi "utasítások" közül válogathat:
Ez utóbbi lehetőséget teremt a játékos számára a játék "naplójának" előállítására, a helyzetelemzéshez szükséges adatok kiíratására, a fotontorpedó útjának vizsgálatára, irány- és távolságszámításokra stb.
A fentiekből már érezhető, hogy ez a játék valamilyen absztrakt "katonásdi", amelyben természetesen nemcsak a játékos űrhajója mozog, hanem a "Klingon" flottát is irányítja a számítógép. A játék részben determinisztikus elemekből áll elő (pályakijelölés, célzás stb.), részben pedig véletlenszerű folyamatok is beleszólnak. Csak példaként: a csillagbázison javításra kerülő űrhajó sohasem készül el "idejében", mert a szerviz mindig alábecsüli a javításhoz szükséges időt...
A Star-Trek szabályrendszere eléggé összetett; megtanulni, megérteni csak ismételt játékok során lehetséges. A játék jó vagy unalmas voltáról megoszlanak a vélemények. A tudományos-fantasztikus irodalom és "elmesport" hívei érdekesnek és gondolatébresztőnek tartják; a tizenévesek gyorsan képesek a játékszabályokat megtanulni, ők is szívesen játszanak vele; sokan azonban úgy vélik, hogy a bonyolult játékrendszer megtanulása után a játékból szerezhető szórakozás messze a várakozáson alul marad.
A Stark-Trek vitathatatlanul a legsikeresebb, legelterjedtebb számítógépes játék. Az Egyesült Államokban évente mintegy 25 alkalommal rendeznek Star-Trek konvenciókat, melyeken sok ezer érdeklődő vesz részt. A játék leírása elérhető szinte az összes népszerű programnyelven: FORTRAN, APL, PL/1 stb. Vannak továbbfejlesztett változatok is. Ezek egyikénél a Klingon flotta kétfajta hajóból tevődik össze: a Romulans-ok láthatatlanok, a Tholian-ok pedig csoportosan támadnak. A program a tudományos-fantasztikus regényekből ismert "időutazást" is lehetővé teszi, ez azonban nagyon veszélyes. (Tárkapacitás igénye: kb. 100 k szó.)
Elkészült a játék "fordított" változata is: itt a számítógépes játékot kockadobásokkal játszható táblás játékká alakították át. A játék ugyan kissé hosszadalmas így, mert napokig vagy hetekig is tarthat, de állítólag annyira érdekes, hogy "az órák csak úgy repülnek". - És még egy apróság: azok a trikók, amelyeken a mélykék ég csillaghátterében az Enterprise ezüstös képe csillog, nagyon kelendőek...
4.3. Biológiai folyamatok szimulációja
A biológiai folyamatok a játéklehetőségek szempontjából két nagyobb csoportra oszthatók.
Az egyik csoportba azok a jelenségek tartoznak, amelyeket mindenki ismer, vagy pontos ismeret híján is eléggé jól "érez". Ilyen jelenségcsoport egy faj létszámának változása. Mindenki tudja pl. biztosan, hogy egyetlen nyúlpár két hónap alatt nem fog megtízszereződni, de nem biztos, hogy pontos választ tud adni arra a kérdésre, hogy az eredeti nyúlpár hat év alatt hány utódot hozhat létre. Az "érzések" felületes, pontatlan következtetésekre vezetnek, így aztán nem meglepő, hogy ezekre a biológiai folyamatokra játékokat lehet alapozni.
A második csoport fontos biológiai törvények lefolyásának modellezésén alapul. Ha egyáltalán a játék szót ezekben az esetekben használhatjuk, azért tehetjük, mert itt bizonyos esetekben a jól ismert játékok egyszerű komponenseiből összetevődő olyan-folyamatok szerepelnek, amelyek meglepőek és ezért újra és újra megismétli őket az ember. Kicsit hitetlenkedve, kicsit csodálkozva, önfeledten és érdek nélkül, vagyis igazán játszik velük.
Ebben a fejezetben először olyan játéklehetőségekről írunk, amelyek alapja a véletlen, majd olyanokról, amelyek determinisztikusak. Néhány biológiai jelenségnek mind a sztochasztikus, mind a determinisztikus modelljét megemlítjük.
4.3.1. Sztochasztikus játékok
Az itt ismertetésre kerülő játékok M. Eigen Nobel-díjas kémikus könyvén alapulnak, amelynek címe: "A játék, a természettörvények vezérelte véletlen". A könyv az anyagszerveződés és az élet fejlődésének kérdéseiről szól, és illusztrációként jó-néhány játékot ír le.
A játékok többségét négyzet alapú lemezen levő 8x8-as lyukakba helyezett színes golyókkal és különleges dobókockákkal lehet játszani (4.6. ábra). A játékmezőre felkerülő vagy onnan lekerülő golyók sorsáról a dobókockák és egy-egy játék adott szabályrendszere intézkedik. A különleges dobókockák szerepe könnyen érthető, ha pl. arra gondolunk, hogy két oktaéder feldobásával a tábla egyetlen helyét jelölhetjük ki véletlenszerűen.
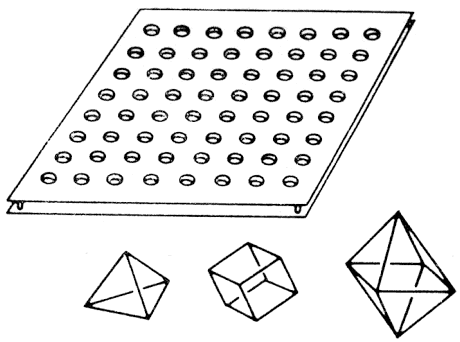
4.6. ábra: Biológiai szimulációs játékok eszközei: a tábla és a dobókockák
A játékok tehát - elvben - számítógép nélkül is játszhatók. Valóságban azonban az összetettebb jelenségek lefutásának vizsgálatához 200...500 kockadobás is szükséges, ami a játékot vontatottá teszi. Az is meglehetősen nehezíti a játékot, hogy tetraéder vagy oktaéder alakú dobókockákat magunknak kell csinálnunk, melyek ezért biztosan "cinkeltek" lesznek, így aligha várható a dobások eredményének egyenletes eloszlása.
Több játéknál korlátot jelent a játéktér kicsiny volta is, nagyobb játéktéren pedig a játékidők nyúlnak túl hosszúra. A következőkben olyan játékokat mutatunk be, melyek számítógépes megoldást igényelnek, ha a "természet által vezérelt véletlen jelenségek" fölötti szemlélődésünk játék jellegét meg akarjuk tartani és nem kívánunk a részletekben elveszni. A játékok lényegéről csak némi benyomást kaphatunk, részletesebb magyarázatukra nem térünk ki.
Ingadozás: 4x4-es mezőre 8 fehér és 8 fekete golyót helyezünk. A fej vagy írás dönt arról, hogy fehér vagy fekete golyót helyettesítünk ellenkező színű golyóval. A játék vége (az egyik színű golyók "kipusztulása") gyorsabban elérhető, ha a körülzárt golyók egyszerre változtatják színüket.
Egyensúly: 8x8-as mezőre véletlenszerűen elhelyezünk 32 fehér és 32 fekete golyót. Két oktaéder feldobásával "megcímzünk" egy elemi cellát, az itt található golyót levesszük és egy ellenkező színűt rakunk a helyére.
Minden vagy semmi: A játék az előző elrendezésben indul, a szabály azonban most más: a megcímzett golyó "megduplázódik", vagyis leveszünk egy ellenséges golyót, és a saját színűt tesszük ennek is a helyére.
(A három játék közötti különbséget leginkább a végeredményen mérhetjük le. A 4.7. ábra a végállapotok valószínűségeloszlását tünteti fel. Ennek ismeretében a játék kimenetelére már becsületes fogadásokat is lehet kötni.)

4.7. ábra: Az "ingadozás" (1), "egyensúly" (2) és a "minden vagy semmi" (3) játékok végeredményének valószínűségei
Kiválasztódás: A 8x8-as játékmezőn véletlenszerűen elhelyezünk 32-32 különbözőszínű golyót. Két oktaédert dobunk fel, és felváltva a következő két szabály szerint járunk el:
A játékot érdemes úgy is játszani, hogy több különböző színű golyó van kezdetben a táblán. A végeredmény: egy szín mindig "eluralkodik", a többi "kipusztul". Érdekes változat az, amelynél a különböző színű golyók "szelekciós értéke" különböző. Itt minden oktaéder-kettős feldobása után egy hagyományos kockát is feldobunk, és az ezen található számértéktől függően veszünk le, ill. duplázunk golyókat. Ha pl. piros golyót csak akkor veszünk le, ha a kockán 1-et találunk, de bármilyen (2...6) értéknél megduplázzuk és a sárga golyót mindig levesszük, de csak akkor duplázzuk, ha a kocka 1-et mutat, akkor a játék nyilván a piros színű golyók elszaporodásával fog végződni.
Bolyongás két dimenzióban. A 4.8. ábra szerinti elrendezésben zajlik a játék. A négy játékos mindegyike négy azonos színű golyót kap. A játékosok sorban két tetraéderrel dobnak, amelynek oldalain 0, 0, +, - jelek szerepelnek. + + vagy - - eredménynél a játékos egy figurával a starthelyre léphet. A továbbiakban a figura az ábrán feltüntetett irányba léphet a dobás eredményétől és a játékos választásától függően. A játék célja: minél előbb mind a négy figurával a CÉL-ba eljutni. A játéktér szélén azonban már csak két irányban lehet haladni. A játékban az ellenfél figuráit ki lehet ütni, akár a CÉL előtt közvetlenül is. Így tehát ez a játék eléggé hasonlít a nálunk is ismert "Ki nevet a végén" elnevezésű társasjátékhoz.
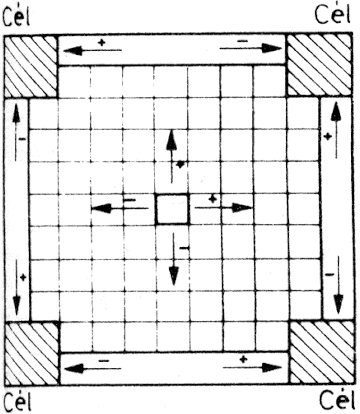
4.8. ábra: Játéktábla a "bolyongáshoz"
Küzdelem: A 8x8-as játékmezőn kezdetben meghatározott számú zöld, sárga és piros golyót helyezünk el. Két feldobott oktaéderrel megcímzett golyók átalakulnak attól függően, hogy szomszédságukban milyen színű golyókat találunk. Vagyis:
zöld
sárga
piros
kék
játékszabály legfontosabb részét, az állapotátmeneti mátrixot a 4.1. táblázat tartalmazza. A kék színű golyók a további játékban nem vesznek részt, azokat le kell venni.
| Szomszédos mező | Megcímzett mező |
|||
üres |
zöld |
sárga |
piros |
|
| mind üres | zöld |
- |
- |
piros |
| zöld | zöld |
- |
zöld |
piros |
| sárga | zöld |
zöld |
- |
piros |
| piros | zöld |
- |
sárga |
piros |
A játék a 4.9. ábrán látható változásokra vezet. Ezeket egyszerűen értelmezhetjük, ha arra gondolunk, hogy a zöld golyó füvet jelent, a sárga és a piros pedig nyulat és rókát. Így a játék egy ekológiai rendszer modellje is lehet.
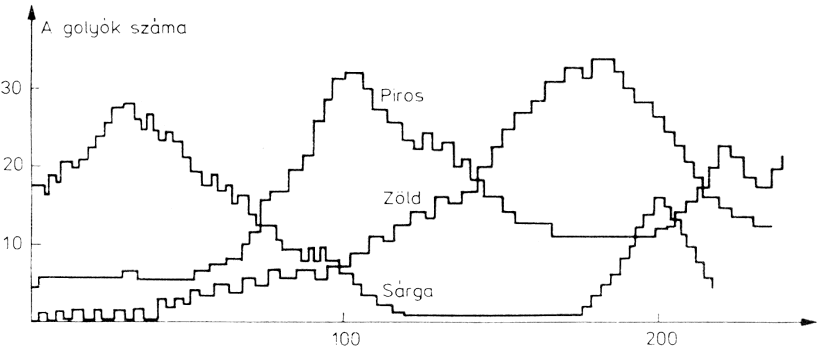
4.9. ábra: A küzdelem során változó golyók száma
RNS-játék: Kezdetben minden játékos kap egy 80 gyöngyszemből álló felfűzött láncot, amelyen az egyes gyöngyszemek (piros, kék, zöld, sárga) véletlenszerű sorrendben helyezkednek el. A játék célja a lánc olyan összehajtogatása, hogy az egymással szembekerülő piros-zöld, kék-sárga párokból minél több álljon elő (4.10. ábra).
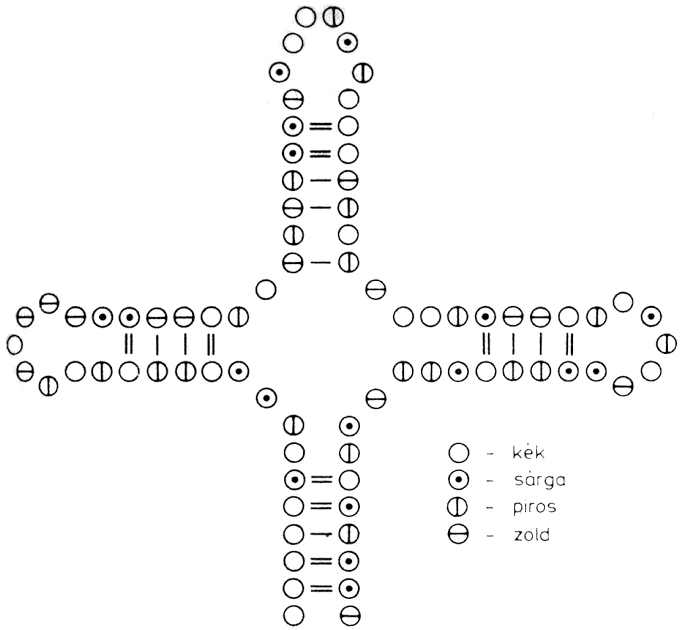
4.10. ábra: Egy RNS-lánc kialakulása
Egy tetraéderrel végzett dobások révén mód nyílik bizonyos "mutációk" létrehozására, vagyis egyes helyeken levő gyöngyszemek cseréjére. A játék kiértékelése során a piros-zöld pár kettő, a sárga-kék három pontot ér. Mint az ábrából is látható, a "levélszerű" kialakítás nagyobb nyereségre vezet.
Eigen játékai tehát valódi játékoknak is elfogadhatók, nevük azonban utal arra, hogy ezek nem csupán felelősség nélküli időtöltést nyújtanak, hanem bizonyos biológiai folyamatok modelljei. A könyv még sok más játékot is tartalmaz. Megtalálható benne az életjáték (life) (részletesen Id. a 4.3.3. pontban) és több más olyan játék, ahol a golyók bizonyos csoportjainak kitüntetett jelentősége és szerepe van (pl. a go játék). Találunk itt betűjátékokat, amelyekből szavakat kell kirakni és olyan szóátalakítási játékokat, ahol a kezdőszóból kell eljutni egy másik szóig, miközben az egyes betűk véletlenszerűen változnak.
E játékok számítógépes programjai viszonylag könnyen elkészíthetők. Ha grafikus, vagy kvázigrafikus képernyős megjelenítő is rendelkezésre áll, a játékok igen látványossá is tehetők. Ilyen típusú játékokat a számítógépes oktatási módszerek közé is szívesen beiktatnak (Id. az 5.3. pontot).
4.3.2. Populációjátékok
Az előző szakasszal ellentétben most egy vagy több faj egyedeinek számát nem véletlenszerű események irányításával követjük nyomon, hanem ezek "okaként" állandó paraméterű differenciálegyenletet fogunk megoldani. Ez a módszer is nagyon érdekes, sokfajta jelenség részletes elemzését teszi lehetővé.
Ha egyetlen faj egyedeinek számát az idő függvényében x(t)-vel jelöljük, akkor az időegység alatt keletkező új egyedek száma
lesz, vagyis az új egyedek száma a már életben levő egyedek számával lesz arányos. Ha a pozitív állandó, akkor a faj létszáma exponenciálisan növekszik. Az exponenciális növekedésnek azonban rendszerint korlátai vannak; a túlnépesedés, a táplálék véges mennyisége az elszaporodást mérsékeli, így a következő matematikai modell a jelenséget pontosabban írja le:
ahol a és b a folyamat állandó paraméterei. Bár ez a differenciálegyenlet nemlineáris, még létezik analitikus megoldása. Az analitikus megoldásokról azonban le kell mondani akkor, ha a rendszer egyidejűleg több fajt is tartalmaz, és e fajok versengenek a táplálékforrásokért. Legyen x1(t) és x2(t) két különböző faj. Ekkor az ún. Volterra egyenletek:
Most a két populáció egymást is "eszi", ezért szorzatukkal arányosan csökken a szaporodás aránya. Kicsit hasonló összefüggéshez jutunk, ha olyan rendszer viselkedését írjuk le, amelyikben az egyik faj a másikból él, vagyis
Itt az x1 faj x2 jelenléte nélkül exponenciálisan elszaporodna, x2 pedig X1 jelenléte nélkül kihal. Az x2 tehát "megeszi" x1-et; x1 szolgál x2 táplálékául. Valahogy így: a nyulak rókák nélkül elszaporodnának, a rókák nyulak nélkül kihalnak. A két faj egyedeinek - az adott esetben a nyulak számára végzetes - találkozásainak száma a két faj létszámának szorzatától függ, ahogyan első közelítésben az autók "találkozásainak" vagyis a "koccanásoknak" a száma is az autók számának négyzetével arányos.
További módosítási lehetőségként a fajok számának alakulását külső tényezők is befolyásolhatják: pl. terménybetakarítás, vadászat stb. Így azután egy n fajt tartalmazó rendszerben az i-edik fajra általánosan a következő összefüggés írható fel:
ahol az utolsó tag a kívülről történő beavatkozást jelenti. (Ez persze nem csupán csökkentő célzatú lehet, hanem pozitív irányú változást is jelenthet, pl. ivadéktelepítés, tenyészállatok beszerzése stb.)
A fenti típusú differenciálegyenletek vizsgálatának igen fontos eszköze a digitális számítógép, ahol a kezdeti feltételek és a folyamat paramétereinek ismeretében gyorsan megkaphatjuk a megoldást jelentő időfüggvényeket.
(Megjegyezzük, hogy alapjában véve hasonló jellegű összefüggések modellezik a járványok lefolyását, a sikerszíndarabok pénztárai előtt jegyért sorban állók számát, az ismeretek megszerzésének és elfelejtésének társadalmi méretű változásait, a lézerek működésének alapjait, az egymást vaktában lövöldöző ellenséges hadseregek létszámának alakulását stb.)
Az előbb említett nyúl-róka rendszerből könnyen készíthetünk számítógépes demonstrációs programot. Ha a differenciálegyenlet-rendszert Euler-módszerrel oldjuk meg, akkor a következő egyszerű rekurziós formulához jutunk el:
ahol N a nyulak, R a rókák száma.
A (k+1)-edik időpontban tehát az egyedek száma a k-adik időpontbeli értékektől és a folyamat paramétereitől függ.
Az előbbieken alapuló, de bizonyos irányban bővített és játékosabb programot közlünk. A játék alaphelyzete a következő: a játékos egy állatfarm vezetője. Kezdetben az állatállomány 100 fiatal, 100 felnőtt és 100 öreg állatból áll. Ha az állományt tápláljuk, de értékesítésre egyetlen állatot sem veszünk el belőle, akkor száma növekszik. Közben azonban összetétele is megváltozik, mivel a k-adik ídőpontbeli állomány a (k+1)-edikben jelentősen, módosul. A módosulás oka, hogy az öregek és felnőttek szaporodnak (nem egyforma arányban) a fiatalokból felnőttek lesznek, az öregek egy része pedig elpusztul (4.11. ábra).
Az állatállománnyal azonban gazdálkodni is kell. Ennek lényege az, hogy minden esztendő végén előre "szerződésben kikötött" darabszámú és összetételű állatot kell értékesítésre átadni. Az egyes állatfajták eladási ára, ill. évenkénti költsége adott (ld. a 4.11b ábrát). A szerződést úgy kell megkötni, hogy 10 éven át a szállítási kötelezettségnek eleget tudjon a játékos tenni, azonban nem csupán az állomány elfogyása számít végzetes hibának, hanem az is, ha az egy meghatározott értéknél nagyobbá válik, vagyis túlszaporodik.
Állapot diagram
Összefüggések
x1(k+1) = ax2(k)+bx3(k)
x2(k+1) = x1(k)
x3(k+1) = x2(k)+cx3(k)Példa:
(a =0,7; b=0,4; c=0,6)
Gazdasági paraméterek:
költség / év eladási ár 4.11. ábra: Egy biológiai-gazdasági játék vázlata
Az állatállomány külső beavatkozás nélküli változásait az állapotdiagram és az azt leíró összefüggések mutatják. A számpélda a k-adik esztendőben 110 fiatal, 120 felnőtt, 130 öreg egyedből álló állománynak az összefüggésekből számítható értékeit tünteti fel a k+1-edik esztendőben. A gazdasági paraméterek megadott értékei melletti eredményeket találunk a mintafutások közölt részleteiben.
A program a játékostól három számot kér: az évenként átadni kívánt fiatal, felnőtt és öreg állatok számát. Ezután következik a gazdálkodás, majd a pénzügyi végeredmény. Ez úgy áll elő, hogy az eladási árból levonjuk az állatok tartási költségeit, valamint az állatállomány kezdő és végértéke közötti különbség abszolút értékét. A játék célja: megtalálni azt a három számot, amelynél a végösszeg maximális.
A program úgy kezdődik, hogy közli saját paramétereit, majd kérésre kiírja-rajzolja az állatállomány egymást követő években történő változásait abban az esetben, ha közben nem adunk el egyetlen darabot sem.
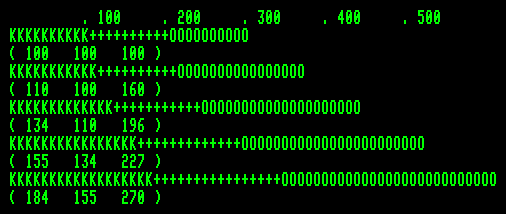
Ennek alapján kell megbecsülni az eladni kívánt állatok számát. A figyelmes olvasó észreveheti, hogy 10 fiatal zérus felnőtt és 60 öreg állat évenkénti eladása esetén az állomány állandó szintű és összetételű marad. Ha ezeket az adatokat adjuk meg, akkor a pénzügyi értékelés:
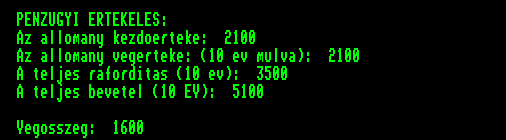
Ez nem rossz gazdálkodás, de mint látni fogjuk, nem is a legjobb. Ha az eladásra kerülő állatok számát 10, 20, 25-re választjuk, akkor az állomány száma és összetétele stabil lesz, de a gazdálkodás eredménye az előző esethez képest eléggé siralmas. Végösszeg: 497.5
A játék tehát azon alapul, hogy egy ismert, de nagyon összetett rendszer viselkedését kell előírt határok közé szorítani, ill. valamifajta optimumra törekedni. A feladat csak ismételt próbálkozásokkal oldható meg - a rendszer nemlinearitása (a "levadászásának" az állomány értékétől független volta) azonban a viszonyokat igen nehezen áttekinthetővé teszi. Az eddig közölt eredményekből ugyanis kinek jutna eszébe, hogy a játéknak a szerzők által ismert legmagasabb végeredménye a (0, 0, 80) értéknél adódik? (Végösszeg: 2652.5)
Ha a játék paramétereit módosítjuk, újabb (ismeretlen maximális végeredményű) játékhoz jutunk. A módosításra a 22, 30, 40 címkéjű sorokban, ill. a 86 és 110 utasításokban van mód. Az évenkénti változások kiszámítása a 620...635 sorokban történik.
2 REM MARHAK
4 PRINT "Egy marha-farm tulajdonosa kezdetben 100-100-100 fiatal, felnott"
5 PRINT "es oreg allata van. Ezek szaporodnak meghatarozott szabalyok"
6 PRINT "szerint. A marhakereskedovel 10 esztendore kell szerzodest kotni"
7 PRINT "ugy, hogy minden ev vegen ugyanannyi fiatal felnott es oreg"
8 PRINT "allatot fog on atadni. A jatek celja, hogy minel nagyobb legyen"
9 PRINT "a gazdalkodasbol szarmazo bevetel. (Rossz gazdalkodast jelent,"
10 PRINT "ha az allatok tulsagosan elszaporo dnak, vagy valamelyik ev"
11 PRINT "vegen nem sikerul a vallalt allatszamot atadnia.)"
21 PRINT
22 LET S=.7
30 LET T=.4
40 LET U=.6
45 GOSUB 700
46 DIM X(3),L(3),A(10),F(3),Y(3)
50 LET X(1)=100:LET X(2)=100:LET X(3)=100
55 LET L(1)=0:LET L(2)=0:LET L(3)=0
56 GOSUB 710
57 INPUT H
58 IF H=0 THEN 80
59 GOSUB 720
60 FOR K=1 TO 5
65 GOSUB 560
70 GOSUB 620
75 NEXT K
76 FOR J=1 TO 3
77 LET X(J)=100
78 NEXT J
79 PRINT :PRINT
80 PRINT "Mennyi legyen az evente eladott fiatal, felnott es oreg allatok szama"
81 INPUT L(1),L(2),L(3)
82 PRINT "Ohajtja az allomany evenkenti valtozasat diagrammon abrazolva? (0/1)";:INPUT M
86 LET A(1)=3*X(1)+10*X(2)+8*X(3)
87 PRINT
95 LET D=0
96 IF M=0 THEN 100
97 GOSUB 720
100 FOR Q=1 TO 10
104 IF M<>0 THEN GOSUB 560
109 LET P=2
110 LET D=(X(1)+3*X(2)+3*X(3))/P+D
115 GOSUB 620
120 FOR R=1 TO 3
125 IF X(R)<0 THEN 205
130 NEXT R
131 IF X(1)+X(2)+X(3)>700 THEN 207
135 NEXT Q
140 PRINT
150 PRINT "PENZUGYI ERTEKELES:"
155 PRINT "Az allomany kezdoerteke: ";
165 LET A(10)=3*X(1)+10*X(2)+8*X(3)
170 PRINT A(1)
171 PRINT "Az allomany vegerteke: (10 ev mulva): ";A(10)
175 PRINT "A teljes raforditas (10 ev): ";D
180 PRINT "A teljes bevetel (10 EV): ";
185 LET B=(3*L(1)+10*L(2)+8*L(3))*10
190 PRINT B
194 PRINT
195 PRINT "Vegosszeg: ";B-D-ABS(A(10)-A(1))
200 GOTO 650
205 PRINT "A szerzodest nem tudja teljesiteni!"
206 GOTO 650
207 PRINT "Az allomany tulszaporodott!"
209 GOTO 650
560 FOR J=1 TO 3
562 LET Y(J)=INT(X(J)/10+.5)
564 NEXT J
570 FOR Z=1 TO Y(1)
572 PRINT "K";
574 NEXT Z
580 FOR Z=1 TO Y(2)
582 PRINT "+";
584 NEXT Z
590 FOR Z=1 TO Y(3)
591 PRINT "O";
592 NEXT Z
593 PRINT
600 PRINT "(";X(1);" ";X(2);" ";X(3);")"
605 RETURN
620 LET F(1)=INT(S*X(2)+T*X(3)-L(1))
625 LET F(2)=INT(X(1)-L(2))
630 LET F(3)=INT(X(2)+U*X(3)-L(3))
633 FOR I=1 TO 3
634 LET X(I)=F(I)
635 NEXT I
636 RETURN
650 END
700 PRINT "A jatek beepitett parameterei (evenkenti ertekek):":PRINT
701 PRINT ,"Az oregek szaporodasi aranya:",T
702 PRINT ,"A felnottek szaporodasi aranya:",S
703 PRINT ,"Az oregek tulelesi aranya:",U
704 PRINT
705 PRINT "Penzugyi adatok: fiatal felnott oreg"
706 PRINT "Tartas koltseg: 1 3 3"
707 PRINT "Eladasi ar: 3 10 8"
708 PRINT
709 RETURN
710 PRINT "Akarja megismerni hogy az allomany hogyan szaporodik,"
711 PRINT "ha nem ad el egyetlen darabot sem (0 / 1)?"
712 RETURN
720 PRINT :PRINT
721 FOR Q=0 TO 4
722 PRINT TAB(10+Q*10);".";(Q+1)*100;
723 NEXT Q
724 PRINT
725 RETURN
4.3.3. Életjáték
Az életjáték (eredeti nevén The game of life) John Conway-tól, a cambridge-i egyetem matematikusától származik. Ez a játék amellett, hogy sok más matematikai és logikai játékhoz hasonlóan nagyon szórakoztató és érdekes, több aktuális tudományos probléma modellezésének alapgondolatát is hordozza.
Maga az alapötlet - feltehetően - Neumann Jánosnak, az önmagukat reprodukáló automatákra (az ún. sejtautomatákra) vonatkozó elméletének alapján született. Így - természetesen nagyon egyszerűsített formában - tartalmazza ennek az ötletnek a lényegét, hogy ti. nagyszámú, egyszerű és egyforma elemből olyan magasszintű automata "állítható össze", amely a benne tárolt információ hatására képes saját maga is azonos bonyolultságú automata reprodukálására.
A játék ugyanakkor már nevével is utal arra, hogy létrehozója az élővilág jelenségeivel való hasonlóságot is felfedezett benne. Egyrészt az élővilágban megfigyelhető növekedés, változás, szaporodás és pusztulás menetét, másrészt azt a tényt, hogy a soksejtű élőlények egyes sejtjeinek a szervezetben játszott szerepét nemcsak maga sejt, hanem a környező sejtek is megszabják.
A játék manuális formában egy nagy (elvileg végtelen) négyzethálós táblán - papíralapon - játszható. Itt az egyes sejteket korongok vagy bábúk képviselhetik. A játék alapötletének megfelelően azonban nevezzük a játéktábla négyzeteit a továbbiakban celláknak, a figurákat pedig sejteknek. (Ezt a szóhasználatot a számítógépes változatnál is meg fogjuk tartani.)
A játék kezdetén tetszés szerinti cellákba sejteket helyezünk. Egy cellának tehát két lehetséges állapota van, vagy üres, vagy sejtet tartalmaz és a kezdeti állapot olyan módon jellemezhető, hogy megmondjuk, melyik cella nem üres. Ebből az alapállapotból azután újabb elrendeződések sorozata jön létre a Conway által nagy körültekintéssel kidolgozott ún. genetikai törvények alapján. Maguknak az elemi sejteknek a sorsa háromféle lehet:
A túlélés, elpusztulás és születés szabályait Conway olyan módon szabta meg, hogy az egymást követő elrendezések (nevezzük ezeket nemzedékeknek) egymásutánja minél nagyobb változatosságot mutasson. Ugyanakkor olyan módon választotta ezeket a szabályokat, hogy egy elrendezésről puszta rátekintéssel ne mondhassuk meg, hogy mi lesz annak a sorsa az elkövetkező nemzedékek során. A genetikai törvények megválasztásánál a következő szempontokat tartotta irányadónak:
Az alapvető célkitűzés tehát az volt, hogy az elrendezések (nemzedékek) tulajdonságait ("jövőjét") ne lehessen közvetlenül "megjósolni". Maguk - a túlélést, születést, elpusztulást szabályozó - genetikai törvények rendkívül egyszerűek és szemléletesek. A sejtek sorsát szomszédjaik száma fogja megszabni. Tekintsünk először a 4.12. ábrára, ahol jól láthatjuk, hogy egy adott cellának nyolc szomszédja van (négy ortogonálisán, négy diagonálisan), amely környezet megszabja a törvény hatóterületét is.
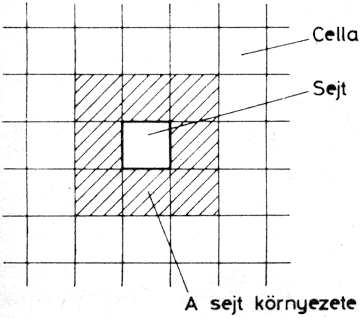
4.12. ábra: Egy adott cella környezete, amely a genetikai törvény hatóterületét megszabja
Maguk a szabályok a következők:
Az is nagyon fontos része a szabályoknak, hogy a születések és elhalások egyszerre következnek be és nem egymás után. Tehát a nemzedékváltás nem fokozatosan, hanem az egész táblán egyszerre, egy lépésben zajlik le. Gyakorlatban - még a manuális játék keretei között maradva - az új nemzedéket a következőképpen származtathatjuk a régiből:
Ha a kezdeti elrendezést nulladik nemzedéknek tekintjük, ilyen módon létrejött az első nemzedék. Ha most már a szabályok szerinti döntéseket a sejtek sorsára vonatkozóan ismét meghozzuk, létrejön a következő - a második - generáció, majd tovább folytatva a harmadik, negyedik, ötödik stb. Azt fogjuk találni, hogy bár a törvények nagyon egyszerűek, a népesség állandóan meglepő módon változni fog, és ezenkívül sokszor nagyon szép és érdekes alakzatok kialakulását is nyomon kísérhetjük. A különböző kialakuló alakzatoknak Conway neveket is adott, amelyeket a biológiából vagy a mindennapi életből vett.
Manuális módon az egyes alakzatok sorsát nyomon követni, változásainak fázisait kialakítani meglehetősen fáradságos dolog. Ezért már a játék őskorában is ezt számítógépes program segítségével végezték. Ugyancsak számítógéppel keresték vissza vagyis határozták meg azokat a kezdőhelyzeteket, amelyek érdekes változásokra vezettek.
A következőkben most bemutatunk néhány jellemző alakzatot és annak várható élettörténetét, hogy a játékot ezek kiválasztásával még érdekesebbé tehessük. A gyakorlatban, ha rendelkezésünkre áll, mindig képernyős megjelenítőn játsszunk és ne "hard-copy" eszközön (teletype-on vagy sornyomtatón), mivel így a sokszor nagyszámú érdekes nemzedék sorsát sokkal gyorsabban kísérhetjük nyomon.
Lássunk először néhány olyan egyszerű elrendezést, amelyek nagyon hamar teljesen kipusztulnak, mivel minden sejtjük elhal (4.13. ábra). Az ábra c részében ábrázolt diagonális sejtlánc bármilyen hosszú lehet, akkor is elpusztul, csupán a hosszával arányosan késleltetve, mivel minden generációváltáskor a két legszélső sejtje hal meg.
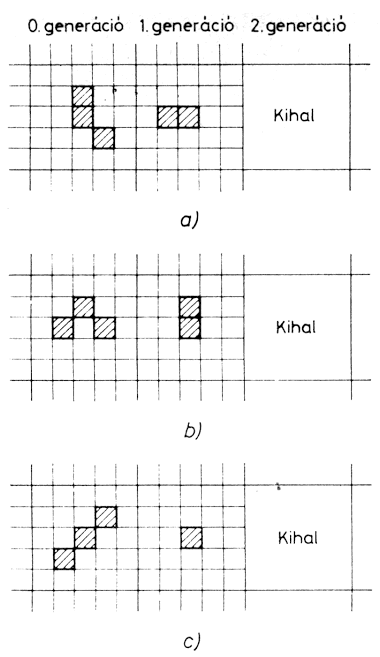
4.13. ábra: A második nemzedékben kihaló sejtrendszerek
A 4.14. ábrán mutatjuk be a tengődésnek a legegyszerűbb formáját. Itt már az első nemzedékváltás után kialakul egy olyan alakzat, amely stabilan megmarad és többé nem változik. Ezt a formát Conway egyébként blokknak nevezte. Hasonló módon nem változó (tengődő) végalakzatok a 4.15. ábrán láthatók is, amelyek sorrendben a következő neveket kapták: cső, tó, kígyó, méhsejt, hajó, cipó.
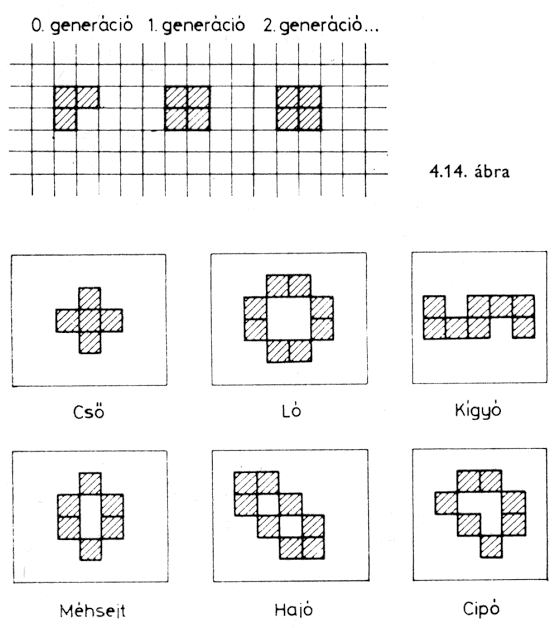
4.14, 4.15. ábra: Néhány gyakori tengődő alakzat
Sokszor különböző alakzatok ugyanabba a végállapotba jutnak. Jól megfigyelhetjük ezt a 4.16. ábrán, ahol három különböző kezdési alakzat végső sorsa a méhsejtalakzatban való tengődés.
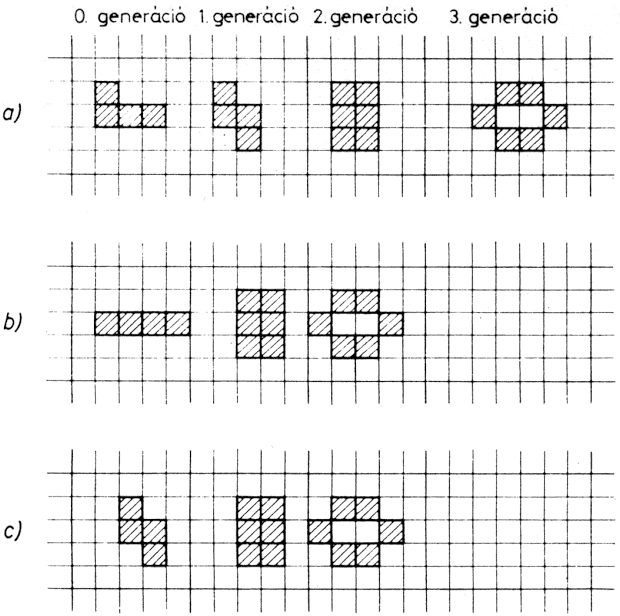
4.16. ábra: Küldönböző kezdeti állapotok azonos tengődő állapotokhoz vezethetnek
Az önmagát ciklikusan ismétlő, pulzáló elrendezések legegyszerűbbikét a 4.17. ábrán láthatjuk. Ez az ún. villogó, amely minden második generációban visszanyeri eredeti alakját.
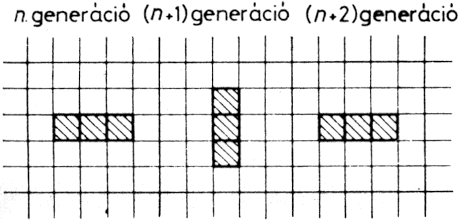
4.17. ábra: Egyszerű ciklukosan ismétlődő elrendezés
Hasonló tulajdonságú alapelrendezéseket mutatunk be a 4.18. ábrán. Az egyes alakzatok neve a rajz sorrendjében: béka, vészjel, óra.
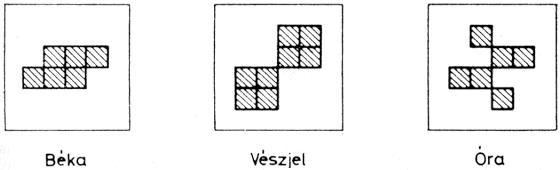
4.18. ábra: Kétciklusú pulzáló alakzatok
Nagyon érdekes alakzat a 4.19. ábrán látható ún. vitorlázórepülő. Ez minden negyedik generációban visszaalakul eredeti formájába, de eközben átlósan jobbra lefelé mozog. Ezzel szemben a 4.20. ábrán látható tizenkét sejtből álló alakzat tizenötös periódussal lüktet, és ugyanakkor képes a feléje megfelelő irányból érkező vitorlázórepülőt elnyelni. (Ezért ezt "faló"-nak nevezték el.)
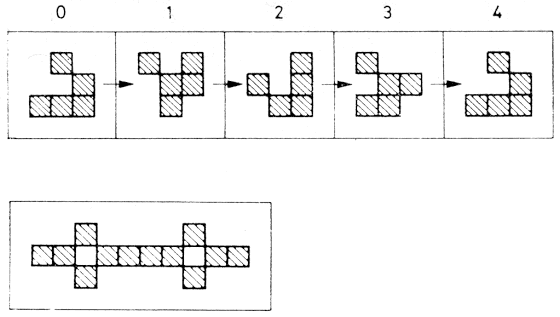
4.19. ábra: A vitorlázórepülő mozgása
4.20. ábra: A vitorlázórepülőt elnyelni képes faló alakzat
Conway egyik alapkérdésére - hogy ti. létezik-e olyan alakzat, amely vég nélkül növekszik - keresték a választ, amikor a 4.21. ábrán látható öt sejt hosszú és változatos életét nyomon kísérték. Ez az elrendezés csak 1103 generáció után jut el végső állapotába. (Ez hat össze nem ütköző, tehát szabadon mozgó vitorlázórepülőt, nyolc álló blokkot, négy méhsejtet, négy villogót és két hajót tartalmaz.) Később számítógéppel sikerült olyan elrendezést létrehozni, amely egyre csak szaporodik, így kellő idő után bármilyen nagyszámú sejtet tartalmazhat.

4.21. ábra: Hosszú életű elrendezés
A játék sok meglepetést tartogat számunkra és a kialakuló különféle alakú elrendezések változásának nyomon kísérése önmagában is nagyon érdekes és szórakoztató. Társasjátéknak azonban nem nevezhető ebben a formában. Ezért egy továbbfejlesztett változatát is kidolgozták. Ezt már két játékos játszhatja és tulajdonképpen az eredeti életjáték szabályainak figyelembevételével két ellenséges sejttípus harca egymás ellen. A játékot 5x5 négyzetet tartalmazó táblán (amely ismét a megjelenítő ernyője vagy a teletype papírja) játszhatjuk. Az egyik játékos sejtjeit a * szimbólum, a másikét a # szimbólum reprezentálja. A két szimbólum egymással egyenértékű az eredeti életjáték szabályainak figyelembevételével, kivéve mikor a három szomszédos sejt egy újat generál egy üres cellahelyen. Ekkor ui. a többségi elv érvényesül, vagyis olyan sejtfajta jön létre, amelyből a három közül legalább kettő van jelen.
A játék kezdetén mindkét játékos 3-3 sejtet helyezhet el a táblán azok X és Y koordinátáinak a megadásával. (Ha mindkét játékos azonos cellát választ, a sejtek "kiirtják" egymást, és így a cella üres marad.) Ezután az életjáték szabályai szerint kerül feldolgozásra a tábla állása. Minden egymást követő fordulóban mindegyik játékos egy sejtet helyezhet el arra törekedve, hogy minél többet semmisítsen meg a másik fél sejtjeiből. A játék addig tart, amíg egyik játékosnak már nincs több élő sejtje.
5. Társadalmi jelenségeket szimuláló játékok
E fejezetben azokról a szimulációs lehetőségekről számolunk be, amelyek célja valamely társadalmi jelenség utánzása. A "társadalmi" szót elég tágan értelmezzük: ide tartozónak tekintünk mindent, ami kisebb-nagyobb embercsoportok tevékenységét, mozgását, változását érinti.
A számítógépes szimuláció elsősorban a gazdasági élet tervezése, irányítása terén hozott értékes eredményeket. Ugyancsak sokat ígérő a számítógépeknek mint oktatási segédeszközöknek a megjelenése is. Oktatók és tanítványok kisebb erőfeszítéssel juthatnak el céljukig: a tananyag mélyebb és gyorsabb elsajátításáig.
Az igen nagy embercsoportokra készített számítógépes szimulációk - pl. történelmi helyzetelemzések - már sokkal szerényebb eredményeket szolgáltattak. Az ok nyilvánvaló: minél több változót kell figyelembe venni, minél bonyolultabb az egyes elemek közötti összefüggés, annál nehezebb pontos modellt készíteni.
E fejezet tartalmát úgy válogattuk össze, hogy az esetenként túl bonyolult vagy túlegyszerűsített modellek játéklehetőségeit igyekeztünk kiemelni. Ennek során bizonyos szóhasználati problémákkal is szembe kellett néznünk, pl. a gazdasági játékoknak nevezett témakör jóval meghaladja az általunk játéknak nevezett fogalmat.
5.1. Gazdasági játékok
Eléggé érthető módon a számítógépes szimuláció a gazdaságirányítással, gazdaságtervezéssel foglalkozó szakemberek érdeklődését is felkeltette. Létrehoztak olyan modelleket, amelyek segítségével egy-egy nemzet gazdasági viszonyai vizsgálhatók és készítettek olyanokat, melyek egy vagy több vállalat azonos piacon való tevékenységét hivatott utánozni. Mindkét modelltípus - a makro- és a mikroviszonyokat tükröző - nagyon fontos és érdekes eredményekre vezethet. Az átfogó közgazdasági modellek közül már említettünk egyet, az ún. Római Klub jelentését. A mikrorendszerek pedig kitűnő gyakorló eszközök lehetnek a cégek vezetői, piackutatói, beruházástervezői stb. részére. Ez a fajta modell tehát a már ugyancsak említett repülőgép-szimulátorhoz hasonlít: biztonságban, komoly következmény nélkül lehet "bravúrokat" végrehajtani rajtuk, kockázatos manőverbe kezdeni, a szakadék szélén táncolni.
A gazdaság egészére vonatkozó modellek nyilvánvalóan annál hasznosabbak, minél pontosabbak, minél részletesebbek. Mivel nekünk a gazdasági modellek játéklehetőségeit kell számba vennünk, megelégedhetünk egyszerűbb változataikkal is. Így pl. az 5.1. ábrán egy viszonylag egyszerű rendszert mutatunk be. A rajzon a C fogyasztás, a P árszínvonal, a W bérszínvonal és az M pénztömeg közötti összefüggéseket tüntettük fel. Az ábrán látható blokkvázlat elemei között számos D késleltetőelem foglal helyet - ezekről feltesszük, hogy mindegyik pontosan egy időegységnyi (mondjuk három hónap vagy félév) eltolást jelent a kimenet és bemenet között.
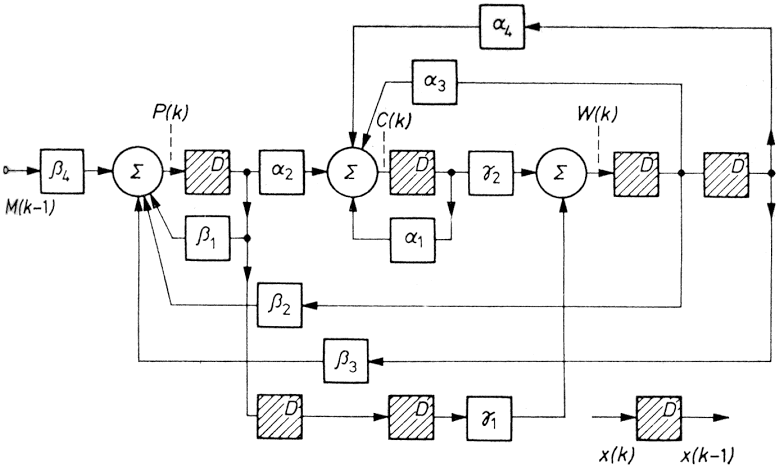
5.1. ábra: Egy makroekonómiai modell részletes blokkvázlata
A blokkvázlat alapján elég nehéz a viszonyokat áttekinteni, azonban a vázlat által leírt rendszerre vonatkozó egyenletek viszonylag egyszerűen felírhatok és értelmezhetők. Így tehát:
ahol alfa, béta, gamma a folyamat állandó értékű paraméterei; C(k) jelenti C értékét a k-adik vizsgálati időpontban; P(k-3) pedig P értékét három időegységgel k-1 megelőzően. Az egyenletek "jelentése" könnyen kiolvasható a fenti formulákból. Az árszínvonal pl. a megelőző időszak árszínvonalától, a bér - hosszabb, két időegységnyi - megelőző értékétől, és a pénztömeg előző értékétől függ. Hasonlóképpen értelmezhető a többi egyenlet is.
(E modell valódi értékét ne firtassuk. Változói amúgy is nagyon összetett, nehezen mérhető, esetleg ellentmondásosan definiálható mennyiségek. Kissé határozottabb fogalmazásban: ne ezekből az egyenletekből akarjuk az alapvető közgazdasági összefüggéseket megérteni. Tekintsük őket esetlegeseknek, de nem minden ésszerűség nélkülieknek.)
Az egyenletrendszer szabályszerű matematikai elemzéséből kiderül, hogy melyek az állapotváltozók, és mi tekinthető vezérlőváltozónak. Esetünkben P, C, W ún. endogén változó, míg az egyetlen, a rendszer befolyásolására felhasználható változó az M. Az 5.1. ábra már ezt a képet tüntette fel. A bemenő mennyiség időfüggvényének és a rendszer paramétereinek ismeretében a szimuláció nagyon egyszerűen kivitelezhető, mivel az egyenletrendszer számítógép-programmá való átfogalmazása szinte semmi szellemi munkát sem igényel.
A fenti példa nagyon egyszerű viszonyok közepette mutatta be, hogyan készíthetők átfogó gazdasági modelljátékok. Nyilván jóval bonyolultabb a helyzet akkor, ha a modell paramétereit egy nemzetgazdaság számszerű kiértékelésével állítják elő, - ilyenkor sokkal több változót vesznek figyelembe. A modell próbája ezek után az lesz, hogy helyesen írja-e le a múltat. Ha igen, akkor nagyon csábító - bár nem feltétlenül helyes - gondolat az, hogy a szimulációt tovább kell folytatni, és akkor a jövőben bekövetkező változásokra is kaphatunk információt. - A makrogazdasági modellek mellett gyakran találkozunk összetett kiértékelő függvényekkel, amelyekkel a gazdálkodás hatékonysága mérhető. Így pl. a szakirodalomban leírást találunk egy gazdasági oktatójátékról, amely egy zárt gazdaság egyik ága húsz esztendős történetének adataiból indult ki. Első lépésként a játékosoknak meg kell becsülniük a következő évek állami kiadásait és a jövedelemadó mértékét oly módon, hogy a munkanélküliség a lehető legkisebb legyen. Második lépésben azonban egy ún. J jóléti értéket kell optimalizálniuk, amely a következő kvalitatív összefüggéssel adott:
ahol C: az árukra és a szolgáltatásokra fordított fogyasztói kiadások, G: azonos célra az állam által kiadott pénzösszeg; I: az infláció aránya; U: az átlagos munkanélküliség; B: a folyószámlák egyenlege; CP: beruházások, tőkeáramlás.
A játék azért lesz érdekes, nemtriviális, mert a gazdálkodást 12 évig kell folytatni, és a jóléti tényező átlagértéke ad számot a siker mértékéről.
5.2. Vállalati játékok
A gazdasági játékok második nagy csoportját a viszonylag kisebb gazdasági egységekre vonatkozó vállalati játékok jelentik. Ezek többsége az 5.2. ábra szerinti sémának megfelelően zajlik: a játékos (ill. játékosok) felkészül a feladatra, tanulmányozza a problémát, majd ennek alapján beavatkozási javaslatot tesz (dönt). Javaslatát a játékvezetőnek adja át, aki a javaslatokat számítógépen szimulálva lefuttatja, értékeli és az eredményeket közli a játékossal, aki ennek ismeretében újra dönt stb.
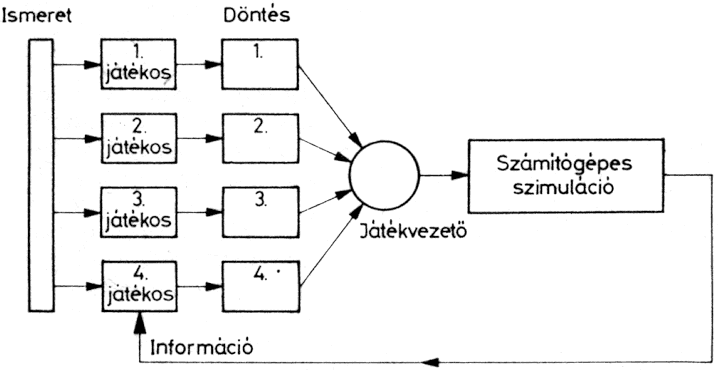
5.2. ábra: A vállalati játékok általános sémája
A vállalati játékok leggyakoribb témái:
Ezek a játékok a játék stílusát, stratégiáját tekintve két nagy csoportra oszthatók. Az egyik csoportban azok a játékok találhatók, amelyeknél a játékosok egymástól függetlenül dönthetnek - a játékos a szimulált rendszerrel egyedül áll szemben. A másik csoportban, pl. egy, a piacokért folytatott "küzdelemben", a játékosok döntései egymás további lépéseit is befolyásolják. Gondoljunk arra, hogy a munkaerőtartalék nagysága, az új munkaerő beállításának lehetősége egy-egy iparág korlátozott számú szakmunkásának helyzetétől függ. Az egymással a munkaerőért versenyző vállalatok közösen szabják meg a munkerőpiac jellemzőit. Hasonló a helyzet pl. a reklámköltségek megtérülése esetén is: ha sokan költenek sokat reklámra, akkor annak hatékonysága csökken, ill. bizonytalanná válik.
A vállalati játékok rendszerint eléggé összetett programrendszeren alapulnak. A programrendszerben az egymással kölcsönhatásban levő egységek mennyiségi és időbeli jellemzőit egyaránt meg kell adni. Természetesen a mennyiségek csak úgy választhatók meg, hogy a játékosok által ismert vagy értelmezhető helyzetet reprezentáljanak. Közepes méretű játékok ilyen paramétereinek száma 50...200 közötti - ebből az is kitűnik, hogy a játékok tervezése sem könnyű feladat.
A vállalati játékok többségének matematikai alapja valamiféle egyenletrendszer ismételt megoldása. A determinisztikus eljárásrészek mellett azonban sok paraméter értékét vagy annak egy részét valószínűségi változó adja - ez biztosítja a játék életszerűségét.
Talán már az eddig elmondottakból is érezhető, a vállalati játékok fogalomköre nem fedi egészen a könyvünkben ez ideig használt számítógépes játék elnevezést. A különbség elsősorban abból adódik, hogy e játékok egy részénél a játékosok írásban nyilatkoznak döntéseikről, a játékvezető van csak kapcsolatban a számítógéppel, a játékosok pedig csak jókora időkéséssel kapják meg az eredményeket. Előfordul tehát az, hogy a játékosok a számítógépet nem is látják, periferiális eszközeivel sem találkoznak. Ez a fajta "játék" tehát már kinő a szórakoztató időtöltés kategóriájából és inkább vezetők, menedzserek, közgazdászok képzésének, továbbképzésének eszköze.
A gazdasági játékok befejező részeként arról adunk információt, hogy egyszerű - esetleg gyermetegnek is minősíthető - játékok leírása is megtalálható a szakirodalomban. Elsőként azt a játékot említjük, amely a tőzsdézésre készít fel. Ennek során a játékos meghatározott összeggel és adott nagyságú részvényköteggel indul. A játék minden periódusában változnak a részvények árfolyamai, így a játékos nyer, veszít - szerencséjétől függően. Az árfolyamok tendenciáit megfigyelve, mód lesz arra, hogy a játékos huzamosabban nyerjen, bár minden egyes tranzakciójáért értékaranyos jutalékot kell fizetnie.
Néhány játék zárt gazdasági rendszereket "szimulál". Az egyikben pl. a játékosnak földet kell adnia-vennie élelmiszerért. Az élelmet egyrészt saját állampolgárai számára kell biztosítani, másrészt pedig ebből kell esetleges vásárlásait fedezni. A változók közötti egyszerű összefüggések következtében a játék kevéssé változatos, csak a véletlenszerűen bekövetkező elemi csapások - járvány, sáskák - teszik színesebbé. A játék szűk lehetőségeit leginkább az mutatja, hogy a leglényegesebb változót - a földterület-élelmiszer átszámítási tényezőt - nem a játékos határozza meg, hanem ez tőle függetlenül, véletlenszerűen változik. A játék egy másik változatában a mezőgazdaság mellett eladható nyersanyagforrások is megjelennek, azonban ennél is az egyes játékfázisokat frappánsan kommentáló szövegrészletek kötik le a játékos érdeklődését, nem pedig a gazdasági-logikai feladat.

...pedig a gazdasági játékokban én voltam a legügyesebb!...
5.3. Oktatójátékok
A számítógépek egyre növekvő szerepet töltenek be az alap-, a közép- és a felsőfokú oktatásban. A számítógéppel segített oktatás (CAI: Computer Aided Instruction) különböző formákban jelenik meg: néha csak tanári segédeszköz; máskor egy adott tananyag programozott feldolgozásával siet a tanulók segítségére; az is előfordul, hogy könyvtárnyi ismeretanyag található meg az oktatási programcsomagban, és műholdat is felhasználnak az oktatási hálózat kommunikációs eszközeként.
A számítógépes oktatás külön "szakma", jellegzetes módszerekkel, eljárásokkal és jellegzetes számítógép-konfigurációval. A nagyszámítógépekhez rendszerint különleges programnyelvek is rendelkezésre állnak, amelyekkel aktív pedagógusok viszonylag egyszerűen tudnak oktatóprogramokat szerkeszteni. Ezeken az ún. szerzői nyelveken készültek el a legnagyobb méretű oktatórendszerek. Példaképpen a PLATO rendszert említjük, amelynek háttere mintegy 5000 emberévnyi programozói munkát testesít meg.
Persze a kisgépgyártó, forgalmazó vállalatok is bekapcsolódtak a versenybe, így nagyon sok kisgéphez is rendelkezésre állnak a különböző tantárgyak oktatásához szükséges programcsomagok.
Az oktatás és játék kapcsolatát vizsgálva először is le kell szögeznünk, hogy a játékos oktatást nem tekintjük oktatójátéknak. Ez utóbbin valami olyat értünk, aminek során a tanuló játékszerű helyzetbe kerül, valamilyen stratégia alapján megold egy játék színezetű feladatot, meghatározott pedagógiai céllal. E cél lehet az, hogy a tanuló saját maga fedezze fel a feladatmegoldás módszerét, de lehet az is, hogy a feladat megoldásából vonjon le következtetést.
Ebben az értelemben e könyv számos játékát lehetne oktatójátéknak tekinteni. A mozgást utánzó játékok fizikát, a véletlenen alapuló játékok valószínűségszámítást stb. taníthatnak. Értékük ilyen szempontból igen magas lehet, bár aligha képes bárki komoly tanulmányok nélkül pusztán a játékokon keresztül egy-egy tudományterület alapjait megismerni.
A feladat megoldásából levonható következtetés illusztrálására egy példát mutatunk.

5.3. ábra: Hogyan kell a lovasnak haladnia, ha a lehető legrövidebb idő alatt akar a városba érni?
Az 5.3. ábra szerint egy lovas indul a folyótól A távolságra levő tanyáról a városba. Útja során azonban meg kell itatnia a lovát, ezért a folyót is érintenie kell. Feltéve, hogy a lovas állandó sebességgel halad, próbálkozással kell megkeresni azt a pontot, amelynél a folyót érintve legrövidebb idő alatt jut el a városba. A számítógép a tanuló válaszait mindig értékeli, és közli vele az utazás időtartamát, valamint az ábrán látható két háromszög adatait, vagyis oldalhosszúságaikat és szögeiket. A feladat célja nyilvánvalóan az, hogy rávezesse a tanulót a fénytöréssel kapcsolatos fontos fizikai elvekre. Az ismételt, más A, B és C értékekkel történő feladatmegoldásokból leszűrhető az az általános eredmény, hogy a minimális utazási időhöz az ábrán jelölt két szögnek egyenlőnek kell lennie.
Ilyen típusú oktatójátékok megfelelő szaktárgyi ismeret és némi fantázia birtokában könnyűszerrel előállíthatok. A játékok tervezésénél azonban a tanulók életkorát, érdeklődési körét, előismereteit stb. is figyelembe kell venni.
5.4. Történelmi játékok
Az elmúlt években egy eddig elhanyagolt játékforma kezdett elterjedni és bizonyos körökben jókora népszerűségre tett szert. Azokra a "történelmi"-nek nevezhető játékokra gondolunk, amelyek kiinduló alapja egy jól ismert történelmi helyzet, vagy embercsoportok hirtelen megjelenése egy adott társadalmi forma keretei között. Példaképpen a nálunk is ismert játékra, a diplomacy-ra utalunk, mely az első világháborút utánozza állandóan változó térképekkel és a diplomáciai manipulációk sűrű szövedékével. Nem lehet célunk e játékok ismeretközlő és tudatformáló hatásait értékelni, népszerűségük és terjedésük miatt azonban erről a játékkategóriáról is meg kell emlékeznünk.
A számítógépek természetszerűleg önmagukban alkalmasak történelmi helyzetek és változások szimulálására is, azonban ezek igen összetett volta, a szabályok önkényes jellege stb. miatt nem vezettek túl sok használható eredményre. A lehetőségek számának, a szabályok rögzítésének útját járva azonban csak igen "sovány" eredményre számíthatunk.
Ez a helyzet pl. a Polgárháború elnevezésű számítógépes játéknál is. Ez a program az amerikai polgárháború ütközeteit "szimulálja". A számítógép által közölt adatok alapján a játékos bizonyos mértékig "beavatkozik" a történelembe azzal, hogy stratégiát választ, valamint intézkedik a rendelkezésre álló pénzösszeg felhasználásával. A játékos által begépelt számok és a csata kimenetele lazán kapcsolódnak egymáshoz. Mindenesetre ha a játékos sokat költ élelmezésre és zsoldra, akkor a hadsereg hangulata jó lesz, a dezertálok száma kicsi, és a csata megnyerésének esélyei növekednek. - Bár a program a játékos aktív közreműködését igényli, igazi játékértéke kicsiny. Nem elhanyagolható tény azonban az, hogy ismételt lejátszása során a játékos megtanulja a dátumokat, a hadseregek parancsnokainak nevét, az ütközet eredményét stb. (A játéknak a történelemszemlélet-formáló hatását ne firtassuk...)
5.5. Helyzetjátékok
A társadalom kisebb nagyobb csoportjainak életét, mozgását szimuláló játékok sorában meg kell emlékeznünk egy olyan programegyüttesről is, amelynek témaköre nem erőszakolható be a fejezet előző alpontjai közé. Jobb szó híján helyzetjátékoknak nevezzük azokat a programokat, amelyek kisebb - esetleg alkalomszerű - társulások viselkedését szimulálják. Rögtön példával támasztjuk alá a nem egészen pontos témakörülírást: elkészült egy szimulációs rendszer, amelyet leginkább "diplomamegszerző játéknak" nevezhetünk. A játékos célja egy felsőoktatási intézmény végbizonyítványának megszerzése, amelyet korlátos mértékű energiáival óhajt elérni. Energiáit azonban a tanuláson kívül intenzív sportolásra, sok időt igénylő szórakozásra is felhasználja. Hogyan kell gazdálkodnia, ha a vizsga-eredményeknél valamelyest a véletlen is szerephez jut?
A témakör szerteágazó voltát egy másik - a szakirodalomban említett - programmal is illusztrálhatjuk: itt a tudományos kutatási eredmények gyakorlatba történő átültetése jelenik meg a játékra módot adó konfliktushelyzetként.
A legnépszerűbb helyzetjátékok azonban a különböző sportágakhoz kapcsolódnak. Elsősorban a csapatjátékok - futball, kézilabda, kosárlabda, jégkorong - alkalmasak a szimulációhoz. A csapat "erejét", a labda útját, a játék jellegzetes eseményeit stb. viszonylag könnyen lehet a számítógép, véletlenszám-generátora segítségével utánozni. Ha a program a részletekről kicsit változatos módon rendszeresen tájékoztat, a hatás olyasmi lesz, mintha egy alapvetően vizuális élményt nyújtó sporteseményről rádióközvetítést hallgatnánk.
A témakör irodalmában elég bő választékot találunk a különféle sportágakra vonatkozó játékokból.

Vajon közben mit fog lépni?
6. Miből, hogyan készíthetünk számítógépes játékokat?
Alig valószínű, hogy létezik olyan ember, aki a számítógépes játékokkal találkozva ne akarná azokat módosítani, ne akarna újakat készíteni. A számítógép különleges szerszám: aktivitásra, konstrukcióra serkenti azokat, akik megismerik. Jól mutatják ezt a jelenséget a személyi számítógépek elterjedésével együtt szaporodó folyóiratok, amelyek egyik legnépszerűbb "profilja" a számítógépes játékok közlése.
Az aktív játékkészítés kapcsán óhatatlanul az jut az ember eszébe, hogy e mögött is rejtőzik valami olyan pszichológiai tényező, mint mondjuk a karácsonyi ajándékozásnál, ti. az ajándék kitalálása, elkészítése sokkal nagyobb örömet és kielégülést okoz, mintha sajátmagunk kapunk ajándékot. A játékok - néha csak egyszerű tréfák - ötletének számítógépprogrammá fogalmazása, a program javítása és csiszolgatása nem kis szórakozást jelent készítőjének. A játékkészítés közben szerzett ismeretek pedig előbb-utóbb valahol majd kamatoztathatók lesznek.
Ebben a fejezetben példákat adunk arra, hogyan lehet számítógépes játékokat készíteni. Elsőként az awari nevű játék kapcsán azt mutatjuk be, miként alakíthatunk egy meglevő programot, hogyan bővíthetjük, változtathatjuk új játékká. A nyelvi játékok bemutatásával azt illusztráljuk, hogy ugyancsak véges számítógép-kapacitással is eléggé meghökkentő hatású szövegeket állíthatunk elő. Az ilyen "frázisgenerátorral" előállított mondatok kísértetiesen hasonlítanak a bürokratikus nyelvezetre, valamint arra a stílusra, amelynél a mondanivaló hiányát közhelyszerű kifejezések áradata helyettesíti.
A befejező részben két szokatlan, valószínűségszámításon alapuló játékot közlünk és néhány ötletet, amelyek még kidolgozva nincsenek, de talán felkeltik az Olvasó érdeklődését, lelkesedését, és rövidesen maga is hozzálát ilyenfajta játékok készítéséhez.
6.1. Awari
Az awari (mancala) Afrikában és Ázsiában népszerű játék. Két játékos játssza, de mód van arra, hogy versenyszerű bajnokságot szervezzenek, ilyenkor sokan válnak a játékban érdekeltté. A játék népszerűségének oka kettős. A játéktábla nagyon könnyen biztosítható, mindössze néhány pálcika és pár tucat kavics vagy gyümölcsmag szükséges hozzá. Emellett a játék eléggé összetett gondolkodást, figyelmet és gyakorlatot kíván.
A játékhoz gyakran egy fából készített eszközt: táblát használnak. Ennek képét a 6.1 ábra mutatja.

6.1. ábra: Az awari (mancala) játék fából készülő táblája
6.2. ábra: Az awari játék tálkáinak számozása és a gyűjtőtálkák elhelyezése (az 1-6. 2-5, 3-4 tálkapárokat tekintjük egymással szembenlévőnek)
A játék lényege: mindkét, egymással szemben elhelyezkedő játékosnak 6-6 tálkája van, kezdetben ezek mindegyikében ugyanannyi (pl. 3 vagy 6) "babszem" foglal helyet. A játékos kiválaszt egy tetszőleges tálkát, kézbe veszi az itt található magokat és "vetni" kezd. Ez annyit jelent, hogy az óramutató járásával ellenkezően minden szomszédos tálkába belepottyant egy magot. Ha saját tálkáinak végére ért, a műveletet az ellenfél tálkáiban folytatja. Az utolsóként lehelyezett mag - bizonyos feltételek teljesülése mellett - lehetővé teszi egy vagy több mag eltávolítását. A játék célja: minél több magot levenni, ill. többet, mint az ellenfél.
A játéknak számos változata van. Először azt a változatot ismertetjük, amelyikhez programot is közlünk. Itt a játékosok tálkái mellett elhelyezett gyűjtőtálkáknak a játékban is van szerepük (6.2. ábra). A játék menetét néhány példán keresztül ismertetjük. Ha pl. az 1. játékos a hármas számú tálkáján található magokat veszi kézbe és velük "lép", akkor ennek eredménye:
|
|
||||||||||||||||||||||||||||
kiinduló helyzet |
a lépés végrehajtása |
Ha a hatos számú tálkát választja a játékos, akkor egy mag a saját gyűjtőtálkájába pottyan, és ez az ő "nyeresége" lesz. Tehát:
|
|
||||||||||||||||||||||||||||
kiinduló helyzet |
a lépés végrehajtása |
Ha az utolsóként lepottyantott mag üres tálkába kerül, akkor - feltéve hogy az ezzel szemben levő tálka nem üres mindkét tálkát kiürítheti és a nyereséget saját gyűjtőtálkájába helyezheti. A játék során igyekezni kell minél több ilyen lépést tenni, Példa:
|
|
||||||||||||||||||||||||||||
kiinduló helyzet |
a lépés végrehajtása |
Ez a lépés tehát 9 maggal növelte a gyűjtőtálka tartalmát (egy egység a "vetés" eredménye, a többi a szemben levő "elrablásából" származik). Rabolni saját és ellenfél magokat egyaránt lehet.
A játék szabályait mindössze egyetlen dologgal kell bővítenünk: ha az utolsóként lehelyezett mag a saját gyűjtőtálba kerül, tetszőleges tálkával újra léphetünk. (Ha ennek utolsó magja is a gyűjtőtálkába jut, akkor már az ellenfél következik.)
A játék akkor fejeződik be, ha valamelyik játékos a magok számának több mint felét már saját tálkájába begyűjtötte, vagy pedig akkor, ha valamelyik játékos összes tálkája kiürült.
A játék egy másik változatánál (Nigéria) kezdetben minden tálkában négy mag foglal helyet. A játék szabályai szerint, ha az utolsó mag olyan tálkába kerül, amelynek tartalma négy magnál nagyobb, akkor ennek tartalmával tovább kell folytatni a lépést, míg az utolsó mag az ellenfél térfelére nem kerül. Ha az utolsó mag olyan saját tálkába kerül, amelyben ezzel együtt három vagy négy lett a magok száma, akkor a tálka teljes tartalmát a játékos saját gyűjtőtálkájába helyezheti. A gyűjtőtálkának e változatban semmi külön szerepe - és így helyértéke - sincs. A játék akkor fejeződik be, ha az utolsó mag bármelyik térfélen üres tálkába kerül, vagy pedig három, vagy annál kevesebb mag van már csak a táblán. Ez esetben ezek a magok azt a játékost illetik, amelyiknek térfelén találhatók. Aki a játék befejeztekor nem tudja gyűjtőtálkája tartalmával saját térfelének kezdőhelyzetét visszaállítani, az a vesztes.
A játék szabályrendszere tehát viszonylag egyszerű, elemi számolgatásokkal megbecsülhető az egyes lépések következménye. Egy játékos egy adott állapotnál maximálisan hatféle lépés közül választhat, így tehát a saját lépés és az ellenfél lehetséges lépésének összes kombinációszáma 6x6=36. Ez a játék tehát nagyon alkalmas arra, hogy belőle számítógépes játékprogramot is csináljunk.
A továbbiakban az eddigiekben közölt játékoknál részletesebben ismertetjük a közölt - gyakorlatilag Minmal-BASIC - számítógépprogramot. Ezt elsősorban azért tesszük, mert az awari játékok a számítógépes játékok szerkesztésének, módosítási lehetőségeinek, hibáinak bemutatására igen alkalmasak.
A program működéséről áttekintő képet a 6.3. ábra alapján kaphatunk.
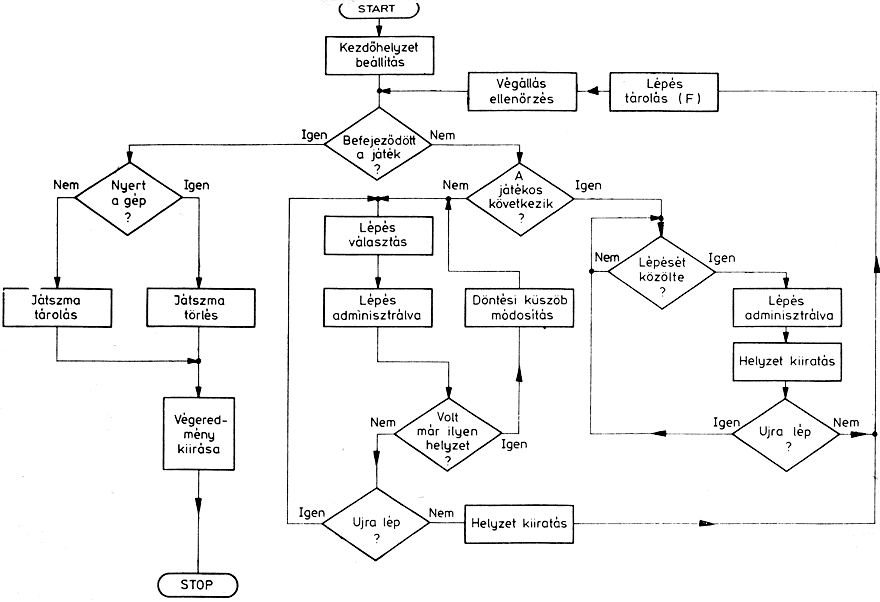
6.3. ábra: Az awarit játszó program rövidített folyamatábrája
A program:
5 PRINT "AWARI"
7 PRINT "CREATIVE COMPUTING, MORRISTOWN, NEW JERSEY"
15 DIM B(13),G(13),F(50)
16 LET N=0
20 PRINT :PRINT :LET E=0:LET Q=0
25 FOR I=0 TO 12
26 LET B(I)=3
27 NEXT I
30 LET C=0:LET F(N)=0:LET B(13)=0:LET B(6)=0
35 GOSUB 500
40 PRINT "MIT LEP";:GOSUB 110
45 IF E=0 THEN 80
50 IF M=H THEN GOSUB 100
55 IF E=0 THEN 80
60 PRINT "AZ EN LEPESEM ";:GOSUB 800
65 IF E=0 THEN 80
70 IF M=H THEN PRINT ",";:GOSUB 800
75 IF E>0 THEN 35
80 PRINT :PRINT "VEGE A JATEKNAK"
85 LET D=B(6)-B(13)
86 IF D<0 THEN PRINT "EN NYERTEM";-D;"PONTTAL!":GOTO 20
90 LET N=N+1
92 IF D=0 THEN PRINT "DONTETLEN":GOTO 20
95 PRINT "ON NYERT";D;"PONTTAL":GOTO 20
100 PRINT "ISMET!";
110 INPUT M
115 IF M<7 AND M>0 THEN LET M=M-1:GOTO 130
120 PRINT "SZABALYTALAN LEPES!":GOTO 100
130 IF B(M)=0 THEN 120
140 LET H=6:GOSUB 200
150 GOTO 500
200 LET K=M:GOSUB 600
205 LET E=0
206 IF K>6 THEN LET K=K-7
210 LET C=C+1
212 IF C<9 THEN LET F(N)=F(N)*6+K
215 FOR I=0 TO 5
216 IF B(I)<>0 THEN 230
220 NEXT I
225 RETURN
230 FOR I=7 TO 12
232 IF B(I)<>0 THEN LET E=1:RETURN
235 NEXT I
500 PRINT :PRINT " ";
505 FOR I=12 TO 7 STEP-1
506 GOSUB 580
510 NEXT I
515 PRINT :LET I=13:GOSUB 580
520 PRINT "-----------------------";:PRINT B(6):PRINT " ";
525 FOR I=0 TO 5
526 GOSUB 580
530 NEXT I
535 PRINT :PRINT :RETURN
580 IF B(I)<10 THEN PRINT " ";
585 PRINT B(I);:RETURN
600 LET P=B(M):LET B(M)=0
605 FOR P=P TO 1 STEP-1
606 LET M=M+1
608 IF M>13 THEN LET M=M-14
610 LET B(M)=B(M)+1
612 NEXT P
615 IF B(M)=1 AND M<>6 AND M<>13 AND B(12-M)<>0 THEN 625
620 RETURN
625 LET B(H)=B(H)+B(12-M)+1:LET B(M)=0:LET B(12-M)=0:RETURN
800 LET D=-99:LET H=13
805 FOR I=0 TO 13
806 LET G(I)=B(I)
808 NEXT I
810 FOR J=7 TO 12
812 IF B(J)=0 THEN 885
815 LET M=J:GOSUB 600
820 FOR I=0 TO 5
822 IF B(I)=0 THEN 845
825 LET L=B(I)+I:LET R=0
830 IF L>13 THEN LET L=L-14:LET R=1:GOTO 830
835 IF B(L)=0 AND L<>6 AND L<>13 THEN LET R=B(12-L)+R
840 IF R>Q THEN LET Q=R
845 NEXT I
850 LET Q=B(13)-B(6)-Q
852 IF C>8 THEN 875
855 LET K=J
856 IF K>6 THEN LET K=K-7
860 FOR I=0 TO N-1
862 IF F(N)*6+K=INT(F(I)/6^(7-C)+.1) THEN LET Q=Q-2
870 NEXT I
875 FOR I=0 TO 13
876 LET B(I)=G(I)
877 NEXT I
880 IF Q>=D THEN LET A=J:LET D=Q
885 NEXT J
890 LET M=A:PRINT CHR$(42+M);:GOTO 200
900 FOR I=0 TO N-1
992 PRINT B(I)
995 NEXT I
999 END
A programban való tájékozódáshoz néhány jelölés ismerete is szükséges. Ezek a következek:
A program legfontosabb részei:
A program még több apró - feltétel-ellenőrző - részletet tartalmaz. Ezek szerepe azonban a főrészek azonosítása után már könnyen kitalálható.
Most vizsgáljuk meg a gép játékmódszerét. A számítógép "gondolatban" minden egyes tálkájának tartalmával lép, majd e lépést követően megvizsgálja az ellenfél összes lehetséges lépését. A saját lépése eredményeként szerzett pontokból levonja az ellenfél húzása utáni R eredményt és a lehetséges kombinációk közül azt választja, ahol ez a Q szám a legnagyobb. A gép tehát egy lépéssel előre gondolkodik. Az így megvalósuló játékmódszer eléggé nagy játékerőt képvisel és a játékosnak csak többszöri próbálkozás után sikerül a gépet megvernie. Ebbe azonban jelentősen beleszól az a tény is, hogy a játszma első lépését a játékos teszi.
A számítógép az előzőek szerint választott lépését "ellenőrzi", vagyis megnézi, hogy a játék során - döntetlen vagy vesztett játszmában - a játszma azonos számú lépésénél ezt már nem választotta-e. Ha igen, akkor a lépésválasztáshoz szükséges feltétel (Q ![]() Q-2) értékét csökkenti, így az adott - legjobbnak tűnő - lépés helyett kissé rosszabbat választ, de ezzel az ellenfelet és saját magát is új utakra készteti, amely esetleg saját győzelméhez vezet. A játszma lépéseinek tárolása kissé szokatlan módon történik. Ha a játszma egyes lépései ,1, a2, a3 ...a9 számokból állnak, ahol a számok 1...6-ig terjednek és a választott tálkákra utalnak, akkor a számítógép a játék menetét az
Q-2) értékét csökkenti, így az adott - legjobbnak tűnő - lépés helyett kissé rosszabbat választ, de ezzel az ellenfelet és saját magát is új utakra készteti, amely esetleg saját győzelméhez vezet. A játszma lépéseinek tárolása kissé szokatlan módon történik. Ha a játszma egyes lépései ,1, a2, a3 ...a9 számokból állnak, ahol a számok 1...6-ig terjednek és a választott tálkákra utalnak, akkor a számítógép a játék menetét az
formában tárolja. A program eredeti változatában ezt a megoldást azért választották, mert így kilenc lépést lehet egy hat decimális jegyű szám segítségével ábrázolni, áthidalva így a BASIC korlátozott pontosságát és megtakarítva igen sok tárhelyet.
A számítógép így bizonyosfajta tapasztalatot gyűjt, ami a játék során fokozatosan növekszik. Nagyon fontos azonban az a tény, hogy a számítógép nem veszít sorozatban játszmákat egyforma módon. Ez a valódi játékos számára azt az illúziót nyújtja, mintha ellenfele nagyon okos lenne, ill. az emberéhez hasonló "lelki" adottságai lennének.
A gép döntési módszere, stratégiája azonban több szempontból fogyatékos. Legsúlyosabb hibája, hogy a kettős (ismételt) lépéseket külön-külön analizálja és nem egyetlen lépésként. A gép csak akkor lép olyat, amelynél az utolsó mag saját gyűjtő tálkájába kerül, ha erről a lépésről önmagában eldöntötte, hogy az adott helyzetben a legelőnyösebb. Saját második lépési lehetőségét teljesen újként, az előzőtől függetlenül kezeli. Nagyon érdekesen mutatkozik ez meg abban, ha a program 810. sorában a saját lépésvizsgálat irányát megfordítjuk. Ha ui. J = 12 értékkel kezdődik a vizsgálat, akkor a saját gyűjtőtálkába való belépésnek a valószínűsége valamivel nagyobb. A gép így gyakrabban jut kettős lépésekhez, nyerési esélyei fokozódnak. Hibája a számítógép döntési rendszerének az is. hogy bár a vesztett játszmák értékelésénél a döntési küszöb számértéke csökken, de az így választott - a legjobbhoz legközelebb álló - lépés több hasonlóból véletlenszerűen alakul ki, különösebb megfontolás nélkül.
E fogyatékosságok ellenére a program jól játszik, nem lebecsülendő ellenfél. A program részleteinek megismerése azonban szinte óhatatlanul továbbfejlesztési ölteteket, újabb játéklehetőségeket sugall. Így pl. - néhány programsor módosításával - elérhető, hogy a számítógép a játékos helyett is lépjen. Ezzel a játékos teljesen megszabadul a gondolkodástól és azt figyelheti, hogyan játszik a számítógép saját magával. Mivel a gép mindkét ellenfél részére pártatlanul és ugyanolyan szabályok szerint dönt, a játék általában hosszú és elég érdekes lesz. Azt sem nehéz elérni, hogy a számítógép két különböző "felfogásban" játsszon, pl. a 810. sor már említett két változatát használja.
Az igazi továbblépést azonban az jelenti, ha a számítógép nem csupán a saját és az ellenfél lépését vizsgálja, hanem ezt még egyszer megismétli. Így a kettős lépések előnyei rögtön kiderülnének, a játék sokkal nagyobb mélységben lenne átlátható. Ennek ára azonban az, hogy a program eredeti változata szerinti 36 lépés átvizsgálása helyett most már 6^4=1296 esetet kellene végignéznie. Ez azonban nemcsak a számítási időt növelné meg, hanem a részeredmények tárolására időlegesen fellépő tárhelyigényt is. Ügyesen alkalmazott alfa-béta eljárás ezen némiképpen segíthetne, de a játszma lelassulását csak nagyobb sebességű számítógéppel vagy a gépi nyelvhez közelebbi programozással lehetne ellensúlyozni.
Nagyon érdekes játékváltozatot jelentene, ha a gép a játszma végét előre figyelné. Gondoljunk arra, elvben lehetséges az, hogy a játék nagyon hamar befejeződik, mert az egyik játékos rekeszei teljesen kiürülnek. Így ha a számítógép nyerésre áll, célja lehet saját gyűjtőtálkája tartalmának növelése helyett saját térfelét gyorsan kiürítve meglepetésszerű győzelmet kierőszakolni. Ezt a stratégiát azonban elég nehéz programozni.
A program nagyszámú bővítési lehetősége közül kettőt említünk. Ha a játék egyes állásait a képernyős megjelenítőn mutatjuk meg, akkor látványosabb, áttekinthetőbb ábrázolást is alkalmazhatunk, pl. az egyes tálkák tartalmának megfelelő számú csillaggal. Villogó feliratok segítségével hívhatjuk fel a figyelmet arra, hogy kinek a lépése következik stb. Igen szórakoztatóvá teheti a játékot, ha annak részeredményeit kommentáló megjegyzések jelennek meg; dicsérve, bosszantva a játékost.

Amióta a főnök vett egy számítógépet, már ezt sem érdemes játszani...
6.2. Nyelvi játékok
A beszélt emberi nyelvek általában kimeríthetetlen játéklehetőségeket tartogatnak. Erre utalnak a televízió, a rejtvény újságok, irodalmi hetilapok által népszerűsített és néha valóságos játéklázzá váló nyelvi játék ötletek. (Szóvicckészítés, a szavak félreértelmezése, a csacsi-pacsi, szavak összerakása betűkből stb.)
A számítógép - elsősorban a korlátozott tárkapacitású és működési sebességű minigépre gondolunk - a nyelvi játékok terén csak mérsékelt lehetőségekkel rendelkezik. Ennek oka elsősorban az, hogy a beszélt nyelv szabályai rendszerint igen nagyszámúak és nem nagyon nevezhetők logikusnak, legalábbis a számítógépek vagy a matematikai egzaktság szintjén. A ragozás, a magánhangzó illeszkedés összetett szabályai, helyesírási gondok stb. utalhatnak arra, hogy a számítógépek nyelvi játékokra való programozása igen fáradságos munka, és a várható eredmény sem tűnik annyira értékesnek, hogy a munkába belekezdjünk. Súlyos hibája a számítógépeknek, hogy nem értik meg a szavakat; a számítógépek számára az értelmes vagy értelmetlen alfanumerikus karaktersorok egyformák, ha szintaktikus hibát nem tartalmaznak. A szavak, mondatok "megértésére" - struktúrák és relációk létrehozására - csak a mesterséges intelligencia kutatások néhány központi helyén találunk programokat, és ezek is eléggé gyermekded értelmi színvonallal ruházzák fel a számítógépeket.
Egy rövid példával érzékeltetni kívánjuk azt, hogyan értelmezi a beszélt nyelveken megjelenő szöveget a számítógép. A "nyelvprocesszálás" nagyon bonyolult feladat: az értelmezni kívánt mondat elemeinek és struktúrájának alapos vizsgálatát igényli, majd a számítógép tárában elhelyezett értelmező rendszer sorra veszi a lehetséges - a mondatban implicite benne rejlő - módosulatokat. Valahogy így:
INPUT: Jancsi adott Juliskának egy aszpirint.
OUTPUT:
Jancsi azt hiszi, hogy Juliskának aszpirinre van szüksége.
Juliska beteg.
Juliska szeretné jobban érezni magát.
Juliska majd megemészti az aszpirint.
Meg kell említenünk azt is, hogy számos alkalommal írtak már beszélgetőprogramokat. Ezek azon alapulnak, hogy a számítógép "beszélget" egy meghatározott helyzetben levő emberrel, mondjuk egy kórházban,- így tehát viszonylag kis számú, a helyzetre jellemző szót, szókapcsolatot kell csak a számítógépnek felismernie, és ezekből kell válaszait, kérdéseit megfogalmazni. Ha a program összeállításánál az "optimista" szemléletet juttatták uralomra, akkor a számítógép a beszélgetés során azt fogja sugallni a páciensnek. A kórházi betegtársakkal ellentétben a számítógép inkább csak szerencsés kimenetelű műtétekről ad számot, persze mértékkel adagolva az ilyeneket, nehogy beszélgető partnere gyanút fogjon. Állítólag a beszélgetőprogramok nagyon jó hatásúak, annak ellenére, hogy a páciens tudja, hogy a terminál mögött mindössze csak egy számítógép rejtőzik.
A beszélgetőprogramok egyik legrégebbi változatát az időjárás témaköréből írták: régi emberi gyarlóság az időjárásról társalogni, akár hosszasan is, az információnyerés legkisebb esélye nélkül. A program általánosan semmitmondó kifejezéseken és szófordulatokon kívül figyelembe vette a pillanatnyi meteorológiai helyzetet, azt összehasonlította a tárban tárolt nevezetesebb időjárási anomáliákkal. "Bezzeg éppen 28 évvel ezelőtt - éppen amikor a királynőt koronázták - akkor milyen szépen sütött a nap..." - típusú mondatokkal szinte a mindennapi élet gyakori fordulataihoz jutunk vissza. (Talán nem meglepő: a programot először Angliában készítették el...).
A számítógépes nyelvi játékok elterjedésének van egy nagy akadálya: ha a nyelvi játék pl. angol nyelvű, akkor az szinte lefordíthatatlan magyarra (és viszont), mert a játékok rendszerint az illető nyelvre jellemző szabályrendszeren alapulnak.
A számítógépes nyelvi játékok viszonylag kis száma nem jelenti azonban azt, hogy a nyelvtudományok bizonyos részeinek feladatai ne lennének számítógéppel megoldhatók. A számítógépek sokat segíthetnek a rendezés munkáiban, szótárkészítésben - még az olyan szokatlan feladványban is, mint pl. a szóvégződések szerinti szórendezés. Ezt az igen tág kört azonban nem érintjük, a továbbiakban olyan egyszerű programokat közlünk, amelyeknek eredménye hosszabb-rövidebb ideig szórakoztatónak, komikusnak tűnik. A játék tulajdonképpen a program megírásában vagy módosításában rejlik. A nyelvi programok írása azért hasznos időtöltés, mert érdekes megközelítését nyújtja a nyelvtani kérdéseknek, és jó gyakorlatot jelent ahhoz, hogy megtanuljuk: korlátozott lehetőségekkel hogyan lehet a nyelvi szabályok ketrecrendszeréből kicsit kibújni.
6.2.1. Beszámolókészítés
A számítógép véletlenszám-generátorának felhasználásával egy jól megválasztott szótárból szinte sohasem ismétlődő szövegáradatot tudunk kelteni. Nem közömbös azonban az, hogy milyen szavakból, kifejezésekből állítjuk elő a szótárt, és mennyire ügyesen választjuk meg mondatszerkesztési módszerünket, hogy a keltett szöveg "stílusa" változatos, emberszerű legyen.
Beszámolók (jelentések) készítésére szinte már mindenki rákényszerült: munkahelyi csoportok, intézmények, egyének egyaránt írnak beszámolókat. Ezek gépies voltának kihasználásával - komikus vonásainak kihangsúlyozására - készült a "beszámolóíró" program. A program működése a 6.4. ábra alapján tekinthető át:
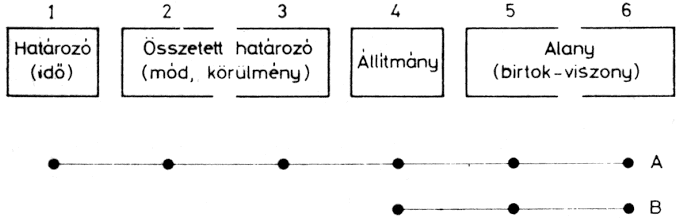
6.4. ábra: A frázisgenerátor A és B típusú mondatainak előállítási vázlata
A számítógép szótárában elhelyezkedő szavak hat csoportra oszlanak. Az egyes csoportokhoz olyan szavak, szócsoportok vagy mellékmondatok tartoznak, amelyeknek a helye a mondatban rögzített. A mondatok felépítése általában a következő: az (1) határozót (többnyire időhatározó) a (2) összetett mód-, és (3) helyhatározó követi, majd a (4) állítmány következik, végül a mondat (5, 6) alanya zárja a sort. A számítógép véletlenszerűen válogat az egyes mondatrészekhez tartozó szótárból, két különböző mondatszerkezetet hozva létre (A és B). A rövidebb mondat a stílust "élénkíti". A program a mondatokat bekezdésekké tördeli - egy bekezdésben 3...6 mondat található. Három bekezdés ad egy oldalt.
A szótár feltöltése a lehetséges állítmányok összeállításával kezdődik. Mivel a program "beszámoló", ezért a (4) állítmányok, ill. bővítményes szerkezetek mindig sikerről, diadalról adnak számot. A mondat (5,6) alanya munkatervből, környezeti viszonyokból adódhat. Az időhatározó, ill. kezdő mellékmondat is némiképpen magán viselheti a környezet nyomait. A (2, 3)-ban megjelenő szavak többsége a hivatalos nyelv és a pongyola fogalmazások vadhajtásaiból állítható elő.
A program megindulásakor megkérdi, hogy hány oldalnyi szöveget kell generálnia, valamint azt, hogy kinek számára készüljön. Ez utóbbi információt tulajdonképpen semmire sem használja, csupán az utolsó oldal utolsó bekezdésében helyezi el azt egy előre megírt (a beszámolókban nem ritka) tartalmú mondatban. A program gondoskodik arról, hogy a legelső bekezdés időhatározóval kezdődjék. A program által készített szöveg:

A mondatok nehézkessége, a bennük felbukkanó igazi jelentés nélküli szavak a szöveget "életszerűvé" teszik, és ebből keveset von le az, hogy a program a szavak elválasztásának semmiféle szabályát sem használja. (Ennek programozása ui. meghaladná a kisgépek lehetőségeit.)
Alább a teljes - Minimal-BASIC - programot közöljük. Látható, hogy annak túlnyomó részét (a 300-914 sorok között) a szótár teszi ki. Mivel itt a szavakkal, mondatrészekkel semmiféle műveletet nem végzünk az egyszerű egymásután íráson kívül, a feladat programrésze igen egyszerű. Említést érdemel azonban az, hogy a szótár részeit PRINT szubrutinok formájában fogalmaztuk meg.
50 REM BESZAMOLO
55 RANDOMIZE
60 PRINT TAB(34);"BESZAMOLO"
70 PRINT :PRINT "HANY OLDAL LEGYEN";
85 INPUT L
90 PRINT "KINEK KESZUL;
95 INPUT A$
100 PRINT :PRINT
120 LET B=3*L
130 FOR K=1 TO B
140 LET M=INT(4*RND(3))+3
150 FOR I=1 TO M
160 IF I=1 THEN PRINT " ";
170 IF K*I=1 THEN 250
175 IF RND<.3 THEN 232
179 LET W=INT(12*RND+1)
180 ON W GOSUB 801,802,803,804,805,806,807,808,809,810,811,812
189 LET W=INT(13*RND+1)
190 ON W GOSUB 821,822,823,824,825,826,827,828,829,830,831,832,833
199 LET W=INT(11*RND+1)
200 ON W GOSUB 841,842,843,844,845,846,847,848,849,850,851
209 LET W=INT(14*RND+1)
210 ON W GOSUB 861,862,863,864,865,866,867,868,869,870,871,872,873,874
219 LET W=INT(12*RND+1)
220 ON W GOSUB 881,882,883,884,885,886,887,888,889,890,891,892
229 LET W=INT(13*RND+1)
230 ON W GOSUB 901,902,903,904,905,906,907,908,909,910,912,913,914
231 GOTO 270
232 LET W=INT(14*RND+1)
233 ON W GOSUB 861,862,863,864,865,866,867,868,869,870,871,872,873,874
234 LET W=INT(13*RND+1)
235 ON W GOSUB 821,822,823,824,825,826,827,828,829,830,831,832,833
236 LET W=INT(12*RND+1)
237 ON W GOSUB 901,902,903,904,905,906,907,908,909,910,911,912
240 GOTO 270
250 ON INT(4*RND+1) GOSUB 801,802,803,804
260 GOTO 189
270 NEXT I
280 PRINT
290 NEXT K
300 PRINT " A FENTI MUNKAKAT AZ ";A$;
305 PRINT " TULAJDONKEPPEN CSAK ERKOLCSI TAMOGATASBAN RESZESITETTE. IGEN CELSZERU LENNE, HA AZ ";A$;
315 PRINT " A TOVABBIAKBAN ANYAGILAG IS RESZT VALLALNA EZEKBOL A HASZNOS ES JELENTOSEGTELJES KUTATASOKBOL."
330 END
801 PRINT "AZ ELMULT EVBEN ";:RETURN
802 PRINT "A MULT ESZTENDOBEN ";:RETURN
803 PRINT "TAVALY ";:RETURN
804 PRINT "A BESZAMOLASI IDOSZAKBAN ";:RETURN
805 PRINT "JELENTOS EREDMENYKENT ";:RETURN
806 PRINT "ELONYOS VALASZTAS VOLT, HOGY ";:RETURN
807 PRINT "HASONLOKEPPEN ";:RETURN
808 PRINT "SZELESKORU ELISMEREST SZERZETT, HOGY ";:RETURN
809 PRINT "AZ EVES TERVNEK MEGFELELOEN ";:RETURN
810 PRINT "A TAVLATI TERV SZERINT ";:RETURN
811 PRINT "A TUDOMANY ES TERMELES KAPCSOLATAT FOKOZTA, HOGY ";:RETURN
812 PRINT "PARTEREINKKEL EGYUTTMUKODVE ";:RETURN
821 PRINT "A CAMAC RENDSZER ";:RETURN
822 PRINT "A CAMAC MODULOK ";:RETURN
823 PRINT "A KISSZAMITOGEPEK ";:RETURN
824 PRINT "AZ MSI VALTOZATU KISGEP ";:RETURN
825 PRINT "AZ IPARI ALKALMAZASOK ";:RETURN
826 PRINT "A RENDSZERTELEPITES ";:RETURN
827 PRINT "A MIKROPROCESSZOROK ";:RETURN
828 PRINT "A HIEARCHIKUS RENDSZERTELEPITES ";:RETURN
829 PRINT "A SZAMITOGEPES VEGELLENORZES ";:RETURN
830 PRINT "A MOZGOKOCSIS LABORATORIUM ";:RETURN
831 PRINT "A SZAMITOGEPES MERORENDSZEREK ";:RETURN
832 PRINT "A MOBIL LABORATORIUM ";:RETURN
833 PRINT "AZ IPARI MERORENDSZEREK ";:RETURN
841 PRINT "TEKINTETEBEN ";:RETURN
842 PRINT "VONATKOZASABAN ";:RETURN
843 PRINT "TERULETEN ";:RETURN
844 PRINT "KIALAKITAS KAPCSAN ";:RETURN
845 PRINT "MEGVALOSITASA SORAN ";:RETURN
846 PRINT "KONSTRUKCIOJANAL ";:RETURN
847 PRINT "TEMA LEZARASANAL ";:RETURN
848 PRINT "KOVETELMENYEK KIELEGITESE CELJABOL ";:RETURN
849 PRINT "KOORDINACIOJANAK FOKOZASARA ";:RETURN
850 PRINT "TEREN AZ LSI ARAMKOROK ALKALMAZASANK KEZDETEKENT ";:RETURN
851 PRINT "TEREN FOLYTATOTT INTENZIV MUNKA KOVETKEZTEBEN ";:RETURN
861 PRINT "BEFEJEZODOTT ";:RETURN
862 PRINT "LEZARULT ";:RETURN
863 PRINT "ELKESZULT ";:RETURN
864 PRINT "MEGVALOSULT ";:RETURN
865 PRINT "FUNKCIONALISAN KIEGESZULT ";:RETURN
866 PRINT "SIKERES BEMUTATON VETT RESZT ";:RETURN
867 PRINT "ATGONDOLT RENDSZERANALIZIST IGENYEL ";:RETURN
868 PRINT "MEGFONTOLASRA KERULT ";:RETURN
869 PRINT "SZERZODO PARTNEREINK RESZERE ELKESZULT ";:RETURN
870 PRINT "GAZDASIGLAG IGEN HASZNOSNAK BIZONYULT ";:RETURN
871 PRINT "KOMOLY UZLETKOTESEKET TETT LEHETOVE ";:RETURN
872 PRINT "MEGERDEMELT SIKERT HOZOTT ";:RETURN
873 PRINT "AZ INTEZETBEN FOLYO EGYEB MUNKAKHOZ KAPCSOLODOTT ";:RETURN
874 PRINT "SZAKMAI SZINTUNKET JELENTOSEN EMELTE ";:RETURN
881 PRINT "A KORSZERU PERIFERIALIS ESZKOZOK ";:RETURN
882 PRINT "AZ INTEZETI TERMINAL HALOZAT ";:RETURN
883 PRINT "A MIKROPROCESSZOR ";:RETURN
884 PRINT "ANNAK ";:RETURN
885 PRINT "AZ ADADBEVITEL ";:RETURN
886 PRINT "AZ ENBER-GEP KAPCSOLAT ";:RETURN
887 PRINT "A SZAMITOGEPES ELLENORZES ";:RETURN
888 PRINT "A SOFTWARE ";:RETURN
889 PRINT "A HARDWARE ";:RETURN
890 PRINT "A KISSZAMITOGEPEKRE TORTENO ADAPTACIO ";:RETURN
891 PRINT "A HATTERTAROLOK ";:RETURN
892 PRINT "A PROGRAMCSOMAG ";:RETURN
901 PRINT "KONSTRUKCIOJA. ";:RETURN
902 PRINT "ILLESZTO RENDSZERE. ";:RETURN
903 PRINT "MERORENDSZERE. ";:RETURN
904 PRINT "TESZT RENDSZERE. ";:RETURN
905 PRINT "DOKUMENTACIOJA. ";:RETURN
906 PRINT "KIERTEKELESE. ";:RETURN
907 PRINT "BEMERESI UTASITASA. ";:RETURN
908 PRINT "ELEMZO VIZSGALATA. ";:RETURN
909 PRINT "TUDOMANYOS KONCEPCIOJA. ";:RETURN
910 PRINT "ALKALMAZAS TECHNIKAJA. ";:RETURN
911 PRINT "IMPLEMENTALASA. ";:RETURN
912 PRINT "KONCEPCIOJANAK KIALAKITASA. ";:RETURN
913 PRINT "GAZDASAGOSSAGANAK VIZSGALATA. ";:RETURN
914 PRINT "MAS MEGOLDASOKKAL TORTENO OSSZEHASONLITASA. ";:RETURN
A fenti elven alapuló program különböző "tematikákra" alkalmazható. Mindenütt, ahol a szöveg egyes részei, szófordulatai, bizonyos kifejezései uralkodóvá válnak, ott ezek véletlenszerű egymás után következései már az "igazi" benyomását keltik. Létezik eléggé jó szerelmeslevél-író program, és valószínű, hogy "közhelyszótár" felhasználásával viszonylag egyszerűen lehetne pl. Jonesco stílusát utánzó abszurd drámát íratni számítógéppel.
6.2.2. Versírás
A számítógépeket már nagyon sokszor programozták versírásra és egyik-másik számítógépes verset más nyelvre le is fordítottak. Ennek ellenére számítógépes "költészet" nem létezik. Ha ui. a verset úgy definiáljuk, mint hosszabb-rövidebb verbális szakaszok egymásutánját, amelyben- meghökkentő, de asszociatíve nem egymáshoz rendelhető szavak következhetnek egymás után nagyon kevés ritmikai és formai megkötéssel, akkor a számítógép tud verset írni. Félő azonban, hogy ezt a definíciót sem az irodalmárok, sem a költők nagy része nem fogadná el.
Játszani azonban mégis lehet. Vegyük elő Weöres Sándor "Téma és variációk" c. művét. Ennek első mondata ill. versszaka:
"Ma szép nap van, csupa sugárzás, futkosnak a kutyák az árokszélen és mindenki remekül tölti az időt, még a rabkocsiból is nóta hangzik."
A szavak azután összekeverednek, és a tizedik változat már ilyen:
"Ma szép rabkocsi van, csupa töltés, sugárzik a remek napba és kutyás árokszélek hangzanak a futkosásba, még az idő is nótázza mindenkinek."
Ehhez a játékhoz hasonlót a számítógép is tud csinálni. Akár ugyanezekből a szavakból is.
A fentihez hasonlóan érdekes játékra nyílik mód akkor, ha egy-egy kedvelt vagy éppenséggel nem szeretett költő verseinek jellemző szavaiból, szófordulataiból íratunk véletlenszerűen "verseket". A szavak és stílusjegyek megállapításához nem "mesterségbelieknek" elsősorban a paródiákat ajánljuk.

A költő
6.2.3. Szóradar
A szóradar népszerű játék. Abból áll, hogy az egyik játékos gondol egy ötbetűs szót, a másik ötbetűs szavakkal "lő rá". Válaszként közlik vele, hogy a találatok (betűegyezések száma) mennyi (ld. a 2.1.3. szakaszt: mastermind).
A játék azon alapul, hogy a magyar nyelvben az ötbetűs szavak eléggé gyakoriak (ahogy pl. az angolban a négybetűsek), ezért az a játékos, aki "próbálkozik", részben logikai készségére, részben nyelvismeretére van utalva. Jó játékosok 8...12 szóval körülhatárolják a kitalálandó szót, persze őket is érhetik meglepetések.
Kétféle számítógépes program képzelhető el: az egyik passzív, a másik aktívan játszik. A passzív játékos csupán adminisztrál, gondolkodnia szinte semmit sem kell. Ha az aktív játékos közöl egy új szót, akkor annak minden betűjével végig kell vizsgálnia az "elrejtett" szót, minden egyes betűjét és az egyezéseket össze kell számolni. (Itt a játék módosulatai között némi eltérés található.)
A számítógép tehát itt csak következetesen, pontosan kiértékel. Érdekesebb a játék, ha a számítógép tárában néhány száz szó van "eldugva" és a játékos a számítógéptől kap - véletlenszerűen - egy feladványt. Még érdekesebb az a játék, amelynél több ezer ötbetűs szó van tárolva, a számológép tehát aktív játékot folytathat ennek alapján. A számítógép taktikája: úgy kell a következő kérdező szót megválasztani, hogy
6.3. Zenegenerálás
A zenegenerálás elnevezést megkülönböztetésül használjuk: a számítógéppel előállított - a kompozíció nevet eléggé ritkán megérdemlő - "műveket" kívánjuk ezzel az igazi alkotásoktól elválasztani. Ma már vitathatatlan, hogy a számítógépekkel végzett zenemű-analízisek nagyon értékes ismeretekkel gazdagították a zenetudományt: a számítógép segédeszközként szerepel bizonyos fajta elemző kutatásokban. Terjednek a számítógép vezérlésű "zeneszerzámok" is, az egyre divatosabb szintetizátorok, hang-technikai trükköket megvalósító berendezések is gyakran tartalmaznak már kisszámítógépeket.
Mindezek ellenére a számítógéppel végzett (segített) legmagasabb rendű zenei tevékenység - a komponálás - eléggé gyér sikereket vallhat csak magáénak. Az utcán nem fütyülnek komputerslágereket és a sznobok is leszoktak már a számítógéppel komponált koncertek látogatásáról. Az ok nagyon kézenfekvő: a zene, a zene élvezete részleteiben és egészében igen kevéssé ismert pszichológiai folyamatokon alapul, ezért mesterséges vagy gépi eszközökkel nehéz sikeres műveket alkotni.
E fejezet bevezetésében változatos alapokon nyugvó játékokat ígértünk. Ebben joggal foglalhat helyet egy egyszerű számítógépes zenegeneráló eljárás leírása is. Természetesen nem jutunk messzire, a játék szintjén maradunk.
A zeneszerzés folyamata - erősen egyszerűsítve - két lépésből áll: ki kell találni az egymást követő hangok magasságát és időtartalmát (ritmusát), valamint le kell írni ezeket egyfajta konvencionális módon (kotta). A számítógép véletlenszám-generátora ismét ideális eszköznek mutatkozik hosszú számsorozatok keltésére, ezeket valamilyen egyszerű eljárással hangmagasságokká, ill. időtartamokká alakíthatjuk. Egy ilyen módon előállított kompozíció látható a 6.5. ábrán. Az egymást követő hangok magassága és időtartama között semmiféle összefüggés sincs, minden hang egyforma valószínűséggel jelenik meg. A kottát bármilyen hangszeren lejátszva kellemetlen élményben lesz részünk: a mű csupa meglepetés, egyetlen hangját, hangcsoportját sem érezzük előre. Nagyon fárasztó ilyen "zenét" hallgatni.

6.5. ábra: A hangok véletlenszerűen követik egymást
Valamivel kellemesebb élményt nyújt a fizikából jól ismert jelenség, a Brown-mozgás utánzásával készülő zene. Itt a véletlenszámokat arra használjuk fel, hogy két egymást követő hang közötti távolságot szabjuk meg. Ez a fajta zene tehát egy közepes hangmagasság körül ingadozik, "bolyong". A 6.6. ábrán közölt részlet már sokkal kellemesebb benyomást tesz, mint az előző. Most viszont a zenét unalmasnak érezzük, a részeg emberek tántorgó mozgását véljük felfedezni benne.

6.6 ábra: Brown-mozgáson alapuló zene
A zene statisztikai vizsgálatai során kiderült, hogy az ember számára kellemesnek tűnő hangsorozatokban a hangteljesítmény frekvenciaspektruma 1/f jellegű. Eszerint tehát a teljesen véletlen zenét azért nem éreztük jónak, mert az 1/f^0=1, vagyis "fehér zaj", a Brown-mozgást imitáló zene pedig 1/f^2 frekvenciaspektrumú. Az egyik teljesen kötetlen egymásutánja a hangoknak, a másik túlságosan kötött. Vajon milyen zenéhez jutunk, ha az egyes hangok magassága az őket megelőzőktől nem lesz teljesen független?
Az 1/f zene előállításának a szakirodalomban közölt módszere a következő: Vegyünk három dobókockát, amelyek különböző színűek (kék, zöld, piros). Ha e három kockát együtt dobjuk fel, akkor 3 és 18 közötti számot kapunk eredményül. Ez a 16 szám feleljen meg sorban 16 különböző hangmagasságnak. A három kocka egyszeri feldobása után azonban az új hangjegyeket a következő táblázat által elrendelt kockafeldobásokkal kapjuk meg:
vagyis első lépésként csak a piros kockával dobnak újra, második lépésben a zöld kocka kerül sorra, majd a piros és a zöld együtt stb.
Kézenfekvőnek tűnik a gondolat: vajon egy megfelelően programozott számítógép nem tudna-e valamilyen módon egy dallamot lejátszani? Erre jó néhány számítógépnél viszonylag egyszerű lehetőség kínálkozik. A PDP-8 típusú számítógépek pl. a JUMP utasítások végrehajtásánál egy impulzust szolgáltatnak. Ha ezen impulzusok frekvenciáját program segítségével változtatjuk, akkor ezekkel az impulzusokkal egy hangszóróban különböző magasságú hangokat kelthetünk. Lehet olyan fordítóprogramot szerkeszteni, amelybe egy kotta hangjegyeit kódolva betápláljuk, majd a fordítóprogram elkészíti azt a gépi utasításokból álló tárgyprogramot. Az előbb említett utasításból származó impulzus felhasználásával - kissé uniszónó orgonahatást keltve - a hangszóróból megszólalhat a kívánt dallam. A kisszámítógépek egy részébe a hangszórót eleve beépítik: ezzel ui. a programok futásának ellenőrzése, a hibakeresés bizonyos körülmények között egyszerűbbé válhat.
6.4. Szindbád, részeg-golf és egyebek
A mese szerint Szindbád egyszer megmentette a szultán életét. Jutalmul elvonultak előtte egyesével a hárem hölgyei, mindegyik fellebbentette arcfátylát és Szindbádnak választania kellett egyet a hölgyek közül. A választás azonban nem volt könnyű, csak az éppen ott álló hölgyet választhatta, aki már elvonult előtte, azt már nem kérhette. Itt tehát az érdekes kérdés: ha Szindbád tudja, hogy éppen százan fogják megmutatni arcukat, hogyan tudná a legszebbet kiválasztani közülük?
Mivel "szép" nőarcokat nehéz a számítógép-perifériákon generálni, ezért a hölgyek szépségére (pontosabban a játékos ízlésétől függő "kívánatosságára") számadatok utalhatnak. Az elvonuló | hölgyek nevével egyidejűleg a derékbőségükre, ill. mellbőségükre vonatkozó adatok 1 is feltűnnek. Ha a játékos választott már, de nem az optimálisát, akkor a felvonulás tovább folytatódik, és könnyen lehet, hogy a "legszebb" csak ezután érkezik; a játékos i tehát vesztett.
A számítógépprogram a jellemző adatokat egy adott értékintervallumban véletlen-szerűen generálja, a sorbaállítás is újra és újra véletlenszerű. A játékos tehát csak valamilyen jól megválasztott stratégiával nyerhet. Egy lehetséges megoldás szerint a várható létszám egy meghatározott töredékéig csak figyel, de semmiképpen nem választ. Ezzel megállapítja, hogy melyik volt az addig előfordult legmagasabb érték. A következő szakaszban pedig azonnal kiválasztja azt, akinek számértéke a megfigyelési szakasz maximumánál nagyobb. Ha ilyen nincs, a legutolsót választja, ami rendszerint, bár nem feltétlenül, a játékos vereségét jelenti.
A részeg-golf játék alaphelyzete a következő: két játékos golfozik (leegyszerűsítve: minél kisebb ütésszámmal igyekszik a labdát a lyukba belejuttatni), amelyik egy játszmát megnyer, az köteles egy pohár martinit meginni. Ennek hatására azonban rosszabbul játszik. Kérdés: hogyan kell az erősebb vagy a gyengébb játékos helyzetében "taktikázni", hogy neki legyen előbb 10 nyert játszmája?
A két játékos eléggé különböző képességű. Ennek ellensúlyozására azonban az alkohol "játékrontó" hatása sem azonos. Míg a rosszabb játékos valószínűséggörbéje poharanként egy egységgel csúszik jobbra, addig az ügyesebb játékosra jobban hat az ital, ő poharanként 1,5-tel rosszabb teljesítményt nyújt.
A játék során a számítógép az egyik játékos; az élő játékos választja meg, hogy ő a jobbik vagy rosszabbik játékos kíván lenni. Az élő játékosnak van némi előnye a géppel szemben: a gép mindig a pillanatnyi állapotának megfelelően játszik és ő próbálkozik először. Az élő játékos választhat: ő is becsületesen próbálkozik - legjobb tudása szerint - vagy pedig készakarva elveszti a játszmát a géppel szemben. Ez a taktikai veszteség - különösen többször egymás után - a gép által képviselt játékos játékát alaposan leronthatja.
A számítógépesítésre alkalmas játékok száma igen nagy. Az ún. üldözéses játékokban az üldöző és üldözött mozgáslehetőségei lényegesen különböznek. A 6.7. ábra egy ilyen helyzetet ábrázol: egymásra merőleges utcákból felépített városban rendőrautó igyekszik elfogni a bankrablók autóját. A rendőrautónak (kissé szokatlanul) be kell tartania a közlekedési szabályokat, ezért vagy előző irányának megfelelően mozoghat, vagy pedig csak jobbra fordulhat. Időegységenként két utcányit halad, ellentétben a rablók autójával, amely lassabban mozog, de a közlekedési szabályokat nem tartja be.
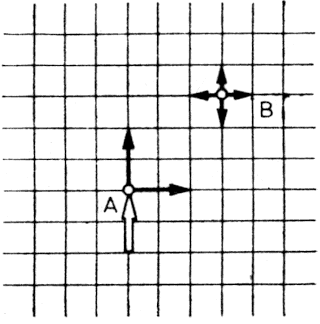
6.7. ábra: A rendőrök és a rablók autója különbözőképpen mozog
Ha mindkét autó ismeri egymás pillanatnyi helyzetét, mi a rendőrautónak és a rablók autójának az optimális stratégiája? (Feltéve, hogy a rendőrautó akkor fogja el a rablókat, ha egy egységnyire megközelíti őket.) A választ a szakirodalomban megtaláljuk: A 6.8. ábrán azt látjuk, hogy a körrel jelölt pontba érkező rendőrautó a környezetében levő pontokon elhelyezkedő rablóautót hány lépéssel képes elfogni. Az ábrából az tűnik ki, hogy ha a rablóautó a számokkal jelölt területrészen kívül helyezkedik el, a rendőrök sohasem érik utói, feltéve, hogy stratégiája helyes.
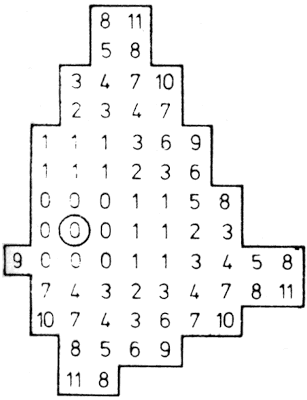
6.8. ábra: A rendőrautó csak akkor képes a rablók autóját elfogni, ha az utóbbi a számokkal jelölt területen tartózkodik
Hasonló jellegű játék vázlatát látjuk a 6.9. ábrán. Itt a mozgás egyenlő oldalú háromszögekből kialakuló térrészen zajlik, a két jármű mozgáslehetőségeit az ábra mutatja: a gyorsabb jármű irányváltoztatási lehetősége kisebb.
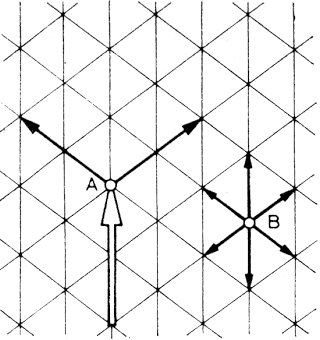
6.9. ábra: Az ámoksofőr és a részeg gyalogos mozgáslehetőségei
Mindkét játék programozása viszonylag egyszerű, célszerűen a rablót játszhatja az élő játékos, és a gyorsabb, de kevésbé kanyarodóképes játékost a számítógép. A számítógép - a megoldás birtokában - eléggé jól játszhat, és az élő játékost sokszor térdre kényszeríti, mielőtt az a játék fortélyait kitanulja.

Üldözéses játék
Egy kép felér sok ezer szóval. Ez igaz a számítástechnika gyakorlatára is. Az elmúlt évek fejlődése egyre újabb hardware-eszközöket, egyre fejlettebb programnyelveket és software-csomagokat, a kettő együtt pedig az ember és a számítógép kapcsolat új módszereit és teljesen új alkalmazási területeket hozott létre. Ennek hatására jött létre a napjainkban is rohamosan fejlődő számítógépes grafika (grafikus információbevitel, -feldolgozás és -kivitel), valamint az ember és a számítógép "párbeszédes" formájú együttműködését biztosító interaktív számítógépes grafika.
Ez a számítástechnika szempontjából rendkívül jelentős fejlődés ugyanakkor egyre több számítógép-konfigurációnál biztosít különböző szintű feltételeket játékok és játékos alkalmazások számára is.
A játékok nagyon nagy része már eredetileg is ezek, melyek számítógépesítéséhez most már hardware- és software-eszközök is rendelkezésre állnak. Ezek az eszközök ugyanakkor teljesen újfajta játékok kialakítását is lehetővé teszik.
Ilyen hardware-eszközök pl. az alfanumerikus kimeneti perifériák, melyek a legegyszerűbb, kvázigrafikusnak tekinthető kirajzolást tesznek lehetővé. E kimeneti perifériák egyik csoportja az információt papírra rögzíti (hard-copy berendezések), mint pl. a sornyomtató, teletype vagy villamos írógép, másik csoportja pedig egy televízióhoz hasonló ún. alfanumerikus megjelenítő, amely a képernyőjén (soft-copy) adja ki az információt, és az információ karaktereit az ún. karaktergenerátor pontokból alakítja ki. A karakterek megfelelő elrendezésével és megválasztásával jól használható diagramokat, hisztogramokat, nomogramokat állíthatunk elő, sőt ezek egyszerűbb ábrák rajzolását is lehetővé teszik.
A sornyomtatók, villamos írógépek egy fontos csoportja a karaktereket mátrixban elrendezett pontokból állítja elő, ezek a mátrixnyomtatók. Az alfanumerikus megjelenítőknek szintén van egy csoportja, mely a mátrixnyomtatók és a felhasználó által definiált szimbólumokat használja. E megjelenítők karakter-, ill. szimbólumgenerátorai: REPROM-ok, vagyis csak olvasható, de különböző tartalommal többször is feltölthető, félvezetős tárak. Ezek átírásával a rajzolást jobban szolgáló speciális szimbólumokat (pl. a fehérből a fekete felé haladó szürkeségi sornak megfelelő tónusú vagyis fedettségű pontot) is létrehozhatunk.
Az előbb ismertetett legegyszerűbb kimeneti perifériák egy része azonban olyan kiképzésű, hogy nem csupán információt visz ki, mivel egybe van építve egy bemeneti perifériával. Ez a bemeneti periféria általában az írógép betű/jel elrendezésének megfelelő felépítésű billentyűzet. A billentyűzetnek, a tényleges adatbevitelen kívül két további fontos feladata is van. Egyrészt hardware-úton teszi lehetővé - a kimeneti perifériával együtt - a számítógéppel való párbeszédet (pl. a képernyőn megjelenő kérdésre adott választ), másrészt a billentyűzet segítségével bevitt karakterek elrendezésével egyszerűbb ábrák rajzolhatók, ill. a már kirajzolt elrendezésekben kiválasztott pozíciók jelölhetők ki.
A kimeneti perifériák közül igazi grafikus ábrázolást biztosítanak a különböző rajzgépek. Ezek felépítése lehet síkasztalos és dobos. Működésük alapelve: digitális vagy növekményes (vagyis adott írótoll helyzethez képest csak adott irányú és nagyságú relatív elmozdulást biztosító) és analóg (az írótoll véghelyzet abszolút koordinátái szerinti elmozdulást biztosító). A rajzgép lehet külső vezérlésű, amely csak elemi utasításokat képes végrehajtani és belső vezérlésű, amelynek ún. pályagenerátora is van. Üzemmódja szerint lehet közvetlen (on-line), amikor a rajzgép periferikus berendezésként csatlakozik a számítógéphez, ill. közvetett (off-line), amikor a rajzinformáció valamilyen közbenső adattár (pl. lyukszalagos, mágnesszalagos tár stb.) közvetítésével jut el a független rajzgéphez. A korszerű rajzgépek - hasonlóan a modern képernyős megjelenítőkhöz - többszínű rajzolást is lehetővé tesznek.
A képernyős megjelenítő grafikus ábrázolást lehetővé tevő típusa a grafikus megjelenítő. Ennek képernyőjén való megjelenítésnél a képcső elektronsugara vagy az ábra alakját követi közvetlenül, vagy a televíziónál is megszokott módon szisztematikusan tapogatja végig a képernyőt, az ábrát tulajdonképpen elemi ábraelemekből - pontokból - rakva össze. Az előbbi az ún. tetszőleges eltérítést biztosító grafikus megjelenítő, az utóbbi pedig a raszter típusú megjelenítő. A grafikus megjelenítő esetében az ábrát speciális generátorok: pontgenerátor, vektorgenerátor, karaktergenerátor, egyenesgenerátor, körívgenerátor stb., által létrehozott elemekből állíthatjuk össze. A raszter típusú megjelenítőnél viszont az ábrát az egyes képpontok (melyek különböző fényerejűek, ill. színűek lehetnek) felvillantásának az engedélyezésével, ill. tiltásával generálhatjuk. A korszerű képernyős megjelenítők mindkét kategóriája intelligens, azaz maga is programozható az ezekbe beépített egy vagy több processzor (ma már általában mikroprocesszor) segítségével. A processzorok a vezérlés és a külvilággal való kapcsolat szervezését is nagymértékben egyszerűsítik.
A bemeneti perifériák egyik csoportjának olyan grafikus beviteli eszközei vannak, melyek közvetlenül a képi információval való kapcsolatot is lehetővé teszik.
Ilyen grafikus beviteli eszközök:
Ezek segítségével a számítógép és a felhasználó a képi információn keresztül hathat egymásra, képi párbeszédben oldva meg a feladatot. A módszert interaktív számítógépes grafikának nevezik és egyre nagyobb szerepet kap a számítástechnikában.
Maguk a grafikus rendszerek vagy önállóak, vagy egy nagy számítógép végberendezései (termináljai) lehetnek.
A bemeneti perifériák másik csoportja a grafikus (képi) információ bevitelét önállóan végzi. Ide tartoznak az ábrák manuális bevitelét biztosító, kézi nyomkövetésen alapuló digitalizálok és kézi rajzolást átalakító grafikus táblák. Egy másik alcsoport már a képek automatikus átalakításának és bevitelének az eszköze. Ezekhez tartoznak a különféle automatikus képletapogatók (scanner-ek), amelyek legismertebb, legegyszerűbb formája a televíziós kamera.
A hardware-eszközök korántsem teljes felsorolása után röviden foglalkozunk a számítógépes grafika software-eszközeivel is.
A software-eszközöket a többé-kevésbé általános célú hardware-eszközöknél sokkal nagyobb mértékben, az alkalmazások szabják meg. A két legfontosabb alkalmazási terület:
A képfeldolgozás feladatai szerint csoportosíthatók:
A software-eszközök a különböző célú programcsomagok. Ilyenek pl. egy rajzgép ábrázolásformáit megvalósító alapsoftware, a képi információ tárolását megvalósító adatstrúktura (pl. file-szervezés), kétdimenziós transzformációk (definiált képrészek eltolása, méretváltoztatása vagy elforgatása), képrészek kivágása (elhatárolás, ablak-képzés, "gumioptikázás" stb.), háromdimenziós ábrázolás (különböző perspektívák, eltakart vonalak kiküszöbölése, árnyékolás stb.) programcsomagjai.
A software eszközök közé tartoznak a különböző grafikus ábrázolást segítő programnyelvek is. Különböző szinten valósítják meg a programozást (képgenerálást és grafikus manipulációkat), az interaktív működésnél a parancsok és a párbeszédek feldolgozását. Ezek lehetnek általános célúak vagy feladatorientáltak. Szintjüket tekintve alacsony (assembly) vagy magas szintűek. (A speciális programnyelvek mellett különösen hasznosak az általános célú magasszintű nyelvek pl. ALGOL, LISP, PL/1, APL grafikus orientációjú kiegészített változatai.)
A játékos számítógépes grafika alkalmazásainak körét nagyon nehéz lenne definiálni. A helyzet ui. az, hogy bár a rajz, az ábra, a képi információ általában nagyon sok esetben a számítógép és ember közötti kapcsolat eszköze vagy a játék megjelenési formája, mégis a játék lényegét nem csupán a rajzos megjelenés jelenti. Így azt az utat választjuk, hogy definiálás helyett ismét néhány jellemző példán keresztül mutatjuk be a lehetőségeket. Mégis - az áttekintés kedvéért - valamiféle kategorizálásra törekszünk és ebben rendezőként a számítógép-konfigurációk (hardware-, ill. software-erőforrások) által nyújtott lehetőségeket választjuk (Id. a 7.2. ábrán látható táblázatot).
| Hardware eszköz | Játékos alkalmazás (példa) |
| Alfanumerikus kimeneti periféria (villamos íróírógép, teletype, sornyomtató, képernyős megjelenítő) | Kvázigrafikus ábrázolás karakterekkel (Labirirtus) |
| Alfanumerikus be-, ill. kimeneti periféria (alfa-numerikus display, teletype, képernyős megjelenítő) | Kvázigrafikus párbeszéd (Bogár) |
| Kvázigrafikus kimeneti periféria (raszter képernyős megjelenítő, mátrix nyomtató) | Tónusos képábrázolás (Fényképezés) |
| Grafikus kirajzolás (rajzgép, grafikus képernyős megjelenítő) | Vonalas képi ábrázolás (Computer Art) |
| Interaktív mozgó ábrázolás (grafikus, kvázigrafikus képernyős megjelenítő és speciális bemeneti eszköz) | Mozgó ábra megjelenítés a játékos által vezérelve (Holdraszállás) |
| Egyszerű interaktív mozgó ábrázolás (Célszámítógép és speciális bemeneti eszköz) | Mozgó ábra megjelenítés a játékos által vezérelve (tv-játékok) |
A legegyszerűbb számítógépnek (kis- vagy mikroszámítógépeknek vagy termináloknak) is van valamiféle alfanumerikus kimeneti perifériája. A karakterek segítségével így egyszerű diagramokat rajzolhatunk, sőt még figuratív ábrákat is összeállíthatunk. A sornyomtató ugyanakkor arra is felhasználható, hogy kétszintű (fekete-fehér) ábrázolás mellett különböző árnyalatokat (szürkeségi szinteket) tartalmazó képeket is előállítsunk vele. Ilyenkor az első kinyomtatást második, harmadik, negyedik stb. is követi, amelyek hatására azonos karakterpozíciókba kerülő betűk és jelek egymásra nyomtatódnak. Nyolc szürkeségi szintet pl. a következő egymásra nyomtatott karakterekkel biztosíthatunk:
Szürkeségi szint Nyomtatott karakterek 1 (fehér) betűköz (blank) 2 - 3 = 4 +, x 5 x, * 6 +, x, = 7 0, x, * 8 (fekete) 0, M, W, #
A grafikus megjelenítők és a rajzgépek két olyan számítógép alkalmazási terület létrejöttét is lehetővé tették, ahol a játékos alkalmazás határvonala elég elmosódott. Az egyik ilyen terület a számítógépes művészet (Computer Art), ahol a játékos célból előállított érdekes, esztétikus ábrák és a tényleges művészi alkotások között nehéz meghúzni a határvonalat.
Eddigiekben - bár ezt külön nem hangsúlyoztuk - csak statikus (mozdulatlan, illő) ábrázolásról beszéltünk. A korszerű számítógépek képernyős megjelenítői (mind a vonalrajzoló típusok, mind a raszter rendszerűek) azonban képesek dinamikus (mozgó) ábrák létrehozására is. Az alapelvet a filmtől kölcsönözték, ahol a mozgás látszatát álló képek egymástól csak kissé eltérő sorozatának egymás utáni megjelenítésével keltik. Esetünkben azonban a kívánt mozgásnak megfelelően módosított álló képeket a számítógép generálja. Ha a mozgás - a képernyős megjelenítő és a számítógép utasításaiban megfogalmazva - nem túlságosan bonyolult, a képmódosítás egy "állókép kocka" ideje alatt elvégezhető, így a mozgókép létrehozásának nincs akadálya. Természetesen itt is nehéz egyértelműen válaszolni arra a kérdésre, hogy egy szimulált holdraszállás vagy repülőgép landolás érdekes játék-e, vagy egy nagy jelentőségű kiképzési eszköz. A határvonalat talán a szimuláció szintje, a valóság megközelítésének mértéke jelentheti. A dinamikus, mozgó ábrázolással összekapcsolt szimuláció ugyanakkor nagyon hasznos oktatási segédeszköz is. A számítógépes megelevenítés: az animáció pedig a nagyon munkaigényes rajzfilmkészítés egyre jelentősebb gyakorlati segédeszközévé is vált az utóbbi időben. A félvezetős integrált áramköri technológia fejlődése két eredményével közvetlenül is hozzájárult a grafika játékos alkalmazásainak nagyarányú terjedéséhez. Egyrészt létrehozta a mikroszámítógépek egy új kategóriáját, a személyes használatú számítógépet (PERCOM: personal-computer). A nagybonyolultságú integrált áramkörök segítségével a PERCOM típusokhoz közönséges televíziós készülék (vagy monitor) csatlakoztatható alfanumerikus és tv-raszter rendszerű megjelenítőként. A PERCOM egyik fő alkalmazása - egyebek mellett - a számítógéppel segített játék. Az egyszerű tv-rendszerű megjelenítő alkalmazásával ezek köre a grafikus (ill. kvázigrafikus) játékokra is kiterjeszthető. Másrészt a tv-készülékek és az LSI áramkörök házasságából létrejöttek a ma már mindenki által jól ismert tv-játékok. Ezek egyre újabb, érdekesebb és összetettebb grafikus játékokat biztosítanak számunkra.
7.1. Grafikus játékok
A rajz, az ábraformában való információkiadás igénye talán egyidős a számítástechnikával. A kezdeti vázlatos ábrázolás eszközei a különféle szöveges (alfanumerikus) kivitelt biztosító perifériák voltak. Ezek ma is megtalálhatók még a legegyszerűbb konfigurációkban is. A karakterekkel való rajzolás jól felhasználható a játékos alkalmazásoknál is.
A 7.3. ábrán egy jól ismert játék: az útvesztő vagy labirintus egy változatát mutatjuk be. Láthatjuk az ábrából, hogy annak előállítására csak karaktereket (I,- , :, .) használtunk fel. Így ez az ábra bármilyen alfanumerikus periféria felhasználásával kinyomtatható.
7.3. ábra: Számítógéppel generált labirintus (útvesztő)
Magát a labirintust - amelynek mindig csak egyetlen bejárata és kijárata és ezeket összekötő egyetlen átjárható útja van az alább található Altair BASIC program segítségével állíthatjuk elő. A program számára megszabhatjuk - perifériás eszközeink dimenzióival (vagyis a soronkénti és oszloponkénti maximális karakterszámokkal) összhangban - a labirintus méreteit (vagyis a függőleges és a vízszintes "cellaszámot") is. A program a BASIC véletlenszám-generátorok segítségével minden esetben különböző elrendezésű útvesztőt fog létrehozni.
10 PRINT TAB(32);"LABIRINTUS"
20 PRINT TAB(15);"CREATIVE COMPUTING MORRISTOWN, NEW JERSEY"
30 PRINT:PRINT
100 INPUT "MI LEGYEN A SZELESSEG ES HOSSZUSAG";H,V
102 IF H<>1 AND V<>1 THEN 110
104 PRINT "ERTELMETLEN DIMENZIOK!":GOTO 100
110 DIM W(H,V),V(H,V)
120 PRINT
130 PRINT
160 Q=0:Z=0:X=INT(RND(1)*H+1)
165 FOR I=1 TO H
170 IF I=X THEN 173
171 PRINT ".--";:GOTO 180
173 PRINT ". ";
180 NEXT I
190 PRINT "."
195 C=1:W(X,1)=C:C=C+1
200 R=X:S=1:GOTO 260
210 IF R<>H THEN 240
215 IF S<>V THEN 230
220 R=1:S=1:GOTO 250
230 R=1:S=S+1:GOTO 250
240 R=R+1
250 IF W(R,S)=0 THEN 210
260 IF R-1=0 THEN 530
265 IF W(R-1,S)<>0 THEN 530
270 IF S-1=0 THEN 390
280 IF W(R,S-1)<>0 THEN 390
290 IF R=H THEN 330
300 IF W(R+1,S)<>0 THEN 330
310 X=INT(RND(1)*3+1)
320 ON X GOTO 790,820,860
330 IF S<>V THEN 340
334 IF Z=1 THEN 370
338 Q=1:GOTO 350
340 IF W(R,S+1)<>0 THEN 370
350 X=INT(RND(1)*3+1)
360 ON X GOTO 790,820,910
370 X=INT(RND(1)*2+1)
380 ON X GOTO 790,820
390 IF R=H THEN 470
400 IF W(R+1,S)<>0 THEN 470
405 IF S<>V THEN 420
410 IF Z=1 THEN 450
415 Q=1:GOTO 430
420 IF W(R,S+1)<>0 THEN 450
430 X=INT(RND(1)*3+1)
440 ON X GOTO 790,860,910
450 X=INT(RND(1)*2+1)
460 ON X GOTO 790,860
470 IF S<>V THEN 490
480 IF Z=1 THEN 520
485 Q=1:GOTO 500
490 IF W(R,S+1)<>0 THEN 520
500 X=INT(RND(1)*2+1)
510 ON X GOTO 790,910
520 GOTO 790
530 IF S-1=0 THEN 670
540 IF W(R,S-1)<>0 THEN 670
545 IF R=H THEN 610
547 IF W(R+1,S)<>0 THEN 610
550 IF S<>V THEN 560
552 IF Z=1 THEN 590
554 Q=1:GOTO 570
560 IF W(R,S+1)<>0 THEN 590
570 X=INT(RND(1)*3+1)
580 ON X GOTO 820,860,910
590 X=INT(RND(1)*2+1)
600 ON X GOTO 820,860
610 IF S<>V THEN 630
620 IF Z=1 THEN 660
625 Q=1:GOTO 640
630 IF W(R,S+1)<>0 THEN 660
640 X=INT(RND(1)*2+1)
650 ON X GOTO 820,910
660 GOTO 820
670 IF R=H THEN 740
680 IF W(R+1,S)<>0 THEN 740
685 IF S<>V THEN 700
690 IF Z=1 THEN 730
695 Q=1:GOTO 830
700 IF W(R,S+1)<>0 THEN 730
710 X=INT(RND(1)*2+1)
720 ON X GOTO 860,910
730 GOTO 860
740 IF S<>V THEN 760
750 IF Z=1 THEN 780
755 Q=1:GOTO 770
760 IF W(R,S+1)<>0 THEN 780
770 GOTO 910
780 GOTO 1000
790 W(R-1,S)=C
800 C=C+1:V(R-1,S)=2:R=R-1
810 IF C=H*V+1 THEN 1010
815 Q=0:GOTO 260
820 W(R,S-1)=C
830 C=C+1
840 V(R,S-1)=1:S=S-1:IF C=H*V+1 THEN 1010
850 Q=0:GOTO 260
860 W(R+1,S)=C
870 C=C+1:IF V(R,S)=0 THEN 880
875 V(R,S)=3:GOTO 890
880 V(R,S)=2
890 R=R+1
900 IF C=H*V+1 THEN 1010
905 GOTO 530
910 IF Q=1 THEN 960
920 W(R,S+1)=C:C=C+1:IF V(R,S)=0 THEN 940
930 V(R,S)=3:GOTO 950
940 V(R,S)=1
950 S=S+1:IF C=H*V+1 THEN 1010
955 GOTO 260
960 Z=1
970 IF V(R,S)=0 THEN 980
975 V(R,S)=3:Q=0:GOTO 1000
980 V(R,S)=1:Q=0:R=1:S=1:GOTO 250
1000 GOTO 210
1010 FOR J=1 TO V
1011 PRINT "I";
1012 FOR I=1 TO H
1013 IF V(I,J)<2 THEN 1030
1020 PRINT " ";
1021 GOTO 1040
1030 PRINT " I";
1040 NEXT I
1041 PRINT
1043 FOR I=1 TO H
1045 IF V(I,J)=0 THEN 1060
1050 IF V(I,J)=2 THEN 1060
1051 PRINT ": ";
1052 GOTO 1070
1060 PRINT ":--";
1070 NEXT I
1071 PRINT "."
1072 NEXT J
1073 END
A következő egyszerű rajzos játék, amelyet bemutatunk, a bogár (eredeti neve: Bug) A játék célja: részekből rakni össze (test, nyak, fej, csápok, farok, lábak) egy bogarat, mielőtt a számítógép befejezné a saját maga bogárrajzát. A játékos és a számítógép felváltva "dobnak kockát" (azaz a program véletlenszerűen kiválaszt egy számot 1 és 6 között), amely egy-egy testrésznek felel meg. A részek csak megfelelő sorrendben használhatók fel, vagyis nem ér semmit a nyak, amíg nincs test, vagy nem lehet a bogárnak addig feje, amíg nincs nyaka stb. Minden új rész hozzáadása után a program - kívánságra (a megfelelő kérdésre adott válasz függvényében) - kirajzolja a játékos és a számítógép "bogarát". Egy ilyen rajzot abban az állapotban, amikor az egyik fél már nyert, vagyis kész a bogár rajza, láthatunk a 7.4. ábrán.

7.4. ábra: A bogárjáték által kirajzolt ábra
Egy tv-kamerával és a hozzákapcsolt A-D konverterrel számítógépes fényképet készíthetünk, amelyet a programban definiált módon el is torzíthatunk (számítógépes karikatúrakészítés). A képeket sornyomtató, mátrixnyomtató alkalmazásával papírra is kinyomtathatjuk.
A grafikus ábrázolás alapeleme a pont. A pont definiálása azonban az alkalmazott grafikus eszköz típusától függően különböző. így egy pont megadható:
Ez utóbbival, mivel a játékok számára kiemelkedő fontosságú, kicsit részletesebben is foglalkozunk.
Blokknak tekintünk adott számú egymáshoz rendelt pontcsoportot. A megjelenítendő felületet ezek után ezen blokkokkal fedjük le, hasonlóan ahhoz, ahogy egy falfelületet csempékkel borítunk be. A 7.5. ábrán bemutatott 12 pontból álló sort és 12 pontból álló oszlopot tartalmazó mezőt 2x3 pontból álló blokkokkal "fedtük le". (Mind az egyes pontokat, mind a blokkok elemeit a felfrissítő tárban 1 és 0 bit képviseli aszerint, hogy a pont "látható" vagy nem, megjelenített vagy nem.)
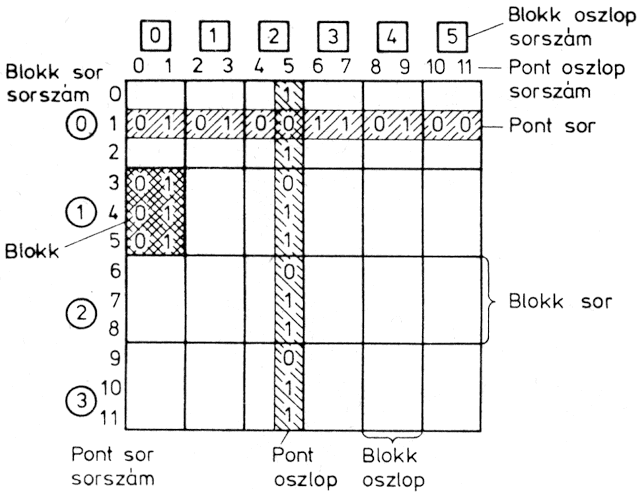
7.5 ábra: Pont ábrázolása blokkok segítségével
Az egyes blokkokhoz, a karakterek megjelenítéséhez hasonlóan, kódokat rendelünk, amelyek a 2x3 pontból álló blokk esetén a bitelrendezést is megadják (7.6. ábra).
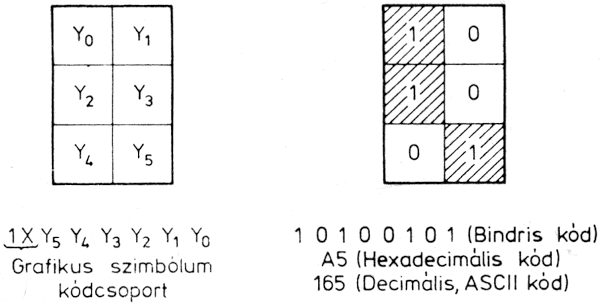
7.6. ábra: Blokk-kód ás bitelrendezés kapcsolata
Több egymáshoz kapcsolódó blokk segítségével különféle alakzatok jeleníthetők meg.
Adott n sor, ill. m oszlop sorszámú pont esetén a megfelelő - az adott pontot tartalmazó blokk - blokksor, ill. blokkoszlop száma egyszerűen meghatározható. Ezek birtokában, ha az egyes blokkoknak megfelelő byte-ok egymás utáni tárhelyeken vannak, a vonatkozó tárcím is egyszerűen képezhető. Legyenek pl. a keresett pont koordinátái: n=7, m=5. Az ennek megfelelő tárhely címeltérése (a 0,0 sorszámú blokk címéhez képest):
(a maradékot figyelmen kívül hagyva), ahol k a blokkban levő sorok száma; I az egy sorban levő blokkok száma; p a blokkban levő oszlopok száma. Így a címeltérés
A blokkon belüli bit a maradékok alapján határozható meg. Ha a sormaradék: 0 az Y0 vagy Y1, 1 az Y2 vagy Y3, 2 az Y4 vagy Y5, ill., ha az oszlop maradék: 0 az Y0, Y2 vagy Y4, 1 az Y1, Y3 vagy Y5 jelű bitről van szó (ld. 7.6. ábrát).
Esetünkben
7/ 3 = 2 a maradék 1, tehát Y2 vagy Y3 bitről van szó,
5/2 = 2 a maradék 1, tehát Y1 vagy Y3 vagy Y5 bitről van szó.
A kívánt bit, amely mindkettőt kielégíti, az Y3 jelű.
Gyakorlati feladatok esetén a következő négy dolgot tehetjük: egy adott bitet - vagyis annak megfelelő pontot - 1 értékűre (látható pont), vagy 0 értékűre (nem látható, "üres" pont) állíthatjuk be; komplementálhatunk (látható pont "eltűnik" és fordítva); vagy az adott helyen levő értéket megvizsgálhatjuk. A blokknak megfelelő byte-ból a kívánt bitet M maszk segítségével választjuk ki. Ha ez a bit pl. az Y3 helynek felel meg, akkor a maszkban csak ebben a bitpozícióban lesz 1 érték.
M3 = 00001000
Az egyes blokkoknak megfelelő kódokat a kép összeállításánál speciális billentyűzet (grafikus karakterek) segítségével is megadhatjuk, ami a rajzolást és képösszeállítást sokkal gyorsabbá teszi.
7.2. Számítógépes művészet és animáció
A számítógépes grafikának, mint már korábban említettük, két sajátos alkalmazási területe alakult ki az elmúlt években: a számítógépes művészet és az animáció. Ezekről, játékos vonatkozásaikat figyelembe véve, nem felejtkezhetünk meg. A számítógépes művészetnek - bár más ágai (zene, szobrászat, építészet, színművészet, tánc stb.) - is nagymértékben fejlődnek, most csak a grafikus vonatkozásait érintjük röviden.
Minden számítógép, amely nyomtatott formában képes karaktereket kiadni, alkalmas játékos rajzok készítésére. Ezek az idősebb generáció igényei szerint csinos hölgyeket szoktak ábrázolni vagy elsősorban gyermekek számára különféle állatfigurákat. Ez képviseli tehát a számítógépes művészet legalsó fokát és kellő türelemmel és fantáziával viszonylag rövid idő alatt bárki elő tud ilyen ábrákat állítani. Példaként a 7.7. ábrán be is mutatunk egy ilyen művet, amelynek generáló programját is közöljük.

7.7. ábra: Nyuszi ábrázolása karakterek segítségével
100 PRINT TAB(33);"NYUSZI"
110 PRINT TAB(15);"CREATIVE COMPUTING MORRISTOWN, NEW JERSEY":PRINT
115 DIM B(5)
120 FOR I=0 TO 5
125 READ B(I)
128 NEXT I
160 PRINT
170 READ X
171 IF X>128 THEN 450
172 IF X<0 THEN 160
180 PRINT TAB(X);:READ Y
190 FOR I=X TO Y
195 LET J=I-6*INT(I/6)
200 PRINT CHR$(B(J));
210 NEXT I
220 GOTO 170
290 DATA 78,89,85,83,90,73
300 DATA 1,2,-1,0,2,45,50,-1,0,5,43,52,-1,0,7,41,52,-1
310 DATA 1,9,37,50,-1,2,11,36,50,-1,3,13,34,49,-1,4,14,32,48,-1
320 DATA 5,15,31,47,-1,6,16,30,45,-1,7,17,29,44,-1,8,19,28,43,-1
330 DATA 9,20,27,41,-1,10,21,26,40,-1,11,22,25,38,-1,12,22,24,36,-1
340 DATA 13,34,-1,14,33,-1,15,31,-1,17,29,-1,18,27,-1
350 DATA 19,26,-1,16,28,-1,13,30,-1,11,31,-1,10,32,-1
360 DATA 8,33,-1,7,34,-1,6,13,16,34,-1,5,12,16,35,-1
370 DATA 4,12,16,35,-1,3,12,15,35,-1,2,35,-1,1,35,-1
380 DATA 2,34,-1,3,34,-1,4,33,-1,6,33,-1,10,32,34,34,-1
390 DATA 14,17,19,25,28,31,35,35,-1,15,19,23,30,36,36,-1
400 DATA 14,18,21,21,24,30,37,37,-1,13,18,23,29,33,38,-1
410 DATA 12,29,31,33,-1,11,13,17,17,19,19,22,22,24,31,-1
420 DATA 10,11,17,18,22,22,24,24,29,29,-1
430 DATA 22,23,26,29,-1,27,29,-1,28,29,-1,4096
450 END
Az igazi művészet és a számítógépes grafika egymásra hatásáról vallanak gyakorló - számítógépes eszközöket is felhasználó - képzőművészek. Bár a gyakorló, a számítógépes grafikában jártas szakemberek számára az egyes formák és alakzatok megadása természetes és egyszerű, mégis talán érdemes egy művészeti-alkotás-kategória számára kidolgozott program (Diagonal White) ábramegadását röviden bemutatnunk.
A program segítségével a 7.8. ábrán látható elrendezéshez hasonló - színben és az alakzatok kialakításában különböző - alkotások készíthetők.

7.8. ábra: Diagonal white (Edward Zajec alkotása)
A felhasználható elemek a következők: függőleges, vízszintes és ferde vonalak síklapok meghatározására, színek megadása (a három alapszín: sárga, piros, kék, valamint fehér, szürke és fekete). A színek és az alakzatok egymáshoz vannak rendelve. A derékszögű alakzatok alapszínűek, a nem derékszögűek pedig szürkék vagy feketék.
A mű "megalkotása" röviden a következőképpen történik.
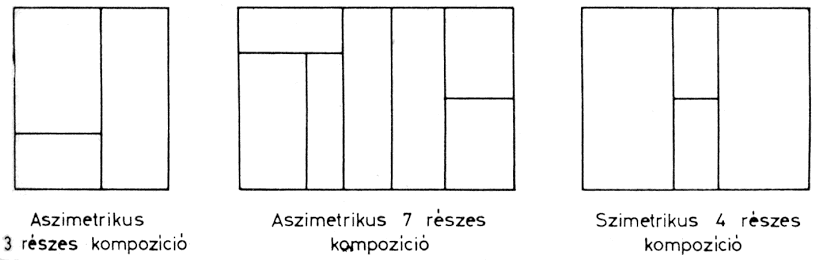
7.9. ábra: A kompozíció kialakítása
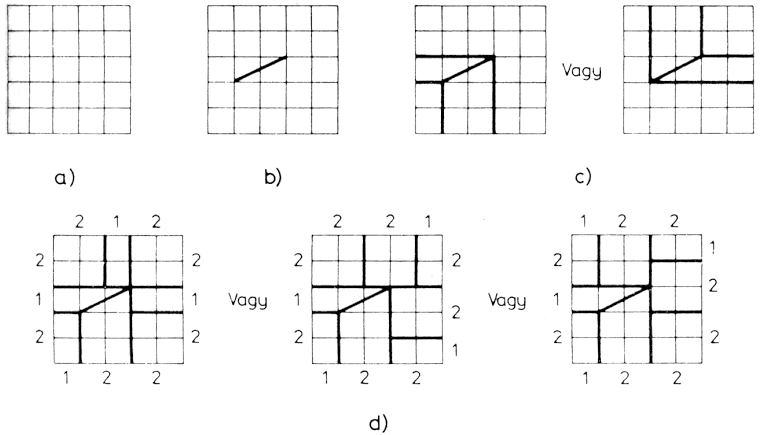
7.10. ábra: Az alakzat kidolgozása
Az ismertetett szabályok alapján létrehozott elrendezést mutattuk be a 7.8. ábrán.
A 7.11. ábrán - könyvünk nyomdatechnikai lehetőségeinek megfelelő - számítógépes grafikai alkotást mutatunk be, amely esztétikai szempontból már jogosan művészi produktumnak tekinthető.

7.11. ábra: Példa számítógépes művészeti alkotásra
Szemben az ismertetett statikus (álló) képekkel, az animáció időben változói képmegjelenítést jelent. Maga a számítógép és a hozzá kapcsolódó grafikus megjelenítő eszközök nagyon alkalmasak az animáció létrehozására, a relatív helyzet, alak stb. megváltozás generálására és mozgóképszerű megjelenítésére.
Mivel állóképeinek segítségével nem lehet bemutatni az animáció tényleges eredményét, így csak a lehetőségek körének illusztrálására szorítkozunk.
A 7.12. ábrán egy igen egyszerű tv-játék képét mutatjuk be. Itt a játék vezérlése a "labda" megadott szabályok szerinti mozgását biztosítja Ebben az esetben és a már korábban bemutatott 4.3. ábrán látható "holdraszállás" esetén is az animáció interaktív, tehát az ember (a játékos) által a valódi időtartományban befolyásolható.

7.12. ábra: TV-játék, a legegyszerűbb interaktív animáció
Ilyen számítógéppel közvetített interaktív animáció megvalósításához a már ismertetett hardware-erőforrások (digitális számítógép, megfelelő tárak, beavatkozó-, bemeneti-, kimeneti eszköz) mellett természetesen megfelelő software-rendszerre is szükség van, melynek legfontosabb elemei a következők:
8. A játékok királynője: a sakk
A sakk indiai eredetű játék, Indiából jutott el a IX. században Görögországba, majd a mórok közvetítésével Spanyol- és Olaszországba. A sakk sok szempontból egyedülálló és kiemelkedik a játékok sorából. A szabályai világosan definiáltak, ugyanakkor a játék elég összetett ahhoz, hogy a valóságos élet problémáihoz hasonlatos legyen. Így még sokszázéves gyakorlat és intenzív tanulmányozás után is felkelti a kezdő érdeklődését és ugyanakkor a szakértő számára is sok lehetőséget tartogat.
A sakk gazdag története elegendő "anyagot" szolgáltatott a sakktudás értékeléséhez és a különböző játékstílusok analizálásához. A sakk egyben az intelligenciavizsgálatok tudományos eszközévé is vált.
A digitális számítógépek megjelenése együtt járt egy új tudományág kialakulásával is, amelyet mesterséges intelligencia kutatásoknak neveznek. Ezen a területen végzett kutatómunka célja olyan feladatoknak számítógépekkel való megoldása, amelyek általában emberi intelligenciát kívánnak. Ezen feladatok között - olyan alapproblémák mellett, mint az egyik nyelvről a másikra való gépi fordítás, a beszéd és alakfelismerés, és általában az automatikus problémamegoldás - hamarosan felmerült a számítógépekkel való sakkjáték is. Mivel az ember - a számítógéppel ellentétben - képes olyan nem egzakt feladatokat, mint pl. a sakkjátszmában a következő lépés kiválasztása, nagyon jól megoldani, Botvinnik, az egykori sakkvilágbajnok azt javasolta, hogy a számítógépet kell megtanítani az emberhez hasonló viselkedésre. Mások - figyelembe véve a számítógép eltérő tulajdonságait - el tudnak képzelni olyan jó hatásfokú sakkprogramokat, amelyek az embertől egészen eltérő módon játszanak. A mai napig elsősorban az első módszer látszott járhatóbbnak, vagyis szimulálni az emberi sakkjátékos játékát, egyben kihasználni a számítógép az embert messze meghaladó képességeit a számolás sebességében és abban, hogy nem követ el hibát a kalkulációban.
Ennek alapján - figyelmen kívül hagyva két fontos tényezőt: a feladat-összetettséget és hiányos ismereteinket az emberi sakkjátékos tényleges "feladatanalíziséről" és feladatmegoldási készségéről - optimista előrejelzések születtek arról, hogy a világ legjobb sakkjátékosa hamarosan egy számítógép lesz. Egy sok helyen idézett 1958-as becslés szerint ennek tíz éven belül - vagyis 1968-ban - be kellett volna következnie. Ezzel szemben a sakkprogramok legújabb generációja még ma sem érte el a sokkal szerényebb célt, a mesterszintű játékos képességét. Így a "küzdelem" tovább tart, és egyre növekvő számban készülnek olyan számítógépprogramok, amelyek különböző szinten képesek sakkozni.
A számítógéptudomány művelőit különböző indítékok vezérlik, amikor sakkjátszó programokat hoznak létre. Az egyik nagy csoport csupán arra kíváncsi, hogy milyen "erős" programot képes létrehozni. Ezek legjobbjai "sportnak" is tekintik a program-készítést és időről időre összemérik erejüket a különböző nemzeti és világbajnokságokon.
Mások sokkal átfogóbb célként az emberi gondolkodás, koncepcióformálás és problémamegoldás megértésének szolgálatában foglalkoznak a számítógépes sakkal. Ezek a szakemberek olyan komplex, gyakorlati feladatok megoldásához keresnek segédeszközöket, mint pl. egy repülőgép automatikus leszállítása vagy valamilyen betegség diagnosztizálása. Melléktermékként, de korántsem mellékesen, hasznot remélnek az oktatás terén is a számítógépes sakktól. Ha a számítógépprogram képes a sakkozás összetett feladatát részfeladatokra bontani és így megoldani, ebből az ember is tanulhat feladatmegoldási módszert.
A félvezetős áramköri technológia utóbbi időben bekövetkezett nagyarányú fejlődése - és ezen belül is a mikroprocesszorok megjelenése - két formában is tömeges - elsősorban szórakoztató célú - gépi sakkozást tett lehetővé. Megjelentek a sakkozásra képes elektronikus eszközök és az egyre jobban terjedő mikroszámítógépekhez alkalmazható sakkprogramcsomagok (pl. Checkmate, Chess Challenger, Compuchess stb.) Elsősorban szórakozás céljából egyre többen próbálnak kis rendszereken futtatható sakkprogramot írni. Ezzel tulajdonképpen egy új irányzat, a mikroszámítógépes sakk is megjelent.
Nemzeti büszkeségünk megsértése nélkül nem felejthetjük el, hogy a "gépesített" sakk hosszú idővel előbb keletkezett, mint maga a számítógép. Itt Kempelen Farkas által 1770-ben konstruált híres sakkozógépre gondolunk (8.1. ábra), amely minden ellenfelet megvert, magát Napóleont is. A Török néven híressé vált gépben ugyan egy ember is el volt rejtve, de ez a találmány újszerűségéből keveset von le, hiszen az ember nem volt a közönség számára látható, hanem rafináltan elhelyezett tükrök és rések segítségével belülről tájékozódott.

8.1. ábra: Kempelen Farkas sakkautomatája
A számítástechnika elterjedésének kezdetén 1950-51-ben olyan klasszikusok alapozták meg műveikkel a sakkprogramokat, mint Shannon vagy Turing.
A számítógépes sakkozás a '60-as évek közepén kezdődött modern korszakát két iskola és az ennek megfelelő két program uralja. Az egyik az amerikai Northwestern Egyetem CHESS (3.0...4.6. változatok), a második a moszkvai Vezérléstudományok Intézetének KAISSA nevű programja. Utóbbi kidolgozását Botvinnik, minden idők egyik legnagyobb sakkozója is segítette tanácsaival. Az IFIP (International Federation of Information Processing; az információfeldolgozás nemzetközi egyesülete) világkongresszusokkal párhuzamosan szervezett számítógépes sakkvilágbajnokságokon is ezek a programok szerepeltek a legjobban. Az eddig megrendezett két világbajnokság közül Stockholmban a KAISSA program nyert 1974-ben, míg 1977-ben Torontóban a CHESS 4.6 diadalmaskodott, amely akkor egy szupergyors CDC CYBER 170 sorozatú számítógépen futott.
Mivel sakkozás céljára még a leggyorsabb univerzális számítógépek is lassúnak bizonyultak, a sakkprogramban gyakran szereplő eljárások hardware (vagy mikroprogramozott) közvetlen megvalósításával próbálják javítani a programok futási idejét. Így pl. a MIT-nél Richard Greenblatt olyan célprocesszort valósított meg, amely a "sakkjátékorientált" alapvető utasításokat körülbelül 40 ns alatt hajtotta végre. Ez természetesen a "nyers erő" módszerével az elemzés mélységének növelését teszi lehetővé, ami persze nem vezet közvetlenül a játékerő növelésére. A számítógépes sakk tehát napjainkban is él, amit a publikációk növekvő száma is bizonyít.
A sakkjáték ma már annyira elterjedt, hogy az alapvető - az egyes figurák mozgását megszabó - szabályokat szinte mindenki ismeri. A játék folyamán a két hadsereg - a világos és a sötét - katonái, a figurák felváltva lépnek. A játék célja az ellenfél királyának matthelyzetbe, vagyis olyan helyzetbe hozása, amikor a királyt olyan pozícióban támadja egy ellenséges figura, hogy az nem képes elmenekülni. Ekkor az összes számba jövő mezőket vagy saját figurái foglalják el, vagy az ellenfél tartja ellenőrzése alatt, és nincs lehetőség a támadót leütni vagy a támadás vonalába egy saját figurát behozni. A sakkjáték azon jellemzője is közismert, hogy a végcél - az ellenfél királyának matthelyzetbe hozása - nem érhető el közvetlenül. Ehelyett - ezt megelőzően - közbeeső, szerényebb célokat kell kitűzni és megvalósítani, vagyis anyagi vagy helyzeti előnyt elérni. Csak így lehetséges az anyagilag vagy pozíció szempontjából előnyös játszmát matthelyzetté alakítani.
Mivel a sakk "véges" játék - vagyis véges számú megengedett elrendezés van - legalábbis elvileg lehetséges minden érvényes folytatást előállítani. Ezt olyan módon hajthatnánk végre, hogy minden megengedett lépést és az ellenfél által erre adott lehetséges válaszlépést, majd az ismét következő ellenlépést stb. létrehoznánk egészen addig, amíg vagy a világos, vagy a sötét király matthelyzetbe nem jut, esetleg döntetlen állás alakul ki. Ezután a lehetséges lépések fáján végighaladva a játékos - a már ismertetett minimax eljárást használva - megtalálhatná a számára legkedvezőbb lépést.
Egy gyors matematikai számítással azonban rögtön meggyőződhetünk arról, hogy gyakorlatban nincs lehetőség valamennyi lehetséges lépés nyomon követésére az egész sakkjátszma folyamán. Ha pl. egy kezdőállásban 10 lehetséges lépés van, erre ismét 10 lehetséges ellenlépés, majd ismét 10 megengedett válaszlépés, csupán hat - egyik fél által megtett -, ún. féllépést figyelembe véve, 10^6 = 1 millió végállást kellene értékelni. Ha most már azt is figyelembe vesszük, hogy egy tipikus mesterjátszmában átlagosan 42 lépés (84 féllépés) van, és pozíciónként átlagosan 38 különféle lépés lehetséges, a megvizsgálandó állások száma elméletileg 38^84, amelyet a világ legnagyobb és leggyorsabb számítógépével sem lehetne elfogadható időn belül analizálni.
A mesterjátszmák alaposabb vizsgálata ugyanakkor egy további érdekes eredményre is vezetett. Kimutatható, hogy egy adott állásban a "jó" lépések átlagos száma nem több, mint 1,76. így egy adott esetben a megvizsgálandó pozíciók száma nagymértékben lecsökken, már csak 1,76^84. Ha el akarjuk képzelni, hogy ez is még milyen nagy szám, elég arra gondolnunk, hogy 4,6 milliárd év, azaz 10^18 másodperc telt el a Föld kialakulása óta. Ha az egyes állások értékelését a számítógép 1 másodperc alatt végzi el, akkor 420 "földtörténetnyi" idő kellene a mesterszintű játék végigelemzéséhez. Ebből egyértelműen következik, hogy a sakkjátékos (és így a számítógép is) szelektív vizsgálatot kell, hogy végezzen az exponenciálisan növekvő állásszám ésszerű keretek között tartása érdekében.
8.1. A sakktábla gépi ábrázolása
8.1.1. A postaláda típusú reprezentáció
Ennél az ábrázolásnál minden egyes sakktáblamezőnek egy postaláda - a tárban egy vagy több szó - felel meg. Az adott című tárrész tartalmazza az adott sakktáblamezőre vonatkozó információt, ill. annak az aktuális értékét. Ebben az ábrázolási módban az egyes figurákhoz számokat rendelünk, amelyeket majd később az értékelésnél fel fogunk használni. (Pl. +1 a világos gyalog, +2 a világos huszár, +3 a világos futó stb., ill. -1 a sötét gyalog, -2 a sötét huszár, -3 a sötét futó stb.) Az üres mezőt a zérus tartalom jellemzi. A tábla 8x8 mezejéből való kilépést korszerű programoknál egy 10x12 mezőből álló elméleti tábla segítségével reprezentálják, ahol a 8x8 mezőn kívüli részhez tartozó tárak tartalma valamilyen specifikus szám, pl. 99. A huszárok szélső sávból való - két mezőnek megfelelő - "ugrásait" figyelembe véve a 12x 12 mezőből álló elrendezés először logikusabbnak látszana. Ha viszont a 10x12 mezőbe álló elrendezést gondolatban egy hengerpaláston képzeljük el - vagyis a két "szél" találkozik - azonos eredményt kapunk kevesebb tárhely alkalmazásával. A számítógép az adott mezőhöz tartozó tárhely tartalma alapján azonnal képes eldönteni az ott levő figura típusát és színét, ill. a tábla "elhagyását".
Egy adott táblapozícióban egy adott figura számára lehetséges lépések egyszerűen meghatározhatók a mezők címe közötti reláció alapján. Rendeljük pl. az egyes mezőkhöz a 8.2. ábra szerint a tárcímeket.
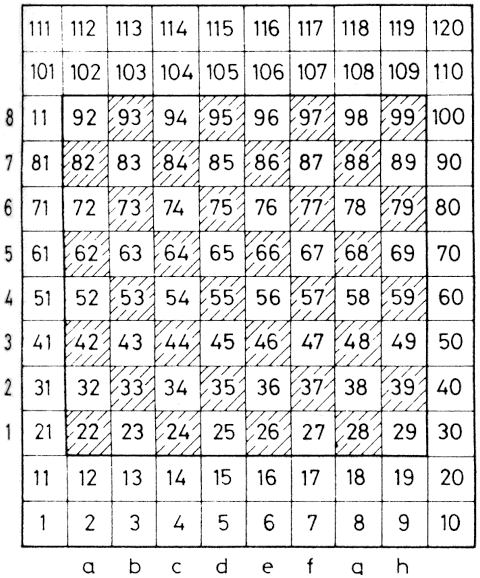
8.2. ábra: A sakktábla postaláda típusú ábrázolása
Az ábrán a vastag 8x8 mezőből álló sakktáblán kívüli címek tartalma az előző megállapodás szerint 99, vagyis a táblán kívüli mezőt jelent. Most, ha pl. egy figura valamelyik sakktáblamezőn áll, a lehetséges lépések - az adott helyzethez tartozó - címhez adott címmódosító értékekkel nyerhetők. Ezen címmódosítók huszár esetén a következők: +8, +19, +21, +12, -8, -19, -21, -12. Így pl. egy világos huszára Hf3 vagyis 47 című helyről a következő mezőkre léphet:
Látható, hogy ha a fenti számítást pl. a 92 címnek megfelelő Ha8 sarokpozícióban álló figurára végezzük el, az elméletileg lehetséges 8 lépés közül 6 a táblán kívül lesz, amit a kiszámított címek 99 tartalma fog jelezni. (92+8=100, 92+19=111, 92+21=113, 92+12=104, 92-21=71, 92-12=80.) A lehetséges király lépések hasonló módon a következő címkülönbségekkel számíthatók: -1, +9, +10, +11, +1, -9, - 10, -11. Az, hogy a lépés megengedett-e, a címkülönbséggel módosított eredeti cím, vagyis az új cím tartalmának ellenőrzésével dönthető el. Ha a tartalom 99, a lépés illegális (a táblán kívül van a mező). Ha a tartalom pozitív, akkor a világos figura lépése nem megengedett, mivel azon a helyen már egy világos figura áll. Ezzel szemben, ha a tartalom negatív, a mezőn sötét figura tartózkodik (hogy milyen, azt majd a számérték, alapján ki lehet értékelni), a lépés tehát ütést fog jelenteni. A zérus tartalom üres mezőt jelent, amelyet a figura általában elfoglalhat.
Futó, bástya és a vezér lehetséges mozgása ugyancsak hasonló elven számítható. Futó esetén az XY címet (pl. 46 esetén X = 4 és Y=6) a négy lehetséges iránynak megfelelően X+n,Y+n; X+n,Y-n; X-n,Y+n; X-n,Y-n módosítjuk, ahol n = 1, 2, 3, ... Világos futó esetén az egy irányba való címmódosítás (n-növelés) végértékét vagy pozitív tartalom (azonos színű figura áll a kiszámított helyen), negatív tartalom (ütés) vagy 99 értékű tartalom (a tábla széle jelzi). Ezután a számítást a következő irányban folytatjuk.
A bástya lehetséges lépéseit hasonló módon, de a ZW címtől kezdve a Z,W+n; Z,W-n, Z+n,W; Z-n,W alapján számíthatjuk. A vezér esetén a futó és a bástya algoritmusa szerinti számítást egyaránt el kell végeznünk. Itt most nem említettünk olyan összetett lépéseket, mint a sáncolás, vagy az "en passant" gyalog elfogás. Természetesen a fenti algoritmusok alapján elkészített lépésgenerátorunkat a gyakorlatban ezekkel a kissé összetettebb műveletekkel is ki kell egészíteni.
8.1.2. Bittérkép vagy bittábla
Ez az ábrázolás a digitális számítógépek utasításrendszerében rejlő lehetőségeket jobban kihasználja. Itt nem tártartalmat rendelünk a tábla egy mezőjéhez, hanem egy-egy 64 bites szót (vagy szócsoportot) minden figuratípushoz. Hatféle figura lévén, hat szó szükséges ebben az ábrázolásmódban a világos, és másik hat szó a sötét figurák pozíciójának ábrázolásához. (Gyalogok, bástyák, huszárok, futók, király, vezér pozíciójának megadására.) A 64 bites szó minden egyes bitje egy sakktáblamezőnek felel meg, amelynek az értéke jelzi, hogy abban a pozícióban egy adott típusú figura tartózkodik-e (pl. 1 = van figura, 0=nincs figura). Ezt az eljárást ezért bittérképnek vagy bittáblának szokás nevezni. Hasonló módon - további bittérképek segítségével - további fontos információkat is tárolhatunk (pl. az összes világos, ill. sötét figura helyzetét, a világos figurák által támadott mezőket stb.).
Ennek a módszernek az előnyét különösen a korszerű számítógép utasításrendszere által nyújtott lehetőségek tükrében érthetjük meg. Mint ismeretes, két bináris operandus ÉS műveletének eredménye abban a helyértékben fog 1 bit értéket tartalmazni, ahol a két eredeti szó mindegyikében logikai 1 érték volt. A logikai VAGY művelet esetén 1 érték fog megjelenni azon pozíciókban, amelyek 1 értéket tartalmaztak bármelyik szó adott helyértékében.
Ezeket az egyszerű műveleteket a sakkjáték programozásánál is alkalmazhatjuk. Legyen a feladat például a Hf3 pozíciójú világos huszár összes lehetséges lépésének az előállítása. Legyen ebben az ábrázolásmódban a 64 bit (azaz egy térkép) a tárban egy-egy táblapozícióhoz rendelve, amely az adott mezőn álló huszár lehetséges lépéseit tárolja. Most a számítógép először előveszi a tárból a lehetséges huszár lépéseket tároló bittérképek közül az f3 pozícióhoz tartozót, majd a világos figurák jelenlegi állását tartalmazó térképet. Ez utóbbit negálva (a 0 értékeket 1-re változtatva és viszont) egy olyan térképhez jutunk, amely azt jelzi logikai 1 bit pozíciókkal, hogy melyik táblamezőben nincs világos figura. Ezen térkép ÉS művelete a lehetséges huszárlépések térképével adja az adott pozícióhoz tartozó megengedett huszárlépéseket. Amelyik bitpozícióban a művelet elvégzése után 1 értéket kapunk, a huszár annak megfelelő mezőre léphet vagy üthet. Itt az eredményt csupán két tárhely és két logikai művelet segítségével kaptuk meg, ami lényegesen kevesebb, mint ahányra a "postaláda" ábrázolása és eljárás esetén szükségünk lett volna.
Tekintsünk egy további egyszerű, a sakkban előforduló feladatot. A középjáték folyamán a világos meg akarja határozni, hogy milyen támadási lehetőségei vannak. Például azt vizsgálja, hogy a következő lépésben valamelyik huszárjával "villába" tudja-e fogni (vagyis egyszerre meg tudja-e támadni) a sötét vezért és királyt. Hogy erre a kérdésre választ tudjon adni, a következő részfeladatok megoldására van szükség:
Egy sakkjátékos számára elég, ha egy pillantást vet a táblára, hogy erre a három kérdésre válaszolni tudjon. Gondoljuk végig ennek a feladatnak a megoldását a "postaláda" és a "bittérkép" reprezentáció alkalmazása esetén is, hogy a két módszer lehetőségeivel kicsit közelebbről megismerkedjünk.
A "postaláda" módszert alkalmazva először a huszár nyolc címmódosító értékét (+8, +19, +21, stb.) kell a sötét király pozíciójához adnunk és ezt tárolnunk. Ezek címezők a sötét király huszárral való megtámadásának lehetséges helyei. Ezután ugyanezt a műveletet a sötét vezérre is el kell végezni, megkapva a vezér megtámadásának kiindulási helyeit. Ebben az esetben az a helyes "stratégia", ha a vezérre vonatkozó mezők számított értékeit rögtön összehasonlítjuk a királyállás számított értékeivel. Ha megegyező értékeket találunk, ellenőriznünk kell az ehhez tartozó tárhely tartalmát is (nem 99-e, mert akkor ez a tényleges táblán kívül esik, tartalma nem 1-6 közötti pozitív érték-e, mert akkor már világos figura van ezen a mezőn). Ha a vizsgálat eredménye szerint a mező elfoglalható, megoldottuk az első részfeladatot és megállapítottuk, hogy van olyan mező, ahonnan a sötét királyt és vezért egyszerre megtámadhatnánk egy huszárral.
Most a második részfeladat szerint azt kell meghatároznunk, hogy valamelyik világos huszár tartózkodik-e egy lóugrásnyira ettől a mezőtől. Adjuk a huszárnak megfelelő nyolc címmódosító értékét a "villa" mező címéhez, és ezután vizsgáljuk meg ezen címek tartalmát. A +2-t tartalmazó mezőn világos huszár áll.
Végezetül azt kell megvizsgálnunk, hogy nem támadja-e a "villa" pozíciót egy sötét figura. Elég fárasztó művelet lenne, ha minden sötét figura lehetséges lépését ki kellene kalkulálnunk és ezeket - pl. itt - a villához tartozó mező értékével összevetnünk. Általában minden lépés előtt ki kell számítani és tárolni kell minden figura lehetséges támadási pozícióját, ez az értékelés része. Ezek az adatok azután ismételten felhasználhatók a lehetséges lépések egymást követő analizálása során. Mindenesetre az alapkérdésünk megválaszolásához (ha a válasz az egyes részkérdésekre pozitív, tehát végigcsináljuk az egész számítást) legalább 50 számítógép-utasítást végre kell hajtani.
Vizsgáljuk meg most ugyanezt a problémát a bittérkép módszer alkalmazása esetén. Először elővesszük a tárból a sötét király, a sötét vezér és a világos huszárok jelenlegi helyzetéhez tartozó potenciális huszárlépések bittérképeit. Ezután az összes világos figura bittérképének a negáltját (ahol nincs világos figura azon a pozíción logikai 1 érték van) egy logikai ÉS művelet segítségével összehasonlítjuk az előbb említett három bittérkép ÉS művelettel egyesített formájával. (Ez olyan tárkoordinátákat tartalmaz, ahonnan egy huszárlépéssel mindhárom figura elérhető.) Ha ezen művelet eredménye nem zérus, akkor a "villa" mező létezik. Végezetül a sötét összes figurája által támadott mezők bittérképét hozzuk logikai ÉS kapcsolatba az előző eredménnyel. Ha ennek a műveletnek az eredménye zérus, ez azt jelenti, hogy a "villa" számára alkalmas mezőt a sötét figurák nem támadják. A bittérkép módszer alkalmazásával a megoldáshoz csak öt adatbeolvasás műveletre, egy NEM és négy ÉS műveletre volt szükség, amely jelentős hatásfok-növekedést jelent a "postaláda" módszerrel szemben.
Jelenleg nagyon sok számítógépes sakkprogram használ bittérképeket olyan feladatok megoldására, mint pl. lépésgenerálás és a figurák közötti alapvető relációk rögzítése, ahogy azt a fenti egyszerű gondolatmenetben is láttuk. Természetesen a bittérkép sokkal összetettebb problémák ábrázolására is alkalmas. Ilyen formában rögzíthetjük az olyan kérdésre adott (és kiszámított) választ is, mint például melyek azok a mezők, amelyeket egy adott futó elfoglalhat például három lépésben, a jelenlegi tábla-konfiguráció korlátozásait figyelembe véve. Az ún. tanácsadó programok is kiterjedten használják a bittérképeket az alakfelismerés jellegű eljárások részeként.
8.2. A lépéskiválasztás módszerei
8.2.1. Statikus értékelés
A sakkprogram által megoldandó alapvető feladat a következő legjobb lépés kiválasztása a sok lehetőség közül. Itt a program számára - hasonlóan a sakkjátékoshoz - egyetlen lehetőség előretekinteni és megvizsgálni az adott lépésre adható válaszlépéseket, majd az erre adható viszontlépéseket stb. Ez a vizsgálat természetesen az adott állásban a lehetséges lépésvariációk nagy száma miatt teljes "szélességében", ill. a lépések folyamán a variációk felszaporodása miatt teljes "mélységében" nem végezhető el. Így a lehetséges lépések közül valamilyen algoritmus szerint választani kell majd (Id. később). Az értékelést nem a játék végéig előre kalkulálva, hanem - az emberhez hasonlóan - valamilyen közbeeső "kvázistatikus" állásnál fogjuk elvégezni.
Az alapvető értékelési szempontok a következők:
További tényezők, amelyek figyelembe vehetők:
Az alapgondolat tehát az, hogy ezeket (és még sok egyéb) az állásra vonatkozó tényezőket a "kvázistatikusnak" tekintett állásban súlyozni kell fontosságuk szerint, és ezeket összeadva meghatározni az adott állásnak az értékét. Az értékelő üggvény tehát additív.
Az állásból nem közvetlenül következő további javasolt szempontok közül néhányat bemutatunk:
A gyakorlati - számítógép utasításokkal realizált - értékelőprogram alapvető része egy sakkprogramnak. Az értékelés ugyanakkor természetesen nem lehet független a kombinációk között szelektáló algoritmustól. Ha nagyon nagy számú kombinációt vizsgálunk meg, az értékelőprogram nagyon sokszor fut (pl. minden egyes lépés kiválasztásánál 10 000... 100 000 alkalommal). Ilyenkor minden egyes tényező értékét (információ-futásidő-növekedés) kritikusan kell szemlélni a program futási idejének szempontjából és ennek alapján lehet dönteni, hogy "érdemes-e" alkalmazni őket.
Persze, ha csak kisszámú variációt veszünk számításba, komplex és lehetőleg minden "algoritmizálható" tényezőt tartalmazó értékelést használunk.
Eddigi értékelési módszereinket statikusnak hívhatjuk, mivel az értékelési algoritmus a játék folyamán nem, vagy csak kismértékben változik, így a számítógép nem úgy játszik, mint egy igazi sakkjátékos játszana. A jövő sakkprogramjai azért bizonyosan a játék különböző körülményeihez jobban alkalmazkodó, változó értékelőfüggvényeket fognak használni. Ilyen "feltételes" értékelőfüggvény pl. a következő szempontokat is figyelembe veheti:
A programozástechnika olyan jól ismert módszerei, mint a hierarchikus program-struktúra, beleértve a döntési táblázatok használatát, jól alkalmazhatók az eljárás megvalósításában.
8.2.2. A sakkjátékfa és alkalmazása
A legtriviálisabbnak látszó megoldás az lenne, ha valamennyi megengedett lépést generálnánk, majd az ellenfél lehetséges válaszainak figyelembevételével újabb ellenlépéseket hoznánk létre olyan mélységig, amely már az értékeléshez megfelelőnek látszik. Ennek az A típusú stratégiának nevezett eljárásnak az alkalmazása során jelentős nehézségek merülnek fel. A lehetséges szabályos lépések száma egy adott állásban (átlagosan kb. 38), és a szükséges mélység (6... 10 féllépés azaz 3...5 lépés) rendkívül sok végállást hoz létre. Minden állásban az átlagos 38 lehetséges lépést feltételezve
2 féllépés esetén 4 féllépés esetén 6 féllépés esetén
végállás alakulhat ki.
Az "exponenciális robbanás" - vagyis az a tény, hogy a "mélységgel" (a lépések számával) a végállások száma exponenciálisan nő - megoldhatatlan nehézséget jelent az A típusú stratégia alkalmazásánál.
Az egymást követő lépések sorozata nagyon szemléletesen ábrázolható egy fával, amit esetünkben sakkjátékfának nevezhetünk. Az eredeti állás a fa törzse, amely a lépések főágaiban, az ellenlépések nagy ágaiban, az újabb ellenlépések kis ágaiban stb. folytatódik. Minden olyan hely a fán, ahol egy nagyobb ág kisebb ágakra bomlik, csomópontot alkot. Ezen csomópontok közbenső táblaállásokat fognak jelenteni (8.3. ábra).
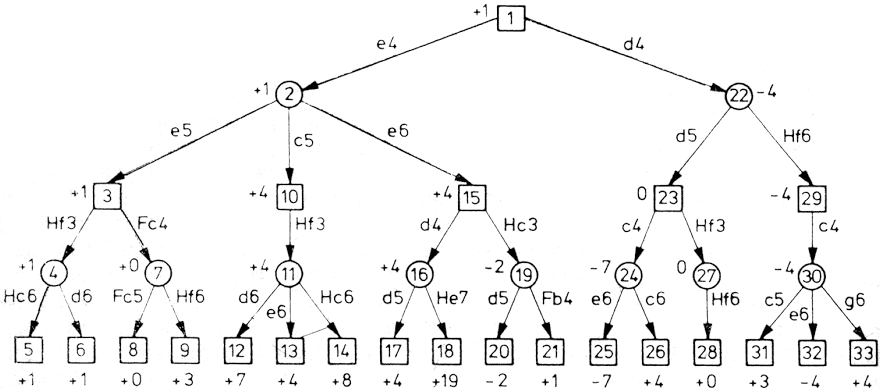
8.3. ábra: Példa a sakkjátékfára
Az "exponenciális robbanás" problémájának megoldására javasolták az ún. B típusú stratégiát. Ennek az a lényege, hogy a potenciálisan lehetséges lépéseknek csak egy kis alcsoportját vesszük figyelembe. Ha pl. 6 féllépés (3 lépéspár) mélységű analizálásnál minden csomópontban 38 helyett csak 5 folytatást veszünk számításba, a végállások száma 386 helyett "csak" 5^6= 15 625 lesz. Mivel egy adott állásban - a gyakorlat szerint - soha sincs öt értelmes lépésnél több, ez az eljárás nagyon előnyösnek látszik. "Csupán" arra van szükség, hogy minden egymást követő lépés után (azaz csomópontban) az értelmes (plauzibilis) lépéseket (faelágazásokat) kiválasszuk, és a többit figyelmen kívül hagyjuk. A számítógépprogramot képessé kell tenni arra, hogy kiválassza ezen plauzibilis lépéseket ahhoz, hogy ezt a megoldást a gyakorlatban alkalmazhassuk. Az erre a célra tervezett szubrutint plauzibilis lépésgenerátornak szokták nevezni. Ezzel rendkívül bonyolult problémával a későbbiekben még részletesebben foglalkozunk.
Fogadjuk el egyelőre, hogy lehetséges elfogadható statikus értékelőfüggvény és egy plauzibilis lépésgenerátor kidolgozása, és nézzük meg, hogy ezt a két alapvető eszközt hogyan használhatjuk fel a következő lépés kiválasztására egy adott állásban.
Szerkesszük ehhez meg a sakkjátékfát, és alkalmazzuk az értékelésnél a Neumann által javasolt - és már korábban ismertetett - klasszikus minimax eljárást. A lépést az alaphelyzetből a fán adott mélységig (lépésszámig) előre haladva választjuk ki. Minden csomópontban a számítógép azt fogja feltételezni, hogy a lépésre következő játékos mindig a számára legjobb alternatívát fogja választani. A legjobb ebben az esetben a statikus értékelőfüggvény segítségével határozható meg. Ha a lépést a világos szempontjából választjuk meg, az értékelésnél pl. a nagy számok jelentik az előnyös és a kis számok jelzik a hátrányos helyzetet. A gép a páratlan csomópontokban (azaz amikor világos lépése következik) maximumot fog keresni, míg a páros csomópontokban (amikor a sötét lép) a minimumot fogja képezni.
A sakkjátékfa analizálásakor a számítógép által követett eljárás legjobban talán egy példa segítségével mutatható be. Tekintsük az igazi kezdő állást, amikor minden figura a táblán van. Szokás szerint világos teszi az első lépést. Tételezzük fel, hogy a számítógép négy féllépésnek megfelelő mélységben analizál, és a lépéseket a plauzibilis lépésgenerátor segítségével választja ki. Ennek figyelembevételével nyerhetjük a 8.3. ábrán látható sakkjátékfát. Az ábrán a négyzetek jelentsék azokat az állásokat, amikor világos lépése következik, míg a köröknél sötét lép. Az egymást követő állásokat összekötő utak mindegyike olyan lépést jelent, amely a számítógép számára plauzibilisnek látszik. A fa csomópontjait különböző sorrendben állíthatjuk elő. Általában először a mélységnek megfelelően haladunk végig, de lehetőség van a szélesség szerinti generálásra is, amikor egy adott szinten valamennyi csomópontot megvizsgáljuk, mielőtt mélyebbre haladnánk. Ábránkon a csomópontokat az első eljárás sorrendjének megfelelően számoztuk. A legalul elhelyezkedő (vizsgálatuk szempontjából végső) állások alatti számok az állás értékelésének eredményei. Ezeket a számokat egy nagyon egyszerű értékelőfüggvény alkalmazásával nyertük.
Legyen LV és LS világos, ill. sötét számára rendelkezésre álló lehetséges lépések száma az adott állásban. Legyen SV és SS a sáncoláshoz minimálisan szükséges lépésszám világos, illetve sötét számára, és legyen CV és CS egyenlő azzal a számmal, ahány központi mezőt (d4, d5, e4, e5) világos, ill. sötét figurák támadnak. Legyen ezekután a KF értékelőfüggvényünk pl. a következő módon definiálva:
KF=(LV-LS)+3(SS-SV)+3(CV-CS)
Világos szempontjából a nagyobb szám jelenti a jobb állást.
Az értékeléshez tehát meg kell határoznunk először az egyes tényezők értékét.
Pl. ezek az 5. végpozícióban a következők:
LV5=27; LS5=29; SV5=2; SS5=3; CV5=3; CS5=3;
(Ezek a számértékek - a sakktáblán az 5. lépés után előálló állást felállítva - könnyen ellenőrizhetők.) Ezen értékekkel:
KF5=27-29+3(3-2)+3(3-3) = +1
Láthatjuk, hogy még ilyen nagyon egyszerű értékelőfüggvény esetén is elég munkaigényes számításra van szükség.
A legjobb lépés kiválasztásához a számítógép a minimax eljárást fogja erre a sakktáblafára alkalmazni. Meg fogja vizsgálni először a 4. csomópontból kiinduló ágak értékelésének eredményét, és a minimális értéket (+1) fogja "felvinni" ,azaz hozzárendelni a 4. csomóponthoz, mivel itt sötét jön lépésre. Ezután hasonló módon elvégzi ugyanezt a 7., 11., 16., 19., 24., 27. és 30. csomópontokra, kiválasztva a minimumnak megfelelő 0, +4, +4, -2, -7, +0 és -4 értékeket.
A számítógép ezután az alapcsomópont irányába haladva maximumot fog képezni a 3. csomópontnál, mivel most világos lép. Ennek megfelelően kiválasztja a kapcsolódó 4. és 7. csomóponthoz vezető ágak értékei közül a nagyobbat (+1). Hasonló módon eljárva az azonos "szinten" levő 10., 15., 23. és 29. csomópontokban, a +4, +4, +0 és -4 értékeket kapjuk. Ezután a 2. és 22. csomópontokban (amelyek ismét sötét lépései) elvégezve a minimalizálást, a kapott értékek +1 és -4. Végezetül maximumképzéssel az alapcsomópontban a 2. felé vezető utat, azaz az e4 lépést fogja a számítógépprogram kiválasztani. Bár számunkra ez az eljárás most talán nehézkesnek tűnik, azonban a számítógép számára nagyon egyszerű feladatot jelent. Csak azt kell figyelnie, hogy mikor kell minimalizálni és mikor maximalizálni, és az ennek megfelelő legkisebb, ill. legnagyobb számérték kiválasztása primitív programozási lépésekkel elvégezhető. A minimax eljárás jól implementálható eljárásnak bizonyult a következő lépés kiválasztásához.
Ha most még egyszer végiggondoljuk az eljárás folyamán követett stratégiát, könnyen beláthatjuk, hogy a vizsgálatnál a fából jelentős részek elhagyhatók, és ezzel együtt jelentős gépidőt is megtakaríthatunk. Példáinkban, ha már az ismertetett módon hozzárendeltük a +1 értéket a 4. csomóponthoz, előre is tudhatjuk, hogy a 3. csomóponthoz tartozó maximumképzésnél ez nem lehet kisebb, mint +1. így nyilvánvaló, hogy nem érdemes időt vesztegetni a 9. pozíció értékelésére, mivel az ezt megelőző 8. pont értéke csak +0 volt, ennek alapján a 7. csomópont felé vezető út érdektelen.
Hasonló módon belátható, hogy a 9., 19., 20., 21., 29., 30., 31., 32. és 33. csomópont is kihagyható a minimax-útkeresésnél. A gyakorlati esetekben, ahol egy csomópontból sokkal nagyobb számú ág indul, és a vizsgálatot is nagyobb mélységnek (pl. 5-6 féllépésnek) megfelelően végezzük, ez a "tisztítás" hatalmas keresési idő megtakarítást eredményez. Az ilyen módon módosított eljárás, amelyet alfa-béta algoritmusnak szoktak nevezni (ld. a 2.1.1. pontot), olyan esetekben is megvalósíthatóvá teszi a minimax eljárást, amikor annak alkalmazását a végrehajtási időigény irreálissá tenné. A módosított megoldás ugyanazt az eredményt adja, mint a teljes minimax eljárás.
Az alfa-béta algoritmus alkalmazásánál alfával jelöljük a világos legjobb értékét, míg bétával sötét legjobb értékét, a vizsgálatnál mindig az aktuális értéket tekintve. Az eddigiek alapján az is könnyen belátható, hogy az alfa-béta algoritmust alkalmazó minimax eljárás hatásosságát nagymértékben tovább fokozhatjuk az egymás után generált és vizsgált lépések sorrendjével. Ha ui. először világos legjobb lépését és sötét legjobb válaszát vesszük figyelembe, a nagyszámú gyengébb alternatíva elhagyható. A korszerű számítógépes sakkprogramok nagy jelentőséget tulajdonítanak a lépések olyan sorrendbe állításának, hogy minden egyes csomópontban az "erős" lépéseket vegyék először figyelembe.
A lépések sorrendjének megállapítására a programok különféle heurisztikus eljárásokat (vagyis általános érvényű gyakorlati szabályokat, más néven "ökölszabályokat") alkalmaznak. Lássunk csak ismét néhány ilyen szabályt, természetesen a teljesség igénye nélkül, pusztán illusztrációként.
Fontos szabály, hogy először az összes ütéseket kell megvizsgálni. Ütések ugyanakkor a fa méretét is csökkentik azáltal, hogy figurákat távolítanak el a tábláról.
Másik általánosan használt heurisztikus eljárás az előzőekben erősnek talált lépések tárolása és ismételt kipróbálása. Ilyen előzőleg szereplő "gyilkos" lépésekre való "visszaemlékezés" módszerét gyakran "gyilkos heurisztikának" szokták nevezni.
Maga az alfa-béta algoritmust alkalmazó minimax eljárás persze nem az egyetlen fakiértékelő módszer. A sokféle módszer közül a "heurisztikus keresés" vagy más néven "fokozatos mélyítés" módszerének alapgondolatát mutatjuk be még vázlatosan.
A vizsgálat itt csak a fa "jelentős" részeire korlátozódik. Az egymás után következő vizsgálatok mindig mélyebbek, mint az ezt megelőző analízisek. A kezdőponttól elindulva a keresés itt is a fastruktúra szerint folyik, de minden szinten a következő lépést a legjelentősebb irányba tesszük. A jelentőségértéket (ami a statikus értékelés eredménye, valamint a lépésmélység és az állás állandósultsága mértékének kombinációja - (az utóbbiról később még szólunk) rendeljük hozzá az egyes facsomópontokhoz. A szelektív vizsgálat ezen módszere közeledni próbál az emberi sakkjátékhoz, feltételezve, hogy a fa nagyon kis részében is elegendő információ van a legjobb lépés kiválasztásához.
Kiegészítő információként kiterjedten használnak helyzet-, ill. alakzatfelismerő jelzéseket, pl. figurák lekötésének, sekknek vagy olyan közismert állásoknak a jelzésére, mint a "villa".
8.2.3. Nyugalmi állapot
Ahogy a sakkjátékfa mentén előretekintünk lépésről lépésre, talán a legnehezebb feladat annak eldöntése, hogy egy csomópont alkalmas-e arra, hogy az értékeléshez szükséges végpontnak tekinthessük. A legsúlyosabb hiba a korai értékelés, vagyis amikor a számítógép azt a jelentős hibát követi el, hogy statikus értékelést végez egy olyan helyen, amely korántsem tekinthető statikusnak vagy más szóval nyugalmi állapotnak. Az emberek által játszott sakkjáték háborújában jól tudjuk, hogy igazán nyugalom soha sincs, mégis jól elhatárolhatók az egyes csaták vagy hadjáratok. Ezek határa a kvázi nyugalmi állapot, ahol megállapítható az anyagi helyzet (figurák számának értékelése) vagy ennél finomabban a helyzet a figurák pozíciója alapján. Pl. csere közben végzett elemzés világos lépése után figyelmen kívül hagyva az ezután következő sötét ellenlépést, természetesen fordított eredményt ad. Hasonló módon egy futó vagy huszár éppen úton lehet egy nagyon jó pozíciójú mező felé, az értékelésnél egy elég gyenge pozíciójú mezőn tartózkodva. Ezek a nagyon leegyszerűsített példák is illusztrálják, hogy milyen nagyon nehéz úgy programozni egy számítógépet, hogy megértse a helyzetet és eldöntse, hogy az adott pozíció aktív, vagy statikusnak tekinthető.
Sok program a helyzet hiányos megértéséből származó hibákat ismét heurisztikus eljárásokkal próbálja kompenzálni. Így pl. az ütési sorozatokat addig folytatja, ameddig azok tényleg befejezettnek tekinthetők, tehát újabb ütés nem következik. Sajnos ez nem segít a pozícióelőny olyan egyszerű eseteinél sem, mint egy figura lekötése, amely persze később anyagi előnyt is hozhat.
A sakkadás, mint cél is jelentős hibaforrás lehet. Sok olyan helyzet van ugyanis, ahol sorozatosan adható sakk minden további eredmény nélkül. Sajnos a számítógép abban is gyenge, hogy különbséget tegyen egy támadó és egy céltalan sakkadás között. A legtöbb program ezt a problémát úgy "oldja meg", hogy korlátozza a sorozatban sakkot adó lépések számát, ha azok nem vezetnek anyagi nyereségre vagy mattra.
A nyugalmi állapot elérésének bizonytalanságát a sakkprogramok a mélység növelésével is kompenzálják. Ez a nyers erő módszer a számítógépek sebességének növekedésével automatikusan is adódik. A legtöbb sakkal kapcsolatos fogalom ui. világosan mélységfüggő. Ezek megértésére a program a vizsgálatba bevont lépésszám növelésével egyre inkább alkalmassá válik. Pl. állandó két féllépés mélységű vizsgálat esetén, amelyet sakk- és ütésvizsgálattal egészítünk ki, a számítógép el fog nézni egy egyszerű villamanővert. Megnövelve a mélységet négy féllépésre, a program megérti a "villát" és olyan lépéseket fog választani, hogy ezt az egyszerű csapdát elkerülje.
Az állandó mélységű vizsgálatnál persze sokkal célravezetőbb a nyugalmi állapot elérésének megállapítása. Erre vonatkozóan a heurisztikus keresés módszerének leírásánál már bemutattunk egy megoldási módozatot.
8.2.4. Plauzibilislépés-generátorok
Amint azt a stratégiák bemutatásánál már láttuk, a nyers erőn alapuló, minden lehetséges kombinációt figyelembe vevő A típusú stratégia nem biztosítja - a rendkívül nagyszámú megvizsgálandó kombináció miatt -, hogy a program elegendő mélységig előrenézhessen. Ilyen program alapján a számítógép csak nagyon gyenge sakkjátékra képes. Marad tehát a B típusú stratégia szerinti játék, de ennek - mint szintén láttuk- az a feltétele, hogy a csomópontokba helyes stratégiával válasszunk ki néhány jó lépést és csak ezeket analizáljuk. Így a megvizsgálandó lépésszám rendkívüli módon csökken és ezzel a vizsgálati mélység a szükségesnek megfelelően növelhető. Pl. csupán három kombinációt (vagyis faelágazási irányt) vizsgálva csomópontonként, 12 féllépés mélység esetén 531 441 végpozíciónk lesz. (Ezzel szemben 30 kombináció és már négy féllépés esetén ez a szám 810 000). Gyakorlati esetekben a szélesség az egyre mélyebb rétegekben csökken. (Pl. 15, 15, 9, 9 és 7 változat lehetséges az első, második, harmadik, negyedik és ötödik féllépés után.)
A lehetséges lépések közül a legjobbnak vagy a szokásos terminológiával, a plauzibilisnek a kiválasztása a plauzibilislépés-generátorprogramjának a feladata. A számítógép az emberi sakkjátékból ismét heurisztikus módszerek segítségével próbál minél több tapasztalatot átvenni. Egy gyakorlati program pl. körülbelül 50 ilyen eljárást használ. Ismét csak példaként néhányat ezek közül bemutatunk, amelyek a lépés kiválasztásában szerepet játszanak:
Egy igazán intelligens plauzibilislépés-generátort nagyon nehéz készíteni. Ezt megint csak legjobban néhány példán keresztül tudjuk illusztrálni. Az alapvető probléma ezekben a valóságos sakkmérkőzésekből vett példákban, hogy a győzelemhez sokszor elengedhetetlen - pozíciónyerésért hozott - jelentős anyagi áldozatot a számítógép nem képes plauzibilisnek tekinteni.
Nézzük a 8.4. ábra szerinti állást (a játék Kirdetzoff és Kahn között 1918-ban Koppenhágában folyt).

8.4. ábra: Állás a 16. lépés után (Világos: Kirdetzoff, sötét Kahn)
Sötét lép, és számos plauzibilis lépés látszik jónak számára. A futó felfejlődése hasznosnak tűnik, mivel így a bástyák megduplázhatok. A d-vonali gyalog védtelen, így egy azt védő lépés is plauzibilisnek látszik. A világos b-gyalog is leüthető, egyúttal nyomást gyakorolva az a1 mezőn álló bástyára is. Valamennyi felsorolt lépés ésszerűnek látszik, azonban sötét győzelmet jelentő lépése Vf3: volt! A játék a következőképpen folytatódott: 17. gV:, Fh3+ 18. Kg1, Be6 19. Vc7, Bae8 20. Bf1, Be1 és világos feladta. A Vc7 lépés világos számára feltétlen szükséges volt, hogy megelőzze a Bg6++ lépést. A példa jól demonstrálja, hogy a pozícióelőny sokszor értékesebb az anyagi fölénynél.
A második példa az 1974. évi magyar bajnokságon Adorján és Tompa közötti mérkőzés, amely sötét 24. lépése (Hh5) után a 8.5. ábra szerint állt.

8.5. ábra: Állás sötét 24. lépése után. (Világos: Adorján, sötét: Tompa; Magyar Bajnokság, 1974)
Ebben az aktív állásban több, látszólag támadó lépés látszik jónak világos számára. A játék azonban a következőképpen folytatódott: 25. Vh5:, gh: 26. Bg3+, Fg7 27. Hf5, Vf8 28. Hg7:, de: 29. He6+, Kh8 30. Fe5:+, f6 31. Bf6: sötét feladta. Ismét egy olyan vezér áldozatot láthattunk, amely olyan pozícióelőnyt eredményezett, hogy megérte a nagy anyagi áldozatot. Az anyagi áldozatot követő lépések mindkét példában győzelemre vezettek, de nem olyan sakkadási vagy ütési sorozaton keresztül, amely a fa mély, de keskeny szeletének analizálásával nyilvánvaló lehetett volna.
A legtöbb sakkprogram kénytelen a plauzibilislépés-generátor jellemzői között nagy súlyt helyezni az anyagi tényezőkre egyszerűen azért, mert e nélkül nem képes elfogadható módon játszani. Ha a pozíció súlya egyenértékű lenne az anyagi erővel, az azzal járna, hogy a program rendszeresen "elszórná" anyagi erejét nem kellően megalapozott áldozatokkal. Ez pedig az esetek többségében a játék elvesztését jelentené, így egy elfogadható plauzibilitás-függvény automatikusan kizárja azokat az áldozatokat, amelyek sok esetben a sakkjáték izgalmát adják.
Az anyagi áldozaton túlmenően vannak olyan kiváló lépések, amelyet a "született tehetség" rögtön észrevesz, de az állás statikus analizálása alapján a plauzibilislépés-generátor biztosan "kihagy". A 8.6. ábra állásánál sötétnek egy gyalog előnye van és a
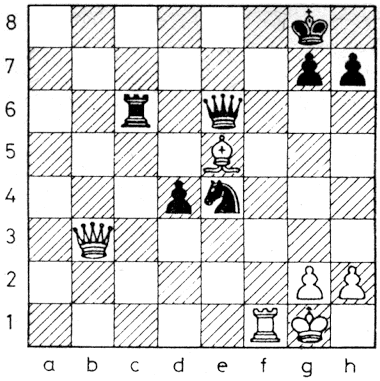
8.6. ábra: Világos legjobb lépése csak hosszú analizálás után található meg
világos vezér jelenleg védtelen. Világos lépése következik. Gyalogot nyerhet a (1.) Ve6:+ , Be6: (2.) Fd4: lépésekkel, vagy egyszerűen tarthatja pozícióját a vezérrel megvédve az ugyancsak védtelen futóját a Vb5 vagy Vb8+ lépéssel. Bármelyik e lépések közül nagyon plauzibilis lenne a számítógép számára, mivel így anyagi előnyhöz jutna, ill. megvédené figuráit. A helyes lépés azonban Fd6 mind a vezért, mind a futót védtelen helyzetben hagyja. Ha sötét válasza Vb3:, akkor Bf8+ és matt. Ha sötét válasza Bd6:, akkor Vb8+ és ismét matt. Ha sötét a futót a huszárral üti le, akkor Ve6:+ és nyer. Csak nagyon bonyolult dinamikus analízis alapján lehet kimutatni, hogy a Fd6 lépés helyes, amire egy statikus alapon működő plauzibilislépés-generátor képtelen.
A legígéretesebb folytatások tehát gyakran nem következnek az állás felületes analizálásából. Ez a probléma az ismertetett stratégiák közvetlen következménye. Ennek kiküszöbölésére új eljárásokkal kísérleteznek, amelyekre azonban itt már - bonyolultságuk miatt - nem térünk ki.
8.2.5. A horizont hatás
A plauzibilislépés-generátor kialakításának nehézségei miatt számos sakkprogram kénytelen a teljes szélességben való keresés módszeréhez visszatérni. Ez azonban nem tesz lehetővé hosszú távú tervezést és a vizsgált lépésszámon (a horizonton) kívül eső lehetőségek automatikus figyelmen kívül hagyását jelenti. Ezt a problémát horizont hatásnak szokták nevezni.
Lássunk egy gyakorlati esetet ismét, hogy erről a problémáról is elképzelésünk legyen. A 8.7. ábra szerinti állásnál a számítógép a világos.
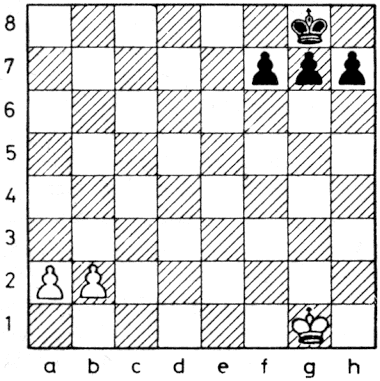
8.7. ábra: Világos lép és nyer
Az állás statikus analizálása alapján sötétnek gyalog előnye van, így egy döntetlen ajánlatot a program sötét feltételezett előnye alapján azonnal elfogadna. A világos nyerő helyzetét egy kezdő sakkozó is rögtön látja, mivel sötét nem tudja megakadályozni az a gyalog bevitelét. Egy versenyekről is ismert program az alfa-béta algoritmust alkalmazó eljárással analizálta ezt az állást a minden változatot figyelembe vevő teljes szélességgel. Maga az állás nagyon egyszerű, de a végcél a szokásos mélységnek megfelelő horizonton kívül esik.
A sakkprogram a CDC 6400 gépen futott, így a futási idők erre a számítógépre vonatkoznak, amelynek sebessége kb. 1 millió művelet/s. Három féllépés mélységű vizsgálatnál a gép 148 csomópontot vizsgált végig 0,3 másodperc alatt és a következő folytatást választotta:
Az állást sötét számára ítélte kedvezőnek -107 értékkel (a mínusz előjel jelzi sötét előnyét, egy gyalog értéke pedig 100). Nyilvánvaló, hogy a számítógép félreértette az állást, mivel a helyes lépés a4 és világos egyértelműen nyerő pozícióban van. Növeljük a vizsgálat mélységét. Öt féllépés esetén a gép 900 csomópontot vizsgált meg 2,1 másodperc alatt és a következő változatot választotta:
A számítógép még mindig vak és most az állást -115-nek értékeli.
Hét féllépésnek megfelelő vizsgálat 8,6 másodpercig tartott (4523 csomópont figyelembevételével) és eredménye a következő volt:
Az értékelőfüggvény aktuális értéke most -116. Kilenc féllépés esetén a program végre megtalálta a helyes folytatást, mivel itt már öt világos lépést vett figyelembe, ami elég ahhoz, hogy a gyalog elérje a nyolcadik sort. 48273 csomópont 96,5 másodpercig tartó vizsgálata után a következő változatot választotta a gép:
A számítógép még most sem érti egészen a helyzetet, mivel a sötét áldozattal a világos gyalog továbbhaladását a horizontot túlra tolja. Tulajdonképpen a helyes folytatást itt is egy másik cél, a gyalogos nyerés hozta létre. Csak 11 féllépés mélység esetén párosul ez a helyes lépésválasztás a valódi céllal.
A horizont hatás tehát értelmetlen anyagi áldozatokra és pozícióvesztésre vezethet. Ez is egyértelműen mutatja, hogy javítani kell a program tulajdonságait, hogy minél jobban különbséget tudjon tenni aktív és nem aktív csomópontok között.
8.3. A megnyitás és a végjáték
Van két olyan szakasza a sakkjátéknak, ahol az eddig ismertetett lépéskiválasztási eljárások nem, vagy csak nagyon rossz eredménnyel alkalmazhatóak. Ez a két szakasz a megnyitás és a végjáték. A megfelelő játékstratégia kiválasztása és megvalósítása - különösen a végjátékra - a számítógépes sakkprogramok legnehezebb feladata.
További problémát okoz, hogy bár az emberi sakkjáték három elég jól elkülönülő részre bontható - megnyitásra, középjátékra és végjátékra - ezek határvonalának a definiálása (amikor tehát stratégiát kell váltani) nagyon nehéz és határok számítógépes programmal való meghatározása szinte megoldhatatlan feladat. A megfelelő színvonalú játék biztosításához ezenkívül arra is szükség lenne, hogy az átmenet az egyik szakaszhoz választott stratégiából a másikra sima legyen, tehát a program képes legyen a határvonalon az ehhez szükséges információt átadni és átvenni.
8.3.1. A megnyitás
A sakkjáték megnyitása az egyes figurák felfejlődését biztosítja olyan mezőkre, ahol azok hatásosan fognak tudni harcba szállni sokszor 20 vagy 30 féllépéssel később. Mivel ezek a lépések bizonyosan messze a gép horizontján kívül esnek, a megnyitás szakaszában a figurák felfejlődését tisztán heurisztikus alapon kell véghezvinni (pl. a középső mezők ellenőrzése, huszárok pozíciója, sáncolás előkészítése stb.). Mivel ezek az ökölszabályok nem biztosítanak megfelelő színvonalú megoldást, a legtöbb sakkprogram készítő elhatározta, hogy a szokásos - a sakkjátékosok által is használt - stratégiát fogja használni, vagyis nagyszámú szabványos megnyitást memorizál, és a megnyitásnál ezek lépéseit követi.
Maga a számítógép valóban könnyen programozható könyv szerinti megnyitások alapján való játékra. Tulajdonképpen csak az elkészítéséhez szükséges munka korlátozza az ún. megnyitáskönyvtár nagyságát. A szokásos versenyeken is szereplő programok manapság 3 000 és 10 000 lépés közötti nagyságú könyvtárral rendelkeznek, de a jövőben elérik a 100 000-es nagyságrendet is. A gépek sebessége növelésének eredményeként a program gyorsan hozzá tud férni a könyvtárban tárolt lépésekhez, így a számítógép a megnyitást rendkívül gyorsan képes játszani. (Ez nagyon hasznos a versenyjátszmáknál, ahol a játék ideje korlátozott és a megnyitás alatti időmegtakarítás jól hasznosítható a középjáték időigényes kalkulációinál.)
Sajnos azonban a számítógépes sakk esetén ez a megoldás sem tökéletes. Ismerjük a tudományos életből az ún. McMurphy "törvényt", amely szerint, ha valami elromolhat, az el is fog romlani, mégpedig olyan módon, hogy a legtöbb kárt okozza. Sajnos ez az alapelv a tárolt megnyitáskönyvtár alapján játszó számítógépprogram esetén is hatni fog. Előbb vagy utóbb - függetlenül a könyvtár nagyságától - az előkészített lépések tára ki fog merülni, és a számítógépnek saját magának kell "gondolkoznia", vagyis kalkulálnia. A probléma abból származik, hogy a könyvtárból való kilépéskor nem a számítógép által létrehozott állásból kell folytatni a játékot, és nem segíthetnek a nagymesterek ötletei és tervei, amelyek az egyes megnyitó lépések választását irányították, mert ezek már nem állnak a számítógép rendelkezésére. Így nem marad más lehetőség, mint hogy a számítógép a saját statikus értékelése alapján meghatározza, hogy az egyes figurák megfelelő pozícióban vannak-e. Természetesen a számítógép azt fogja találni, hogy nem, mivel az értékelőfüggvény nem olyan okos, mint a nagymester. Ennek az lesz a következménye, hogy a könyvtárból való kilépés után az első néhány lépést a gép arra fogja vesztegetni, hogy az állást az értékelőfüggvényével összhangban átrendezze. Érdekes, hogy a sakkozóprogram e hibája nagyon hasonlít azon kezdő sakkjátékos játékára, aki betanult néhány megnyitást anélkül, hogy megértette volna azok lényegét.
Ezen a nehézségen két módon lehet segíteni. Az egyik mód olyan könyvtárak szervezése, amelyek a lépések sorozatán túlmenő bizonyos információt is tárolnak. Ezek az információk a kilépéskor az értékelőfüggvényt képesek úgy módosítani, hogy a stratégiának megfelelően bizonyos figurák adott mezőkre való lépését erősítse. Ez lehetővé teszi a megnyitás végének a középjátékba való sima átvitelét.
Másik út olyan megnyitás választása, amely összhangban van a program játékstílusával. Pl. ha a számítógép értékelőfüggvénye az anyagi tényezőket a pozíciójellemzők elé helyezi, helyes olyan könyvtári lépéseket választani, amelyek gyorsan aktív pozícióhoz vezetnek. Vagy ha pl. az értékelő függvény a gyalogelrendezés figyelembevételére különösen alkalmas, olyan megnyitást kell választani, amely kettős vagy magányos gyalogokat is megenged. A számítógép stílusához a legjobban alkalmazkodó megnyitások kiválasztása persze nagyon nehéz feladat.
8.3.2. A végjáték
A végjáték egyértelműen a gépi sakk legbonyolultabb problémája és ennek következtében mind a mai napig leggyengébb pontja. A gyakorlati sakkjátszmáknál jól ismert, hogy a győzelmi terv sokszor 20, vagy még több lépés megfelelő véghezvitelét jelenti. Ilyen mélységben az összes kombinációt figyelembe vevő teljes szélességnek megfelelő keresés teljesen lehetetlen, így a végjátékban fel kell adni az alfa-béta algoritmust alkalmazó minimax eljárást és valamilyen más stratégiát kell választani.
Egyik ígéretes módszer a heurisztikus sáv szerinti vizsgálat, vagyis a fa csupán olyan részének a figyelembevétele, amely valamilyen adott célhoz, pl. gyalogbevitelhez tartozik. Ennél a stratégiánál persze arra is szükség van, hogy a gép képes legyen felismerni, hogy a végjáték már megkezdődött, valamint a megfelelő célt kitűzni. A helyzetfelismerés, amely ezen két döntéshez szükséges, szintén nem egyszerű feladat, de az alakfelismerés korszerű módszereivel megoldható.
Egy másik stratégia alapja a tipikus végjáték-kategóriák analizálása. Ennek alapján lehetőség van ezekhez alkalmazkodó programok létrehozására, amelyek ezen tipikus végjátékokat algoritmikus módszerekkel képesek megoldani. Pl. külön eljárás van király és bástya vagy király és gyalog végjátékokra, ez a módszer tehát nem általános megoldást, csak részmegoldást ad a végjáték problémájára.
A feladat bonyolultságának bemutatására lássunk most is egy példát! Legyen csupán egyetlen gyalog (és természetesen a két király) a táblán, és ebben az esetben használjunk egy speciális szubrutint (ONEPAWN) az állás vizsgálatára, értékelésére és a helyes folytatás meghatározására. A program először meghatározza a gyalog helyzetét, az ellenfél királyának pozícióját, és megvizsgálja, hogy a potenciálisan nyerésre álló fél királya valóban olyan mezőn áll-e, amely nyerést tesz lehetővé. Pl. ha a világos c4-en áll és a sötét király f7 mezőn, ha világos következik lépésre, akkor fog nyerni, ha királya az "X"-szel jelölt mezők valamelyikén van (8.8. ábra). Egyébként a játszma döntetlenül végződik.
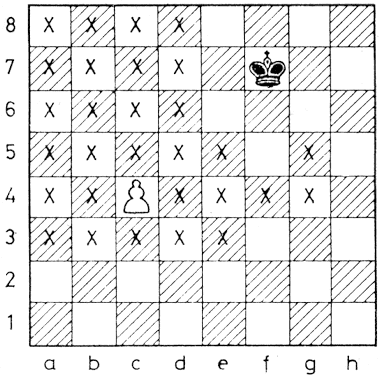
8.8. ábra: A világos gyalog bevihető, ha a világos lép, és királya valamelyik X-szel jelölt mezőben van
Egy rövid tesztsorozat segítségével megállapítható, hogy a világos király egy megjelölt mezőn tartózkodik-e. Nyilvánvaló, hogy eltérő "maszk"-ot kell használni, ha a világos gyalog az a4-en, a sötét király pedig d7-en van. A ONEPAWN szubrutin kb. 300 különböző maszk segítségével képes az összes lehetséges elrendezést megvizsgálni.
Több gyalogot (de csak gyalogot) tartalmazó állás értékelésére képes PEASANT program tulajdonságait (erejét és gyengeségét) ismét néhány példával illusztráljuk. A 8.9. ábra egyszerű állása esetén a program öt féllépésnek megfelelő vizsgálattal megtalálta a helyes folytatást (d5).
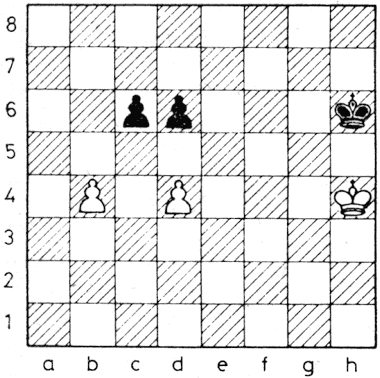
8.9. ábra: Világos indul és nyer
A 8.10. ábra szerinti állásnál a program négy és öt féllépés mélység esetén h3-t, hét és nyolc féllépés esetén Kh5-t választotta, és csak kilenc féllépés után találta meg a helyes Kg5 folytatást.
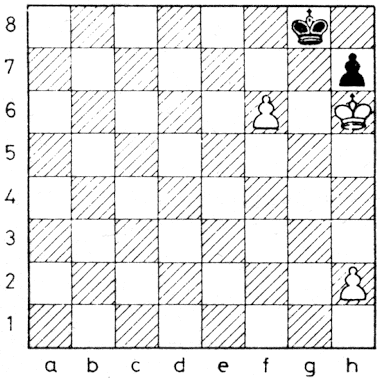
8.10 ábra: Világos indul és nyer