Szabványos PASCAL
Programozás és algoritmusok
Dr. Pongor György, 1989
Tartalom
Bevezető 2. Algoritmusok egész, valós logikai és karakteres adatokkal 3. További adattípusok, típusdefiníció |
5. Mutató típus, dinamikus változó 6. További adattípusok 7. További szabályok |
4. Szegmensek: Eljárások, Függvények
Ez a fejezet a nagyobb programok megírásához szükséges eszközökkel, az eljárásokkal és a függvényekkel foglalkozik. Részletesen tárgyal egy érdekes lehetőséget: a rekurziót, amely megfelelő használat esetén nagyon megkönnyíti az algoritmusok megfogalmazását.
Az eljárások és függvények olyan nyelvi eszközök, amelyek segítségével egy-egy utasításcsoport a program többi részétől elkülöníthető, névvel látható el, és a program további részében e névvel lehet rá hivatkozni. Ezt a hivatkozást az eljárás, illetve függvény hívásának nevezzük. A hívás az eljárás, illetve függvény utasításainak végrehajtását jelenti minden olyan helyen, ahol a nevét a programba írjuk. Így lehetőségünk van arra, hogy ismétlődő programrészeket csak egyszer kelljen megadni: ezeket a programrészeket egy-egy eljárásba tesszük, mindazon helyeken, ahol a programrész végrehajtására szükség van, csak az eljárás nevét kell leírni.
Az eljárásokat és függvényeket közös néven szegmenseknek nevezzük.
Szegmensek használata nemcsak azért előnyös, mert jelentősen megrövidíthetik programunkat, hanem azért is, mert összetett programok részekre bontásával, azaz szegmentálásával a program áttekinthetőbbé, jobban követhetővé tehető, így kisebb a valószínűsége, hogy hibát követünk el benne. Ez a szempont legalább olyan fontos, mint az előző.
4.1.1. Példa:
Készítsünk programot nyolcas számrendszerbeli, azaz oktális egész számok öt alapműveletének elvégzésére! A bemeneti adatok alakja:
operandus1 művelet operandus2
ahol a művelet + - * / és % lehet, az utóbbi kettő jelölje most az egész osztást és a maradékképzést!
Az operandusok előjel nélküliek és a nyolcas számrendszer értelmében csak a '0' ...'7 ' tartományba eső számjegyeket tartalmazhatják.
Megoldás:
A feladat megoldását először szegmensek nélkül, majd eljárásokkal mutatjuk be.
Mivel a Pascal nyelvben nincs oktális számrendszerbeli beolvasás - a számokat csak tízes számrendszerben tudjuk közvetlenül beolvasni -, a bemeneti adatokat karakterenként fogjuk feldolgozni. Egész számok karakterenkénti beolvasására, sőt 16-os számrendszerbeli beolvasásra is láttunk már példát a 2.11 alfejezetben, ezért ennek a változatnak megértése nem okozhat gondot:
program oktalis_kalkulator (input,output);
var op1,op2,eredmeny,hely: integer;
ch,muveletijel,elojel: char;
e: packed array[1..6] of char; { eredmeny karakteresen }
begin
repeat {szamitasok ciklusa}
read(ch); {elso karakter beolvasasa}
while ch=' ' do read(ch); { szokozok kiszurese }
op1:=0; {elso operandus beolvasasa}
repeat
op1:=8*op1+ord(ch)-ord('0');
read(ch);
until (ch<'0') or (ch>'7');
while ch=' ' do read(ch); { szokozok kiszurese }
muveletijel:=ch; { muveleti jel elrakasa }
read(ch);
while ch=' ' do read(ch); { szokozok kiszurese }
op2:=0; { masodik operandus beolvasasa }
repeat
op2:=8*op2+ord(ch)-ord('0');
read(ch);
until (ch<'0') or (ch>'7');
case muveletijel of { muvelet elvegzese }
'+': eredmeny:=op1+op2;
'-': eredmeny:=op1-op2;
'*': eredmeny:=op1*op2;
'/': eredmeny:=op1 div op2;
'%': eredmeny:=op1 mod op2
end;
e:=' '; { eredmeny karakterekke alakitasa }
if eredmeny<0 then elojel:=' '
else elojel:=' ';
eredmeny:=abs(eredmeny);
hely:=6; { eredmeny utolso karakterenek indexe }
repeat
e[hely]:=chr(eredmeny mod 8+ord('0'));
hely:=hely+1;
eredmeny:=eredmeny div 8;
until eredmeny=0;
e[hely]:=elojel;
writeln(' = ',e); { eredmeny kiirasa }
readln;
until eof { nincs tobb adat }
end.
Most írjuk meg ugyanezt a programot eljárások felhasználásával!
A program megírásakor azt a gondolatmenetet követjük, amit egy ilyen program megalkotásakor a programozó általában szokott: először azt tervezzük meg, hogy melyek lesznek a program legfontosabb részei, majd ezeket a nagyobb részeket bontjuk le egyre kisebb műveletekre egészen addig, amíg végül a Pascal nyelv utasításaihoz nem jutunk. Ezt a nagyobb egységtől a kisebbek felé, felülről lefelé (top-down) haladó programtervezési módszert követtük általában eddig is, de most a szegmensek használatával közvetlen nyelvi segítséget is kapunk hozzá.
A program általános szerkezete:
repeat { számítások ciklusa }
beolvasas; { adatok beolvasása }
szamitas; { eredmény kiszámítása }
kiiras; { eredmény kiírása }
until eof; { nincs több adat }
A Pascal nyelvben természetesen nincs olyan utasítás, hogy beolvasas vagy kiiras, de a beolvasást, illetve a kiírást végző műveleteket összefoghatjuk egy-egy eljárássá, és ezeknek az eljárásoknak adhatjuk például a fenti neveket.
A beolvasas eljárást például így is megadhatjuk, azaz deklarálhatjuk:
procedure beolvasas;
begin
kovkar; { elso karakter beolvasasa }
szokozszures; { szokozok atolvasasa }
operandusolv(op1); { elso operandus beolvasasa }
szokozszures; { szokozok atolvasasa }
muveletolv; { muveleti jel beolvasasa }
szokozszures; { szokozok atolvasasa }
operandusolv(op2); { masodik operandus beolvasasa }
end;
A procedure szó is kulcsszó, és azt jelenti, hogy egy eljárás deklarációja következik. Ez után áll az eljárás neve, vagyis az eljárásra ilyen néven lehet majd hivatkozni.
Ez a deklaráció is pontosan követi a program tervezésekor alkalmazott, felülről lefelé haladó gondolatmenetünket, de ismét tartalmaz olyan utasításokat, amelyek nem elemei a Pascal nyelvnek. Ezért további lebontásra, további eljárások deklarálására van szükség:
{ kovetkező karakter beolvasasa }
procedure kovkar;
begin
read(ch);
end;
Ez az eljárás már nem szorul további lebontásra, finomításra, hiszen olyan utasítást tartalmaz, amely eleme a Pascal nyelvnek. Talán furcsa, hogy olyan eljárást deklaráltunk, amely mindössze egyetlen utasítást tartalmaz, de bizonyos esetekben ez is indokolt lehet, mint erre a teljes program megismerése után majd visszatérünk.
{ szokozok atolvasasa }
procedure szokozszures;
begin
while ch=' ' do kovkar;
end;
Ez az eljárás sem szorul további magyarázatra.
{ operandus beolvasasa }
procedure operandusolv(var op: integer);
begin
op:=0;
repeat
op:=8*op +ord(ch)-ord('0');
kovkar;
until (ch<'0') or (ch>'7');
end;
Itt egy operandus, azaz egy nyolcas számrendszerbeli szám értékét kellett beolvasni, méghozzá úgy, hogy ezt a programrészletet az első és a második operandus beolvasására is fel lehessen használni. Amikor ezt az eljárást a beolvasas eljárásban használjuk, az operandusolv név után zárójelben megadjuk azt is, hogy az adott esetben melyik változóba történjen meg a szám beolvasása - hasonlóan ahhoz, ahogyan egy Pascal-beli read utasításban zárójelek között megadjuk, hová történjen a beolvasás. Az eljárást tehát úgy kell megírnunk, hogy felhasználásakor meg lehessen adni, az adott esetben hová tegye az eredményt, az eljárás hívásakor pedig az ennek megfelelő konkrét változót kell megadni. Ezt a megfeleltetést paraméterezésnek, más szóval paraméterátadásnak nevezzük.
Az eljárás deklarációjában, a neve után, zárójelek között adjuk meg, hogy az eljárásnak hány és milyen típusú paramétere van, és azt is, hogy az eljáráson belül hogyan nevezzük ezeket a paramétereket. Az eljárások fejrészében megadott paramétereket formális paramétereknek nevezzük, mert az eljárás a műveleteket látszólag ezekkel végzi. Az eljárás használatakor megadott paramétereket aktuális paramétereknek nevezzük, hiszen az eljárás adott használatakor ténylegesen ezek értékét használja, illetve változtatja meg. Az eljárás aktivizálásakor természetesen pontosan annyi és olyan típusú paramétert kell megadni, ahány és amilyen típusú formális paramétere az adott eljárásnak van.
Mindez ugyanígy igaz a függvényekre is. A szegmenseknek - tehát az eljárásoknak és függvényeknek - tetszőleges számú paraméterük lehet, ezek pedig tetszőleges típusúak, sőt még eljárások és függvények is lehetnek.
Visszatérve mintaprogramunkhoz, a beolvasas eljáráshoz, már csak a muveletolv eljárás deklarálása van hátra:
procedure muveletolv;
{ muveleti jel beolvasasa }
begin
muveletijel:=ch; { muveleti jel elrakasa }
kovkar;
end;
A még nem deklarált eljárások:
procedure szamitas;
{ eredmeny kiszamitasa }
begin
case muveletijel of { muvelet elvegzese }
'+': eredmeny:=op1+op2;
'-': eredmeny:=op1-op2;
'*': eredmeny:=op1*op2;
'/': eredmeny:=op1 div op2;
'%': eredmeny:=op1 mod op2
end;
end;
procedure kiiras;
{ eredmeny kiirasa }
procedure szamiras(n: integer);
begin
if n>7 then szamiras(n div 8);
write(n mod 8 :1); { utolso szamjegyek }
end;
begin { kiiras }
write (' = ');
if eredmeny<0 then write('-'); { negativ elojel }
szamiras(abs(eredmeny));
writeln; readln;
end;
A kiiras eljárást egyszerűbben is meg lehetett volna oldani, de ezzel a változattal az volt a célunk, hogy felvillantsuk az eljárások használatának néhány további lehetőségét, nevezetesen az eljáráson belül deklarált eljárást és a rekurziót. A rekurzióról most csak annyit bocsátunk előre, hogy egy szegmensben használjuk magát a szegmenst, ahogyan például a szamiras eljárásban használtuk saját magát. Ennek megértéséhez részletesebben kell ismernünk a szegmensek működését.
Miután deklaráltuk minden részletét, össze lehet állítani a teljes programot. Az eljárások azonosítóit a többi azonosítóhoz hasonlóan csak deklarációjukat követően használhatjuk, ezért meg kell állapítanunk, melyik eljárás melyiket használja, hogy azt deklaráljuk elsőként, amelyik nem hivatkozik egy másikra, majd azokat, amelyek csak erre hivatkoznak stb.
A számítás nem hivatkozik más eljárásra, a kiiras eljárás pedig csak a saját, belső eljárását, szamiras-t használja, amely csak önmagát hívja.
Több sorrend is megengedett, egy lehetséges megoldás szerint a teljes program:
program oktalis_kalkulator_2 (input,output);
var op1,op2,eredmeny: integer;
ch,muveletijel: char;procedure kovkar;
{ kovetkezo karakter beolvasasa }
begin
read(ch);
end;procedure szokozszures;
{ szokozok atolvasasa }
begin
while ch=' ' do kovkar;
end;procedure operandusolv(var op: integer);
{ operandus beolvasasa }
begin
op:=0;
repeat
op:=8*op +ord(ch)-ord('0');
kovkar;
until (ch<'0') or (ch>'7');
end;procedure muveletolv;
{ muveleti jel beolvasasa }
begin
muveletijel:=ch; { muveleti jel elrakasa }
kovkar;
end;procedure beolvasas;
{ adatok beolvasasa }
begin
kovkar; { elso karakter beolvasasa }
szokozszures; { szokozok atolvasasa }
operandusolv(op1); { elso operandus beolvasasa }
szokozszures; { szokozok atolvasasa }
muveletolv; { muveleti jel beolvasasa }
szokozszures; { szokozok atolvasasa }
operandusolv(op2); { masodik operandus beolvasasa }
end;procedure szamitas;
{ eredmeny kiszamitasa }
begin
case muveletijel of { muvelet elvegzese }
'+': eredmeny:=op1+op2;
'-': eredmeny:=op1-op2;
'*': eredmeny:=op1*op2;
'/': eredmeny:=op1 div op2;
'%': eredmeny:=op1 mod op2
end;
end;procedure kiiras;
{ eredmeny kiirasa }
procedure szamiras(n: integer);
begin
if n>7 then szamiras(n div 8);
write(n mod 8 :1); { utolso szamjegyek }
end;
begin { kiiras }
write (' = ');
if eredmeny<0 then write('-'); { negativ elojel }
szamiras(abs(eredmeny));
writeln; readln;
end;begin { foprogram }
repeat; { szamitasok ciklusa }
beolvasas; { adatok beolvasasa }
szamitas; { eredmeny kiszamitasa }
kiiras; { eredmeny kiirasa }
until eof; { nincs tobb adat }
end.
Az eljárásokat tehát - és a függvényeket is - a változók után, a program utasításrésze előtt kell deklarálni.
Most nézzük meg azt, hogy hogyan történik az eljárások aktivizálása! A teljes program végrehajtása továbbra is a program utasításrészének végrehajtását jelenti. Ha ebben hivatkozunk valamelyik eljárásra, az azt jelenti, hogy amikor a program végrehajtása az eljáráshivatkozáshoz ér, áttér az eljárás utasításrészének végrehajtására, de előzőleg megjegyzi, hogy honnan lépett át oda.
Az eljárás ilyen aktivizálását eljáráshívásnak nevezzük, az eljárást aktivizáló utasítást pedig - ami az eljárás nevének és, ha vannak, akkor aktuális paramétereinek megadásából áll - eljárásutasításnak nevezzük Az eljárásutasítás tehát önálló utasítás és végrehajtása az eljárás hívását jelenti.
Az eljárás végrehajtása során, mint láttuk, az eljárás utasításrészét hajtja végre a gép, majd ennek befejeztével visszatér az eljáráshívást közvetlenül követő utasításhoz. Ezt az teszi lehetővé, hogy híváskora gép megjegyezte, honnan lépett át az eljárásba.
A programban például a szamitas utasítás végrehajtása ennek az eljárásnak az utasításrészében a case utasítás végrehajtását jelenti.
Ha az eljárás további eljárást is hív, akkor annak aktivizálása ugyanilyen módon történik, de a gép egy másik, új helyen jegyzi meg, hol kell az újabb hívás után a hívó eljárást folytatni, azaz a visszatérési címek nem keverednek össze. Egy újabb hívás egy újabb helyre teszi el a visszatérési címet, egy visszatérés során pedig mindig az utoljára eltett visszatérési címen folytatódik annak a programrésznek a végrehajtása, ahonnan a hívás történt.
A beolvasas eljárás például hívja a szokozszures eljárást, az pedig hívja a kovkar eljárást. kovkar ilyen aktivizálásakor a gép azt tartja számon, hogy hol kell folytatni a kovkar-ból, a szokozszures-ből és a beolvasas-ból történő visszatéréskor. Mindez a programozótól függetlenül, automatikusan történik, Pascal programok írása közben nem is kell erre figyelmet fordítanunk. Annak azonban, aki most ismerkedik a nyelvvel, ez az ismeret segíthet az eljárások működésének megértésében.
A beolvasas eljárást egyetlen helyről hívjuk, ezért abból mindig ugyanoda térünk vissza. Az operandusolv eljárást két helyen aktivizáljuk, a szokozszures eljárást három, a kovkar-t négy helyen is hívjuk. Az előbb ismertetett mechanizmus segítségével minden egyes hívás után az adott hívást követő utasításhoz tér vissza a gép.
Most térjünk vissza arra, miért volt érdemes a kovkar eljárást deklarálni annak ellenére, hogy az csak egyetlen utasítást tartalmaz. Ez a programok hordozhatóságával, karbantarthatóságával függ össze. Bár milyen számítás eredménye csak akkor használható, ha látjuk, milyen bemeneti adatokból keletkezett. Ez a program jelenlegi változatában nem írja ki a beolvasott adatokat, azaz feltételezi, hogy a gép ezt a programtól függetlenül elvégzi. Ez teljesül is a legtöbb interaktív rendszerben, ahol tehát a felhasználó egy képernyő előtt ülve írja be a bemeneti adatokat, és ezeket a gép a beírással egyidejűleg a képernyőre visszaírja, így a felhasználó láthatja, hol tart a beírással. Ilyenek például a személyi számítógépek is.
Ha azonban a program a bemeneti adatokat például lyukkártyáról vagy mágneslemezről olvassa be, és az eredményeket nyomtatóra írja, akkor az eredmények előtt nem íródnak ki automatikusan a bemeneti adatok. Ilyen alrendszerekben a programozó feladata, hogy gondoskodjon a beolvasott adatok kiírásáról. A programunkban ehhez mindössze egy helyre, a kovkar eljárásba kell egy write(ch) utasítást beszúrni:
{ kovetkező karakter beolvasasa }
procedure kovkar;
begin
read(ch);
write(ch);
end;
Az eljárások nélküli változatban, hét helyen van read (ch) utasítás, tehát a kiírást is hét helyre kellene beszúrni. Ráadásul ezek közül három olyan, hogy a read(ch) utasítás egy-egy while utasítás do-ja után egyedül áll, tehát ezeken a helyeken még begin ... end párokat is be kell iktatni.
Ha nem használnánk a kovkar eljárást, hanem helyette mindenütt read (ch) lenne, szinte biztos, hogy a program módosításakor megfeledkeznénk e helyek valamelyikéről vagy a begin ... end párról.
Miután nagy vonalakban megismerkedtünk az eljárásokkal, nézzünk néhány egyszerű példát programban definiált függvényekre is!
4.1.2. Példa:
Deklaráljunk függvényt, amely a radiánban adott szög tangensét számítja ki!
(A szabványos Pascal nyelvben nincs tangensfüggvény.)
Megoldás:
Egy szög tangensét például szinuszának és koszinuszának hányadosaként lehet kiszámítani, ezek a függvények pedig léteznek a Pascalban.
function tan(x:real):real;
begin
tan:=sin(x)/cos(x)
end;
Egy függvény deklarációja tehát a function (kiejtése: fanksön, magyarul: függvény) szóval kezdődik, ezt követi a deklarálandó függvény neve, majd - az eljáráshoz hasonlóan - a formális paraméter, illetve paraméterek megadása. Most egyetlen formális paraméterünk van, ez valós típusú. A formális paramétereket az eljárástól eltérően kettőspont, majd típusazonosító követi, ez adja meg, hogy függvényünk milyen típusú értéket állít elő.
A függvény utasításrészében kiszámítottuk a kívánt értéket és azt egy értékadó utasítással rendeltük hozzá a függvény nevéhez. Az így definiált függvényt kifejezésekben használhatjuk, ugyanúgy, mint a szabványos függvényeket, tehát például értékadó utasításokban, feltételvizsgálatokban stb.:
z:=3*tan(fi);
alfa:=33; {fok} q:=tan(alfa/180*pi);
f:=tan(1);
ahol z, fi, alfa, q és f valós változók, pi=3.14... konstans.
A függvény hívása tehát akkor történik meg, amikor a gép a függvényhivatkozást tartalmazó kifejezés kiértékeléséhez ér. A függvény végrehajtása nagyon hasonló az eljárás végrehajtásához, azaz a gép először megjegyzi, hol kell folytatnia a hívást tartalmazó kifejezés kiértékelését, majd áttér a függvény utasításrészének végrehajtására. Ebben legalább egyszer végre kell hajtania egy értékadást a függvény nevére, megadva azt az értéket, amit a függvény a hívását tartalmazó kifejezéshez szolgáltat. Ha több ilyen értékadás is történik, akkor az utoljára adott érték lesz érvényes. Amikor a függvény utasításrészének végrehajtása befejeződött, a gép visszatér a hívást tartalmazó kifejezés további kiértékeléséhez.
4.1.1. Feladat:
Deklaráljon egy-egy függvényt tízes, kettes alapú, illetve tetszőleges logaritmus meghatározására!
4.1.2. Feladat:
Deklaráljon függvényeket árkusz szinusz és árkusz koszinusz meghatározására!
4.1.3. Feladat:
Deklaráljon függvényt, amely megadja egy tömb elemeinek maximális értékét!
4.1.4. Feladat:
Definiáljon függvényt, amely megadja a paraméterként kapott hexadecimális számjegy ('0'.'9', 'A'...'F') értékét egész számként!
4.1.5. Feladat:
Deklarálja az előbbi feladat függvényének fordítottját: ez egy 0...15 közötti számértékhez meghatározza a hexadecimális számjegyet!
4.1.6. Feladat:
Deklaráljon függvényeket a második fejezetben megismert gyökkeresési módszerek megvalósítására!
4.1.7. Feladat:
Deklaráljon függvényeket a második fejezetben megismert numerikus integrálási módszerek megvalósítására!
4.1.8. Feladat:
Ismételje át a lottószámok előállításakor használt véletlenszám generátor függvény működését!
A függvény tehát a következőkben különbözik az eljárástól:
4.2. Lokális és globális változók, azonosítók hatásköre
4.2.1. Példa:
Készítsünk függvényt, amely megadja a paraméterként kapott egész szám faktoriálisát!
Megoldás:
n faktoriális értéke könnyen meghatározható az első n egész szám összeszorzásával, ennek alapján megkísérelhetjük a függvény deklarálását:
{ >>> Hibas! <<< }
var g:integer;
...
function faktorialis(n:integer):integer;
begin
faktorialis:=1;
for g:=2 to n do
faktorialis:=faktorialis*g
end;
Ebben a megoldásban két hiba is van, az egyik a tévedésből előírt rekurzió, a másik a for utasítás használatából következik.
Tipikus hiba:
Ha egy függvény nevét bárhol kifejezésben használjuk, akkor az a függvény hívását jelenti, még akkor is, ha ez nem állt szándékunkban. A fenti példában a faktorialis függvényazonosító egy értékadó utasítás jobb oldalát megadó kifejezésben is előfordul, és ez a faktorialis függvény hívását jelentené. Szerencsére ennek a függvénynek van paramétere is, tehát a híváskor meg kellene adni az aktuális paramétert. Ezt a fordítóprogram is hiányolni fogja és szintaktikai hibát jelez, hiszen a függvény neve után egy szorzásjel következik, és nem zárójelek között lévő paraméter. Ha e függvénynek nem lenne paramétere, akkor nem is volna szintaktikailag hibás, tehát a hibát nem tudná jelezni a fordítóprogram, Ez azt jelentené, hogy a függvényben hívjuk magát a függvényt, és abban ismét csak hívjuk magát a függvényt, és így tovább a végtelenségig, illetve addig, amíg el nem fogy a gép memóriája a visszatérési címek tárolására. Már esett róla szó, hogy amikor egy szegmens hívja saját magát, azt rekurziónak vagy rekurzív hívásnak nevezzük. Ez sok feladat megoldásához nagyon hasznos módszer, ezért külön foglalkozunk majd vele. Most azonban nem akartunk rekurziót.
Ezt a problémát úgy oldhatjuk meg, hogy külön változót használunk a szorzások elvégzéséhez és csak a végeredményt másoljuk be a függvény nevébe:
{ >>> Hibas! <<< }
var g,f:integer;
...
function faktorialis(n:integer):integer;
begin
f:=1;
for g:=2 to n do
f:=f*g;
faktorialis:=f
end;
A megmaradt (szintaktikai) hiba nem olyan súlyos, mint az előző esetben, és inkább csak stílusbeli fogyatékosságnak tűnik, pedig nem az.
A függvény ugyanis használja az f és g munkaváltozókat, amelyek az ábra szerint valahol a függvény előtt vannak deklarálva. Ezek értékét a függvény megváltoztatja, ráadásul g értékét úgy, hogy az a for utasítás befejeztével, tehát a függvény befejezése után is meghatározatlan lesz.
Ha tehát ezeket a változókat valahol a függvényen kívül is használjuk, akkor az ott beállított értéket a függvény minden figyelmeztetés nélkül elrontja, ami nagyon kellemetlen, összetett programok esetén nehezen felderíthető hibákhoz vezethet.
Elvileg megoldás lenne a problémára az is, ha gondosan ügyelünk, hogy az ilyen munkaváltozókat másutt semmire se használjuk, de a valóságban erre szinte lehetetlen vigyázni.
Úgy kell tehát deklarálnunk ezeket a munkaváltozókat, hogy semmi közük ne lehessen a függvényen kívüli - akár azonos nevű - nyelvi elemekhez, legyenek azok változók, konstansok vagy például függvények. Erre az ad lehetőséget, hogy a szegmenseknek, így a függvényeknek is lehetnek saját változóik. Ezeket a szegmensben deklaráljuk, a szegmens utasításrésze előtt ugyanis ugyanúgy lehet definiálni és deklarálni dolgokat, mint a programok utasításrésze előtt.
Ezzel tehát a jó megoldás:
function faktorialis(n:integer):integer;
var f,g:integer; { a fuggveny sajat lokalis valtozoi }
begin
f:=1;
for g:=2 to n do
f:=f*g;
faktorialis:=f
end;
A for utasításnál már találkoztunk azzal a szabállyal, hogy a for utasítás ciklusváltozója csak lokálisváltozó lehet (bár a legtöbb omplementáció rugalmasabb). Így az előző változatban g használata szintaktikailag is hibás, de f használata már nem. Ettől függetlenül f-et is érdemes lokálissá tenni.
A definíciós-deklarációs részt és a hozzá tartozó (begin...end által határolt) utasításrészt együtt blokknak nevezzük.
Egy program a program fejrészéből, egy blokkból és végül a pontból áll, egy szegmens deklarációja pedig a szegmens fejrészéből, egy blokkból és a záró pontosvesszőből.
A blokk
1. A blokk egy program vagy egy eljárás, illetve függvény része. Fontos szerepe van az azonosítók hatáskörének meghatározásában.
2. Alakja:
blokk:

címkedeklarációs rész:
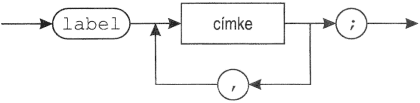
konstansdefiníciós rész:

típusdefiníciós rész:
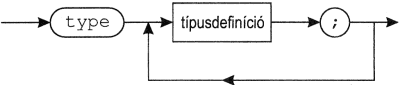
változódeklarációs rész:

eljárás- és függvénydeklarációs rész:
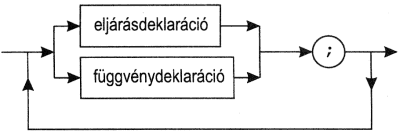
utasításrész: utasításcsoport
3. Ha egy blokk tartalmaz címkedeklarációs részt, akkor az abban deklarált címkék deklarációs pontjai azok a helyek, ahol a címkék a címkedeklarációs részben előfordulnak. Érvényességi körük ez a blokk, és mindegyikhez pontosan egy utasításnak kell tartoznia a blokk utasításrészében: amely utasítás előtt a címke áll. (d)
4. Az utasításrész tartalmazza azokat a műveleteket, azaz utasításokat, amelyeket a blokk aktivizálásakor végre kell hajtani.
5. Egy blokk végrehajtása a következőket jelenti:
létrejön a blokkban deklarált lokális változók egy külön, minden előzőtől különböző készlete a deklarációjukban megadott típussal. A lokális változók értéke a blokkba lépéskor meghatározatlan, a blokk végrehajtásának befejeztével a program paraméterek kivételével megszűnnek;
végrehajthatóvá válnak a blokkban deklarált eljárások és függvények;
végrehajtódik a blokk utasításrészét jelentő utasításcsoport, ennek befejezése jelenti a blokk végrehajtásának befejezését;
ha a blokk egy végrehajtásakor a blokk lokális címkéjére, változójára, eljárására vagy függvényére hivatkozunk, akkor ez a blokk éppen érvényes végrehajtásához tartozó címke, változó, eljárás, illetve függvény hivatkozását jelenti; (e)
- ha a blokk egy függvényhez tartozik és a blokkból nem goto-val lépünk ki, akkor a blokkban értékadást kell végrehajtani a függvény nevére.
Magyarázatok, megjegyzések:
(a) Deklarálni azokat a nyelvi eszközöket lehet, amelyek valamilyen tárcímmel kapcsolatosak: címkék, változók, eljárások és függvények.
Definiálni ezzel szemben olyanokat lehet, amelyek nem kapcsolódnak tárhelyhez, csak valamilyen tulajdonságot vagy állandó értéket képviselnek: konstans- és típusazonosítók.
Mivel ennek a megkülönböztetésnek nincs nagy jelentősége, az egyszerűség kedvéért többször is azonos értelemben használjuk a deklaráció és definíció szavakat.(b) A különböző definíciós és deklarációs részeknek és az utasításrésznek pontosan ilyen sorrendben kell követniük egymást. Előfordulhat, hogy a blokkban nincsen sem definíció, sem deklaráció, csak utasításrész.
(c) Az egyes deklarációs és definíciós részeket rendre a label, const, type és var foglalt szavak vezetik be, az eljárás- és függvénydeklarációs részt az első procedure vagy function foglalt szó kezdi. Ez a rész akár függvény, akár eljárás deklarációjával kezdődhet.
(d) Az érvényességi kör és hatáskör kifejezéseket azonos értelemben használjuk.
(e) Ha egy eljárás hívja önmagát - ezt rekurziónak nevezzük -, akkor például a harmadik szintű rekurzív végrehajtás során mindezek a nyelvi elemek a blokk harmadik szintjéhez tartozó külön készletet jelentik, és ezek teljesen függetlenek a második és az első híváshoz tartozó ugyanilyen elemektől. Így a harmadik szintű végrehajtás során nem érhetők el a második szint címkéi, változói stb., és ugyanígy az első szinthez tartozók sem.
Most vizsgáljuk meg, milyen kapcsolat van a blokkban és a blokkon kívül definiált vagy deklarált azonosítók között!
Tekintsük például a következő programot:
program faktorialis;
const fmax=7;
var g:integer;
function faktorialis(n:integer):integer;
var f,g:integer; { a fuggveny sajat lokalis valtozoi }
begin
f:=1;
for g:=2 to n do
f:=f*g;
faktorialis:=f
end;
{ a program utasitasresze }
begin
write('Szam: ');read(g);
if g>fmax then writeln('A szam tul nagy!')
else writeln(g:3,' faktorialisa = ',faktorialis(g):6)
end.
A program definíciós-deklarációs részében három azonosítót definiáltunk: az fmax konstansot, a g változót es a faktorialis függvényt. Ezeket definícióiknak megfelelő módon használhatjuk a program utasításrészében.
A legkülső szintet, azaz a program elején definiált azonosítókat és a program utasításrészét együtt röviden főprogramnak nevezzük. Ebbe tehát nem tartoznak bele azok az azonosítók és címkék, amelyeket valamelyik eljárásban vagy függvényben definiáltunk.
A faktorialis függvényben is deklaráltunk két azonosítót: f és g egy-egy változót jelent.
Amikor a függvényben az f, illetve a g azonosítót használjuk, akkor ezek a függvényben deklarált változókat jelentik. Ez az f változó esetén magától értetődő, hiszen a programban máshol nincs is ilyen azonosító deklarálva, g nevű változó azonban kettő is előfordul.
Ha egy szegmensben definiálunk egy azonosítót, akkor a szegmens további részében ez az azonosító az itt definiált dolgot jelenti. Példánkban tehát, amikor a g azonosítót a függvényen belül használjuk, ez a függvényben deklarált változóra való hivatkozást jelent és semmi köze a főprogramban deklarált ugyanilyen nevű változóhoz.
Ha viszont a függvényben az fmax azonosítót is használnánk, akkor ez azt a konstanst jelentené, amit a program elején, még a függvény előtt definiáltunk:
program faktorialis;
const fmax=7;
var g:integer;
function faktorialis(n:integer):integer;
var f,g:integer; { a fuggveny sajat lokalis valtozoi }
begin
if n>fmax then begin
writeln('A szam tul nagy!');
faktorialis:=0
end
else begin
f:=1;
for g:=2 to n do
f:=f*g;
faktorialis:=f
end
end;
{ a program utasitasresze }
begin
write('Szam: ');read(g);
writeln(g:3,' faktorialisa = ',faktorialis(g):6)
end.
Ha egy azonosítót annak a blokknak az utasításrészében használunk, amelynek a deklarációs részében az azonosítót deklaráltuk, akkor az azonosítót lokálisnak nevezzük. Ha ez például egy változónak a neve, akkor lokális változóról, ha konstansé, akkor lokális konstansról beszélünk. Ilyen lokális változó a faktorialis függvényben f és g, de lokális azonosító a főprogramban max, g és faktorialis is, hiszen ezeket a főprogramban definiáltuk, illetve deklaráltuk.
Globálisnak azt az azonosítót nevezzük, amit olyan blokkban használunk, amely maga nem tartalmazza az azonosító deklarációját, de ez a blokk egy olyan másik blokkban van, amelyben az azonosítót deklaráltuk. Ilyen a második változatban, a függvényben fmax konstans azonosítója.
A lokális azonosítókat csak a blokkjukban használhatjuk, a blokk befejeztével nem érhetők el.
Így például a főprogramban nem használhatnánk az f változót, hiszen az csak a függvényen belül értelmezett.
Azt, hogy egy azonosító a program mely részeiben használható, és ott milyen értelemben, az azonosítók érvényességi körére vonatkozó szabályok adják meg.
Ehhez nagyon hasonló szabályokkal a with utasításnál már találkoztunk. Ott a mezőneveknek, mint önálló azonosítóknak az érvényességi köre a with utasítás végéig terjedt.
Visszatérve a hibás példákra, a második fejezetben a for utasítás szabályai között szerepelt az is, hogy for utasítás ciklusváltozója csak lokális változó lehet, így a g változót kötelesek vagyunk afaktorialis függvényben deklarálni. (Bár a legtöbb megvalósítás megengedőbb.)
Ez a szabály azért hasznos, mert megóv bizonyos hibáktól: ha egy globális változót például for utasítás ciklusváltozójaként munkaváltozónak használnánk, akkor elrontanánk a külső blokkban tárolt értéket.
Érvényességi kör
1. Az érvényességi kör vagy más néven hatáskör a program szövegének azon része, ahol az adott azonosító vagy címke egy adott értelemben használható, azaz egy adott jelentése van. Az adott szimbólum érvényességi köre több szövegrészből is állhat. (a)
A definiálási pont a program szövegében az a hely, ahol az adott azonosító vagy címke az érvényességi körében rá jellemző tulajdonságait megkapja. (b)
2. A címkék, illetve különböző jellegű azonosítók definíciós pontját, illetve érvényességi körét a következő szabályok adják meg:
Címke definíciós pontja az a hely, ahol a blokk címkedeklarációs részében az adott címkét deklaráljuk, érvényességi köre a blokk további része, a 3. szabályban megadott kivétellel.
Konstans-, típus-, változó-, eljárás- és függvényazonosító definíciós pontja az a hely, ahol egy blokk megfelelő definíciós, illetve deklarációs részében definiálva, illetve deklarálva van, érvényességi köre pedig a blokk további része, a 3. pontban megadott kivétellel.
Eljárás és függvény formális paraméterének, valamint illeszkedő tömbparaméterek indexhatárainak definíciós pontja az a hely, ahol az a formális paraméterlistán előfordul, érvényességi köre az őt közvetlenül tartalmazó formális paraméterlista további része és a hozzá tartozó blokk a 3. pontban megadott kivétellel. (c)
- a rekord definíciójában vagy deklarációjában az adott mezőnevet közvetlenül tartalmazó mezőnévlista további része,
- a with utasítás rekordlistáján a mezőt tartalmazó rekord megadásától a with utasítás végéig, a 3. pontban megadott kivétellel,
- a rekordváltozó.mezőnév alakú hivatkozás.
Az előre deklarált input, illetve output állományváltozó deklarációs pontja az a hely, ahol a program paraméterei között előfordul, érvényességi köre a teljes program, a 3. szabályban megadott kivétellel.3. Ha egy azonosítónak vagy címkének egy A tartományban van a definíciós pontja, az A tartomány lenne az érvényességi köre, de ezen belül van egy B tartomány amelyben ugyanilyen azonosítónak vagy címkének definíciós pontja van, és B tartomány az érvényességi köre, akkor az A-ban definiált azonosító, illetve címke érvényességi körébe nem tartozik bele a B tartománynak az azonosító vagy címke definíciós pontját követő része, és semmilyen további, B-n belüli tartomány (Ezt az esetet az azonosító vagy címke újradefiniálásának nevezzük.) Ilyen beágyazott tartomány blokk, vagy with utasítás is lehet.
4. Ha az azonosítónak vagy címkének egy tartományban van definíciós pontja, akkor ugyanebben a tartományban ugyanilyen azonosítónak vagy címkének nem lehet újabb definíciós pontja, legfeljebb egy ebbe a tartományba ágyazott másik tartományban, ezzel az esettel a 3. szabály foglalkozik.
5. Minden, a programban használt azonosítónak és címkének kell, hogy legyen definíciós pontjai, ez adja meg az adott azonosító, illetve címke jelentését és érvényességi körét.
6. Ha az azonosító vagy címke az érvényességi körén belül a definíciós pont után fordul elő, azt az azonosítóra vagy címkére, való hivatkozásnak nevezzük. Az azonosítónak vagy címkének a hivatkozás helyén érvényes tulajdonságait a definíciós pontban hozzárendelt tulajdonságok adjak meg. Érvényességi körén kívül nem hivatkozhatunk sem az azonosítóra, sem a címkére.
7. Az azonosítóra, vagy címkére való minden hivatkozásnak az azonosító, illetve címke definíciós pontja után kell állnia, azaz egyetlen hivatkozás sem előzheti meg a program szövegében a neki megfelelő definíciós pontot, kivéve egy esetet: a típusdefiníciós részben egy új mutatótípus definiálásakor hivatkozhatunk olyan típusazonosítóra, amely az így definiált mutatótípus által mutatott változó típusát adja meg, és a mutatótípus definíciójáig nem definiáltuk. Az így hivatkozott típus definíciójának ugyanabban a típusdefiníciós részben kell lennie, mint a rá hivatkozó mutatótípus definíciójának.
Magyarázatok, megjegyzések:
(a) Az érvényességi kör fontos tulajdonsága, hogy milyen értelemben használható benne az adott címke vagy azonosító. Előfordulhat ugyanis, hogy például egy azonosító a program szövegének egyes részein különböző dolgokat jelent: az egyik részben változót, a másikban adattípust, a harmadikban pedig újra egy változót, ami más, mint az előző.
Az érvényességi kör tehát az azonosító vagy címke egy adott jelentésének megfelelő szövegrészek együttese.(b) Bár a Pascal nyelvben a konstansokat és típusokat definiálni, a címkéket, változókat és szegmenseket pedig deklarálni kell, nincs olyan fogalom, hogy "deklarációs pont", a deklarált nyelvi elemek, például azonosítók, illetve címkék esetére is a "definíciós pont' kifejezést használjuk.
(c) A formális paraméterek érvényességi körébe tehát nem tartozik bele az ugyanazon formális paraméterlistán megadott formális eljárás- vagy függvényparaméter formális paraméterlistája. Így helyes például a következő eljárásfej:
procedure eljaras(a,b:real;function fv(p,a,z:integer):char;z:xhar);
...Itt a és z nem ugyanabban a formális paraméterlistában fordul elő kétszer. Hibás azonban a következő:
function ffvv(var m,n:integer;procedure p(ch:char);
p,n:array[g..m:integer] of real):char;
...Ennél m, p, illetve n második definíciós pontja is ugyanabban a formális paraméterlistában van.
Vegyünk még egy kicsit összetettebb példát az azonosítók érvényességi körére!
program ppp...
var a,b,c:real; { a foprogram valtozoi }
...
procedure p; { p eljaras deklaracioja }
var g,c,k:har; { p eljaras lokalis valtozoi }
begin { p utasitasresze }
...
c:='q' { hivatkozas p lokalis valtozojara }
...
end; { proc. p }
function f:real { f fuggveny deklaracioja }
const c=1E-6; { f lokalis konstansa }
var c1,c2,a:integer; { f lokalis valtozoi }
begin { f utasitasresze }
...
c1:=trunc(a*c); { c itt f lokalis konstansa }
...
if k<>'.' then... { hibas! k csak p-ben letezik }
p; { p eljaras hivasa }
...
end; { funct. f. }begin { foprogram }
c:=1/100; { hivatkozas a foprogram valtozojara }
...
p; { p eljaras hivasa }
a:=f+10.6; { f fuggveny hivasa }
...
end.
A példában c három különböző dolgot is jelent: a főprogramban valós, a p eljárásban pedig karakter típusú változó, az f függvényben viszont valós konstans.
Az f függvényben nem hivatkozhatunk a k változóra, hiszen az p lokális változója, a p eljáráson kívül nem használható.
A főprogramban hívhatjuk akár a p eljárást, akár az f függvényt, de a p eljárást hívhatjuk f-ből is, hiszen a p azonosító globális az f szempontjából, (hiszen az f-et tartalmazó blokkban deklaráltuk, és amikor f-et deklaráljuk, akkor p már deklarálva van). Nem hivatkozhatnánk azonban f-re p-ben, hiszen amikor p-t deklaráljuk, f még nincs megadva.
f és p is hívhatná saját magát (rekurzió), mert bár e hívások helyéig deklarációjuk nem fejeződött még be, a hívásukhoz szükséges információk rendelkezésre állnak: a szegmens neve, a paraméterek száma és típusa, függvény esetén az eredmény típusa.
Ha mégis arra lenne szükségünk, hogy p is hívhassa f-et, azaz f és p is közvetett módon rekurzívan hívhassa magát, ahhoz további nyelvi elemre: a forward direktívára lesz szükségünk. Ezt majd a szegmensekre vonatkozó szabályoknál ismerjük meg.
A lokális változóknak van még egy érdekes tulajdonságuk: a gép csak addig foglal le memóriát a számukra, amíg a deklarációjukat tartalmazó szegmens végrehajtása tart. Ez azt jelenti, hogy a szegmens hívásakor a gép lefoglal megfelelő mennyiségű memóriát a szegmens lokális változóinak, majd a szegmens végrehajtásának végén, közvetlenül a hívás helyére való visszatérés előtt ezt a memóriaterületet ismét szabaddá teszi. Így a lokális változók valóban csak addig foglalják a memóriát, ameddig arra szükség van. Ebből az is következik, hogy a szegmensbe belépve a lokális változók értéke meghatározatlan, illetve a bennük tárolt értékek a szegmens befejeztével elvesznek. Ez azért van így, mert egyáltalán nem biztos, hogy ugyanabba a szegmensbe ismét belépve ugyanazt a memóriaterületet fogja a gép a lokális változók számára lefoglalni. Ha mégis, akkor lehet, hogy azt közben megváltoztatta valamely azóta végrehajtott programrész.
A szegmensek paraméterei az érvényességi kör szempontjából szintén lokálisak, azaz csak a szegmensben használhatók, ebbe beleértendők a szegmensben deklarált további szegmensek is. Mivel egy azonosítót egy szegmensben csak egyféle értelemben lehet használni, nem lehet azonos nevű formális paraméter és más lokális elem, például változó vagy konstans, hiszen ha erre hivatkozunk, akkor nem lehet eldönteni, hogy ez a formális paramétert vagy a lokális elemet jelenti-e.
4.3. Adatátadás a szegmens és a hívó programrész között
Ahhoz, hogy a szegmensek egyáltalán műveleteket végezhessenek a hívó programrész számára - legyen az a főprogram, vagy valamely más szegmens - a műveletek számára adatokat kell onnan átvenniük, illetve a műveletek eredményét valamilyen formában át kell adniuk. Előfordulhat az is, hogy egy szegmens nem vesz át adatot, mert például éppen az a feladata, hogy a hívó programrész számára adatokat olvasson be a gép billentyűzetéről, vagy mert olyan számítást végez, amihez nincs szüksége bemeneti adatokra. Lehetséges az is, hogy nem ad át eredményt a hívó programrésznek, mert a feladata kiírás vagy grafikonrajzolás, és ehhez a szegmensnek csak bemeneti adatokra van szüksége. Sőt az is előfordulhat, hogy a hívó szegmenstől nem is vesz át és nem is ad vissza adatot, mert például egyedüli feladata egy hibaüzenet kiírása:
procedure hiba;
begin
writeln;writeln('Hiba! 0-val valo osztas!')
end;
A szegmensek és a hívó programrész közötti adatátadásra a paramétereket, a globális változókat és a függvények értékeit használhatjuk.
A különböző adatátadási módok vegyesen is használhatók, azaz egy szegmens egyidejűleg használhat globális változókat és paramétereket is adatátadásra. A szegmens és a paraméter jellegétől függ, hogy mikor melyiket érdemes használni.
Adatátadás globális változókkal
A globális változók az adatátadás legegyszerűbb módját jelentik, hiszen amikor a hívó programrész és a hívott szegmens ugyanazokat - a szegmens számára globális - változókat használja valamilyen közös adat tárolására, akkor az olyan postaládaként működik, amelybe a címzett és a feladó, azaz a hívó programrész és a hívott szegmens is tehet be, illetve ahonnan mindkettő vehet ki adatokat, azaz mindketten egyidejűleg lehetnek címzettek és feladók is.
A globális változók használatának hátránya, hogy az adatátadás módja merev, vagyis a szegmens mindig ugyanazokkal a változókkal dolgozik.
Előnye, hogy nem kell a szegmens minden egyes hívásakor aktuális paraméterként megadni, rövidebb és gyorsabb lesz az eljárás, illetve függvény hívása.
Akkor használunk globális változót adatok átadására, ha a szegmens egyébként is mindig ugyanazokkal a változókkal dolgozik (mint a telefonkonyv5 program).
Adatátadás változóparaméterekkel
Nézzünk egy eljárást, ami két változó értékét felcseréli:
procedure csere(var x,y:integer);
var tmp:integer;
begin
tmp:=x;x:=y;y:=tmp
end;
A formális paraméterlistán var x,y:integer szerepel, itt a var kulcsszó jelzi, hogy úgynevezett változóparaméterről van szó. A var kulcsszóval már találkoztunk, ez jelzi egy blokkban a változódeklarációs rész kezdetét is, itt azonban más a jelentése.
A változóparaméter kétirányú adatátadást tesz lehetővé a hívó programrész és a szegmens között: a hívó programrész is tud vele a szegmensnek adatot átadni, és a szegmens is a hívó programrésznek.
Mivel a változóparaméterrel részben az a célunk, hogy a szegmens értéket adhasson át a hívó programrésznek, ezt csak úgy teheti meg, hogy megváltoztatja a formális paraméternek megfelelő aktuális paraméter értékét. Tehát az aktuális változóparaméter csak változó lehet, konstans vagy kifejezés nem, hiszen ezek értékét a hívó programrész nem változtathatná meg.
A szegmens végrehajtása alatt a formális változóparaméterrel végzett minden művelet - például a paraméter értékének felhasználása vagy megváltoztatása - úgy történik, mintha mindezt közvetlenül az aktuális paraméterrel tennénk, tehát mintha a szegmens végrehajtása alatt a formális paraméter teljesen azonos lenne az aktuális paraméterként megadott változóval.
Akit érdekel, hogy ez a gépen belül hogyan történik, annak megemlítjük, hogy a gép a híváskor az aktuális paraméter memóriabeli címét adja át a szegmensnek, mely ennek a címnek a segítségével fér hozzá a változó értékéhez, illetve változtatja meg azt.
A változóparaméter használatának előnye, hogy kétirányú adatátadást tesz lehetővé a szegmens és környezete között. Másik előnye, hogy a szegmens egyes hívásainál az aktuális paraméter más és más lehet, a szegmens tehát mindig az éppen aktuális változóval dolgozik.
Hátránya, hogy az aktuális paramétert minden hívásnál meg kell adni, és ez némi többletmunkával jár a globális változó használatához képest.
Adatátadás értékparaméterekkel
A 4.1.2. példában deklarált tan függvény egyetlen formális paramétere előtt nincs ott a var kulcsszó, ez ugyanis úgynevezett értékparaméter.
Az értékparaméterre az jellemző, hogy csak a szegmens felé közvetít értéket, a szegmensből kifelé nem. Ez azt jelenti, hogy ha a szegmensben megváltoztatjuk egy formális értékparaméter értékét, akkor ettől kezdve a szegmensen belül ezt az új értéket jelenti, de a megfelelő aktuális paraméter értéke nem változik meg.
Ennek demonstrálására nézzük a következő programot:
program pr;
var a,b:integer;
procedure pr(x:integer;var y:integer);
begin
writeln('Elejen: a=',a,' b=',b,' x=',x,' y=',y);
x:=x+1;y:=y+1;
writeln('Vegen: a=',a,' b=',b,' x=',x,' y=',y)
end;
begin
a:=10;b:=20;
pr(a,b);
writeln('Utana: a=',a,' b=',b)
end.
A pr eljárás első paramétere értékparaméter, a második, az összehasonlítás kedvéért, változóparaméter, bejárásban közvetlenül a belépés után, majd a formális paraméterek értékének megváltoztatása után is kiírjuk az a és b globális változók, valamint az x és y formális paraméterek értékét. a és b lesz az eljárás aktuális paramétere is.
A program a következőket írja ki:
Elejen: a=10 b=20 x=10 y=20
Vegen: a=10 b=21 x=11 y=21
Utana: a=10 b=21
Átírásokból is látható, hogy az x és y formális paraméterek átveszik az aktuális paraméterek értékét, illetve, hogy az eljárásbeli értékadások mindkettőt megváltoztatják. Ennek csak a b aktuális paraméterre van hatása, hiszen b aktuális változóparaméter, a-ra azonban, amely aktuális értékparaméter, nincs hatása.
Az értékparamétert tehát a szegmens olyan lokális változójához hasonlíthatjuk, amelyet a szegmens hívásakor a gép az aktuális paraméter értékével tölt fel.
Az értékparaméter belső megvalósítása egyébként úgy történik, hogy híváskor a gép először meghatározza az aktuális paraméter értékét, majd elteszi egy erre a célra lefoglalt memóriaterületre. Azaz, ha az aktuális paraméter változó volt, akkor ennek a változónak az értékét lemásolja erre a külön memóriaterületre. A formális paraméterre való hivatkozás ennek a külön területnek a használatát jelenti, így ennek nincs hatása az aktuális paraméterre, akkor sem, ha megváltozna az értéke.
Az aktuális értékparaméter tehát konstans, illetve kifejezés is lehet, hiszen ezeknek az értékét kapja meg a formális paraméter. A tan függvény hívásakor láthatunk példákat különböző jellegű aktuális értékparaméterekre.
Az értékparaméter használatának előnye, hogy az aktuális paraméter konstans, illetve kifejezés is lehet, és hogy a szegmensen belüli műveletek nem tudják megváltoztatni, például hibás működés esetén elrontani az aktuális paraméter értékét.
Hátránya, hogy tárolásához külön memóriaterületre van szükség, tehát ha például egy nagy tömb a paraméter, akkor erről az egész tömbről készül másolat - azaz a tömb értéke a szegmens végrehajtása alatt két példányban lesz jelen a memóriában. Ha ezt a gép memóriakapacitása nem tenné lehetővé, akkor inkább változóparamétert kell használni a tömb paraméterként való átadására.
Adatátadás függvény értékével
Függvény értéke egyszerű típus, illetve mutatótípus lehet (a mutatótípussal az 5. fejezet foglalkozik).
Akkor használjuk, ha a szegmens eredménye egyetlen érték, és azt kifejezésben, például értékadásban, illetve feltételvizsgálatban is használni akarjuk.
A függvények is használhatnak egyébként akár globális változókat, akár változóparamétereket, tehát nem csak egy értéket adhatnak át a hívó programrésznek. Mégis akkor részesítjük előnyben a függvényt az eljárással szemben, ha a szegmens elsődleges eredménye egyetlen érték.
Az adatátadás különböző módjai így foglalhatók össze:

4.4. A szegmensek mint paraméterek
A 2.10. fejezetben, a simpsonmodszer olyan program volt, amely a sin(x)/x függvény határozott integrálját számítja ki adott intervallumban, Simpson-módszerrel.
Gyakran visszatérő probléma olyan függvény határozott integráljának meghatározása, amelynek nincs primitív függvénye. Jó lenne olyan módszert találni, amely tetszőleges függvény esetén használható.
Megjegyzendő: sem a Turbo Pascal, sem a HiSoft-Pascal nem teszi lehetővé szegmensek paraméterként történő átadását, így ezen megvalósításokban nem használható az ebben a fejezetben bemutatandó megoldás.
4.4.1. Példa:
Készítsünk függvényt, amely tetszőleges függvény határozott integrálját képes meghatározni, ha adott az integrálandó függvény Pascal függvényként, az integrálás alsó és felső határa, valamint a felbontásban szereplő pontok száma!
Megoldás:
Az integrálközelítő összeg meghatározását végző függvény az integrálandó függvényt is paraméterként fogja megkapni, így ugyanaz az integráló módszer tetszőleges függvényre használható lesz.
Pontossága miatt a Simpson-módszert választjuk:
function simpson(function f(p:real):real;also,felso:real;n:integer);
{ simpson integral }
{ f - integralando fuggveny, p - ennek parametere }
{ also, felso - integralasi hatarok, n - pontszam }
var x,suly,t,h:real; { lokailis valtozok }
k:integer;
begin
if odd(n) then n:=n+1; { paros pontszam kell }
t:=f(also)+f(felso); { kezdeti ertekek }
suly:=4;h:=(felso-also)/n;
x:=also+h;
for k:=1 to n-1 do begin
t:=t+suly*f(x);
x:=x+h;suly:=6-suly
end;
simpson:=t+h/3
end;
Ha fenti függvénnyel például a sin(x)/x függvényt akarjuk integrálni, akkor ehhez először azt is Pascal függvény formájában kell deklarálnunk:
function sinxpx(x:real):real;
begin
if x=0 then sinxpx:=1
else sinxpx:=sin(x)/x
end;
Itt x=0 helyen a függvényt határértékével helyettesítettük, hogy ne történhessen nullával osztás.
Ha ki szeretnénk írni sin(x)/x határozott integrálját a 0.1-től 10-ig vett intervallumra 20 ponton számolva, azt a következőképpen tehetjük meg:
write(simpson(sinxpx,0.1,10,20));
A simpson függvény deklarációjában az első paraméter az integrálandó függvény. Ennek a fejét kell a formális paraméterek között megadni, hogy hívásakor paramétereinek száma, típusa, illette az általa adott eredmény típusa ismert legyen. Amikor az integrálásban az f függvényt hívjuk, akkor ez a simpson hívásakor aktuális paraméterként megadott függvény hívását jelenti. Ez lehet a sinxpx, vagy tetszőleges más függvény, amelynek egyetlen valós paramétere van, és valós értékű.
A paraméterként használt szegmensek érdekessége még, hogy az aktuális paraméterként átvett függvényt illetve eljárást akár az azt aktuális paraméterként használó sz szegmens előtt, akár az után deklarálhatjuk, hiszen közvetlenül, azaz deklarációjában egyik sem hivatkozik a másikra, csak akkor kerülnek kapcsolatba, amikor az sz szegmenst hívjuk. Ez azért lehetséges, mert a formális paraméterlistából, vagyis az itt megadott szegmensfejből minden, a paraméterként hívott szegmens hívásához szükséges információ kiderül, kivéve, hogy melyik az sz által hívandó szegmens. Ezt pedig elég az sz szegmens hívásakor megadni.
4.4.1. Feladat:
Készítsen olyan függvényeket a második fejezetben megismert gyökkeresési, illetve integrálási módszerekhez, amelyek az összes adatot és a használt függvényt is paraméterként veszik át!
A paraméterként használt szegmensekre további mintapélda található a rekurzióról szóló 4.5 alfejezetben.
"-És hol van ez a könyv?
- A könyvben - hangzott a válasz"...
[0] 188. oldal
Rekurzióról akkor beszélünk, ha egy eljárás vagy függvény közvetlenül vagy közvetve hívja saját magát Közvetlen a rekurzió, ha egy a szegmens az utasításrészében magát a-t hívja; közvetett, ha egy a szegmens egy másik b szegmenst hív, amely hívja a-t, akár közvetve, akár közvetlenül.
Ez első hallásra egy komplikáltan megoldott végtelen ciklusnak tűnik, és ha hibásan alkalmazzuk, valóban az is lehet belőle, kivéve, hogy a végtelen rekurzió előbb-utóbb lefoglalja az összes rendelkezésre álló memóriát, és így programunk meghal. Sok feladat megoldása azonban rekurzív módon fogalmazható meg legkönnyebben, és rekurzív eljárással vagy függvénnyel valósítható meg legegyszerűbben.
A rekurzív algoritmusok egyik tipikus esete, amikor a feladatot ugyanannak a feladatnak egy, vagy több egyszerűbb, illetve kisebb méretű esetére vezetjük vissza, ezekhez megint csak kisebb méretű esetek megoldása kell, míg végül olyan szintre jutunk, ahol már olyan egyszerű, vagy kis méretű a feladat, hogy további visszavezetés nélkül is megoldható.
4.5.1. Példa:
Oldjuk meg az úgynevezett Hanoi tornyai problémát!
Adott három rúd: a, b és c. Az a rúdon induláskor n darab különböző átmérőjű lyukas korong van, nagyság szerint felfelé csökkenő sorrendben:
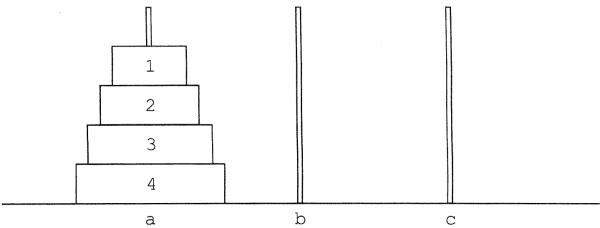
Át keli rakni a tornyot a c rúdra a következő szabályok betartásával:
n bemeneti adat.
Olyan megoldást szeretnénk, amely lépésről lépésre megadja, melyik korongot honnan hová kell tenni.
A feladat onnan kapta a nevét, hogy állítólag Hanoi közelében egy kolostorban 64 aranykorongból álló tornyot raknak át az ott élő szerzetesek az előbbi szabályok szerint, minden nap egyetlen korongot mozgatva. A legenda szerint a világvége akkor fog bekövetkezni, ha befejeződik a torony átrakása.
Megoldás:
A megoldás ötlete: 2 magasságú tornyot úgy kell átrakni, hogy az 1. korongot áttesszük b-re, ekkor a 2. korong áttehető c-re, majd a b-re félretett korong áttehető c-re.
A megoldás n magasságú toronyra általánosított gondolatmenete:
Ha n>0 akkor:
n-1 magasságú torony átrakása a-ról b-re,
az n-edik korong átrakása a-ról c-re,
n-1 magasságú torony átrakása b-ről c-re,
egyébként semmit sem kell csinálni.
A feladatot eggyel alacsonyabb torony kétszeri átrakására és egy korong mozgatására vezettük vissza. A legegyszerűbb az az eset, amikor 0 magasságú tornyot kell mozgatni, ekkor ugyanis semmit sem kell csinálni.
A gondolatmenetnek megfelelő eljárás:
procedure hanoi(n:integer;honnan,mivel,hova:char);
begin
if n>0 then begin
hanoi(n-1,honnan,hova,mivel); { atrakas a kisegitore }
writeln(n:3,' korongot tedd ',honnan,' rudrol ',hova,' rudra');
hanoi(n-1,mivel,honnan,hova) { atrakas kisegitorol vegsore }
end
end;
Az előbbi eljárás például a
hanoi(3,'a','b','c')
hívás esetén a következőt írja ki:
1. korongot tedd a rudrol c rudra
2. korongot tedd a rudrol b rudra
1. korongot tedd c rudrol b rudra
3. korongot tedd a rudrol c rudra
1. korongot tedd b rudrol a rudra
2. korongot tedd b rudrol c rudra
1. korongot tedd a rudrol c rudra
A tornyok induláskor és az egyes mozgatások után:
Induláskor:
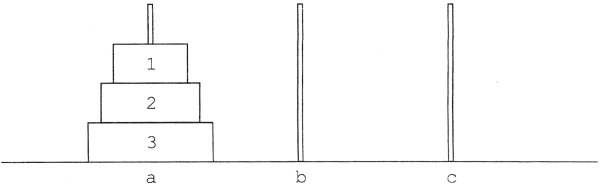
1. korongot tedd a rúdról c rúdra:
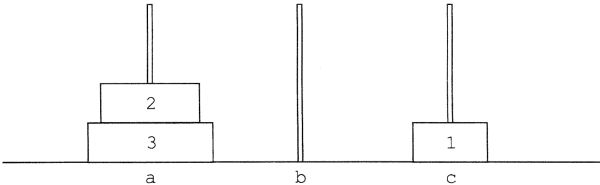
2. korongot tedd a rúdról b rúdra:
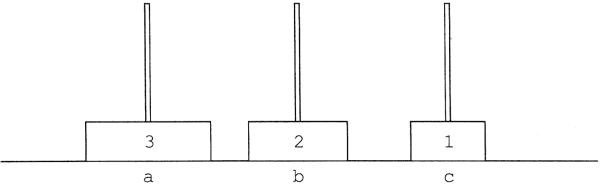
1. korongot tedd c rúdról b rúdra:
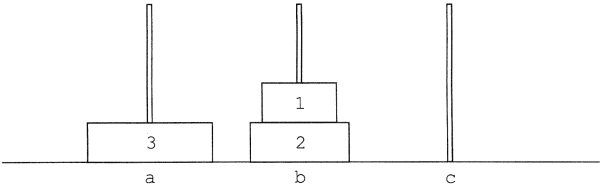
3. korongot tedd a rúdról c rúdra:
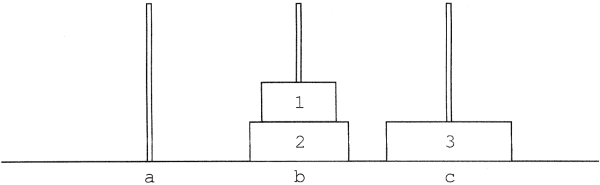
1. korongot tedd b rúdról a rúdra:
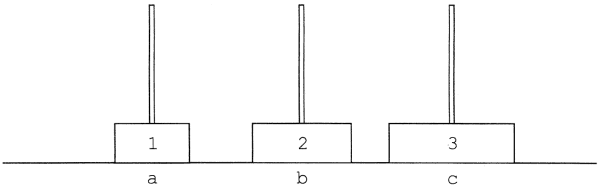
2. korongot tedd b rúdról c rúdra:

1. korongot tedd a rúdról c rúdra:

Az algoritmus elemzése nagyon hasonlít a teljes indukcióra.
Nulla magasságú torony esetén jól működik, hiszen nem ír ki semmit.
Egy magasságú torony esetén is jól működik, hiszen kétszer hívja magát nulla magasságú toronyra, arról már tudjuk, hogy helyes; ezen kívül egy sort ír ki, amely az n-edik elemet mozgatja a honnan rúdról a hova rúdra, itt éppen az 1. elemet az a rúdról a c-re, tehát ez is helyes.
Ha n-1 magasságú tornyot helyesen rak át, akkor n magasságút is, hiszen ezt a megoldás gondolatmenete és az ennek teljesen megfelelő eljárás az n-1 magasságú torony honnan rúdról mivel rúdra való mozgatásával kezdi, amit feltevésünk szerint helyesen old meg. Ekkor a honnan rúdon egyedül az n-edik korong marad, ezt áttesszük a hova rúdra, majd a mivel rúdra félretett n-1 magasságú tornyot áttesszük végleges helyére, a hova rúdra.
A Hanoi eljárás, és általában a rekurzív szegmenshívások működésének teljes megértéséhez még azt is látnunk kell, miért nem keverednek össze az egyes hívások adatai, azaz hogyan tartja nyilván a gép a hívások szintjeit, az egyes hívásokhoz tartozó paramétereket, illetve ha vannak, a lokális adatokat. Ehhez már mindent ismerünk, csak fel kell eleveníteni az ide tartozó ismereteket:
A gép a szegmens hívásakor megjegyzi, hogy hol kell folytatni a szegmens befejezése után a programot, ezt minden egyes híváskor egy-egy újabb helyen jegyzi meg, így az egyes hívásokhoz tartozó visszatérési címek nem keverednek össze. Amikor befejeződött a szegmens végrehajtása, a visszatérési cím számára lefoglalt hely felszabadul.
Az értékparaméterek számára a gép a szegmens hívásakor külön helyet foglal, értéküket kiszámítja és ide helyezi, a szegmens pedig a formális értékparaméterek értékeit erről a helyről veszi elő. Minden egyes hívásnál külön területet használ, így az egyes hívások értékparaméterei nem keverednek össze. Ezt a területet a szegmensből visszatérve felszabadítja.
Az előzőekhez teljesen hasonló módon minden egyes hívásnál külön területet használ a lokális változóknak is, ez a szegmens befejeztével szintén felszabadul.
Mivel az előbbi három dologhoz a memóriaterület lefoglalása, használata és felszabadítása nagyon hasonlóan történik, ezeket a gép együtt végzi. Az adott híváshoz tartozó visszatérési címet, értékparaméter értékeket, illetve lokális változókat minden szegmenshívásnál egy elkülönített - a három dolog együttes tárolására elegendő - memóriaterületen tárolja; ezt nevezzük szegmensmezőnek. A szegmensmező tehát addig létezik, amíg a hozzá tartozó szegmenshívás érvényben van, tehát a szegmensbe történő adott belépéstől a hozzá tartozó kilépésig.
Hozzá kell tenni, hogy ugyanebben a szegmensmezőben tárolja a gép a változóparaméterek címeit is.
Az adott szegmens végrehajtásakor a gép mindig az utoljára lefoglalt szegmensmező adatait, tehát paramétereit, lokális változóit, illetve a kilépéskor az abban tárolt visszatérési címét használja.
A szegmensmezők számára a gép memóriát a veremből (angolul: stack, kiejtése: sztek) foglalja, ezért a szegmensmezőt gyakran veremkeretnek is nevezik.
A szegmensmezők létrehozásának, használatának, illetve felszabadításának megértéséhez most ismét végigkövetjük a Hanoi (3,'a','b','c') hívás végrehajtásának menetét, de minden egyes utasítás végrehajtása után feltüntetjük a szegmensmezők tartalmát is. Az újonnan lefoglalt szegmensmezőt az előzőek fölé írjuk, így mindig a legfelső lesz az, amihez az eljárás hozzáfér.
Egyszerűsíti a dolgot, hogy a Hanoi eljárásnál nincs változóparaméter és lokális változó.
Azért, hogy a működés könnyebben legyen követhető, megszámoztuk az egyes utasításokat és visszatérési címeket:
Kezdő hívás:
{1} hanoi(3,'a','b','c') { 1. cím }
eljárás:
procedure hanoi(n:integer;honnan,mivel,hova:char);
begin
if n>0 then begin
{2} hanoi(n-1,honnan,hova,mivel); { 2. cím }
{3} writeln(n:3,' korongot tedd ',honnan,' rudrol ',hova,' rudra');
{4} hanoi(n-1,mivel,honnan,hova) { 3. cím }
end
end;
A következő táblázat mindig az egyes utasítások utáni helyzetet mutatja, ha a torony h magassága 0, 1, 2, illetve 3.
Feltüntetjük azt is, mit ír ki a gép:
(Nem ír ki semmit, hiszen nincs mit mozgatni.)
1. korongot tedd a rúdról c rúdra
1. korongot tedd a rúdról b rúdra
2. korongot tedd a rúdról c rúdra
1. korongot tedd b rúdról c rúdra
1. korongot tedd a rúdról c rúdra
2. korongot tedd a rúdról b rúdra
1. korongot tedd c rúdról b rúdra
3. korongot tedd a rúdról c rúdra
1. korongot tedd b rúdról a rúdra
2. korongot tedd b rúdról c rúdra
1. korongot tedd a rúdról c rúdra
Alacsonyabb tornyok esetén még viszonylag egyszerű az események részletes nyomonkövetése, magasabb tornyok esetén már csak azt érdemes figyelni, mi történik a legfelső, tehát a Hanoi eljárás pillanatnyi hívása által hozzáférhető adatokkal.
A rekurzív hívások egymásba ágyazását érzékeltethetjük úgy is, hogy a bemutatott Hanoi eljárás első utasítása elé (közvetlenül a begin után) beszúrjuk a következő, nyomkövetést segítő utasítást:
writeln(' ':40-2*n,' Hanoi (',
n:1,',',honnan,',',mivel,',',hova,')');
Ha így futtatjuk le az eljárást hármas magasságú toronyra, akkor a következő eredményt kapjuk:
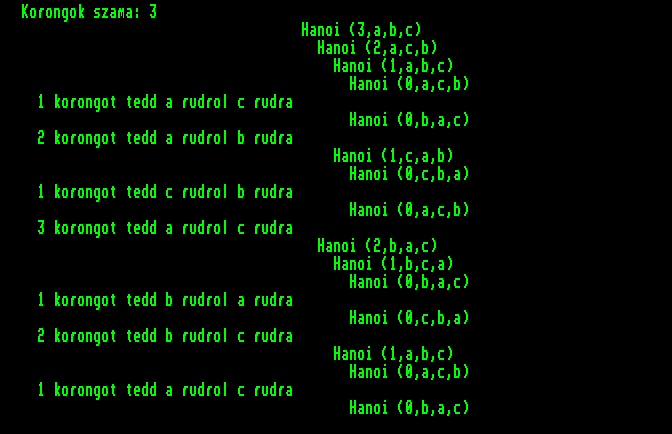
4.5.1. Feladat:
Módosítsa a Hanoi eljárás megoldását úgy, hogy feleannyi eljáráshívásra legyen csak szükség!
Ha rekurzív eljárást vagy függvényt írunk, természetesen nem kell mindig ilyen részletességgel átgondolnunk és megterveznünk az adatok és paraméterek különböző szintjeit és a szegmensmezők egymásra épülését, ezt ugyanis a gép elintézi helyettünk. Elég, ha a paraméterek jellegére (érték- vagy változóparaméter) és a lokális-globális változók megválasztására alkalmazzuk azokat a megfontolásokat, amelyeket a 4. fejezet elején megismertünk, és vigyázunk arra, hogy a rekurzió véget érjen, azaz valóban egyszerűbb esetekre vezessük vissza a megoldást.
Vizsgáljuk meg, mekkora az n magasságú Hanoi-torony átrakásához szükséges mozgatások m száma!
2
3
4
...
3
7
15
...
Általában, ha n magasságú torony átrakásához m(n) mozgatás kell, akkor n+1 magas toronyhoz
m(n+1) = 2*m(n)+1
mozgatás. Ebből m(n) kifejezhető n függvényében, de az előbbi táblázatból is kitalálható:
m(n)=2^n-1
Tehát a lépésszám a torony magasságának exponenciális függvénye, ami nagyon meredek növekedést jelent. n=64 esetén például m(64) körülbelül 1.8446744074*10^19, és ezek szerint a világvégéig körülbelül 5.0539024859*10^16 év van még hátra.
A rekurzív megoldás hatékonyságának érzékeléséhez javaslom az Olvasónak, hogy a feladatot oldja meg rekurzió nélkül, azaz úgy, ahogyan a szerzeteseknek naponta a következő korongot át kell tenniük: adott a három rúdon a torony valamilyen elrendezése, és egyetlen korongot kell áttenni úgy, hogy az a megoldás irányába változtasson a korongok elrendezésén.
A Hanoi-probléma nagyon jó a rekurzió szemléltetésére, de kicsi a gyakorlati jelentősége, hacsak a világvégé eljövetelének időpontjára tett becslést nem vesszük túl komolyan.
Most egy olyan eljárás következik, amely valódi problémát old meg rekurzióval, nagyon hatékonyan.
4.5.2 Példa:
Készítsünk eljárást táblázatban tárolt adatok nagyság szerint növekvő sorrendbe rendezésére és alkalmazzuk a telefonkonyv1 programban! A módszer legyen az úgynevezett gyorsrendezés (angolul: quick-sort, kiejtése: kvik szort)!
Megoldás:
A módszer lényege egy felosztási módszer: kiválasztjuk a táblázat tetszőleges elemét, nevezzük ezt alapelemnek, mert a többit ehhez fogjuk viszonyítani. Ezután először balról, azaz a táblázat elejétől indulva addig lépegetünk, amíg ennél az alapelemnél csupa kisebb elemet találunk. Ha egy elem nagyobb vagy egyenlő, akkor ott megállunk és a táblázat jobb oldalától, tehát végétől haladunk balra, de most akkor állunk meg, ha az alapelemnél nem nagyobb egy elem. Ekkor felcseréljük ezt a két elemet, és a következő, eggyel nagyobb, illetve kisebb indexű elemnél folytatjuk a keresést és cserét, egészen addig amíg valahol, remélhetőleg középtájon össze nem érünk. Például, ha alapelemnek a középsőt választjuk:
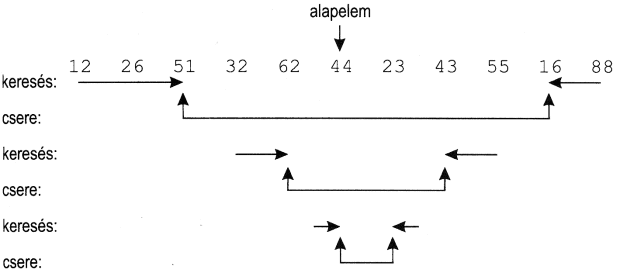
Az algoritmus után a táblázat azon a helyen, ahol összeértünk, két részre osztható; a bal oldalon lévő elemek egyike sem nagyobb, mint a jobb oldalon lévők:
12 26 16 32 43 23 44 62 55 51 88
A határ itt a 23 és 44 között van.
A táblázat teljes rendezettségéhez szükséges, hogy a felosztást külön-külön tovább folytassuk a táblázat két részére, majd annak két részére stb., amíg a felosztandó rész hossza 1 nem lesz.
A telefonkonyv1 programban először deklarálnunk kell egy elem típust.
program gyorsrendezes;
const nevhossz=30;szamhossz=13;tablahossz=100;
type nevt=array[1..nevhossz] of char;
szamt=array[1..szamhossz] of char;
elem=record
nev:nevt;
telszam:szamt;
end;
var tabla:array[1..tablahossz] of elem;
...
A teljes gyorsrendezés eljárás az előbbi definíciókkal:
procedure gyorsrendezes(tol,ig:integer);
var bal,jobb:integer;
csere:elem; { segedelem cserehez }
alapkulcs:nevt;
begin
bal:=tol;jobb:=ig; { intervallum hatarainal indul }
alapkulcs:=tabla[(tol+ig) div 2].nev; { viszonyitasi alap }
repeat { felosztas }
while tabla[bal].nev<alapkulcs do { felosztas }
bal:=bal+1; { kereses balrol }
while tabla[jobb].nev>alapkulcs do
jobb:=jobb-1; { kereses jobbrol }
if bal<=jobb then begin { nem kerultek el egymast }
csere:=tabla[bal]; { csere }
tabla[bal]:=tabla[jobb];
tabla[jobb]:=csere;
bal:=bal+1;jobb:=jobb-1 { kovetkezonel folytatjuk }
end
until bal>jobb; { elkerultek egymast }
if tol<jobb then gyorsrendezes(tol,jobb);
if bal<ig then gyorsrendezes(bal,ig)
end;
A táblázat rendezését a következő eljáráshívással hajthatjuk végre:
gyorsrendezes(1,utolso);
Például úgy, hogy a case-konstans listát még egy esettel bővítjük:
'r': BEGIN
Gyorsrendezes(1,utolso);
Writeln('Kesz')
Ez a módszer az átlagos végrehajtási időt tekintve tényleg igen gyors. Ha a felosztás valóban középen osztja két szakaszra az intervallumot, akkor a felosztások, azaz a rekurzív hívások száma log2n. Minden felosztásnál - ha részenként is, de - a teljes n hosszúságú táblázaton végig kell menni. Így az összehasonlítások teljes száma: n*log2n.
Az algoritmus hatékonysága szempontjából az a legrosszabb eset, ha a kiválasztott alapelem a vizsgált intervallumban éppen a legkisebb, vagy a legnagyobb. Ekkor ugyanis a felosztás csak ezt az egy elemet választja le. Ha az a szerencsétlen eset állna elő, hogy minden felosztás ilyen, akkor az algoritmus n^2-tel arányos összehasonlítást végez, tehát a leglassúbbak egyikévé válik. Ennek az esetnek azonban nagyon kicsi a valószínűsége.
További rekurzív algoritmusok találhatók a szegmensek szabályainak ismertetése után és az 5. fejezetben, a dinamikus adatszerkezeteknél.
4.5.2. Feladat:
Vizsgálja meg az azonosítók hatáskörét a gyorsrendezes eljárásban!
4.5.3. Feladat:
Próbáljon rendezni különböző táblázatokat a gyorsrendezes eljárással és a 3. fejezetben megismert rendezési módszerekkel, hasonlítsa össze a futási időket!
Mikor ne használjunk rekurziót?
Aki megismerte a rekurziót, könnyen abba a hibába eshet, hogy a módszer kényelmessége és eleganciája miatt akkor is használja, amikor nincs rá szükség, mivel a feladat egyszerűbben és hatékonyabban oldható meg egyszerű ciklus vagy ciklusok használatával.
Vannak problémák, amelyek természetükből adódóan rekurzívan oldhatók meg legkényelmesebben, például a gyorsrendezés vagy a Hanoi tornyai. De sok olyan feladat is van, amelyet megfogalmazni rekurzívan kényelmes, megoldani mégis ciklussal érdemes.
A ciklusokat azért említjük a rekurzióval kapcsolatban, mert mindig helyettesíthetők rekurzióval.
Tipikus példa erre a Fibonacci-számok kiszámítása. Emlékeztetőül: a nulladik ilyen szám 0, az első 1, a továbbiak pedig az őket közvetlenül megelőző kettő összegeként kaphatók meg. Az első néhány Fibonacci- szám tehát: 0 1 1 2 3 5 8 13 21 ...
Maga a definíció rekurzív, ezért az n-edik Fibonacci-szám kiszámítására első ötletünk egy rekurzív függvény lehet:
function fibonacci1(n:integer):integer;
begin
if n<=1 then fibonacci1:=n
else fibonacci1:=fibonacci1(n-1)+fibonacci1(n-2)
end;
Ez a megoldás elegáns ugyan, de van egy nagy hibája: növekvő n esetén rohamosan nő a végrehajtási idő. Ez onnan adódik, hogy az n-edik szám kiszámításához kell az n-1-edik és az n-2-edik, az n-1-edikhez az n-2-edik és az n-3-adik kiszámítása, így az n-2-edik Fibonacci számot kétszer kell az n-edik érdekében kiszámítani, az n-3-adikat hasonló okból 3-szor, az n-4-ediket 5-ször stb. A következő ábrái nyilak jelzik, hogy melyik Fibonacci-számhoz melyik előző kiszámítása szükséges, így a függőlegesen egymás alá kerülő nyilak száma megadja, hogy az adott Fibonacci-számot hányszor kell kiszámítani:
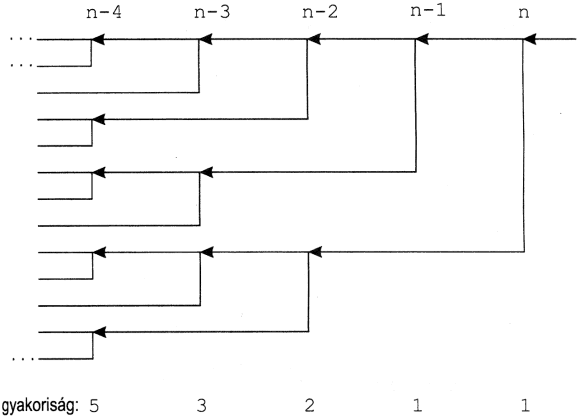
Láthatjuk, hogy ezek a gyakoriságértékek éppen a Fibonacci-számok, az n-k-adik értéket éppen Fibonacci(n-k+1)-szer fogjuk kiszámítani.
Mivel n növekedésével a Fibonacci-számok exponenciálisan nőnek, nem csoda, hogy rohamosan növekszik a futási idő.
A legegyszerűbb megoldás az, ha nem rekurzívan számolunk, hanem nullától felfelé egy ciklusban:
function fibonacci2(n:integer):integer;
var g,f,f1,f2:integer;
begin
if n=0 then fibonacci2:=0
else begin
f:=1;f1:=0;
for g:=2 to n do begin
f2:=f1;f1:=f; { elozo ertekek megorzese }
f:=f1+f2 { kovetkezp ertek }
end;
fibonacci2:=f
end
end;
Ez minden értéket csak egyszer számol ki, tehát a végrehajtási idő arányos n-nel.
A másik tipikusan rossz példa a rekurzióra a faktoriális kiszámítása. Erre a 4.2-1. példában láttunk egy nem rekurzív függvényt, de a megoldást rekurzívan is megfogalmazhatjuk:
function faktorialis(n:integer):integer;
begin
if n=0 then faktorialis:=1
else faktorialis:=n*faktorialis(n-1)
end;
Ehhez hasonlóan rossz példa a rekurzióra a binomiális együtthatók kiszámítását végző függvény is.
A binomiális együtthatókat szokás az úgynevezett Pascal-háromszög segítségével ábrázolni, ebben a szélső elemek értéke 1, a többi pedig a felette balra, illetve jobbra lévő egy-egy elem összege:
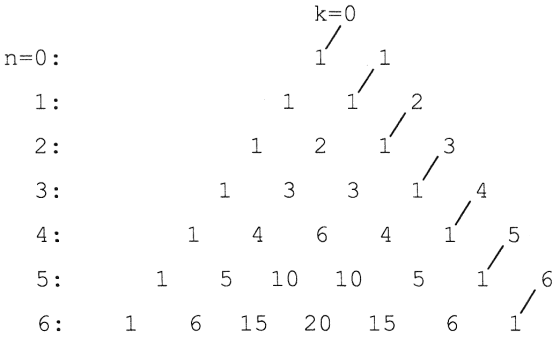
A fenti ábrának megfelelően jelölje n azt, hogy az adott szám hányadik sorban, k pedig azt, hogy hányadik ferde oszlopban van; mindegyiket nullától számozzuk.
Az n-edik sor k-adik elemét jelöljük Binom(n,k)-val, ekkor a belső elemekre:
Binom(n,k) = Binom(n-1,k-1) + Binom(n-1,k)
A binomiális együtthatókat meghatározó rekurzív függvény:
function binom1(n,k:integer):integer;
begin
if (k=0) or (k=n) then binom1:=1
else binom1:=binom1(n-1,k-1)+binom1(n-1,k)
end;
Nagy n esetén ez is meglehetősen lassú, hiszen például Binom(n, k) meghatározásához kétszer kell kiszámítani Binom(n-2,k-1) értékét, háromszor Binom(n-3,k-2) és Binom(n-3,k-1) értékét, a végzendő műveletek száma n növekedésével itt is közel exponenciálisan nő.
Ha gyorsabb megoldást keresünk, elvileg felhasználhatjuk a következő azonosságot:
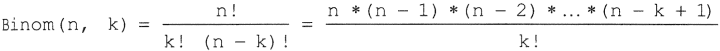
ahol a felkiáltójel faktoriálist jelent.
Az így számoló függvény:
function binom2(n,k:integer):integer;
var b,g:integer;
begin
b:=n;
for g:=n-k+1 to n-1 do b:=b*g; { szamlalo }
for g:=2 to k do b:=b div g; { nevezo }
binom2:=b;
end;
A módszer hátránya, hogy a rekurzív módszernél például Binom(18,7)=31824 is kiszámítható 16 bites egészeket használó gépeken, itt azonban a számláló meghatározásakor lényegesen kisebb n értéknél is átlépjük maxint értéket. A módszer némileg javítható, ha valós b munkaváltozót használunk, de ez nagy n esetén kerekítési és így pontossági problémákat okozhat.
4.5.5. Feladat:
Miért használtunk b munkaváltozót a binom2 függvényben ahelyett, hogy mindjárt binom2-ben végeztük volna a szorzásokat és osztásokat?
Javíthatjuk a rekurzív módszer hatékonyságát úgy is, hogy a már kiszámított értékeket eltesszük egy tömbbe, és csak akkor számolunk rekurzív módon, ha a tömb még nem tartalmazza a keresett binomiális együtthatót.
Legyen a regib:array[0..m,0..m] of integer tömb globális a binom3 függvényre nézve, és a függvény első hívása előtt kapjon ilyen kezdeti értéket:
for sn:=0 to m do begin { sorok }
regib[sn,0]:=1;regib[sn,sn]:=1; { szelso elemek }
for sk:=1 to sn-1 do { oszlopok }
regib[sn,sk]:=0 { belso elemek }
end;
ahol m konstans értékét maxint értékétől függően kell megválasztani, sn és sk pedig egész típusú segédváltozók.
function binom3(n,k:integer):integer;
begin
if regib[n,k]=0 then { meg nincs kiszamitva }
regib[n,k]:=binom3(n-1,k-1)+binom3(n-1,k);
binom3:=regib[n,k]
end;
Vegyük észre, hogy az 1 értékű szélső elemeket strázsának használtuk, így a binom3 függvényben nem kellett külön figyelnünk, hogy a Pascal-háromszög szélére értünk-e.
Ha egyébként programunkban sokszor van szükség binomiális együtthatókra, akkor legegyszerűbb előre kiszámolni azokat, majd az így kapott tömbből szükség esetén elővenni.
A
binom:array[0..m,0..m] of integer;
tömb így tölthető fel:
for sn:=0 to m do begin
binom[sn,0]:=1;binom[sn,sn]:=1;
for sk:=1 to sn-1 do
binom[sn,sk]:=binom[sn-1,sk-1]+binom[sn-1,sk]
end;
Mi nem rekurzió?
4.5.4. Példa:
Készítsünk függvényt két egész érték maximumának meghatározására!
Megoldás:
A megoldás magától értetődő:
function max(a,b:integer):integer;
begin
if a>b then max:=a else max:=b
end;
4.5.5. Példa:
Az előbbi max függvény segítségével hogyan lehet 3, 4, 5 stb. darab egész szám maximumát meghatározni?
Megoldás:
Három szám: p, q és r maximumát például így tehetjük s-be:
s:=max(p,q);
s:=max(s,r);
de ezt a két lépést össze is vonhatjuk:
s:=max(max(p,q),r);
Ez nem rekurzív hívás, hiszen a külső max függvény hívása előtt a gépnek először meg kell határoznia a paraméterek értékét. Ehhez tehát meghívja a max függvényt p és q értékével, majd amikor az befejeződött, ismét hívja max-ot, paraméterként az előbb kapott értéket és r értékét adva át.
Figyeljük meg, hogy a max függvénynek mindig csak egy hívása van érvényben, először csak a p és q paraméterű, másodszor pedig az előbb kapott érték és r a paraméter.
Hogy ez nem rekurzió, az onnan is látszik, hogy max deklarációjában nem hívjuk a max függvényt sem közvetlenül, sem közvetve.
4 darab szám maximuma hasonló módon számítható ki:
w:=max(max(p,q),max(r,s));
amit írhatunk más módon, például így is:
w:=max(p,max(q,max(r,s)));
4.5.6. Feladat:
Készítsen rekurzív és nem-rekuzív függvényt is az úgynevezett Csebisev polinom kiszámítására!
Ennek értékét az n fokszám és az x valós paraméter határozza meg a következő módon:
T(0,x) = 1
T(1,x) = x
T(2,x) = 2x^2-1
T(n,x) = 2xT(n-1,x)-T(n-2,x)
Szegmensek, azaz eljárások és függvények deklarációja és hívása
Az eljárások és függvények deklarálásának szabályait együtt adjuk meg. Ahol egy szabály mindkettőre vonatkozik, ott a közös "szegmens" szót használjuk az "eljárás, illetve függvény" kifejezés helyett.
Az első 7 szabály a szegmensek deklarációjának, a többi pedig a szegmensek hívásának szabályaival foglalkozik.1. Az eljárásdeklaráció formai szabályai:
eljárásdeklaráció:
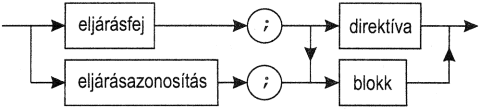
eljárásfej:

eljárásazonosítás:
procedure azonosító
direktíva:
forward
(a)
2. A függvénydeklaráció forma szabályai:
függvénydeklaráció:
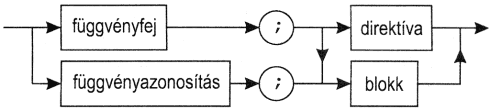
függvényfej:
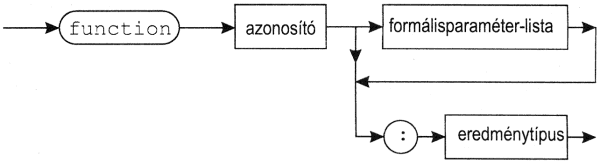
ahol eredménytípus:
egyszerűtípus-azonosító vagy mutatótípus-azonosító
(b)
függvényazonosítás:
function azonosító
3. A forward használata:
A szegmens deklarációjának - ahogy az az előbbi szabályokból is kiderült - három alakja lehet, ezeket rendre a szegmensdeklaráció első, második és harmadik alakjának nevezzük:első alak:

második alak:

harmadik alak:

Az első alak a szegmens deklarálásának legegyszerűbb és leggyakoribb módját mutatja. Akkor használjuk, ha az így deklarált szegmens blokkjában nem hivatkozunk olyan további szegmensre, amelyet csak ez után deklarálunk.
A második és harmadik alakot akkor használjuk, ha olyan szegmenst akarunk deklarálni, amely közvetett módon hívja saját magát, azaz közvetetten rekurzív: olyan szegmenst hív, amely - közvetve vagy közvetlenül - ezt a szegmenst hívja és ezzel a szegmenssel azonos szinten van deklarálva.
Ilyenkor először a szegmens deklarációjának második alakját használjuk, amely megadja mindazokat az információkat, amelyek e szegmens hívásához szükségesek, azaz hogy eljárásról vagy függvényről van-e szó, mi ennek a neve, milyenek a formális paraméterei, függvény esetén milyen az eredmény típusa.
Ezt kell, hogy kövessék a szegmens által hívott további szegmensek deklarációi, majd ugyanilyen névvel a harmadik alakú szegmensdeklaráció, amely megadja ugyanennek a szegmensnek a blokkját.
A harmadik alak a szegmensazonosítással kezdődik. Ez abban különbözik a szegmensfejtől, hogy nincs benne formális paraméterlista, és függvény esetén eredménytípus-megadás sem, hiszen mindezeket az ugyanezen szegmenshez tartozó második, azaz forward-os alakban már megadtuk. A harmadik alakban használt eljárás-, illetve függvényazonosító ugyanaz, minta forward-os alakban, ezzel adjuk meg, hogy melyik fej tartozik hozzá. E harmadik alak tartalmazza az elvégzendő tevékenységeket leíró blokkot. Mivel ebben a blokkban hivatkozni akarunk olyan szegmensre, amely az ehhez tartozó második alak használatakor még nem volt deklarálva, a harmadik alakú deklarációnak a hivatkozott szegmensek deklarációi után kell állnia.
A második és harmadik alakot mindig párban használjuk, mégpedig ilyen sorrendben. Ugyanabban a szegmensdeklarációs részben kell lenniük, de a kettő között általában - de nem kötelezően - további szegmensek deklarációi is szerepelnek.
Az itt következő példa tipikus esetet mutat. Az A eljárás és a B függvény kölcsönösen hívja egymást:
...
{ A, masodik alak }
procedure A (p1,p2:integer); forward; { az A eljaras feje }
{ B, első alak }
function B(v :char):real; { a B függvény feje }
var v1,v2:char;
begin { B utasitasresze }
...
A(ord(v1,122); { az A eljaras hivasa }
...
end;
procedure A; { az A eljaras azonositasa }
var g:integer;
begin
...
if B('q')*3<... then ... { B hivasa }
...
end;Először A fejét adtuk meg, amely tartalmazza az a formális paramétereinek specifikációját is, majd a B függvényt, amely hivatkozhat az a eljárásra, hiszen ehhez előzőleg már megadtuk a fejét. Ezek után következik A azonosítása és a blokkjának megadása, melyben hivatkozunk a B függvényre. Mivel a formális paramétereit előzőleg már megadtuk, erre itt nincs szükség.
4. Függvény blokkjában legalább egy értékadó utasításnak kell szerepelnie, amelynek bal oldalán a függvény neve áll.
Hiba történik, ha a függvény végrehajtása úgy fejeződik be, hogy nem goto utasítással lépünk ki a függvény blokkjából és nem történt meg az értékadó utasítás végrehajtása a függvény nevére.5. Formális paraméterek:
formálisparaméter-lista:

formálisparaméter-szakasz:
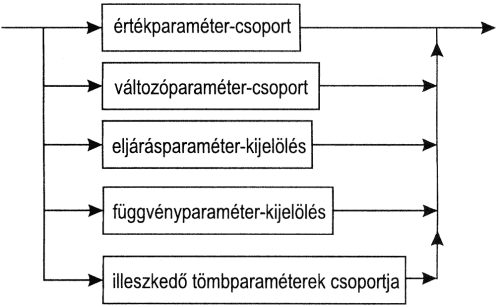
értékparaméter csoport:

változóparaméter-csoport:

eljárásparaméter-kijelölés:
eljárásfej
függvényparaméter-kijelölés:
függvényfej
Az illeszkedő tömbparaméterekre vonatkozó szabályokat a 7. pont adja meg.
5.1. A formálisparaméter-listán megadott értékparaméter-azonosító, változóparaméter-azonosító, eljárásazonosító, függvényazonosító, valamint az illeszkedő tömbparaméter azonosítója az illető azonosítót mint a formálisparaméter-listához tartozó szegmens formális paraméterét definiálja. Definíciós pontja az a hely, ahol a formális paraméterek listáján előfordul, hatásköre pedig az ezeket közvetlenül tartalmazó formálisparaméter-lista további része és ha van, akkor a formálisparaméter-listához tartozó blokk. (d)
5.2. Értékparaméter a szegmensben úgy használható, mint egy változó, amelynek a típusát az utána átló típusazonosító adja meg. Ez a típus nem lehet adatállomány (file) vagy olyan összetett típus, amelynek van adatállomány típusú eleme.
A neki megfelelő aktuális paraméter olyan kifejezés lehet, amelynek az értéke értékadáskompatibilis a formális paraméter típusával. A formális paraméter e kifejezésnek a szegmens hívásakor érvényes értékét kapja meg.
Az értékparaméter tehát a hívás helyéről a szegmens blokkja felé közvetít értéket, fordítva, azaz a szegmensből a hívás helye felé nem.5.3. A változóparaméternek megfelelő aktuális paraméternek vagy változónak, vagy formális érték- -vagy változóparaméternek kell lennie, típusának pedig kompatibilisnek kell lennie a formális változóparaméter típusával. Az aktuális paraméterként használt változóhoz illetve formális paraméterhez a hozzáférés a szegmens hívásakor történik meg és ez a hozzáférés marad érvényben a szegmens teljes végrehajtása során. (e)
A formális változóparaméter úgy használható, mint egy változó, kivéve, hogy nem lehet for utasítás ciklusváltozója. A formális változóparaméterre tett hivatkozás a neki megfelelő aktuális paraméterre történő hivatkozást jelenti, így például a formális változóparaméter értékének megváltoztatása a neki megfelelő aktuális paraméter értékének megváltoztatását okozza. Ily módon a változóparaméterek segítségével a szegmensek értékeket adhatnak vissza a hívó programrésznek.
Aktuális változóparaméter nem lehet sem változórekord vezérlőmezője, sem packed összetett típus eleme. (f)
Adatállomány (file) csak változóparaméter lehet.
5.4. Eljárásparaméter aktuális paraméterének olyan eljárás azonosítójának kell lennie, amely a programban van deklarálva - azaz nem lehet előre deklarált eljárás és paraméterlistája, ha van, egybevág a neki megfelelő formális paraméter paraméterlistájával. (A paraméterlisták egybevágóságát a 6. szabály írja le.)
A szegmens blokkjában a formális paramétereljárásra tett hivatkozás az aktuális paraméterként megadott eljárásra történő hivatkozást jelenti.
5.5. Függvényparaméter aktuális paraméterének olyan függvény azonosítójának kell lennie, amely a programban van deklarálva - tehát nem előre deklarált függvény -, paraméterlistája, ha van, egybevág a neki megfelelő formális paraméter paraméterlistájával, eredménytípusa pedig azonos vele. (g)
A szegmens blokkjában a formális paraméter függvényre tett hivatkozás az aktuális függvény paraméterre történő hivatkozást jelenti.
6. Két paraméterlista egybevág, ha ugyanannyi paramétert tartalmaz, és ezek a paraméterek páronként rendre egybevágnak.
Két paraméter egybevág, ha a következő öt feltétel bármelyike teljesül:
azonos típusú értékparaméterek:
azonos típusú változóparaméterek;
mindkettő eljárásparaméter, amelyeknek vagy nincs paraméterük, vagy a paraméterlistájuk egybevág;
mindkettő függvényparaméter, amelyek eredménytípusa kompatibilis, és amelyeknek vagy nincs paraméterük, vagy paraméterlistájuk egybevág;
- mindkettő illeszkedő tömbparaméter, amelyek egybevágóak.
Két illeszkedő tömbparaméter egybevágó, ha a következő négy feltétel mindegyike teljesül:
- mindkettő értékparaméter vagy mindkettő változóparaméter;
- indextípus-azonosítójuk ugyanazt a típust adja meg;
- vagy az elemtípusukat megadó típusazonosítók adnak meg azonos típust, vagy az elemtípusukat megadó illeszkedőtömb-kijelölések egybevágóak;
- mindkettő pakolt vagy pakolatlan illeszkedő tömbparaméter.
7. Illeszkedő tömbparaméter (c) (k)
illeszkedö tömbparaméterek csoportja:

változó illeszkedő tömbparaméterek csoportja:

érték illeszkedő tömbparaméterek csoportja:

illeszkedő tömbparaméter kijelölése:

pakolt illeszkedő tömbparaméter kijelölése:
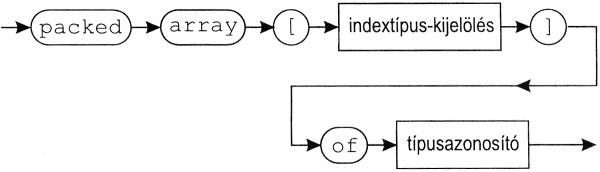
(h)
pakolatlan illeszkedő tömbparaméter kijelölése:
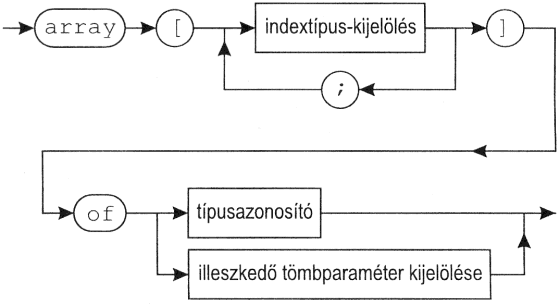
indextípus-kijelölés:

ahol alsó indexhatár:
azonosító
felső indexhatár:
azonosító
Például:array[u..v:t1] of array [j..k:t2] of t3
helyett
array[u..v:t1;j..k:t2] of t3
használható.
Az alsó és felső indexhatárt megadó azonosítók definíciós pontja az a hely, ahol az indextípus-kijelölésben előfordulnak, hatáskörük pedig az ezeket közvetlenül tartalmazó formális paraméterlista további része és ha van, akkora formális paraméterlistához tartozó blokk. (d) A szegmens végrehajtása alatt az alsó indexhatár a megfelelő aktuális paraméter megfelelő indexének deklarált legkisebb lehetséges értékét, a felső pedig deklarált legnagyobb értékét adja meg, típusa az indextípus-kijelölésben megadott típus. Az indexhatárokat megadó azonosítók nem konstansok és nem is változók, de használatukra a konstansokra vonatkozó szabályok érvényesek, kivéve, hogy nem definiálhatunk felhasználásukkal további konstansokat és nem használhatjuk őket intervallumtípus megadásában, tehát tömb indextartományának megadásában sem. (k)
A változó illeszkedő tömbparaméterek használatára egyebekben ugyanazok a szabályok érvényesek, mint az egyéb típusú változóparaméterekre.
Az érték illeszkedő tömbparaméterekre általában ugyanazok a szabályok érvényesek, mint az egyéb típusú értékparaméterekre, kivéve, hogy formális illeszkedő tömbparaméter nem használható aktuális érték illeszkedő tömbparaméternek, legfeljebb annak olyan indexes eleme, amely maga nem illeszkedő tömbparaméter típusú, (i)
- t1 indextípusa kompatibilis t2-vel;
- t1 indextípusának legkisebb és legnagyobb értéke a t2 által megengedett zárt intervallumba esik;
- t1 elemtípusa megegyezik a formális illeszkedő tömbparaméter elemtípusával, vagy az elemtípusokra is teljesül az itt felsorolt 4 szabály;
- vagy mindkettő pakolt, vagy mindkettő pakolatlan.
Egy illeszkedő tömbparaméter-csoport elemeinek megfelelő aktuális tömbparamétereknek azonos típusúaknak kell lenniük. (j)
A formális illeszkedő tömbparaméter típusa olyan tömbtípus, amely minden egyéb tömbtípustól különbözik, elemtípusát a megfelelő illeszkedő tömbparaméter kijelölésének utolsó elemeként megadott típusazonosító adja meg, indextípusát pedig az aktuális paraméter neki megfelelő indextípusa.
- Nem lehet olyan illeszkedő tömbtípust definiálni, amely a string, azaz karakterlánc típusnak felel meg. (l)
8. Eljárás hívása az úgynevezett eljárásutasítással történik, alakja:
eljárásutasítás:
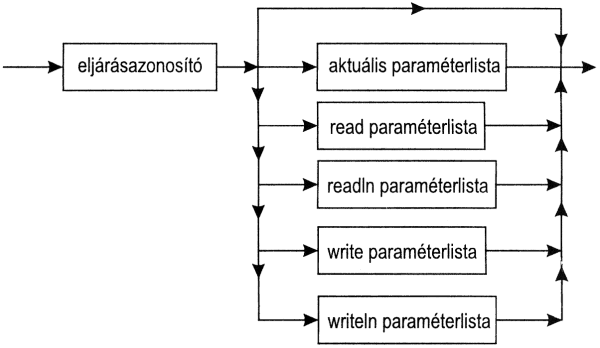
aktuális paraméterlista:
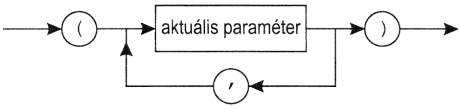
ahol aktuális paraméter lehet:
- kifejezés
- változóhivatkozás
- eljárásazonosító
- függvényazonosító
Az eljárásutasításban read paraméterlista, readln paraméterlista, write paraméterlista, és writeln paraméterlista csak akkor adható meg, ha az előtte álló eljárásazonosító az előre deklarált read, readln, write, illetve writeln. (Ezeknek az eljárásoknak a használata részletesen az adatállományok leírásánál található meg, itt csak a teljesség kedvéért tettünk említést róluk.)
9. Ha az eljárásnak van formális paramétere, akkor az eljárásutasításban meg kell adni egy aktuális paraméterlistát, amely
- ugyanannyi elemet tartalmaz, mint a hívott eljárás formális paraméterlistája;
- az aktuális paramétereknek a felsorolás sorrendjében rendre a formális paramétereknek megfelelő kifejezéseknek, változóhivatkozásoknak, eljárásazonosítóknak, illetve függvényazonosítóknak kell lenniük, ahogyan azt az 5. szabály megadja.
Az aktuális értékparaméterek értékének kiértékelése, illetve az aktuális változóparaméterekhez való hozzáférés az eljárás hívásakor, a hívott eljárás blokkjának végrehajtása előtt történik meg, az aktuális változóparaméterekhez való hozzáférés az eljárás blokkjának végrehajtása alatt nem változik. (e)
Az egyes aktuális paraméterek meghatározásának egymás közötti sorrendje megvalósításfüggő. (n)
10. Az eljárásutasítás végrehajtása a következő módon történik:
a gép meghatározza az aktuális paramétereket és átadja azokat az eljárásnak a paraméterek jellegének megfelelően;
végrehajtja az eljárás blokkját (amely tartalmazhat további szegmenshívásokat is); (o)
ha az eljárás blokkja azért fejeződik be, mert a blokk végrehajtása során elértük a blokk végét, akkor visszatér az eljárás hívását közvetlenül követő helyre;
11. A függvény hívása a függvény azonosítójának és - ha vannak paraméterei, akkor - az aktuális paramétereknek egy kifejezésben való megadásával történik. A kifejezés állhat csak magának a függvénynek a hívásából is.
függvényhívás:

12. Ha a függvénynek van formális paramétere, akkor a függvényhívásban meg kell adni egy aktuális paraméterlistát, amelyre ugyanazok a szabályok érvényesek, mint amiket a 8. és 9. pont az eljárások paramétereiről leír.
13. A függvény végrehajtása az eljárásutasítás végrehajtásával (10. pont) azonos módon történik azzal a kiegészítéssel, hogy
a függvény blokkjának végrehajtása során legalább egy értékadásnak kell történnie a függvény azonosítójára az 5. szabály szerint;
Magyarázatok, megjegyzések:
(a) A Pascal nyelvben a forward az egyetlen szabványos direktíva, de néhány megvalósítás továbbiakat is használ. A leggyakoribb az extern vagy external direktíva, ez olyan szegmens használatát jelenti, amelyhez tartozó blokk a programon kívül van deklarálva és általában valamilyen könyvtárból vehető elő, legtöbbször lefordított alakban.
(b) Függvény eredménytípusa tehát nem lehet összetett típus.
(c) Illeszkedő tömbparamétert csak a Pascal nyelv úgynevezett 1-es szintű, azaz teljes megvalósításának kell tudnia kezelni, a 0-s, azaz alapszintű megvalósításnak nem. A gyakorlatban használt Pascal rendszerek (ideértve a Turbo Pascalt és a HiSoft-Pascalt is) szinte mind 0-s szintűek.
(d) Egy példa a formális paraméterek hatáskörének bemutatására:
type t=...;
...
procedure pr(a,b:t; c:real; var t:char; { t innentol formalis par. }
function fv(p1,a:real):boolean; var z=integer);
var ... { pr eljaras lokalis valtozoi }
begin
...
if fv(z*2.5,c-3) then ...
...
a:=... { a itt a pr eljaras formalis parametere }
...
end;
Itt a, b, c, t, fv és z a pr eljárás formális paraméterei. Hatáskörük ott kezdődik, ahol formális paraméterként definiálva vannak, és a pr végéig tart, de nem tartozik bele fv paraméterlistája, ahol például a segítségével az fv függvény második paraméterének típusát adjuk meg.
t először még mint a pr eljárás a és b paraméterének típusát megadó típusazonosító szerepel, csak később következik formális paraméterként való definiálása.
p1 nem formális paramétere a pr eljárásnak, mivel nem pr formális paramétereinek listáján szerepel, hanem az fv nevű függvényparaméter első paraméterét nevezi meg. fv második paraméterének a az azonosítója, ez tehát fv paraméterlistáján más jelentéssel bír, mint a pr eljárás többi részében, p1 és a ilyen értelmű hatásköre csak fv paraméterlistájának végéig tart, mivel az fv függvényhez nem tartozik blokk. Ebből látható, hogy az fv paraméterlistáján használt p1 és a nevek nem is lényegesek, hiszen csak fv formális paramétereinek számát és típusát adjuk meg segítségükkel, a továbbiakban sehol sem hivatkozunk rájuk.(e) Az, hogy az aktuális változóparaméterhez való hozzáférés állandó marad a szegmens végrehajtása során, például így szemléltethető:
program varparam;
var t:array[1..10] of integer;
g:integer;
procedure p(var par:integer);
begin
writeln('Elejen: g = ',g,' par = ',par);
g:=g+1;
writeln('Vegen: g = ',g,' par = ',par);
end;
begin
for g:=1 to 10 do
t[g]:=g; { t feltoltese }
g:=3;
p(t[g]); { t[3] az aktualis parameter}
writeln('Utana: g = ',g,' t[g]= ',t[g]);
end.A fenti program a következőt írja ki:
Elejen: g = 3 par = 3
Vegen: g = 4 par = 3
Utana: g = 4 t[g]= 4(f) Azt, hogy miért nem lehet aktuális változóparaméter egy packed összetett változó eleme, egy példán mutatjuk be:
...
var t:packed array[1..10] of boolean;
...
procedure pr(var log:boolean;...);
...
begin
...
log:=... { ertekadas a formalis, tehat az aktualis paramterenek }
...
end; { pr eljaras vege }
begin
...
pr(t[g]); { hibas! }
...Ha például ezt a programrészletet a Pascal-8000 fordítóprogrammal próbálnánk lefordítani (ami egyébként a most bemutatásra kerülő szintaktikai hiba miatt nem is sikerülne), a következő történne: mivel a gép az önálló boolean változókat, és így a log formális paraméter értékét is 4 byte-on tárolja, a log-ra vonatkozó értékadás a memória 4 byte-ját változtatná meg. Az aktuális paraméter - hibásan - egy packed tömb eleme, ilyen esetben a gép egy-egy logikai értéket 1-1 byte-on tárol. Az eljáráson belül nem lehet eldönteni, hogy később melyik esetben fogunk teljes hosszúságú, és mikor a pakolt tárolásnak megfelelően rövidebb aktuális paraméteri használni. Az eljárásban mindig 4 byte-os értékadás történik a normál logikai adattípusnak megfelelően. Így ha megengednénk ezt az aktuális paramétert, akkor abban 4 egymást követő byte, tehát 4 szomszédos tömbelem is megváltozna, és ez nyilvánvalóan hibát okozna.
(g) Ha mégis szükségünk lenne arra, hogy egy előre deklarált függvényt adjunk meg aktuális függvényparaméterként, akkor deklaráljunk olyan függvényt, amely pontosan azt adja eredményül, mint a szabványos:
{ Hatarozott integral numerikus meghatarozasa }
function integral(function f(p:real):real;...):real;
{ Az elso parameter az integralando fuggveny }
... { az integral fuggveny tovabbi resze }Ha ezzel akarjuk integrálni a sin függvényt, akkor a
v:=integral(sin,...)
függvényhívás az 5.5 szabály értelmében formailag hibás, ezért deklaráljunk egy sinus nevű függvényt:
function sinus (x:real):real;
begin
sinus:=sin(x); {az elore deklaralt sin függvényt hívjuk }
end;Ezt már megadhatjuk aktuális paraméternek, hiszen sinus nem előre deklarált függvény:
v:=integral(sinus,...)
Érdemes még megjegyezni, hogy e helyettesítő függvényt közvetlenül nem deklarálhatjuk sin nevűre, hiszen ez rekurzív, mégpedig végtelen rekurzív hívást jelentene. Ha mégis ragaszkodunk hozzá, hogy továbbra is sin legyen a paraméterként átadható szinuszfüggvényünk neve, először egy közvetítő függvényt kell deklarálnunk, ez lehet például az előbb megadott sinus függvény, majd ezzel deklarálhatjuk a paraméterként is átadható sin függvényt:
function sin(x:real):real;
begin
sin:=sinus(x);
end;Fontos, hogy a sinus és sin deklarációk ilyen sorrendben legyenek.
Hasonló megoldásokat használhatunk, ha előre deklarált eljárást akarunk formális paraméterként átadni, bár erre sokkal ritkábban van szükség.
(h) Pakolt illeszkedő tömbparaméternek tehát csak egy indexe lehet.
(i) Ez a szabály azt mondja ki, hogy egy teljes érték illeszkedő tömbparaméter semmilyen formában nem adható át aktuális paraméterként további szegmensnek, tehát a következő példában az elj4-en belül feltüntetett egyik eljáráshívás sem megengedett:
...
type tt=array[1..10] of real;
...
procedure elj1(p1:tt;...);
... begin ...end;
procedure elj2(var p2:tt;...);
... begin ...end;
procedure elj3(p3:array[a..f:integer] of real;...);
... begin ...end;
procedure elj4 (p4:array[al..fel:integer] of real;..);
begin
...
elj1(p4,...); { hibasak! a tipusok nem azonosak, }
elj2(p4,...); { mivel az illeszkedo tombpar. kulon tipust kevisel }
elj3(p4,...); { hibasak! formalis ertek illeszk. tomb parameter }
elj4(p4,...); { nem lehet aktualis illeszkedo tombpar. }
...
end;(j) Tekintsük például a következő definíciókat:
var
t1,t2:array[1..10] of real;
t3,t4:array[1..20] of real;
...
procedure pr(a,b:array[tol..ig:integer] of real;
c,d:array[al..fel:integer] of real;)
...
begin
...
end;Itt a pr eljárás a és b formális paramétere egyetlen paramétercsoportban szerepel, míg c és d egy ettől függetlenben.
A szabály értelmében helyesek a következő hívások:pr(t1,t2,t3,t4)
pr(t3,t4,t1,t2)
pr(t1,t2,t2,t2)
pr(t1,t1,t1,t1)mert az egyes paramétercsoportok elemeinek megfelelő aktuális paraméterek azonos típusúak voltak. Hibás viszont a következő két hívás:
pr(t2,t3,t4 ,t3) { t2 es t3 tipusa kulonbozik }
pr(t4,t3,t3,t1) { t3 es t1 tipusa kulonbozik }(k) Az illeszkedő tömbparaméter fogalmát a Pascal nyelv szabványának megalkotói arra szánták, hogy egységes és rögzített formában váljon lehetővé adott eljárással vagy függvénnyel különböző méretű tömbök feldolgozása.
E paramétertípussal például két különböző méretű tömb elemeinek átlagát a következő módon határozhatjuk meg:
var
t1:array[1..10] of real;
t2:array[1..100] of real;
function atlag(t:array[also..felso:integer] of real):real;
var g:integer;
s:real;
begin
s:=0;
for g:=also to felso do s:=s+t[g];
atlag:=s/(felso-also+1);
end;
...
begin
...
write(' t1 atlaga = ',atlag(t1),' t2 atlaga = ',atlag(t2));
...Itt az atlag eljárás egyetlen paramétere olyan illeszkedő tömbparaméter, amely értékparaméter, elemtípusa real, és egyetlen indexe van: az egészek egy intervalluma.
A write utasításban először t1, majd t2 elemeinek átlagát számoltatjuk ki vele; az also, illetve felso nevű indexhatárok értéke az első esetben 1 és 10, a másodikban 0 és 100 lesz, az aktuális tömbparaméterek deklarált indexhatárainak megfelelően. Ezeket az also és felso nevű értékeket az eljárásban tetszőleges kifejezésben felhasználhatjuk, természetesen értéket nem kaphatnak.
Az illeszkedő tömbparaméter tehát nemcsak az aktuális paraméterként megadott tömb értékét közvetíti a szegmens és a külvilág között, hanem annak indexhatárait is a szegmens felé.Az illeszkedő tömbtípus nem adattípus abban az értelemben, ahogyan más adattípusok, így például nem lehet ilyen típusazonosítót, sőt változót sem deklarálni, csak szegmens paramétertípusa lehet ilyen.
String típusú illeszkedő paraméter azt jelentené például, hogy az ilyen formális paraméter értékét egyetlen write utasítással ki lehetne írni, vagy a <, > stb. relációs műveleteket el lehetne vele végezni. Ez nemcsak azért nem lehetséges, mert bár a stringtípus hasonlít a tömbre, mégsem valódi tömbtípus, hanem azért sem, mert valahogyan biztosítani kellene, hogy az index alsó határa 1 legyen. Ez például a következő illeszkedő tömbparaméter kijelölést tenné szükségessé:packed array[1..hossz:integer] of char
ami ellentmond a 7. szabályban megadott alaknak.
A különböző jellegű formális paramétereknek megfelelő aktuális paraméterek összefoglalva:
formális paraméter: aktuális paraméter: értékparaméter
változóparaméter
eljárásparaméter
függvényparaméter
érték-illeszkedő tömbpar.
változó-illeszkedő tömbpar.kifejezés
változóhivatkozás
eljárásazonosító
függvényazonosító
tömbváltozó-hivatkozás
tömbváltozó-hivatkozásTermészetesen további szabályokat is be kell tartani a paraméterek típusára, a szegmensparaméterek formális paraméterlistájára stb. vonatkozóan.
(n) E szabály értelmében az egyes megvalósítások eltérhetnek abban, hogy melyik aktuális paramétert határozza meg a gép először, másodszor stb.
(o) A blokk végrehajtásának megkezdésekor a blokk lokális változóinak értéke meghatározatlan, így első felhasználásuk előtt értéket kell kapniuk. A blokkból kilépve a lokális változók értéke elvész, ezért ha ugyanezen blokkba újra belépünk, a lokális változók értéke ismét meghatározatlan lesz.
(p) Ha a függvény blokkjából goto utasítással lépünk ki, nincs értelme a függvény értékéről beszélni, hiszen félbeszakad a függvény hívását tartalmazó kifejezés feldolgozása, így a függvény értékének felhasználása nem történik meg. Ilyenkor nem okoz hibát, ha a goto-val történt kilépésig a függvény azonosítója nem kapott értéket.
Közvetett rekurzió
"- Mindent, ami megtörténik - mondta - feljegyzel.
- Minden, amit feljegyzek, megtörténik - szólt a felelet."
[0] 188. oldal
4.5.6. Példa:
Készítsen programot, amely kifejezéseket ún. fordított lengyel alakúra hoz. Az átalakítandó kifejezésekben az egyszerűség kedvéért csupa egykarakteres szimbólum szerepel (=, #, <, >, +, -, *, /), és a kifejezés végét olyan karakter - például szóköz vagy újsor jel - jelzi, amely nem tartozik a megadottak közé. A # karaktert a <> (nem egyenlő) jelölésére használjuk.
A kifejezések lengyel alakja, illetve fordított lengyel alakja abban különbözik az általunk megszokottól, hogy nem tartalmaz zárójelet, a műveleteknek nincs precedenciájuk, a kiszámítás sorrendjét a kifejezés felírási sorrendje határozza meg, és a lengyel alaknál a műveleti jel az operandusok előtt, a fordított lengyel alaknál pedig az operandusok után áll. Ezért az általunk megszokott alakot szokás még a kifejezés infix alakjának, a lengyel alakot - amely ezt a nevet első alkalmazója, Jan Lukasiewicz lengyel matematikus után kapta -, prefix alaknak, a fordított lengyel alakot pedig posztfix alaknak is nevezni.
Példák:
(infix)
(posztfix)
(prefix)a
a+b
(a+b)
a/b
a/b*c
a*b-c
(a*b)-c
a*(b-c)
a+b/c
(a+b)/c
a<b*(c-d)a
ab+
ab+
ab/
ab/c*
ab*c-
ab*c-
abc-*
abc/+
ab+c/
abcd-*<a
+ab
+ab
/ab
*/abc
-*abc
-*abc
*a-bc
+a/bc
/+abc
<a*b-cd
Megoldás:
Az előbbi példákból látható, hogy a fordított lengyel alakra való átalakításkor a műveleti jelet a két operandus mögé kell tennünk, és ha a teljes operandus zárójelben van, akkor egyszerűen elhagyhatjuk a zárójeleket.
Az összeg fordított lengyel alakra való átalakításának gondolatmenete tehát:
Teljesen hasonló módon alakítható át a tag és a kifejezés is.
A tényező átalakítása eltér ezektől; itt a kezdő- és végzárójeleket kell csak eltüntetni:
A kifejezések fordított lengyel alakra való átalakítását végző teljes program:
program Forditott_Lengyel (input,output);
var ch:char; {kovetkezo karakter}
function betu:boolean; {igaz, ha ch betu}
begin
betu:= (ch>='a') AND (ch<='z') OR (ch>='A') AND (ch<='Z')
end;
procedure kifejezes; forward;
procedure tenyezo;
begin
if ch='(' then begin {zarojellel kezdodik}
read(ch);
kifejezes {kifejezes atalakitasa, utana ch=')'}
end
else if betu then write(ch);
read (ch) {')' vagy betu utani karakter olvasasa}
end;
procedure tag; {tag atalakitasa}
var muvelet:char;
begin
tenyezo;
while (ch='*') or (ch='/') do begin
muvelet:=ch; {muveleti jel felretetele}
read(ch); {kovetkezo tenyezo eleje}
tenyezo; {tenyezo atalakitasa}
write(muvelet); {muveleti jel kiirasa}
end
end;
procedure osszeg; {osszeg atalakitasa}
var muvelet:char;
begin
tag; {elso tag atalakitasa}
while (ch='+') or (ch='-') do begin
muvelet:=ch; {muveleti jel felretetele}
read(ch); {kovetkezo tag eleje}
tag; {tag atalakitasa}
write(muvelet) {muveleti jel kiirasa}
end
end;
procedure kifejezes; {kifejezes atalakitasa}
var muvelet:char;
begin
osszeg; {elso osszeg atalakitasa}
while (ch='=') or (ch='#') or (ch='<') or (ch='>') do begin
muvelet:=ch; {muveleti jel felretetele}
read(ch); {kovetkezo osszeg eleje}
osszeg; {osszeg atalakitasa}
write(muvelet) {muveleti jel kiirasa}
end
end;
begin {foprogram}
repeat {kifejezesek ciklusa}
read(ch); {elso karakter atalakitasa}
kifejezes; {kifejezes atalakitasa}
writeln; readln;
until eof
end.
Figyeljük meg, hogy a program négy eljárása a következő sorrendben hivatkozik egymásra: kifejezes osszeg - tenyezo - tag.
Ezek tehát közvetve hívják magukat, ezt közvetett rekurziónak nevezzük. A rekurzió itt azért nem végtelen, mert ha a következő beolvasott karakter nem bal zárójel, akkor tenyezo nem hívja kifejezes-t.
A forward direktíva használata ebben az esetben egyébként elkerülhető lenne, hiszen a főprogramban e négy eljárás közül csak kifejezes-t hívjuk, így a többi három ennek belső eljárása is lehetne:
procedure kifejezes; {kif. lokalis valtozoja}
procedure tenyezo; {lokalis eljarasok}
...
procedure tag;
...
procedure osszeg;
...
begin {kif. utasitasresze}
...
end;
A kifejezések fordított lengyel alakját néhány zsebszámológépen is használják, mert az így megadott kifejezés nagyon könnyen kiértékelhető. A beolvasott számokat rendre egy táblázat - az úgynevezett kalkulátor-verem - tetejére kell tenni, amikor pedig a műveleti jel jön, a műveletet a verem tetején levő két számmal kell elvégezni: az operandusokat el kell távolítani a verem tetejéről, és az eredményt kell oda betenni.
5. Mutató típus, dinamikus változó
"Muirávkitna
dárnok ylorák idnárok sonodjalut."
[0] 191. oldal
5.1. A dinamikus változó fogalma
A tömb és a rekord is olyan adattípus, amelynek mérete, azaz elemeinek száma a program megírásakor eldől, azon a program futása közben már nem lehet változtatni. Nem változtatható a program futása során ezeknek az összetett típusoknak a szerkezete sem, ehhez is a program szövegén kellene változtatni.
A mutatók segítségével létrehozott dinamikus adattípus éppen azt teszi lehetővé, hogy adatszerkezetünknek - bizonyos határokon belül - akár a méretét, akár az alakját a program futása közben megváltoztathassuk.
Nézzük meg a következő definíciókat, illetve deklarációkat:
type
mut=^r; { r-re mutato tipus definialasa }
r=record { ilyen adatra mutat a mut tipusu valtozo }
ertek:real;
kovetkezo:mut
end;
...
var p1,p2,pp:mut; { mutato, azaz pointer valtozok }
A fenti példában definiáltunk egy r rekordtípust, amely két mezőből áll: az ertek valós, a kovetkezo pedig mut típusú, ezt a típusazonosítót r előtt definiáltuk. Ez azonban HiSoft-Pascalban nem megengedett, ott a következő deklarációt kell használni:
type
r=record
ertek:real;
kovetkezo:^r
end;
mut=^r; { r-re mutato tipus definialasa }
...
var p1,p2,pp:mut; { mutato, azaz pointer valtozok }
mut definíciójában az r típusazonosító előtti felfelé mutató nyíl (hatványozás jele) azt jelzi, hogy mut mutató típust ad meg, ebben a példában olyat, amely r típusú adatra tud mutatni. Azért használjuk itt azt a kifejezést, hogy "tud mutatni", mert az, hogy egy mut típusú változó egy adott pillanatban valójában mire mutat, a program végrehajtása során dől el. A mutató szó helyett a magyar szaknyelvben is gyakran használjuk a pointer megnevezést, ezért a továbbiakban vegyesen alkalmazzuk e kettőt, teljesen azonos értelemben.
A p1, p2 és pp változók mut típusúak, azaz mutatók, mut definíciója értelmében r típusú adatra mutathatnak.
Amikor az ilyen deklarációs részű blokk végrehajtása elkezdődik, akkor például p1, és minden vele együtt deklarált változó értéke meghatározatlan. Ha azt akarjuk, hogy valóban létezzen egy olyan változó, azaz memóriaterület, amelyre pl. mutat, akkor ezt a változót először létre kell hozni.
Erre a new előre definiált eljárást használhatjuk:
előtte:
new(p1)utána:
A fenti ábrán a kérdőjelek azt jelzik, hogy az adott változónak, illetve mezőnek meghatározatlan az értéke.
A new eljárás tehát létrehoz, pontosabban lefoglal egy adatterületet. Ez esetünkben r típusú, és a paraméterként megadott pl. mutató változó értékét úgy állítja be, hogy az rámutasson erre a most lefoglalt területre.
Hogy pontosan hol van a számítógép memóriájában ez az adatterület, és hogy pontosan mit jelent, hogy p1 rámutat erre, a Pascal nyelven programozó számára lényegtelen. Ha segít a fentiek megértésében, akkor tekintsük úgy, hogy a gép valahol fenntart egy tárterületet a new eljárással létrehozandó adatok számára, a new végrehajtásakor ebből foglal le megfelelő méretű részt, a new paramétereként megadott mutatóba pedig ennek a területnek a címét teszi. Annak az adatterületnek, amelyet így osztunk fel, heap a neve (kiejtése: híp, magyarul: "kupac" vagy "halom").
Maga a p1 változó mindaddig létezik, amíg a deklarációját tartalmazó blokk végrehajtása tart. Az ilyen változókat statikus változóknak nevezzük, mert számuk, szerkezetük és méretük a program megírásakor eldől. Az eddig a fejezetig megismert minden változó ilyen statikus változó volt.
Ezzel szemben a p1 által mutatott területet dinamikus változónak nevezzük, mert csak a program futása során jön létre. Az is csak ekkor dől el, hogy hány ilyen változót hozunk létre, illetve, hogy milyen lesz ezek kapcsolata, hogyan kapcsolódnak az ilyen adatok egymáshoz.
A p1 mutatóváltozóra egyszerűen a változó azonosítójának leírásával hivatkozhatunk, amint ezt a new eljárásban is tettük.
A p1 által mutatott területre p1^ alakban lehet hivatkozni, azaz a mutatóváltozó után egy felfelé mutató nyilat írunk, mintegy jelezve, hogy p1 erre mutat. Ez a terület ebben a példában r típusú, azaz rekord.
Ennek a rekordnak az elemeire ugyanúgy hivatkozhatunk, mint bármelyik rekord elemeire, tehát a rekord megadása után egy pont, majd mezőnév következik. Például az ertek mező megadása:
p1^.ertek
A mutató, a mutató által megadott dinamikus változó, illetve ennek adott részei az alábbi összefoglaló ábra szerint adhatók meg. Az éppen hivatkozott részt vastagabb keret határolja, típusát zárójelben adtuk meg:
Az így megadott rekord elemei ugyanúgy használhatók, mint egyéb rekordok elemei, azaz értéket adhatunk nekik, beolvashatjuk, és kiírhatjuk őket, ha ezt típusuk megengedi. Például a p1^.ertek mezőnek a
p1^.ertek:= -4.67
utasítás ad értéket.
p1^.kovetkezo a dinamikus változónak egy mut típusú mezőjét adja meg, ami szintén mutathat egy másik dinamikus adatra. Tegyük fel, hogy p1 és p2 is egy-egy, egymástól különböző dinamikus változóra mutat, ekkor
p1^.kovetkezo:=p2
hatására a két dinamikus változó egymás után láncolódik a következő módon:
Ekkor arra van szükség, hogy egy mutató típusú érték egy másikba értékadó utasítással átmásolható legyen, ami valóban megengedett művelet.
5.1.1. Példa:
Készítsünk programrészletet, amely beolvas k darab valós számot és ezeket elhelyezi dinamikus változók k elemű láncában. A láncelemek e fejezetben bemutatott példa szerinti r típusúak legyenek! k az első bemeneti adat.
Megoldás:
A beolvasott szám értékét az ertek mezőkben tároljuk, a dinamikus adatok egymáshoz kapcsolására pedig a kovetkezo mezőt használjuk.
Legyen j és k egész típusú változó, ezzel a programrészlet:
read(k);
new(p1);
read(p1^.ertek);
p2:=p1;
for j:=2 to k do begin
new(p2^.kovetkezo);
p2:=p2^.kovetkezo;
read(p2^.ertek);
end;
...{ adatok szama }
{ elso elem letrehozasa }
{ elso adat beolvasasa }
{ eloszor p2 is ide mutat }
{ kovetkezo elem letrehozasa }
{ p2 tovabblep az uj elemre }
{ kovetkezo ertek beolvasasa }
Tegyük fel, hogy a beolvasott számok a következők voltak:
5 1.2 2 3.6 4.9 5.1
Ekkor az előbbi programrészlet utasításainak végrehajtása a következő adatszerkezettel szemléltethető:
utasítások:
read(k);
new(p1);
read(p1^.ertek);
p2:=p1;
hatásuk:
new(p2^.kovetkezo); { kovetkezo elem letrehozasa }
p2:=p2^.kovetkezo; { p2 tovabblep az uj elemre }
read(p2^.ertek); { kovetkezo ertek beolvasasa }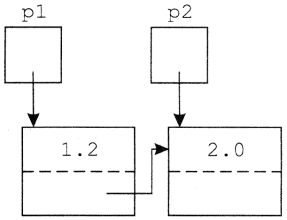
new(p2^.kovetkezo); { kovetkezo elem letrehozasa }
p2:=p2^.kovetkezo; { p2 tovabblep az uj elemre }
read(p2^.ertek); { kovetkezo ertek beolvasasa }
Végül, azaz a programrészlet teljes lefutása után a következőt kapjuk:
A következő módon írhatjuk ki a lánc elemeinek tartalmát:
pp:=p1;
writeln(pp^.ertek);
while pp<>p2 do begin
pp:=pp^.kovetkezo;
writeln(pp^.ertek)
end;{ a lanc elejerol indulunk }
{ elso ertek kiirasa }
{ meg nem ertunk a vegere }
{ pp tovabblep a kovetkezore }
{ kovetkezo ertek kiirasa }
Itt a pp mutató értéke rendre végigmegy a p1-gyel mutatott elemtől a p2-vel megadottig a beolvasáskor felépített láncon, és minden egyes lépésben kiírjuk az éppen aktuális elem ertek mezőjének értékét.
Akkor áll le a ciklus, ha pp az utolsó elemre mutat. Ehhez az kell, hogy megvizsgálhassuk két mutatótípus egyenlőségét, amire a Pascal nyelv lehetőséget is ad: két azonos típusú mutató értékét összehasonlíthatjuk az = és a <> összehasonlító műveletekkel.
A lánc elemeinek kiírását megoldhatjuk így is:
pp:=p1;
writeln(pp^.ertek);
for j:=2 to k do begin
pp:=pp^.kovetkezo;
writeln(pp^.ertek)
end;{ a lanc elejerol indulunk }
{ elso ertek kiirasa }
{ tovabbi elemek }
{ pp tovabblep a kovetkezore }
{ kovetkezo ertek kiirasa }
Tipikus hibák:
A mutató típus használatakor nagyon könnyen elkövethetjük azt a hibát, hogy a ciklust eggyel előbb vagy eggyel később fejezzük be, mint ahogyan kellene. Ilyenkor nagyon gyakori, hogy a ciklusban léptetett mulató az utolsó lépésben értelmetlen vagy meghatározatlan értéket kap, és ez általában a program megszakításához vezet.
Íme, néhány hibás megoldás:
Az utolsó elemet nem írja ki:
{ hibas! az utolso elemet nem irja ki }
pp:=p1;
repeat
writeln(pp^.ertek);
pp:=pp^.kovetkezo
until pp=p2;
Az első elemet nem írja ki:
{ hibas! az elso elemet nem irja ki }
pp:=p1;
repeat
pp:=pp^.kovetkezo;
writeln(pp^.ertek)
until pp=p2;
Legalább kételemű láncnál működik csak jól:
{ hibas! legalabb ketelemu lancnal mukodik csak jol }
pp:=p1;
writeln(pp^.ertek);
repeat
pp:=pp^.kovetkezo;
writeln(pp^.ertek)
until pp=p2;
Az utolsó elemet nem írja ki:
{ hibas! az utolso elemet nem irja ki }
pp:=p1;
repeat
writeln(pp^.ertek);
if pp<>p2 then pp:=pp^.kovetkezo
until pp=p2;
Az utolsó lépésben pp^.kovetkezo értéke meghatározatlan, hisz a lánc létrehozásakor nem kapott értéket:
{ hibas! az utolso lepesben pp^kovetkezo erteke meghatarozatlan }
pp:=p1;
for g:=1 to k do begin
writeln(pp^.ertek);
pp:=pp^.kovetkezo
until pp=p2;
Meg kell említeni, hogy az eddig jónak tekintett megoldások sem tökéletesek, hiszen elvileg az is lehet, hogy a lánc egyetlen elemet sem tartalmaz, azaz nulla hosszúságú. Ennek az esetnek a megfelelő kezeléséhez meg kell ismernünk a nil értéket.
Ahhoz, hogy a kiírást elvégezhessük, az eddig látott módszerekben vagy azt kellett ismernünk, hogy hány elemből áll a lánc, vagy pedig a lánc elejére és végére is kellett mutasson egy-egy mutató.
Arra is van azonban lehetőség, hogy a lánc végét az utolsó elemben a továbbmutató pointer értéke jelezze. Az egyik módszer az, hogy ebbe a mutatóba nil értéket teszünk. nil a Pascal nyelv egyik foglalt szava, és olyan mutatóértéket jelent, amely minden mutató típussal kompatibilis és nem mutat sehová. Szerepe éppen az, hogy a dinamikus adatszerkezetek végét nil-lel jelezzük, így tehát az utolsó elem továbbmutató pointerébe nil értéket teszünk.
Az 5.1.1.példa programrészletét egészítsük ki a végén a
p2^.kovetkezo:=nil; { ez jelzi a lánc végét }
utasítással. A nil értéket az ábrákon a megfelelő mutatóba húzott vízszintes vonallal fogjuk jelölni:
Ekkor a láncban tárolt adatok kiírásának ciklusa így is megadható:
pp:=p1;
while pp<>nil do begin
writeln(pp^.ertek);
pp:=pp^.kovetkezo
end;{ a lanc elejerol indulunk }
{ nem ertunk a vegere }
{ meg nem ertunk a vegere }
{ kovetkezo ertek kiirasa }
{ pp tovabblep a kovetkezore }
A nil segítségével most már kényelmesen kezelhetjük a nulla hosszúságú adatszerkezeteket is, mert az üres láncot úgy jelezzük, hogy az első elemre mutató pointer lesz nil értékű.
5.1.2. Példa:
Készítsünk programrészletet, amely adatok végéig olvas be valós számokat és ezeket egy láncban helyezi el, a láncelemek a fejezet elején bemutatott deklaráció szerinti r típusúak legyenek!
Megoldás:
A gondolatmenet:
üres lánc létrehozása,
amíg van bemeneti adat:
új elem lefoglalása,
beláncolása a többi elem elé,
szám beolvasása az új elembe.
Az ennek megfelelő programrészlet az eddig is használt definíciókat és deklarációkat feltételezve:
p1:=nil; { ures lanc letrehozasa }
while not eof do begin { van meg bemeneti adat }
new(p2); { uj elem lefoglalasa }
p^2.kovetkezo:=p1; { belancolas a tobbi elem ele }
p1:=p2; { ez lett az uj elso elem }
read(p2^.ertek) { szam beolvasasa az uj elembe}
end;
Az így létrehozott adatszerkezet az egyes utasítások végrehajtása után, feltételezve az előbbi (5 1.2 2 3.6 4.9 5.1) bemeneti adatokat:
p1:=nil; { ures lanc letrehozasa }
new(p2); { uj elem lefoglalasa }
P^2.kovetkezo:=p1; { belancolas a tobbi elem ele }
p1:=p2; { ez lett az uj elso elem }
read(p2^.ertek) { szam beolvasasa az uj elembe}
new(p2); { uj elem lefoglalasa }
P^2.kovetkezo:=p1; { belancolas a tobbi elem ele }
p1:=p2; { ez lett az uj elso elem }
read(p2^.ertek) { szam beolvasasa az uj elembe}
new(p2); { uj elem lefoglalasa }
p^2.kovetkezo:=p1; { belancolas a tobbi elem ele }
p1:=p2; { ez lett az uj elso elem }
read(p2^.ertek) { szam beolvasasa az uj elembe}
Végül, azaz a programrészlet teljes lefutása után a következőt kapjuk:
Ez tehát egy olyan lánc, amelynek ertek mezői a beolvasott számokat tartalmazzák, mégpedig ha a lánc elejétől, p1-től indulunk, éppen a beolvasással ellentétes sorrendben. A láncban tárolt értékeket például így írathatjuk ki:
pp:=p1; { pp a lanc elejere mutat }
while pp<>nil do begin { a lanc vegeig megyunk }
writeln(pp^.ertek); { kiiras }
pp:=pp^.kovetkezo { tovabblep a kovetkezore }
until pp=p2;
Ez a megoldás helyesen fog működni akkor is, ha a lánc üres, azaz ha p1 értéke nil.
Ha a számokat a beolvasás sorrendjében akarjuk kiíratni, akkor a lánc végétől kellene visszafelé haladni, ez azonban közvetlenül nem lehetséges. A következő rekurzív eljárás mégis megoldja ezt. Alapötlete az, hogy a láncot úgy kell fordított sorrendben kiírni, hogy először ki kell írni az adott elemet követő lánc tartalmát (fordított sorrendben), majd magát az elemet:
{ lancolt lista forditott sorrendu kiirasa }
procedure visszafeleir(p:mut);
begin
if p<>nil then begin { nem ures a lanc }
visszafeleir(p^.kovetkezo);
write(p^.ertek)
end
end;
Hívása:
visszafeleir(p1);
Ha az 5.1.1 példát tömb segítségével akarjuk megoldani, akkor már a program megírásakor szükségünk van az adatok legnagyobb lehetséges számára. Itt a tárolható számok számát csak az korlátozza, hogy mekkora memóriát használhatunk dinamikus adatok tárolására. Igaz, most nemcsak a tényleges adatot, hanem adatonként egy mutató értékét is tárolnunk kell, a dinamikus adatszerkezetek kellemes tulajdonságai miatt azonban ez sokszor bőven megéri.
A legfontosabb tulajdonságok megismerése után lássuk a mutató típusra és a dinamikus adatokra vonatkozó szabályokat!
A mutató (pointer) típus, dinamikus változó:
1. A mutatók, illetve a mutatók áltat megadott változók segítségével olyan adatszerkezeteket lehet létrehozni a számítógép főtárában, amelyek mérete és szerkezete a program végrehajtása során megváltoztatható. Ezért a mutatók segítségével létrehozott adatszerkezeteket dinamikus adat szerkezeteknek is nevezzük.
2. A mutató típus formai szabályai:
mutató típus:
^alaptípus
(a)
ahol alaptípus: típusazonosító
(b)
2. Egy típusdefiníciós részben az alaptípus definíciója a rá mutató típus definíciója után is állhat, de még ugyanabban a típusdefiníciós részben kell lennie. Így tehát egy mutató típus azonosítójának definiálását nem kell feltétlenül megelőzni az alaptípus-azonosító definíciójának (mint minden más hasonló típushivatkozásnál).
Így például megengedett a következő:
type
...
pq=^q; { q itt meg nincs definialva }
q=record { q definicioja ugyanabban a tipusdefinicios reszben van }
u,w:integer;
kov:pq
end;
...
var p1,p2:pq;(l)
4. A mutató típusú változó értékkészletébe a nil érték, valamint mutatóértékek egy halmaza tartozik, a mutatóértékek egy-egy különböző, a mutató alaptípusának megfelelő változóra mutatnak. A nil kulcsszóval képviselt érték minden mutató típussal kompatibilis és nem mutat változóra. (d)
A mutatókhoz tartozó változók értéke dinamikus abban az értelemben, hogy e mutatott változók a program végrehajtása során létrehozhatók és megszüntethetők; létrehozásukra a new, megszüntetésükre a dispose előre deklarált eljárást használhatjuk.
(HiSoft-Pascalban dispose helyett a release kulcsszó használandó erre a célra.)5. Mutató típusú változóval a következő műveletek végezhetők:
- értéket kaphat értékadó utasítással, mégpedig azonos típusú mutatótól vagy nil-től, valamint get és new eljárással; (e)
- értéke kiírható put eljárással; (e)
(Mutatók között tehát csak ez a két reláció értelmezett.)
= egyenlőség vizsgálata; két mutató értéke akkor egyenlő, ha ugyanarra a dinamikus változóra mutatnak, vagy mindkettő értéke nil <> - érték- és változóparaméterként átadható eljárásnak, illetve függvénynek;
- függvény típusa lehet mutató.
6. Dinamikus változónak a mutató típusú változó által hivatkozott (mutatott) változót nevezzük, típusát a mutató alaptípusa adja meg.
dinamikus változó:
mutatóváltozó^
Ebben a definícióban a "mutatóváltozó" mutató típusú változót jelent, (c)
Hibát okoz, ha úgy hivatkozunk dinamikus változóra, hogy a mutatóváltozó értéke nil vagy meghatározatlan. (g)
7. Dinamikus változók előre deklarált eljárásai:
new(p) new(p,k1,k2,...,kn)
Az itt megadott k értékek csak a létrehozott dinamikus változó által lefoglalt tárméretet befolyásolják, a vezérlőmezők értékei a létrehozott rekord többi mezőjéhez hasonlóan meghatározatlanok lesznek. (h)
Hiba történik, ha a későbbiekben a dinamikus változó olyan változata lesz aktív, amely eltér a new eljárásban kijelölt változattól.
Hiba történik, ha a new eljárás ezen második alakjával létrehozott dinamikus változó egészére hivatkozunk, akár kifejezésben, akár értékadó utasítás bal oldalán, akár aktuális paraméterként; vagyis az így létrehozott dinamikus változónak csak a mezőire hivatkozhatunk. (i)dispose(q)
Hiba történik, ha q értéke dispose hívásakor nil vagy meghatározatlan, vagy ha a dinamikus változót a new előre definiált eljárás második alakjával hoztuk létre.dispose(q,j1,j2,...,jm)
Hiba történik, ha q értéke dispose hívásakor nil vagy meghatározatlan. Hiba történik, ha a dinamikus változót a new eljárás második alakjával hoztuk létre és az akkor megadott k paraméterek n száma nem egyezik meg a dispose-ban megadott j paraméterek m számával.
Hiba történik továbbá, ha az aktív változatok a q által mutatott dinamikus változóban nem felelnek meg rendre a dispose-ban megadott j értékeknek. (m)8. Dinamikus változóval mindazok a műveletek elvégezhetők, amelyeket a mutatóváltozó alaptípusa megenged. Kivétel, hogy dinamikus változó nem lehet for utasítás ciklusváltozója, és a new eljárás második alakjával létrehozott dinamikus változó nem használható kifejezésben, értékadó utasítás bal oldalán, valamint aktuális paraméterként. (i)
9. A dinamikus változót csak a new előre definiált eljárással lehet létrehozni és csak a dispose előre definiált eljárással lehet megszüntetni. A dinamikus változó addig létezik, amíg a dispose előre definiált eljárással meg nem szüntetjük, vagy a program végrehajtása be nem fejeződik. (k) (n)
Magyarázatok, megjegyzések:
(a) Némely (régebbi) gép karakterkészletéből hiányzik a ^ karakter, helyette azonos értelemben használhatjuk a felfelé mutató nyilat vagy a @ karaktert is.
(b) A mutató típus megadásánál tehát a t után egy típusazonosítónak kell állnia, új típus megadása nem használható. Így tehát hibás:
type ptip=^array[1..10] of char;
helyette írjuk például a következőt:
tombtip=array[1..10] of char;
ptip=^tombtip;(c) A dinamikus változónak tehát nincs saját azonosítója, éppen az az egyik legjellemzőbb tulajdonsága, hogy csak mutató segítségével tudjuk elérni.
A 3. pontbeli definíciók és deklarációk esetén például p1^ dinamikus változó típusa q rekord, és így a rekordoknál megszokott módon hivatkozhatunk e rekord mezőire:
p1^.w egész típusú,
p1^.kov pedig pq, tehát q-ra mutató pointer típusú.(d) A nil értéket arra használjuk, hogy jelöljük vele: a nil értékű mutató nem mutat semmilyen dinamikus változóra. A nil értékű mutató és a meghatározatlan értékű mutató között lényeges különbség van. A nil érték vizsgálható például = vagy <> relációval, illetve értékadó utasítással átmásolható egy másik mutató változóba. A meghatározatlan értékű mutató értékére való bármilyen hivatkozás (például egyenlőségvizsgálat) hibát okoz - ugyanúgy, mint bármilyen más, tetszőleges típusú és meghatározatlan értékű változó értékének használata.
(e) Nem szerencsés egy mutatónak get-tel értéket adni, mivel ez feltételezi, hogy a számítógép főtárában a dinamikus változók ugyanazon a helyen érhetők el, mint ahol a get-tel beolvasandó állomány létrehozásakor voltak. Ez a feltételezés a gyakorlatban szinte sohasem teljesül, ezért feltétlenül kerüljük a mutatók vagy mutatót is tartalmazó adatszerkezetek put és get segítségével való mozgatását.
(f) Két különböző típusú mutató még akkor sem hasonlítható össze, ha az összehasonlítás pillanatában mindkettő nil értékű.
(g) Mutatóváltozó értéke akkor lehet meghatározatlan, ha még nem kapott értéket, vagy a dispose előre definiált eljárás első paramétereként használtuk.
(h) Közvetlenül a new eljárás ezen alakjának használata után ajánlatos a létrehozott rekordban a változó részek vezérlőmezőit a new-ban használt k1...kn értékre beállítani.
(i) Ez a szabály talán furcsának tűnik, hiszen egy rekord típusú adatnak a használata éppen azt jelenti, hogy a teljes rekordot egyetlen egységként is tudjuk kezelni.
Ha a változó résszel is rendelkező rekordot a new eljárás első alakjával hozzuk létre, akkor minden változó részben a legnagyobb, leghosszabb változat számára történik meg a helyfoglalás, mégpedig azért, hogy a rekord használatakor bármelyik változat elférjen a létrehozott dinamikus változóban.
Ezzel szemben a new eljárás második alakjával létrehozott dinamikus változóban csak pontosan annyi hely lesz, amelyben a new-ban használt k értékekkel kijelölt változat elfér.
Nézzük meg a különbséget egy példán, az egyes mezőkre valamilyen hosszértékeket feltételezve:
type
p=^r;
r=record
a,b:integer;
c:real;
case v1:boolean of
true: (d:real);
false: (e:char)
end;
var p1,p2:p;
rv:r;
{ 2+2=4 byte }
{ 6 byte }
{ 1 byte }
{ 6 byte }
{ 1 byte }
{ r-re mutato pointerek }
{ r tipusu statikus valtozo }A fenti r állandó része 4+6=10 byte, változó része v1=true esetén 1+6=7 byte, míg v1=false esetén 1+1=2 byte hosszú, a teljes rekord maximális hossza így 10+7=17 byte.
Ha a new(p1) eljáráshívással foglalunk helyet egy ilyen r típusú dinamikus változónak, a maximális, 17 byte-os rekord jön létre. Ha azonban new(p2,false) módon hozunk létre egy r típusú rekordot, akkor csak 10+2=12 byte-os.
Érthető, hogy a p2^:=p1^ vagy a p2^:=rv értékadás hibát okoz, hiszen 17 byte-os változók értékét akarjuk 12 byte-osba másolni.
Megengedettek azonban például a következő értékadások:
p1^:=rv ; { p1^-t new első alakjával hoztuk létre }
p2^.a:=p1^.b; { p2^ mezőjére hivatkoztunk }
rv.d:=p2^.c-3.1; { p2^ mezőjére hivatkoztunk }(j) Ez a szabály nem azt jelenti, hogy ha egy adott pillanatban p1 és p2 ugyanarra a dinamikus változóra mutat, és így p1 és p2 értéke azonos, akkor a dispose(p1) hatására p2 értéke is megváltozna, hiszen p1 és p2 egymástól független változók, az egyik értékének megváltozása - például meghatározatlanná válása - nem befolyásolhatja a másik értékét. A szabály értelme az, hogy a dispose(p1) végrehajtása után p2 értékét meghatározatlannak kell tekinteni, hiszen az a változó, amelyre mutatott, már megszűnt.
Mi több, bizonyos megvalósításokban az is előfordulhat, hogy a dispose(p1) hatására p1 értéke fizikailag nem is változik meg, így pl. egy if p1=p2 then ... vizsgálat a két mutató értékét egyenlőnek találja, de ezzel a vizsgálattal már hibát követtünk el, hiszen a dispose végrehajtása után nincs jogunk e mutatók értékét vizsgálni, meghatározatlannak kell tekintenünk őket.(k) Így például, ha a dinamikus változót eljárásban hozzuk létre, az eljárásból kilépve nem szűnik meg - mint például az eljárás lokális változói -, csak akkor, ha a program befejeződik, vagy ha dispose-t adunk ki rá.
(l) Elvileg megengedett lenne tehát a következő definíciós sorrend is:
type r=record
a,b:real;
k:^r
end;
pr=^r;de az így definiált pr típus nem lesz kompatibilis az r rekord k mezőjével, hiszen a típusdefiniálás szabályainak értelmében pr definíciója egy új, minden előzőtől különböző adattípust vezet be, még akkor is, ha ez mindenben megfelel a k mező típusának. (HiSoft-Pascalban azonban ezt a formát kényszerülünk használni!)
(m) Ajánlatos ezért a dispose második alakjában a rekordváltozó részeinek vezérlőmezőit használni a j értékek megadására, hiszen ezeket a (h) megjegyzés szerint létrehozásukkor a megfelelő értékekkel töltöttük fel.
(n) Ha egy egyirányú láncolt lista első elemét dispose eljárással megszüntetjük, akkor annak csak az első elemével lefoglalt tárterület szabadul fel, de a lánc többi eleme is hozzáférhetetlenné válik, azaz elvész, hiszen azokat csak az első elemen keresztül tudjuk elérni. Ha tehát egy teljes láncot akarunk megszüntetni, minden elemére külön-külön kell alkalmazni a dispose eljárást.
Például, ha a 3. szabály definícióit és deklarációit tekintjük, és feltételezzük, hogy p1 egy olyan lánc elejére mutat, amelynek utolsó elemében kov értéke nil; akkor ez a lánc a következő módon szüntethető meg:
while p1<>nil do begin { nem ertunk a lanc vegere }
p2:=p1^.kov; { kovetkezo elem }
dispose(p1); { elem megszuntetese }
p1.=p2 { tovabblepes }
end;
5.2. Tipikus adatszerkezetek dinamikus adatokkal
Dinamikus adatokkal tetszőlegesen sok különböző adatszerkezet létrehozható annak megfelelően, hogy az adott feladat, illetve az adott algoritmus mit kíván meg. Ezek közül most csak néhányat tudunk áttekinteni. A legtöbbet használt szerkezetek az egy és két irányban láncolt lista és a bináris fa, ezeket mutatjuk be.
A dinamikus adatszerkezetek bemutatására ugyanazt a példát oldjuk meg, mint a táblázatkezelési módszereknél a 3.10.1. példánál, de most nem kell a programban megadnunk egy táblázat maximális méretét, tehát azt, hogy legfeljebb hány bejegyzésre számítunk.
5.2.1. Példa:
Készítsünk programot telefonszámok nyilvántartására: lehessen a nyilvántartásba új nevet és telefonszámot felvenni, a meglévők közül név alapján telefonszámot kapni, egy adott névhez tartozó bejegyzést törölni, illetve a nyilvántartás összes adatát kilistázni!
Megoldás:
A program használata és általános szerkezete itt is azonos a különböző adatszerkezetek használata esetén, mint a 3.10. fejezetben megismert táblázatkezelési módszereknél, de már szegmenseket is használhatunk, és áttekinthetőség kedvéért a szegmensek a főprogrammal csak paramétereken keresztül cserélnek adatokat.
Egy irányban láncolt lista rendezetlen adatokkal
Ilyen szerkezetet használtunk az 5.1 alfejezetben a mutató típussal való ismerkedéskor, de most egy adatelemben a nevet, a telefonszámot és a következő elemre mutató pointert tároljuk. Az adattípusok:
mutato=^elem;
elem=record
nev:nevt;
telszam:szamt;
kovetkezo:mutato
end;
a szükséges globális változók:
elso,
keresett,
elozo:mutato;(A lánc elejére mutat)
(A keresett,)
(illetve az azt megelőző elemre mutat.)
Az új adatelemet az eddigiek elé, a lánc elejére iktatjuk be:
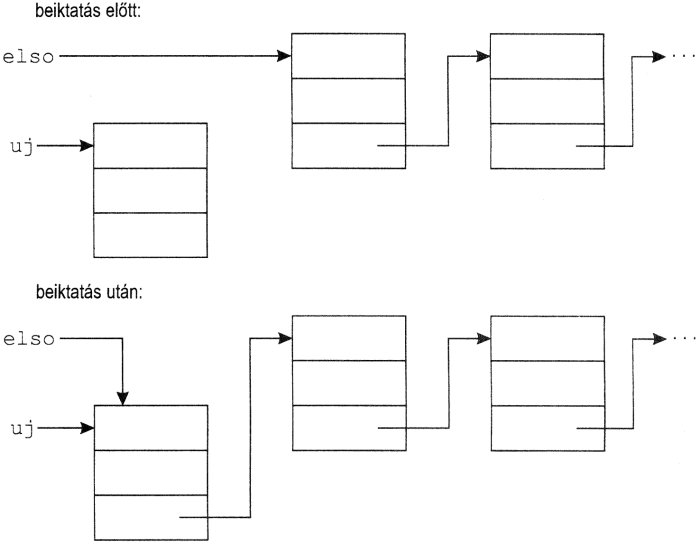
A keresés nagyon hasonlít a táblázatkezelési módszereknél megismert lineáris kereséshez: a lánc elejétől addig lépegetünk az elemeken, amíg a keresett nevet meg nem találjuk, vagy a lánc végére nem jutunk.
A láncból úgy lehet egy elemet törölni, hogy először a kiiktatandó elemet megelőző elemben a mutatót a kiiktatott elem utánira állítjuk:
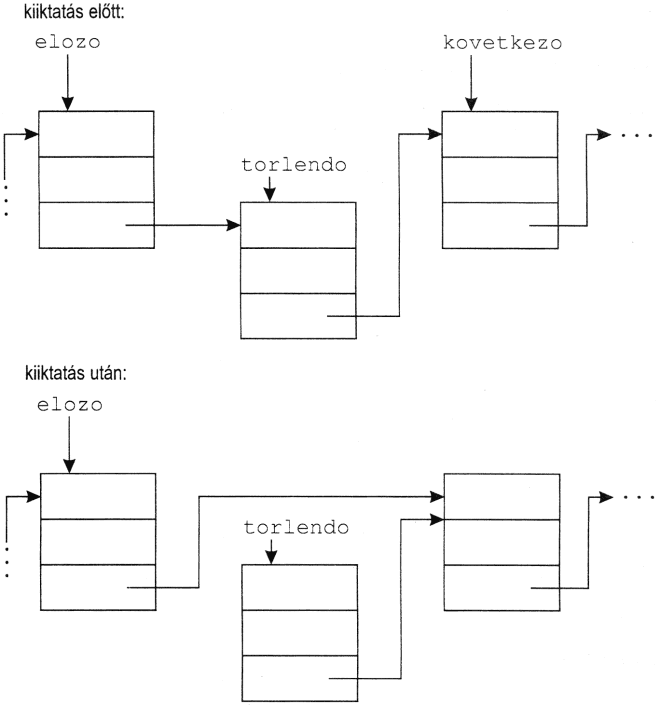
Ezt követően a dispose eljárással megszüntethetjük a feleslegessé vált elemet.
A Turbo Pascal program:
program telefonkonyv6;
const nevhossz=30;
szamhossz=16;
type nevt=string[nevhossz];
szamt=string[szamhossz];
mutato=^elem;
elem=record
nev:nevt;
telszam:szamt;
kovetkezo:mutato
end;
var parancs,ch:char;
ujnev:nevt;
ujszam:szamt;
megvan:boolean;
elso,keresett,elozo:mutato;procedure Kezdes(var e:mutato);
begin
e:=nil { elso elem mutatoja }
end;procedure Menu;
begin
Writeln;
Writeln('''u'' - uj nev');Writeln('''k'' - kereses');
Writeln('''t'' - torles');Writeln('''l'' - listazas');
Writeln('''v'' - vege');
Write('Parancs: ');
repeat
Readln(parancs)
until parancs in ['u','k','t','l','v']
end;procedure Kereses(knev:nevt;eleje:mutato;
var megvan:boolean;
var keresett,elozo:mutato;var sz:szamt);
begin
if eleje=nil then megvan:=false { ures a lanc }
else begin { nem ures }
keresett:=eleje; { elejetol keresunk }
repeat
megvan:=knev=keresett^.nev; { nev egyezik? }
if not megvan then begin { tovabblepes }
elozo:=keresett;
keresett:=keresett^.kovetkezo
end
until megvan or (keresett=nil);
if megvan then sz:=keresett^.telszam
end
end;procedure Ujelem(ujnev:nevt;ujszam:szamt;var elso:mutato);
var uj:mutato;
begin
new(uj); { uj elem letrehozasa }
with uj^ do begin { uj elem kitoltese }
nev:=ujnev;
telszam:=ujszam;
kovetkezo:=elso { tobbi ele kerul }
end;
elso:=uj { ez lesz az uj elso }
end;procedure Kiiras(elso:mutato);
begin
while elso<>nil do
with elso^ do begin
Writeln(nev,' : ',telszam);
elso:=kovetkezo
end
end;procedure Torles(torlendo,elozo:mutato; var elso:mutato);
begin
if torlendo=elso then { elso elemet kell torolni }
elso:=torlendo^.kovetkezo
else
elozo^.kovetkezo:=torlendo^.kovetkezo;
Dispose(torlendo) { elem felszabaditasa }
end;begin
Kezdes(elso);
repeat
Menu;
if (parancs='u') or (parancs='k') or (parancs='t') then begin
Write('Nev: ');readln(ujnev);
Kereses(ujnev,elso,megvan,keresett,elozo,ujszam)
end;
case parancs of
'u': if megvan then Writeln('Mar van ilyen nev!')
else begin
Write('Telefonszam: ');Readln(ujszam);
Ujelem(ujnev,ujszam,elso)
end;
'k': if megvan then Writeln('Telefonszam: ',ujszam)
else writeln('Nincs ilyen nev a listan!');
't': if megvan then Torles(keresett,elozo,elso)
else Writeln('Nincs ilyen nev a listan!');
'l': Kiiras(elso);
'v': begin
Write('Valoban be akarja fejezni?');
repeat
Readln(ch)
until (ch='i') or (ch='n');
if ch='n' then parancs:=ch
end
end
until parancs='v'
end.
HiSoft-Pascalban a típusdefiníciót a következőképen kel megadni:
TYPE nevt=ARRAY[1..nevhossz] OF char;
szamt=ARRAY[1..szamhossz] OF char;
elem=RECORD
nev:nevt;
telszam:szamt;
kovetkezo:^elem
END;
mutato=^elem;
A dispose helyett pedig a release kulcsszó használandó.
Szabványos Pascal-ban a nevt és szamt típusokat a következőképen kell deklarálni:
nevt=packed array[1..nevhossz] of char;
szamt=packed array[1..szamhossz] of char;
A módszer hatékonysága ugyanolyan, mint a lineáris keresésé.
Ha az általunk használt Pascal megvalósítás nem tartalmaz semmilyen kiterjesztést karakterfüzérek beolvasására, használhatjuk a következő eljárásokat a név és a telefonszám beolvasására:
procedure szokozszures;
begin
while ch<=' ' do read(ch);
end;procedure nevolvasas(var n:nevt);
var k:integer;
procedure szoolvasas;
begin
repeat
n[k]:=ch;k:=k+1;read(ch);
until (ch<=' ') or (k>nevhossz);
end;
begin
szokozszures; { szokozok kihagyasa }
k:=1;szoolvasas; { nev elso szava }
if k<nevhossz then szoolvasas; { nev masodik szava }
for k:=k to nevhossz do n[k]:=' ';
end;procedure telszamolvasas(var tsz:szamt);
var k:integer;
begin
szokozszures; { szokozok kihagyasa }
k:=1;
repeat
tsz[k]:=ch;k:=k+1;read(ch);
until (ch<=' ') or (k>szamhossz);
for k:=k to szamhossz do tsz[k]:=' ';
end;
A két eljárást az alábbi formában hívhatjuk meg:
nevolvasas(ujnev);
telszamolvasas(ujszam);
5.2.1. Feladat:
Alakítsa át a telefonkonyv6 programot úgy, hogy a lánc végén strázsát használ: induláskor nem üres a lánc, hanem van egy eleme, amelyet mindig a lánc végén hagyunk és egy utolso:mutato változó mutat rá. Amikor keresni kell, a keresett nevet először ebbe az elembe írjuk be, így nem kell a lánc végét is figyelni.
Vigyázzon, hogy a kiírásnál ezt az elemet hagyja figyelmen kívül!
5.2.2. Feladat:
Oldja meg ugyanezt a feladatot ismét egy irányban láncolt listával, de az adatokat nagyság (ábécé) szerint tárolja!
A módszer előnye az előzővel szemben, hogy keresésnél átlagosan a lánc feléig kell csak menni, hiszen ha a keresettnél nagyobb elem következik, akkor a keresett név a lánc további részében már nem lehet.
Oldja meg a feladatot strázsa nélkül és strázsával is!
5.2.3. Feladat:
Az eddigi módszerekben, ha törölni kellett, vagy nagyság szerint rendezett lánc esetén új elemet kellett be-szúrni, a lánc elején máshogyan kellett eljárni, mint a lánc többi részén. Készítsük el a feladat megoldását úgy, hogy a lánc elején is legyen egy strázsa! (Ebbe semmit nem kell tenni, mert értékét nem is vizsgáljuk, a keresést a második elemtől végezzük. Ez az elem csak arra való, hogy egy új elem beláncolásakor és törlésekor egyszerűbbé tegye a programot. így sohasem kell a lánc legelejére elemet beszúrni, vagy onnan elemet törölni.)
A telefonkonyv6 programban bemutatott megoldásban kényelmetlenséget okozott, hogy az elem törléséhez szükségünk volt a törlésre váró előtti elemre mutató pointer értékére. Hasonló problémával találkozunk beszúrásnál a rendezett, egy irányban láncolt listával kapcsolatban. Egy elem törlése, illetve új elem beszúrása megoldható némi trükkel akkor is, ha nem ismerjük az előző elemre mutató pointert.
Legyen torlendo a láncból kiiktatásra kerülő elem mutatója és m egy másik mutatóváltozó, a típusok pedig az előbbi mintapélda szerintiek. Ekkor a kiiktatás így oldható meg:
m:=torlendo^.kovetkezo; { torlendo utani elem }
torlendo^:=m^; { teljes kovetkezo elem atmasolasa }
Itt tehát valójában nem a torlendo-vel megadott elemet iktattuk ki, hanem az arra következőt, s amelynek a tartalmát előbb átmásoltuk abba, amire torlendo mutat.
Ezek után az m által mutatott elem szabadítható fel:
dispose(m)
Hasonló módon oldható meg egy uj pointer által megadott új elem beiktatása a koveto pointer által megadott elem elé. Itt is az elemek tartalmát rendezzük át úgy, mintha az új elem megelőzné az őt követőt:
uj^:=koveto^; { tartalom atmasolasa }
koveto^.kovetkezo:=uj; { uj elem beiktatasa a lancba }
with koveto^ do begin { ez vette at az uj elem szerepet }
nev:=ujnev;
telszam:=ujszam
end;
Két irányban láncolt lista rendezett adatokkal, strázsával
Az előbb tárgyalt probléma úgy is megoldható, hogy az elemekben nemcsak a következő, hanem a megelőző elemre mutató pointert is tároljuk, így minden elemből nagyon egyszerűen elérhetjük mindkét szomszédját.
A következő mintaprogramban a két irányban láncolt listát ábécé szerint rendezett adatok tárolására fogjuk használni, a lánc mindkét végén strázsával.
Az adattípusok:
mutato=^elem;
elem=record
nev:nevt;
telszam:szamt;
kovetkezo,elozo:mutato
end;
A globális adatok:
elso,
keresett:mutato;(A lánc elejére mutat.)
(A kerfesett elemre mutat.)
A Turbo Paslcal program:
program telefonkonyv7;
const nevhossz=30;
szamhossz=16;
type nevt=string[nevhossz];
szamt=string[szamhossz];
mutato=^elem;
elem=record
nev:nevt;
telszam:szamt;
kovetkezo,elozo:mutato
end;
var parancs,ch:char;
ujnev:nevt;
ujszam:szamt;
megvan:boolean;
elso,keresett:mutato;procedure Kezdes(var e:mutato);
begin
new(e);
with e^ do begin
new(kovetkezo);
with kovetkezo^ do begin
kovetkezo:=nil;elozo:=e;
nev:=chr(255)
end
end
end;procedure Menu;
begin
Writeln;
Writeln('''u'' - uj nev');Writeln('''k'' - kereses');
Writeln('''t'' - torles');Writeln('''l'' - listazas');
Writeln('''v'' - vege');
Write('Parancs: ');
repeat
Readln(parancs)
until parancs in ['u','k','t','l','v']
end;procedure Kereses(knev:nevt;eleje:mutato;
var megvan:boolean;
var keresett:mutato;var sz:szamt);
begin
keresett:=eleje^.kovetkezo;
while knev>keresett^.nev do
keresett:=keresett^.kovetkezo;
megvan:=knev=keresett^.nev;
if megvan then sz:=keresett^.telszam
end;procedure Ujelem(ujnev:nevt;ujszam:szamt;ezele:mutato);
var uj,ezutan:mutato;
begin
ezutan:=ezele^.elozo;
new(uj);
with uj^ do begin
nev:=ujnev;
telszam:=ujszam;
kovetkezo:=ezele;
elozo:=ezutan
end;
ezutan^.kovetkezo:=uj;
ezele^.elozo:=uj
end;procedure Kiiras(elso:mutato);
begin
elso:=elso^.kovetkezo;
while elso^.kovetkezo<>nil do
with elso^ do begin
Writeln(nev,' : ',telszam);
elso:=kovetkezo;
end;
end;procedure Torles(torlendo:mutato);
begin
with torlendo^ do begin
elozo^.kovetkezo:=kovetkezo;
kovetkezo^.elozo:=elozo;
end;
Dispose(torlendo)
end;begin
Kezdes(elso);
repeat
Menu;
if (parancs='u') or (parancs='k') or (parancs='t') then begin
Write('Nev: ');readln(ujnev);
Kereses(ujnev,elso,megvan,keresett,ujszam)
end;
case parancs of
'u': if megvan then Writeln('Mar van ilyen nev!')
else begin
Write('Telefonszam: ');Readln(ujszam);
Ujelem(ujnev,ujszam,keresett)
end;
'k': if megvan then Writeln('Telefonszam: ',ujszam)
else writeln('Nincs ilyen nev a listan!');
't': if megvan then Torles(keresett)
else Writeln('Nincs ilyen nev a listan!');
'l': Kiiras(elso);
'v': begin
Write('Valoban be akarja fejezni?');
repeat
Readln(ch)
until (ch='i') or (ch='n');
if ch='n' then parancs:=ch
end
end
until parancs='v'
end.
A kétirányú láncolás és a strázsa miatt több helyen jelentősen egyszerűsödött a program.
A kereséshez szükséges lépések száma az 5.2.2 feladatban megfogalmazottak szerint átlagosan fele a rendezetlen lánc esetén szükségesnek, feltéve, hogy az egyes telefonszámokat azonos gyakorisággal keressük.
Bináris fa
Ha lényegesen akarunk javítani a dinamikus adatszerkezetben a keresések hatékonyságán, az adatokat úgy kell tárolni, hogy a bináris kereséshez hasonlóan lehetőleg minden lépésében feleződjön azon elemek száma, amelyeket a további műveletekben figyelembe kell venni.
Ehhez nem volt elég, hogy az adatokat nagyság szerint rendezve láncban tároltuk: közvetlenül nem tudtunk hozzáférni egy részlánc középső eleméhez, csak egyenként lépegetve az elemeken.
A fákat, esetünkben bináris fát alkalmazó keresési módszer átlagosan a tárolt elemek számának logaritmusával arányos számú lépésben képes egy elemet megkeresni, beiktatni vagy törölni.
A bináris fa olyan adatszerkezet, amelynek elemeiben a ténylegesen tárolandó adatokon, esetünkben a néven és a telefonszámon kívül még két mutatót tárolunk. Az egyik azoknak az elemeknek a részfájára mutat, amelyekben a kulcs kisebb, mint az adott elemben; a másik pedig olyan részfára, amelyben nagyobb. A részfa szintén bináris fa, ugyanilyen szerkezettel, de a teljes fának csak egy részét alkotja; a bal részfa az adott elemnél kisebbeket, a jobb pedig a nagyobbakat.
Az így megadott tartalmú fákat szokás még rendezőfáknak is nevezni, mégpedig azért, mert bennük az elemek balról jobbra nagyság szerint növekvő sorrendben, azaz mintegy rendezve szerepelnek. Használhatunk más tartalmú faszerkezeteket is, azok azonban már nem rendezőfák. Ilyen speciális fának tekinthető például a kupac, amelyben minden elem pl. nagyobb vagy egyenlő, mint az alatta levő elemek.
A bináris fához szükséges típusok:
mutato=^elem;
elem=record
nev:nevt;
telszam:szamt;
bal,jobb:mutato
end;
A legelső elemet, tehát amelyiknek csak leszármazottai vannak, őse nincs, gyökérelemnek szoktuk nevezni, az erre mutató pointerre pedig hagyományosan a gyoker (gyökér) azonosítót használjuk.
Egy lehetséges faszerkezet:
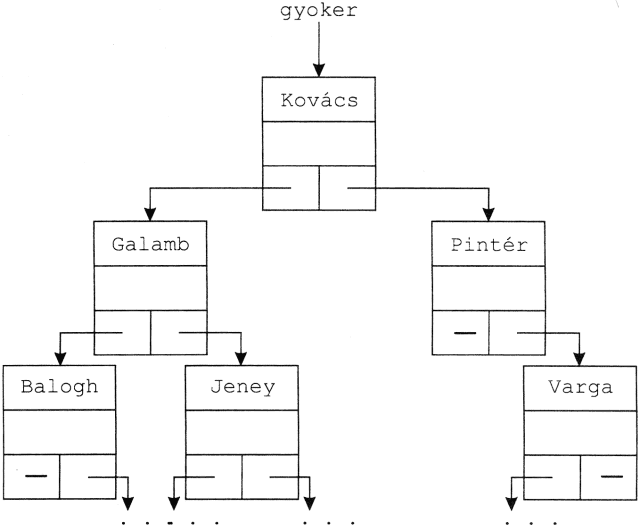
A fa elnevezés onnan származik, hogy az adatszerkezet az egyes elemeknél elágazhat, és azért bináris, mert kétfelé ágazhat el. Mint a fenti ábrából is látható, ez nem jelenti azt, hogy valóban minden elemnek van két további ága: csak azt, hogy lehet. Végül minden ág olyan elemben végződik, amelyen nem lóg további elem, ezeket a fa leveleinek nevezzük. Ha egy adott irányban nem folytatódik a fa, akkor azt itt is a megfelelő pointer nil értéke jelzi.
Egy elem keresése a következő módon történik. A gyökérelemtől indulunk. Ha ebben a kulcs megegyezik a keresettel, akkor megtaláltuk. Ha a keresett kulcs kisebb, akkor balra, egyébként pedig jobbra lépünk tovább a következő elemre.
Ha nem találjuk meg a fában az elemet, ezt az jelzi, hogy a keresett elem által kijelölt irányban egyszer csak nem lehet tovább haladni, mert az a pointer nil.
Új elemet úgy tudunk a fába iktatni, hogy üres fa esetén az új elem lesz a gyökérelem, egyébként pedig a gyökérelemtől indulunk és megkeressük az új elem helyét: balra lefelé haladunk, ha az új elem kulcsa kisebb, mint a fa adott eleméé, és jobbra, ha nagyobb. Előbb-utóbb a fa egyik szélső eleméhez érünk, erre az új elemet a megfelelő irányba felfüggesztjük. Az új elem beiktatása tehát keresésből, majd a tényleges új elem felvételéből áll.
Ez a módszer automatikusan biztosítja, hogy a fa a kulcsok szerint balról jobbra rendezett legyen, azaz a fa minden elemére teljesül, hogy bal oldali utódai - azok az elemek, amelyek az adott elemből a bal mutatóval érhetők el - mind kisebb, a jobb oldaliak pedig mind nagyobb, vagy legfeljebb egyenlő kulcsúak lesznek.
A fa tartalmát - összes elemét - több módszerrel is kiírhatjuk. Kulcsok szerint növekvő sorrendben például úgy, hogy minden elemnél először kiírjuk a bal oldali részfáját, majd magát az elemet, végül a jobb oldali részfáját.
Ez az algoritmus már sugallja, hogy a fán végzett műveleteket legkényelmesebben rekurzív eljárások formájában tudjuk megadni. Ez nem is meglepő, mert a fa maga is rekurzív adatszerkezetnek tekinthető: minden fa és annak minden részfája vagy üres, vagy egy gyökérelemből és annak bal és jobb oldali részfájából áll.
Egy elem törlése már nem fogalmazható meg ilyen egyszerűen. Ha a törlésre kijelölt elem levél (azaz nincs utódja), vagy csak egy utódja van, könnyen kiiktatható, hiszen az esetleg meglévő egyetlen utódot a kiiktatott elem helyére függesztjük.
Elem törlése bináris rendezőfából, ha csak egy utódja van:
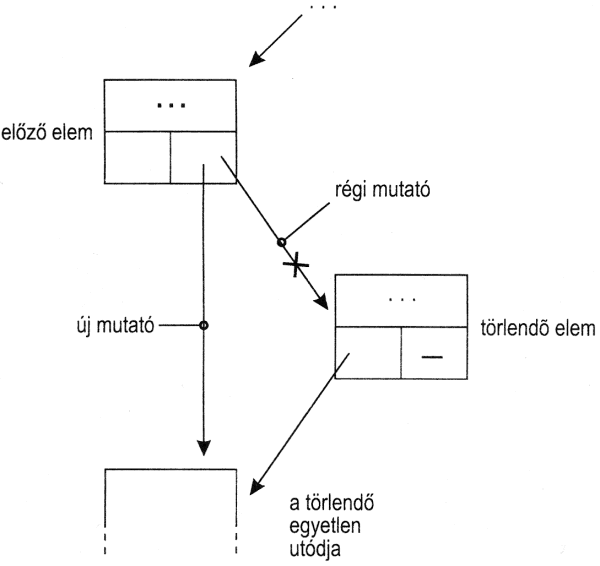
Más a helyzet, ha a törlésre kijelölt elemnek két utódja is van, ezeket ugyanis nem lehet egyetlen elem he-lyére betenni. Ráadásul a törlés után is meg kell maradnia a rendezettségnek, azaz a törölt helyére kerülő új elemnek minden bal oldali utódnál nagyobbnak és minden jobb oldalinál kisebbnek kell lennie.
A feladat például úgy oldható meg, hogy a törlendő elem bal oldali részfájának legjobboldalibb elemét áttesszük a törlendő elem helyére. Ehhez először kivesszük ezt a legjobboldalibb elemet az eredeti helyéről, majd a törlendő elem helyére iktatjuk be. Legjobboldalibb elemnek azt az utolsó elemet nevezzük, amely az adott részfában annak gyökerétől jobbra lépegetve érhető el. Ennek a kulcsa biztosan nagyobb a bal oldali részfa, és kisebb a jobb oldali részfa minden eleménél.
Elem törlése a bináris rendezőfából, ha két utóda van:
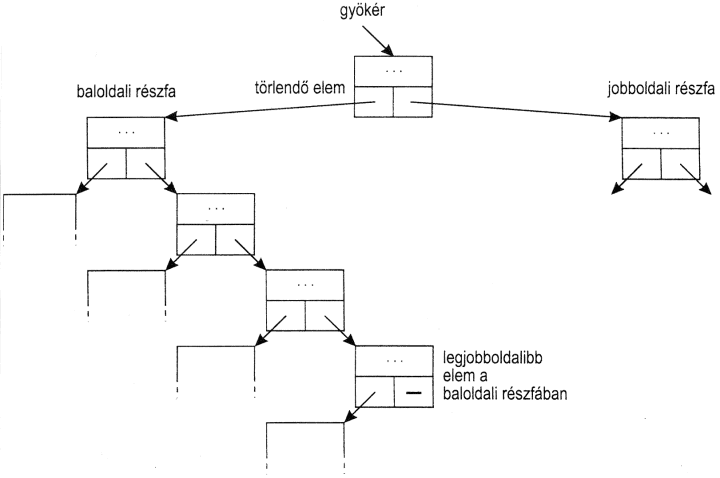
A feladat megoldható egyébként szimmetrikusan a másik oldallal is: tehát úgy, hogy a törlendő elem jobb oldali részfájának legbaloldalibb elemét hozzuk fel a törlendő helyére stb.
A szükséges típusokat már megadtuk, az algoritmushoz szükséges globális változó:
gyoker:mutato; (gyökérelem)
A Turbo Pascal program:
program telefonkonyv8;
{$A- }
const nevhossz=30;
szamhossz=16;
type nevt=string[nevhossz];
szamt=string[szamhossz];
mutato=^elem;
elem=record
nev:nevt;
telszam:szamt;
bal,jobb:mutato
end;
var parancs,ch:char;
ujnev:nevt;
ujszam:szamt;
megvan:boolean;
gyoker:mutato;procedure Kezdes(var gy:mutato);
begin
gy:=nil { ures fa }
end;procedure Menu;
begin
Writeln;
Writeln('''u'' - uj nev');Writeln('''k'' - kereses');
Writeln('''t'' - torles');Writeln('''l'' - listazas');
Writeln('''v'' - vege');
Write('Parancs: ');
repeat
Readln(parancs)
until parancs in ['u','k','t','l','v']
end;procedure Kereses(knev:nevt;gy:mutato;
var megvan:boolean;var sz:szamt);
begin
if gy=nil then megvan:=false { ures fa }
else
with gy^ do begin
megvan:=knev=nev; { nev egyezik? }
if megvan then sz:=telszam
else
if knev<nev then Kereses(knev,bal,megvan,sz)
else Kereses(knev,jobb,megvan,sz)
end
end;procedure Ujelem(ujnev:nevt;ujszam:szamt;var gy:mutato);
begin
if gy=nil then begin { ures (resz-)fa }
New(gy); { uj elem letrehozasa }
with gy^ do begin { uj elem kitoltese }
nev:=ujnev;telszam:=ujszam;
bal:=nil;jobb:=nil
end
end
else { nem ures a fa }
with gy^ do begin
if ujnev<nev then
Ujelem(ujnev,ujszam,bal)
else Ujelem(ujnev,ujszam,jobb)
end
end;procedure Kiiras(gy:mutato);
begin
if gy<>nil then
with gy^ do begin
Kiiras(bal); { kisebb elemek kiirasa }
Writeln(nev,' : ',telszam);
Kiiras(jobb) { nagyobb elemek kiirasa }
end
end;procedure Torles(tnev:nevt;var gy:mutato);
var torolt,bj,ebj:mutato;
begin
if gy<>nil then { nem ures a (resz-)fa }
with gy^ do begin
if tnev=nev then begin { megtalaltuk }
torolt:=gy; { a gyokerelem a torlendo }
if bal=nil then gy:=jobb { nincs bal reszfa }
else
if jobb=nil then gy:=bal { nics jobb reszfa }
else begin { van mindket reszfa }
bj:=bal; { bal reszfa... }
while bj^.jobb<>nil do begin { ...legbaloldalibb... }
ebj:=bj; bj:=bj^.jobb { ...elemenek keresese }
end;
if bj<>bal then begin { gyoker bal gyereke }
ebj^.jobb:=bj^.bal; { lejebb volt }
bj^.bal:=bal
end;
bj^.jobb:=jobb;gy:=bj { bj elem gyoker helyebe lep }
end;
Dispose(torolt) { torolt elem felszabaditasa }
end
else { nem a gyokerelem torlendo }
if tnev<nev then Torles(tnev,bal) { bal reszfarol torol }
else Torles(tnev,jobb) { jobb reszfarol torol }
end
end;begin
Kezdes(gyoker);
repeat
Menu;
if (parancs='u') or (parancs='k') or (parancs='t') then begin
Write('Nev: ');readln(ujnev);
Kereses(ujnev,gyoker,megvan,ujszam)
end;
case parancs of
'u': if megvan then Writeln('Mar van ilyen nev!')
else begin
Write('Telefonszam: ');Readln(ujszam);
Ujelem(ujnev,ujszam,gyoker)
end;
'k': if megvan then Writeln('Telefonszam: ',ujszam)
else writeln('Nincs ilyen nev a listan!');
't': if megvan then Torles(ujnev,gyoker)
else Writeln('Nincs ilyen nev a listan!');
'l': Kiiras(gyoker);
'v': begin
Write('Valoban be akarja fejezni?');
repeat
Readln(ch)
until (ch='i') or (ch='n');
if ch='n' then parancs:=ch
end
end
until parancs='v'
end.
Ez a fejezet további három adattípust mutat be: a felsorolt típust, a halmazt és az adatállományt.
6.1.1. Példa:
Definiáljunk adatszerkezetet, amely egy üzlet heti nyitvatartási idejének tárolására alkalmas: melyik nap mikor nyit, illetve zár.
Megoldás:
Eddigi ismereteink alapján a következők valamelyikét választanánk:
type
nyitvatartas1=array[1..7,1..2] of real;
{ 1: nyitas, 2 :zaras}
nyitvatartas2=array[1..7] of record
nyit,zar:real
end;
El kell döntenünk azt is, hogy a hét napjait hogyan osztjuk el az 1...7 intervallumon, azaz hétfő legyen-e az 1-es, vagy inkább a vasárnap.
Ha ez megvan, készítsünk programrészletet, amely beolvassa egy nyitva:nyitvatartas1; tömbbe az időpontokat:
for k:=1 to 7 do
for g:=1 to 2 do read(nyitva[g,k]);
{ hibas! }
Remélem, az Olvasó is felfedezte a hibát! A gondot itt az okozza, hogy ennél a megoldásnál a hét napjait nekünk, a programozóknak kellett valamilyen módon kódolnunk, vagyis az eredeti jelentés, a hét napjainak neve helyett egész számokat alkalmazunk. Nem szerencsés a nyitás és zárás, mint 1, illetve 2 index sem, ennél már a rekord használata is természetesebb.
Például:
nyitzar:nyitvatartas2;
változó esetén:
for k:=1 to 7 do
with nyitzar[k] do read(nyit,zar);
Ennél sokkal jobb lenne, ha a beolvasást így írhatnánk:
for nap:=hetfo to vasarnap do
for nyitzar:=nyit to zar do
read(nyitva[nap,nyitzar]);
Ez megtehető a következő definíciók és deklarációk segítségével is:
const
hetfo=1; vasarnap=7;
nyit=1; zar=2;
type nyitvatartas3=array[hetfo..vasarnap,nyit..zar] of real;
var
nyitva:nyitvatartas3;
nap,nyitzar:integer;
Ez már olvashatóbbnak tűnik, de nem véd meg attól a hibától, amit az első esetben a beolvasáskor elkövettünk: ha véletlenül felcseréljük az indexeket, ez csak a program futásakor derül ki, hiszen mindkét tömbindex az egész típus intervalluma. Ha azt akarjuk, hogy az ilyen hiba már a fordításkor, azaz szintaktikai hibaként kiderüljön, akkor a két indexnek alapvetően más adattípust kell választani.
A probléma megoldását a felsorolt típus használata jelenti. Ennek segítségével ugyanis a hét napjainak, valamint a nyitásnak és a zárásnak a jellemzésére is saját, minden mástól különböző adattípust definiálhatunk:
type
hetnapja=(hetfo,kedd,szerda,csutortok,pentek,szombat,vasarnap);
nyztip=(nyit,zar);
Így a zárójelben megadott azonosítók lesznek a definiált adattípus lehetséges értékei, formálisan hetnapja, illetve nyztip típusú konstansok azonosítói.
A megfelelő definíciók és deklarációk:
type nyitvatartas=array[hetnapja,nyztip] of real;
var nyitva:nyitvatartas;
nap:hetnapja;
nyitzar:nyztip;
Ezekkel már valóban így végezhető el a beolvasás:
for nap:=hetfo to vasarnap do
for nyitzar:=nyit to zar do
read(nyitva[nap,nyitzar]);
Ha ebben a programrészletben cserélnénk fel véletlenül az indexeket, akkor az valóban szintaktikai hibát jelentene, tehát már a program fordításakor kiderülne.
A felsorolt típus
1. A felsorolt típus értékek egy rendezett készletét jelenti, amelyet az ezen értékeket jelentő azonosítók felsorolásával definiálunk. Nem előre definiált típus, azaz minden felsorolt típust a programban definiálni kell.
2. A típusmegadás formája:
felsorolt típus:
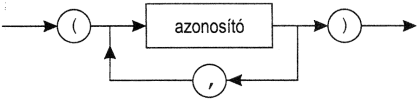
3. A felsorolt típus a definíciójában szereplő azonosítókkal képviselt értékeket veheti fel. Amikor egy azonosítót egy felsorolt típus definíciójában a zárójelek közötti listán megadunk, ezzel az azonosítót az adott felsorolt típus konstansának definiáljuk. A konstans definíciós pontja az azonosító megadásának helye.
A felsorolt típus definíciója így egyszerre jelenti a típus, vagy az ilyen típusú adat, valamint az értékkészletét jelentő konstansok azonosítóinak definiálását is. (a)
Például atype ujj=(kis,gyurus,nagy,mutato,huvelyk)
definíció esetén ujj a felsorolt típus azonosítója, az értékkészletet a zárójelben megadott kis...huvelyk nevek jelentik, melyek ezzel a definícióval ujj típusú konstansokat jelentenek.
4. A felsorolt típus egyben sorszámozott is. A definiáláskor felsorolt konstansazonosítók ord értékei a felsorolás sorrendjében rendre 0, 1,..., azonosítók száma -1.
Az előbbi példában ígyord(kis)=0
ord(gyurus)=1
ord(huvelyk)=45. Felsorolt típusú adattal a következő műveletek végezhetők:
- előfordulhat összehasonlító kifejezésben;
- felsorolt típusú változó értéket kaphat értékadó utasítással, valamint get és read eljárással;
- értéke kiírható put és write eljárással;
- érték- és változóparaméterként átadható eljárásnak, illetve függvénynek;
- függvény típusa lehet felsorolt típus;
- lehet halmaz elemtípusa, állhat in művelet bal oldalán;
- használható ciklusváltozóként for utasításban;
- lehet case utasítás szelektora;
- lehet tömb indextípusa;
- lehet változó rekord vezérlőtípusa.
6. Felsorolt típusú adatok összehasonlításának eredménye megegyezik ord értékeik összehasonlításának eredményével, azaz ha f1 és f2 kompatibilis felsorolt típusú, akkor pl. f1<f2 akkor és csak akkor igaz, ha ord(f1)<ord(f2). (c)
Az összehasonlítás eredménye boolean típusú.
Kompaibilis felsorolt típusú adatokra használható összehasonlító műveletek:
= egyenlőség; <> < kisebb, azaz a bal oldali a felsorolásban előrébb áll-e, mint a jobb oldali; > nagyobb, azaz a bal oldali a felsorolásban hátrább áll-e, mint a jobb oldali; <= kisebb vagy egyenlő; >= nagyobb vagy egyenlő. 7. Felsorolt típusok függvényei; az f-fel jelölt paraméter valamilyen ft felsorolt típusú:
- integer értékű:
ord(f) az f érték sorszámát adja meg, az ft típus megadásakor az értékek listáján legelöl álló elem ord értéke 0, a következőé 1 stb.
- A paraméter típusával megegyező, azaz ft típusú:
succ(f) a következő, azaz eggyel nagyobb ord értékű elemet adja meg, ha az létezik, egyébként hiba történik,
pl. succ(gyurus) = nagy
de succ(huvelyk) már hibát okoz, hiszen nincs ilyen érték.pred(f) Az előző, azaz eggyel kisebb ord értékű elemet adja, ha az létezik, egyébként hiba történik,
pl. pred(gyurus) = kis
de pred(kis) már hibát okoz.Magyarázatok, megjegyzések:
(a) Ha egy felsorolt típusú változót csak egy helyen használunk, akkor nem kell külön a típust, majd az ilyen változót deklarálnunk, hanem közvetlenül a változót is deklarálhatjuk felsorolt típusúnak.
Például:var gy1,gy2:(alma,korte,szilva,barack);
Itt nem típust definiáltunk először, hanem felsorolt típusú változót. Ez is definiálta az alma.barack konstansokat.
Ha először nem egy adott felsorolt típus azonosítóját, majd utána ilyen típusú változót, vagy ilyen elemtípusú összetett változót definiálunk, hanem pl. a felsorolt típust először egy változó deklarációjában adjuk meg, akkor később ezt a típust az első ilyen változó deklarációjában felsorolt konstansok segítségével kifejezett intervallumtípussal tudjuk megadni:gy3:alma..barack;
vanotthon:set of alma..barack;Ilyenkor mégis szerencsésebb, ha először definiáljuk a megfelelő típus azonosítóját, és később azt az azonosítót használjuk:
type gyumolcs=(alma,korte,szilva,barack);
var gy1,gy2:gyumolcs ;
gy3:gyumolcs;
vanotthon:set of gyumolcs;Ez a megoldás azért is jobb, mert például szegmens paraméterének illetve függvénynek a típusát csak típusazonosítóval adhatjuk meg, intervallummal nem.
(b) Felsorolt típusú értéket tehát nem lehet text típusú állományból read, vagy readln eljárással beolvasni, illetve text típusú állományba write, vagy writeln eljárással kiírni. A kiíráskor az ord értéket, vagy megfelelő stringet szoktak használni.
Ha mégis erre lenne szükségünk, akkor több megoldást is választhatunk:
repeat
read(ch)
until ch<>' '; { szokozok atlepése }
case ch of
'K': u:=kis;
'G': u:=gyurus;
'N': u:=nagy;
'M: u:=mutatu;
'H': u:=huvelyk
end;ahol ch char típusú, u pedig ujj típusú változó.
A felsorolt típusú konstans nevének megfelelő karakterláncokat olvasunk be és megfelelő tömbök segítségével keressük ki a felsorolt típusú értéket.
- Az adott érték ord értékét olvassuk be, és ebből határozzuk meg a felsorolt típusú adatot. (d)
(c) A relációs műveletek ilyen definíciója miatt felesleges a felsorolt típusú adatok hasonlítása helyett ord értékeik összehasonlítását használnunk, hiszen az nemcsak hosszabb, de áttekinthetetlen is.
(d) Ha valamiért mégis szükségünk lenne az ord függvény inverzére egy adott felsorolt típusnál, akkor például a 3. szabály ujj típusára ilyen függvényt definiálhatunk:
function ujjfv(n: integer):ujj ;
{ megadja az n ord értékű ujjat }
var u:ujj;
begin
u:=kis; {elso ertek}
while ord(u)<>n do
u:=succ(u); { kereses }
ujjfv:=u;
end;Ezt a függvényt például a
var u:ujj;
deklaráció esetén így használhatjuk:
u:=ujjfv(4);
ami u-nak a huvelyk értéket adja.
Vegyük észre, hogy ha a függvény paramétere a példában negatív vagy nagyobb 4-nél, akkora succ függvény végrehajtásakor végül hiba fog történni.
A felsorolt típust elsősorban olyankor használjuk, ha a programon belül egy érték néhány esetének valamilyen nevet akarunk adni. Ilyen lehetne például a személyi adatok nyilvántartásában a családi állapot. Az ennek megfelelő adattípus:
csaladi_allapot=(egyedulallo,hazas,elvalt,ozvegy);
Ilyen még például a színek felsorolása, vagy a bizonyítványban a tantárgyak nevének megadása is.
6.1.2. Példa:
Gyakran előfordul interaktív programokban, hogy egy kérdésre igen-nem választ kell adni.
Készítsünk függvényt, amely beolvas egy karaktert, és megadja, hogy az igen vagy nem válasznak felel-e meg!
Megoldás:
type ignem=(nem,igen);
...
function valasz:ignem;
var ch:char;
begin
repeat
read(ch)
until (ch='I') or (ch='i') or (ch='Y') or (ch='y') or (ch='N') or (ch='n');
if (ch='n') or (ch='N') then valasz:=nem
else valasz:=igen
end;
Sajnos, a felsorolt típusú adat nem olvasható be és nem is írható ki közvetlenül text típusú adatállományba, ezért elsősorban belső adatábrázolásra használjuk.
Az előző példában látható eljárásban meglehetősen körülményesen lehetett megfogalmazni, hogy a beolvasott karaktert melyik 6 esetben fogadtuk el helyes válasznak. A kényelmes megfogalmazás az lenne, hogy a beolvasott karakter benne van-e az i, I, y, Y, n, N karakterek halmazában.
Ez a Pascal nyelvben így írható le:
until ch in ['I','i','Y','y','N','n'];
Hasonlóan, a függvény értékének beállítása így történhet:
if ch in ['n','N'] then valasz:=nem
else valasz:=igen;
Itt a szögletes zárójelben felsorolt értékekből a gép az értékek típusának megfelelő halmazt készít, az in
művelet pedig egy összehasonlítást végez, amely akkor igaz, ha a bal oldalán megadott érték benne van a jobb oldalán megadott halmazban.
Ennek a halmaz létrehozásához használt szögletes zárójelnek semmi köze sincs a tömböknél használt index-zárójelhez, és úgy tudjuk tőle megkülönböztetni, hogy nincs közvetlenül előtte azonosító, legfeljebb műveleti jel.
A 3.4. fejezetben, a 3.4.2. példában a lottószámok előállításakor minden újonnan kisorsolt számról meg kellett vizsgálni, hogy előfordult-e már. Ezt a matematikában úgy fogalmaznánk, hogy az új szám benne van-e az előzőleg kisorsolt számok halmazában.
A már kisorsolt számok halmazának tárolására deklarálhatunk olyan változót, amelyben az 1-től 90-ig terjedő számok lehetnek benne:
program lotto;
var k,uj:integer;
szamok:set of 1..90;
begin
szamok:=[]; { ures halmaz }
for k:=1 to 5 do begin
repeat
uj:=trunc(random*90+1) { kov. veletlen ertek }
until not(uj in szamok); { egyik elozovel sem egyezik }
szamok:=szamok+[uj] { uj elem halmazba rakasa }
end;
for k:=1 to 90 do
if k in szamok then write(k:4);
writeln
end.
Ez a változat megoldja a számok nagyság szerinti kiírását is, hiszen 1-től 90-ig haladva vizsgáljuk meg, hogy az adott szám benne van-e a kisorsoltak között, és ha igen, akkor kiírjuk.
Ebben a programban két további halmazműveletet is látunk. Az egyik az üres halmaz létrehozása, ez olyan szögletes zárójelpárral érhető el, amelyben semmi sincs; a másik a halmazok egyesítése, azaz uniója, hi-szen az új számot + műveleti jellel tettük a halmazba.
A halmaz (set) típus
1. A halmaz típus a matematikában megszokotthoz hasonló halmazműveletek végrehajtását teszi lehetővé.
2. Alakja:
halmaz típus:

ahol elemtípus: sorszámozott típus
(a)
Pl.
set of char
set of 1..1103. Ha s egy t típus intervallumtípusa, akkor a set of s típusú adattal végzett halmazművelet eredményét set of t típusúnak, a packed set of s típusú adattal végzett halmazművelet eredményét pedig packed set of t típusúnak tekintjük. (b)
4. Halmazértéket az elemtípusának megfelelő értékekből a halmazgenerátorral tudunk létrehozni:
halmazgenerátor:
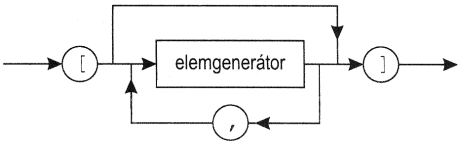
elemgenerátor:
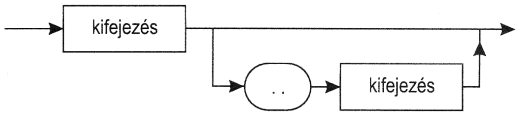
A kifejezések értékének a halmaz elemtípusával kompatibilis sorszámozott típusúnak kell lennie.
Jelöljük t-vel a halmazgenerátorban használt kifejezések típusát; ekkor a halmazgenerátorral létrehozott érték vagy set of t, vagy packed set of t típusú - ahogyan azt a vele képzett kifejezésben a környezet megkívánja.A [] halmazgenerátor üres halmazértéket jelöl, mely minden halmazzal kompatíbilis.
Az [x] halmazgenerátor - ahol x egy kifejezés olyan halmazértéket jelöl, amelynek egyetlen eleme van: x.
Az [x..y] halmazgenerátor - ahol x és y egy-egy kifejezés és x<=y -, olyan halmazértéket hoz létre, amelynek x-től y-ig rendre minden érték eleme x-et és y-t is beleértve, míg x>y esetén üres halmazt hoz létre.
Az [u,v] halmazgenerátor - ahol u és v is akár a fenti x-nek akár x..y-nak megfelelő elemgenerátor lehet olyan halmazt hoz létre, amelyben mind az [u] mind a [v] halmazgenerátorral létrehozott halmazok elemei benne vannak, röviden:
[u,v]=[u]+[v]
A fenti halmazgenerátorokban az x-szel és y-nal jelölt kifejezések, illetve az u-val és v-vel je¬lölt elemgenerátorok kiértékelésének sorrendje megvalósításfüggő.
Példák:
[5] egyelemű halmazérték, melynek csak az 5 egész szám az eleme, ['0'..'9'] set of char vagy packed set of char típusú érték, amelyben minden számjegy benne van, és csak a számjegyek, ['A'..'Z'] [8,11..22] egészekből álló halmazérték, melynek elemei: 8, 11, 12, 13...20, 21, 22 [he..pe] [5*Z+3..7] ha z=0, akkor [3..7] értékű,
ha z=1, akkor üres halmaz stb.5. A t1 és t2 halmaz típusok kompatibilisek, ha kompatibilis elemtípus halmaz típusai és vagy mindkettő, vagy egyik sem packed.
6. A t2 halmaz típust értékadás-kompatibilisnek nevezzük t1 halmaztípussal a v1:=v2 irányban - ahol v1 változó t1, v2 kifejezés pedig t2 típusú -, ha a t2 típusú érték minden eleme t1 elemtípusának megengedett tartományában van. (c)
7. Halmazzal végezhető műveletek:
Halmaz típusú változó értéket kaphat értékadó utasítással és get eljárással.
Hiba történik, ha az értékadásban szereplő halmazértéknek van olyan eleme, amely nincs benne a halmaz típusú változó elemtípusának megengedett értéktartományában.Értéke kiírható put eljárással.
- Használható halmazkifejezésben. Halmazkifejezés operandusai csak kompatibilis halmazok lehetnek, a kifejezés eredményének típusát a 3. szabály adja meg.
* metszet- azaz közösrész képzés: h1*h2 halmaznak azok az értékek az elemei, amelyek mind h1-nek, mind h2-nek elemei; + egyesítés, azaz unió: a h1+h2 halmaznak mindazon értékek elemei, amelyek akár h1-nek, akár h2-nek elemei; - halmazkülönbség képzés: h1-h2 halmaznak azok és csak azok az értékek elemei, amelyek h1-nek elemei de h2-nek nem.
= egyenlőségvizsgálat: két halmaz akkor egyenlő, ha mindkettő üres, vagy ha pontosan ugyanazon értékek az elemeik; <> <= >=
- Ha az első opersrdus sorszámozott típusú kifejezés, a második pedig ilyen elemű halmaz típus:
in halmaz eleme vizsgálat: e in h akkor igaz, ha az e érték eleme a h halmaznak, egyébként hamis. (e) Magyarázatok, megjegyzések:
(a) Mivel halmaz elemtípusa csak sorszámozott típus lehet, nem képezhető set of real és set of string sem (például string=packed array[1. .80] of char definíció mellett).
(b) Ha például
v1:set of 'A'..'Z';
v2:set of '0'..'9';akkor bármelyik szerepel is egy halmazkifejezésben, a kifejezés típusa set of char lesz.
(c) Tekintsük a következő változódeklarációkat:
charhalm:set of char;
szjegyhalm:set of '0'..'9';
betuhalm:set of 'A'..'Z'A 6. szabály értelmében a charhalm:=szjegyhalm és a charhalm:=betuhalm értékadás mindig elvégezhető, szjegyhalm:=charhalm csak akkor végezhető el, ha charhalm csupa számjegy elemeket tartalmaz, vagy üres;
betuhalm:=charhalm csak akkor végezhető el, ha charhalm csak 'A' és 'Z' közötti karaktereket tartalmaz, vagy üres;
szjegyhalm:=betuhalm csak akkor végezhető el, ha betuhalm üres, hiszen a számjegyek zárt sorozatot alkotnak, tehát nem lehet közöttük betű;
betuhalm:=szjegyhalm csak akkor végezhető el, ha szjegyhalm üres, vagy az adott megvalósításban a számjegyek az 'A'..'Z' intervallumban vannak (de ez sem az ASCII, sem az EBCDIC karakterkészletre nem teljesül).
(d) A Pascal nyelvben a halmazoknál nincs műveleti jel a valódi részhalmaz vizsgálatára. Ezt például úgy jelölhetnénk, hogy h1<h2, és az lehetne a jelentése, hogy h1 valódi részhalmaza h2-nek, ha h2-nek van olyan eleme, amely nem eleme h1-nek, de h1 minden eleme eleme h2-nek. Ezt az összehasonlítást pótolhatjuk a következő kifejezéssel:
(h1<=h2) and (h1<>h2)
Hasonlóan, a nem létező h1>h2 valódi részhalmaz vizsgálat helyett használhatjuk a
(h1>=h2) and (h1<>h2)
kifejezést.
(e) Az e in h relációt kifejezhetjük az előbbi lehetőségekkel ilyen módon is:
[e]*h<>[]
vagyis az e-t tartalmazó egyelemű halmaz és a h halmaz metszete nem üres halmaz.
6.2.1. Példa:
Készítsünk programot, amely azzal segít a bevásárlásban, hogy megadja, melyik üzletekbe kell elmenni, ha bizonyos árukat szeretnénk megvenni!
Tételezzük fel, hogy rendelkezésünkre állnak az egyes üzletek árukészletei, azaz hogy melyik üzletben mit lehet venni. A program egy futása során tetszőleges számú bevásárláshoz adjon tanácsot.
Megoldás:
A következő egyszerűsítéseket tesszük:
Az üzletekben a keresett áruk készletét úgy adjuk meg, hogy felsoroljuk az áruk kódszámait, amelyek pozitív számok lehetnek egy adott értékig, majd 0-val jelezzük az áruk megadásának végét.
A program részletes elemzése a megjegyzések alapján könnyen elvégezhető:
program bevasarlas;
const maxarukod=250;
type arukod=1..maxarukod; { aruk kodja }
aruk=set of arukod; { a ruk halmaza }
uzlet=(skala,corvin,florian,sugar); { uzletek }
var valasztek:array[uzlet] of aruk; { uzletek valaszteka }
teljesvalasztek:aruk; { uzletek teljes valaszteka }
igeny:aruk; { amit keresunk }
hol:uzlet; { hol akarunk vasarolni }
procedure arukkiirasa(a:aruk);
var aru:arukod;
begin
for aru:=1 to maxarukod do
if aru in a then write(aru:4);
end;
procedure arukbeolvasasa(var a:aruk);
var aru:integer;
begin
writeln('Irja be az aruk kodjait, fejezze be 0-val!');
a:=[];
repeat
read(aru);
if (aru>=1) and (aru<=maxarukod) then
a:=a+[aru] { kovetkezo aru hozzadasa }
else if aru<>0 then
writeln('Az 1...',maxarukod,
' tartomanyban kell lennie, vagy 0')
until aru=0;
writeln;
if a<>[] then begin
write('Beolvasott arukodok: ');
arukkiirasa(a);
writeln
end;
writeln;
end;
procedure valasztekbeolvasasa;
var hol:uzlet;
begin
writeln('Uzletek valasztekanak beolvasasa');
teljesvalasztek:=[];
for hol:=skala to sugar do begin
write(ord(hol)+1,'. uzlet valaszteka: ');
arukbeolvasasa(valasztek[hol]);
teljesvalasztek:=teljesvalasztek+valasztek[hol]
end
end;
begin
valasztekbeolvasasa;
repeat
writeln;write('Kovetkezo igeny: ');
arukbeolvasasa(igeny);
if igeny<>[] then begin
if igeny<=teljesvalasztek then write('Mindent megkap')
else begin
write('Nem kaphato: ');
arukkiirasa(igeny-teljesvalasztek);
writeln(', ne is keresse!');
write('A tobbi megtalalhato')
end;
igeny:=igeny*teljesvalasztek; { igenyek redukalasa }
hol:=skala;
while (hol<sugar) and not (igeny<=valasztek[hol]) do
hol:=succ(hol); { tovabb keresunk }
if igeny<=valasztek[hol] then { itt minden megvan }
writeln('a(z) ',ord(hol)+1,'. uzletben')
else begin { nincs meg minden egy helyen }
writeln(', de vegig kell jarni a kovetkezo helyeket:');
hol:=skala;
repeat
if igeny*valasztek[hol]<>[] then begin { van mit venni }
write(ord(hol)+1,'. uzlet, itt van:');
arukkiirasa(igeny*valasztek[hol]);writeln;
igeny:=igeny-valasztek[hol]
end;
if hol<sugar then hol:=succ(hol)
until igeny=[] { mindent vettunk }
end;
igeny:=[1];
writeln;writeln('irjon 0-at, hogy befejezze')
end
until igeny=[]
end.
6.3. Az adatállomány (file) típus
Az adatállományok olyan adatok, amelyek az összes többitől eltérően általában nem a gép főtárában, azaz memóriájában helyezkednek el, hanem valamilyen egyéb adathordozón, így például mágneslemezen vagy mágnesszalagon. Adatállományok segítségével kezeljük a programok elsődleges adatbeviteli és kiírási eszközeit is, melyek személyi számítógépeknél tipikusan a billentyűzet, illetve a képernyő.
Az adatállományok, vagy angol nevükön file-ok (kiejtése: fájl) teszik lehetővé, hogy a program a "külvilággal", így a program használójával is, kapcsolatot tartson, azaz onnan adatokat olvasson be, illetve oda eredményeket írjon ki. A számítógépek legtöbbje nagyon sokféle műveletet képes file-okkal végezni, de hogy miket és hogyan, az erősen függ a gép lehetőségeitől, valamint a programok futási környezetétől, például az operációs rendszertől. A szabványos Pascal nyelv e lehetőségek közül csak a legegyszerűbbeket tartalmazza; nem véletlen, hogy az egyes Pascal megvalósítások között éppen az adatállományok kezelésében van a legnagyobb különbség. (HiSoft-Pascal-ban pedig egyáltalán nincs a file-típus megvalósítva.) Ha valaki hatékony adatállománykezelő programot akar írni egy Pascal megvalósításban, akkor nagyon jól teszi, ha alaposan áttanulmányozza gépe és Pascal rendszere kézikönyveit.
A legfontosabb adatállománykezelő műveletekkel már a 2.13. fejezetben már megismerkedtünk. Most először a file-okra vonatkozó szabályok következnek, majd néhány mintapélda azok használatára.
Az állomány (file) típus
1. Az adatállományok, vagy más néven állomány típusú adatok abban térnek el a többi adattípustól, hogy
- lehetővé teszik a program és a külvilág, például a program és felhasználója, illetve két program közötti információcserét; (a)
- olyan nagy mennyiségű adat tárolását is lehetővé teszik, amely egyszerre nem férne el a gép belső memóriájában; (b)
- az adatok a program végrehajtása előtt is létezhetnek, illetve lehet, hogy a program lefutása után is létezni fognak. (b,c)
2. File típus megadásának formai szabályai:
állománytípus:

ahol elemtípus: típus
File elemtípusa tetszőleges adattípus lehet, kivéve file típus, vagy bármilyen összetett típus, amelynek van file típusú eleme. (d)
3. Az adatállomány pillanatnyi értékét a következők határozzák meg:
- az adatállomány kiírási vagy beolvasási állapotban van-e;
- ha kiírás alatt van, akkor melyek a már kiírt értékek, és mi ezek sorrendje (e);
4. Egy adatállomány akkor üres, ha egyetlen értéket sem tárol.
5. Két adatállomány akkor egyenlő, ha mindkettő üres állomány, vagy minden elemük rendre megegyezik.
6. "Adatok vége" állapotban van egy adatállomány,
- ha beolvasás alatt van és nincs további beolvasható értéke,
- vagy ha kiírás alatt van.
7. A text típusú előre definiált állományt az jellemzi, hogy
- sorokból áll,
- egy sor karakterekből és a sor végén sorvége jelből áll (f,g),
8. A text típusú adatállományra használható minden előre deklarált eljárás és függvény, amely a file of char típusú adatállományra is használható.
Az eoln előre deklarált függvényt és a readln, writeln, page előre deklarált eljárásokat csak text típusú adatállományra lehet alkalmazni. (h)
9. A bufferváltozó olyan változóhivatkozás, amely egy adatállomány egyetlen elemét adja meg, és ez az egyetlen eleme, amelyet egy adott pillanatban közvetlenül el lehet érni. (Maga a buffer szó itt átmeneti tárolót jelent.)
Jelölése:bufferváltozó:
adatállomány-változó^
Az adatállomány-változó egy tetszőleges elemtípusú adatállományt jelent, beleértve a text típusú adatállományt is.
A bufferváltozó típusát az adatállomány-változó elemtípusa adja meg.
A bufferváltozóra hivatkozás adatállomány-változóra való hivatkozást jelent.
Hiba történik, ha egy adatállomány értéke megváltozik, miközben a bufferváltozóhoz hozzáférünk. (i)
10. Adatállománnyal végezhető műveletek:
- változóparaméterként átadható eljárásnak és függvénynek; (j)
- adatállomány, illetve elemeinek értéke megváltoztatható a 12. pontban leírt előre deklarált eljárások segítségével;
- az adatállomány aktuális elemére hivatkozhatunk bufferváltozó segítségével. (k)
11. Bufferváltozóval végezhető műveletek: mindazok, amelyeket a bufferváltozó típusa, tehát az adatállomány elemtípusa megenged, kivéve, hogy bufferváltozó nem lehet for utasítás ciklusváltozója.12. Az adatállományokra alkalmazható előre deklarált eljárások és függvények ismertetése következik.
Itt f tetszőleges adatállomány-változót, így f^ ennek bufferváltozóját jelöli.
Hiba történik, ha a most következő előfeltételek valamelyike nem teljesül közvetlenül az adott eljárás használata előtt.
Az itt ismertetendő hatásoknak valamikor a következő file-művelet végrehajtása előtt kell bekövetkezniük, file-műveletnek számít a bufferváltozóhoz való hozzáférés is. A hatások pontos bekövetkezésének időpontja megvalósításban definiált. (l)
Eljárások:
| rewrite(f) | Az f állományt megnyitja írásra (m), azaz olyan állapotba hozza, hogy utána put-tal vagy write-tal írni lehessen bele. Előfeltételek: - Hatások: f üressé válik és felírási állapotba kerül, f^ teljesen meghatározatlanná válik, tehát ha f file tartalmazott eddig értékeket, akkor azok a rewrite hatására elvesznek, azaz a file tartalma törlődik. |
| put(f) | Felírja az f^ bufferváltozó értékét az f file-ba, tehát ft értékét az f állomány végéhez csatolja. Előfeltételek: f felírási állapotban legyen, f^ tartalma nem lehet meghatározatlan. Hatások: f^ értékét f-hez csatolja, f^ tartalma teljesen meghatározatlanná válik és f felírási állapotban marad. Előtte tehát a bufferváltozót a kiírandó értékkel fel kell töltenünk. |
| reset(f) | Az f állományt megnyitja olvasásra (m), azaz olyan állapotba hozza, hogy utána a file elemei a get vagy read eljárással rendre beolvashatok és a bufferváltozóból felhasználhatók legyenek. Előfeltételek: az f file tartalma ne legyen meghatározatlan. Hatások: az f adatállomány olvasási állapotba kerül, és ha f nem üres, akkor f első elemének értékét a gép f^-ba olvassa, ezzel át is lépi f első elemét és eof(f) értéke false lesz, egyébként, tehát ha f üres, akkor f^ teljesen meghatározatlanná válik és eof (f) értéke true lesz. (n) |
| get(f) | Beolvassa az f file következő elemének értékét az ft bufferváltozóba. Előfeltételek: az f file beolvasási állapotban legyen és f nem lehet adatok vége állapotban, azaz eof(f) értéke false kell, hogy legyen. Hatások: beolvasási állapotban marad. Ha van még további eleme f-nek, akkor a következő elem értéke f^-ba kerül és eof(f) értéke false lesz, míg ha nincs további eleme f-nek, akkor f^ értéke teljesen meghatározatlanná válik és eof(f) értéke true lesz. Az f file beolvasási állapotban marad. |
A read és write előre definiált eljárások használata a nem text előre definiált típusú állományokkal a következők szerint történik:
Jelöljön v egy, az f adatállomány elemtípusával értékadás-kompatibilis változót, e pedig f elemtípusával értékadás-kompatibilis kifejezést. A v változóra hivatkozás nem azt jelenti, hogy v aktuális változóparaméter, v pakolt összetett változó eleme is lehet.
| read(f,v) | azonos a
utasításcsoporttal, azaz a bufferváltozó értékét a v-vel jelölt változóba másolja és beolvassa a következő értéket. (o)
azonos a
utasításcsoporttal. Vagyis több - tetszőleges számú - változó értékét is beolvashatjuk egyetlen read eljáráshívás segítségével, a változók rendre az f file egymást követő elemeinek értékeit kapják. |
| write(f,e) | azonos a
utasításcsoporttal, tehát az e kifejezés értékét kiírja f-be. (p)
azonos a
utasításcsoporttal, azaz több - tetszőleges számú - kifejezés értékét is kiírhatjuk egyetlen write eljáráshívás segítségével, a kiírt értékek rendre a paraméterként felsorolt kifejezések értékei lesznek. |
Függvény:
| eof(f) | értéke true, ha nincs az f file-nak további eleme, egyébként - tehát
ha van további eleme - false. Ha elhagyjuk az eof függvény paraméterét, akkor az előre deklarált input állományra vonatkozik. (q) |
Az itt ismertetett eljárások és a függvény eiső vagy egyetlen paramétere tehát mindig valamilyen adatállomány típusú változó. Ez a paraméter csak text típusú file esetén hagyható el, ezt részletesen a 13., illetve 14. pont ismerteti.
13. A text előre definiált állományra a writeln, page és readln előre deklarált eljárások és az eoln előre deklarált függvény is használható, a write és read eljárások pedig további lehetőségeket is adnak.
A továbbiakban t egy text típusú állományt, v pedig a kiírandó, illetve beolvasandó érték típusának megfelelő értéket, illetve változót jelöli.Függvény:
| eoln(t) | értéke true, ha t^ bufferváltozó éppen egy sorvége jelet tartalmaz. Hiba történik, ha eoln(t) hívásakor t meghatározatlan, vagy eof(t) igaz. Ha elhagyjuk az eoln függvény paraméterét, akkor az előre deklarált input állományra vonatkozik. (r) |
Eljárások:
| read | Alakja: |

| Itt t egy text típusú állományt jelöl, a változó típusa pedig az előre definiált char, integer, vagy ezek intervalluma, illetve az előre definiált real típus lehet. Ha t nincs megadva, akkor az eljárás az előre deklarált input állományból olvas. A 12. pontban megadotthoz hasonlóan
azonos a
utasításcsoporttal. read(t,v) jelentése v típusától függ.
azonos a
utasításcsoporttal, ugyanúgy, mint a 12. pontban leírtaknál, v itt is lehet packed összetett változó eleme. Ha v típusa integer - az előre definiált egész típus -, ennek intervalluma, vagy real - az előre definiált valós típus - akkor read(t,v) hatására egy előjeles egész, illetve valós számnak megfelelő karaktersorozat beolvasása történik meg a következő módon:
|
|
| readln | Alakja: |
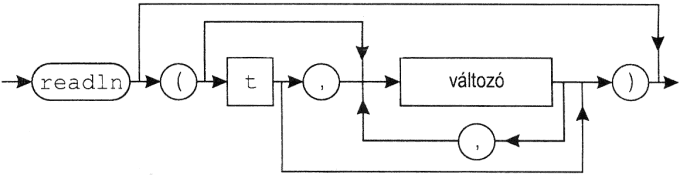
| Itt t és a változó típusára ugyanazok a szabályok érvényesek, mint a read eljárásnál. Ha t megadása, vagy a teljes paraméterlista hiányzik, akkor a művelet az előre deklarált input állományra vonatkozik.
azonos a
utasításcsoporttal,
pedig azonos a
utasításcsoporttal. A readln tehát a beolvasás után következő beolvasandó sor első karakterére állítja a t^ bufferváltozót azzal, hogy átlépi a sor további részét a sorvége jelig, valamint magát a sorvége jelet is. |
|
| write | Az eljárás text típusú állományra alkalmazva egész, valós, logikai, karakter, illetve karakterlánc típusú értékek karaktersorozat formájában történő kiírását teszi lehetővé. Alakja: |
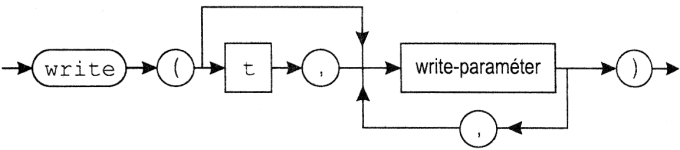
write-paraméter:

A t adatállomány-változónak előre definiált text típusúnak kell lennie. Ha nincs megadva, a művelet az előre deklarált output állományra vonatkozik.
Hiba történik, ha t értéke definiálatlan, vagy ha t nem kiírás állapotban van.
azonos a
utasításcsoporttal. A write-paraméterben szereplő kifejezés típusa, valamint a mezőhossz és törtrészhossz határozza meg a kiírás tényleges alakját. Törtrészhossz csak valós érték kiírásakor adható meg. A mezőhossz és a törtrészhossz egész értékű kifejezés lehet, hiba történik, ha bármelyikük értéke kisebb egynél. Ha nincs megadva mezőhossz, akkor a kiírás egy alapérték szerint történik. Ez az alapérték karaktertípusnál 1, karakterlánc típusnál a karakterláncban található karakterek száma, míg egész, valós és logikai típusú érték kiírásakor megvalósításban definiált. Ahhoz, hogy a további mintapéldákban pontosan lehessen látni a kiírás alakját, a kiírt karaktersorozat elején megjelenített szóközöket egy-egy ~ jelöli.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| writeln | Alakja: |
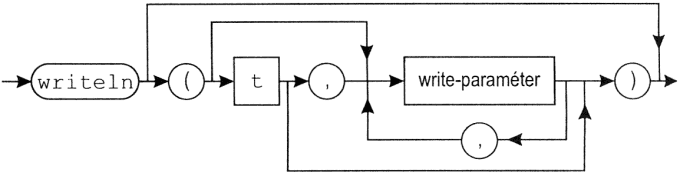
A t adatállomány-változónak előre definiált text típusúnak kell lennie. Ha nincs megadva, a művelet az előre deklarált output állományra vonatkozik.
egyenértékű a
utasításcsoporttal; writeln(t) hatására egy sorvége jel íródik ki a t text típusú adatállományba. A writeln lényegében befejezi a kiírandó sort, a következő kiírás új sor elejéről indul. Ez a képernyőn - megvalósítástól függően - a sor maradék részének változatlanul hagyását vagy törlését okozza, nyomtatott kiírás esetén a sor további része üresen marad. |
|
| page | Alakja: |

A t paraméter - ha van - előre definiált text típusú; ha pedig nincs megadva, akkor a művelet az előre deklarált output állományra vonatkozik. A page eljárás pontos hatása megvalósításban definiált, utána a kiírás általában új lapon, illetve üres képernyőn folytatódik. Ha történt már kiírás az állomány rewrite-tal való megnyitása óta, és az utoljára kiírt jel nem sorvégejel, akkor először egy sorvége jelet ír ki, és csak az után történik meg az új lap kezdését jelentő művelet. Ha olyan állományt olvasunk be, amelyre kiírásakor page eljárást hajtottak végre, a hatás megvalósításfüggő. |
14. Előre deklarált állományok:
Két előre deklarált állomány létezik, az input és az output, mindkettő előre definiált text típusú.Ha a programparaméterek között bármelyikük szerepel, akkor ez egyben definíciós pontja. Érvényességi tartománya a programblokk, és úgy tekintendő, mintha a reset (input), illetve a rewrite (output) eljárás a program első utasításának végrehajtása előtt megtörtént volna, tehát ezen állományokat nem kell az első használat előtt megnyitni. (x)
Ha a programban bármelyikükre reset-et vagy rewrite-ot hajtunk végre, annak hatása megvalósításban definiált. (z)
15. A Pascal nyelv szabványa több kérdést nem rögzít a file-okkal kapcsolatban:
- Milyen az adatok tényleges tárolási módja?
- Hogyan határozza meg a gép a file első és utolsó elemét?
- Mi a kapcsolat a programban definiált állományok és a programon kívüli, például az operációs rendszer által kezelt file-ok között? (x)
- Mikor és hogyan történik egy adatállomány lezárása (close)? (y)
- Mit jelent, ha egy adatállomány meg van adva a programparaméterek között?
Magyarázatok, megjegyzések:
(a) Ez az információcsere tipikusan azt jelenti, hogy a géphez csatolt billentyűzeten beírt adatokat file-műveletek segítségével tudjuk a programban olvasni, illetve a géphez kapcsolt képernyőn tudjuk az adatokat megjeleníteni. Más esetekben például mágneslemezről olvasunk be adatokat és sornyomtatóra írunk ki stb.
(b) Az adatokat valamilyen külső adathordozón (pl. mágneslemezen, mágnesszalagon) is tudjuk tárolni - természetesen csak akkor, ha ezt az adott gép lehetővé teszi. Ezt értjük nagy mennyiségű adat tárolásán, vagy a program élettartamán kívül is tárolt adat fogalmán.
(c) A Pascal nyelv szabványa nem nyilatkozik arról, hogy melyek azok az állományok, amelyek a program lefutása után is megmaradnak, illetve melyek azok, amelyek csak ideiglenesen, a program befejeződéséig léteznek. Erről az adott megvalósítás kézikönyvei adnak felvilágosítást.
(d) File elemtípusa tehát lehet összetett típus, pl. tömb vagy rekord, és általában összetett típus eleme is lehet file típusú, csak file eleme nem lehet file típusú.
Például:
type
f1=file of array[1..100] of real;
f2=array[1.10] of text;
hibas=file of record { hibas! }
a,b:integer;
c:text; { elemeben file is van }
end;(e) Az adatállományok értékét tehát nemcsak a bennük tárolt értékek sorozata, hanem a feldolgozás, illetve létrehozás pillanatnyi állapota is meghatározza, hiszen ettől függ például a bufferváltozó értéke, illetve a put vagy get eljárás végrehajtásának hatása.
(f) A sorvége jelet megvalósító karakterek - ha vannak egyáltalán ilyenek - tényleges számáról és tárolásuk módjáról a Pascal szabványa nem nyilatkozik. Az ASCII kódot használó gépek legtöbb esetben kocsivissza (ord értéke: 13), vagy kocsivissza és soremelés (az utóbbi ord értéke 10) karaktert használnak a sorvége jelzésére. Lyukkártyát használó gépek esetén nincs külön ilyen karakter, a sorvége jelet az állítja be, hogy a lyukkártya végére értünk.
(g) A sorvége jel csak a sort alkotó karakterek után állhat, tehát sor közben nem, hiszen éppen az a jelentése. Előfordulhat azonban, hogy egy sor a sorvége jelen kívül egyetlen további karaktert sem tartalmaz, azaz két sorvége jel van közvetlenül egymás után.
(h) A text és a file of char típusok tehát különböznek, hiszen sorvége karakter csak text típusú állományban lehet, és eoln, readln, writeln és page eljárás is csak text típusú állományra alkalmazható. Ezen kívül integer és real érték beolvasását és kiírását text állománnyal elvégezhetjük, file of char típusúval azonban nem.
Ennek a megkülönböztetésnek nincs nagy jelentősége, a legtöbb megvalósítás nem is tesz különbséget.(i) Adatállomány értékének megváltozását jelenti a put vagy get eljárás végrehajtása is. Például:
var g:integer;
f:file of array[1..10] of integer;
...
function fv:integer;
begin
get(f); { megvaltozik f file erteke }
fv:=f^[g]
end;
...
begin
...
f^[fv]:=8; { hibas! f^ bufferhez valo hozzaferes kozben }
... { fv megvaltoztatja az f file erteket }(j) Állomány tehát értékparaméterként nem adható át eljárásnak vagy függvénynek. Ez ugyanis azt jelentené, hogy az eljárásban például a file további elemei beolvashatok lennének, majd amikor kilépünk az eljárásból, a file eredeti értékét, tehát eredeti pozícióját is vissza kellene állítani. Vagy - ami ehhez hasonlóan nagyon nehezen lenne megvalósítható - az eljárásba való belépéskor automatikusan másolatot kellene készíteni a file-ról, mint minden értékparaméter értékéről, sőt, a másolatban a file adott pozíciójára kellene lépni, az eljárásban pedig a file típusú értékparaméter a másolatot jelentené.
(k) Az állománytípus az egyetlen adattípus, amelyre - azaz a teljes állományra - nem alkalmazható az értékadó utasítás (:=), illetve az egyenlőségvizsgálat (= <>). Ugyanígy nem alkalmazhatók e műveletek olyan összetett típusra sem, amelynek file típusú eleme van.
(l) A hatás bekövetkezést idejének ilyen, első olvasásra pontatlannak tűnő definíciója azért indokolt, mert lehetővé teszi, hogy az adott file-művelet tényleges befejeződése előtt folytatódjon a program végrehajtása és csak a következő file-művelet elkezdése előtt kelljen megvárni az előző művelet befejeződését. Ez a programnak és a beolvasás-kiírás műveletének egyidejű végrehajtását is lehetővé teszi, ami jelentősen csökkentheti a program futási idejét. A legtöbb gép egyébként is alkalmas ilyen egyidejűségre, hiszen általában más részei végzik a program, és mások a file-műveletek végrehajtását.
(m) A file-ok írásra vagy akár olvasásra való megnyitását a megnyitás szó angol megfelelőjével open műveletnek nevezik, gyakran a magyar nyelvű szakirodalomban is.
(n) Meg kell különböztetnünk a létező, de üres állományt a meghatározatlan értékű állománytól. Előbbinek reset-tel való megnyitása nem okoz hibát és ezután eof(f) értéke azonnal true értékű lesz, utóbbi pedig gyakorlatilag olyan állományt jelent, amelyet sohasem nyitottak meg írásra, így nincs is értelme olvasásra megnyitni.
(o) A read eljárás így magába foglalja a get eljárás végrehajtását is, tehát mindazoknak az előfeltételeknek teljesülniük kell, amelyek a get-re vonatkoznak, egyébként hiba történik. Hasonló módon a get-re vonatkozó hatások is érvényesek.
(p) Az előző megjegyzéshez hasonló a kapcsolat a write és a put eljárás előfeltételei és hatásai között, kivéve, hogy az f^ bufferváltozónak nem kell meghatározottnak lennie.
(q) Emlékeztetünk a 6. szabályra, mely szerint kiírás alatt lévő állománynál mind rewrite, mind put végrehajtása után eof(f) értéke végig true marad, hiszen nincs az f állománynak további eleme.
(r) Ha az eoln(t) igaz, akkor a t^ bufferváltozó értéke szóköz karakter, mint azt a sorvége jel 7. szabálybeli definíciója megadja.
(s) Egy egész szám beolvasása egyenértékű például a következő algoritmussal:
procedure readint(var t:text;var n:integer);
{ egesz szam beolvasasa }
var negativ:boolean;
begin
{ vezeto szokozok es sorvegjelek atugrasa }
while t^=' ' do get(t);
negativ:=t^='-';
if (t^='+') or (t^='-') then get(t); { elojel atlepese }
if (t^>='0') and (t^<='9') then begin { szamjegy jott }
n:=0;
repeat { szamjegyek beolvasasa }
n:=n*10+ord(t^)-ord('0'); { szam ertekenek kiszam. }
get(t);
until (t^<'0') or (t^<'9');
if negativ then n:=-n; { elojelvaltas }
end
else hiba; { nem szamjegy jott }
end; { proc. readint }A hiba eljárás például a következő lehet:
procedure hiba;
begin
writeln;writeln('Szamjegynek kell kovetkeznie!')
end;Egy valós szám beolvasása például a következő algoritmussal írható le:
procedure readreal(var t:text;var r:real);
{ valos szam beolvasasa }
var negativ:boolean;
hert:real;
kitevo,g:integer;
function szamjegy:boolean { t^ szamjegy? }
begin
szamjegy:=(t^>='0') and (t^<='9')
end;
procedure elojel; { elojel feldolgozasa }
begin
negativ:=t^='-';
if (t^='+') or (t^='-') then get(t)
end;
begin
while t^=' ' do get(t); { vezeto szokozok
es sorvegejelek kihagyasa}
elojel;
if szamjegy then begin { mantissza elso szamjegye }
r:=0;
repeat
r:=r*10.0+ord(t^)-ord('0');
get(t)
until not szamjegy;
if t^='.' then begin { tizedes pont }
get(t); { pont atlepese }
if szamjegy then begin { van szamjegy a pont utan }
hert:=10.0; { szamjegy helyiertekenek reciproka }
repeat { tortresz szamjegyei }
r:=r+(ord(t^)-ord('0'))/hert;
hert:=hert*10.0;
get(t);
until not szamjegy
end
else hiba { nem szamjegy jott . utan }
end; { tortresz feldolgozasa }
if negativ then r:=-r; { mantissza elojele }
if (t^='E') or (t^='e') then begin { van kitevo }
get(t); { E atlepese }
elojel; { kitevo elojele }
if szamjegy then begin { van szamjegy a kitevoben }
kitevo:=0;
repeat { kitevo szamjegyei }
kitevo:=kitevo*10+ord(t^)-ord('0');
get(t);
until not szamjegy;
if negativ then hert:=1/10.0
else hert:=10.0;
for g:=1 to kitevo do r:=r*hert
end
else hiba { nem szamjegy jott }
end { kitevo feldolgozasa }
end
else hiba { elojel utan nem szamjegy jott }
end; { proc. readreal }(t) Egy egész típusú érték kiírása a következő eljárással ekvivalens:
procedure writeint(var f:text;n,mezohossz:integer);
{ egesz ertek kiirasa }
const maxszamjegy=6; { megvalositasfuggo }
var jegyek:array[1..maxszamjegy] of char; { szam szamjegyei }
g,k:integer;
elojel:char;
begin
if n<0 then elojel:='-' else elojel:=' ';
n:=abs(n);g:=1;
repeat
jegyek[g]:=chr(n mod 10+ord('0'));
g:=g+1; { jegyek indexe }
n:=n div 10 { utolso szamjegy elhagyasa }
until n=0;
if elojel='-' then begin
jegyek[g]:='-';g:=g+1
end;
for k:=1 to mezohossz-g do
write(f,' '); { vezeto szokozok }
for k:=g downto 1 do
write(f,jegyek[k]) { elojel, szamjegyek }
end; { proc. writeint }A maxjegyszam-nak legalább az adott megvalósítás definiált maxint decimális számjegyeinek száma+1-nek kell lennie.
(u) A valós szám lebegőpontos alakban történő kiírásának pontos módját a következő eljárás adja meg:
procedure wrrealexp(var t:text;r:real;mezohossz:integer);
{ valos szam kiirasa kitevos alakban }
const kitevohossz=2; { kit. jegyeinek sz., megvalosiatasfuggo }
kitevojel='E'; { E vagy e megvalositasto fuggoen }
var kitevo,torthossz,jegy,g,h:integer;
kerekito:real;
begin
if r<0 then write(t,'-') else write(t,' '); { elojel }
r:=abs(r);
if r=0.0 then begin { a kiirando ertek 0 }
write('0.0');
if mezohossz<kitevohossz+6 then { tul kicsi }
mezohossz:=kitevohossz+6;
for g:=1 to mezohossz-4 do write(' ');
end
else begin { az ertek nem 0 }
kitevo:=0;
while r>10.0 do begin { normalizalas 1..10 koze }
r:=r/10.0;
kitevo:=kitevo+1
end;
while r<1.0 do begin
r:=r+10.0;
kitevo:=kitevo-1;
end;
if mezohossz>=kitevohossz+6 then { tortresz hossza }
torthossz:=mezohossz-kitevohossz-5
else torthossz:=1;
kerekito:=1/2;
for g:=1 to torthossz do
kerekito:=kerekito/10.0; { leptetes jobbra }
r:=r+kerekito; { ki nem irt resz kerekitese }
if r>=10 then begin {normalizalas 10 ala}
r:=r/10.0;
kitevo:=kitevo+1;
end;
jegy:=trunc(r); { egeszresz }
write(t,jegy:1,'.');
r:=r-jegy; { marad a tortresz }
for g:=1 to torthossz do begin { tortresz jegyei }
r:=r*10.0; { maradek balra lep egy dec. helyet }
jegy:=trunc(r); { kovetkezo szamjegy }
write(t,jegy:1);
r:=r-jegy { maradek kepzese }
end;
write(t,kitevojel);
if kitevo>=0 then write(t,'+')
else write(t,'-'); { kitevo elojele }
kitevo:=abs(kitevo);
h:=1;
for g:=1 to kitevohossz-1 do
h:=h*10; { kitevo nagysagrendje }
for g:=1 to kitevohossz do begin
write(t,kitevo div h:1);
kitevo:=kitevo mod h;
h:=h div 10
end
end { a szam nem nulla }
end; { proc. wrrealexp }(v) A valós szám fixpontos kiírását a következő eljárás adja meg:
procedure wrrealfix(var t:text;r:real;mezohossz,torthossz:integer);
{ valos ertek kiirasa fixpontos alakban }
var elojel:char;
egeszhossz,teljeshossz,jegy,g:integer;
n:real;
begin
if r=0.0 then begin { nulla az ertek }
for g:=1 to mezohossz-torthossz-2 do
write(t,' '); { vezeto szokozok }
write(t,' 0.0');
for g:=1 to torthossz-1 do
write(t,' ') { vegso szokozok }
end
else begin { nem nulla }
if r<0 then elojel:='-' else elojel:=' ';
r:=abs(r);
n:=1/2; { kerekito ertek meghatarozasa }
for g:=1 to torthossz do n:=n/10.0;
r:=r+n; { kerekites }
egeszhossz:=1; n:=10.0;
while r>=n do begin { egeszresz hosszanak meghat. }
egeszhossz:=egeszhossz+1;
n:=n*10.0
end;
teljeshossz:=egeszhossz+torthossz+2;
{ +2: elojek, tizedespont }
for g:=1 to mezohossz-teljeshossz do
write(t,' '); { vezeto szokozok }
write(t,elojel);
for g:=1 to egeszhossz do begin { egeszresz kiirasa }
n:=n/10.0;
jegy:=trunc(r/n); { kovetkezo szamjegy }
write(t,jegy:1);
r:=r-jegy*n { kiirt ertek kivonasa }
end;
write(t,'.'); { tizedespont }
for g:=1 to torthossz do begin { tortresz jegyei }
r:=r*10.0; { kovetkezo szamjegy egessze valik}
jegy:=trunc(r); { kovetkezo szamjegy }
write(t,jegy+1);
r:=r-jegy { maradek kepzese }
end
end { nem nulla }
end; { proc wrrealfix }(w) A legtöbb megvalósításban (így a Turbo Pascalban és a HiSoft-Pascalban is) az alapértelmezés szerinti mezőszélesség true értékre 4, false értékre pedig 5. Ez nem nagyon szerencsés, mert táblázatok kiírásánál a logikai értéktől függően elcsúszhatnak a sorok. Ezért mindig érdemes mezőhosszt is megadni, például 5 értékűt, ekkor a true érték elé egy szóköz is kiíródik.
(x) A külső adatállományok és a program belső file-jai közötti kapcsolatot általában a nyelv további, a szabványoshoz képest bővítést jelentő utasításai adják meg, mint például a Turbo Pascalban az assign. Az, hogy a nyelv szabványa nem rögzíti ezt az összerendelést, lehetővé teszi, hogy az adott megvalósításban az adott gépnek, illetve programozási környezetnek legjobban megfelelő kiterjesztéseket alkalmazzák, ugyanakkor rontja a programok hordozhatóságát.
(y) A file lezárásán (angolul: close, kiejtése: klóz) azt értjük, hogy ennek segítségével közöljük a program futási környezetével - pl. az operációs rendszerrel hogy a file létrehozása, illetve olvasása befejeződött; ekkor ugyanis a file tényleges tárolásának megfelelően további műveleteket is kell végezni.
(z) Íme egy teljes program, amely az input file tartalmát sorszerkezetének megtartásával átmásolja az output file-ba:
program copytext(input,output) ;
var ch:char;
begin
while not eof do
if eoln then begin
readln;writeln;end { sor vege }
else begin
read(ch);write(ch)
end
end.Tipikushiba, ha az adatok végét (eof) csak a sorok végén vizsgáljuk, ezt [1], [2], [14], sőt [16] is elköveti:
...
while not eof do begin { hibas! }
while not eoln do begin { sor kozben is lehet }
read(ch);write(ch) {adatok vege!}
end;
readln;writeln
end;
...
6.3.1. Példa:
Készítsünk programot, amely egy a adatállomány végéhez hozzáírja a b adatállomány tartalmát. Legyenek azonos t elemtípusúak.
Megoldás:
Ha egy adatállományba írni akarunk, akkor előtte ki kell adni rá a rewrite műveletet. Ez törli az állomány előző tartalmát, tehát állományhoz nem tudunk közvetlenül hozzáírni.
Az a állomány tartalmát először át kell másolnunk egy i ideiglenes állományba, majd innen vissza, és amikor ez kész, akkor folytatjuk a kiírását b tartalmával. Mivel ehhez összesen 3 másolás kell, érdemes erre a feladatra eljárást használni. Ne feledjük, hogy állomány csak változó paraméter lehet!
program file_egyesites(a,b);
type t=...;
ft=file of t;
var a,b,i :ft;
procedure masol(var innen,ide:ft);
begin
while not eof(innen) do begin
ide^:=innen^;
put(ide);get(innen)
end
end; { proc. masol }
begin { foprogram }
reset(a);rewrite(i);masol(a,i); { a --> i }
rewrite(a);reset(i);masol(i,a); { i --> a }
reset(b);masol(b,a) { b --> a }
end.
6.3.2. Példa:
Készítsünk deklarációkat és eljárásokat, amelyekkel a 3.10. fejezetben bemutatott, tömböt használó telefonkönyv programot kiegészítve lehetővé válik az adatok állományba mentése, illetve a program indulásakor onnan a visszaállítás!
Megoldás:
A feladat megoldásának a lineáris és bináris kereséshez illeszkedő változatát készítjük el, a csonkításos keresés a 6.3.1 feladat lesz.
Adatdeklarációk:
type
...
elem=record
nev:nevt;
telszam:szamt
end;
var
...
tabla:array[1..tablahossz] of elem;
f:file of elem; { ebbe tarol, illetve innen olvas }
Az eljárások:
procedure kimentes;
var k:integer;
begin
rewrite(f)
for k:=1 to utolso do
write(f,tabla[k])
end;
procedure visszaallitas;
begin
utolso:=0;
reset(f);
while not eof(f) do begin
utolso:=utolso+1;
read(f,tabla[utolso])
end
end;
Ugyanezt a módszert a telefonkonyv5 nevű Turbo Pascal programunkban így lehet megvalósítani:
program telefonkonyv5a;
...
procedure kimentes;
var k:integer;
begin
assign(f,'telefon.dat');
rewrite(f);
for k:=1 to utolso do
write(f,tabla[k]);
close(f)
end;procedure visszaallitas;
begin
utolso:=0;
assign(f,'telefon.dat');
{$I-}
reset(f);
{$I+}
if ioresult=0 then
while not eof(f) do begin
utolso:=utolso+1;
read(f,tabla[utolso])
end
else writeln('Uj telefonkony nyitasa!')
end;
6.3.1. Feladat:
Készítsen eljárásokat a csonkításos kereséshez használt táblázat tartalmának file-ba mentésére és visszaállítására!
6.3.2. Feladat:
Készítsen eljárásokat a dinamikus adatszerkezetekben tárolt telefonkönyv (5.2-1. - 5.2-7. példa) adatainak file-ba mentésére, illetve visszaállítására!
Ez a fejezet olyan szabályokat tartalmaz, amelyek a Pascal nyelvnek részét képezik ugyan, de nem igényelnek didaktikus tárgyalást.
Program
1. A program szó itt egy teljes Pascal programot jelent. (a)
2. Alakja:
program:

programfej:

programparaméterek:
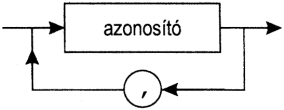
3. A program azonosítójának, azaz a program nevének nincs jelentősége a program működése szempontjából.
4. Programparaméter lehet az előre deklarált input vagy output adatállomány-változó azonosítója, de lehet a program blokkjának változódeklarációs részében deklarált változó azonosítója is. (b)
A programparaméterek és a program számára külső adatok közötti kapcsolat adatállomány típusú programparaméterek esetén a megvalósításban definiált, más típusúaknál megvalósításfüggő.5. A program végrehajtása a program blokkjának végrehajtását jelenti, így a program akkor fejeződik be, ha a gép a program blokkjának utolsó utasítását is végrehajtotta.
Magyarázatok, megjegyzések:
(a) A Pascal nyelv szabványa nem foglalkozik azzal az esettel, amikor egy program részeit több lépésben, külön-külön fordítjuk le és a teljes programot e részekből szerkesztjük össze, hanem úgy tekinti, hogy a teljes program egyetlen összefüggő szöveg lefordításának eredménye.
A legtöbb megvalósítás lehetővé teszi a több részben történő fordítást is, ez általában néhány további egyszerű nyelvi elem és egy szerkesztőprogram (Linkage Editor) használatát jelenti. Ezekről a lehetőségekről az egyes Pascal fordítók kézikönyvei adnak tájékoztatást.(b) A szabványos input és output állományok text típusúak, a rájuk vonatkozó további tudnivalók az adatállományok leírásánál találhatók.
A goto utasítás:
1. Alakja:
goto címke
2. A goto utasítás hatására a program végrehajtása a címkével megjelölt utasítással folytatódik.
3. A goto utasítással csak a következő esetekben lehet a goto-ban megadott címkéjű utasításra ugrani: (a)
3.1. A címkével ellátott utasítás magába foglalja a goto utasítást.
3.2. A címkével ellátott utasítás a goto utasítást is tartalmazó utasítássorozat egyik utasítása.
3.3. A címkével ellátott utasítás annak a blokknak az utasításrészében szerepel, amely tartalmazza a goto utasítást.4. A goto utasítással kiléphetünk blokkból is (3.3. szabály), ennek hatására megszakad az elhagyott blokkok (eljárások, illetve függvények) végrehajtása. Annak a blokknak a végrehajtása folytatódik, amely a goto-ban hivatkozott címkét tartalmazza, valamint azon blokkoké is, amelyek végrehajtása még nem fejeződött be a címkét tartalmazó blokk aktivizálásakor. (b) (c)
Magyarázatok, megjegyzések:
(a) E szabályok lényegében azt jelentik, hogy goto utasítással vagy azonos szinten lévő utasításra, vagy összetett utasításból, illetve blokkból kifelé lehet ugrani. Így tehát nem lehet kívülről összetett utasításon belülre vagy blokkba ugrani.
Néhány példa helyes és hibás goto utasítás illusztrálására:
while do begin
88: if ... then begin
...
goto 88; {kiugras osszetet utasitasbol }
end;
...
goto 88; { ugras azonos szinten levo utasitasra }
...
repeat
...
if ... then goto 88; { kilepes osszetett utasitasbol }
until ...;
end; { while }
...
goto 88; { hibas! a while utasitason belulre ugorna }
if ... then goto 88; { hibas , mint az elozo }(b) Ha goto utasítással blokkot hagyunk el, akkor ez azt is jelenti, hogy felszabadul az a memóriaterület, amelyet a blokk lokális változói és értékparaméterei elfoglaltak. Ha a goto utasítással több, egymásba ágyazott blokkból is kilépünk, akkor minden elhagyott blokkra megtörténik a memóriaterületek felszabadítása. Emiatt egy blokkból való kiugrás az egyszerű vezérlésátadáson kívül további műveletek végrehajtását is jelenti.
(c) A goto utasítás használata idegen a strukturált programozási nyelvek, így a Pascal nyelv stílusától. A tapasztalat azt mutatja, hogy ha goto-val ugrálunk, az rontja a programok olvashatóságát, megbízhatóságát, ezért használatát kerülni kell.
Csak akkor fogadható el goto alkalmazása, ha egyébként túl bonyolult vagy fáradságos megoldást kellene alkalmazni. Ilyen eset például, ha a program egy többszörösen beágyazott belső blokkjában kiderül, hogy olyan, általában a program által felfedezett hibából származó esettel állunk szemben, ami a program további végrehajtását lehetetlenné vagy értelmetlenné teszi. Ilyenkor elfogadható megoldás, ha - megfelelő hibaüzenet kiírása után - goto-val lépünk ki a program legutolsó end-je előtt álló címkére:
program proba;
label 9999;
...
procedure pr...
...
function fv...
...
begin
...
if eof then begin
writeln;writeln('Tul keves az adat!');
goto 9999 { ugras a program vegere }
end;
...
end; { fv blokkjanak vege }
begin { pr eljaras utasitasresze }
...
a:=fv... { fv hivasa }
end; { pr eljaras vege }
begin { foprogram kezdete }
... pr... { pr eljaras hivasa }
9999:
end.Ezt a befejezést egy hibajelző változó beállításával és annak vizsgálata alapján az egyes blokkokból lépcsőzetesen kilépve is elérhetnénk, de az túl bonyolult lenne.
Érdemes megfigyelni, hogy a 9999 címke után álló end nem utasítás, de a címke után egy üres utasítás áll.A legtöbb megvalósításban létezik egy - általában halt, abort vagy exit nevű - utasítás, amely megszakítja a program működését és tetszőleges utasítás, illetve blokk belsejében is használható. Ennek a megoldásnak az az előnye a goto-val történő kilépéshez képest, hogy legtöbb esetben az így megszakított program jelzi a futtatási környezetnek, illetve az operációs rendszernek, hogy a program hiba miatt fejezte be a működését. Így lehetővé teszi például, hogy a környezet ne indítson el olyan további programokat, amelyek felhasználnák a hiba miatt megszakított program eredményeit. További előnye a halt, abort illetve exit ilyen használatának, hogy több megvalósítás (pl. a Turbo Pascal) nem engedi meg a blokkból goto-val való kilépést. (A HiSoft-Pascal megengedi.) Ilyenkor ezek a szabványos Pascal nyelvben nem létező utasítások valóban a legkényelmesebb megoldást jelentik.
Az üres utasítás
1. Alakja:
2. Az üres utasítás lényegében egy tényleges utasítás hiányát jelenti: ahol a programban egy utasításnak kellene állnia, de nem írunk oda semmit.
3. Az üres utasítás végrehajtása semmilyen tevékenységgel sem jár, tehát nincs hatása.
Magyarázatok, megjegyzések:
(a) Üres utasítást ott használunk, ahol a Pascal nyelv formai szabályai értelmében utasításnak kellene állnia, de a program működése semmilyen tevékenységet nem igényel. Pl.:
if feltétel then { üres utasítás }
else utasítás;Itt a then és else között nincs semmi, azaz csak üres utasítás van, a megjegyzés nem utasítás. Átírhatnánk az előbbi programrészletet a következő alakra is:
if not feltétel then utasítás;
vagyis a feltétel megfordításával inkább az else ágat hagyjuk el, és ez általában olvashatóbb megoldás is, mint az előző.
Előfordulhat azonban olyan eset is, amikor valamiért éppen az előző, üres then ággal rendelkező változat tűnik természetesebbnek.(b) Az előbbi esetnél sokkal gyakoribb, hogy a repeat utasításban az until szó előtt, vagy utasításcsoportban a záró end előtt (fölösleges) pontosvessző áll. Ha ezeknek az utasításoknak a szintaktikai szabályait megnézzük, azt látjuk, hogy bennük a pontosvessző utasításokat választ el, így a záró until, illetve end szó előtti pontosvessző is. Itt azonban a pontosvessző és a záró kulcsszó között üres utasítás van:
repeat
ut1;
...
utn; { ures utasitas }
until feltétel;begin
ut1;
...
utn; { ures utasitas }
end;
Szimbólumelválasztók:
(1) A Pascal nyelv szimbólumait szóközök, megjegyzések és újsor jelek választhatják el egymástól. Két nyelvi elem között és a program első eleme előtt tetszőleges számú elválasztó lehet. Legalább egy elválasztónak kell lennie két egymást követő azonosító, foglalt szó, címke és előjel nélküli szám között.
Egy szimbólum (pl. foglalt szó, azonosító, szám) belsejében nem lehet elválasztó.
Például:
begin alfa
a begin foglalt szót és az alfa azonosítót jelent, ezzel szemben a
beginalfa
egyetlen azonosítót.
Megjegyzés (komment)
1. Alakja:

(a)
2. A program működése nem változik, ha a megjegyzés helyére egy szóköz kerül. (b)
Magyarázatok, megjegyzések:
(a) A megjegyzés ilyen definíciója nem teszi lehetővé megjegyzések egymásba ágyazását.
Ez például akkor lenne előnyös, ha a program különböző változatainak kipróbálásakor olyan programrészeket tennénk { és } kommentzárójelek közé, amelyek már maguk is tartalmaznak megjegyzést.A megjegyzés egyébként több sor hosszúságú is lehet.
(b) A megjegyzés tehát nem befolyásolja a program működését, de szolgálhat a nyelv egyes szimbólumainak elválasztására.
Helyettesítő szimbólumok
Vannak olyan gépek, amelyeken nem használható minden, a Pascal nyelvben használt karakter. Tipikusan ilyen karakter a kapcsos zárójel vagy a felfelé mutató nyíl. Ezeken a gépeken a hiányzó karakterek helyett olyan egy- vagy kétkarakteres szimbólumok alkalmazhatók, amelyek gyakorlatilag minden gépen megtalálhatók.
(a) (b)
Ha az adott megvalósításban létezik az eredeti karakter is, akkor abban az eredeti és a helyettesítő változat azonos értelemben használható. (A HiSoft-Pascal azonban nem ismeri a helyettesítő szimbólumokat.)
Mivel az eredeti és a helyettesítő szimbólumok teljesen egyenértékűek, megengedettek a következő esetek is:
tomb[3.)
(* a megjegyzes vegen mas all }(c)
Magyarázatok, megjegyzések:
(a) Az újabb billentyűzeteken felfelé mutató nyíl helyett helyett csak ^ jel van. Ilyenkor ez is használható, azonos értelemben.
(b) A kétkarakteres változatok karakterei együtt, közvetlenül egymás után írva jelentik a megfelelő szimbólumot, így karaktereik között nem állhat elválasztó, például szóköz sem.
(c) A zárójelváltozatok ilyen vegyes használata rontja a program áttekinthetőségét, ezért inkább vagy csak az egyik, vagy csak a másik változatot használjuk. Az egykarakteres változat az áttekinthetőbb.
7.7. Az adattípusok összefoglalása
Az adattípusokat több szempont szerint is csoportosíthatjuk.
Az egyik lehetséges felosztás csoportjai és alcsoportjai:
A Pascal nyelv szabványa ezt a csoportosítást használja, bár a mutató típust sorolhatnánk az egyszerű típus nem sorszámozott alesetéhez is, hiszen egyetlen értéket tárol és nincs ord értéke. Ilyen felosztásnál a függvény eredménytípusa is egyszerűbben lenne meghatározható: röviden "egyszerű típus" lenne, míg a szabvány szerint "egyszerű és mutató típus". Az, hogy a mutató típust mégsem az egyszerű típushoz sorolják, abból adódhat, hogy bár maga a mutató egy értéket tárol, mégis mindig valamilyen összetett típussal, legtöbbször rekorddal kapcsolatban használjuk, tehát nagyon erősen kapcsolódik az összetett típusokhoz is.
A másik lehetséges felosztás az előre definiált, azaz szabványos típusokat és a programban definiálandó típusokat választja szét:
"Akinek lába volt, akár kurta, akár nyurga, görbe, vagy egyenes,
az mind táncolt, s akinek hangja volt, akár szép, akár csúnya,
mély, vagy magas, az mind énekelt és nevetett."
[0] 257. oldal
[0] Michael Ende:
A Végtelen Történet
(Árkádia, Budapest, 1985)
Ez egy csodálatos mese, mely - mint minden igazán csodálatos mese - nem csak mese.
[1] Kathleen Jensen - Niklaus Wirth:
A Pascal programozási nyelv
(Felhasználói kézikönyv és a nyelv formális leírása)
(Műszaki Könyvkiadó, Budapest, 1982)
Ez annak a könyvnek a fordítása, amelyben a nyelv alkotója először tette szélesebb kör számára is hozzáférhetővé a Pascal nyelv többé-kevésbé pontos leírását. Az "eredeti" Pascal nyelvet tartalmazza, melytől a későbbi szabvány meglehetősen sok helyen eltér, de a szabvány megjelenése előtt ezt tartották a nyelv hivatkozási alapjának.
Tömör összefoglaló, több lényeges kérdéssel nem foglalkozik, a nyelv megismerésére is csak korlátozottan alkalmas, a programozással most ismerkedőknek nem ajánlható.
[2] Gordon Erzsébet - Körtvélyesi Gézáné - Sós Zoltán - Székely Zoltán:
PASCAL programozási nyelv
(SzÁMALK, Budapest, 1982.)
Hosszú ideig ez volt a nyelv magyarul is elérhető legpontosabb leírása, de megírásakor csak a szabvány előzetes változatára [4] támaszkodhatott, ezért még nem a végleges szabvány szerint mutatja be a Pascal nyelvet.
Nyelvezete és az anyag bemutatási módja kezdők számára is jól használható könyvvé teszi, egyes kérdéseket (pl. rekurzió, mutató típus) azonban nem tárgyal fontosságának megfelelő mélységben. A könyv III. része egyes megvalósítások sajátosságait írja le a teljesség igénye nélkül.
[3] Niklaus Wirth:
Algoritmusok + Adatstruktúrák = Programok
(Műszaki Könyvkiadó, Budapest, 1982.)
Egyes érdekes programozási feladatok megoldásának különböző lehetőségeit tárgyalja, emellett összefoglalja a megoldások leírására használt Pascal nyelv tulajdonságait is.
Több helyen kibővíti a nyelvet olyan elemekkel, amelyek az adott algoritmus számára hasznosak. Elsősorban azok számára ajánlható, akik mélyebben érdeklődnek a programozás módszertana, a szép, biztonságos és hatékony programírás kérdései iránt. Tanulságos példáit olvasmányos stílusban ismerteti.
[4] A. M. Addyman - R. Brewwer - D. G. Burnett-Hall - R. M. DeMorgan - W. Findlay - M. J. Jackson - D. A. Joslin - M. J. Rees - D. A. Watt - J. Welsh - B. A. Wickmann:
A Draft Description of Pascal
(Software - Practice and Experience,
Vol.9, pp.381-424 1979.)
A Pascal nyelv szabványának előzetes változatát adja, a szabványoktól megszokott tömör nyelvezettel. Sok irodalom - tévesen - ezt tekinti a szabványnak, így [2] is.
[5] British Standard Specification for Computer Programming Language Pascal
BS 6192:1982
A jelenleg érvényes szabvány a Pascal programozási nyelvre, melyet az ISO-ban változtatás nélkül átvettek.
[6] Specification for Computer Programming Language Pascal, ISO 7185-1983
(International Standards Organization, 1983.)
A nyelv jelenleg érvényes szabványa, [5] betű szerinti átvétele.
[7] IEEE Standard Pascal Computer Programming Language
An American National Standard
ANSI/IEEE 770 X3.97-1983
(The Institute of Electrical and Electronics Engineers, Inc. New York, 1983. jan. 7.)
A Pascal nyelv szabványa az Amerikai Egyesült Államokban. Szinte teljesen megfelel az ISO szabványnak. Néhány kevésbé jelentős és nem nagyon szerencsés változtatást is tartalmaz, például nem ismeri az illeszkedő tömbparamétert.
[8] Kis Ottó - Kovács Margit:
Numerikus módszerek
(Műszaki Könyvkiadó, Budapest, 1973.)
A legfontosabb numerikus módszerek tömör és jól érthető összefoglalóját adja a szükséges matematikai háttérrel és sok példával. Különösen jól használhatóvá teszi a könyvet, hogy a legtöbb algoritmus ALGOL nyelvű programját is tartalmazza. Ez a két nyelv hasonlósága miatt a Pascalban programozók számára is szinte közvetlenül felhasználható.
Akinek gondot okozna az ALGOL nyelv egy-egy eleme, annak a könyv első fejezete rövid, de jól követhető ALGOL tankönyvet tartalmaz.
[9] Turbo Pascal Reference Manual
Version 3.0
(Borland International Inc., 1985.)
Az IBM-PC típusú, illetve ezzel kompatibilis személyi számítógépeken legnépszerűbb, Pascal programok fejlesztésére és a nyelv tanulására hatékonysága és könnyű kezelése miatt kiválóan alkalmas programrendszer hivatkozási kézikönyve. A Pascal nyelv ezen megvalósításának jellemzőit, valamint a programcsomaghoz tartozó teljesképernyős szövegszerkesztő használatát írja le, a megkötések és bővítések teljes ismertetésével, sok mintapéldával. Kitér a fordítóprogram Z80-as mikroprocesszort használó gépeken, CP/M operációs rendszer alatt használható változatára is.
[10] PASCAL 8000 Reference Manual
Az IBM 360, 370, illetve ezekkel kompatibilis (pl. ESZR) számítógépeken elterjedten használt, hatékony fordítóprogram hivatkozási kézikönyve. A nyelv megvalósításának pontos leírása, mely a futtatáshoz szükséges rendszervezérlő parancsokat is részletezi.
[11] I. M. Szobol:
A Monte-Carlo módszerek alapjai
(Műszaki Könyvkiadó, Budapest, 1981.)
A könyv alapvető jelentőségű a véletlenszámokat is használó algoritmusok tervezéséhez. Foglalkozik álvéletlenszámok előállításának, ellenőrzésének, valamint különböző matematikai és mérnöki problémák véletlenszámokon alapuló megoldásának kérdéseivel, különös tekintettel a számítógépek alkalmazására.
[12] D. E. Knuth:
A számítógép-programozás művészete I-III
(Műszaki Könyvkiadó, Budapest, 1987.)
A számítógépes algoritmusok majd 20 éve világszerte legnépszerűbb, összefoglaló, enciklopédikus igényű könyvsorozatának fordítása. Az első kötet az alapvető algoritmusokkal, a második a szeminumerikus, például véletlenen alapuló algoritmusokkal, a harmadik pedig a keresési és rendezési módszerekkel foglalkozik.
[13] R. Baumgartner - S. Hansjakob - W. Prawl:
Turbo-Pascal
Elmélet és gyakorlat
(NOVOTRADE RT, Budapest, 1987.)
Nem a [9]-ben leírt Turbo Pascal rendszer kézikönyve, hanem főleg operációs rendszertől függő, érdekes és trükkös megoldások, valamint további algoritmusok gyűjteménye, a szükséges elemzésekkel együtt. Sajnos sok olyan programja is kihasználja a Turbo Pascal sajátosságait, amely első pillantásra teljesen szabványosnak tűnik. Ha más Pascal rendszerrel akarjuk ezeket a programokat használni, nagyon körültekintőnek kell lennünk.
[14] Kathleen Jensen - Niklaus Wirth:
A Pascal programozási nyelv
Felhasználói kézikönyv és a nyelv formális leírása (az ISO Pascal szabvány szerint)
2., bővített kiadás
(Műszaki Könyvkiadó, Budapest, 1988)
[1] bővített, módosított kiadása, mely már [6] szerint tárgyalja a Pascal nyelvet.
[15] Turbo Pascal Version 6.0 Programmer's Guide
Turbo Pascal Version 6.0 User's Guide
Turbo Pascal Version 6.0 Library Reference
(Borland International Inc., 1990)
A Turbo Pascal megvalósításnak e könyv második kiadása előkészítésekor legújabb változatait tárgyalják részletesen.
A Turbo Pascal 6.0 változata lényeges bővítéseket tartalmaz mind a szabványos nyelvhez, mind pedig a [9]-ben leírt 3.0 változathoz képest, ezek közül talán a leglényegesebb az ún. objektumorientált kiterjesztés és az interaktív változat beépített nyomkövetési lehetősége.
[16] Pongor György:
Szabványos PASCAL
Programozás és algoritmusok
(Novotrade, 1988)
Ennek a könyvnek az első kiadása, mely most átdolgozva került az Olvasó kezébe.
Vissza az Enterprise könyvekhez
Vissza a Spectrum könyvekhez