A Pascal programozási nyelv
Felhasználói kézikönyv és a nyelv formális leírása
Kathleen Jensen - Niklaus Wirth Az eredeti mű: |
Fordította: Szabó Zoltán, Mikolás Zoltán Lektorálta: Bakos Tamás |
Tartalom
Előszó az átdolgozott kiadáshoz
A Jensen-Wirth szerzőpáros Pascal-leírása közel egy évtizede a legfontosabb tankönyve a nyelvvel ismerkedőknek, s egyszersmind kézikönyve a Pascal-programozóknak. A hetvenes évek folyamán a Pascal népszerűsége a legmerészebb várakozásokat is felülmúlva robbanásszerűen nőtt, s napjainkra világszerte az egyik legáltalánosabban használt programnyelvvé vált. Míg régebben - legalábbis az Egyesült Államokban - a gyakorlati szakemberek gyakran nagyobb érdeklődést mutattak a nyelv iránt, mint a tudományos és oktatási intézmények, ma az egyetemek többségén a Pascal a programozástanítás nyelvi eszköze. A Pascal mindinkább kiszorítja a PL/1-et és az ALGOL-60-at, sőt egyes újításai még a FORTRAN korszerűsített változataiba is beépültek.
A Pascal User Group (Pascal Felhasználói Csoport) és a Pascal News (Pascal Hírek) munkatársaiként tanúi lehettünk a nyelv elterjedésének. 1971-ben még csak egy számítógéprendszeren futott Pascal fordítóprogram, 1974-ben már tízen, 1979-re több, mint nyolcvanon. Ma valamennyi korszerű gépen rendelkezésre áll a nyelv; a mindenhová bevonult személyi számítógépek, az intelligens munkaterminálok elképzelhetetlenek a Pascal nyelv nélkül.
Az 1977-es southamptoni Pascal-konferencián felmerült kérdések [10] hatására kezdődött meg a szervezett munka egy hivatalosan elfogadott, nemzetközi Pascal-szabvány kidolgozására. A résztvevők igyekeztek összegyűjteni és egységesen megválaszolni mindazokat a kérdéseket, amelyek felmerültek, ha valaki a Jensen-Wirth műben lefektetett definíciók alapján Pascal fordítót próbált írni. E munka eredményeként született meg az ISO 7185 Pascal Szabvány [11], a Pascal hivatalos definíciója, amely a Jensen-Wirth könyv átdolgozását is szükségessé tette.
Az átdolgozással nem az volt a célunk, hogy a könyv vegye át a szabvány szerepét. Helyesebbnek láttuk, ha csupán a szabványnak megfelelően módosítjuk az anyagot, s így minél inkább megőrizzük olvasmányosságát és eleganciáját, amely - véleményünk szerint - a szabványtól megkülönbözteti. Korszerűsítettük a szintaxis leírását (Wirth EBNF-rendszerét alkalmaztuk), javítottunk a Felhasználói kézikönyv programpéldáinak stílusán. Akik a könyvet korábbi kiadásból ismerik, különösen hasznosnak találhatják az E. függeléket, amelyben a szabvány által szükségessé tett változtatásokat foglaltuk össze.
Végül úgy érezzük, nem lenne teljes a könyv, ha nem emlékeznénk meg arról, hogy a Pascal programnyelv nevét Blaise Pascalról, a XVII. századi francia matematikusról és filozófusról kapta, aki számológép-építéssel is foglalkozott. Köszönettel tartozunk Roberto Minionak és Niklaus Wirth-nek a könyv átdolgozásának támogatásáért, Henry Ledgard-nak mindig a legjobbkor jött és hasznos tanácsaiért, Elise Oranges-nak a határidők betartásához nyújtott lelkiismeretes segítségéért, William W. Porternek a grafikáért és Linda Strzegowskinak a könyv szedéséért.
Andy Mickel
Jim Miner
Minneapolis, USA,
1984. november
Előszó az első kiadáshoz
A Pascal programozási nyelv első, vázlatos formáját 1968-ban fogalmaztuk meg. Szellemében az új nyelv az ALGOL-60 és az ALGOL-W vonalát követte. 1970-ben, intenzív fejlesztési munka eredményeként, elkészült az első működő fordítóprogram, majd egy évvel ezután megjelentek a nyelvvel kapcsolatos publikációk [1], [8], Egyre növekedett az igény, hogy más számítógépekre is elkészüljön a nyelv fordítóprogramja. Ez, valamint a Pascal kétéves alkalmazása során szerzett tapasztalatok néhány módosítást tettek szükségessé. Így került sor 1973-ban a Revised Report (Átdolgozott Jelentés) kiadására, ill. a nyelv ISO karakterkészlettel való leírására.
Az Olvasó két részből álló könyvet tart a kezében. Az első rész a Felhasználói kézikönyv, a második a nyelv formális leírása, az átdolgozott Jelentés. A kézikönyvet azoknak szánjuk, akik foglalkoztak már számítógép-programozással és most a Pascal programnyelvvel szeretnének megismerkedni. Éppen ezért e kézikönyvet tankönyvnek szántuk, amely a Pascal különböző tulajdonságait számos példán keresztül szemlélteti. Függelékként csatoltuk az összefoglaló táblázatokat és a szintaxis leírását.
A könyv második részének az a célja, hogy tömör összefoglaló leírást adjon a programozók, a fordítóprogram-készítők és a nyelv egyéb felhasználói részére. Az átdolgozott Jelentés (Revised Report) az ún. standard Pascalt definiálja, amely a nyelv különböző változatainak közös alapját képezi.
Azt ajánljuk, amennyiben az Olvasó kézikönyvünket tankönyvként használja, tartsa magát a kézikönyv szerkezetéhez, és olvasás közben fordítson különös figyelmet a példaprogramokra. Inkább olvassa el újra azokat a részeket, amelyek nehézséget okoznak. Ha a beviteli és a kiviteli eljárásokkal kapcsolatban kérdések merülnek fel, különösen nagy szükség lehet a 13. fejezet ismételt átolvasására.
A könyv a standard Pascalt írja le. A standard Pascal feldolgozása az elsődleges követelmény, amit a fordítóprogram-készítő támaszt az általa megvalósított rendszerrel szemben. Csak a standard Pascalban leírt nyelvi lehetőségekkel élhet az a programozó, aki egyik számítógépről a másikra átvihető portábilis programot akar írni. A nyelv különböző megvalósított változatai természetesen ehhez képest további szolgáltatásokat is tartalmazhatnak, ezeket azonban mindenképpen kiterjesztésként kell kezelni.
A könyv sokak munkájának eredménye. Külön köszönettel tartozunk a Zürichi Műszaki Egyetem Informatikai Intézete (Institut für Informatik, ETH Zürich) munkatársainak, valamint John Larmouth-nak, Rudy Schildnek.Olivier Lecarme-nak és Pierre Desjardins-nek bírálataikért, javaslataikért, bátorításukért.
A Pascal-megvalósítás, amely könyvünk megjelentetését lehetségessé és ugyanakkor szükségessé tette, Urs Ammann és munkatársa, Helmut Sandmayr munkája.
Kathleen Jensen
Niklaus Wirth
ETH Zürich,
Svájc, 1974. november
1.1. A Pascal programok felépítése
A következőkben abból indulunk ki, hogy az Olvasónak, ha csak minimálisan is, vannak számítástechnikai ismeretei, és nagyjából tudja, milyen felépítésű egy számítógépprogram. Ebben a fejezetben ezeket a többé-kevésbé hézagos ismereteket szeretnénk felfrissíteni, tudatosítani.
Egy algoritmus vagy számítógépprogram mindig két fő részből áll: az elvégzendő tevékenységekből (műveletek) és az ezek által kezelt adatok leírásából. A tevékenységeket ún. utasításokkal, az adatokat ún. deklarációkkal és definíciókkal adjuk meg.
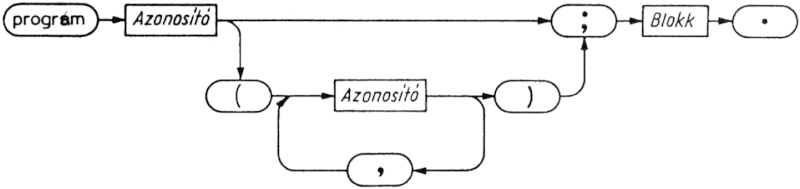
A program programfejre és blokknak nevezett törzsre tagolódik. A fej nevet ad a programnak, és felsorolja a program paramétereit. A paraméterek (állomány típusú) változók, és a számítás argumentumait, ill. eredményeit reprezentálják. A blokk hat részből áll, amelyek közül - az utolsót kivéve - bármelyik üres is lehet. A hat rész sorrendje kötelezően a következő:
Blokk = Címkedeklarációs rész
Konstansdefiníciós rész
Típusdefiníciós rész
Változódeklarációs rész
Eljárás és Függvénydeklarációs rész
Utasításrész
Mutatja ezt az alábbi program is:
Program Inflacio (Output);
{ Turbo Pascal }
{ Legyen az inflacio gyorsasaga evi 7, 8, ill. 10%!
Kerdes, hogy milyen mertekben devalvalodik valamely
valuta (frank, dollar, font, marka, rubel, jen vagy
holland forint) 1, 2, ..., n ev alatt. }const MaxEv=10;
var Ev: 0..MaxEv;
Tenyezo1, Tenyezo2, Tenyezo3: Real;begin
Ev:=0;
Tenyezo1:=1.0; Tenyezo2:=1.0; Tenyezo3:=1.0;
Writeln(' Ev 7% 8% 10%'); Writeln;
repeat
Ev:=Ev+1;
Tenyezo1:=Tenyezo1*1.07;
Tenyezo2:=Tenyezo2*1.08;
Tenyezo3:=Tenyezo3*1.10;
Writeln(Ev:3,Tenyezo1:7:3,Tenyezo2:7:3,Tenyezo3:7:3)
until Ev=MaxEv
end.
Az első rész felsorolja az adott blokkban definiált összes címkét. A második rész a konstansok "szinonimáit" definiálja, azaz azonosítókat vezet be, amelyek aztán az illető konstansok helyett írhatók. A harmadik típusdefiníciókat tartalmaz, a negyedik pedig a változók definícióit. Az ötödik kijelöli az alárendelt programrészeket (vagyis az eljárásokat és a függvényeket). Az utasításrész az elvégzendő tevékenységeket adja meg.
1.2. Szintaxisdiagramok
A program előbb leírt vázlatos szerkezetét pontosabban fejezi ki az 1.1. ábrán látható szintaxisdiagram. A Program szótól elindulva, ha az ábrán a nyilakat követve végighaladunk, minden lehetséges út egy szintaktikusan helyes programot ad. Az ábra téglalapjai a beírttal azonos nevű szintaxisdiagramokat helyettesítenek. A téglalapok jelentését tehát ezek a részletes szintaxisdiagramok definiálják (1.2. ábra). A Pascal programban ténylegesen előforduló ún. terminális szimbólumokat ovális alakú mezőbe írjuk. (A Pascal teljes szintaxisának leírása a D. függelékben található.)

1.1. ábra. Program szintaxisdiagramja
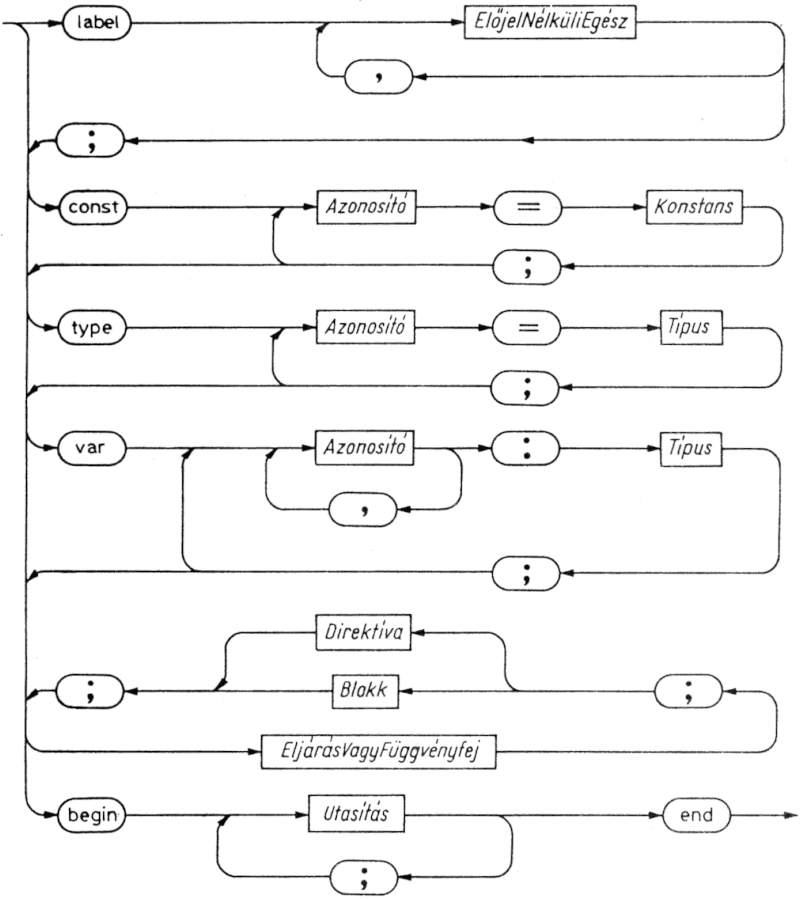
1.2. ábra. Blokk szintaxisdiagramja
1.3. Az EBNF
A szintaxisleírás másik lehetséges módját a kiterjesztett (Extended) Backus-Naur-forma (EBNF) alkalmazása jelenti, ahol a szintaktikai egységeket szavak és füzérek, más szóhasználattal literálok vagy karakterláncok jelölik. A szavak jelentése az egyes egységek jellegére, tartalmára utal, míg a füzérek a nyelvben ténylegesen használt szimbólumok. A füzéreket idézőjelek határolják.
Ha egy szintaktikai egységekből álló sorozatot kapcsos zárójelek ({ és } ) közé írunk, ez a sorozat nullaszori vagy többszöri ismétlését jelenti. Az alternatívákat függőleges vonallal ( | ) választjuk el egymástól. A gömbölyű zárójelek ( ( és ) ) csoportosításra szolgálnak, a szögletes zárójelek ( [ és ] ) pedig azt fejezik ki, hogy a közéjük írt szintaktikai egységek, ill. füzérek elhagyhatók. (A Pascal teljes EBNF-leírása a D. függelékben található.)
Az 1.1. ábra programját pl. a következő formulák, ún. képzési szabályok írják le:
Ebből a szemszögből nézve úgy is mondhatjuk, hogy valamely X azonosító hatásköre vagy értelmezési tartománya az a teljes blokk, amelyben X-et definiáltuk, ideértve tehát azokat a blokkokat is, amelyeket X-szel azonos blokkban definiáltunk. (Vegyük észre, hogy példánk esetében minden azonosító különböző kell, hogy legyen. A 4.7. szakaszban foglalkozunk majd azzal az esettel, amikor nem kell feltétlenül minden azonosítónak különbözőnek lennie.)
P
A
B
Q
R
SM, P, A, B, Q, R, S
P, A, B
A, B
B
Q, R, S
R
S
1.5. Összehasonlítás más programnyelvekkel
ALGOL, PL/1 vagy FORTRAN ismeretekkel rendelkező programozók talán hasznosnak találják, ha a Pascal tulajdonságait ezekkel a nyelvekkel összehasonlítva is megfogalmazzuk. Ilyen szempontból a Pascal következő jellemzőit sorolhatjuk fel:
Azok, akik először találkoznak a Pascallal és még nem volt alkalmuk mélyebben megismerni a nyelvet, gyakran nehezményezik, hogy bizonyos "népszerű" eszközök nincsenek meg benne. Példaként említik a többi között a hatványozó operátort, a füzérek konkatenációját, a dinamikus tömböket, a logikai értékekkel végzett aritmetikai műveleteket, az automatikus típusátalakítást, az automatikus deklarációt. Ezek nem tévedésből, hanem szándékosan maradtak ki a nyelv eszköztárából. Egyes esetekben engedélyezésük kevésbé hatékony programozási megoldásokra csábítana, más esetekben pedig úgy éreztük, hogy ellentétben állna céljainkkal: az áttekinthetőséggel, a megbízhatósággal, a "jó programozási stílussal". Nem utolsósorban pedig szigorúan meg kellett rostálnunk a rengeteg rendelkezésre álló programozási eszközt, hiszen azt akartuk, hogy a fordítóprogram viszonylag tömör és hatékony legyen, hogy minden felhasználó hatékonyan és gazdaságosan alkalmazhassa - az is, aki kis programokat ír, s a nyelvnek csak kevés eszközét használja, de az is, aki nagy programokat készít, s a nyelv minden lehetőségét igyekszik kiaknázni.
2. Jelölések: szimbólumok és elválasztok
A Pascal programok szimbólumokból és szimbólum-elválasztókból (röviden elválasztókból) állnak. A szimbólumok a következő csoportokba sorolhatók: speciális szimbólumok, szószimbólumok (alapszavak), azonosítók, számok, füzérek, címkék és direktívák. A következő szakaszban az elválasztókkal foglalkozunk.
2.1. Elválasztók
A szóközt, a sor végét és a magyarázatot (megjegyzést, commentet) elválasztóként használjuk. A Pascal szimbólumok belsejében elválasztó (sem annak része) nem szerepelhet. Bármely két azonosító, szám vagy alapszó között azonban legalább egy elválasztót kell alkalmazni.
A magyarázat (comment) { vagy (* jellel kezdődik (nem füzér belsejében), és } vagy *) zárja le. A magyarázat tetszőleges, karakterekből és sorvégekből álló jelsorozat lehet, de { -et vagy *) -ot nem tartalmazhat. Ha a programszövegben a magyarázat helyére szóközt írunk, a szöveg jelentése nem változik.
A szóközök, üres sorok (sorvégek) és magyarázatok közbeiktatása gyakran olvashatóbbá teszi a Pascal programot.
2.2. Speciális szimbólumok és alapszavak
A következőkben a Pascal programokban használatos speciális szimbólumokat és alapszavakat tekintjük át. Fontos, hogy a kétkarakteres speciális szimbólumok között nincs elválasztó! A speciális szimbólumok:
+ - * /
. , : ;
= <> < <= > >=
( ) [ ]
Egyes speciális szimbólumokat más jelekkel pótolhatunk:
[ helyett (.
] helyett .)
^ helyett @
Az alapszavakat a kézzel írt programban általában aláhúzzuk: így jelezzük, hogy karaktereik egyetlen, rögzített jelentésű szimbólumot alkotnak. Ezeket a szavakat kizárólag a Pascal definíciójában lefektetett összefüggésben szabad használni. Alapszó sosem lehet azonosító! Az alapszavak egyszerűen kis- vagy nagybetűk sorozatai; kezdetük vagy végük jelölésére nincs szükség speciális karakterekre. Az alapszavak:
and end nil set array file not then begin for of to case function or type const goto packed until div if procedure var do in program while downto label record with else mod repeat
2.3. Azonosítók
Az azonosítók a konstansok, típusok, tartományhatárok, változók, eljárások és függvények jelölésére szolgáló nevek. Betűvel kell kezdődniük, amely után viszont betűk és számok tetszőleges kombinációja állhat. Az azonosítók hossza nincs korlátozva, a fordítóprogram valamennyi karakterüket értékesnek tekinti. Az összetartozó kis- és nagybetűk azonosnak számítanak.
2.1. ábra. Betű szintaxisdiagramja

2.2. ábra. Számjegy szintaxisdiagramja

2.3. ábra. Azonosító szintaxisdiagramja
Példák azonosítókra:
Telefonkonyv Gyok3 Pi h4g X
EzEgyNagyonHosszuDeAzertHelyesAzonosito
EzEgyNagyonHosszuDeAFentiektolKulonbozoAzonosito
A BetukEsSzamok azonosító megegyezik a betukesszamok azonosítóval.
Hibás azonosítók:
7Torpe arraay Szint.4 Gyok.3 Tizedik_Bolygo
Bizonyos ún. standard azonosítók előre definiáltak (pl. sin, cos). Az alapszavakkal (pl. array) ellentétben nem kell az így megadott definíciókhoz ragaszkodnunk, tehát bármelyik standard azonosító újradefiniálható. Ennek az az oka, hogy a standard azonosítók a programban úgy szerepelnek, mintha egy, az egész programot körülvevő hipotetikus blokkban deklaráltuk volna őket. A Pascal összes standard azonosítóját megadtuk a C. függelékben.
2.4. Számok
A számokat - egész és valós értékeket - decimális írásmódban írjuk. A számok előtt előjel (+ vagy -) állhat; az előjel nélküli számok esetén nem szabad előjelet használni!
A számok vesszőt nem tartalmazhatnak. A valós számokat tizedestörtként és/vagy 10 hatványaival írjuk le. A kitevő előtt egy E (vagy e) betű áll, jelentése: "...-szer 10 a ... hatványon". Figyeljük meg, hogy ha a szám tizedespontot tartalmaz, a pont előtt és után is legalább egy-egy számjegynek kell állnia!

2.4. ábra. Előjel nélküli egész szintaxisdiagramja

2.5. ábra. Előjel nélküli szám szintaxisdiagramja
Előjel nélküli számok:
3
03
6272844
0.6
5E-8
49.22E+08
1E10
Hibásan felírt számok:
3,487,159
XII
.6
E10
5.E-16
3.487.159
2.5. Füzérek
Az egyszeres idézőjelek (aposztrófok) közé zárt karaktersort füzérnek (string) nevezzük. Ha aposztrófot tartalmazó füzérre van szükségünk, a megfelelő helyen két aposztrófot kell írni.

2.6. ábra. Füzér szintaxisdiagramja
Példák:
'a'
'.'
'3'
'begin'
'BNV''86'
' Ez 33 karakteres fuzer.'
2.6. Címkék
A címkék előjel nélküli egész számok, amelyeket Pascal utasítások megjelölésére használunk. Értékük 0 és 9999 közé kell, hogy essen.
Példák:
13
00100
9999
2.7. Direktívák
A direktívák eljárás- és függvényblokkokat helyettesítő nevek. Szintaxisuk megegyezik az azonosítókéval (l. a 12. fejezetet).

2.7. ábra. Direktíva szintaxisdiagramja
3. Az adat fogalma: egyszerű adattípusok
Az adat szó gyűjtőfogalom. Adatnak tekintünk minden objektumot, amivel (amin) a számítógép műveleteket végez. A hardver és a gépi kód szintjén minden adatot valamilyen bináris számsor (bitsorozat) ábrázol. A magas szintű programozási nyelvek lehetővé teszik, hogy elvonatkoztassunk a konkrét ábrázolásmód részleteitől. Mindebben igen jelentős szerepet játszik az adattípus fogalma.
Az adattípus határozza meg, hogy egy változó milyen értékeket vehet fel és milyen műveletek végezhetők rajta. A program minden változójának valamilyen (de csakis egyetlen) típushoz kell tartoznia. Bár a Pascalban meglehetősen összetett adattípusok is előfordulhatnak, minden összetett (strukturált) adattípus végső soron egyszerű, strukturálatlan adattípusokból épül fel.
A Pascal több, egymástól független, de az alkalmazás szempontjából célszerűen egyszerre megadható adattípus megadására is lehetőséget ad. Ennek eszközei a strukturált és a mutató típusok, amelyekkel a 7-11. fejezetben foglalkozunk.
Adattípusok:
A Pascal egyszerű típusait tovább bonthatjuk a megszámlálható (ordinal) típusok csoportjára és a valós (real) típusra. A megszámlálható típust vagy a programozó definiálja - ekkor felsorolt (enumerated), ill. résztartomány (subrange) típusról van szó -, vagy előredefiniált, standard típusazonosító jelöli: ez a Boolean (logikai), az Integer (egész) vagy a Char (karakter) azonosítók valamelyike lehet. A valós típust a Real standard típusazonosítóval jelöljük.

3.1. ábra. Egyszerű typus szintaxisdiagramja
A felsorolt típusokat a típushoz tartozó (különböző) értékek halmaza és az azon értelmezett lineáris rendezés jellemzi. A típus definíciójában az egyes értékeket azonosítókkal jelöljük. A résztartomány típusok olyan megszámlálható típusok, amelyek egy korábban deklarált megszámlálható típus értéktartományának korlátozásával: egy legkisebb és egy legnagyobb érték megadásával jönnek létre. A felsorolt és a résztartomány típusokkal a 6. fejezetben foglalkozunk.
3.1. Megszámlálható típusok
A megszámlálható- adattípusok valamilyen véges és rendezett értékhalmazt írnak le. (Matematikai értelemben a megszámlálhatóság fogalmának gyakorlatilag csak végtelen halmazok esetében van jelentősége, hiszen a véges halmazok triviálisan megszámlálhatok. Könyvünkben ugyan kizárólag véges halmazokról van szó, ennek ellenére a definíciók hasonlósága miatt a most bevezetett típuscsoportot megszámlálhatónak nevezzük.) A megszámlálható típushoz tartozó értékeket egyértelműen megfeleltetjük a 0, 1, 2,... természetes számoknak, tehát minden értéknek sorszáma van. (Ez a leképezés az egész típus esetében triviális.) Minden megszámlálható típusnak van egy legkisebb és egy legnagyobb értéke. A legkisebb érték kivételével mindegyik értékhez tartozik egy őt megelőző érték. A legnagyobb érték kivételével mindegyik értékhez tartozik egy őt követő érték.
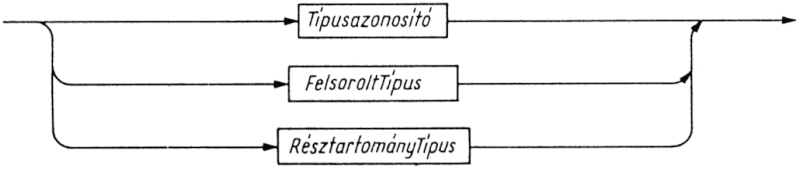
3.2. ábra. Megszámlálható típus szintaxisdiagramja
Tetszőleges megszámlálható típusú argumentumra alkalmazhatjuk a következő standard függvényeket:
| succ(x) | eredménye az X-et követő érték. |
| pred(x) | eredménye az X-et megelőző érték. |
| ord(x) | eredménye az X érték sorszáma. |
Az =,<>,<,<=,>= és > relációs operátorok minden megszámlálható típusra alkalmazhatók, feltéve, hogy mindkét operándusuk azonos típusú. A rendezést az értékek sorszáma határozza meg.
3.2. A logikai (boolean) típus
Boolean érték csak a két logikai igazságérték, a hamis, ill. az igaz lehet. Ezeket a false (hamis) ill. a true (igaz) azonosítóval jelöljük.
Logikai operandusokra alkalmazva logikai értéket szolgáltatnak a következő logikai operátorok (a logikai operátorok felsorolását l. a B. függelékben):
| and | logikai konjunkció (ÉS művelet), |
| or | logikai diszjunkció (VAGY művelet), |
| not | logikai negálás |
Az összes relációs operátor (=, <>,<=, <, >, > =, in) logikai értéket szolgáltat. A "<>" szimbólum jelentése: "nem egyenlő". Lényeges, hogy a logikai típus definíciója értelmében false < true, s így a fenti logikai és relációs operátorok segítségével mind a 16 Boole-algebrai művelet kijelölhető. Ha pl. P és Q logikai értékek,
alakban fejezhető ki.
Standard (beépített vagy élőredeklarált) logikai függvények - azaz logikai értéket szolgáltató standard függvények - pl. a következők (a standard függvények összefoglalását l. az A. függelékben):
| odd(I) | értéke igaz, ha az I egész szám páratlan, egyébként hamis, |
| eoln(F) | sor vége (end of line), részletesebben l. a 10. fejezetet, |
| eof(F) | állomány vége (end of file), részletesebben l. a 10. fejezetet. |
3.3. Az egész (integer) típus
Az egész típusú értékek az egész számoknak - az adott Pascal-megvalósításban definiált - részhalmazához tartoznak.
Az alábbi aritmetikai operátorok egész operandusokra alkalmazva egész értéket szolgáltatnak:
| * | szorzás, |
| div | osztás a törtrész elhagyásával (Az eredmény tehát nem kerekített!), |
| mod | maradékképzés: legyen Maradék = A-(A div B)*B; ekkor ha Maradék < 0, akkor A mod B = Maradék + B egyébként A mod B = Maradék |
| + | összeadás, |
| - | kivonás. |
Minden megvalósításban megvan a MaxInt standard konstansazonosító, amely azt a legnagyobb egész értéket jelöli, amellyel az adott rendszerben még valamennyi egészekre értelmezett művelet végrehajtható. Ha A és B két egész típusú kifejezés, az
A op B
művelet helyes végrehajtása csak akkor biztosított, ha
abs(A op B) <= MaxInt
abs(A) <= MaxInt és
abs(B) <= MaxInt
Négy fontos standard függvény szolgáltat egész eredményt:
| abs(I) | az eredmény: I abszolút értéke, |
| sqr(I) | az eredmény: I négyzet, feltéve, hogy I <= MaxInt div I. |
| trunc(R) | R valós érték, az eredmény: R egészrésze. (A törtrészt a művelet levágja. Így pl. trunc(3.7) = 3 és trunc(-3.7) = -3.) |
| round(R) | valós érték, az eredmény az R-nek megfelelő kerekített egész. Ha R >= 0, akkor round(R) =trunc(R+0.5), ha R < 0, akkor round(R) = trunc(R-0.5). |
Ha I egész típusú változó, akkor
| succ(i) | a "következő" egészt, (I+1)-et, |
| pred(i) | a megelőző egészt, (I-1)-et szolgáltatja. |
3.4. A karakter (char) típus
A karakter típusú értékek valamilyen véges és rendezett karakterhalmaz (jelkészlet) elemei. Ilyen halmazt kommunikációs célokból minden számítógépes rendszerben definiálnak. Ezek a karakterek állnak rendelkezésünkre a be-, ill. kiviteli berendezéseken. Sajnos szabványos karakterkészlet, amit egységesen alkalmaznának, nem létezik, ezért az elemek definíciója és rendezése szigorúan rendszerfüggő (l. a G. függeléket).
Az aposztrófok (egyszeres idézőjelek) közé zárt jel karakter típusú értéket jelöl.
Példák:
'*' 'G' '3' '''' 'X'
(Az aposztróf karaktert két, aposztrófok közé zárt aposztróffal jelöljük.)
A karakter típus definiálásakor azonban a rendszertől függetlenül feltételezzük, hogy:
Példák:
succ('5') = '6'
'A' < 'B'
'a' < 'b'
Az adott jelkészlet és a természetes számok egy részhalmaza (a karakterek sorszámai) között két standard függvény, az ord és a chr segítségével kölcsönös és egyértelmű leképzés létesíthető.
| ord(C) | a C karakter sorszáma az adott rendezett karakterkészletben; |
| chr(I) | az I sorszámú karakter. |
Azonnal látszik, hogy ord és chr egymás inverz függvényei, tehát:
chr(ord(C))=C és ord(chr(I))=I
Az előbbi függvényekkel egy adott karakterkészlet rendezését a következőképpen értelmezhetjük:
C1 < C2 akkor és csak akkor, ha ord(C1) < ord(C2).
Ezt a definíciót az összes relációs operátorra (=, <>, <, <=, >=, >) általánosíthatjuk. Ha R egy ilyen operátor, akkor
C1 R C2 akkor és csak akkor, ha ord(C1) R ord(C2).
Ha a pred, ill. a succ standard függvény argumentuma karakter típusú, a függvényeket a következőképpen értelmezzük:
pred(C) = chr(ord(C)-1)
succ(C) = chr(ord(C)+1)
Megjegyzés: A karaktert megelőző, ill. követő karakter az adott jelkészlettől függ. A két értéknek csak akkor van értelme, ha a készletben létezik az adottat megelőző, ill. követő karakter.
3.5. A valós (real) típus
A valós típusú értékek a valós számok - adott Pascal-megvalósításban definiált - részhalmazának az elemei.
A valós típusú operandusokkal végzett műveletek mindig közelítő eredményt szolgáltatnak: az eredmény pontossága attól függ, milyen fordítóprogrammal (géppel) dolgozunk. A Reál az egyetlen nem megszámlálható egyszerű típus. A valós értékekhez nem rendelhetünk sorszámot, sem megelőző vagy követő értéket.
Abban az esetben, ha az alábbi operátoroknak legalább az egyik operandusa valós (a másik egész típusú is lehet), a következő műveletek valós értéket szolgáltatnak:
| * | szorzás, |
| / | osztás (mindkét operandus lehet egész, de az eredmény mindig valós), |
| + | összeadás, |
| - | kivonás. |
Valós argumentumokra alkalmazva valós eredményt ad az
abs(R) és az sqr(R)
standard függvény. Az előbbi eredménye R abszolút értéke, az utóbbié R négyzete, feltéve, hogy az nem esik már kívül a valós számoknak az adott megvalósításban megengedett tartományán.
Az alábbi standard függvények valós és egész argumentumokon egyaránt valós eredményt szolgáltatnak:
| sin(x) | az X radiánban megadott érték szinusza, |
| cos(x) | az X radiánban megadott érték koszinusza, |
| arctan(x) | X arkusz tangense radiánban, |
| ln(x) | X természetes (e alapú) logaritmusa, X>0, |
| exp(x) | exponenciális függvény (e az X-ediken), |
| sqrt(x) | X négyzetgyöke, X>=0 |
Figyelmeztetés! A valós típus ugyan az egyszerű típusok között van, de nem mindig használható ugyanúgy, mint a többi egyszerű (megszámlálható) típus. Külön ki kell emelnünk, hogy a pred és a succ függvény valós argumentumra nem alkalmazható, továbbá tilos valós értéket tömb és case utasítás indexelésére, for utasítás vezérlésére, halmaz alaptípusának definiálására, ill. résztartomány típusban használni!
4. A programfej és a deklarációs rész
Mint már említettük, minden program fejből és blokkból (törzsből) áll. A blokk két részre tagolódik: a deklarációs részre, amely az összes, a programra nézve lokális objektum definícióját tartalmazza, és az utasításrészre, amely az ezen objektumokon elvégzendő műveleteket, tevékenységeket adja meg.
![]()
4.1. ábra. Program szintaxisdiagramja
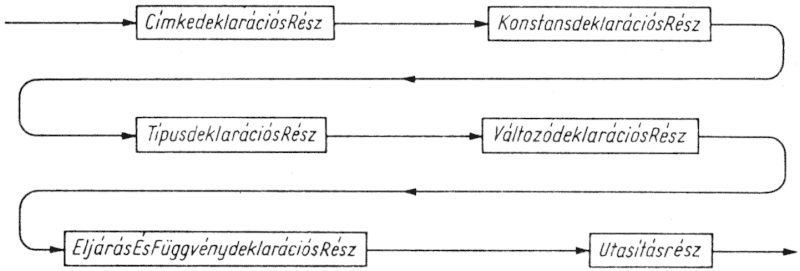
4.2. ábra. Blokk szintaxisdiagramja
![]()
4.3. ábra. Utasításrész szintaxisdiagramja
4.1. A programfej
A fej nevet ad a programnak (a név egyébként magában a programban nem lényeges), és felsorolja a program paramétereit, amelyek a programon kívüli objektumokat jelölnek, és amelyeken keresztül a program a környezettel kapcsolatot tart. Ezeket az objektumokat (többnyire állományokról van szó, l. a 10. fejezetet) külső (external) objektumoknak nevezzük. A paramétereket ugyanúgy kell deklarálni, mint a közönséges lokális változókat, de deklarációjuknak a programot alkotó blokkban kell állnia (l. a 4.5. szakaszt).

4.4 ábra. Programfej szintaxisdiagramja
4.2. A címkedeklarációs rész
A címkék segítségével a program tetszőleges utasítását jelzéssel láthatjuk el. A címkét az utasítás elé kell írni, a címke után kettőspont áll. (Címkével jelölhetjük ki pl. egy goto utasítás célpontját.) Felhasználása előtt azonban minden címkét deklarálnunk kell a címkedeklarációi miben. A deklarációt a programban a label (címke) alapszó vezeti be. A címkedeklarációs rész általános alakja:

4.5. ábra. Címkedeklarációs rész szintaxisdiagramja
A címke előjel nélküli, 0 és 9999 közé eső egész szám.
Példa:
label 13,00100,99;
4.3. A konstansdefiníciós rész
A konstansdefinícióban egy konstans helyett, annak szinonimájaként, egy azonosítót vezetünk be. A konstansdefiníciós rész a const szimbólummal kezdődik, s általános alakja:

4.6. ábra. Konstansdefiníciós rész szintaxisdiagramja
ahol a konstans szám (esetleg előjeles) konstansazonosító, karakter vagy füzér lehet.
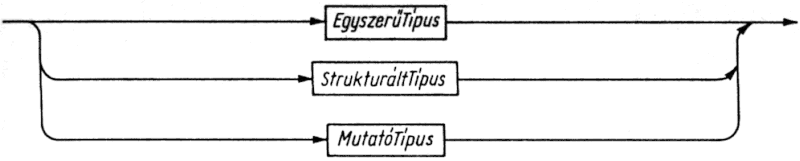
4.9. ábra. Típus szintaxisdiagramja
Típusazonosítókra több példát is talál az Olvasó a következő fejezetekben.
4.5. A változódeklarációs rész
Az utasításokban szereplő összes változót változódeklarációban kell megadni. A deklaráció, hacsak nem programparaméterről van szó, meg kell, hogy előzze a változó felhasználását.
A változódeklarációban az új változóhoz azonosítót és adattípust rendelünk, mégpedig oly módon, hogy egyszerűen leírjuk az azonosítót, majd a változó típusát. A változódeklarációs részt a var szimbólum vezeti be. Általános alakja a 4.10. ábrán látható.
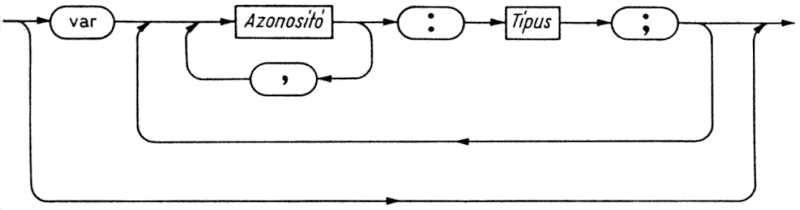
4.10. ábra. Változódeklarációs rész szintaxisdiagramja
Példa:
var Gyok1, Gyok2, Gyok3: Real;
Darab, I: Integer;
Megvan: Boolean;
Betu: Char;
A programfej paraméterlistájában felsorolt (külső objektumokat, rendszerint állományokat jelölő) azonosítókat - az Input és az Output kivételével - a program változódeklarációs részében deklarálni kell. Az Input és az Output azonosítókat, ha szerepelnek, a fordítóprogram automatikusan szövegállományként deklaráltnak tekinti (l. a 10. fejezetet).
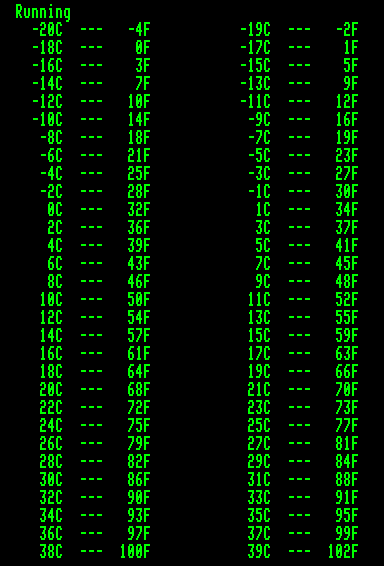
program Atszamit (Output);
{Turbo Pascal}
{Atszamitas Celsius fokbol Fahrenheit fokba}
{ A konstans- es tipusdefinicios, ill. a
valtozodeklaracios reszt szemlelteto program }
const Eltolas = 32;
Szorzo = 1.8;
AlsoHatar = -20;
Felsohatar = 39;
Elvalaszto = ' ---'; Terkoz = ' ';
type Celsiustartomany = AlsoHatar..Felsohatar;
{resztartomany tipus}
var Fok: CelsiusTartomany;
begin
for Fok:= AlsoHatar to FelsoHatar do
begin
Write(Output,Fok:5,'C');
Write(Output,Elvalaszto,Round(Fok*Szorzo+Eltolas):5,'F');
if Odd(Fok) then Writeln(Output)
else Write(Output,Terkoz)
end;
Writeln(Output)
end.
A program eredménye:
4.6. Az eljárás- és függvénydeklarációs rész
Felhasználása előtt minden eljárás- vagy függvényazonosítót deklarálni kell. Az eljárás- és függvénydeklaráció ugyanolyan alakú, mint a program - fejből és blokkból áll. A témával részletesen (példákkal) a 12. fejezetben foglalkozunk. Az eljárás olyan szubrutin, amelyet eljárásutasítással hívhatunk be. A függvény olyan szubrutin, amely eredmény értéket szolgáltat, s így kifejezésekben is előfordulhat.
4.7. Az azonosítók és a címkék hatásköre
Egy (konstans-, típus-, változó-, eljárás- vagy függvény-) azonosító vagy címke deklarációja, ill. definíciója mindaddig érvényes, míg a deklarációt, ill. definíciót tartalmazó blokkban vagyunk, hacsak az azonosítót vagy címkét egy alárendelt blokkban újra nem deklaráljuk, ill. definiáljuk. Ekkor a belső blokkban az új deklaráció (definíció) lesz érvényes. Azt a program-területet, amelyen egy változó vagy címke deklarációja, ül. definíciója hatályos, a változó vagy címke hatáskörének nevezzük.
A program blokkban deklarált, ill. definiált azonosítókat globálisnak mondjuk. Az azonosítók (címkék) lokálisak arra a blokkra nézve, amelyben deklaráltuk (definiáltuk) őket, és globálisak azokra a blokkokra nézve, amelyek a deklarációjukat tartalmazó blokkba ágyazottak. (A példákat l. az 1.4. szakaszban.)
Tilos egy azonosítót egyazon szinten és hatáskörön belül egynél többször deklarálni! Hibás tehát a következő deklaráció:
var X: Integer;
X: Real;
5. A tevékenység fogalma
A számítógépes program alapvető tulajdonsága a tevékenység. Más szóval, a programnál mindenképpen csinálnia kell valamit az adataival, még akkor is, ha ez a tevékenysége abból áll, hogy nem csinál semmit! A tevékenységeket utasítások írják le. Az utasítások lehetnek egyszerűek (mint pl. az értékadó utasítás) vagy strukturáltak. Az utasítástípusokat az 5.1. szintaxis diagramon tekinthetjük át.

5.1. ábra. Utasítás szintaxisdiagramja
5.1. Az értékadó utasítás és a kifejezések
A legalapvetőbb utasítás az értékadó utasítás. Hatására egy újonnan kiszámított - egy kifejezés által meghatározott - érték rendelődik valamilyen változóhoz. Az értékadó utasítás alakját az 5.2. ábra szintaxisdiagramja mutatja.

5.2. ábra. Értékadó utasítás szintaxisdiagramja
A := szimbólum az értékadás jele, és nem szabad összetévesztenünk az = relációs operátorral. Az "A:= 5" utasítás jelentése: "A aktuális értékének helyére az 5 érték kerül", vagy egyszerűen "A legyen egyenlő 5-tel!"
A változó (5.3. ábra) lehet teljes változó, amely egy egyszerű, strukturált vagy mutató típus adatainak tárolásához szükséges teljes tárterületet lefoglalja. Strukturált típusok esetében (L. a 7...10. fejezetet) azonban lehet elemi vagy pufferváltozó is, amely a teljes tárterület egy elemét jelöli ki. Végül mutató típusok esetében megkülönböztetünk mutatott változókat, amelyek a mutatók által indirekt módon megadott tárrekeszek leírására szolgálnak.
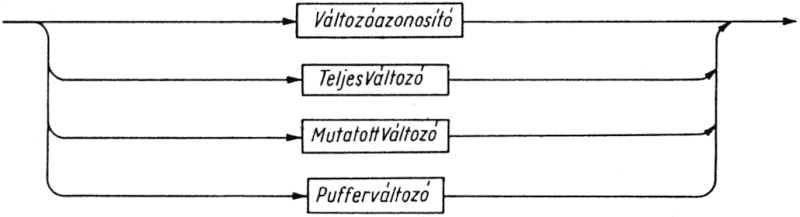
5.3. ábra. Változó szintaxisdiagramja
A kifejezés operátorokból és operandusokból áll. Az operandusok lehetnek konstansok, változók, tömbparaméter-indexhatárok (l. a 12. fejezetet) vagy függvénykifejezések. (A függvénykifejezés egy függvény kiértékeléséről gondoskodik. A standard függvényeket l. az A. függelékben; a felhasználó által definiált függvényekkel a 12. fejezetben foglalkozunk.)
A kifejezés egy számítás kijelölése: előírja valamilyen érték kiszámításának a módját. A kifejezés kiértékelése a megszokott algebrai szabályoknak megfelelően, balról jobbra haladva, az operátorprecedencia figyelembevételével történik. A kifejezések tényezőkből, tagokból és egyszerű kifejezésekből épülnek fel.
Elsőként a tényezők értékelődnek ki. A tényezők lehetnek konstansok, változók, függvénykifejezések, tömbparaméter-indexhatárok vagy halmazgenerátorok (l. a 9. fejezetet). Ha egy logikai értéket leíró tényezőre a not operátort alkalmazzuk, ismét tényezőt kapunk. Tényezőt alkot a zárójelek közé zárt kifejezés is, amely az előtte és mögötte álló operátoroktól függetlenül értékelődik ki.
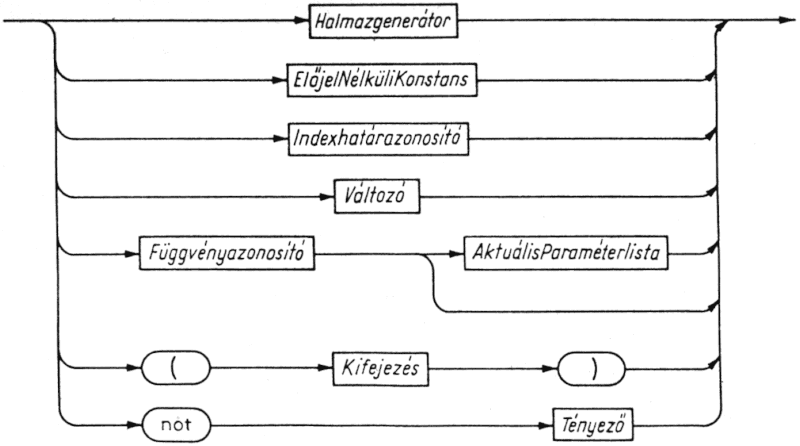
5.4. ábra. Tényező szintaxisdiagramja
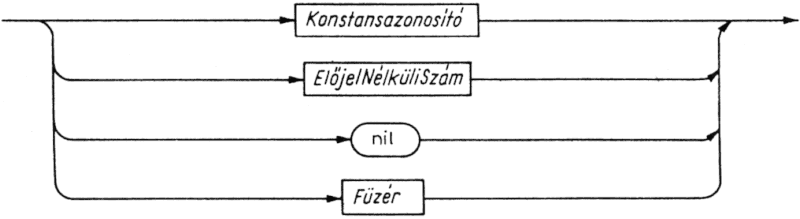
5.5. ábra. Előjel nélküli konstans szintaxisdiagramja

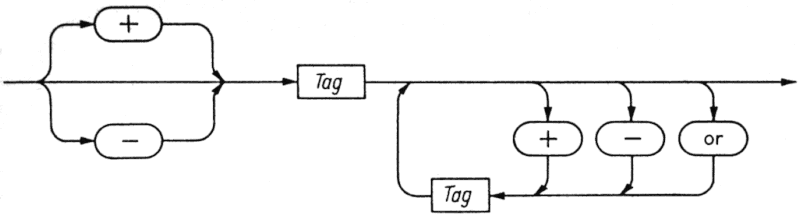
5.6. ábra. Tag szintaxis diagramja
A tényezők után a tagok kiértékelése következik. A tag legegyszerűbb esetben egyetlen tényezőből áll, de általában multiplikatív operátorokkal (*, /, div, mod, and) elválasztott tényezők sorozata.
Harmadikként az egyszerű kifejezések értékelődnek ki. Ezek legegyszerűbb esetben egyetlen tagból, általában pedig additív operátorokkal (+, -, or) elválasztott tagok sorozatából állnak. Első tagjukat előjel operátor (+, -) előzheti meg, amely azonban nem kötelező.
Mindezek után kerülhet csak sor a kifejezések kiértékelésére. A kifejezések valamilyen relációs operátorral (=, <>, <, <=, >=, >, in) összekapcsolt két egyszerű kifejezésből vagy egyetlen egyszerű kifejezésből állnak (5.7. és 5.8. ábra).
5.7. ábra. Egyszerű kifejezés szintaxisdiagramja
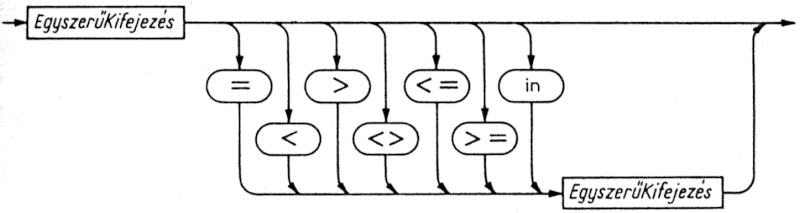
5.8. ábra. Kifejezés szintaxisdiagramja
Példák:
2*3-4*5 (2*3)-(4*5) = -14 15 div 4*4 (15 div 4)*4 = 12 80/5/3 (80/5)/3 = 5.333 4/2*3 (4/2)*3 = 6.000 Sqr(Sqr(3)+11*5) = 8.000
Ha az Olvasó bizonytalannak érzi magát, nézze át a következő táblázatot, amely pontosan megadja az operátorok precedencia-sorrendjét!
Operátor Besorolás not Logikai negáció (a legnagyobb precedenciával). *, /, div, mod, and Multiplikatív operátorok (a precedenciájuk a második legnagyobb). +, -, or Additív operátorok (precedenciájuk sorrendben a harmadik). =, <>, <, <=, >=, ,>, in Relációs operátorok (a legkisebb precedenciával).
(Az operátorok részletes leírása a B. függelékben található.)
A logikai kifejezések érdekes tulajdonsága, hogy értéküket már akkor ismerhetjük, mielőtt az egész kifejezést kiértékeltük volna. Tegyük fel pl., hogy X = 0. Ekkor az
(X>0) and (X<10)
kifejezésről már az első tényező kiértékelése után tudjuk, hogy értéke hamis, s a második tényezővel már nem is kell foglalkoznunk. Ez azt jelenti, hogy az első tényező értékétől függetlenül a programozónak mindig gondoskodnia kell a második tényező helyes felírásáról is. Ha tehát feltételezzük, hogy az A tömb indexhatárai 1 és 10, a következő programpélda hibás!
X:= 0;
repeat
X:= X+1
until (X>10) or (A[X]=0)
(Vegyük észre, hogy ha egyik A[l] sem zérus, a program az A[11] elemre mutat!)
Az értékadás - az állományokat kivéve (l. a 10. fejezetet) - tetszőleges típusú változóra vonatkozhat. A változó (vagy függvény) és a kifejezés azonban az értékadás szempontjából kompatibilis kell, hogy legyen.
A következőkben az értékadás-kompatibilitás valamennyi lehetséges esetét felsoroljuk:
Példák:
Gyok1:= Pi*X/Y
Gyok2:= -Gyok1
Gyok3:= (Gyok1+Gyok2)*(1.0+Y)
BajVan:= Homerseklet > Forrpont
Darab:= Darab+1
Fok:= Fok+10
SqrPr:= Sqr(Pr)
Y:= Sin(X)+Cos(Y)
5.2. Az eljárásutasítás
Az egyszerű utasítások másik fontos fajtája az eljárásutasítás, amely az utasításban megnevezett eljárás végrehajtását idézi elő. Az eljárás olyan alprogram, amelybe valamely, az adatokon végzendő tevékenységcsoportot fogunk össze. Könyvünkben eddig a Read, a Readln, a Write és a Writeln eljárást használtuk: segítségükkel olvastuk be, ill. írtuk ki az adatokat, ill. eredményeket. Az eljárásutasítással részletesen a 12. fejezetben foglalkozunk.
5.3. Az összetett és az üres utasítás
Az összetett utasítás feladata annak biztosítása, hogy összetevői adott sorrendben hajtódjanak végre. Az utasítászárójel szerepét a begin és az end alapszó tölti be. Itt jegyezzük meg, hogy az utasításrész, azaz a program törzse mindig összetett utasítás formáját ölti (5.9. ábra).

5.9. ábra. Összetett utasítás szintaxisdiagramja
5.1. program:
Program BeginEndPelda(output);
{Turbo Pascal}
{ Az osszetett utasitas szemleltetese. }
var Osszeg:integer;
begin
Osszeg:=3+5;
Writeln(Output,Osszeg:5,-Osszeg:5)
end.
A program eredménye:
8 -8
A Pascal a pontosvesszőt nem az utasítás lezárására, hanem az utasítások elválasztására használja; a pontosvessző tehát nem tartozik az utasításhoz. A pontosvesszővel kapcsolatos pontos szabályokat a D. függelék szintaxisleírása tartalmazza. Ha előbbi példánkban a második utasítás után pontosvesszőt tettünk volna, a fordítóprogram ezt a pontosvessző és az end szimbólum közötti üres utasításként értelmezte volna, melynek hatására semmilyen tevékenység nem történik. Ez nem lett volna baj, mert ezen a ponton megengedhető az üres utasítás. A rossz helyre tett pontosvesszők azonban problémákat okozhatnak (l. az 5.5. szakasz if utasításokkal kapcsolatos példáját).
5.4. Ciklusutasítások
A ciklusutasítások bizonyos utasítások ismételt végrehajtását biztosítják. Ha előre (az ismétlések megkezdése előtt) ismerjük a ciklusok számát, általában a for utasítás fejezi ki legalkalmasabban a feladatot, ellenkező esetben a repeat vagy a while utasítást célszerű használni.
5.4.1. A while utasítás
A while utasítás alakja az 5.10. ábrán látható. A do alapszó utáni utasítás lehet, hogy egyszer sem hajtódik végre.
![]()
5.10. ábra. While utasitás szintaxisdiagramja
A ciklust vezérlő kifejezésnek logikai típusúnak kell lennie. Az utasítás végrehajtása előtt a gép kiértékeli a kifejezést; ha az igaz, végrehajtja az utasítást, egyébként kilép a while utasításból. Mivel a kifejezést a gép minden ciklus előtt kiértékeli, ügyelnünk kell arra, hogy a lehető legegyszerűbb alakban írjuk fel.
5.2. program:
Program WhilePelda(Output);
{Turbo Pascal}
{ A H(N) = 1 + 1/2 + 1/3 + ... + 1/N harmonikus sor
N-edik reszosszegenek kiszamitasa while ciklussal. }
var N: integer;
H: real;
begin
Write('N = ');Readln(Input,N);Write(Output,N);
H:=0;
while N>0 do begin
H:= H+1/N;
N:= N-1
end;
Writeln(Output,H)
end.
A program eredménye:
10 2.9289682540E+00
A követező program az X valós értéket az Y hatványkitevőre emeli, ahol Y nem negatív egész. Egyszerűbb, láthatóan helyes megoldást kapunk a belső while utasítás elhagyásával - ekkor az Eredmeny változó értékét úgy kapjuk, hogy X-et Y-szor önmagával szorozzuk. Figyeljük meg azonban az Eredmeny*Hatvany(Alap,Kitevo) = Hatvany(X,Y) ciklusinvariánst! A belső while utasítás az Eredmeny-t és Hatvany(Alap,Kitevo)-t változatlanul hagyja, ezáltal nyilvánvalóan javítja az algoritmus hatékonyságát.
5.3. program:
Program Hatvanyozas(Input,Output);
{Turbo Pascal}
{ Hatvany(X,Y) (X,Y) kiszamitasa termeszetes kitevore.
Hatvany(X,Y) jelentese: "X az Y-adikon". }
var Kitevo,Y:Integer;
Alap,Eredmeny,x: Real;
begin
Write(Output,'X = ');Readln(Input,X);
Write(Output,'Y = ');Readln(Input,Y);
Eredmeny:= 1; Alap:= X; Kitevo:= Y;
while Kitevo>0 do begin
while not odd(Kitevo) do begin
Kitevo:= Kitevo div 2;
Alap:= Sqr(Alap)
end;
Kitevo:= Kitevo-1;
Eredmeny:= Eredmeny*Alap
end;
Writeln(Output,X,'^',Y,' =',Eredmeny)
end.
5.4.2. A repeat utasítás
A repeat utasítás általános alakja az 5.11. ábrán látható.

5.11. ábra. Repeat utasitás szintaxisdiagramja
A repeat és az until szimbólum közötti utasítássorozat legalább egyszer végrehajtódik. Minden ciklus után kiértékelődik a logikai kifejezés. Az ismételt végrehajtások mindaddig folytatódnak, amíg a kifejezés igaz (true) értékűvé nem válik. Minthogy a kifejezés minden ciklusban kiértékelődik, fontos, hogy a lehető legegyszerűbb alakban írjuk fel.
5.4. program:
Program RepeatPelda(Output);
{Turbo Pascal}
{ A H(N) = 1 + 1/2 + 1/3 + ... + 1/N harmonikus sor
N-edik reszosszegenek kiszamitasa repeat ciklussal. }
var N: integer;
H: real;
begin
Write('N = ');Readln(Input,N);Write(Output,N);
H:=0;
repeat
H:= H+1/N;
N:= N-1
until N=0;
Writeln(Output,H)
end.
A program eredménye:
10 2.9289682540E+00
A fenti program akkor hajtódik helyesen végre, ha N>0. Az Olvasóra bízzuk annak vizsgálatát, mi történik, ha N<=0. Ugyanennek a programnak a while utasítással megoldott változata minden N-re (N=0-ra is) helyes eredményt ad.
Figyeljük meg, hogy bár a repeat utasítás utasítássorozatokat hajt végre, a begin . end zárójelpár alkalmazása felesleges (de nem lenne hiba)!
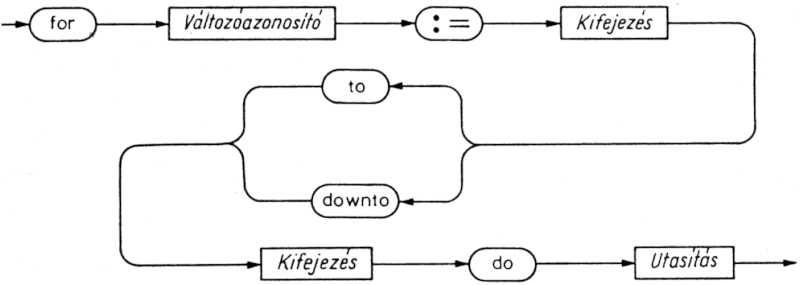
5.4.3. A for utasítás
A for utasítás egy utasítás ismételt végrehajtását biztosítja, miközben az ún. ciklusváltozójának folyamatosan növekvő vagy csökkenő értéket ad. Általános alakja az 5.12. ábrán látható.
5.12. ábra. For utasítás szintaxisdiagramja
5.5. program:
Program ForPelda(Output);
{Turbo Pascal}
{ A H(N) = 1 + 1/2 + 1/3 + ... + 1/N harmonikus sor
N-edik reszosszegenek kiszamitasa for ciklussal. }
var I,N: integer;
H: real;
begin
Write('N = ');Readln(Input,N);Write(Output,N);
H:=0;
for I:= N downto 1 do
H:= H+1/I;
Writeln(Output,H)
end.
A program eredménye:
10 2.9289682540E+00
A ciklus változója a for alapszó után áll. Megszámlálható típusúnak kell lennie, és ugyanabban a blokkban kell deklarálni, ahol a for utasítás szerepel. A kezdő- és a végérték a ciklusváltozó típusával kompatibilis megszámlálható típushoz kell, hogy tartozzon. A ciklusváltozót a ciklusmag utasítása nem módosíthatja. Sem magában a for utasításban, sem pedig az azt tartalmazó blokkban deklarált eljárásokban vagy függvényekben nem szerepelhet tehát értékadás bal oldalán, Read vagy Readln eljárásban vagy másik for utasítás ciklusváltozójaként.
A kezdő- és a végértéket a gép csak egyszer határozza meg. A to (downto) használata esetén, ha a kezdőérték a végértéknél nagyobb (kisebb), az utasítás nem hajtódik végre. Ha viszont végrehajtására sor kerül, hiba, ha a ciklusváltozó nem veheti fel a kezdő- vagy végértéket. Normális esetben a for utasításból kilépve a ciklusváltozó értéke határozatlan lesz.
5.6. program:
program Koszunusz(Input,Output);
{Turbo Pascal}
{ A koszinuszfuggveny ertekenek kiszamitasa sorbafejtessel:
Cos(x) = 1 - Sqr(x)/(2*1) + Sqr(x)*Sqr(x)/(4*3*2*1) - ...}
const Epszilon=1e-7;
var Szog: Real {Radian};
Szog2: Real {Szog a negyzeten};
Sor: Real {A Cos sora};
Tag: Real {A sor kovetkezo tagja};
I,N: Integer {A kiszamitando Cos-ertekek szama};
Ktv: Integer {A kovetkezo tag kitevoje};
begin
Write('Szamitasok darabszama: ');Readln(Input,N);
for i:=1 to N do begin
Write('Szog = ');Readln(Input,Szog);
Tag:=1; Ktv:=0; Sor:=1;
Szog2:=Sqr(Szog);
while Abs(Tag)>Epszilon*Abs(Sor) do begin
Ktv:=Ktv+2;
Tag:=-Tag*Szog2/(Ktv*(Ktv-1));
Sor:=Sor+Tag
end;
Writeln(Output,Szog,Sor,(Ktv div 2):5)
{A konvergenciakriterium altal megkovetelt tagszam}
end
end.
A következő program az f(X) valós értékű függvényt ábrázolja oly módon, hogy a függőlegesen futó X tengely mentén a megfelelő koordinátájú pontokba egy-egy csillagot nyomtat. A csillagok helyzetét a következőképpen határozzuk meg: kiszámítjuk Y = f(X) értékét, megszorozzuk egy léptéktényezővel, a szorzatot a legközelebbi egész számra kerekítjük, végül hozzáadunk egy konstanst, hogy a csillag előtt ennyi hely üresen maradjon.
5.7. program:
program Rajzolo1(Output);
{Turbo Pascal}
{ Az f(x)=exp(-x)*sin(2*pi**x) fuggveny abrazolasa }
const XLeptek= 16 {az 1 abszcisszaegysegre juto sorelemek szama};
YLeptek= 32 {az 1 ordinataegysegre juto karakterpoz. szama};
ZerusY= 34 {az x-tengely helye};
XHatar= 32 {A grafikon sorokban kifejezett hossza};
var Delta: real {lepeskoz az abszcisszan};
KetPi: real {2*Pi = 8*ArcTan(1.0)};
X,Y: real;
Pont,YPozicio: integer;
begin
Delta:=1/XLeptek;
KetPi:=8*ArcTan(1.0);
for Pont:=0 to XHatar do begin
X:=Delta*Pont; Y:=Exp(-X)*Sin(KetPi*X);
YPozicio:= Round(YLeptek*Y)+ZerusY;
repeat
Write(Output,' ');
YPozicio:= YPozicio-1
until YPozicio=0;
Writeln(Output,'*')
end
end.
Végül tekintsük a következő (5.8.) programot:
program Sorosszegek(Output);
{Turbo Pascal}
{ Szamitsuk ki negyfelekeppen az
1 - 1/2 + 1/3 - ... + 1/9999 - 1/10000 sorosszeget:
(1) sorrendben, balrol jobbra (SBJ),
(2) a pozitiv es negativ tagokat balrol jobbra osszeadva,
majd a ket osszeget egymasbol kionva (BJPoz-BJNeg).
(3) sorrendben, jobbrol balra (SJB),
(4) a pozitiv es negativ tagokat jobbrol balra osszeadva,
majd a ket osszeget egymasbol kivonva (JBPoz-JBNeg). }
var SBJ, BJPoz, BJNeg, SJB, JBPoz, JBNeg,
KovPozBJ, {balrol jobbra haladva a kov. pozitiv tag}
KovNegBJ, {balrol jobbra haladva a kov. negativ tag}
KovPozJB, {jobbrol balra haladva a kov. pozitiv tag}
KovNegJB: Real {balrol jobbra haladva a kov. negativ tag};
Tagpar: Integer {a tagparok szama};
begin
SBJ:=0; BJPoz:=0; BJNeg:=0;
SJB:=0; JBPoz:=0; JBNeg:=0;
for Tagpar:=1 to 5000 do begin
KovPozBJ:=1/(2*Tagpar-1);
KovNegBJ:=1/(2*Tagpar);
KovPozJB:=1/(10001-2*Tagpar);
KovNegJB:=1/(10002-2*Tagpar);
SBJ:=SBJ+KovPozBJ-KovNegBJ;
BJPoz:=BJPoz+KovPozBJ;
BJNeg:=BJNeg+KovNegBJ;
SJB:=SJB+KovPozJB-KovNegJB;
JBPoz:=JBPoz+KovPozJB;
JBNeg:=JBNeg+KovNegJB
end;
Writeln(Output,SBJ);
Writeln(Output,BJPoz-BJNeg);
Writeln(Output,SJB);
Writeln(Output,JBPoz-JBNeg);
end.
A program eredménye:
6.9309718302E-01
6.9309718053E-01
6.9309718306E-01
6.9309718300E-01
Miért tér el a négy "azonos" összeg?
5.5. Feltételes utasítások
A feltételes utasítás több utasítást tartalmaz, s ezek közül egyet jelöl ki végrehajtásra. A Pascal kétféle feltételes utasítást biztosít: az if és a case utasítást.
5.5.1. Az if utasítás
Az if utasítás csak akkor engedélyezi egy utasítás végrehajtását, ha egy bizonyos feltétel teljesül (tehát ha egy logikai kifejezés igaz értékű). Ha a kifejezés értéke hamis, akkor vagy a következő utasításra lépünk, vagy az else szimbólum utáni utasítás hajtódik végre.
Az if utasítás alakja az 5.13. ábrán látható.

5.13. ábra. If utasítás szintaxisdiagramja
Az if és a then között álló kifejezés Boolean típusú kell, hogy legyen. Figyeljük meg, hogy az első forma nem más, mint a második alak speciális, rövidebb változata, ahol az alternatív utasítás az üres utasítás. Vigyázat: az else előtt sohasem állhat pontosvessző! Az
if P then begin S1; S2; S3 end; else S4
programrészlet tehát hibás. Talán még inkább csalóka a következő szöveg:
if P then; begin S1; S2; S3 end
Itt az if a then és a pontosvessző közötti üres utasítás végrehajtását vezérli, így az if utasítást követő összetett utasítás mindig végrehajtódik. Az
if kifejezés1 then if kifejezés2 then utasítás1 else utasítás2
konstrukció szintaktikai kétértelműségét úgy oldhatjuk fel, hogy hatását az alábbi feltételes utasítással tekintjük egyenértékűnek:
if kifejezés1 then
begin if kifejezés2 then utasítás1
else utasítás2
end
Ismét figyelmeztetjük az Olvasót, hogy nagy árat fizethet, ha az if utasítást nem kellő körültekintéssel fogalmazza meg. Tegyük fel pl., hogy n db egymást kölcsönösen kizáró feltétel n számú különféle tevékenységet vált ki. Jelölje a feltételeket rendre C1, ... , Cn, a tevékenységeket S1, ..., Sn. Legyen P(Ci) annak valószínűsége, hogy Ci értéke igaz, és legyen mondjuk P(Ci) >= P(Cj) ha i<j. Ekkor a leghatékonyabb if utasítássorozat:
if C1 then S1
else if C2 then S2
else ...
else if C(n-1) then S(n-1) else Sn
Ha valamelyik feltétel teljesül, a hozzá tartozó utasítás végrehajtásával az if utasítás befejeződik, s így a hátralevő feltételvizsgálatokat átugorhatjuk.
Ha Found logikai típusú változó, akkor az if utasítás következő példánkban felesleges. (Ez szintén gyakori hiba!)
if Kulcs = KeresettÉrték then Found:= True else Found:= False
Sokkal egyszerűbb ezt így leírni:
Found:= (Kulcs = KeresettÉrték)
5.9. példaprogram:
program ArabRomai(Output);
{Turbo Pascal}
{ Ketto hatvanyainak kiirasa arab es romai szamokkal }
var Maradek, Szam: integer;
begin
Szam:=1;
repeat
Write(Output,Szam,' ');
Maradek:=Szam;
while Maradek>=1000 do begin
Write(Output,'M');
Maradek:=Maradek-1000
end;
if Maradek>=900 then begin
Write(Output,'CM');
Maradek:=Maradek-900
end
else if maradek>=500 then begin
Write(Output,'D');
Maradek:=Maradek-500
end
else if Maradek>=400 then begin
Write(Output,'CD');
Maradek:=Maradek-400
end;
while Maradek>=100 do begin
Write(Output,'C');
Maradek:=Maradek-100
end;
if maradek>=90 then begin
Write(Output,'XC');
Maradek:=Maradek-90
end
else if Maradek>=50 then begin
Write(Output,'L');
Maradek:=Maradek-50
end
else if Maradek>=40 then begin
Write(Output,'XL');
Maradek:=Maradek-40
end;
while Maradek>=10 do begin
Write(Output,'X');
Maradek:=Maradek-10
end;
if Maradek=9 then begin
Write(Output,'IX');
Maradek:=Maradek-9
end
else if Maradek>=5 then begin
Write(Output,'V');
Maradek:=Maradek-5
end
else if Maradek=4 then begin
Write(Output,'IV');
Maradek:=Maradek-4
end;
while Maradek>=1 do begin
Write(Output,'I');
Maradek:=Maradek-1
end;
Writeln(Output);
Szam:=Szam*2
until Szam>=5000
end.
A program eredménye:
Ismételten felhívjuk a figyelmet arra, hogy az if utasítás egy-egy ága csak egyetlen utasítás végrehajtását vezérelheti. Ezért, ha egy feltételhez több utasítást kötünk, összetett utasítást kell használnunk.
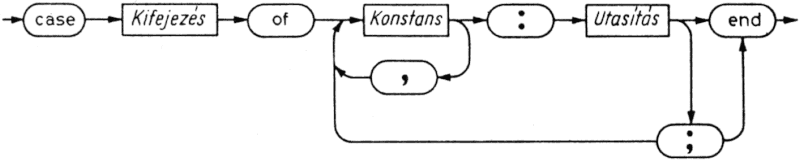
5.5.2. A case utasítás
A case utasítás egy szelektornak nevezett kifejezésből és egy utasításlistából áll. Mindegyik utasításhoz egy, a szelektorral azonos típusú konstans tartozik. A szelektor csak megszámlálható típusú lehet. A case utasítás a szelektor aktuális értékéhez tartozó utasítást jelöli ki végrehajtásra. Hibát jelent, ha az utasításlista egyik tagja előtt álló konstans sem egyezik meg a szelektor aktuális értékével. A kijelölt utasítás elvégzése után a vezérlés a case utasítás utánra kerül.
Az utasítás alakja az 5.14. ábrán látható.
5.14. ábra. Case utasítás szintaxisdiagramja
Példák:
(Tegyük fel, hogy var i: Integer; eh: Char;)
case i of
0: x:= 0;
1: x:= Sin(x);
2: x:= Cos(x);
3: x:= Exp(x);
4: x:= Ln(x)
endcase Ch of
'a', 'A', 'e', 'E', 'i',
'I', 'o', 'O', 'u', 'U':
AngolMagarlhangzo:= AngolMaganhangzo + 1;
'+', '-', '*', '/', '=', '>', '<',
'.', ',', '"', '?', '!', ':', ';', """:
irasjel: = irasjel + 1
end
Megjegyzések: A case utasításlista tagjai előtt álló konstansok nem címkék (l. a 4.2. és 5.7. szakaszt), goto utasítással rájuk ugrani nem lehet, sorrendjük tetszőleges.
Bár a case utasítás hatékonysága a megvalósítástól függ, általánosságban azt mondhatjuk, hogy akkor célszerű használni, ha több, egymást kölcsönösen kizáró utasításunk van, s mindegyiket ugyanolyan valószínűséggel választhatjuk ki.
5.6. A with utasítás
A with utasítást rekord (strukturált) típusú változókkal kapcsolatban alkalmazzuk, így a 8.3. szakaszban tárgyaljuk.
5.7. A goto utasítás
A goto olyan egyszerű utasítás, amely azt jelzi, hogy a további programvégrehajtást programszöveg valamely más pontján, mégpedig az adott címke helyén kell folytatni.
![]()
5.15. ábra. Goto utasítás szintaxisdiagramja
Minden címke
A címkének és a rá hivatkozó goto utasításnak az alábbi feltételek közül legalább egynek meg kell felelnie:
Példaként tekintsük a következő programrészletet:
label 1; {A blokk}
...
procedure B; {B blokk}
label 3, 5;
begin
goto 3;
3: Writeln('Jó napot!');
5: if P then begin S; goto 5 end; {while P do S}
goto 1;
{emiatt korán kilépünk B-ből}
Writeln('Viszonthallásra!')
end; {B blokk}
begin
B;
1: Writeln('Még beszélnénk!')
{Az A blokkban "goto 3'' nem megengedett}
end {A blokk}
Tilos kívülről egy strukturált utasítás belsejébe ugratni. Éppen ezért a következő példák hibásak.
Hibás példák:
for I:= 1 to 10 do
begin S1;
3: S2
end;
goto 3
if B then goto 3;
...
if B1 then 3; S
A goto utasítást csak olyan szokatlan, rendkívüli esetekben alkalmazzuk, amikor meg kell bontanunk egy algoritmus természetes felépítését. Hasznos szabály: kerüljük az ugrási utasítás alkalmazását, ha utasítások ismételt vagy feltételes végrehajtását akarjuk kifejezni! Az ilyen ugrások ugyanis nem engedik, hogy a program szövegszerkezete (statikus struktúrája) a számítás tényleges menetét, struktúráját tükrözze. A program szöveges és számítási (statikus és dinamikus) szerkezete közötti megfelelő kapcsolat hiánya pedig nagymértékben rontja a program áttekinthetőségét, és jelentősen megnehezíti a program helyességének ellenőrzését. Ha egy Pascal programban goto utasítások vannak, ez gyakran annak a jele, hogy a programozó még nem tanult meg eléggé "Pascalban gondolkodni". (Más programozási nyelvekben a goto-ra szükség van.)
6. Felsorolt és résztartomány típusok
Az előzőekben megismerkedtünk a Boolean, a Char, az Integer és a Real standard típusazonosítókkal, amelyekkel az általuk jelölt előredefiniált (standard) típusokra hivatkozhatunk. Most két olyan módszert mutatunk be, amellyel új megszámlálható típusokat hozhatunk létre. Az első eredményeként egy olyan új - ún. felsorolt (enumerated) - típust kapunk, amely egyetlen más típushoz sem kötődik, míg a második egy meglévő megszámlálható típus értékkészletének valamely részhalmazát definiálja önálló - ún. résztartomány (subrange) - típusként.
6.1. Felsorolt típusok
A felsorolt típusok definíciójában értékek valamely rendezett halmazát adjuk meg oly módon, hogy felsoroljuk az értékeket jelölő konstansazonosítókat.
Az elsőként felsorolt konstans sorszáma 0, a másodiké 1 stb.

6.1. ábra. Felsorolt típus szintaxisdiagramja
Példa:
type Szín=(Feher, Voros, Kek, Sarga, Lila, Zold, Narancs, Fekete);
Nem=(Ferfi, No);
Nap=(Hetfo, Kedd, Szerda, Csutortok, Pentek, Szombat, Vasarnap);
Operatorok=(Plusz, Minusz, Szor, Per);
Foldresz=(Afrika, Antarktisz, Ausztralia, Azsia, Europa, DelAmerika, EszakAmerika);
Hibás példa:
type Munkanap = (Hetfo, Kedd, Szerda, Csutortok, Pentek, Szombat);
Szabadnap = (Szombat, Vasárnap);
(mert Szombat típusa kétértelmű).
Az Olvasó már ismeri a logikai standard típust, amelynek definíciója:
type Boolean=(False, True);
Ez automatikusan definiálja a false és a true konstansazonosítót, ill. hogy false < true.
Az =, <>, <, <=, >=, > relációs operátorok minden felsorolt típusra alkalmazhatók, feltéve, hogy mindkét oldal azonos típusú. Az értékek rendezését felsorolásuk sorrendje határozza meg.
Megszámlálható (és így felsorolt) típusú argumentumon értelmezett standard függvények az alábbiak:
succ(X) az X utáni érték, pl. succ(Kek)=Sarga pred(X) az X előtti érték, pl. pred(X) pred(Kek)=Voros ord(X) X sorszáma, pl. ord(Kek)=2
Ha C és C1 Szin típusúak (l. fent), B logikai típusú és S1, ..., Sn tetszőleges utasítások, akkor van értelmük a következő utasításoknak:
for C:=Fekete downto Voros do S1;
while (C1<>C) and B do S1;
if C> Feher then C:= pred(C);
case C of
Voros, Kek, Sarga: S1;
Lila: S2;
Zold, Narancs: S3;
Feher, Fekete: S4
end;
A 6.1. program felsorolt típusú adatokon végzett műveletekre mutat néhány példát.
program TegnapMaHolnap(Output);
{Turbo Pascal}
{ A felsorolt tipus szemleltetese }
type HetNapjai= (H,K,Sze,Cs,P,Szo,V);
Mikor= (Mult,Jelen,Jovo);
var Nap:Hetnapjai;
Tegnap,Ma,Holnap: HetNapjai;
Ido:Mikor;
begin
Ma:=V {A Pascalban felsorolt tipusu ertekeket nem
lehet az Inputrol olvasni };
Ido:= Jelen;
repeat
if Ido=Jelen then begin {Milyen nap volt tegnap?};
Ido:=Mult;
if Ma=H then Tegnap:=V else Tegnap:=Pred(Ma);
Nap:=Tegnap
end
else if Ido= Mult then begin {Milyen nap lesz holnap?}
Ido:= Jovo;
If ma= V then Holnap:=H else Holnap:=Succ(Ma);
Nap:= Holnap
end
else begin {Ido= Jovo; visszaallitas jelenre}
Ido:=Jelen;
Nap:=Ma
end;
case Nap of
H: Write(Output,'Hetfo');
K: Write(Output,'Kedd');
Sze: Write(Output,'Szerda');
Cs: Write(Output,'Csutortok');
P: Write(Output,'Pentek');
Szo: Write(Output,'Szombat');
V: Write(Output,'Vasarnap')
end;
Writeln(Output,Ord(Ido)-1:3)
until Ido= Jelen
end.
6.2. Résztartomány típusok
Egy típust definiálhatunk úgy is, hogy valamely, már előzőleg definiált megszámlálható típus egy részhalmazát, résztartományát adjuk meg. Az eredeti típust a résztartomány típus alaptípusának (host type) nevezzük. A résztartományt egyszerűen a tartomány legkisebb és legnagyobb konstansának megadásával definiáljuk. Az alsó határ a felsőnél nagyobb nem lehet A valós típusból résztartomány nem képezhető, mivel a Real nem megszámlálható típus.
![]()
6.2. ábra. Résztartomány típus szintaxisdiagramja
Az alaptípus szabja meg, hogy a résztartomány típusok értékein milyen műveletek értelmezhetők. Mint mondtuk, a megszámlálható típusok értékadás-kompatibilitásának feltétele, hogy a változó és a kifejezés ugyanahhoz a megszámlálható típushoz, ill. annak egy-egy résztartományához tartozzon, és a kifejezés értéke a változó típusa által meghatározott zárt intervallumba essen. Induljunk ki pl. az alábbi deklarációból:
var A:1..10; B:0..30; C:20..30;
Itt A, B és C skalár alaptípusa az egész típus, így az
A:=B; C:=B; B:=C;
értékadások mind helyes utasítások, bár végrehajtásuk esetleg lehetetlen. Ezért mindenütt, ahol könyvünkben megszámlálható típusokról szólunk, állításaink ezek résztartományaira is vonatkoznak, bár ezt nem mindig hangsúlyozzuk.
Példa:
type Napok=(Hetfo, Kedd, Szerda, Csutortok, Pentek, Szombat, Vasarnap)
{felsorolt tipus} ;
Munkanapok = Hetfo..Pentek {napok resztartomanya };
Index = 0..63 {az egesz tipus resztartomanya};
Betu = A..Z {a karakter tipus resztartomanya};
TermeszetesSzamok = 0..MaxInt;
PozitivSzamok = 1..MaxInt;
A résztartomány típusok a feladatra orientált problémamegfogalmazás eszközei. A gépi megvalósítást végző szakember szempontjából alkalmazásuk tármegtakarítást tesz lehetővé, és módot ad az értékadások futásidőben történő ellenőrzésére (l. pl. a 7.1. programot). Egy 0..200 típusúnak deklarált változó pl. sok rendszerben lehet, hogy csak egy byte-ot (8 bitet) foglal el, egy Integer változó viszont több byte-ot köthet le.
7. Strukturált típusok - tömbök
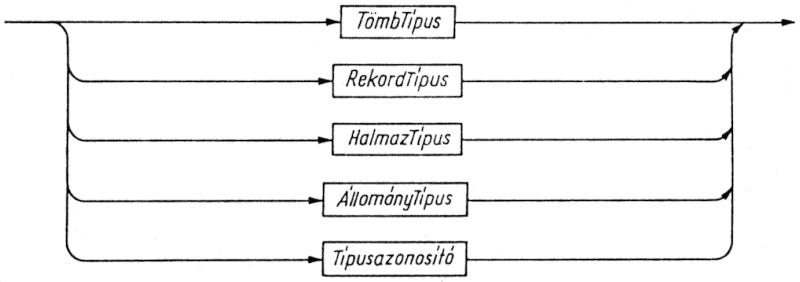
Az egyszerű (megszámlálható és valós) típusok strukturálatlan típusok. A Pascal rajta kívül strukturált és mutató típusokat különböztet meg. Ahogyan a strukturált utasítások is más utasításokból felépülő egységek, a strukturált típusok is más típusokból felépülő konstrukciók. A strukturált típust az elemek (összetevők) típusa(i) és legfőképpen a strukturálás módja jellemzik.
Strukturált adattípusok:
7.1. ábra. Strukturált típus szintaxisdiagramja
Bármelyik strukturálási módot választjuk, mindig lehetőségünk van a számunkra legkedvezőbb belső adatábrázolás előírására. A típusdefiníció elé a packed (tömörített) szimbólumot írva utasíthatjuk a fordítóprogramot, hogy takarékosan gazdálkodjon a tárkapacitással, még akkor is, ha ez az elvégzendő kifejtési és tömörítési műveletek miatt esetleg a futási idő és a kód hosszabbodását vonja maga után. A felhasználó dolga, hogy él-e ezzel a lehetőséggel, enged-e a hatékonyságból a helyigény csökkentése kedvéért. (A hatékonyságra és a tárigényre gyakorolt hatások tényleges alakulása a gépi megvalósítástól függ, és az is lehet, hogy az eredő hatás végül is zérus.)
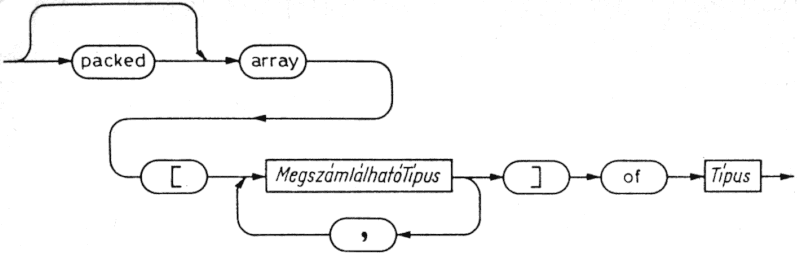
7.1. A tömb (array) típus
A tömb rögzített számú elemből áll (ezt a tömb létrehozásakor definiáljuk). Az elemek mind azonos típushoz, az ún. elemtípushoz tartoznak. Az egyes elemekre a tömbváltozó nevével és az azt követő, szögletes zárójelben álló ún. indexszel hivatkozhatunk. így az elemek explicit módon jelölhetők, és közvetlenül hozzáférhetők. Az index maga is lehet számítási eredmény, típusa az ún. indextípus. Mivel az egyes elemek elérési ideje nem függ a szelektor (index) értékétől, a tömböt közvetlen elérésű struktúrának nevezzük.
A tömb definíciójában mind az elemtípust, mind az indextípust meg kell adni. A definíció alakja:
type A = array [T1] of T2;
ahol A egy új típusazonosító, T1 az indextípus, amely csak megszámlálható típus lehet. T2 pedig tetszőleges típus.
A tömbstruktúra segítségével egy névvel több, azonos jellemzőkkel rendelkező változót foghatunk össze. A tömbváltozó deklarációja a teljes struktúrának nevet ad. A teljes tömbváltozókra két művelet megengedett: az értékadás és az elemkijelölés. Az utóbbi úgy történik, hogy a tömbváltozó neve után szögletes zárójelben egy megszámlálható kifejezéssel megadjuk a kívánt elem indexét. Az így kijelölt elemváltozóra mindazok a műveletek megengedettek, amelyek az adott tömb típus elemének a típusához tartozó változókra általában értelmezettek.
7.2. ábra. Elem típus szintaxisdiagramja
Példák változódeklarációra:
Tar: array[0..Max] of Integer
Beteg: packed array [Napok] of Boolean
Példák értékadásra:
Tar[I+J]:= X
BetegfHetfo]:= true
(A példák természetesen feltételezik, hogy a bennük használt segédazonosítókat korábban már definiáltunk.)
A 7.1. és a 7.2. program a tömbök alkalmazását szemlélteti. Az Olvasó gondolja meg, hogyan kellene kibővíteni a 7.2. programot - tömb alkalmazásával és a nélkül -, ha egynél több függvényt akarnánk ábrázolni!
program MinMax(Input,Output);
{Turbo Pascal}
{ Adott lista legnagyobb es legkisebb elemenek kivalasztasa }
const MaxMeret=16;
type ListaMeret=1..MaxMeret;
var Elem: ListaMeret;
Min,Max,Elso,Masodik: Integer;
A:array[Listameret] of Integer;
begin
for Elem:=1 to MaxMeret do begin
Write(Output,Elem,'. elem: ');Readln(Input,A[Elem])
end;
Min:=A[1]; Max:=Min; Elem:=2;
while Elem<MaxMeret do begin
Elso:=A[Elem];
Masodik:=A[Elem+1];
if Elso>Masodik then begin
if Elso>Max then Max:=Elso;
if Masodik<Min then Min:=Masodik
end
else begin
if Masodik>Max then Max:=Masodik;
if Elso<Min then Min:=Elso
end;
Elem:=Elem+2
end;
if Elem=MaxMeret then
if A[MaxMeret]>Max then Max:=A[MaxMeret]
else if A[MaxMeret]<Min then Min:=A[MaxMeret];
Writeln(Output,Max,Min:6)
end.
7.2. program:
program Rajzolo2(Output);
{Turbo Pascal}
{ Az f(x)=exp(-x)*sin(2*Pi**x) fuggveny abrazolasa }
{ az X-tengely felrajzolasaval }
const XLeptek= 16 {az 1 abszcisszaegysegre juto sorelemek szama};
YLeptek= 32 {az 1 ordinataegysegre juto karakterpoz. szama};
ZerusY= 34 {az x-tengely helye};
XHatar= 32 {A grafikon sorokban kifejezett hossza};
YHatar= 68 {A grafikon karakterpoziciokban kifejezett szelessege};
type Tartomany=1..YHatar;
var Delta: real {lepeskoz az abszcisszan};
KetPi: real {2*Pi = 8*ArcTan(1.0)};
X,Y: real;
Pont: integer;
Hely, YPozicio, Futashatar: Tartomany;
Ykar: array[Tartomany] of Char;
begin
Delta:=1/XLeptek;
KetPi:=8*ArcTan(1.0);
for Hely:=1 to YHatar do
Ykar[Hely]:=' ';
for Pont:=0 to XHatar do begin
X:=Delta*Pont; Y:=Exp(-X)*Sin(KetPi*X);
YKar[ZerusY]:=':';
YPozicio:= Round(YLeptek*Y)+ZerusY;
YKar[YPozicio]:='*';
if YPozicio<ZerusY then Futashatar:=ZerusY
else Futashatar:=YPozicio;
for Hely:=1 to Futashatar do
Write(Output,YKar[Hely]);
Writeln(Output); YKar[YPozicio]:= ' '
end
end.
Mivel T2 tetszőleges típus lehet, a tömbök elemei strukturáltak is lehetnek. Abban a speciális esetben, amikor T2 is tömb, az eredeti A tömböt többdimenziósnak mondjuk. Egy M többdimenziós tömb deklarációját tehát a következőképpen írhatjuk fel:
var M: array[A..B] of array[C..D] of T;
és ekkor M[l] [J] M l-edik elemének (T típusú) J-edik komponensét jelöli.
Többdimenziós tömböknél az alábbi kényelmes, rövidebb írásmódot szokás alkalmazni:
var M: array [A..B, C..D] of T;
ill.
M[I,J]
M-et mátrixnak is tekinthetjük, és azt mondhatjuk, hogy M[I,J] az M mátrix l-edik elemének J-edik komponense, vagyis az M mátrix l-edik sorának a J-edik oszlopba tartozó eleme.
Mindez nem korlátozódik csupán két dimenzióra, mert T megint lehet strukturált típusú. A típus (rövid) alakja általában:
7.3. ábra. Tömb típus szintaxisdiagramja
Ha n számú indextípust adunk meg, a tömböt n-dimenziósnak mondjuk, a tömb egy elemét pedig n darab indexkifejezéssel jelöljük ki.
Ha A és B két azonos típusú tömbváltozó, akkor - feltéve, hogy az egyik tömb elemei rendre felvehetik a másik elemeinek értékét, azaz:
A[i]:= B[i]
minden, az indextípushoz tartozó i-re végrehajtható az elemenkénti értékadás helyett a következő, rövidebb alakot használhatjuk:
A:= B
7.3. példaprogram:
program MatrixSzorzas(Input,Output);
{Turbo Pascal}
{ Matrixszorzas }
const m=4; p=3; n=2;
var i: 1..m;
j: 1..n;
k: 1..p;
Osszeg: Integer;
A: array[1..M,1..P] of Integer;
B: array[1..P,1..N] of Integer;
C: array[1..M,1..N] of Integer;
begin
for I:=1 to M do begin {A es B elemeinek feltoltese }
for K:=1 to P do begin
Write(Output,'A[',I,',',K,']=');Readln(Input,A[I,K])
end;
Writeln(Output);
end;
Writeln(Output);
for K:=1 to P do begin
for J:=1 to N do begin
Write(Output,'B[',K,',',J,']=');Readln(Input,B[K,J])
end;
Writeln(Output);
end;
Writeln(Output);
{Az A es B matrix szorzatat tartalmazo C matrix eloallitasa}
for I:=1 to M do begin
for J:=1 to N do begin
Osszeg:=0;
for K:=1 to P do
Osszeg:=Osszeg+A[I,K]*B[K,J];
C[I,J]:=Osszeg;
Write(Output,Osszeg:5)
end;
Writeln(Output)
end;
Writeln(Output)
end.
Figyeljük meg, hogy az előbbi programban az A, B és C tömb indextípusa rögzített volt. Hogy általánosított, programkönyvtárba tehető mátrixszorzó alprogramot írhassunk, szükségünk van egy olyan eszközre, amellyel az index típusokat megfelelően beállíthatjuk. A Pascalban erre a célra az illeszkedőtömb- paraméterek szolgálnak (l. a 12.1.2. pontot); használatukat a 12.4 szakasz (Mátrixszorzás2) szemlélteti.
7.2. Füzér típusok
A füzért korábban mint aposztrófok közé tett jelsorozatot definiáltuk (l. a 2.5. szakaszt). Az egy jelből álló füzér a standard karaktertípushoz (l. a 3.4. szakaszt), az N (N>1) jelei tartalmazó füzér pedig a
packed array[1..N] of Char
definícióval megadott típushoz tartozó konstans. Az ilyen típust füzér típusnak nevezzük.
Ha az A tömbváltozó és az E kifejezés azonos elemszámú füzér típushoz tartozik, megengedett az
A:= E
értékadás. Ugyanígy, két azonos elemszámú füzért a relációs operátorokkal (=, <>, <, >, <= és >=) összehasonlíthatunk; a rendezésnél az első elem (A[1]) számít a legértékesebbnek, s a sorrendet a standard Char típus értéksorrendje szabja meg.
7.3. Tömörítés (pack) és kifejtés (unpack)
A tömörített tömbök egyes elemeihez gyakran nehéz hozzáférni. Így a feladattól, ill. az adott nyelvi megvalósítástól függően kívánatos lehet, hogy a programozó a tömb elemeinek tömörítését, ill. kifejtését egyetlen művelettel végezze. Ez a Pack (tömörítés) és az Unpack (kifejtés) standard eljárások segítségével valósítható meg. Legyen U egy
array[A..D] of T {T állomány típust nem tartalmazhat};
típusú tömörítetlen, P pedig egy
packed array [B..C] of T
típusú tömörített tömbváltozó, ahol
Ord(D)-Ord(A) >= Ord(C)-Ord(B)
Ekkor
Pack (U, I, P)
U-nak az l-edik elemtől kezdődő részét P-be tömöríti, míg
Unpack (P, U, I)
U-nak az I-edik elemtől kezdődő részébe fejti ki P-t.
8. Rekord (record) típusok
A rekord talán a legrugalmasabb szerkezet. A rekord típus gyűjtőfogalom, ugyanis a rekord olyan szerkezet, amelyben teljesen eltérő tulajdonságú részek fordulhatnak elő. Tegyük fel, hogy pl. egy személy adatait szeretnénk nyilvántartani. Ismert a név, a magasság, a nem, a születési idő, az eltartottak száma és a családi állapot. Ezenkívül ha az illető nős, férjezett vagy özvegy, adott az (utolsó) házasságkötés időpontja; ha elvált, tudjuk a (legutóbbi) válás dátumát, és hogy ez az első válása vagy sem; ha pedig nőtlen vagy hajadon, nincs szükségünk több adatra. Mindezt az információt egyetlen rekordba foglalhatjuk, amelyben minden adatelemhez külön-külön hozzáférhetünk.
8.1. Rögzített rekordok
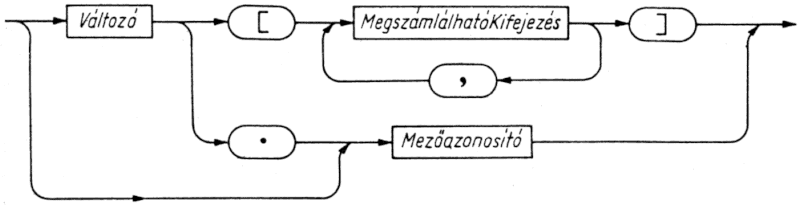
Pontosabban fogalmazva a rekord rögzített számú, mezőnek nevezett elemből felépülő adatszerkezet. A tömbtől eltérően az elemeknek nem kell azonos típusúaknak lenniük, és kifejezéssel nem indexelhetők. A rekord típus definíciója megadja az egyes elemek típusát, és minden elemhez egy ún. mezőazonosítót rendel. Teljes rekordváltozókra a Pascal két műveletet enged meg: az értékadást és az elemkiválasztást. A mezőazonosító hatásköre az a legbelső rekord, amelyben definiáltuk.
Azért, hogy a kiválasztott elem típusa közvetlenül a programszöveg alapján, a program végrehajtása nélkül is leolvasható legyen, a rekordszelektorban nem valamilyen számított index érték, hanem rögzített mezőazonosító áll.
Egyszerű példaként tegyük fel, hogy a +bi alakú komplex számokkal akarunk számításokat végezni, ahol a és b valós szám, i pedig -1 négyzetgyöke. "Komplex" nevű standard típusunk nincs. A programozó azonban könnyen definiálhat a komplex számok ábrázolására alkalmas rekordot. Ebben a rekordban két, Real típusú mezőnek kell lennie, amelyek a valós, ill. a képzetes részt írják le. Ezt az alábbi szintaxisok segítségével fejezhetjük ki:

8.1. ábra. Rekord típus szintaxisdiagramja
8.2. ábra. Mezőlista szintaxisdiagramja

8.3. ábra. Fix rész szintaxisdiagramja

8.4. ábra. Rekordszakasz szintaxisdiagramja
A fenti szabályok alkalmazásával a következő definícióra és deklarációra juthatunk:
type Komplex = record Re, lm: Real end;
var Z: Komplex;
ahol Komplex a típusazonosító, Re és lm mezőazonosítók, Z pedig egy Komplex típusú változó, azaz egy kételemű, két mezőből álló rekord (l. a 8.1. programot).
program KomplexAritmetika(Output);
{Turbo Pascal}
{ Muveletek komplex szamokkal }
const Novekmeny=4;
type Komplex= record Re, Im: Real end;
var X,Y: Komplex;
Par: Integer;
begin
X.Re:=2;X.im:=5; {X kezdoerteke}
Y:=X; {Y kezdoerteke}
for Par:=1 to 5 do begin
Writeln(Output,'X= ', X.Re:5:1, X.Im:6:1,'i');
Writeln(Output,'Y= ', Y.Re:5:1, Y.Im:6:1,'i');
{X+Y}
Writeln(Output,'Osszeg= ',
X.Re+Y.Re:5:1, X.Im+Y.Im:6:1,'i');
{X*Y}
Writeln(Output,'Szorzat= ',
X.Re*Y.Re-X.Im*Y.im:5:1, X.Re*Y.Im+X.Im*Y.Re:6:1,'i');
Writeln(Output);
X.Re:=X.Re+Novekmeny;
X.Im:=X.Im-Novekmeny
end
end.
A program eredménye:
A rekord valamely elemére (mezőjére) úgy hivatkozhatunk, hogy leírjuk a rekord nevét, majd egy pont után a mező azonosítóját. A következő két programsor pl. Z-nek 5 + 3i értéket ad:
Z.Re:= 5;
Z.lm:= 3
Ugyanígy definiálhatunk egy dátumot leíró változót is:
Datum = packed record Ev: 1900...2100;
Hó: (Jan, Feb, Marc, Apr, Maj, Jun, Jul, Aug, Szept, Okt, Nov, Dec);
Nap: 1..31
end;
Megjegyzés: A Dátum típus megengedi pl. az április 31-et is!
Egy játék megadása:
Jatek = record Milyen: (Labda, Bugocsiga, Hajo, Baba, Kocka, Tarsas, Modell, Konyv);
Ar: Real;
Kaptam: Datum;
Szeretem: (Nagyon, Elegge, Kicsit, Nem);
Eltort, Elveszett: Boolean
end;
Egy házi feladat jellemzőinek leírása:
Hf= record Tantargy: Tori, Nyelv, Irodalom, Matek, Fiz, Kem);
Kiirva: Datum;
Osztalyzat: 1..5;
Nehezség: 1..10
end;
Ha a rekord maga is egy másik szerkezetbe van ágyazva, a rekordváltozó neve tükrözi ezt a szerkezetet. Tegyük fel, hogy azt szeretnénk nyilvántartani, hogy a család egyes tagjai mikor kaptak utoljára himlőoltást. Az egyik lehetőség, hogy a családtagokat felsorolt típusként, az oltási időpontokat pedig rekordokból álló tömbként definiáljuk:
type Csaladtag = (Apa, Anya, Gyerek1, Gyerek2, Gyerek3);
var OltasDatuma: array [Csaladtag] of Datum;
A legújabb adatokat ekkor az alábbi alakban vehetjük nyilvántartásba:
OltasDatuma[Gyerek3].Ev:= 1986
OltasDatuma[Gyerek3].Ho:= Apr;
OltasDatuma[Gyerek3].Nap:= 23
8.2. Változó rekordok
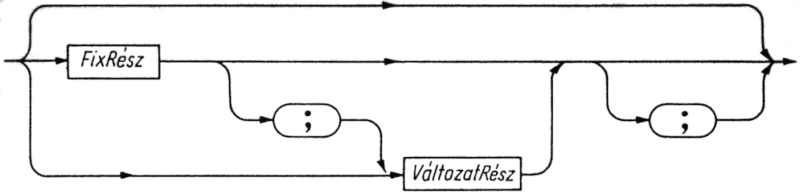
Előfordulhat, hogy olyan információt szeretnénk felvenni egy rekordszerkezetbe, amely más, már a rekordban levő információtól függ. Ilyenkor változórekord-típust adhatunk meg, amelybe bizonyos mezők csak akkor kerülnek be, ha egy másik mező értéke ezt előírja.
A rekord típus szintaxisa lehetőséget biztosít változat rész képzésére is, azaz amint az elnevezés is mutatja, egy rekord típus több változatot is tartalmazhat. Ez azt jelenti, hogy különböző, jóllehet azonos típusúnak mondott változók bizonyos szempontból eltérő szerkezetűek lehetnek. Eltérő lehet az elemek száma és típusa.
Az egyes változatokat egy-egy lista jellemzi, amely a változathoz tartozó elemek deklarációját tartalmazza. A listát zárójelek határolják. Minden ilyen deklarációlista előtt egy vagy több konstans áll, az egész listasort pedig egyetlen case utasítás fogja össze, amely megadja a konstansok típusát (vagyis azt a típust, amely szerint a változatokat különválasztottuk).

8.5. ábra. Változat rész szintaxisdiagramja

8.6. ábra. Változat szintaxisdiagramja
Példaként tegyük fel, hogy létezik egy:
type CsaladiAllapot= (Nos, Ozvegy, Elvalt, NotlenVagyHajadon);
Ekkor egy személy adatait a következő módon írhatjuk le:
type Szemely= record
{az összes személynél közös mezők};
case CsaladiAllapot of
NosVagyFerjezett: ({a kizárólag házas személyekre vonatkozó mezők})
NotlenVagyHajadon: ({a kizárólagos egyedülálló személyekre vonatkozó mezők});
end;
Fontos, hogy a változatok megkülönböztetésére használt ún. kijelölő típus valamennyi lehetséges értéke előforduljon valamelyik változat előtt. Fenti példánk tehát csak akkor helyes ha a változatfelsorolásban a NosVagyFerjezett és a NotlenVagyHajadon után az Ozvegy és az Elvalt konstans is megjelenik.
Többnyire maga a rekordelem (mező) jelöli ki, hogy éppen melyik változata "hatályos". A fent definiált személyi rekordban pl. valószínűleg szerepel egy
CsA: CsaladiAllapot
közös mező. Ebben a gyakran előforduló esetben lerövidíthetjük a programot, ha a kijelölési végző elem, az ún. kijelölő mező deklarációját magába a case utasításba írjuk, az alábbi példa szerint:
case CsA: CsaladiAllapot of
Mielőtt a személyi adatokat megpróbálnánk változórekord-szerkezetben megadni, célszerű külön összefoglalni a szükséges információkat.
I. Személy
(A) név (vezetéknév, keresztnév);
(B) magasság (természetes szám);
(C) nem (férfi, nő);
(D) születési idő (év, hó, nap);
(E) eltartottak száma (természetes szám);
(F) családi állapot:
ha nős, férjezett vagy özvegy:
(a) a házasságkötés dátuma (év, hó, nap)
ha elvált:
(a) válás dátuma (év, hó, nap),
(b) első válás, (false, true)
ha nőtlen vagy hajadon.
A 8.7. ábra illusztrációképpen két, különböző adatokkal rendelkező személy "nyilvántartási lapját" mutatja.
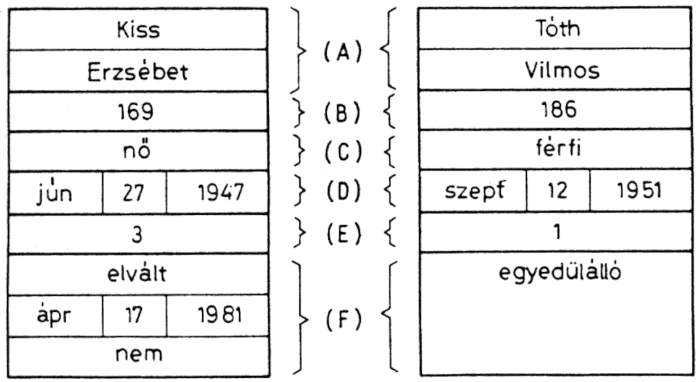
8.7. ábra. Két "nyilvántartási lap" minta
A Személy rekord ezek alapján a következőképpen írható fel:
type Fuzer15= packed array[1..15] of Char;
CsaladiAllapot= (NosVagyFerjezett, Ozvegy, Elvalt, NotlenVagyHajadon);
Datum= packed record
Ev: 1900..2100;
Ho: (Jan, Feb, Marc, Apr, Maj, Jun, Jul, Aug, Szep, Okt, Nov, Dec);
Nap: 1..31;
end;
TermeszetesSzam= 0..MaxInt;
Szemely= record
Nev: record Vezeteknev, Utonev: Stringl5 end;
Magassag: TermeszetesSzam {cm};
Nem: (Ferfi, No);
SzuletesiIdo: Datum;
EltartottakSzama: TermeszetesSzam case CsA: CsaladiAllapot of
NosVagyFerjezett, Ozvegy: (HazassagkotesDatuma: Datum);
Elvalt: (ValasDatuma: Datum; ElsoValas: Boolean);
NotlenVagyHajadon: ()
end {Szemely};
Megjegyzések:
A rekord valamely elemére való hivatkozás lényegében a rekord vázának lineáris rekonstrukciója. Példaként vegyünk egy Személy típusú P változót, és állítsuk elő a 8.7. ábrán második személyének adatait:
P.Nev.Vezetek:= 'Macska';
P.Nev Kereszt:= 'Marton';
P.Magassag:= 186;
P.Nem:= ferfi;
P.Szuletett.Ev:= 1951;
P.Szuletett.Ho:= Szept;
P.Szuletett.Nap:= 12;
P.Eltartottak:= 1;
P.CsA:= NotlenVagyHajadon;
8.3. A with utasítás
A fenti írásmód kissé terjengős lehet, de a felhasználó ugyanezt rövidebben is megfogalmazhatja, mégpedig a with utasítás segítségével. A with utasítás felnyitja az adott rekordváltozó mezőazonosítóit tartalmazó hatáskört, s ily módon a mezőazonosítók változóazonosítókként szerepelhetnek. Ezáltal lehetőséget biztosít a fordítóprogramnak, hogy optimalizálja a with utasításban kijelölt utasítást.
A with utasítás általános alakja a 8.8. ábrán látható.

8.8. ábra. With utasítás szintaxisdiagramja
A with utasítás do utáni utasításában a rekordváltozó kívánt mezőjére egyszerűen a mezőazonosítóval hivatkozunk. Nem tesszük ki tehát a mezőazonosító elé az egész rekord nevét.
Az alábbi with utasítás egyenértékű az előbbi értékadásokkal:
with P do begin
with Nev do begin
Utonev:= 'Marton';
Vezeteknev:= 'Macska'
end;
Magassag:= 186;
Nem:= Ferfi;
with SzuletesIdo do begin
Ev:= 1951; Ho:= Szep; Nap:= 12 end;
EltartottakSzama:= 1;
CsA:= NotlenVagyHajadon;
end
Hasonlóképpen, a
var MaiDatum: Datum;
...
with MaiDatum do
if Ho=Dec then begin
Ho:= Jan; Év:= Ev+1
end
else Ho:= Succ(Ho)
programrészlet egyenértékű a következővel:
var MaiDatum: Datum;
...
if MaiDatum.Ho=Dec then begin
MaiDatum.Ho:= Jan;
MaiDatum.Ev:= MaiDatum.Ev+1
end
else MaiDatum.Ho := Succ(MaiDatum.Ho)
Az alábbi programrészlet pedig a korábbi példánkban látott himlőoltás-nyilvántartást végzi:
with OltasDatuma[Gyerek3] do begin
Ev:= 1986; Ho:= Apr; Nap:= 23 end
A with utasítás végrehajtásakor a do utáni utasítás végrehajtása előtt "ráállunk" a kívánt rekordváltozóra. Ha tehát a belső utasításban a rekord változólista valamelyik elemére vonatkozó értékadás áll, az nem változtatja meg a rekordváltozót.
Például:
var Kicsoda: Csaladtag;
...
Kicsoda:= Apa;
with OltasDatuma[Kicsoda] do begin
Kicsoda:= Anya;
Ev:= 1947; Ho:= Jul; Nap:= 7;
end
Itt a with utasítás OltasDatuma[Apa] mezőit állítja be.
Az egymásba ágyazott with utasításokat rövidebben is felírhatjuk. A
with R1, R2, ... , RN do S
alak a
with R1 do
with R2 do
...
with RN do S
utasításnak felel meg.
A P személy adatait megadó előbbi példánkat tehát a következőképpen írhatnánk át:
with P, Nev, SzuletesiIdo do begin
Vezeteknev:= 'Macska';
Utonev:= 'Marton';
Magassag:= 186;
Nem:= ferfi;
Ev:= 1951;
Ho:= Szep;
Nap:= 12;
EltartottakSzama:= 1;
CsA:= NotlenVagyHajadon;
end {with}
Nézzünk most egy példát a mezőazonosítók hatáskörére! Míg
var A: array[2..8] of Integer;
A: 2..8;
hibás, mivel A definíciója nem egyértelmű, a
var A: Integer;
B: Record A: real; B: Boolean end;
szöveg helyes, minthogy az egész A és a valós B.A könnyen megkülönböztethető. Ugyanígy a B rekordváltozó is megkülönböztethető a Boolean B.B-től. A
with B do S
utasításban szereplő S utasításban az A, ill. B azonosító a B.A, ill. a B.B elemet jelöli, az A égész változó nem hozzáférhető.
9. Halmaz (set) típusok
A halmaz (set) típus alkalmazásával tömör alakban dolgozhatunk az egyazon megszámlálható típushoz tartozó értékek együttesével. Pontosabban a halmaz típus alaptípusa hatványhalmazát definiálja. Ez az alaptípusbeli értékek összes részhalmazának halmaza (amely az üres halmazt is tartalmazza). A halmaz is közvetlen elérésű struktúra. Jellemzője, hogy elemei mind ugyanazon - megszámlálható - típushoz tartoznak.
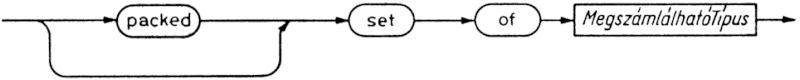
9.1. ábra. Halmaz típus szintaxisdiagramja
Teljes halmazértékekre a következő műveletek megengedettek: az értékadás, az ismert halmazműveletek (pl. egyesítés = unió), az egyenlőség- és részhalmazvizsgálat, valamint az elem- (tartalmazás-) vizsgálat (l. később). A halmazokat elemeikből a halmazgenerálásnak nevezett művelettel hozhatjuk létre.
A Pascal gépi megvalósításai általában korlátozzák a halmazok méretét. Ez a korlát egész kicsiny is lehet (pl. az egy számítógépi szóban levő bitek száma), és közvetlenül behatárolja a halmaz alaptípusok elemszámát.
9.1. Halmazgenerátorok
A halmazokat elemeikből halmazgenerátorok segítségével állíthatjuk elő. A halmazgenerátor a halmazelemek felsorolásából áll. A listát szögletes zárójelek közé írjuk, az egyes elemeket vesszővel választjuk el. Az elemeket megadhatjuk kifejezés formájában - ekkor az elem nem más, mint a kifejezés értéke, de írhatunk a szögletes zárójelek közé AlsóHatár..FelsőHatár alakú tartományt is: ekkor az AlsóHatár, ill. a FelsőHatár kifejezés értéke rögzíti a halmaz értékkészletét. Ha AlsóHatár > FelsőHatár, a halmaznak egy eleme sincs.
A kifejezéseknek egyazon megszámlálható típushoz, a halmazgenerátor típus alaptípusához kell tartozniuk. A [ ] halmazgenerátor minden halmaztípus esetén az üres halmazt jelöli. A halmazgenerátorok nem hordoznak teljes típusinformációt [10], nem mondják meg például, hogy a halmaz tömörített-e vagy sem. Hogy a halmazkifejezésekben a más halmazokkal való kompatibilitást biztosítsuk, a halmazgenerátor típusát egyidejűleg tömörítettnek és kifejtettnek tekintjük.
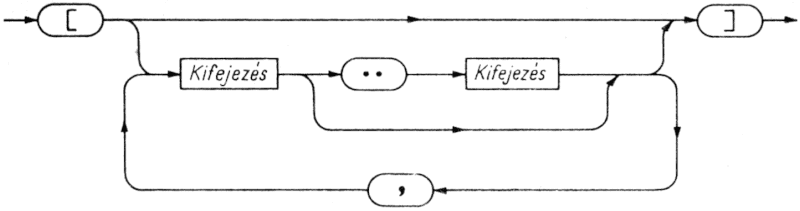
9.2. ábra. Halmazgenerátor szintaxisdiagramja
Példák:
[13]
[i+i, i-j]
['0'..'9']
['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j', 'k', 'l', m, 'n', 'o', 'p', 'q', 'r', 's', 't', 'u', v, 'w', 'x', 'y', 'z']
9.2. Halmazműveletek
Ha X halmazváltozó és E halmazkifejezés, megengedett az
X:= E
értékadás, feltéve, hogy E minden tagja X alaptípusához tartozik, és X, ill. E vagy egyaránt tömörített, vagy egyik sem az. A következő operátorok tetszőleges halmazstruktúrájú operandusra alkalmazhatók. Legyen A és B két azonos típusú halmazkifejezés. Ekkor:
A+B az A-hoz és B-hez tartozó elemek halmaza (a két halmaz egyesítése, uniója); A*B A és B közös elemeinek halmaza (a két halmaz metszete); A-B A azon elemeinek halmaza, amelyek nem tartoznak egyidejűleg B-hez (a két halmaz különbsége).
Halmazoperandusokra öt relációs operátor alkalmazható. Legyen A és B azonos típusú halmazkifejezés, e pedig az alaptípushoz tartozó, megszámlálható típusú kifejezés. Ekkor:
| e in A | elem- (tartalmazás-) vizsgálat. Eredménye True, ha e eleme A-nak, egyébként False. |
| A=B | egyenlőségvizsgálat. |
| A<>B | egyenlőtlenség-vizsgálat. |
| A<=B | részhalmazvizsgálat. Eredménye True, ha A valódi vagy nem valódi részhalmaza B-nek. |
| A>=B | részhalmazvizsgálat. Eredménye True, ha B valódi vagy nem valódi részhalmaza A-nak. |
Példák deklarációra:
type Alapszin = (Voros, Sarga, Kek);
Szin = set of Alapszin;
var Arnyalat1, Arnyalat2: Szin;
Maganhangzok, Massalhangzok, Hangok: set of Char;
Muveletikod: set of 0..7;
osszeadas: Boolean;
K: Char;
Példák értékadásra:
Arnyalat1:= [Voros]; Arnyalat2:= [];
Arnyalat2:= Arnyalat2 + [Succ(Voros)]
Hangok:= ['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', j', 'k', 'l', 'm', 'n', 'o', 'p', 'q', 'r', 's', t', 'u', 'y', 'w', 'x', 'y', 'z'];
Magánhangzók:= ['A', 'E', 'I', 'O', 'U'];
Massalhangzok:= Hangok-Maganhangzok;
Osszeadas:= [2,3]<=Muveleti kod
A halmazműveletek viszonylag gyorsak, s más bonyolultabb vizsgálatok helyett jól alkalmazhatók. Az
if (Ch='A') or (Ch='E') or (Ch='l') or (Ch='O') or (Ch='U') then S
feltételvizsgálatot pl. az alábbi formára egyszerűsíthetjük:
if Ch in ['A' , 'E' , 'I' , 'O' , 'U'] then S
9.1. példaprogram:
program EgeszAtalakitas(Input,Output);
{Turbo Pascal}
{ Szamjegysor beolvasasa es az altaluk kifejezett egesz szamma
alakitasa. Elojel nelkuli szamokat tetelezunk fel. }
var K: Char;
Szamjegyek: set of '0'..'9';
Szam: Integer;
begin
Szamjegyek:=['0'..'9']; { halmaz inicializalasa }
Read(Input,K);
Szam:=0;
while K in Szamjegyek do begin
Szam:= Szam*10+Ord(K)-Ord('0');
Writeln(Output,Szam);
Read(Input,K)
end
{ K az egesz szam utani karaktert tartalmazza }
end.
9.2. példaprogram:
program HalmazMuveletek(Output);
{Turbo Pascal}
{ A halmazmuveletek bemutatasa }
type HetNapjai= (H,K,Sze,Cs,P,Szo,V);
Het= set of HetNapjai;
var EgeszHet,Munka,Szabad: Het;
Nap: HetNapjai;
procedure Vizsgalat(X: Het);
var N:HetNapjai;
begin
for N:=H to V do
if N in X then Write(Output,'X')
else Write(Output,'O');
Writeln(Output)
end {vizsgalat};
begin
Munka:=[]; Szabad:=[]; Egeszhet:=[H..V];
Nap:= Szo;
Szabad:=[Nap]+Szabad+[V];
Vizsgalat(Szabad);
Munka:=Egeszhet-Szabad;
Vizsgalat(Munka);
if Szabad<=EgeszHet then Write(Output,'O');
if Egeszhet>=Munka then Write(Output,'K');
if not (Munka>=Szabad) then Write(Output,'Zsoke');
if [Szo]<=Munka then Write(Output,'Ma ne');
Writeln(Output)
end.
9.3. A programfejlesztésről
A programozás - ha ezen algoritmusok és adatstruktúrák tervezését és megfogalmazását értjük - általában bonyolult folyamat, amely számos részletkérdés és speciális módszer biztos ismeretét követeli meg. Csak kivételes esetben fordul elő, hogy egy feladatnak csak egyetlen jó megoldása van. Többnyire annyi a megoldás, hogy az optimális program kiválasztásához a rendelkezésre álló algoritmusok és számítógépek beható tanulmányozása mellett még azt is részletesen meg kell vizsgálnunk, milyen módon használják majd leggyakrabban a kérdéses programot.
A program tehát sok megfontolás, vizsgálat és tervezői döntés eredményeként jöhet csak létre. A kezdeti fázisban legjobb, ha figyelmünket a globális problémákra összpontosítjuk, s a megoldás első megfogalmazásában, vázlatában csak kevés figyelmet fordítunk a részletekre. A tervezési folyamat előrehaladtával a problémát részfeladatokra bonthatjuk, s fokozatosan tekintetbe vehetjük a feladatspecifikáció részleteit, a rendelkezésre álló eszközök jellemzőit. A probléma ilyen megközelítése szorosan kapcsolódik a lépésenkénti finomítás [2] és a strukturált programozás [4] fogalmához.
Fejezetünk hátralevő részében egy algoritmus kidolgozásának menetét mutatjuk be: egy C. A. R. Hoare által a [4]-ben közölt példát "hangszereltünk át" Pascalra.
A feladat a 2..N tartományba eső prímszámok előállítása, ahol N >= 2. A különböző algoritmusok összehasonlítása után egyszerűsége miatt (mivel sem szorzást, sem osztást nem tartalmaz) az eratosztenészi szita mellett döntünk.
Először szóban fogalmazzuk meg a feladatot:
Bár minden program végrehajtásának első lépése a változók kezdeti értékének beállítása (az inicializálás), a programfejlesztés során gyakran ezt hagyjuk utoljára. A helyes inicializálás előfeltétele, hogy pontosan ismerjük az algoritmus működését. Ha a programot módosítjuk, egyidejűleg a kezdeti értékeket is megfelelően át kell állítani, különben nem futhat a program. (Sajnos az átállítás önmagában nem mindig elegendő!)
Hoare mind a szita, mind a prímszámok ábrázolására 2..N elemű halmaz típust választ. A most következő szöveg - kis módosítástól eltekintve - megegyezik az általa közölt programvázlattal.
program Primszamok1;
{Turbo Pascal}
{ Eratosztenesz szitajanak megvalositasa halmazokkal }
const N=255;
type PozitivSzam= 1..MaxInt;
var Szita, Primek: set of 2..N;
KovPrim, Tobbsz: PozitivSzam;
begin
Szita:=[2..N]; Primek:=[];
KovPrim:=2;
{ a kovetkezo primszam keresese }
repeat
while not (KovPrim in Szita) do
KovPrim:=Succ(KovPrim);
Primek:=Primek+[KovPrim];
Tobbsz:=KovPrim;
while Tobbsz<=N do begin { kiejtes }
Szita:=Szita-[Tobbsz];
Tobbsz:=Tobbsz+KovPrim
end
until Szita=[]
end.
Hoare gyakorlásképpen azt a feladatot adja az olvasónak, hogy írja át ezt a programot így, hogy a halmazok csak a páratlan számokat tartalmazzák. Az egyik lehetséges megoldás az alábbi. Figyeljük meg, milyen szoros a kapcsolat az első változattal!
program Primszamok2;
{Turbo Pascal}
{ Eratosztenesz szitajanak megvalositasa halmazokkal,
csak a paratlan szamok figyelembevetelevel }
const N=255;
type PozitivSzam= 1..MaxInt;
var Szita, Primek: set of 2..N;
KovPrim, Tobbszoros, UjPrim: PozitivSzam;
begin
Szita:=[2..N]; Primek:=[];
KovPrim:=2;
{ a kovetkezo primszam keresese }
repeat
while not (KovPrim in Szita) do
KovPrim:=Succ(KovPrim);
Primek:=Primek+[KovPrim];
UjPrim:=2*KovPrim-1;
Tobbszoros:=KovPrim;
while Tobbszoros<=N do begin { kiejtes }
Szita:=Szita-[Tobbszoros];
Tobbszoros:=Tobbszoros+UjPrim
end
until Szita=[]
end.
A Pascal-megvalósításokkal szemben támasztott egyik tervezési követelmény, hogy a halmazokon végzett alapműveletek viszonylag gyorsak legyenek. Egyes gépi megvalósításokban a halmazok maximális méretét a számítógép szóhosszának megfelelően korlátozzák, s ily módon az alaphalmaz minden elemét egy bit reprezentálja (0 a hiányt, 1 a meglétet jelenti). A legtöbb megvalósítás nem engedne meg pl. 10 000 elemű halmazt. Ezek a megfontolások az adatábrázolás módosítását vonják maguk után (l. a 9.5. programot).
A nagy halmazokat kisebb halmazokból alkotott tömbökként ábrázolhatjuk. Az elemi halmazok méretét (a megvalósítástól függően) úgy választjuk meg, hogy egy halmaz éppen egy számítógépi szónak feleljen meg. A következő programban a második programvázlatot használtuk fel az algoritmus absztrakt modelljeként. A Szita és a Primek halmazokból alkotott tömb, a KovPrim pedig rekord lesz.
9.5. példaprogram:
program Primszamok3(Output);
{Turbo Pascal}
{ a 3..10000 kozotti primszamok meghatrozasa az ebbe a
taromanyba eso paratlan egeszeket tartalmazo szitaval }
const HMer=128 {megvalositasfuggo};
Maxelem=127;
HalmResz=39; {= 10000 div HMer div 2}
type TermeszetesSzam= 0.. MaxInt;
var Szita, Primek: array[0..HalmResz] of set of 0..MaxElem;
KovPrim: record Resz, Elem: TermeszetesSzam end;
T, UjPrim, R, N, Szamlalo: TermeszetesSzam;
Ures: Boolean;
begin
for R:=0 to HalmResz do begin
Szita[R]:=[0..MaxElem];
Primek[R]:=[]
end;
Szita[0]:= Szita[0]-[0]; Ures:= False;
KovPrim.Resz:= 0; KovPrim.Elem:=1;
with KovPrim do
repeat {a kovetkezo primszam keresese }
while not (Elem in Szita[Resz]) do
Elem:=Succ(Elem);
Primek[Resz]:=Primek[Resz]+[Elem];
UjPrim:=2*ELem+1;
T:= Elem; R:=Resz;
while R<=HalmResz do begin { kiejtes }
Szita[R]:=Szita[R]-[T];
R:= R+Resz*2;
T:= T+UjPrim;
while T>MaxElem do begin
R:= R+1; T:= T-HMer
end
end;
if Szita[Resz]=[] then begin
Ures:= True; Elem:=0
end;
while Ures and (Resz<HalmResz) do begin
Resz:= Resz+1;
Ures:= Szita[Resz]=[]
end
until Ures;
Szamlalo:=0;
for R:= 0 to HalmResz do
for N:= 0 to MaxElem do
if N in Primek[R]then begin
Write(Output,2*N+1+R*HMer*2:7);
Szamlalo:=Szamlalo+1;
if (Szamlalo mod 8)=0 then Writeln(Output)
end
end.
10. Állomány (file) típusok
Sok szempontból a legegyszerűbb strukturálási mód a sorbarendezés. Az adatfeldolgozás területén a sorozatot leggyakrabban egy szekvenciális állománnyal (sequential file) írják le. A Pascal egyszerűen a file alapszót használja az olyan adatszerkezet jelölésére, amely azonos típusú elemek sorozatából áll.
Az állományok különleges csoportját alkotják a szöveg- (text) állományok, amelyek j különböző hosszúságú karaktersorok sorozatából állnak. Segítségükkel valósul meg az ember és a számítógéprendszerek közötti írásos kommunikáció.
10.1. Az állományok szerkezete
A sorozat maga definiálja az elemek természetes rendezését. Mindig csak egyetlen elem lehet közvetlenül hozzáférhető. A többi elem az állománybeli sorrendben, az állományon végighaladva érhető el. Az elemek számára - az állomány ún. hosszára - az állomány típusdefiníciója nem tesz megkötést. Ez olyan tulajdonság, amely egyértelműen megkülönbözteti az állományt a tömbtől. Azt az állományt, amely egyetlen elemet sem tartalmaz, üresnek nevezzük, Az állomány típus tehát abban tér el a tömb, a rekord és a halmaz típustól, hogy soros elérésű, azonos típusú elemekből felépülő szerkezet.

10.1. ábra. Állomány típus szintaxisdiagramja
Minden F állományváltozó deklarálásakor automatikusan létrejön egy F^ jelű, az elemek típusához tartozó ún. pufferváltozó is. Ezt olyan ablaknak tekinthetjük, amelyen át megvizsgálhatjuk, kiolvashatjuk a már meglevő elemek értékét, ill. amelyen keresztül az állományhoz új elemeket csatolhatunk (írhatunk). A pufferváltozót bizonyos állományműveletek automatikusan pozícionálják. A teljes állományra vonatkozó értékadás tiltott. Ehelyett a pufferváltozón keresztül egyenként írhatunk új elemeket az állományba. Ha az állomány utolsó elemén túllépünk, a pufferváltozó értéke határozatlanná válik.

10.2. ábra. Pufferváltozó szintaxisdiagramja
A soros feldolgozás, a változó hossz és a pufferváltozó jelenléte már jelzi, hogy az állományok a háttértárral és a perifériákkal hozhatók kapcsolatba. A megvalósítástól függ, pontosan hol és hogyan tároljuk az egyes elemeket, de feltételezzük, hogy az operatív tárban egyidejűleg csak néhány elem van, és csak az az elem érhető el közvetlenül, amelyre F^ mutat.
Ha az F^ ablak az F állomány végén (end of file) túlra kerül, az eof(F) standard logikai függvény True értéket szolgáltat; értéke egyébként False. Az alapvető állománykezelő eljárások:
| Reset(F) | az állományablakot olvasás céljából az állomány elejére állítja vissza. Ha F nem üres, F^-nek F első elemének az értékét adja; eof(F) értéke False lesz. |
| Rewrite(F) | F létrehozása (írása) előtt alkalmazzuk. F aktuális értéke az üres állomány lesz. Az eof(F) True lesz, és megkezdődhet az új állomány beírása. |
| Get(F) | az állományablakot a következő elemre lépteti, azaz az F^ pufferváltozónak ezen elem értékét adja. Ha nincs következő elem, eof(F) True értéket vesz fel, F^ értéke pedig határozatlan lesz. A Get(F) hibát okoz, ha végrehajtása előtt eof(F) True értékű volt, vagy ha F írása közben alkalmazzuk. |
| Put(F) | az F^ pufferváltozó értékét az F állományhoz illeszti. Hibát okoz, ha végrehajtása előtt az eof(F) logikai függvény nem True értékű, vagy ha F olvasása közben alkalmazzuk. Az eof(F) True marad, és F^ határozatlan lesz. |
Elvileg a fenti négy alapvető állomány operátorral és az eof logikai függvénnyel az összes szekvenciális állományírási és -olvasási műveletet ki tudnánk fejezni. A gyakorlatban azonban az állománypozíció léptetése gyakran természetes módon együtt jár a pufferváltozóval végzett műveletekkel. Ezért bevezetünk két új eljárást (Read és Write), amelyek definíciója a következő:
Read(F,X) jelentése (X változó):
begin
X:= F^; Get(F)
endWrite(F,E) jelentése (E kifejezés):
begin
F^: = E; Put(F)
end
A Read és a Write olyan különleges eljárás, amely változó számú aktuális paramétert is elfogad. Ha V1, ..., Vn változók és E1, ..., En kifejezések, akkor:
Read(F,V1, ..., Vn) jelentése:
begin
Read(F, V1); ...; Read(F, Vn)
end
és
Write(F, E1, ..., En) jelentése:
begin
Write(F, E1); ...; Write(F, En)
end
A Read és a Write eljárás bevezetése a rövidebb írásmód mellett azért is előnyös, mert fogalmi egyszerűsítést is jelent, hiszen elhagyható az F^ pufferváltozó, amelynek értéke bizonyos esetekben határozatlanná válik. A pufferváltozó azonban hasznos "előretekintő" (look-ahead) eszköz lehet.
Példák deklarációra:
var Adatok: file of Integer;
A: Integer;var Rajzallomany: file of record
C: Szin;
Hossz: TermeszetesSzam
end;var Klub: file of Szemely;
Sz: Szemely;
Példák állományokra vonatkozó utasításokra:
A:= Adat^; Get(Adatok)
Read(Adatok,A)
Rajzallomány^.C:= Voros;
Rajzallomany^.Hossz:= 17; Put(Rajzallomany)
Klub^:= Sz; Put(Klub)
Write(Klub,Sz)
Az állományok lehetnek valamely programra (eljárásra) nézve lokálisak, de létezhetnek a programtól függetlenül, azon kívül is. Az utóbbi esetben külső (extenal) állományokról beszélünk. A külső állományok a programfej paramétereiként szerepelnek a programban (l. a 4. fejezetet).
A következő két program az állományok használatát szemlélteti. A 10.1. program (normalizálás) valós számokkal kifejezett mérési adatokból álló állományt dolgoz fel - az adatok közvetlenül a műszertől vagy egy másik programtól származhatnak. A 10.2. program (összefésülés) két állományt fésül össze. A két kiinduló állomány vezetéknév szerint rendezett személyi adatokat tartalmaz; ezekből a program egy hasonlóképpen rendezett harmadik állományt hoz létre. Formálisan, ha a kiinduló állományok elemei rendre:
F1, F2, ..., Fm és G1, G2, ..., Gn
ahol F(I+1) >= F(I), ill. G(J+1) >= G(J) minden I-re, ill. J-re, akkor az eredményként előálló H állományra is:
H(K+1) >= H(K), ahol K = 1, 2, ..., (M+N-1).
10.1. program:
program Normalizalas(K_Adatok,E_Adatok);
{MS Pascal}
{ Meresi adatok normalizalasa. A valos szamokbol allo adatallomany
a muszerrol vagy egy masik programbol szarmazik. }
type MeresiAdatok= file of real;
TermeszetesSzam= 0..MaxInt;
var K_Adatok, E_Adatok: MeresiAdatok;
N_Osszeg, Szorzas, Osszeg, K_Ertek: real;
N: TermeszetesSzam;
begin
Reset(K_Adatok); N:=0;
Osszeg:=0.0; N_Osszeg:=0.0;
while not Eof(K_Adatok) do begin
N:=N+1;
Osszeg:=Osszeg+K_Adatok^;
N_Osszeg:=N_Osszeg+Sqr(K_Adatok^);
Get(K_Adatok)
end;
K_Ertek:=Osszeg/N;
Szorzas:=Sqrt((N_Osszeg/N)-Sqr(K_Ertek));
Reset(K_Adatok); Rewrite(E_Adatok);
while not Eof(K_Adatok) do begin
E_Adatok^:=(K_Adatok^-K_Ertek)/Szorzas;
Put(E_Adatok); Get(K_Adatok)
end
end. {normalizalas}
10.2. program:
program Osszefesules(F, G, H);
{MS Pascal}
{ Az F es G vezeteknevek szerint rendezett
allomanyok osszefesulese a H allomanyba. }
type TermeszetesSzam= 0..MaxInt;
Fuzer15= packed array[1..15] of Char;
szemely= record
Nev: record Keresztn, Vezetek: Fuzer15 end;
Magassag: TermeszetesSzam {Centimeter}
end;
var F, G, H: file of Szemely;
FVagyGVege: Boolean;
begin
Reset(F); Reset(G); Rewrite(H);
FVagyGVege:= Eof(F) or Eof(G);
while not FVagyGVege do begin
if F^.Nev.Vezetek < G^.Nev.Vezetek then begin
H^:=F^; Get(F);
FVagyGVege:=Eof(F)
end
else beign
H^:=G^; Get(G);
FVagyGVege:=Eof(G)
end;
Put(H)
end;
while not Eof(G) do begin
Write(H,G^);
Get(G)
end;
while not Eof(F) do begin
Write(H,F^);
Get(F)
end;
end.
10.2. Szövegállományok
Azokat az állományokat, amelyek változó hosszúságú, sorokra tagolt karaktersorozatokból állnak, szövegállományoknak (textfile) nevezzük. A szövegállományokat a Text (szöveg) standard típushoz tartozónak deklaráljuk.
Azt mondhatjuk, hogy a Text típust a (feltételezett) sorlezáró (end-of-line) karakterrel kibővített Char típuson mint alaptípuson definiáljuk. A Text típus tehát nem egyenértékű a (Packed) file of Char-ral. A sorlezáró karakter előállítása, ill. felismerése a következő speciális szövegeljárásokkal történik:
| Writeln(F) | az F szövegállomány aktuális sorának lezárása. |
| Readln(F) | ugrás az F szövegállomány következő sorának elejére (F^ a következő sor első karakterére mutat). |
| Eoln(F) | logikai függvény, amely azt jelzi, hogy az F szövegállomány aktuális sorának végére értünk. (Ha True értékű, akkor F^ a sorlezáró - end-of-line - karakterre mutat és tartalma üres.) |
Ha F szövegállomány és Ch karakterváltozó, akkor az alábbi rövidebb írásmódot alkalmazhatjuk:
| rövid alak: | teljes alak: |
| Write(F,Ch) | F^:= Ch; Put(F) |
| Read(F,Ch) | Ch:= F^; Get(F) |
A Pascalban van két standard szövegállomány típusú változó: az Input és az Output. Ezekkel mint programparaméterek segítségével történik az írásos ember-gép kommunikáció. Az Input és az Output változóval, valamint a Read, a Write, a Readln és a Writeln további változataival a 13. fejezetben részletesen foglalkozunk.
A most következő programvázlatokban, a fenti írásmódot alkalmazva néhány tipikus szövegállomány-műveletet mutatunk be.
(1) Az Y szövegállomány írása. Tegyük fel, hogy P(C) minden végrehajtása során egy (következő) karaktert állít elő, s a C paraméternek ezt a karakterértéket adja. Az aktuális sor végéhez érve a B1 logikai változó True-ra állítódik, az egész szöveg végénél pedig a B2 változó lesz True értékű.
Rewrite(Y);
repeat
repeat P(C); Write(Y,C)
until B1;
Writeln(Y)
until B2
(2) Az X szövegállomány olvasása. Tegyük fel, hogy Q(C) minden végrehajtása egy (következő) C karakter feldolgozását eredményezi. Az egyes sorok végére érve az R tevékenységet kell elvégeznünk.
Reset(X);
while not Eof(X) do begin
while not Eoln(X) do begin
Read(X,C); Q(C)
end;
R; Readln(X)
end
(3) Az X szövegállomány átmásolása az Y szövegállományba, X sorszerkezetének megtartásával.
Reset(X); Rewrite(Y);
while not Eof(X) do begin {egy sor átmásolása}
while not Eoln(X) do begin
Read(X,C); Write(Y,C)
end;
Readln(X); Writeln(Y)
end
Végül egy megvalósítással kapcsolatos megjegyzés: A sorokat célszerűen vezérlő- (control) karakterekkel zárhatjuk le. Az ASCII karakterkészletben pl. a sor végét két karakterrel, a CR (carriage return : kocsi vissza) és az LF (line feed : soremelés) párossal jelöljük. Egyes számítógépek jelkészletéből azonban hiányoznak ezek a vezérlőkarakterek. Ilyenkor a sorvéget valamilyen más módon kell jelezni.
11. Mutató típusok
Mindeddig olyan típusokról volt szó, amelyek az ún. statikus változók deklarálására szolgáltak. Statikusnak mondjuk azt a változót, amelyet a programban deklarálunk, majd ezt követőén azonosítójával jelöljük. Az elnevezés onnan ered, hogy a változó mindvégig "él" annál blokknak (programnak, eljárásnak vagy függvénynek) a végrehajtása során, amelyre nézve lokális (más szóval a változó számára mindvégig helyet foglalunk a tárban). Változók azonban a program statikus szerkezetétől teljesen függetlenül dinamikusan - azaz egy blokk végrehajtása során - is előállíthatok. Az ilyen változót következésképpen dinamikus (dynamic) vagy mutatott (identified) változónak nevezzük.
11.1. Mutató- (pointer) és dinamikus (dynamic) változók
Ezek a változók nem szerepelnek explicit változó deklarációban, és azonosítókkal közvetlenül nem hivatkozhatunk rájuk: létrehozásukra, ill. törlésükre egy-egy standard eljárás, a New ill. a Dispose szolgál. A dinamikus változókra mutató- (pointer-) értékekkel hivatkozhatunk. A mutató fizikailag nem más, mint az újonnan létrehozott változó tárcíme. A mutatóváltozók csak a megfelelő mutató típushoz tartozó értékeket vehetnek fel.

11.1. ábra. Mutató típus szintaxisdiagramja
A mutató típust egy alaptípuson definiáljuk:
type P= ^T;
Egy P mutató típushoz tehát tetszőleges számú érték tartozhat, de ezek az értékek mind egy adott T típus elemeire (T típusú változókra) mutatnak. Emellett mindig eleme P-nek a nil érték, amely semmilyen változóra sem mutat.
Egy dinamikus változót az őt megcímző mutatóértékkel érhetünk el. Ha Ptr-t
var Ptr: P;
-ként deklaráltunk és értékeket kapott, a dinamikus változót Ptr^-lal jelöljük. Ha Ptr értéke nil vagy határozatlan, Ptr^-at észlelve a program hibát jelez.

11.2. ábra. Mutatott változó szintaxisdiagramja
Ha T típusú dinamikus változóra van szükségünk, a New(Ptr) eljárást használjuk. Ez lefoglalja a tárhelyet, és Ptr-nek a változóra mutató értéket ad. A Ptr értéke által kijelölt változó törlésére (a tárhely felszabadítására) a Dispose(Ptr) eljárás szolgál. A Dispose után Ptr értéke határozatlan lesz.
Mutatók alkalmazásával egyszerűen képezhetünk összetett, rugalmas (sőt rekurzív) adatszerkezeteket. Ha a T típus rekordszerkezetű, és egy vagy több P típusú mezőt tartalmaz, akkor tetszőleges, véges gráfnak megfelelő struktúrát hozhatunk létre, amelyben a dinamikus (mutatott) változók a csomópontokat, a mutatók az éleket reprezentálják.
A 11.1. program sorban álló vásárlók kiszolgálását szimulálja, s a várakozók listájának kezelésén keresztül szemlélteti a mutatók használatát. (Az eljárásokkal a következő fejezetben foglalkozunk.)
program Sorbanallas(Input,Output);
{Turbo Pascal}
{ Varokozolista szimulacioja
az elso harom vasarlo kiszolgalasa }
const NevHossz=15;
type NevIndex= 1..NevHossz;
NevFuzer= packed array[NevIndex] of Char;
TermeszetesSzam= 0..MaxInt;
Vasarlomutato= ^Vasarlo;
Vasarlo= record Nev: NevFuzer; Kovetkezo: Vasarlomutato
end;
var Eleje,Vege: Vasarlomutato;
Nev: packed array[NevIndex] of Char;
procedure Nevbeolvasas;
var c:NevIndex;
begin
for c:=1 to Nevhossz do
if Eoln(Input) then Nev[c]:=' '
else begin
Read(Input,Nev[c]);
Write(Output,Nev[c]);
end;
Readln(Input);
Writeln(Output)
end {Nevbeolvasas};
procedure UjVasarlo;
var Uj:Vasarlomutato;
begin
New(Uj);
if Eleje=nil then Eleje:=Uj
else Vege^.Kovetkezo:= Uj;
Uj^.Nev:= Nev;
Uj^.Kovetkezo:= nil;
Vege:= Uj
end {UjVasarlo};
procedure Kiszolgalas(Hanyvasarolt: TermeszetesSzam);
var Kiszolgalando: Vasarlomutato;
begin
while (Hanyvasarolt > 0) and (Eleje <> nil) do begin
Kiszolgalando:=Eleje;
Eleje:= Eleje^.Kovetkezo;
Writeln(Kiszolgalando^.Nev);
Dispose(Kiszolgalando);
Hanyvasarolt:= Hanyvasarolt-1
end
end; {Kiszolgalas}
begin {Sorbanallas}
Eleje:= nil;
while not Eof(Input) do begin {billentyuzeten CTRL+Z}
Nevbeolvasas;
Ujvasarlo
end;
Writeln(Output);
Kiszolgalas(3)
end.
Nézzünk egy másik példát! Tegyük fel, hogy egy adott embercsoportról "adatbankot" szeretnénk felállítani. írjuk le a személyeket ugyanolyan rekordokkal, mint a 8. fejezetben Ha mármost - mint azt a következő séma mutatja - mindegyik rekordba egy mutató típusú mezőt is beiktatunk, a rekordokból láncot vagy összeszerkesztett listát állíthatunk össze. Ehhez könnyen fűzhetünk újabb rekordokat, s egyszerű az egyes adatok visszakeresése is.
type Kapcsolat = ^Szemely;
...
Szemely = record
...
Kovetkezo: Kapcsolat;
...
end;
Az n személyből álló összeszerkesztett listát a 11.3. ábrával szemléltethetjük. Mindegyik négyzet egy-egy személyt jelképez.

11.3. ábra. Láncolt adatok listája
A lista első elemére az Első nevű, Kapcsolat típusú változó mutat. Az utolsó személy Kovetkezo mezője nil. Figyeljük meg, hogy az
Elso^.Kovetkezo^.Kovetkezo
kifejezés a lista harmadik személyére mutat.
Ha feltesszük, hogy egész számokat - pl. testmagasságadatokat - olvasunk be, a fenti láncot a következő kóddal hozhatnánk létre:
var Elso,P: Kapcsolat; I: Integer;
...
Elso:= nil;
for I:= 1 to N do begin
Read(H); New(P);
P^.Kovetkezo:= Elso;
P^.Magassag:=H; TobbiMezolnicializalasa(P^);
Elso:= P
end;
Figyeljük meg, hogy a lista hátulról előrefelé nő! Az elemek elérését úgy biztosíthatjuk, hogy bevezetünk egy újabb Kapcsolat típusú változót - nevezzük ezt mondjuk Pt-nek -, amely szabadon mozoghat a listában. Hogyan érhetjük el ezzel a lánc valamelyik elemét? Példaként tegyük fel, hogy van a listán egy olyan Személy, akinek a Magasság-a 175 cm, és ezt a személyt szeretnénk elérni (megkeresni). A stratégia a következő: Pt-t a Kapcsolatok-on át addig léptetjük, míg a keresett listaelemet meg nem találjuk.
Pt:= Elso;
while Pt^.Magassag <> 175 do Pt:= Pt^.Kovetkezo
Ez a programrészlet a következőt jelenti: "Mutasson Pt az első Személy-re. Ha a vizsgált Személy Magasság-a nem 175, adjuk Pt-nek az általa éppen kijelölt rekord Kovetkezo mezőjében (ebben a másik mutató változóban) tárolt értéket! Folytassuk ezt mindaddig, míg Pt arra a Személy-re nem mutat, akinek a Magasság-a éppen 175."
Vegyük észre, hogy ez az egyszerű keresőutasítás csak akkor működik, ha biztosak vagyunk benne, hogy van legalább egy olyan személy a listán, akinek a Magasság-a 175. De jogos-e ez a feltevés? Ha nem, feltétlenül meg kell vizsgálnunk, nem értük-e már el a lista végét! Elsőként a következő megoldással próbálkozhatnánk:
Pt:= Elso;
while (Pt <> nil) and (Pt^.Magassag <> 175) do
Pt:= Pt^.Kovetkezo
Idézzük fel az 5.1. szakaszban mondottakat! Ha Pt = nil, akkor a Pt^ változó, amelyre a leállási feltétel második tényezőjében hivatkozunk, egyáltalán nem is létezik, programunk tehát hibás. Így erre a helyzetre pl. az alábbi két programrészlet adhat helyes megoldást:
(1)
Pt:= Elso; B:= true;
while (Pt <> nil) and B do
if Pt^.Magassag=175 then B:= false else Pt:= Pt^.Kovetkezo
(2)
Pt:= Elso;
while Pt <> nil do begin
if Pt^.Magassag=175 then goto 13;
Pt:= Pt^.Kovetkezo
end;
13
11.2. A New és a Dispose eljárás
Vessünk fel most egy másik feladatot, és nézzük meg, mi a teendő, ha mondjuk egy újabb személy adatait szeretnénk felvenni a listára! Ilyenkor először létre kell hoznunk egy új (dinamikus) változót: le kell foglalnunk a szükséges tárterületet, s elő kell állítanunk a rá mutató értéket. Ez a New standard eljárással történik.
New(P)
Helyet foglal egy új P^ dinamikus változónak (P^ típusa P alaptípus lesz) létrehoz egy új - P-ével egyező típusú - mutatóértéket, s azt P-hez rendeli. Ha P^ egy változatrekord-típusú változó, akkor New(P) az összes változat számára elegendő helyet biztosít.New(P, C1, ..., Cn)
Helyet foglal egy új, P-ével egyező változatrekord-típusú P^ dinamikus változónak (a rekord n egymásba ágyazott változat részt tartalmaz, az ezekhez tartozó kijelölőmező értékek rendre C1, ..., Cn), létrehoz egy új - P-ével azonos típusú - mutatóértéket, s azt P-hez rendeli.
Figyelmeztetés! Ha valamely P^ rekordváltozót a New eljárás második alakjával állítunk elő akkor ennek a változónak a programvégrehajtás során mindvégig azonos változatban kell szerepelnie. A teljes változóra vonatkozó értékadás tiltott, P^ elemeire azonban megengedett!
A felvetett feladat megoldásának programozásakor az első lépés egy mutatóváltozó bevezetése. Nevezzük ezt NewP-nek. Ekkor a
New(NewP)
utasítással helyet foglalunk egy új Személy típusú változónak.
A következő lépésben az új változót - amelyre NewP mutat - be kell iktatnunk a láncba, mégpedig a Pt által kijelölt listaelem utáni helyre (11.4. ábra).

11.4. ábra. Láncolt adatok listája beillesztés előtt
A beiktatás egyszerűen a mutatók átállításából áll:
NewP^.Kovetkezo:= Pt^.Kovetkezo;
Pt^.Kovetkezo:= NewP
Az eredményt a 11.5. ábra szemlélteti.
11.5. ábra. Láncolt adatok listája beillesztés után
A Pt segédmutatót követő elemet az alábbi utasítással törölhetjük (hagyhatjuk el):
Pt^.Kovetkezo:= Pt^.Kovetkezo^.Kovetkezo
Gyakran célszerű egy listát két, egymást követő mutató segítségével feldolgozni. A törlést ilyenkor úgy érdemes megoldani, hogy az egyik, mondjuk P1 jelű mutató az elhagyandó lista-elem előtti pozícióra, a másik, P2 mutató magára az elemre mutat. Ekkor a törlést az alábbi utasítással írhatjuk le:
P1^.Kovetkezo:= P2^.Kovetkezo
Fel kell hívnunk a figyelmet arra, hogy az így megoldott törlés bizonyos esetekben csökkenti a felhasználható (szabad) tárterületet! Ezen a helyzeten például úgy segíthetünk, hogy pontosan nyilvántartjuk a "kitörölt" (elhagyott) listaelemeket. Az új változókat ekkor nem a New eljárás hívásával hozzuk létre, hanem ebből a - mondjuk Szabad nevű mutatóváltozó segítségével vezetett - nyilvántartásból vesszük (kivéve persze, ha a nyilvántartás üres). Így egy listaelem elhagyása azt jelenti, hogy a kérdéses elemet kiiktatjuk a láncból (listából), és a szabad elemek nyilvántartásába tesszük.
P1^.Kovetkezo:= P2^.Kovetkezo;
P2^.Kovetkezo:= Szabad;
Szabad:= P2
Végül a Dispose standard eljárás használatával a törölt tagok kezelését a gépi megvalósításra bízhatjuk.
Dispose(Q)
Felszabadítja a Q^ dinamikus változó által elfoglalt területet, és törli a Q mutatóértéket. Hívása hibát okoz, ha Q nil, vagy határozatlan. Csak akkor használható, ha Q értékét a New eljárás első alakjával hoztuk létre.Dispose(Q, K1, . ,Kn)
F felszabadítja a Q^ dinamikus változó rekord (amelynek aktív változatait K1, ..., Kn jelöli ki) által elfoglalt területet, és törli a Q mutatóértéket. Hibát okoz, ha Q nil vagy határozatlan. Csak akkor használható, ha Q értékét a New eljárás második alakjával hoztuk létre, és K1, ..., Kn ugyanazokat a változatokat jelöli ki, mint Q létrehozásakor.
A 12. fejezetben két olyan példaprogramot közlünk, amelyben a feladat egy mutató típusok segítségével felépített fastruktúra bejárása (12.6. és 12.7. program).
12. Eljárások és függvények
Amikor valaki már magas fokon elsajátította a számítógép-programozás mesterfogásait, programját egymást követő finomítást lépésekben készíti el. Minden egyes szinten, mindegyik lépésben részfeladatokra bontja a problémát, s ezáltal egy sor részprogramot hoz létre. Meg lehet úgy is írni a programot, hogy ez a tagoltság rejtett maradjon, ez azonban nem kívánatos. Az eljárás és a függvény fogalom lehetővé teszi, hogy a részfeladatokat ténylegesen részprogramokként írjuk meg.
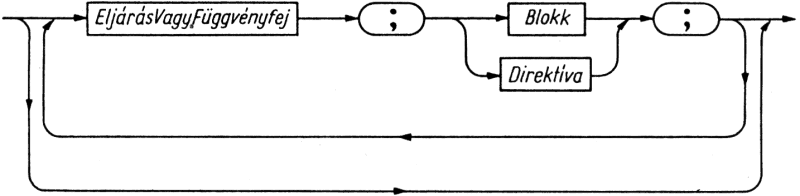
12.1. ábra. Eljárás és függvénydeklarációs rész szintaxisdiagramja

12.2. ábra. Eljárás vagy Függvényfej szintaxisdiagramja
12.1. Eljárások
Könyvünk példaprogramjaiban sokszor találkozhatott az Olvasó a Read, a Readln, a Write és a Writeln standard eljárással. Ebben a szakaszban bemutatjuk, hogyan dolgozhatunk magunk deklarálta (tehát nem standard) eljárásokkal. (Valójában erre már láthattunk példát a 9.2. és a 11.1. programban.)
Az eljárásdeklaráció egy részprogram definiálására, azonosítóval való ellátására szolgál. Ez utóbbi révén a részprogram eljárásutasítással hívható. A deklaráció pontosan olyan alakú mint egy program, csak nem programfej, hanem eljárásfej vezeti be.

12.3. ábra. Eljárásfej szintaxisdiagramja
Példaként tekintsük ismét a 7.1. programot, amely egész számok listájából a legkisebb és a legnagyobb értéket kereste ki! Egészítsük ki a programot azzal, hogy A[1]...A[n]-et rendre megnöveljük valamilyen növekménnyel, majd ismét megkeressük a legkisebb (Min) és a legnagyobb (Max) értéket! A feladatot megoldó következő programban Min-t és Max-ot egy eljárás segítségével határozzuk meg.
Program MinMax2(Input,Output);
{Turbo Pascal}
const MaxMeret = 12;
type Listameret = 1..MaxMeret;
var Novekmeny: Integer;
Elem: ListaMeret;
A: array[ListaMeret] of Integer;
Procedure MinMax;
var Elem: ListaMeret;
Min, Max, Elso, Masodik: Integer;
begin
Min:= A[1]; Max:= Min;
Elem:= 2;
while Elem<MaxMeret do begin
Elso:= A[Elem];
Masodik:= A[Elem+1];
if Elso > Masodik then begin
if Elso > Max then Max:= Elso;
if Masodik < Min then Min:= Masodik
end
else begin
if Masodik > Max then Max:= Masodik;
if Elso < Min then Min:= Elso
end;
Elem:=Elem+2
end;
if Elem = MaxMeret then
if A[MaxMeret] > Max then Max:= A[Maxmeret]
else if A[MaxMeret]<Min then Min:= A[MaxMeret];
Writeln(Output, Max:4, Min:4);
Writeln(Output)
end {MinMax};
begin
for Elem:= 1 to MaxMeret do begin
Write(Output,Elem,'. elem: ');Readln(Input,A[Elem]);
end;
Writeln(Output);
MinMax;
for Elem:=1 to maxMeret do begin
Write(Output,Elem,'. elem: ');Readln(Input,Novekmeny);
A[Elem]:= A[Elem]+Novekmeny
end;
Writeln(Output);
MinMax
end.
Egyszerűsége ellenére ez a program sok fogalom alkalmazását szemlélteti. Ezek:

12.4. ábra. Procedure utasítás szintaxisdiagramja
Ha a 12.1. programot részletesen megvizsgáljuk, kitűnik, hogy MinMax-ot kétszer hívtuk. Azzal, hogy a részprogramot eljárásként írtuk meg, azaz nem írtuk le kétszer ezt a programrészletet, nemcsak gépelési időt takarítottunk meg, hanem tárterületet is. A statikus kódot csak egyszer tároljuk, és a lokális változók területe csak az eljárás végrehajtása során, dinamikusan aktiválódik (a rendszer az eljárásba belépve lefoglalja, majd kilépéskor felszabadítja a tárhelyeket).
Azonban ha ezzel olvashatóbbá válik a program, úgy feltétlenül érdemes eljárásként megírni az olyan programrészeket is, amelyek hívására csak egyszer kerül sor. A rövidebb blokkok mindig áttekinthetőbbek, mint a hosszúak. Érthetőbb és könnyebben ellenőrizhető az a program, amelynek fejlesztési lépéseit eljárások formájában fogalmazzuk meg.
12.1.1. Paraméterlisták
Amikor alprogramokra bontunk fel egy feladatot, gyakran van szükség olyan új változók bevezetésére, amelyek az alprogramok argumentumait, ill. eredményeit tartalmazzák. A programszövegből világosan ki kell derülnie annak, hogy milyen célt szolgálnak ezek a változók.
A 12.2. program az előbbi példa kiterjesztése: szintén egy tömb legkisebb és legnagyobb értékét határozza meg, de az előbbinél általánosabb értelemben, s ezáltal számos újabb, eljárásokkal kapcsolatos fogalom jelentését is bemutatja.
Program MinMax3(Input,Output);
{Turbo Pascal}
const MaxMeret = 12;
type Listameret = 1..MaxMeret;
Lista = array [Listameret] of Integer;
var Elem: ListaMeret;
A,B: Lista;
MinA,MinB,MaxA,MaxB: Integer;
Procedure MinMax(var L: Lista; var Min, Max: Integer);
var Elem: ListaMeret;
Elso, Masodik: Integer;
begin
Min:= A[1]; Max:= Min;
Elem:= 2;
while Elem<MaxMeret do begin
Elso:= L[Elem];
Masodik:= L[Elem+1];
if Elso > Masodik then begin
if Elso > Max then Max:= Elso;
if Masodik < Min then Min:= Masodik
end
else begin
if Masodik > Max then Max:= Masodik;
if Elso < Min then Min:= Elso
end;
Elem:=Elem+2
end;
if Elem = MaxMeret then
if L[MaxMeret] > Max then Max:= L[Maxmeret]
else if L[MaxMeret]<Min then Min:= L[MaxMeret];
end {MinMax};
procedure ReadWrite(var L: Lista);
begin
for Elem:= 1 to MaxMeret do begin
Write(Output,Elem,'. elem: ');Readln(Input,L[Elem])
end;
Writeln(Output)
end {ReadWrite};
begin {foprogram}
ReadWrite(A);
MinMax(A, MinA, MaxA); Writeln(Output);
Writeln(Output,MinA:4, MaxA:4, MaxA-MinA:4);
Writeln(Output);
ReadWrite(B);
MinMax(B, MinB, MaxB); Writeln(Output);
Writeln(Output,MinB:4, MaxB:4, MaxB-MinB:4);
Writeln(Output);
for Elem:=1 to MaxMeret do begin
A[Elem]:=A[Elem]+B[Elem];
Write(Output,A[Elem]:4)
end;
Writeln(Output);
MinMax(A,MinA,MaxA);
Writeln(Output,MinA:4, MaxA:4, MaxA-MinA:4)
end.

12.5. ábra. Formális paraméterlista szintaxisdiagramja
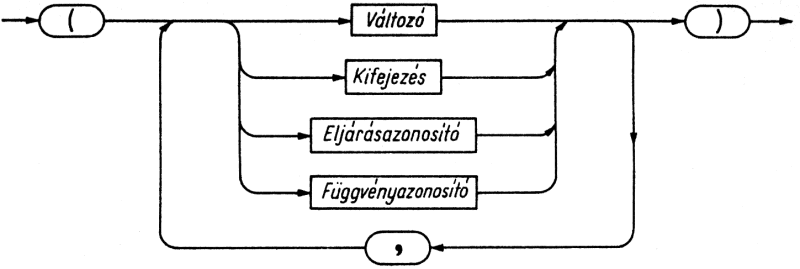
12.6. ábra. Aktuális paraméterlista szintaxisdiagramja
Ha a paraméterrész előtt nem áll szimbólum, akkor a benne szereplő paraméter(eke)t értékparaméter(ek)nek nevezzük. Ilyenkor az aktuális paraméter szükségképpen egy kifejezés (ami a legegyszerűbb esetben egyetlen változó is lehet). A megfelelő formális paraméter a meghívott eljárás valamely lokális változója. Ennek a változónak a kezdeti értékét a hozzá tartozó aktuális paraméter pillanatnyi értéke (tehát a kifejezésnek az eljáráshívás pillanatában felvett értéke) adja. Az eljárás ezután értékadással megváltoztathatja ennek a változónak az értékét; (közben azonban az aktuális paraméter értéke nem változhat. Éppen ezért számítási eredmény sosem lehet értékparaméter. Vigyázat! Állományok vagy állományokból felépülő strukturált változók nem adhatók meg aktuális értékparaméterként, hiszen ez értékadást jelentene!
A 12.3. program azt mutatja, miben különbözik az érték- és a változóparaméter hatása.
program Parameterek(Output);
{Turbo Pascal}
{ Ertek- es valtozoparameterek }
var A,B: Integer;
procedure Osszeadas1(X: Integer; var Y: Integer);
begin
X:= X+1;
Y:= Y+1;
Writeln(Output,X:4,Y:4)
end {Osszeadas};
begin
A:= 0; B:= 0;
Osszeadas1(A,B);
Writeln(Output,A:4,B:4)
end.
A következő táblázatban pontosan összefoglaltuk, hogy a különböző fajtájú paraméterek hogyan jelennek meg a formális, ill. az aktuális paraméterlistában.
formális paraméter aktuális paraméter értékparaméter változóazonosító kifejezés változóparaméter változóazonosító változó eljárásparaméter eljárásfej eljárásazonosító függvényparaméter függvényfej függvényazonosító
A 12.2. program MinMax eljárásában az L tömb egyik elemének értéke sem változott: L nem volt számítási eredmény. Következésképpen ugyanarra az eredményre jutottunk volna, ha L-t értékparaméterként definiáljuk. Hogy megértsük, miért nem ezt a megoldást választottuk, foglalkozzunk egy kicsit a gépi megvalósítással!
Az eljáráshívás valamennyi értékparaméternek új helyet foglal a tárban; ez reprezentálja a lokális változót. Az aktuális paraméter pillanatnyi értéke erre a helyre "másolódik át"; ha kilépünk az eljárásból, ez a tárfelület felszabadul.
Olyan paraméter esetén, amely nem az eljárás eredményét adja át, általában célszerűbb értékparaméterrel dolgozni. Gyorsabb a hozzáférés, és védve vagyunk a téves adatmódosítás veszélyétől. Körültekintéssel kell azonban kezelnünk azt az esetet, amikor valamilyen strukturált (pl. tömb) típusú paraméterrel van dolgunk. Ilyenkor ugyanis az átmásolási művelet meglehetősen időigényes, az átmásolt értékek tárolására lefoglalt terület pedig elég nagy lehet. Példánkban, minthogy az L tömb egyes elemeire csak egyszer hivatkozunk, változóparamétert célszerű használni.
A tömb dimenziószámát egyszerűen MaxMeret újradefiniálásával változtathatjuk meg. Ha a programot valós értékekből álló tömbre akarjuk alkalmazni, csak a típus- és változó definíciókat kell módosítanunk; az utasítások nem egész értékekkel is helyesen működnek.
12.1.2. Illeszkedőtömb-paraméterek
Van azonban egy másik mód is a különböző méretű tömbök eljárásoknak vagy függvényeknek való átadására: ha - változó- vagy értékparaméterként - illeszkedőtömb-paramétert alkalmazunk a formális paraméterlistában. Vigyázat! Az illeszkedőtömb-paraméterek az ISO Pascal-szabványban csak opcionális lehetőségként szerepelnek; egyes megvalósítások nem támogatják őket!
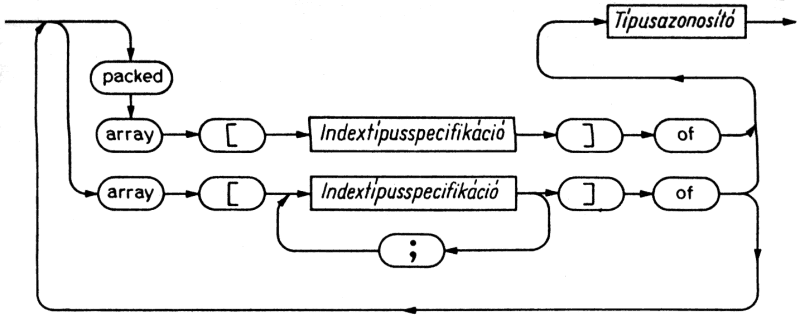
12.7. ábra. Illeszkedőtömb séma szintaxisdiagramja
![]()
12.8. ábra. Index típusspecifikáció szintaxisdiagramja
Az illeszkedőtömb a tömb aktuális méreteit (az egyes dimenziók indexhatárát) indexhatár-azonosítókkal adja meg. Ezek tulajdonképpen csak olvasható (read-only) változók. Az aktuális tömbparaméter indextípusa kompatibilis kell, hogy legyen az illeszkedőtömb indextípus-specifikációjában megadott típussal. Az indextípus legkisebb és legnagyobb értékének is belül kell maradnia az indextípus-specifikációban álló típus zárt intervallumán. Az elemtípusoknak meg kell egyezniük; ha pedig az illeszkedőtömb-paraméter elemtípusa egy másik illeszkedőtömb-paraméter, akkor az aktuális tömbparaméter elemtípusának ehhez illeszkedőnek kell lennie.
Illeszkedőtömb-paraméter csak az utolsó dimenziójában tömöríthető. Az értékparaméterként használt illeszkedőtömb-paraméterekhez az aktuális paraméterlistában változók vagy füzérek tartozhatnak.
A most következő 12.4. program a 7. fejezetben látott MátrixSzorzás program illeszkedőtömb-paramétert alkalmazó változata. A későbbi 12.7. programban pedig különböző hosszúságú füzéreket adunk át egy formális illeszkedőtömb-paraméternek.
program MatrixSzorzas2(Input,Output);
const M= 4;
P= 3;
N= 2;
type Poz= 1..MaxInt;
var A: array[1..M,1..P] of Integer;
B: array[1..P,1..N] of Integer;
C: array[1..M,1..N] of Integer;
Procedure MatrixBe(var X: array[KezdS..VegS: Poz; KezdO..VegO: Poz] of Integer);
var Sor,Oszlop: Poz;
begin
for Sor:=1 to VegS do
for Oszlop:=1 to VegO do
Read(Input,X[Sor,Oszlop])
end {MatrixBe};
procedure MatrixKiiras(var x: array[KezdS..VegS: Poz; KezdO..VegO: Poz] of Integer;
var Sor,Oszlop:Poz;
begin
for Sor:= 1 to VegS do begin
for Oszlop:= 1 to VegO do
Write(Output,X[Sor,Oszlop])
Writeln(Output)
end
end {MatrixKiiras};
procedure Szorzas(var A:array[AkezdS..Avegsor: Poz; AKezdO..AvegO: Poz] of Integer;
var B: array[BKezdS..BVegS: Poz; BKezdO..BVegO: Poz] of Integer;
C: array[CkezdS..CVegS: Poz; CKezdO..CVegO: Poz] of Integer;
S: Integer;
I, J, K: Poz;
begin
if (AKezdS <> 1) or (AKezdO <> 1) or (BKezdS <> 1) or
(BKezdO<> 1) or (CKezdS <> 1) or (CKezdO <> 1) or
(AVegS <> CVegS) or (AVegO <> BVegS) or (BVegO <> CVegO) then {hiba}
else
for I:= 1 to CVegS do begin
for J:= 1 to CVegO do begin
S:= 0;
for K:= 1 to AVegO do
S:= S+A[I,K]*B[K,J];
C[I,J]:= S
end
end
end {Szorzas};
begin
MatrixBe(A);
MatrixKiiras(A);
MatrixBe(B);
MatrixKiiras(B);
Szorzas(A,B,C);
MatrixKiiras(C)
end.
Az illeszkedőtömb-paraméterek itt közölt módon való kezelését sem a Turbo Pascal, sem az MS Pascal nem fogadja el.
12.1.3. Rekurzív eljárások
Ha az eljárás azonosítóját az eljáráson belül használjuk, az eljárást rekurzív módon hajtjuk végre. Vannak feladatok, amelyek megfogalmazása a probléma természetéből adódóan rekurzív, s ezek gyakran szinte kínálják a rekurzív megoldást. Ilyen esetet példáz a 12.5. program.
Az a feladat, hogy írjunk olyan programot, amely a hagyományos (infix) alakban megadott kifejezéseket lengyel (postfix) alakra hozza. Ezt úgy oldjuk meg, hogy mindegyik szintaktikai egységre (kifejezésre, tagra, tényezőre) külön-külön egy-egy konverziós eljárást készítünk. Minthogy ezeket a szintaktikai egységeket rekurzív definícióval adjuk meg, a megfelelő eljárások is rekurzívak lehetnek. Adatként rendelkezésre állnak az
(a+b)*(c-d)
a + b*c-d
(a*b)*c-d
a + b*(c-d)
a*a*a*a
b + c*(d + c*a*a)*b + a
szimbolikus kifejezések, amelyeket a következő EBNF-leírás alapján képeztünk. A bevitel végét pont jelzi.
Kifejezés = Tag {("+" | "-") Tag).
Tag = Tényező {"*" Tényező}.
Tényező = Azonosító | "("Kifejezés")".
Azonosító = Betű.
12.5. program:
program LengyelAlak(Input,Output);
{Turbo Pascal}
{Hagyomanyos kifejezes lengyel (postfix) alakra hozatala}
var C: Char;
procedure Kereses;
label 13;
begin
if Eof(Input) then goto 13;
repeat
Read(Input,C)
until(C<>' ') or Eof(Input);
13:
end {Kereses};
procedure Kifejezes;
var Op: Char;
procedure Tag;
procedure Tenyezo;
begin
if C='(' then begin
Kereses;
Kifejezes;
{C=')'}
end
else Write(Output,C);
Kereses
end {Tenyezo};
begin {Tag}
Tenyezo;
while C='*' do begin
Kereses;
Tenyezo;
Write(Output,'*')
end
end {Tag};
begin {Kifejezes}
Tag;
while (C='+') or (C='-') do begin
Op:= C;
Kereses;
Tag;
Write(Output,Op)
end
end {Kifejezes};
begin {LengyelAlak}
Kereses;
repeat
Kifejezes;
Writeln(Output)
until C='.'
end {LengyelAlak}.
A bináris fa olyan adatstruktúra, amelynél kézenfekvően adódik a rekurzív definíció, s amelyet így szintén rekurzív eljárásokkal dolgozhatunk fel. A fa véges számú csomópontból áll. Ezek halmaza vagy üres, vagy egy csomópontot (gyökeret) tartalmaz, amely két, közös rész nélküli bináris fa - a bal-, ill. jobb oldali részfa - kiindulópontja [6]. Természetes, hogy a bináris fák előállítását, feldolgozását végző rekurzív eljárások is ezt a fajta definíciót tükrözik.
A 12.6. program egy bináris fát épít fel, majd gyökérkezdő, gyökérközepű, és gyökérvégző sorrendben (pre-, in-, ill. postorder) bejárja a fa csomópontjait. Gyökérközepű esetben a bejárást a bal alsó csomóponttal kezdjük, majd balról jobbra, alulról fölfelé tatadunk. Először a bal oldali részfát követjük a gyökérig, majd a jobb oldali részfát járjuk be. A gyökér (a) így a felsorolás közepére kerül. Gyökérvégző esetben szintén a bal alsó csomóponttól indulunk el, de a csomópontokat szintenként csoportosítva járjuk be. A gyökérhez a jobb oldali részfa bejárása után, a felsorolás végén jutunk.
A fát gyökérkezdő alakban adjuk meg, ami azt jelenti, hogy a csomópontokat (melyeket esetünkben egy-egy betű jelöl) a gyökértől kiindulva előbb a bal és csak aztán a jobb oldali részfákon végighaladva soroljuk fel. A 12.9. ábrának megfelelő bemenő betűsor tehát:
abc..de..fg...hi..jkl..m..n..
ahol minden pont egy-egy üres részfát jelöl.
12.9. ábra. Bináris fa adatszerkezet
12.1.4. Eljárásparaméterek
A 12.6. programot úgy is átírhatjuk, hogy paraméterként eljárásokat adunk át. Az eljárásparaméterek eljárásfejként jelennek meg az eljárások és függvények formális paraméterlistájában. A megfelelő aktuális paraméterlistában csak az eljárásazonosítót kell megadni. A 12.7. program az előbbiek mellett azt is bemutatja, hogyan adhatunk át (aktuális) füzérértékeket illeszkedőtömb-paramétereknek.
Óva intjük azonban az Olvasót a rekurzív módszerek fenntartás nélküli alkalmazásától, amelyek "ügyesnek" tűnhetnek ugyan, de nem mindig jelentik a leghatékonyabb megoldást!
Ha valamely P eljárás egy Q eljárást hív és viszont, Q is hívja P-t, s egyikük sincs a másikban deklarálva, akkor vagy P-t, vagy Q-t előzetes (forward) deklaráció formájában előre meg kell adni (l. a 12.3. pontot).
Az A. függelékben felsorolt standard (előre deklarált) eljárások minden szabványos Pascal megvalósításban rendelkezésre állnak. A különféle megvalósításokban ezeken kívül még más előredeklarált eljárások is előfordulhatnak. Minthogy - az összes standard objektumhoz hasonlóan - ezeket is úgy tekintjük, mintha a hatáskörük a felhasználói programot körülvevő, annál tágabb blokkra terjedne ki, nem okoz problémát, ha a programban olyan deklaráció van, amely újradefiniál egy ilyen azonosítót.
Standard eljárások nem adhatók át aktuális eljárásparaméterként.
12.6. program:
program Bejaras(Input,Output);
{Binaris fa bejarasa}
type Mutato= ^Csomopont;
Csomopont= record Info: Char; Bal, Jobb: Mutato end;
var Gyoker: Mutato;
C: Char;
procedure Gyokerkezdo(P:Mutato);
begin
if P<>nil then begin
Write(Output,P^.Info);
Gyokerkezdo(P^.Bal);
Gyokerkezdo(P^.Jobb)
end
end {Gyokerkezdo};
procedure Gyokerkozepu(P:Mutato);
begin
if P<>nil then begin
Gyokerkozepu(P^.Bal);
Write(Output,P^.Info);
Gyokerkozepu(P^.Jobb)
end
end {Gyokerkozepu};
Procedure Gyokervegzo(P:Mutato);
begin
if P<>nil then begin
Gyokervegzo(P^.Bal);
Gyokervegzo(P^.Jobb);
Write(Output,P^.Info)
end
end {Gyokervegzo};
procedure Bevitel(var P:Mutato);
begin
Read(Input,C);
Write(Output,C);
If C<>'.' then begin
New(P); P^.Info:=C;
Bevitel(P^.Bal);
Bevitel(P^.Jobb)
end
else P:=nil
end {Bevitel};
begin {Bejaras}
Bevitel(Gyoker); Writeln(Output);
Gyokerkezdo(Gyoker); Writeln(Output);
Gyokerkozepu(Gyoker); Writeln(Output);
Gyokervegzo(Gyoker); Writeln(Output)
end {bejaras}.
A program eredménye:
abc..de..fg...hi..jkl..m..n..
abcdefghijklmn
cbedgfaihlkmjn
cegfbdilmknjha
12.7. program:
program Bejaras2(Input,Output);
{Binaris fa bejarasa
Eljarasparametereket tartalmazo valtozat}
type Mutato= ^Csomopont;
Csomopont= record Info: Char; Bal, Jobb: Mutato end;
Pozitiv=1..MaxInt;
Szoveg=packed array[1..38] of Char;
var Gyoker: Mutato;
C: Char;
procedure Gyokerkezdo(P:Mutato);
begin
if P<>nil then begin
Write(Output,P^.Info);
Gyokerkezdo(P^.Bal);
Gyokerkezdo(P^.Jobb)
end
end {Gyokerkezdo};
procedure Gyokerkozepu(P:Mutato);
begin
if P<>nil then begin
Gyokerkozepu(P^.Bal);
Write(Output,P^.Info);
Gyokerkozepu(P^.Jobb)
end
end {Gyokerkozepu};
Procedure Gyokervegzo(P:Mutato);
begin
if P<>nil then begin
Gyokervegzo(P^.Bal);
Gyokervegzo(P^.Jobb);
Write(Output,P^.Info)
end
end {Gyokervegzo};
procedure Bevitel(var P:Mutato);
begin
Read(Input,C);
Write(Output,C);
If C<>'.' then begin
New(P); P^.Info:=C;
Bevitel(P^.Bal);
Bevitel(P^.Jobb)
end
else P:=nil
end {Bevitel};
procedure CspontIr(procedure Famuvelet(Start:Mutato);Gyoker:Mutato; Cim: Szoveg);
var K:Pozitiv;
begin
Writeln(Output);
for K:=1 to 38 do
Write(Output,Cim[K]);
Writeln(Output); Writeln(Output);
Famuvelet(Gyoker);
Writeln(Output)
end {CspontIr};
begin {Bejaras}
Bevitel(Gyoker); Writeln(Output);
CspontIr(Gyokerkezdo,Gyoker,'A csomopontok gyokerkezdo sorrendben: ');
CspontIr(Gyokerkozepu,Gyoker,'A csomopontok gyokerkozepu sorrendben: ');
CspontIr(Gyokervegzo,Gyoker,'A csomopontok gyokervegzo sorrendben: ');
end {bejaras2}.
12.2. Függvények
A függvények az eljárásokhoz hasonló jellegű programrészek, amelyek valamilyen - egy kifejezés kiértékeléséhez szükséges - megszámlálható, valós vagy mutató típusú értékkiszámítást végzik. A függvény behívásáról a függvénykifejezés gondoskodik. Ez a függvényt jelölő azonosítóból és az aktuális paraméterek listájából áll. Ezek a paraméterek változók, kifejezések, eljárások vagy függvények lehetnek, és mindig a megfelelő formális paraméterek helyére kerülnek.
A függvénydeklaráció ugyanolyan alakú mint a program, azzal a különbséggel, hogy a függvényfej alakja a 12.10. ábra szerinti.

12.10. ábra. Függvényfej szintaxisdiagramja
Ugyanúgy, mint az eljárásoknál láttuk, a címkedefiníciós részben szereplő összes címke, a konstansdefiníciós részben bevezetett valamennyi azonosító, a típusdefiníciós rész, a változó-, és eljárás- vagy a függvénydeklarációs rész lokális a függvénydeklarációra nézve, amelyet éppen ezért az említett objektumok hatáskörének nevezünk. Hatáskörén kívül a fordítóprogram egyik objektumot sem ismeri fel. A lokális változók értéke az utasításrész kezdetén határozatlan.
A függvényfejbe írt azonosító nevet ad a függvénynek. Az eredmény csak egyszerű vagy mutató típusú lehet. A függvénydeklarációban szerepelnie kell egy ténylegesen végrehajtott, a (függvényazonosítóra vonatkozó (eredmény típusú) értékadásnak. Ez az értékadás szolgáltatja a függvény eredményét.
A 12.8. programban az 5.3. program hatványozási algoritmusát függvénydeklarációként íjuk fel.
Program Hatvanyozas2(Input,Output);
{Turbo Pascal}
{ Hatvany(X,Y) (X,Y) kiszamitasa termeszetes kitevore.
Hatvany(X,Y) jelentese: "X az Y-adikon". }
type Termeszetes=0..MaxInt;
var Pi, PiNegyzet: Real;
Function Hatvany(Alap:Real; Kitevo:Termeszetes):Real;
var Eredmeny: Real;
begin
Eredmeny:=1;
while Kitevo>0 do begin
while not odd(Kitevo) do begin
Kitevo:= Kitevo div 2;
Alap:= Sqr(Alap)
end;
Kitevo:= Kitevo-1;
Eredmeny:= Eredmeny*Alap
end;
Hatvany:=Eredmeny
end {Hatvany};
begin
Pi:=ArcTan(1.0)*4;
Writeln(Output,2.0:11:6,7:3,Hatvany(2.0,7):11:6);
PiNegyzet:=Hatvany(Pi,2);
Writeln(Output,Pi:11:6,2:3,PiNegyzet:11:6);
Writeln(Output,PiNegyzet:11:6,2:3,Hatvany(PiNegyzet,2):11:6);
Writeln(Output,Pi:11:6,4:3,Hatvany(Pi,4):11:6)
end.
Ha a függvény azonosítója a függvényben szereplő bármelyik kifejezésben is megjelenik, akkor rekurzív függvényvégrehajtásról beszélünk. Az F. függelék első példája többek között a rekurzív függvények használatát szemlélteti.
A függvénykifejezés megelőzheti a függvény deklarációt, ha van előzetes deklaráció (l. a 12.3. pontot).
Az A. függelékben felsorolt standard függvények minden szabványos Pascal-megvalósításban rendelkezésre állnak. A különböző megvalósítások további előre deklarált függvényeket is tartalmazhatnak. Standard függvények nem adhatók át aktuális függvény paraméterként.
12.2.1. Függvény paraméterek
A függvények maguk is átadhatók paraméterként eljárásoknak és függvényeknek. A formális függvény paramétert a függvényfejjel, az aktuálisat a függvényazonosítóval adjuk meg. A 12.9. program a megadott függvények értékeiből képezett sor összegét számítja ki.
program Sorosszegek2(Output);
{MS Pascal}
{Kulonbozo szamu tagbol allo sorok osszegenek kiszamitasa}
const MaxTagszam=10;
var Tag: 1..MaxTagszam;
function Szigma(Function F(X: Real): Real; AlsoHatar,Felsohatar: Integer): Real;
var Index: Integer;
Osszeg: Real;
begin
Osszeg:=0.0;
for Index:=AlsoHatar to FelsoHatar do
Osszeg:=Osszeg+F(Index);
Szigma:=Osszeg
end {Szigma};
function SzinuszXSzerX(X: Real): Real;
begin
SzinuszXSzerX:=Sin(X)*X
end {SzinuszXSzerX};
function EgyPerKob(X: Real): Real;
begin
EgyPerKob:=1/Sqr(X)*X)
end {EgyPerKob};
begin {Sorosszegek2}
for Tag:=1 to MaxTagszam do
Writeln(Tag,Szigma(SzinuszXSzerX,1,Tag),Szigma(EgyPerKob,1,Tag))
end.
12.2.2. Mellékhatások
Ha a függvénydeklarációban nem lokális változóra vagy változóparaméterre vonatkozó értékadás történik, mellékhatásról (side effect) beszélünk. Ez gyakran félrevezető, amikor a program szándékolt hatását akarjuk megállapítani, és rendkívül megnehezíti a program ellenőrzését. (Egyes gépi megvalósítások egyenesen megpróbálják megtiltani a mellékhatásokat.) Éppen ezért határozottan óvjuk az olvasót: ne alkalmazzon mellékhatással járó függvényeket! Példaként tekintsük a 12.10. programot.
program Mellekhatas(Output);
{Turbo Pascal}
var A,Z: Integer;
function Becsapas(X: Integer): Integer;
begin
Z:=Z-X {mellekhatas Z-re};
Becsapas:=Sqr(X)
end {Becsapas};
begin
Z:=10;
A:=Becsapas(Z);
Writeln(Output,A:5,Z:5);
Z:=10;
A:=Becsapas(10);
A:=A*Becsapas(Z);
Writeln(Output,A:5,Z:5);
Z:=10;
A:=Becsapas(Z);
A:=A*Becsapas(10);
Writeln(Output,A:5,Z:5)
end.
A program eredménye:
100 0
0 0
10000 -10
12.3. Előzetes (forward) deklarációk
Ha van előzetes deklaráció, az eljárás- (függvény-) hívás megelőzheti az eljárás- (függvény-) deklarációt. Az előzetes hivatkozás alakja a következő. (Figyeljük meg, hogy a paraméterlista és a tulajdonképpeni eredménytípus csak az előzetes hivatkozásban fordul elő!)
procedure Q(X: T); Forward;
procedure P(Y: T);
begin
Q(A)
end;
procedure Q; { a paraméterek itt már nem szerepelnek}
begin
P(B)
end;
13. Szövegállományok be-, ill. kivitele
A 10. fejezetben már szó esett az ember és a számítógép közötti kapcsolat problémájáról.
Az ember és a számítógép egyaránt az alakfelismerésnek nevezett folyamat segítségével "tanul", érti meg az információt. Sajnos azok az "alakok", amelyeket az ember a legkönnyebben felismer (elsősorban a kép és a hang) egészen mások, mint amelyeket a számítógép képes felismerni és értelmezni (elektromos impulzusok). Ez olyannyira így van, hogy az adatok fizikai átadása (átvitele) - amelynek során tehát az ember által olvasható jeleket a számítógép által olvasható jelekké kell alakítani, és viszont - ugyanolyan költséges lehet, mint az átadott információ tulajdonképpeni feldolgozása. (Éppen ezért kiterjedt kutatómunka folyik, hogyan lehetne a fordítási folyamat költségeit - minél nagyobb fokú automatizálással - a minimálisra csökkenteni.)
A fentiekben vázolt kommunikációs feladatot be-, ill. kivitelnek mondjuk.
Az ember beviteli perifériák és adathordozók (pl. billentyűzet, hajlékony mágneslemez, grafikus és rámutató-kiválasztó eszközök, mágnesszalag-kazetta, mágnesszalag, terminál) segítségével adhatja be információit, s az eredményeket kiviteli perifériákon és adathordozókon (pl. sornyomtatón, mágnesszalagon, hajlékony mágneslemezen, mágnesszalag-kazettán, rajzgépen, hanggenerátoron, képernyőn) kapja. Ami ezek többségében közös, az az ember számára olvasható - és az adott számítógéprendszer által meghatározott - karakterkészlet (l. a 3. fejezetet). Ez az a karakterkészlet, amelyen a Pascal a Text standard típust definiálja (l. a 10. fejezetet).
Fontos, hogy minden perifériának megvannak a maga sajátosságai: mindegyik egyéni módon értelmez bizonyos karaktereket vagy karaktercsoportokat (füzéreket). A legtöbb nyomtatón pl. korlátozott a sorszélesség. Sok régebbi sornyomtató a sorkezdő karaktereket nem nyomtatandó vezérlőkarakternek tekinti: az egyik hatására lapot dob, a másikra nem emel sort, felülírja az előző karaktereket stb. Ha valamely perifériának szövegállományt feleltetünk meg, ügyeljünk arra, hogy programunk betartsa az illető periféria sajátosságait!
A szövegállományok a Get és a Put standard eljárás segítségével érhetők el. Ez persze nemegyszer hosszadalmas lehet, hiszen ezeket az eljárásokat úgy definiáltuk, hogy egyszerre csak egy karakterrel tudnak dolgozni. Hogy a helyzetet szemléletesebbé tegyük, képzeljük el a következőt. Van egy természetes szám, amelyet valamely X változóban tároltunk, és ezt a számot ki szeretnénk vinni az Output állományra. Gondoljunk csak arra, mennyire más karakterek fordulnak elő egy szám decimális ábrázolásában, mint a római számos írásmódban (l. az 5.9. programot)! Minthogy általában a decimális ábrázolásra vagyunk kíváncsiak, jó, ha vannak a nyelvben olyan "beépített" standard transzformációs eljárások, amelyek az absztrakt számokat (akármilyen belső, számítógépi alakot is használunk) decimális számjegy sorozattá alakítják (és viszont).
Ezért, hogy megkönnyítsük a szövegállományok olvasását és írását, több irányban is általánosítjuk a Read és a Write standard eljárást.
13.1. Az Input és az Output standard állomány
Az Input (beviteli) és az Output (kiviteli) szövegállomány általában a számítógépes rendszer szokásos be-, ill. kiviteli eszközeit (pl. a billentyűzetet és a megjelenítőt) reprezentálja. Így ez a két állomány a számítógép és az azt felhasználó ember közötti kapcsolat legfontosabb láncszeme.
Minthogy az Input és az Output állományt nagyon gyakran használjuk, azok a szövegállomány-műveletek, ahol az F szövegállomány explicit módon nincs kijelölve, automatikusan e két állomány valamelyikével hajtódnak végre. Részletesen, a táblázat bal oldalán levő műveleteknek a következő műveletek felelnek meg:
Write(Ch) Write(Output,Ch) Read(Ch) Read(Input,Ch) Writeln Writeln(Output) Readln Readln(Input) Eof Eof(Input) Eoln Eoln(Input) Page Page(Output) (l. a 12.4. szakaszt)
Ha bármelyik felsorolt eljárást állományparaméter megadása nélkül használjuk, akkor megállapodásszerűen a művelet automatikusan az Input, ill. az Output állományra vonatkozik. Ebben az esetben viszont a két állománynak feltétlenül szerepelnie kell a programfej paraméter-listájában.
Megjegyzés: A Reset, ill. Rewrite standard eljárás Input, ill. Output állományra való alkalmazásának hatását a gépi megvalósítás határozza meg.
Ennek megfelelően a szövegállományok írását, ill. olvasását a következőképpen fejezhetjük ki: (legyen var Ch: Char; B1, B2: Boolean; legyen P, Q és R három, a felhasználó által definiált eljárás):
repeat
repeat P(Ch); Write(Ch)
until B1;
Writeln
until B2
while not eof do begin
P;
while not eoln do begin
Read(Ch); Q(Ch)
end;
R; Readln
end
A következő két példaprogram az Input és az Output szövegállomány használatát mutatja be. (Gondoljuk meg, hogyan kellene átírnunk a programot, ha a Read, ill. a Write helyett csak a Get, ill. a Put eljárást alkalmazhatnánk!)
program Betugyakorisag(Input,Output);
{MS Pascal}
{ Az Input allomanyban szereplo betuk gyakorisaganak meghatarozasa;
az allomany kiirasa. }
type Termeszetes=0..MaxInt;
var C: Char;
EfSzam:array[Char] of Termeszetes;
Betuk,Nagybetuk,Kisbetuk: set of Char;
begin
Nagybetuk:=['A','B','C','D','E','F','G','H','I','J','K','L','M',
'N','O','P','Q','R','S','T','U','V','W','X','Y','Z'];
Kisbetuk:= ['a','b','c','d','e','f','g','h','i','j','k','l','m',
'n','o','p','q','r','s','t','u','v','w','x','y','z'];
Betuk:= Kisbetuk+Nagybetuk;
for C:='A' to 'Z' do
EfSzam[C]:=0;
for C:='a' to 'z' do
EfSzam[C]:=0;
while not Eof do begin
while not Eoln do begin
Read(C);
Write(C);
if C in Betuk then EfSzam[C]:=EfSzam[C]+1
end;
Readln;
Writeln
end;
for C:='A' to 'Z' do
if C in Nagybetuk then Writeln(C,EfSzam[C]);
for C:='a' to 'z' do
if C in Kisbetuk then Writeln(C,EfSzam[C]);
end.
A következő 13.2. program az Inputot az Outputra másolja, s minden sor elejére beszúr egy sorszámot:
program Sorszamozas(Input,Output);
{MS Pascal}
{Sorszam beirasa a szovegallomanyba}
type Termeszetes=0..MaxInt;
var Sorszam: Termeszetes;
begin
Sorszam:=0;
while not Eof do begin
Sorszam:=Sorszam+1;
Write(Output,Sorszam:4,' ');
while not Eoln do begin
Write(Output,Input^);
Get(Input)
end;
Readln(Input);
Writeln(Output)
end
end.
Ha az Input állományváltozót interaktív terminál beviteli eszközéhez (pl. a billentyűzethez) rendeltük, a legtöbb Pascal-megvalósítás mindaddig nem értékeli ki az Input^ pufferváltozót, amíg értékére a programban ténylegesen nincs szükség. Ez két esetben fordulhat elő: ha Input^-at explicit kifejezésben használjuk, vagy ha a Read és a Readln eljárást, ill. az Eof és az Eoln függvényt alkalmazzuk, amelyek implicit igénybe veszik a pufferváltozót. Bár a gép a programvégrehajtás kezdetén egy implicit Reset(Input)-ot hajt végre, mindaddig nem vár adatokat a terminálról, amíg ilyen értelmű utasítást nem kap - tehát pl. amíg Input^ nem szerepel a programban. Ha a program üzenetet ír ki, s erre választ vár, akkor - ahogy azt általában megszoktuk - a bevitelkérés az üzenet kiírása után következik.
A következő programrészlet ilyen helyzetre mutat példát: kiírunk egy üzenetet, amelyre a felhasználónak válaszolnia kell.
program KerdesValasz(Input,Output);
var MonddMeg: Integer;
...
begin; {Itt történik az Implicit Reset(Input).}
Writeln('Kerek egy 1 es 10 kozotti egesz szamot!');
Read(MonddMeg)
...
13.2. A Read és a Readln eljárás
A Read eljárást a 10.2. szakaszban szövegállományokra definiáltuk. Most egyrészt több (változó számú), másrészt egész (egész résztartomány) és valós típusú paraméterekre is kiterjesztjük az értelmezését.
Jelöljön V1, V2, ..., Vn karakter, egész vagy valós típusú változókat (az előbbi kettő résztartományai is megengedettek), és legyen F egy szövegállomány!
Read(F,V) hibát okoz, ha F-et nem definiáltuk, ha nem F olvasása közben vagyunk, vagy ha Eof(F) = True.
Read(V1, ..., Vn) jelentése:
Read(Input,V1, ..., Vn)
Read(F, V1, ..., Vn) jelentése:
begin Read (F, V1); ...; Read(F,Vn) end
Readln(V1, ..., Vn) jelentése:
Readln(Input,V1,..., Vn)
Readln(F,V1, ..., Vn) jelentése:
begin Read(F,V1); ...; Read(F,Vn); Readln(F) end
Readln hatása: miután beolvasta Vn-t az F szövegállományról, az aktuális sor hátralevő részét átugorja. (A V1, ..., Vn értékek azonban több sorra is átnyúlhatnak.)
Ha Ch egy karakter vagy karakter-résztartomány típusú változó, akkor:
Read(F,Ch) jelentése:
begin Ch:= F^; Get(F) end
Ha valamelyik V paraméter egész (ill. egész résztartomány) típusú, egy előjeles, szükség szerint szóközökkel kezdődő egész számot leíró karaktersorozat olvasódik be. V ekkor a megadott egész értéket veszi fel.
Ha valamelyik V paraméter valós típusú, egy előjeles - Szükség szerint üres karakterrel kezdődő - szám olvasódik be. V ekkor a megadott valós értéket veszi fel.
Ha számokat olvasunk be F-ből, azaz a Read-del számokat keresünk, a szóközöket (üres karaktereket) átugorva sorvégeket is átugorhatunk. F^ továbbra is a szám utolsó jegyét követő első nem számjegykarakterre mutat. Számsorozatokat csak akkor olvashatunk be helyesen, ha az egymást követő számokat szóközökkel vagy sor vége jelekkel választjuk el. A Read a leghosszabb összefüggő számjegysort olvassa be, és ha két számot nem határolunk el, azokat nemcsak a Read, de egyetlen földi halandó sem tudja különválasztani.
Példák:
Olvassunk be és dolgozzunk fel egy számsort, ahol közvetlenül az utolsó szám után egy csillag áll! Legyen F szövegállomány, X egész (vagy valós), Ch pedig karakter típusú változó!
Reset(F);
repeat
Read(F,X,Ch);
P(X)
until Ch='*'
Talán még gyakoribb az a helyzet, amikor semmit sem tudunk a beolvasandó adategységek számáról, és nincs olyan külön szimbólum, amely lezárná az adatsort. Két, jól felhasználható sémát mutatunk be. Mindkettőben a SzokozAtugras eljárással dolgozunk.
procedure SzokozAtugras(var F: Text);
var Kesz: Boolean;
begin
Kesz:= False;
repeat
if Eof(F) then Kesz:= True
else
if F^= ' ' then Get(F)
else Kesz:= True
until kesz
end
Az elsőben egyszerre egy adategységet dolgozunk fel:
Reset(F);
while not Eof(F) do begin
Read(F,X); SzokozAtugras(F);
P(X);
end
A második séma n számból álló adatcsoportokat (szám-n-eseket) dolgoz fel:
Reset(F)
while not Eof(F) do begin
Read(F,X1, ..., Xn); SzokozAtugras(F);
P(X1, ..., Xn);
end
(Ez a program csak akkor működik helyesen, ha az adategységek összes száma n-nek valamilyen többszöröse.)
13.3. A Write és a Writeln eljárás
A Write eljárást a 10.2. szakaszban szövegállományokra definiáltuk. Most több, egész, valós, logikai vagy füzér típusnak megfelelő típusú paraméterre is értelmezzük.
A Write eljárás karakterláncokat (egy vagy több karaktert) illeszt valamilyen szövegállományhoz. Legyen P1, P2, ., Pn a 13.1. szintaxisdiagrammal megadott alakú paraméter, és legyen F szövegállomány. Ekkor Write(F,P) hibát okoz, ha F-et nem definiáltuk, nem F írása közben vagyunk, vagy ha Eof(F) = False.
13.1. ábra. Write paraméterlista szintaxisdiagramja
Write(P1, ...,Pn) jelentése:
Write(Output, P1, ..., Pn)
Write(F,P1, ..., Pn) jelentése:
begin Write(F,P1); ...; Write (F,Pn) end
Writeln(P1, ..., Pn) jelentése:
Writeln(Output, P1, ..., Pn)
Writeln(F,P1, ...,Pn) jelentése:
begin Write(F,P1); ...; Write(F,Pn); Writeln(F) end
A Writeln a P1,...,Pn írását, majd az F szövegállomány aktuális sorának lezárását eredményezi.
Mindegyik Pk paraméter a következő alakú kell, hogy legyen:
e vagy
e:w vagy
e: w: f
ahol e, w és f kifejezések, e az írandó érték. Lehet karakter, egész, valós vagy logikai típusú, de lehet füzér is. w az ún. (legkisebb) mezőszélesség, egy nem kötelező formázási segédeszköz. Pozitív egész értékű kifejezés kell, hogy legyen. Jelentése: az írásra kerülő karakterek száma. Az e értéket általában w számú karakterrel írjuk (az előtte álló szóközökkel együtt). Ha a mezőszélességet nem adjuk meg, a fordítóprogram egy e típusának megfelelő értéket tételez fel. Az f, az ún. törtrészhossz szintén egy választható formázási lehetőséget biztosít, de csak akkor használható, ha e valós típusú, f-nek pozitív egész értékű kifejezésnek kell lennie, és azt mutatja, hogy a tizedespont után még hány számjegy áll.
Ha e karakter típusú, w alapértéke 1. Ezért Write(F,C) f:=C; Put(F)-ből áll.
Ha e egész típusú, akkor w alapértékét a megvalósítás határozza meg. Ha w kisebb, mint az egész szám kiírásához szükséges karakterek száma, a szám akkor is teljes egészében (ha e negatív, akkor előjellel együtt) kiíródik.
Ha e füzér típusú, w alapértelmezés szerint a füzér hossza. Ha w ennél kisebb, e-nek az első w karaktere íródik ki.
Ha e logikai típusú, w alapértéke a gépi megvalósítástól függ. w értékétől függően [(8)-nak megfelelően] a 'true' vagy a 'false' karakterlánc íródik az állományba. Az írásmódot, tehát hogy a 'true', ill. a 'false' szót kis-, ill. nagybetűkkel, vagy mindkettőt alkalmazva írja az eljárás, ugyancsak a megvalósítás szabja meg.
Ha e valós típusú, w alapértékét a megvalósítás határozza meg. Ha w kisebb, mint a valós szám leírásához szükséges karakterek száma, a fennmaradó helyekre (ha e negatív, az előjel helyére is) szóköz kerül. Ha f-et (a törtrész hosszát) nem adtuk meg, e értéke fixpontos, egyébként pedig lebegőpontos, normál alakban íródik ki.
A fixpontos ábrázolás általános alakja a következő karaktersorozat: mínuszjel (csak ha a szám negatív), az egészrészt alkotó számjegyek, egy pont (a tizedespont), végül a törtrészt alkotó számjegyek.
A lebegőpontos ábrázolás általános alakja a következő w karakterből álló füzér: szóköz vagy mínuszjel, egy számjegy, egy pont (a tizedespont), egy számjegysorozat, az E (vagy e) betű, plusz- vagy mínuszjel, végül egy - a megvalósítás által meghatározott hosszúságú -, a kitevőt ábrázoló számjegysorozat. Az első, az E betű előtt álló számjegysorozat hossza w értékétől függ. A decimális lebegőpontos alak előtt bevezető szóközök - az említett előjelpozíció kivételével - nem állhatnak.
A 13.2. ábra valamennyi típus kiírására példát mutat:

13.2. ábra. Példák formázott write utasításokra
13.4. A Page eljárás
A szövegállományok kényelmesebb formázása érdekében a Pascal tartalmaz egy Page(oldal) nevű standard eljárást. Page(F) hatására az eljáráshívás utáni szöveg új "oldalra" kerül (az oldal aszerint értelmezendő, hogy F-et nyomtatjuk, képernyőre írjuk, vagy más módon visszük ki).
Page(F) egy, a megvalósításban meghatározott műveletet végez az F állományon. A legtöbb megvalósításban az eljárás a kívánt hatás eléréséhez szükséges vezérlő- (control) karakter(eke)t - pl. az ASCII FF (FormFeed : lapdobás) karaktert - iktatja az állományba.
Megjegyzések: Ha Page(F) hívása előtt az F állományon utoljára végzett művelet nem Writeln(F) volt, akkor Page(F) először is egy implicit Writeln(F)-et hajt végre. Hiba, ha Page(F) hívásakor F határozatlan vagy nincs írás módban. A megvalósítástól függ, mi történik, ha Page(F) után olvassuk az F állományt.
A nyelv formális leírása
1. Bevezetés
A Pascal nyelv kifejlesztésének hátterében két célkitűzés állt. Az első, hogy olyan nyelvet alkossunk, amely világosan és kézenfekvő módon tükröz bizonyos alapfogalmakat, s így lehetővé teszi, hogy a programozást rendszerbe foglalt, tudományosan megalapozott tantárgyként oktassuk. A második, hogy az új nyelvnek olyan gépi megvalósításait dolgozzuk ki, amelyek a jelenleg elterjedt számítógéptípusokon megbízhatóan és ugyanakkor hatékonyan alkalmazhatók.
Azért merült fel bennem, hogy a programozásoktatás céljaira új nyelvre lenne szükség, mert elégedetlen voltam a jelenleg használatos ismertebb nyelvekkel, amelyekben sok nyelvi eszköz és konstrukció gyakran nem magyarázható meg logikusan, és amelyek bizony nemegyszer ellentmondanak a következetes gondolkodásnak. Elégedetlenségem mellett ama meggyőződésem is sarkallt, hogy az a nyelv, amelyen a diákok először tanulják meg elképzeléseiket kifejezni, mélyrehatóan befolyásolja gondolkodásmódjukat, találékonyságukat, és hogy az ezeket a nyelveket átható rendszertelenség óhatatlanul rányomja bélyegét a diákok programozási stílusára.
Bőségesen van persze okunk a bizalmatlanságra, amikor már megint egy újabb programozási nyelv bevezetéséről hallunk. Kétségkívül alátámasztható valamelyest - ha mással nem, hát rövidlátó üzleti megfontolásokkal - azoknak az álláspontja, akik ellenzik, hogy olyan nyelven tanítsunk programozni, amely még nem terjedt el széles körben. Ha azonban az elterjedtség és az elfogadottság alapján választjuk meg a nyelvet, amelyet oktatni akarunk, akkor a programozás pedagógiai szempontból oly fontos területét egyhelyben topogásra kárhoztatjuk, hiszen a jövőben nyilván azt a nyelvet fogják a legtöbben használni, amit ma leginkább oktatunk. Úgy érzem tehát, hogy feltétlenül érdemes megkísérelnünk a kitörést ebből az ördögi körből.
Egy új nyelvet természetesen nem alkothatunk meg csupán azért, hogy mindenáron újat hozzunk létre. Ha a meglevő nyelvek eleget tesznek az említett követelményeknek és nem akadályozzák a módszeres struktúra kialakítását, a fejlesztőmunkának mindig ezekből kell kiindulnia. Ilyen értelemben a Pascal alapja az ALGOL-60 volt, ez ugyanis bármely más programozási nyelvnél jobban megfelel az oktatás igényeinek. Így a strukturálás elveit és lényegében a kifejezések alakját is az ALGOL-60-ból vettük át. Nem tartottuk volna ugyanakkor helyesnek, hogy a teljes ALGOL-60-at részhalmazként beépítsük a Pascalba, ez esetben ugyanis bizonyos - főként a deklarációkkal kapcsolatos - konstrukciós elvek nem lettek volna összeegyeztethetők azokkal az elvekkel, amelyek a Pascalban az ALGOL-60-hoz képest többletet jelentő eszközök természetes és kényelmes leírását biztosítják.
A Pascal az ALGOL-60-hoz viszonyítva elsősorban az adatstrukturálási lehetőségek terén gazdagabb, mivel véleményünk szerint ezek hiánya a fő oka az ALGOL-60 viszonylag szűk körű alkalmazhatóságának. A rekord- és az állománystruktúrát azért vezettük be, hogy a Pascalt üzleti, ügyviteli jellegű feladatok megoldására is alkalmassá tegyük, vagy legalábbis programozói tanfolyamokon bemutathassuk, hogy a nyelv ilyen feladatok megoldására is eredményesen alkalmazható.
2. A nyelv rövid leírása
Egy számítógépi program két fő részből áll. Az egyik részben a végrehajtandó műveleteket írjuk le, a másikban pedig azokat az adatokat, amelyeket e műveletek kezelnek. A műveleteket ún. utasításokkal, az adatokat pedig deklarációkkal és definíciókkal adjuk meg.
Az adatokat változók értékei szolgáltatják. Minden, a program valamelyik utasításában előforduló változót előzőleg változódeklarációval be kell vezetni, amely ehhez a változóhoz azonosítót és adattípust rendel. A típus lényegében az adott változó által fölvehető értékek készletét írja le, és meghatározza, hogy ezekkel az értékekkel milyen műveleteket lehet végezni. A Pascal nyelvben a típust vagy magában a változó deklarációban lehet megadni, vagy egy típus definíció segítségével típusazonosítót lehet hozzárendelni, azután ezzel a névvel hivatkozni rá
Egyszerű típusok az eleve definiált Real (valós) típus, továbbá a különféle diszkrét (megszámlálható) típusok. Minden egyszerű típus az értékek egy rendezett halmazát határozza meg. A diszkrét típusokat az jellemzi, hogy kölcsönösen egyértelmű hozzárendelés létesíthető értékeik, valamint az egész számok halmaza egy intervallumának elemei között - ez utóbbiakat nevezzük a szóban forgó értékek rendszámainak.
Az alapvető diszkrét típusok a programozó által definiálható felsorolt típusok, valamint az eleve definiált Boolean (logikai), Char (karakter) és Integer (egész) típusok. A felsorolt típusok új értékkészletet, és valamennyi, ehhez tartozó érték jelölésére külön azonosítót vezetnek be. A Char típus értékeit idézőjelek közé tett szöveggel, az Integer és Real típuséit pedig számokkal jelöljük; ezek szintaktikailag különböznek az azonosítóktól. A Char típus értékkészlete és értékeinek grafikus ábrázolása esetenként, az alkalmazott számítógépes rendszer karakterkészletének függvényében változik.
Diszkrét típust definiálhatunk valamelyik alapvető diszkrét típus (az ún. törzstípus) résztartományaként is, mégpedig úgy, hogy megjelöljük a kívánt résztartományt alkotó értékek intervallumának legkisebb és legnagyobb elemét.
A strukturált típusokat elemeik típusának megadásával és a strukturálás módjának megjelölésével definiáljuk. Az egyes strukturálási módokat a strukturált típusú változók elemeinek elérésére szolgáló mechanizmusok különböztetik meg egymástól. A Pascal nyelv a strukturálás négy alapvető módját ismeri: a tömb-, a rekord-, a halmaz- és az állománystruktúrát.
A változók deklarációja során egy azonosítóhoz hozzárendelünk egy típust, és amikor az ezt a változó deklarációt tartalmazó blokkot (l. alább) meghívjuk, az azonosító által megjelölt változó rendelkezésünkre áll. Az ilyen explicit módon deklarált változókat statikusaknak is nevezzük. Változókat azonban végrehajtható utasításokkal is generálhatunk; az ilyen dinamikus generálás egy (az explicit azonosítót helyettesítő) ún. mutatót eredményez, amelynek segítségével később a változóra hivatkozhatunk. Ezeknek a mutatóknak az értékét velük megegyező típusú változókhoz és függvényekhez rendelhetjük hozzá. Minden mutató típushoz tartozik egy rögzített, ún. főtípus, és a mutató típus valamely mutató értéke által kijelölt bármely változónak a főtípushoz kell tartoznia. Az ilyen mutató értékeken kívül minden mutató típus tartalmazza a nil értéket is, amely nem jelöl ki változót. Minthogy a strukturált típusú változók elemei mutató típusúak is lehetnek, egy mutató típus főtípusa pedig maga is lehet strukturált, a mutatók alkalmazása a legáltalánosabb véges gráfok leírását is lehetővé teszi.
A legalapvetőbb utasítás az értékadó utasítás. Ez arról intézkedik, hogy egy kifejezés kiértékelésével kapott érték egy változóhoz (vagy annak egy eleméhez) rendelődjék hozzá. A kifejezések változókból, konstansokból, tömbparaméterek indexhatáraiból, halmazgenerátorokból, továbbá olyan műveleti jelekből és függvényekből állnak, amelyek az említett mennyiségekre hatva valamilyen értéket adnak eredményül. A változókat, konstansokat és függvényeket vagy magában a programban kell deklarálni, vagy standard ("eleve deklarált") objektumokról van szó. A Pascal nyelv a műveleti jelek egy rögzített halmazát értelmezi, e jelek mindegyike úgy tekinthető, mint amely egy, az operandusok típusáról az eredménytípusra való leképezést jelöl. A műveleti jeleket négy csoportra osztjuk.
Az eljárásutasítás a kijelölt eljárás (l. alább) végrehajtásáról gondoskodik. Az értékadó és eljárásutasítások azok a komponensek, "téglák", amelyekből a strukturált utasítások felépülnek. Ez utóbbiak az őket alkotó részutasítások sorrendben, szelektíven vagy ismételten történő végrehajtásáról, gondoskodnak. A sorrendben történő végrehajtás az összetett, a feltételes vagy szelektív végrehajtás az if és case, az ismételt végrehajtás pedig a repeat, while és for utasítások eredménye. Az if utasítás egy logikai kifejezés értékétől függően hajtat végre egy utasítást, míg a case utasítás segítségével több utasítás közül választjuk ki a végrehajtandót, egy diszkrét kifejezés értékének megfelelően. A for utasítást arra használjuk, hogy a ciklusmagot egymás után többször hajtassuk végre, miközben egy ún. ciklusváltozó diszkrét értékek egy sorozatán fut végig. A repeat és a while utasításokat másképpen használjuk.
A Pascal nyelvben ezenkívül egy goto utasítás használatára is lehetőség van, amely azt jelzi, hogy a végrehajtást a program egy másik pontján kell folytatni, ezt a helyet egy címke jelöli, amelyet deklarálni kell.
Az utasításokból, továbbá a címkék, konstansok, típusok, változók, eljárások és függvények deklarációiból blokkokat állítunk össze. A címkékre, konstansokra, változókra, típusokra, eljárásokra és függvényekre csak azon a blokkon belül lehet hivatkozni, ahol deklaráltuk őket, ezért ezeket a blokkra nézve lokálisaknak nevezzük. Azonosítóiknak csak a blokkot alkotó programszövegen belül van értelmük, ezt nevezzük az említett azonosítók hatáskörének. Blokkok az alapegységei a programok, eljárások és függvények deklarációinak is. Ilyen esetekben a blokkhoz egy nevet (azonosítót) rendelünk, amellyel a blokkra hivatkozni lehet. Minthogy az eljárásokat és függvényeket egymásba ágyazhatjuk, a hatáskörök is egymásba ágyazódhatnak.
Az eljárásokhoz és függvényekhez rögzített számú paraméter tartozik. Az eljáráson vagy függvényen belül ezek mindegyikét egy-egy azonosító jelzi, amelyet formális paraméternek nevezünk. Amikor egy eljárást vagy függvényt hívunk, minden paraméteréhez ki. kell jelölni egy aktuális mennyiséget; az eljárás vagy a függvény belsejéből erre a mennyiségre a formális paraméter segítségével hivatkozhatunk. Az ilyen mennyiségeket aktuális paramétereknek nevezzük. Négyféle paramétert különböztetünk meg: az érték-, a változó-, az eljárás- és a függvényparamétereket. Az első esetben az aktuális paraméter egy kifejezés. A formális paraméter, az eljárás vagy függvény hívásának kezdetén az e kifejezés kiértékelésével kapott értéket veszi föl. A formális paraméter lokális változót jelöl. Változóparaméter esetén az aktuális paraméter egy változót jelöl, és a formális paraméter az eljárás vagy a függvény hívása során mindvégig ugyanezt a változót jelöli. Az eljárás- és a függvényparaméterek esetén az aktuális paraméter eljárás-, ill. függvény azonosító.
A függvényeket az eljárásokhoz hasonlóan deklaráljuk, azzal az egyetlen különbséggel, hogy a függvénynek valamilyen eredményt kell adnia, amelynek a függvény deklarációjában előre megadott típushoz kell tartoznia. Az eredménytípus csak egyszerű vagy mutató típus lehet. A függvényeket kifejezések alkotórészeiként is alkalmazhatjuk. A függvény deklarációkon belül kerüljük a nem lokális változóknak való értékadást és más olyan műveleteket, amelyek ún. mellékhatást eredményezhetnek!
3. A jelölésmód és a terminológiák
A szintaktikai egységeket dőlt betűkkel írott szavakkal (metaazonosítókkal) jelöljük, és a kiterjesztett Backus-Naur-forma (EBNF) szabályai szerint definiáljuk [13]. Minden szabály egy EBNF-kifejezés segítségével definiál egy metaazonosítót. Az EBNF-kifejezés egy vagy több, egymástól függőleges vonallal (|) elválasztott, alternatív szókapcsolatból áll. A szókapcsolatnak nulla, egy vagy több eleme van, amelyek mindegyike lehet metaazonosító, idézőjelek közé tett, betűkből álló szimbólum, vagy egy újabb, egymásba skatulyázott kapcsos, szögletes, vagy gömbölyű zárójelek közé zárt EBNF-kifejezés. A kapcsos { és } zárójelek a (nulla- vagy többszöri) ismétlést jelzik, a szögletes [ és ] zárójelek azt, hogy a közéjük zárt tétel opcionális (azaz legfeljebb egyszer szerepelhet, de el is hagyható), végül a gömbölyű ( és ) zárójelek (amelyeket pontosan egyszer alkalmazunk) a bezárt kifejezés együvé tartozását.
A 4. fejezetben az EBNF-szabályok segítségével leírjuk, hogyan képezhetőek a szótári szimbólumok karakterekből; más karakter egyetlen szimbólumban sem fordulhat elő. (A továbbiakban ennek ellenére a teljes magyar karakterkészletet használni fogjuk; ezek nélkül ugyanis az eredeti szövegben használt beszédes változók lefordítása nehézségekbe ütközne, ill. olvasásuk - aki ékezetek híján, akár a táviratokban szokásos módon, a magánhangzó után írt "e" betűvel jelölve az ékezetes betűt - kényelmetlen volna. (A ford.)) Az EBNF-szabályokat az 5-től a 13. fejezetig arra használjuk, hogy a szimbólumok segítségével definiáljuk a programok szintaxisát; ezeket a szimbólumokat - miként azt a 4. fejezetben le fogjuk írni - elválasztójelek választhatják el egymástól (vagy előzhetik meg).
A hiba kifejezés a program olyan tevékenységét vagy állapotát jelzi, amely az érvényes normákat megsérti, és amelyet valamely adott processzor esetleg elmulaszt jelezni.
A rendszer által definiált kifejezés azt jelenti, hogy egy adott Pascal-konstrukció az egyes alkalmazott rendszereken különböző lehet, és hogy minden rendszernek meg kell adnia, hogyan valósítja meg a szóban forgó konstrukciót.
A rendszerfüggő kifejezés azt jelenti, hogy egy adott konstrukció az egyes alkalmazott rendszerekben különböző lehet, de nem szükségképpen adják meg, hogy az illető rendszer hogyan valósítja meg a szóbanforgó konstrukciót.
A bővítés olyan kiegészítő konstrukció, amely általában nem minden rendszerben hozzáférhető, és amely önmagában nem érinti vagy érvényteleníti a standard Pascal konstrukcióit. Az egyes rendszerek igen gyakran tartalmaznak bővítéseket, például további előredefiniált és -deklarált konstansokat, típusokat, változókat, eljárásokat és függvényeket.
Egy standard program nem függhet semmiféle rendszerfüggő konstrukciótól vagy bővítéstől. Ha pedig egy programot több rendszerben is akarunk futtatni, rendkívül óvatosaknak kell lennünk a rendszer által definiált konstrukciók (pl. karakterkészlet vagy az egész számok részére megszabott értékhatárok) alkalmazásával is.
4. Szimbólumok és elválasztok
A program egy, a Pascal szintaktikus szabályainak megfelelően elrendezett szimbólum-sorozat. A szomszédos szimbólumokat az olvashatóság kedvéért gyakran elválasztó-szimbólumokkal határoljuk el. A szimbólumokat a következő csoportokra osztjuk: speciális szimbólumok, azonosítók, direktívák, számok, címkék és karakterfüzérek. Elválasztok a szóköz, a magyarázat és a programszövegben a sorok vége.
SpeciálisSzimbólum = "+" | "-" | "*" | "/" | "=" | "<>" | "<" | "<=" | ">" | ">=" | "(" | ")" | "[" | "]" | ":=" | "." | ".." | ":" | ";" | "^" | Alapszó
Alapszó = "div" | "mod" | "nil" | "in" | "or" | "and" | "not" | "if" | "then" | "else" | "case" | "of" | "repeat" | "untl" | "while" | "do" | "for" | "to" | "goto" | "downto" | "begin" | "end" | "with" | "const" | "var" | "type" | "array" | "record" | "set" | "file" | "function" | "procedure" | "label" | "packed" | "program" |
A standard Pascalban az alábbi módosításokat engedjük meg:
A legtöbb szimbólumot betűkből és számjegyekből állítjuk össze. A füzérek esetétől eltekintve az azonos hangot jelölő kis- és nagybetűk között nem teszünk különbséget.
Betű = "a" | "b" | "c" | "d" | "e" | "f" | "g" | "h" | "i" | "j" | "k" | "l" | "m" | "n" | "o" | "p" | "q" | "r" | "s" | "t" | "u" | "v" | "w" | "x" | "y" | "z".
Számjegy = "0" | "1" | "2" | "3" | "4" | "5" | "6" | "7" | "8" | "9".
Azonosítókkal jelöljük a konstansokat, a típusokat, a változókat, az eljárásokat, a függvényeket, a mezőket és a korlátokat. A direktívákat az eljárások és függvények deklarációiban alkalmazzuk.
Azonosító = Betű {Betű | Számjegy} .
Direktíva = Betű {Betű | Számjegy}.
Egy alapszó, azonosító vagy direktíva karaktersora az általa tartalmazott betűk és számjegyek teljes sorozata. Az azonosítók és direktívák karaktersora nem egyezhet meg egyetlen alapszóéval sem.
Példák azonosítókra (hat különböző karaktersor):
ElsőHely rend EljárásVagyFüggvénydeklaráció
Erzsébet János EljárásVagyFüggvényfej
Az egyes azonosítók karaktersorának deklaráció vagy definíció ad sajátos jelentést, és egy adott azonosító karaktersora nem rendelkezhet más jelentéssel a programnak azon részén belül, amelyet a deklaráció vagy definíció hatáskörének nevezünk (l. a 10. fejezetet).
A számokat a szokásos tízes számrendszerbeli írásmóddal ábrázoljuk. Az előjel nélküli egész és valós számok a standard Integer, ill. Real típusba tartozó konstansok (l. a 6.1.2. pontot). Egy előjel nélküli valós számban a karakterisztika előtt álló "e" betű jelentése: "...-szer 10 a ...-ediken". A standard Maxint konstans rendszer által definiált értéke az a maximális érték, amely egy előjel nélküli egész számnak adható.
ElőjelNélküliSzám = ElőjelNélküliEgész | ElőjelNélküliValós.
ElőjelNélküliEgész = SzámjegyekSorozata.
ElőjelNélküliValós = ElőjelNélküliEgész "." SzámjegyekSorozata ["e" Karakterisztika ] |
ElőjelNélküliEgész "e" Karakterisztika.
Karakterisztika = [Előjel] ElőjelNélküliEgész.
Előjel = "+" | "-".
SzámjegyekSorozata = Számjegy {Számjegy }.
Példák előjel nélküli egész számra:
1
100
00100
Példák előjel nélküli valós számra:
0.1
0.1e0
87.35e+8
1E2
A numerikus értékek szövegállományokból való beolvasása előjeles számok formájában történik (L. a 12. fejezetet).
ElőjelesSzám = ElőjelesEgész | ElőjelesValós.
ElőjelesEgész = [Előjel] ElőjelNélküliEgész.
ElőjelesValós = [Előjel] ElőjelNélküliValós.
A füzérek aposztrófok közé zárt, füzérelemekből álló sorozatok. A füzérelemek a standard Char típusnak a megvalósítás során definiált elemei és vagy két szomszédos aposztrófból állnak, vagy aposztróftól különböző, a megvalósítás során definiált karakterek. Két különböző, füzér-elemként előforduló karakternek a Char típus különböző értékeit kell jelölnie. A két aposztrófból álló füzérelem jelöli az aposztróf karaktert.
Karakterfüzér = " ' " Füzérelem {Füzérelem} " ' ".
Füzérelem = " '' " | BármelyAposztróftólKülönbözőKarakter.
Egy füzér akkor Char típusú konstans, ha egyetlen füzérelemből áll; máskülönben füzér típusú konstans (l. a 6.2.1. pontot), amelynek annyi eleme van, ahány füzérelemből áll.
Megjegyzés: Egy füzér csak egy programsort foglalhat el.
Példák füzérre:
A
';'
' '' '
'Pascal'
'Ez egy karakterfuzer'
Elválasztókat a program bármely két szomszédos szimbóluma között vagy a program első szimbóluma előtt elhelyezhetünk. Legalább egy elválasztónak kell állnia két szomszédos azonosító, direktíva, alapszó, címke, vagy szám között. Elválasztó a szóköz, a program egy sorának a vége és a magyarázat. A program jelentése nem változik meg, ha benne egy magyarázatot szóközzel helyettesítünk.
Magyarázat = ("{" | "(*"){MagyarázatElem} ("{" | "*)").
A MagyarázatElem vagy egy sor vége, vagy egy tetszőleges karaktersorozat, amely nem tartalmazza a "{" vagy a "*)" jelet.
Megjegyzés: Szintaktikailag helyes a magyarázat { ...*) vagy (*... } módon való jelölése is. A {(*) magyarázat ekvivalens a {(} magyarázattal.
5. Konstansok
A konstansdefiníció egy konstansazonosítót vezet be annak az értéknek a jelölésére, amelyet a definícióban szereplő konstans ad meg. Az a konstansazonosító, amelyet éppen definiálunk, nem szerepelhet a definíció "konstans" részében. A konstansdefiniciókat konstansdefiníciós részekbe gyűjtjük össze.
KonstansdefíníciósRész = ["const" Konstansdefinició ";" {Konstansdefinició ";"}].
Konstansdefiníció = Azonosító "=" Konstans.
Konstans = [Előjel] (ElőjelNélküliSzám | Konstansazonosító) | Füzér.
Konstansazonosító = Azonosító.
Az olyan konstansazonosítónak, amely elé ("+" vagy "-") előjelet illesztettünk, Integer vagy Real típusú értéket kell jelölnie.
Három standard, előredefiniált konstansazonosító létezik: a rendszer által definiált, Integer típusú értéket jelölő Maxint, és a Boolean típusú értékeket jelölő false és true (l. a 6.1.2. pontot).
Példa konstansdefiníciós részre:
const N = 20;
Fenysebesség = 2.998e8 {m/s};
Sarkcsillag = 'Polaris';
epsz = 1E-6;
6. Típusok
A típus azon értékek halmazát határozza meg, amelyeket az ilyen típusú változók, kifejezések, függvények stb. fölvehetnek. A típuskompatibilitás szabályai határozzák meg, hogyan alkalmazhatóak különféle típusok egyazon kifejezésben, értékadásban stb.
A típusdefiníció típusazonosítót vezet be a típus megjelölésére. Az a típusazonosító, amelyet éppen definiálunk, nem szerepelhet másként a definíció "típus" részében, mint egy mutató típus főtípusa (l. a 6.3. szakaszt). A típusdefiníciókat típusdefiníciós részekbe gyűjtjük össze. A 6.4. szakaszban láthatunk példát egy típusdefiníciós részre.
TípusdefiníciósRész = ["type" TípusDefiníció ";" {TípusDefiníció ";"}].
Típusdefiníció = Azonosító "=" Típus.
Típusazonosító = Azonosító.
A típusokat a Típus EBNF metaazonosító jelöli. Ha a típus megjelölése pusztán egy típusazonosítóból áll, akkor ugyanazt a (már létező) típust határozza meg, amelyet a típusazonosító jelöl. Ha a típus megjelölése nem csak egy típusazonosítóból áll, akkor egy egészen új típust határoz meg. A típusokat néhány fontosabb tulajdonságuk alapján csoportosítjuk:
Típus = Egyszerű Típus |StrukturáltTípus | MutatóTípus.
6.1. Egyszerű típusok
Az egyszerű típus értékeknek egy rendezett halmazát határozza meg, és vagy a standard Real típussal egyezik meg, vagy valamilyen megszámlálható típus. Egy valós típusazonosító olyan típusazonosító, amely a valós típust jelöli.
EgyszerűTípus = MegszámlálhatóTípus | ValósTípusAzonosító.
ValósTípusAzonosító = Típusazonosító.
A megszámlálható típusokat az különbözteti meg a valós típustól, hogy értékeik és a rendszámok halmaza között kölcsönösen egyértelmű leképezés létesíthető. Minden megszámlálható típus rendszámai az egész számok halmazának részintervallumát alkotják.
Egy megszámlálható típus minden X értékére alkalmazható az alábbi három standard függvény:
| ord(x) | az X-nek megfelelő rendszámot adja meg; az eredmény Integer típusú. |
| succ(x) | az X után következő elemet adja meg. Ez azt jelenti, hogy succ(X) > X és ord(succ(X)) = ord(X)+1 föltéve, hogy X nem a legnagyobb ilyen típusú érték; ha igen, akkor succ(X) hibát eredményez. |
| pred(x) | az X-et megelőző elemet adja meg. Ez azt jelenti, hogy pred(X) < X és ord(pred(X)) = ord(X)-1, föltéve, hogy X nem a legkisebb ilyen típusú érték: ha igen, akkor pred(X) hibát eredményez. |
Egy megszámlálható típus értékeinek rendezését természetesen a hozzájuk tartozó rendszámok rendezésének megfelelően értelmezzük.
Egy megszámlálható típus vagy felsorolt típus, vagy a standard Integer, Char és Boolean típusok egyike, esetleg ezek valamelyikének résztartománya.
MegszámlálhatóTípus = FelsoroltTípus | RésztartományTípus | Típusazonosító.
MegszámlálhatóTípusAzonosító = Típusazonosító.
Egy megszámlálhatótípus-azonosító olyan típusazonosító, amely megszámlálható típust jelöl.
6.1.1. Felsorolt típusok
Egy felsorolt típus teljesen új értékek egy halmazát definiálja és minden egyes érték megjelölésére bevezet egy konstansazonosítót.
FelsoroltTípus = "("Azonosítólista ")".
Azonosítólista = Azonosító {"," Azonosító}.
Az első azonosító jelöli a legkisebb értéket, amelynek rendszáma zérus. A lista minden további azonosítója az őt megelőző azonosító által megjelölt érték után következő értéket jelöli. A konstansazonosítók tehát értékük növekvő sorrendjében szerepelnek a listán.
Példák felsorolt típusra:
(Vörös, Narancssárga, Sárga, Zöld, Kék)
(Treff, Káró, Kör, Pikk)
(Hétfő, Kedd, Szerda, Csütörtök, Péntek, Szombat, Vasárnap)
6.1.2. Standard egyszerű típusok
A Pascal nyelvben az alábbi, előre definiált standard típusazonosítók vannak.
| Real | a valós számok halmazának egy, a konkrét Pascal rendszer által definiált részhalmazát határozza meg. |
| Integer | azon egész számok halmazát jelöli ki, amelyeknek abszolút értéke nem haladja meg a standard MaxInt konstansazonosító rendszer által definiált értékét. Bármely I egész számra ord(I) = I. |
| Boolean | a standard false és true konstansazonosítókkal jelölt igazságértékek halmazát jelöli ki. Megjegyezzük, hogy false < true és ord(false) = 0. |
| Char | egy, a rendszer által definiált karakterkészletet jelöl ki. Az ide tartozó karakterek rendszámát a rendszer definiálja úgy, hogy: |
|
6.1.3. Résztartomány típusok
Egy résztartomány típus által meghatározott értékkészlet valamely más, a résztartomány típus törzstípusának nevezett megszámlálható típus értékkészletének részhalmaza. A résztartomány típus a hozzá tartozó legkisebb és legnagyobb értéket adja meg, és minden, e kettő közé eső értéket tartalmaz.
RésztartományTípus = Konstans ".." Konstans.
Mindkét konstansnak a törzstípushoz kell tartoznia. Az elsőként megadott konstans jelzi a legkisebb értéket, és nem haladhatja meg a legnagyobb értéket kijelölő, másodiknak megadott konstanst.
Példák résztartomány típusra:
1..N
-10..+10
Hétfő..Péntek
6.2. Strukturált típusok
A strukturált típusokat elemeik típusa és strukturálásuk módja jellemzi. Egy strukturált típusban ezenkívül azt is jelezhetjük, milyen módon kívánjuk az adatokat ábrázolni. Egy strukturált típus előtt álló packed szimbólum a program jelentését (két kivételtől eltekintve) nem befolyásolja, csak a fordítóprogramot utasítja, hogy a szóban forgó típus értékeinek tárolásánál takarékoskodjék a hellyel, még ha emiatt kevésbé hatékonyan lehet is majd a struktúra elemeihez hozzáférni; a visszakeresésüket szolgáló kód pedig bonyolultabb lesz. Az ilyen strukturált típust tömörítettnek mondjuk. Az említett két kivétel az, hogy a füzér típusoknak (l. a 6.2.1. pontot) mindig tömörítetteknek kell lenniük, ill. hogy egy aktuális változóparaméter (l. a 11.3. szakaszt) nem lehet eleme valamely tömörített strukturált változónak. Ha egy tömörített strukturált típus valamely eleme maga is strukturált típusú, úgy az elem típusa csak abban az esetben lesz tömörített, ha típusleírásában szintén szerepel a packed szimbólum.
StrukturáltTípus = ["packed"] TömörítetlenStrukturáltTípus | StrukturáltTípusAzonosító.
TömörítetlenStrukturáltTípus = TömbTípus | RekordTípus | HalmazTípus | ÁllományTípus.
StrukturáltTípusAzonosító = Típusazonosító.
A strukturált típusazonosító olyan típusazonosító, amely strukturált típust jelöl.
6.2.1. Tömb típusok
A tömb típus rögzített számú, azonos típusú elemből álló struktúra. Az elemek típusát a tömb elemtípusának nevezzük. Az elemek és az indextípus értékei között kölcsönösen egyértelmű megfeleltetés létesíthető.
TömbTípus = "array" "["Indextípus {"," Indextípus} "]" "of" Elemtípus.
Indextípus = MegszámlálhatóTípus.
Elemtípus = Típus.
Több indextípus is megadható, például így: packed array [T1,T2, ..., Tn] of C.
Ez egyszerűen a
packed array [T1] of array [T2, ..., Tn] of C
jelölés rövidítése. A fenti két jelölés akkor is ekvivalens, ha egyikük elején sem szerepel a packed szimbólum.
Példák tömb típusra:
array [1..100] of Real
array [1..10, 1..20] of 0.99
array [Boolean] of Szin
array [Meret] of packed array ['a'..'z'] of Boolean
Minden tömb típusú érték az indexértékek halmazának egyértékű leképezése az elemtípushoz tartozó értékek halmazára.
Egy tömb típust füzér típusnak nevezünk, ha tömörített, elemtípusa a standard Char típus, indextípusa pedig az Integer 1-től n-ig terjedő résztartománya, ahol n nagyobb, mint 1. A karakterfüzérek (l. a 4. fejezetet) füzér típusú konstansok.
Példák:
packed array [1..FüzérHossza] of Char
packed array [1..2] of Char
6.2.2. Rekord típusok
Egy rekord típus rögzített számú, de egymástól esetleg különböző típusú elemekből áll. Az egyes elemeket, azok típusait, továbbá a rekord típus értékeit a rekord típus mezőlistája írja le.
RekordTípus = "record" Mezőlista "end".
Mezőlista = [(RögzitettRész [";" VáltozatRész] | VáltozatRész) [";"]].
RögzitettRész = Rekordszakasz {";" Rekordszakasz}.
Rekordszakasz = Azonosítólista ":" Típus.
Mezőazonositó = Azonosító.
A mezőlista tartalmazhat egy rögzített részt, amely rögzített számú, mezőnek nevezett elemet ad meg. A rekordszakasz hatására a benne elhelyezett listán felsorolt azonosítók az ugyancsak a rekordszakaszban megadott típusú mezők azonosítói lesznek. A mezőazonosító hatásköre a saját rekordszakaszára, továbbá azokra a mezőkifejezésekre és with utasításokra terjed ki, ahol esetleg alkalmaztuk (l. a 7.2.2. és 9.2.4. pontokat és a 10.2. szakaszt). Egy rekord típuson belül tehát minden mezőazonosító karaktersorának különbözőnek kell lennie.
Példák olyan rekord típusra, amelynek csak rögzített része van:
packed record
Ev: 1900.2100;
Honap: 1 ..12;
Nap: 1..31
endrecord
Vezeteknev, Keresztnev: packed array [1..32] of Char;
Eletkor: 0..99;
Hazas: Boolean
end
Egy mezőlista változat részt is tartalmazhat, amely egy vagy több változatot ad meg. Egy változat szerkezetét és értékeit annak mezőlistájában adjuk meg.
VáltozatRész = "case" Változatszelektor "of" Változat {";" Változat} .
Változat = Konstans {"," Konstans} ":" "('' Mezőlista ")".
Változatszelektor = [Kijelölőmező ":"] KijelölőTípus.
KijelölőTípus = MegszámlálhatóTípusAzonosító.
Kijelölőmező = Azonosító.
A kijelölő típus értékét egy, a változatot megelőző konstansnak kell megadnia. Egy adott változó részben minden ilyen értéknek egyszer és csak egyszer kell szerepelnie. Ha egy változatszelektorban előfordul egy kijelölőmező, akkor ennek azonosítója egy, a kijelölő típushoz tartozó mező mezőazonosítója lesz.
Egy adott változat részből egyidejűleg mindig csak egy változat lehet érvényes. Ha van kijelölőmező, akkor az a változat érvényes, amely előtt a kijelölőmező értéke áll. Kijelölőmező hiányában mindig az a változat van érvényben, amelyhez a rekord legutóbb földolgozott eleme is tartozik.
A mezőlista egy értéke meghatározza a rögzített részben megadott mezők értékeit, valamint a változat rész egy értékét. A változat rész egy értéke egy, az érvényes változatot föltüntető jelzésből, a kijelölőmező (ha egyáltalán létezik) értékéből és az érvényes változat egy értékéből áll.
Példák változat részt is tartalmazó rekord típusra:
record
case NevIsmert : Boolean of
false: ( );
true: (Name: packed array [1..NevMax] of Char)
end
record
X, Y: Real;
Terulet: Real;
case A: Alakzat of
Haromszog: (Oldal: Real; Hajlasszog, Szog1, Szog2: Szog);
Paralelogramma: (Oldal1, Oldal2: Real; Dolesszog, Szog3: Szog);
Kor: (Atmero: Real)
end
6.2.3. Halmaz típusok
Egy halmaz típus lehetséges értékeinek halmaza nem más, mint egy alaptípus értékeiből álló halmaz hatványhalmaza. Egy halmaz típus minden értéke tehát egy nulla vagy annál több elemet tartalmazó halmaz, és minden ilyen elem az alaptípus valamelyik értéke.
HalmazTípus = "set" "of" Alaptípus.
Alaptípus = MegszámlálhatóTípus.
Példák halmaz típusra:
set of Char
packed set of 0..11
6.2.4. Állomány típusok
Az állomány típus egyazon (elemtípusnak nevezett) típushoz tartozó elemek sorozata. A típushoz szervesen hozzátartozik az elemeknek a sorozatban elfoglalt helye, továbbá a mód, mely azt jelzi, hogy az állományt éppen létrehozzuk-e vagy pedig feldolgozzuk. A sorozat elemeinek számát, amelyet az állomány hosszának nevezünk, az állomány típusa nem rögzíti. Az állomány üres, ha hossza 0.
ÁllományTípus = "file" "of" Elemtípus.
Egy állomány típus elemtípusának hozzárendelhető típusnak (l. a 6.5. szakaszt) kell lennie. Ha az állomány feldolgozási módban van, a sorozat bármely eleméhez, továbbá az állomány vége pozícióhoz egyaránt hozzáférhetünk. A generálási módban lévő állományból csak az állomány vége pozícióhoz lehet hozzáférni. Egy állomány tartalmát a standard állománykezelő eljárásokkal és függvényekkel (l. a 11. fejezetet) kezelhetjük.
A standard Text strukturált típusazonosító egy olyan, különleges állomány típust jelöl, amelyben az említett sorozatot sorokra tördeljük. A sorok száma lehet 0 vagy annál több. A sorok karakterekből (Char típusú értékekből) épülnek föl, amelyeket egy speciális sor vége jel követ. Egy sorba kerülhet 0 vagy annál több karakter. A Text típusú változókat szöveg típusú állományoknak nevezzük. Egy nem üres szöveg típusú állományban, ha az feldolgozási módban van, az állomány vége pozíciót közvetlenül megelőző pozíción mindig sor vége jelnek kell állnia. A szöveg típusú állományok kezeléséhez számos további eljárás és függvény áll rendelkezésünkre (l. a 11.5. szakaszt és a 12. fejezetet).
6.3. Mutató típusok
Egy mutató típus abban különbözik az egyszerű és a strukturált típusoktól, hogy értékkészlete dinamikus; a mutató típusú értékek ugyanis a program végrehajtása során keletkeznek és szűnnek meg. Egy mutató típus értékkészlete mindig tartalmaz egy speciális, nil-lel jelölt értéket. Az értékkészlet összes többi elemét a program alkotja meg a standard New eljárás (l. a 11.4.2. pontot) segítségével. Az ilyen értékeket mutatóértékeknek nevezzük, mert mindegyik egy változóra, az ún. dinamikus változóra mutat (l. a 7.3. szakaszt). A dinamikus változóknak mindig a mutató típus főtípusához kell tartozniuk. A mutatóértéket és az általa kijelölt dinamikus változót a standard Dispose eljárás (l. a 11.4.2. pontot) segítségével lehet megszüntetni. A program befejeződésével valamennyi, a program által létrehozott mutatóérték eltűnik.
MutatóTipus = "^" Főtípus | MutatóTípusAzonosító.
Főtípus = Típusazonosító.
MutatóTípusAzonosító = Típusazonosító.
6.4. Példa típusdefiníciós részre
type TermeszetesSzam = 0..Maxint;
Szin = (Voros, Sarga, Zold, Kek);
Arnyalat = set of Szin;
Alakzat = (Haromszog, Paralelogramma, Kor);
Ev = 1900..2100;
Kartya = array[1..80] of Char;
Fuzer18 = packed array [1..18] of Char;
Komplex = record Re, lm: Real end;
Szemelymutato = ^Szemely;
Kapcsolat = (Hazas; Elettars, Egyedulallo);
Szemely = record
Vezeteknev, Keresztnev: Fuzer 18;
SzuletesiEv: Ev;
Neme: (Ferfi, No);
ApjaNeve, AnyjaNeve: Szemelymutato;
Baratai, Gyermekei : file of Szemelymutato;
KorabbiKapcsolatokSzama: TermészetesSzam;
case Allapot: Kapcsolat of
Hazas, Elettars: (Masjellemzo: Szemelymutato);
Egyedulallo: ( )
end;
Matrixindex = 1..N;
NegyzetesMatrix = array [Matrixindex, Matrixindex] of Real;
6.5. Típuskompatibilitás
Két típust kompatibilisnek mondunk, ha az alábbi négy feltétel valamelyike teljesül:
Egy típust hozzárendelhetőnek nevezünk, ha nem állomány típus, és nem is olyan strukturált típus, amelynek valamelyik elemtípusa nem hozzárendelhető.
Egy T2 típusú értékre azt mondjuk, hogy értékadás-kompatibilis egy T1 típussal, ha az alábbi négy feltétel valamelyike teljesül.
Ha a szintaktikus előírások értékadás-kompatibilitást követelnek meg, T1 és T2 pedig kompatibilis megszámlálható vagy kompatibilis halmaz típusok, mindig hiba keletkezik, ha a T2 típusú érték nem tartozik a T1 által meghatározott értékkészlethez.
7. Változók
Egy változóhoz mindig tartozik egy, a változó deklarációja által meghatározott típus. A változó csak ilyen típusú értékeket vehet föl.
Egy változó határozatlan, ha nincs hozzárendelve típusához tartozó érték. Teljesen határozatlannak mondunk egy változót akkor, ha határozatlan és (amennyiben strukturált) valamennyi eleme teljesen határozatlan. A változók létrejöttükkor mindig teljesen határozatlanok. Egy blokk belsejében deklarált változó a blokk aktiválásakor jön létre és megszűnik, amint a blokk nem aktív többé (l. a 10. fejezetet). A dinamikus változók a standard New és Dispose elírások segítségével hozhatók létre, ill. számolhatók fel (l. a 6.3. és a 11.4. szakaszt).
Egy változódeklaráció bevezeti egy vagy több változó azonosítóját, továbbá azt a típust, Melyhez e változók mindegyikének értéke tartozik. A változódeklarációkat változódeklarációs részbe gyűjtjük össze.
VáltozódeklarációsRész = ["var" Változódeklaráció ";" {Változódeklaráció ";"}].
Változódeklaráció = Azonosítólista ":" Típus.
Változóazonosító = Azonosító.
Példa változódeklarációs részre:
var W, X, Y: Real;
Z: Komplex;
I, J: Integer;
K: 0..9;
P, Q: Boolean;
Muveletijel: (Plusz, Minusz, Szorzasjel);
Kontrasztfokozat: array [0..63] of Real;
Lathatosag: array [Szin, Boolean] of Komplex;
Feny: Szin;
F: file of Char;
Arnyalat1, Arnyalat2: set of Arnyalat;
P1, P2: Szemelymutato;
A, B, C; NegyzetesMatrix;
Minneapolis, Zurich: packed record
Terulet: Real;
Lakossag: TermeszetesSzam;
Fovaros: Boolean
end;
A változókat sémáinkban a Változó EBNF metaazonosító jelöli.
Változó = TeljesVáltozó | Elemváltozó | DinamikusVáltozó | Pufferváltozó.
7.1. Teljes változók
Teljes változók a változóazonosítóval megjelölt változók.
TeljesVáltozó = Változóazonosító.
Példák teljes változóra:
Input
P1
Lathatosag
7.2. Elemváltozók
Egy strukturált változó elemei maguk is változók; az elemváltozóval egy strukturált változó valamelyik elemére hivatkozunk. Az elemváltozó szintaktikus szabályai a strukturált változó típusától függően változnak.
Elemváltozó = IndexeltVáltozó | Mezőkifejezés.
Egy strukturált változó valamely eleméhez való hozzáférés vagy az arra való hivatkozás egyúttal azt is jelenti, hogy magához a strukturált változóhoz is hozzá kell férnünk, ill. hivatkoznunk kell rá.
7.2.1. Indexelt változók
Az indexelt változók a tömbváltozók elemei. Egy tömbváltozó nem más, mint egy tömb típusú változó.
IndexeltVáltozó = Tömbváltozó "[" Index {"," Index}"]".
Index = MegszámlálhatóKifejezés.
Tömváltozó = Változó.
Az indexelt változóval a tömbnek azt az elemét érjük el, amelyet az indexkifejezés értéke megjelöl. A hivatkozás idején ennek az értéknek értékadás-kompatibilisnek kell lennie az index-típussal (l. a 6.5. szakaszt). A többszörös indexkifejezések kiértékelésének sorrendje rendszerfüggő.
Példák:
Kontrasztfokozat[12]
Kontrasztfokozat[l+J]
Lathatosag[Voros,True]
Ha egynél több index áll a szögletes zárójelben, mint a fenti Lathatosag[Voros,True] példában is, az egyszerűen a
Lathatosag[Voros] [True]
jelölés rövidítése.
7.2.2. Mezőkifejezések
A mezőkifejezések a rekordváltozók mezőit jelölik. Rekordváltozó az olyan változó, amely rekord típusú.
Mezőkifejezés = [Rekordváltozó "."] Mezőazonosító.
Rekordváltozó = Változó.
A mezőkifejezés a mezőazonosítónak megfelelő mezőt jelöli meg; benne csak a rekordváltozó rekord típusához tartozó mezőazonosítók szerepelhetnek. A with utasításon belül (l. a 9.2.4. fontot) amely kilistázza a rekordváltozót, a rekordváltozó és a "." elhagyható.
Példák mezőkifejezésre:
Z.Re
Lathatosag[Voros,True].lm
P2^.AnyjaNeve
Ha egy rekordváltozó valamelyik változata érvénytelenné válik, az adott változat valamennyi eleme teljesen határozatlan lesz. Ha a változat részben nincs kijelölőmező, és az egyik változathoz tartozó valamelyik elemre hivatkozunk, akkor ez a változat válik érvényessé, az összes többi érvényét veszti. Hibát eredményez, ha egy változat érvénytelen, vagy azzá válik, miközben hozzá akarunk férni vagy hivatkozunk valamelyik elemére. Ha a kijelölőmező határozatlan, a változat rész egyetlen változata sincs érvényben. A kijelölőmező nem lehet aktuális változóparaméter.
7.3. Dinamikus (azonosított) változók
A dinamikus változók jelölik a mutatóváltozók értékeivel megcímzett változókat. A mutatóváltozó egy mutató típusú változó.
DinamikusVáltozó = Mutatóváltozó "^".
Mutatóváltozó = Változó.
Ha egy dinamikus változóhoz hozzá akarunk férni, ahhoz egyúttal a mutatóváltozóhoz is hozzá kell férnünk. Ilyenkor hibát eredményez, ha a mutatóváltozó határozatlan, vagy aktuális értéke nil. Hibát eredményez az is, ha egy változót kijelölő mutatóértéket megsemmisítünk, miközben érvényben marad az általa megcímzett változóra való hivatkozás.
Példák dinamikus változóra:
p1^
p1^.ApjaNeve^
p1^.Baratai^^
7.4. Pufferváltozók
Az állományváltozók nem mások, mint az állomány típusú változók. Minden állományváltozóhoz tartozik egy ún. pufferváltozó.
Pufferváltozó = Állományváltozó "^".
Állományváltozó = Változó.
Ha az állományváltozó Text típusú, akkor a pufferváltozó a Char típusba tartozik; más esetekben a pufferváltozó típusa ugyanaz, mint az állományváltozó állomány típusának elemtípusa. A pufferváltozót az állományváltozó aktuális elemének eléréséhez használjuk. Ha egy állományváltozóhoz tartozó pufferváltozóra hivatkozás van érvényben, hibát okoz minden olyan művelet végrehajtása, amely ennek az állományváltozónak a sorrendjét, pozícióit vagy állapotát megváltoztatja. Ha egy pufferváltozóhoz akarunk hozzáférni, vagy arra hivatkozunk, akkor egyúttal a hozzá tartozó állomány változót is elérjük, ill. hivatkozunk rá.
Az állományváltozók kezelésére szolgáló standard eljárásokat és függvényeket a 11.4, 11.5. szakaszban és a 12. fejezetben ismertetjük.
Ha egy F szöveg típusú állományban Eoln(F) igazzá válik (l. a 11.5.2. pontot), akkor az F^ pufferváltozó a szóköz (' ') karakter típusú értéket fogja fölvenni. F-ben tehát kizárólag Eoln(F) segítségével lehet a sor vége jelet észlelni.
Példák pufferváltozóra:
Input^
P1^.Baratai^
P1^.Baratai^^.Gyermekei^
8. Kifejezések
A kifejezések olyan számítási előírások, amelyek az illető kifejezés kiértékelésekor egy értéket szolgáltatnak, hacsak az az eset nem áll elő, hogy a kifejezés egy függvényt aktivál, és ezt az aktív állapotot egy goto utasítás megszakítja (l. a 9.1.3. pontot és a 10. fejezetet). Az így kapott érték a kifejezésben előforduló konstansok, határok és változók értékétől, továbbá a kifejezés által behívott műveletektől és függvényektől függ.
Kifejezés = EgyszerűKifejezés [Relációsjel EgyszerűKifejezés],
EgyszerűKifejezés = [Előjel] Tag {AdditívMűveletiJel Tag}.
Tag = Tényező {MultiplikatívMűveletiJel Tényező}.
Tényező = ElőjelNélküliKonstans | Határazonosító | Változó | Halmazgenerátor |
Függvénykifejezés | "not" Tényező | "(" Kifejezés ")".
ElőjelNélküliKonstans = ElőjelNélküliSzám | Karakterfüzér | Konstansazonosító | "nil".
Halmazgenerátor = "[" [Elemleírás {"," Elemleírás }] "]".
Elemleírás = MegszámlálhatóKifejezés [ ".."' MegszámlálhatóKifejezés].
Függvénykifejezés = Függvényazonosító [AktuálisParaméterlista].
RelációsJel = "=" | "<>" | "<" | "<=" | ">" | "> = " | "in".
AdditívMűveletiJel = "+" | "-" | "or".
MultiplikatívMűveletiJel = "*" | "/" | "div" | "mod" | "and".
A megszámlálható kifejezés megszámlálható típusú kifejezés. A logikai és az egész kifejezés olyan kifejezés, amelynek típusa Boolean, ill. Integer.
MegszámlálhatóKifejezés = Kifejezés.
LogikaiKifejezés = MegszámlálhatóKifejezés.
EgészKifejezés = MegszámlálhatóKifejezés.
8.1. Operandusok
Egy tagon belül elhelyezkedő multiplikatív műveleti jelnek két operandusa van: a tagnak a műveleti jelet megelőző része és a jelet közvetlenül követő tényező. Egy egyszerű kifejezésben elhelyezkedő additív műveleti jelnek szintén két operandusa van: az egyszerű kifejezésnek az a része, amely műveleti jelet megelőzi, és a jelet közvetlenül követő tag. Egy relációjel két operandusa az azt közvetlenül megelőző és közvetlenül követő egyszerű kifejezés. Egy egyszerű kifejezésben elhelyezett előjel operandusa az előjelet közvetlenül követő tag. Egy tényezőben elhelyezkedő not operandusa a not-ot követő tényező.
Egy műveleti jel operandusai kiértékelésének sorrendje rendszerfüggő. Egy, a szabványhoz illeszkedő programon belül erre nézve semmilyen feltételezést nem kockáztathatunk meg. A rendszer működhet úgy, hogy a két operandus közül először a bal oldalit, de úgy is, hogy először a jobb oldalit értékeli ki, sőt, kiértékelheti a kettőt egyidejűleg is. Néha előfordul, hogy az egyik operandust egyáltalán nem is értékeli ki a másik operandus bizonyos értékei esetén. A (j * (i div j)) kifejezés értékét, ha a j értéke 0, az egyik rendszer tekintheti 0-nak, míg a másik a nullával való osztás miatt hibát jelez.
Egy tényező típusa az őt alkotó részek (pl. változók vagy függvények) típusából állapítható meg. Ha az alkotórészek résztartomány típusúak, akkor a tényező típusa a résztartomány törzstípusa lesz; ha az alkotórészek típusa olyan halmaz típus, amelynek alaptípusa egy résztartomány, akkor a tényező típusa olyan halmaz típus lesz, amelynek alaptípusa ennek a résztartománynak a törzstípusa; minden más esetben viszont a tényező típusa meg fog egyezni alkotórészeinek típusával.
A nil szimbólum minden mutató típushoz hozzátartozik és a nil értéket jelzi.
A halmazgenerátorok halmazértékeket jelölnek. Ha a halmazgenerátor nem tartalmaz elemleírást, akkor az üres halmazt jelöli, amely minden halmaz típushoz hozzá tartozó érték. A halmazérték elemeit minden más esetben le kell írni a halmazgenerátor elemleírásában. Egy halmazgenerátor elemleírásában szereplő valamennyi kifejezésnek ugyanahhoz a típushoz, a halmazgenerátor alaptípusához kell tartoznia. Egy halmazgenerátor típusa lehet tömörített és tömörítetlen és kompatibilis minden olyan halmaztípussal, amelynek alaptípusával a generátor alaptípusa kompatibilis.
Ha egy elemleírás egyetlen kifejezésből áll, akkor azt az elemet írja le, amelynek értéke a kifejezés által megadott érték. Egy a..b alakú elemleírás minden olyan x érték esetére definiál egy elemet, amelyre a < = x < = b. Ha a > b, akkor az a..b leírás nem definiál egyetlen elemet sem. Egy elemleíráson belül a kifejezések kiértékelésének és egy halmazgenerátoron belül az elemleírások kiértékelésének sorrendje rendszerfüggő.
Az egyetlen változóból álló tényező kiértékelése nem jelent mást, mint a változóra való hivatkozást, és eredménye a változó értéke lesz. Ilyen esetben hibát okoz, ha a változó határozatlan.
Az egyetlen függvénykifejezésből álló tényező kiértékelése a függvényazonosító által megjelölt függvény hívását jelenti (l. a 10.3. szakaszt). A formális paraméterek helyébe a megfelelő aktuális paraméterek kerülnek (l. a 11.3. szakaszt). Ha a hívás algoritmusa lefutott, a tényező értéke annak eredménye lesz: hibát eredményez, ha ez az eredmény határozatlan.
8.2. Műveleti jelek
A kifejezések összeállításának szabályai precedenciasorrendet határoznak meg a műveleti jelek négy osztálya között. A legmagasabb precedenciájú a not műveleti jel, ezután következnek az ún. multiplikatív műveleti jelek, majd az ún. additív műveleti jelek, végül a legalacsonyabb precedenciájúak, a relációs jelek. Azonos precedenciájú műveleti jelekből álló sorozat feldolgozása balról jobbra történik. A precedenciaszabályok tükröződnek a Kifejezésekre, Egyszerű-Kifejezésekre, Tag-okra és Tényezőkre vonatkozó (fenti) EBNF-szabályokban is.
A műveleti jeleket operandusaik és eredményük típusa szerint aritmetikai, logikai, halmaz- és relációs műveletek csoportjára is feloszthatjuk.
8.2.1. Aritmetikai műveleti jelek
Az aritmetikai műveleti jelek egész vagy valós operandusokra alkalmazhatók, és eredményül egész vagy valós számot adnak.
Az alábbiakban az egy operanduson ható műveleti jeleket, azaz az előjeleket foglaltuk össze.
Művelet Az operandus típusa Az eredmény típusa azonosság Integer vagy Real ugyanaz, mint az operandusoké előjelváltás Integer vagy Real ugyanaz, mint az operandusoké
Az alábbiakban a két operandusra vonatkozó műveleti jeleket foglaltuk össze:
Művelet Az operandus típusa Az eredmény típusa összeadás Integer vagy Real Integer vagy Real kivonás Integer vagy Real Integer vagy Real szorzás Integer vagy Real Integer vagy Real osztás Integer vagy Real Real osztás Integer Integer modulo Integer Integer
Az összeadás, a kivonás és a szorzás eredménye Integer típusú, ha mindkét operandus Integer típusú. Minden más esetben az eredmény Reál típusú.
Ha y zérus, az x/y alakú tag kiértékelése hibát eredményez.
Az x div y alakú tag kiértékelése hibát eredményez, ha y zérus; minden más esetben az alábbi két feltételt kielégítő értéket eredményez.
abs(x) - abs(y) < abs((x div y)*y) <= abs(x)
x div y = 0, ha abs(x) < abs(y);
minden más esetben x div y pozitív, ha x és y előjele megegyezik, és negatív, ha x és y előjele különböző.
Az x mod y alakú tag kiértékelése hibára vezet, ha y nem pozitív; ha y pozitív, az eredmény olyan k egész szám, hogy x mod y eleget tegyen a következő relációnak:
0 <= x mod y = x - k*y < y
Az egészműveletek esetén, ha mindkét operandus és a helyes eredmény egyaránt a -Maxint..Maxint tartományba esik, akkor egy, a szabványhoz illeszkedő nyelvet megvalósító rendszerben meg kell kapnunk a helyes eredményt. Ha azonban akár az operandusok valamelyike, akár az eredmény kívül esik a -Maxint..Maxint tartományon, a nyelvet megvalósító rendszer maga dönt, hogy helyesen végrehajtja-e a műveletet vagy hibaként kezeli.
Minden, valós eredményt adó műveletet és standard függvényt (l. a 11.5. szakaszt) közelítőnek kell tekinteni. A valós műveletek és standard függvények pontosságát a rendszer definiálja.
8.2.2. Logikai műveleti jelek
A logikai műveleti jelek a következők:
Művelet Az operandus típusa Az eredmény típusa logikai NEM Boolean Boolean logikai ÉS Boolean Boolean logikai VAGY Boolean Boolean
8.2.3. Halmazműveleti jelek
Az alábbiakban a halmazműveleti jeleket foglaltuk össze. A két operandus típusának mindig kompatibilisnek kell lennie (l. a 6.5. szakaszt). Az eredmény típusa tömörített, ha mindkét operandus típusa tömörített és tömörítetlen, ha mindkét operandus típusa ilyen.
Művelet Az operandus típusa Az eredmény típusa egyesítés T alaptípusú halmaz T alaptípusú halmaz differencia T alaptípusú halmaz T alaptípusú halmaz metszet T alaptípusú halmaz T alaptípusú halmaz
8.2.4. Relációs jelek
A relációs jeleket az alábbi táblázatban foglaltuk össze. Az in relációjeltől eltekintve az operandusok típusának vagy kompatibilisaknak kell lenniük, vagy egyikük a Real, másikuk az Integer típus kell, hogy legyen. Az in esetében viszont az első (bal oldali) operandusnak olyan megszámlálható típusúnak kell lennie, amely kompatibilis a második operandus halmaztípusának alaptípusával.
Az x <= y kifejezés, ahol x és y halmaz, pontosan akkor lesz igaz, ha x minden eleme eleme y-nak is, azaz, ha x részhalmaza y-nak.
A kompatibilis füzérek közötti rendezést a Char típusú értékek közötti rendezésnek (l. a 6.1.2. pontot) megfelelően értelmezzük.
Művelet Az operandus típusa Az eredmény típusa egyenlőség egyszerű, mutató, halmaz vagy Boolean Boolean nemegyenlőség egyszerű, mutató, halmaz vagy Boolean Boolean kisebb vagy egyenlő egyszerű vagy füzér Boolean tartalmazás halmaz Boolean nagyobb vagy egyenlő egyszerű vagy füzér Boolean tartalmazás halmaz Boolean kisebb egyszerű vagy füzér Boolean nagyobb egyszerű vagy füzér Boolean eleme diszkrét és halmaz Boolean
Példák tényezőre: Példák tagra: Y
15
(W+X+Y)
sin(X+Y)
[Piros, Sarga, Zold]
[1, 5, 10..19, 60]
not PX*Y
I/(1-I)
Q and not P
(X <= Y) and (Y < W)
Példák egyszerű kifejezésekre: Példák kifejezésekre: X + Kontrasztfokozat[2*L]
-X
P or Q
Arnyalat1 + Arnyalat2
I*J + 1X = 1.5
P <= Q
(I < J) = (J < K)
Sarga in Arnyalat1
9. Utasítások
Az utasítások végrehajthatónak nevezett algoritmikus tevékenységet jelölnek. Egy utasítást megelőzhet egy címke, amelyre a goto utasítások hivatkozhatnak. Az utasításokat utasításrészekbe gyűjtjük össze.
Utasítás = [Címke ":"] (EgyszerűUtasítás | StrukturáltUtasítás).
Utasításrész = ÖsszetettUtasítás.
9.1. Egyszerű utasítások
Egyszerűnek nevezzük az olyan utasítást, amelynek egyetlen valódi része sem alkot utasítást. Az üres utasítás semmiféle szimbólumot nem tartalmaz, és nem jelöl semmilyen tevékenységet.
EgyszerűUtasítás = ÜresUtasítás | ÉrtékadóUtasítás | EljárásUtasítás | GotoUtasítás.
ÜresUtasítás = .
9.1.1. Értékadó utasítások
Az értékadó utasítás segítségével hozzáférhetünk egy változóhoz vagy egy függvényhívás eredményéhez, és ennek aktuális értékét egy adott kifejezés kiértékelésével kapott értékkel helyettesíthetjük.
ÉrtékadóUtasítás = (Változó | Függvény azonosító) ":=" Kifejezés.
Fontos, hogy a kifejezés értéke értékadás-kompatibilis legyen a változó vagy a függvényazonosító típusával (l. a 6.5. szakaszt). A rendszertől függ, hogy a változót, ill. a függvényhívás eredményét a kifejezés kiértékelése előtt vagy után hívja-e be. A változó elérése a változóra való hivatkozással történik, amely az új érték hozzárendelése után érvényét veszti.
Példák értékadó utasításra:
X := Y + Kontrasztfokozat[31]
P := (1 <= I) and (l< 100)
I := Sqr(K) - (l*J)
Arnyalat2 := [Kek, Succ(C)]
9.1.2. Eljárásutasítások
Az eljárásutasítások az eljárásazonosító által megjelölt eljárás végrehajtását írják elő. Egy eljárásutasítás tartalmazhatja azon aktuális paraméterek listáját, amelyek az eljárásdeklarációban (l. a 11.1. szakaszt) definiált, megfelelő formális paramétereket fogják helyettesíteni.
Eljárásutasítás = Eljárásazonosító [AktuálisParaméterlista | WriteParaméterlista].
Ha az eljárásazonosító a standard Write és Writeln eljárások valamelyikét jelöli, akkor az aktuális paramétereknek eleget kell tenniük a WriteParaméterlista esetére előírt szintaktikus szabályoknak. Bármilyen más standard eljárást jelöl az eljárásazonosító, az aktuális paramétereknek meg kell felelniük a 11.4. szakaszban és a 12. fejezetben felállított szabályoknak.
Példák eljárásutasításra:
Kovetkezo
Transzponalt(A, N, N)
Felezés(Fct, -1.0, +1.0, X)
Writeln(Output, 'Cim')
9.1.3. A goto utasítás
A goto utasítás azt jelzi, hogy a feldolgozást a program egy másik pontján, mégpedig a címke által jelzett (l. a 10.1. és 10.3. szakaszt) programpontnál kell folytatni.
GotoUtasítás = "goto" Címke.
Egy címkével ellátott utasításnak és minden, erre a címkére hivatkozó goto utasításnak eleget kell tennie az alábbi két szabály egyikének:
Ezek a szabályok veszik elejét annak, hogy a vezérlést kívülről adjuk át egy strukturált utasítás, eljárás vagy függvény belsejébe. Az első szabály azt is megtiltja, hogy a goto utasítással egy feltételes utasítás egyik "elágazásáról" a másikra adjuk át a vezérlést.
Ha a programpont és a goto utasítás nem ugyanabban az utasításrészben található, minden hívás érvényét veszti (l. a 10.3. szakaszt), amely nem tesz eleget az alábbi két feltétel valamelyikének.
9.2. Strukturált utasítások
A strukturált utasítások más utasításokból épülnek fel. Ezeknek a részutasításoknak a végrehajtási módja szerint osztjuk négy csoportra a strukturált utasításokat: az összetett utasításokat alkotó részutasításokat az előre megadott sorrendben kell végrehajtani, a feltételes utasítás részutasításait csak abban az esetben, ha egy adott feltétel teljesül, a ciklusutasításokéit többször, a with utasításéit pedig kiterjesztett hatáskörben.
StrukturáltUtasítás = Összetettutasítás | FeltételesUtasítás | Ciklusutasítás | WithUtasítás.
Utasítássorozatnak utasítások egy olyan sorozatát nevezzük, amelyeket a leírás sorrendjében kell végrehajtani, hacsak egy goto utasítás másképp nem intézkedik.
Utasítássorozat = Utasítás {";" Utasítás}.
Utasítássorozatokat az összetett utasításokban (l. a 9.2.1. pontot) és a repeat utasításban (l. a 19.2.3.2. alpontot) alkalmazunk.
9.2.1. Összetett utasítások
Az összetett utasításokat alkotó részutasításokat az előre megadott sorrendben kell végrehajtani. Az utasítást alkotó utasítássorozatot a begin és az end alapszavak zárják közre.
ÖsszetettUtasítás = "begin" Utasítássorozat "end".
Példák összetett utasításra:
begin end
begin W:=X; X:=Y; Y:=W end
9.2.2. Feltételes utasítások
A feltételes utasítások az őket alkotó részutasítások közül választják ki az egyiket, és végrehajtják.
FeltételesUtasítás = IfUtasítás | CaseUtasítás.
9.2.2.1. Az if utasítás
Az if utasítás arról intézkedik, hogy a then alapszót követő utasítás végrehajtására csak akkor kerüljön sor, ha a logikai kifejezés értéke igaz. Ellenkező esetben az else alapszót követő utasítást kell végrehajtani, ha egyáltalán van ilyen.
IfUtasítás = "if"LogikaiKifejezés "then" Utasítás ["else" Utasítás].
Megjegyzés: Az
if e1 then if e2 then s1 else s2
utasítás szerkezetéből adódó szintaktikus kétértelműség feloldására a fenti konstrukciót az
if e1 then
begin if e2 then s1 else s2 end
utasítással tekintjük egyenértékűnek.
Példák if utasításra.
if X < 1.5 then W:= X+Y else W:= 1.5
if P1 <> nil then P1 = P1^.ApjaNeve
9.2.2.2. A case utasítás
A case utasítás egy megszámlálható típusú kifejezésből (az ún. esetindexből) és egy utasításlistából áll, amelynek minden elemét egy vagy több, az esetindexszel megegyező típusú konstans előzi meg. Hatására annak az utasításnak a végrehajtására kerül sor, amely előtt az esetindex aktuális értéke áll. Hibát eredményez, ha egyik utasítás előtt sem áll olyan konstans, amely ezt az aktuális értéket jelöli. Minden érték legfeljebb egy esetkonstanssal egyezhet meg.
CaseUtasítás = "case" Esetlndex "of" Eset {";" Eset} [";"] "end".
EsetIndex = MegszámlálhatóKifejezés.
Eset = Konstans {"," Konstans} ":" Utasítás.
Példák case utasításra:
Case MűveletiJel of
Plusz: W:= X+Y;
Minusz: W:= X-Y;
Szor: W:= X*Y
endCase I of
1: Y:=Sin(X);
2: Y:=Cos(X);
3: Y:=Exp(X);
4: Y:=In(X)
end
9.2.3. Ciklusutasítások
A ciklusutasítások bizonyos utasítások ismételt végrehajtásáról gondoskodnak. Ha a szükséges ismétlések számát előre, még az ismétlések megkezdése előtt ismerjük, akkor általában a for utasítás alkalmazása a legcélravezetőbb; más esetekben inkább a while vagy a repeat utasítást használjuk.
Ciklusutasítás = WhileUtasitás | RepeatUtasítás | ForUtasítás.
9.2.3.1. A while utasítás
WhileUtasítás = "while" LogikaiKifejezés "do" Utasítás.
A program ismételten végrehajtja az utasítást mindaddig, amíg a kifejezés értéke hamis nem lesz. Ha a kifejezés értéke már kezdetben hamis, az utasítás végrehajtására egyáltalán nem kerül sor. A
while B do S
utasítás ekvivalens az
if B then begin S; while B do S end
utasítással, hacsak S címkézett utasítást nem tartalmaz.
Példák while utasításra:
while Kontrasztfokozat[l] < X do I:=succ(l)
while I > 0 do begin
if odd(l) then Y:= Y*X;
I:= I div 2;
X:= Sqr(X)
endwhile not Eof(F) do begin
P(F^); Get(F) end
9.2.3.2. A repeat utasítás
RepeatUtasítás = "repeat" Utasítássorozat "until" LogikaiKifejezés.
A program mindaddig ismételten végrehajtja az utasítássorozatot, amíg a kifejezés igazzá nem válik. A
repeat S until B
utasítás ekvivalens a
begin S; if not B then repeat S until B end
utasítással, hacsak S címkézett utasítást nem tartalmaz.
Példák repeat utasításra:
repeat K:= I mod J; I:= J; J:= K until J = 0
repeat
P(F^);
Get(F^)
until Eof(F)
9.2.3.3. A for utasítás
A for utasítás azt jelzi, hogy egy utasítást ismételten végre kell hajtani, miközben egy, a for utasítás ciklusváltozójának nevezett változó értékek egy növő vagy fogyó sorozatát futja be.
ForUtasítás = "for" Ciklusváltozó ":=" Kezdőérték ("to" | "downto") Végérték "do" Utasítás.
Ciklusváltozó = Változóazonosító.
Kezdőérték = MegszámlálhatóKifejezés.
Végérték = Megszámlálható Kifejezés.
A ciklusváltozónak lokálisnak kell lennie arra a blokkra nézve, amelynek utasításrésze a for utasítást tartalmazza (l. a 10.2. szakaszt) és a kezdő- és végérték típusával kompatibilis megszámlálható típushoz kell tartoznia.
Az S utasításról azt mondjuk, hogy veszélyezteti a V változót, ha az alábbi négy eset valamelyike áll fenn:
A for utasításon belül egyetlen utasítás sem veszélyeztetheti a ciklusváltozót. Nem tartalmazhat a ciklusváltozót veszélyeztethető utasítást egyetlen olyan eljárás vagy függvény sem, amelyet ugyanabban a blokkban deklaráltunk, mint magát a ciklusváltozót. Ezek a szabályok azt biztosítják, hogy a ciklusmag utasítása ne módosíthassa a ciklusváltozó értékét.
Legyen T1 és T2 a V-vel megegyező típusú, P pedig Boolean típusú új változó (tehát olyan, amihez egyébként nem lehet hozzáférni). Ekkor a magyarázatként szolgáló megjegyzésektől eltekintve a
for V:= e1 to e2 do S
utasítás ekvivalens a
begin
T1:= e1; T2:= e2;
if T1 <= T2 then begin
{T2-nek értékadás-kompatibilisnak kell lennie a V típusával}
V:= T1; P:= false;
repeat
S;
if V = T2 then P:= true else V:= Succ(V)
until P
end
{V határozatlan}
end
utasítással, a
for V:= e1 downto e2 do S
utasítás pedig a
begin
T1:= e1; T2:= e2;
if T1 >= T2 then begin
{T2-nek értékadás-kompatibilisnak kell lennie a V típusával}
V:= T1; P:= false;
repeat
S;
if V = T2 then P:= true else V:= Pred(V)
until P
end
{V határozatlan}
end
utasítással.
Példák for utasításra:
for I:= 1 to 63 do
if Kontrasztfokozat[I] > 0.5 then write ('*') else write (' ')for I:= 1 to n do
for J:= 1 to n do begin
X:= 0;
for K:= 1 to n do
X:= X + A[I,K]*B[K,J];
C[I,J]:= X
endfor Feny:= Voros to Pred(Feny) do
if Feny in Arnyalat2 then Q(Feny)
9.2.4. A with utasítás
A with utasítás hozzáférést biztosít a listáján szereplő rekordváltozóknak, egy utasítás végrehajtásának erejéig. A hivatkozás addig marad érvényben, amíg ezen utasítás végrehajtása tart.
WithUtasítás = "with"RekordVáltozólista "do" Utasítás.
RekordVáltozólista = Rekordváltozó {"," Rekordváltozó}.
A with utasítás hatására a benne elhelyezett listán szereplő minden rekordváltozóra a hozzá tartozó összes mezőazonosító hatásköre úgy bővül, hogy kiterjedjen a belső utasításra is (l. a 10.2. szakaszt). E kibővült hatáskörön belül a mezőazonosítók anélkül szerepelhetnek egy mezőkifejezésben, hogy a rekordváltozót ismét megadnók. Ezek a mezőazonosítók ilyenkor a hivatkozott változó megfelelő mezejét jelzik. A
with r1, r2, ..., rn do S
jelölés egyszerűen a
with r1 do
with r2 do
...
with rn do S
jelölés rövidítése.
Példa with utasításra:
with Datum do
if Honap = 12 then begin
Honap:= 1; Ev:= Succ(Ev) end
else Honap:= Succ (Honap)
Ez az utasítás ekvivalens az
if Datum.Honap = 12 then begin
Datum.Honap:= 1;
Datum.Ev:= Succ(Datum.Ev)
end
else Datum.Honap:= Succ(Datum.Honap)
utasítással.
10. Blokkok, hatáskör, hívások
A blokkok azok az alapvető egységek, amelyekből a programok (l. a 13. fejezetet), továbbá az eljárások és a függvények (l. a 11. fejezetet) fölépülnek. A hatáskörre vonatkozó szabályok a program statikus (szöveg szerinti) szerkezete alapján határozzák meg, hogy egy adott helyen bevezetett azonosító karaktersorát a programon belül hol használhatjuk. A hívási szabályok a program dinamikus (végrehajtás szerinti) szerkezete alapján azt állapítják meg, hogy egy adott azonosító vagy címke milyen objektumot (például változót) jelöl.
10.1. Blokkok
Egy blokk definíciós és deklarációs részekből áll, amelyek mindegyike lehet üres is, továbbá egy utasításrészből.
Blokk = CímkedeklarációsRész
KonstansdefiníciósRész
TípusdefiníciósRész
VáltozódeklarációsRész
EljárásÉsFüggvénydeklarációsRész
Utasításrész.
A címkedeklarációs rész egy vagy több címkét vezet be, amelyek mindegyike az utasításrészben szereplő valamelyik utasítás előtt áll.
CímkedeklarációsRész = ["label" Számjegysorozat {"," Számjegysorozat} ";"].
Címke = Számjegysorozat.
Egy címke megjelenési formája az az egész szám, amelyet a címkét alkotó számjegysorozat a szokásos tízes számrendszerbeli ábrázolásmód szerint jelöl. Ez az érték nem lehet nagyobb 9999-nél.
10.2. Hatáskör
Egy definíció vagy egy deklaráció bevezeti egy azonosító vagy egy címke karaktersorát, és ehhez speciális jelentést rendel (például azt, hogy a bevezetett karaktersor egy változó azonosítójáé). A programnak azt a részét, amelyben ennek a karaktersornak, valahányszor előfordul, szükségképpen ez a jelentése, összefoglalóan az adott bevezetés (definíció vagy deklaráció) hatáskörének nevezzük. Egy adott karaktersornak - bevezetésének hatáskörén belül - először magában a karaktersor bevezetésében kell előfordulnia. Ez alól a szabály alól egyetlen kivétel van, nevezetesen az, hogy egy típusazonosító karaktersor egy mutató típus főtípusaként (l. a 6.3. szakaszt) az adott karaktersor bevezetését tartalmazó típusdefiníciós rész bármely pontján előfordulhat.
Amint azt ismertetni fogjuk, minden bevezetés a program valamely részére érvényes. Egy bevezetés hatásköre a programnak ez a része, elhagyva belőle azokat a részeket, amelyekre ugyanazon karaktersor egy másik deklarációja érvényes.
Az alábbi deklarációk arra a blokkra érvényesek, amelyben az adott deklaráció előfordul: egy címke a blokk címkedeklarációs részében, egy konstansazonosító a blokk konstansdefiníciós részében vagy egy felsorolt típusban, egy típusazonosító a blokk típusdefiníciós részében, egy változóazonosító a blokk változódeklarációs részében, egy eljárásazonosító egy blokkbeli eljárásdeklarációban (l. a 11.1. szakaszt), és egy függvényazonosító egy blokkbeli függvénydeklarációban (l. a 11.2. szakaszt). Ezeket a címkéket és azonosítókat az adott blokkra nézve lokálisaknak nevezzük.
A standard előre definiált és deklarált azonosítók implicit bevezetése minden programra érvényes.
Egy mezőazonosítónak egy rekord típuson belüli deklarációja a program alábbi részeinek mindegyikére érvényes:
A 3. pont esetben a mezőazonosító rész minden más hatáskörön kívül esik.
Egy paraméterazonosító paraméterlistán való deklarációja (l. a 11.3.1. pontot) a paraméterlistára érvényes. Ha pedig a paraméterlista egy eljárásdeklaráció eljárásfejéhez vagy egy függvénydeklaráció függvényfejéhez tartozik, akkor a paraméterazonosítónak megfelelő változóazonosító, határazonosító, eljárásazonosító vagy függvényazonosító bevezetése a szóban forgó eljárás- vagy függvény deklaráció blokkjára érvényes.
10.3. Hívások
Egy program (l. a 13. fejezetet), eljárás vagy függvény (l. a 11. fejezetet) hívása a program, eljárás vagy függvény blokkjának hívása.
Azt mondjuk, hogy egy blokk hívása a következő objektumok létezését feltételezi, ezek mindegyike csak addig létezik, amíg a hívás érvényben van.
Egy eljárás vagy függvény blokkjának hívása esetén azt mondjuk, hogy az az eljárást, ill. függvényt tartalmazó hívás belsejében van. Ha egy A hívás egy B hívás belsejében van, akkor A minden más olyan hívásnak is a belsejében van, amelynek B a belsejében van.
Egy algoritmusban előforduló eljárásutasítást vagy függvénykifejezést, amely egy blokkot hív, ezen hívás belépési (hívási) pontjának nevezünk.
11. Eljárások és függvények
Eljárásoknak és függvényeknek a program azon részeit nevezzük, amelyeket eljárásutasítások (l. a 9.1.2. pontot), ill. függvénykifejezések (l. a 8.1. szakaszt) hívnak. A programozó szükség szerint deklarálhat új eljárásokat és függvényeket. Az eljárásdeklarációkat és a függvénydeklarációkat az eljárás- és függvénydeklarációs részbe gyűjtjük össze.
EljárásÉsFüggvénydeklarációsRész = {(Eljárásdeklaráció | Függvénydeklaráció) ","}.
Ezen túlmenően a Pascal nyelvet megvalósító minden rendszernek lehetőséget kell adnia több, "előredeklarált" eljárás és függvény alkalmazására. Mint az ilyen esetekben általában, feltételezzük, hogy ezeknek a deklarált hatásköre teljes egészében tartalmazza a szóban forgó programot. Nem okoz tehát bajt, ha a program valamely deklarációja ugyanezt az azonosítót másként definiálja.
11.1. Eljárásdeklarációk
Az eljárásdeklaráció célja, hogy bevezessen egy eljárásazonosítót és hozzárendeljen ehhez az azonosítóhoz egy blokkot, továbbá esetleg egy formális paraméterlistát. Az eljárásazonosítót és a formális paraméterlistát az eljárásdeklaráció eljárásfeje vezeti be.
Az eljárást deklarálhatjuk csupán egyetlen eljárásdeklarációval, amely az eljárásfejből és a blokkból áll. Az eljárások deklarálásának ez a leggyakoribb formája.
Egy eljárás azonban deklarálható "előzetes deklarációval" is: az első eljárásdeklaráció egy eljárásfejből és a forward direktívákból áll, az ugyanazon eljárás- és függvénydeklarációs részben elhelyezett második deklaráció pedig egy eljárásazonosításból és a blokkból. Az eljárásazonosításban elhelyezkedő eljárásazonosítónak meg kell egyeznie az első deklarációban bevezetett azonosítóval. Megjegyezzük, hogy a formális paraméterlistát, ha egyáltalán van, a második deklarációban nem szerepeltetjük.
Eljárásdeklaráció = Eljárásfej ";" Blokk | Eljárásfej ";" Direktíva | Eljárásazonosítás ";" Blokk.
Eljárásfej = "procedure'' Azonosító [FormálisParaméterlista].
Eljárásazonosítás = "procedure" Eljárásazonosító
Eljárásazonosító = Azonosító.
Ha egy eljárásazonosító azon a blokkon belül, ahol deklaráltuk, egy eljárásutasításban szerepel, ez az eljárás rekurzív végrehajtását eredményezi.
Példa eljárásokat tartalmazó eljárás- és függvénydeklarációs részre:
procedure ReadInteger(var F:Text; var X: Integer);
var S: TermeszetesSzam;
begin
while F^<>' ' do
Get(F); S:=0;
while F^ in ['0'..'9'] do begin
S:= 10*S+ord(F^)-ord('0'));
Gef(F)
end;
X:= S
end {ReadInteger};procedure Felezes(Function F(X: Real): Real; A,B: Real; var Z: Real);
var M: Real;
begin {tegyuk fel, hogy F(A)<0 es F(B)>0}
while abs(A-N)>1e-10*Abs(A) do begin
M:= (A+B)/2.0;
if F(M)<0 then A:= M else B:= M
end;
X:= M
end {Felezes};procedure LNKO(M,N: Integer; var X,Y,Z: Integer);
{M es N legnagyobb kozos osztoja X, felteve, hogy M>=0 es N>=0}
{Altalanositott euklideszi algoritmus}
var A1,A2,B1,B2,C,D,Q,R: Integer;
begin
A1:=0; A2:=1;
B1:=1; B2:=0;
C:=M; D:=N;
while D<>0 do begin
{A1*M+B1*N=D, A2*M+B2*N=C es LNKO(C,D)=LNKO(M,N)}
Q:=C div R; R:=C mod D;
A2:=A2-Q*A1; B2:=B2-Q*B1;
C:=D; D:=R;
R:=A1; A1:=A2; A2:=R;
R:=B1; B1:=B2; B2:=R
end;
X:=C; Y:=A2; Z:=B2
{X = LNKO(M,N) = Y*M + Z*N}
end {LNKO};
11.2. Függvénydeklarációk
A függvénydeklaráció célja, hogy bevezessen egy függvényazonosítót és hozzárendeljen ehhez az azonosítóhoz egy eredmény típust, egy blokkot és esetleg egy formális paraméterlistát. A függvényazonosítót, az eredmény típusát és a formális paraméterlistát a függvénydeklaráció függvényfeje vezeti be.
A függvényt deklarálhatjuk csupán egyetlen függvénydeklarációval, amely a függvényfejből és a blokkból áll. A függvények deklarálásának ez a leggyakoribb formája.
Egy függvény azonban deklarálható "előzetes deklarációval" is: az első függvény deklaráció a függvényfejből és a forward direktívákból áll, az ugyanazon eljárás- és függvény deklarációs részben elhelyezett második deklaráció pedig egy függvényazonosításból és a blokkból. A függvényazonosításban elhelyezkedő függvényazonosítónak meg kell egyeznie az első deklarációban bevezetett azonosítóval. Megjegyezzük, hogy a formális paraméterlistát, ha egyáltalán van, továbbá az eredmény típusát a második deklarációban nem szerepeltetjük.
Függvénydeklaráció = Függvényfej ";" Blokk | Függvényfej ";" Direktíva | Függvényazonosítás ";" Blokk.
Függvényfej = "function'' Azonosító [FormálisParaméterlista] ":" Eredménytipus.
Eredménytípus = MegszámlálhatóTípusAzonosító | ValósTípusAzonosító | MutatóTípusAzonosító.
Függvényazonosítás = "function " Függvényazonosító.
Függvényazonosító = Azonosító.
Egy függvénydeklaráció blokkjának legalább egy értékadó utasítást kell tartalmaznia, amely a függvényazonosítóhoz értéket rendel. Ha egy függvényazonosító azon a blokkon belül, ahol deklaráltuk egy függvénykifejezésben szerepel, ez a függvény rekurzív végrehajtását eredményezi.
Példa függvényt tartalmazó eljárás- és függvénydeklarációs részre:
function Gyok(X: Real): Real;
{Newton-modszer}
var X0,X1: Real;
begin
X1:=X; {X>1}
repeat
X0:=X1;
X1:=(X0+X/X0)*0.5
until abs(X1-X0)<Epsz*X1; {epsz=0.0000001;}
Gyok:=X0
end {Gyok};function Max(A: vektor; N: Integer): Real;
{Az A[1], ..., A[N] elemek kozul a maximalis erteket keressuk}
var X: Real;
I: Integer;
begin
X:= A[1];
for I:=2 to N do {X = Max(A[1], ..., A[I-1]}
if X<A[I] then X:=A[I]
Max:=X
end {Max};function LNKO(M,N: TermeszetesSzam): TermeszetesSzam;
{M es N legnagyobb kozos osztojanak meghatarozasa.}
begin
if N=0 then LNKO:=M
else LNKO:=LNKO(M,M mod N)
end;function Hatvany(X: Real; Y: TermeszetesSzam): Real;
{X**Y kiszamitasa}
var W,Z: Real;
I: TermeszetesSzam;
begin
W:=X; Z:=1; I:=Y;
while I>0 do begin {Z*W**I = X**Y}
if odd(i) then Z:= Z*W;
I:=I div 2;
W:=Sqr(W)
end;
Hatvany:=Z
end {Hatvany};
11.3. Paraméterek
A paraméterek teszik lehetővé, hogy egy eljárás vagy függvény minden hívása azokkal az objektumokkal (értékekkel, változókkal, eljárásokkal és függvényekkel) dolgozzék, amelyeket a belépési (hívási) pontban (l. a 10.3. szakaszt) egy aktuális paraméterlista sorol fel. Az eljárás vagy függvényfejben elhelyezett formális paraméterlista határozza meg, hogy ezeket az objektumokat az eljárás vagy a függvény blokkjában milyen azonosítók jelzik, továbbá azt, hogy az aktuális paramétereknek milyen tulajdonságúaknak és típusúaknak kell lenniük.
A standard eljárások és függvények aktuális paraméterei nem mindig tesznek eleget a szokásos eljárásokra és függvényekre vonatkozó előírásoknak (l. a 11.4. és 11.5. szakaszt, valamint a 12. fejezetet).
11.3.1. Formális paraméterlisták
FormálisParaméterlista = "(" FormálisParaméterrész { ";" FormálisParaméterrész. } ")".
FormálisParaméterrész = Értékparaméterspecifikáció | Változóparaméterspecifikáció | Eljárásparaméterspecifikáció | Függvényparaméterspecifikáció.
Egy formális paraméterrész érték-, változó-, eljárás- vagy függvényparamétereket ad meg.
11.3.1.1. Formális érték- és változóparaméterek
Egy érték- vagy változóparaméter specifikáció az azonosítólistáján szereplő valamennyi azonosítót változóazonosítóként határozza meg. Ha a specifikációban egy típusazonosító is szerepel, az a változóazonosítók közös típusát jelöli. Ha illeszkedőtömb-sémát is tartalmaz, akkor a változóazonosítókat illeszkedőtömb-paramétereknek nevezzük, és típusuk az aktuális paraméter típusától függ. Egy adott híváson belül az egyazon formális paraméterrészben definiált valamennyi formális paraméter ugyanolyan típusú.
Megjegyzés: Az illeszkedőtömb-sémák alkalmazására nem minden, a Pascal nyelvet megvalósító rendszerben van lehetőség. Á Pascal nyelvet 0 szinten megvalósító rendszerekben nem alkalmazhatóak, az 1 szinten megvalósítóakban igen.
Értékparaméterspecifikáció = Azonositólista (Tipusazonositó | Illeszkedőtömbséma).
Változóparaméterspecifikáció = "var" Azonosítólista ":" (Típusazonosító | Illeszkedőtömbséma).
Illeszkedőtömbséma = TömörítettIlleszkedőtömbséma | TömörítetlenIlleszkedőtömbséma.
TömörítettIlleszkedőtömbséma = "packed" "array" "[" Indextípusspecifikáció "]" "of" Típusazonosító.
TömöritetlenIlleszkedőtömbséma = "array" "[" Indextípusspecifikáció {";" Indextípusspecifikáció} "]" "of" (Típusazonosító | Illeszkedőtömbséma).
Indextípusspecifikáció = Azonosító ".." Azonosító ":" MegszámlálhatóTípusAzonosító.
Határazonosító = Azonosító.
Az indextípus-specifikációban megadott két azonosító a megszámlálhatótípus-azonosító által megjelölt típusú határazonosítók. Az
array [Alsó1..Felső1: T1; Alsó2..Felső2: T2] of T
illeszkedőtömb-séma egyszerűen az
array [Alsó1 ..Felső1: T1] of array [Alsó2..Felső2: T2] of T
séma rövidítése.
Példa illeszkedőtömb-paramétert bemutató függvénydeklarációra:
function Max(A: array[L..H: Integer] of Real; N: Integer): Real;
{Valasszuk ki az A[L]..A[N] elemek kozul a legnagyobbat}
var X: Real;
I: Integer;
begin
for I:= Succ(L) to N do {X = Max A[L]..A[I-1]}
if X<A[I] then X:=A[I]
Max:= X
end {Max};
11.3.1.2. Formális eljárás- és függvényparaméterek
Egy eljárásparaméter-specifikáció az eljárásazonosítót vezeti be valamilyen, az eljárásfejben definiált, hozzá tartozó formális paraméterlistával együtt.
Eljárásparaméterspecifikáció = Eljárásfej.
Egy függvényparaméter-specifikáció a függvényazonosítót jelöli ki a függvényfejben definiált eredménytípussal és valamilyen hozzá tartozó formális paraméterlistával együtt.
Függvényparaméterspecifikáció = Függvényfej.
11.3.2. Aktuális paraméterlisták
Minden hívási ponton, azaz eljárásutasításnál vagy függvénykifejezésnél egy aktuális paraméterlista adja meg azokat az aktuális paramétereket, amelyekkel az adott hívás során az eljárás vagy függvény formális paramétereit helyettesíteni kell. Ha az eljárásnak vagy függvénynek nincs formális paraméterlistája, akkor a hívásban sem lehet aktuális paraméterlista. Az aktuális és a formális paraméterek közötti megfeleltetés a paraméterek saját listájukon elfoglalt pozícióinak megfelelően történik. Rendszerfüggő, hogy egy lista aktuális paramétereinek behelyettesítésére milyen sorrendben kerül sor.
AktuálisParaméterlista = "(" AktuálisParaméter {"," AktuálisParaméter } ")".
AktuálisParaméter = Kifejezés | Változó | Eljárásazonosító | Függvényazonosító.
Egy adott hívási ponton az ugyanazon formális paraméterrészben definiált illeszkedőtömb-paramétereknek megfelelő valamennyi aktuális paraméter ugyanahhoz a típushoz kell, hogy tartozzék. Ennek a típusnak illeszthetőnek kell lennie (l. a 11.3.4. pontot) a formális paraméterrész illeszkedőtömb-sémájához. Egy híváson belül valamennyi megfelelő formális paraméter ugyanahhoz a típushoz tartozik, ezt a típust az illeszkedőtömb-séma az aktuális paraméter(ek) típusából származtatja (l. a 11.3.4. pontot).
11.3.2.1. Aktuális értékparaméterek
Minden aktuális értékparaméter egy kifejezés. A formális paraméter egy változót jelöl, amelynek kezdőértékként az aktuális paraméter értékét adjuk (l. a 10.3. szakaszt).
Ha a formális paraméter nem illeszkedőtömb-paraméter, akkor az aktuális paraméternek értékadás-kompatibilisnek kell lennie (l. a 6.5. szakaszt) a formális paraméter típusával.
Ha a formális paraméter illeszkedőtömb-paraméter, akkor az aktuális paraméter nem lehet illeszkedő típusú (l. a 11.3.4. pontot).
11.3.2.2. Aktuális változóparaméterek
Az aktuális változóparaméterek változók. A hívás során a formális paraméter azt a változót jelenti, amelyet az aktuális paraméter a hívás kezdetekor kijelöl (l. a 10.3. szakaszt). Az aktuális paraméter nem jelölheti valamely tömörített tömb- vagy rekordváltozó elemét, sem egy kijelölőmezőt.
Ha a formális paraméter nem illeszkedőtömb-paraméter, akkor az aktuális és a formális paraméternek azonos típusúnak kell lennie.
11.3.2.3. Aktuális eljárásparaméterek
Az aktuális eljárásparaméterek eljárásazonosítók. A formális paraméter az aktuális paraméter által megjelölt eljárást jelenti (l. a 10.3. szakaszt). A formális és az aktuális paraméter formális paraméterlistájának, ha egyáltalán van, kongruensnek kell lennie (l. a 11.3.3. pontot).
11.3.2.4. Aktuális függvényparaméterek
Az aktuális függvényparaméterek függvényazonosítók. A formális paraméter az aktuális paraméter által megjelölt függvényt jelenti (l. a 10.3. szakaszt). A formális és az aktuális paraméter eredménytípusának ugyanazt a típust kell jelölnie. A formális és az aktuális paraméter formális paraméterlistájának, ha egyáltalán van, kongruensnek kell lennie (l. a 11.3.3. pontot).
11.3.3. Paraméterlisták kongruenciája
Két formális paraméterlista kongruens, ha elemeik száma megegyezik, és a megfelelő helyen álló formális paraméterek eleget tesznek a következő feltételek valamelyikének:
Két illeszkedőtömb-séma (amelyek mindketten csak egy indextípus-specifikációt tartalmaznak) ekvivalens, ha az alábbi három feltétel mindegyike teljesül:
Példa két ekvivalens illeszkedő tömb-sémára:
array [L1..H1: Integer; L2..H2: Szín] of packed array [L3..H3: T2] of T
array [Also1..Folso1: Integer] of array [Also2..Folso2: Szin] of packed array [Also3..Folso3: T2] of T
11.3.4. Illeszthetőség és illeszkedő típusok
Azt mondjuk, hogy egy T tömb típus (amelynek egyetlen indextípusa van) illeszthető egy (egyetlen indextípus-specifikációval ellátott) S illeszkedőtömb-sémához, ha az alábbi feltételek mindegyike teljesül. Jelölje I az S indextípus-specifikációjának megszámlálhatótípus-azonosítóját!
Ha a szintaktikus szabályok illeszthetőséget követelnek meg, a (2.) feltétel megsértése hibát eredményez.
Azt mondjuk, hogy egy típus a T-ből S által származtatott illeszkedő típus, ha a T-ével azonos indextípusú tömb típus, pontosan akkor tömörített, ha T is az, és elemtípusa vagy megegyezik T elemtípusával, vagy ha S egy másik illeszkedőtömb-sémából épül föl, akkor a T elemtípusából e részséma által származtatott illeszkedő típus. Az indextípus-specifikációban bevezetett határazonosítók az illeszkedő típus indextípusának legkisebb és legnagyobb értékét jelölik.
11.4.1. Állománykezelő eljárások
Több, kifejezetten a szöveg típusú állományok kezelésére definiált standard eljárás van. Ezeket a 12. fejezetben ismertetjük részletesen. Az alábbi eljárások bármilyen f állományváltozóra vonatkozhatnak (l. a 6.2.4. pontot és a 7.4. szakaszt).
Rewrite(f) eredményeképpen f egy üres sorozatot tartalmazó, generálási módban lévő állomány lesz; Put(f) hibát eredményez, ha f határozatlan, ha f nem generálási módban van, vagy ha az f^ pufferváltozó határozatlan. Az f-beli elemsorozat végére beilleszti f^ értékét; Reset(f) hatására f feldolgozási módba kerül, és a benne elhelyezkedő sorozat első pozíciójára állunk rá. Ha ez a sorozat üres, Eof(f) értéke igazzá, f^ pedig teljesen határozatlanná válik, minden más esetben Eof(f) értéke hamis lesz, és f^ a sorozat első pozícióján elhelyezkedő értéket veszi föl; Get(f) hibás, ha f határozatlan, vagy Eof(f) igaz. Hatására az állományban áttérünk a következő elemre, ha ilyen egyáltalán létezik, és f^ ennek az értékét veszi fel, ha az állománynak nincs következő eleme, Eof(f) értéke igazzá válik, f^ pedig teljesen határozatlan lesz.
Az alábbi definíciókban, valahányszor f előfordul, mindig ugyanazt az állomány változót jelenti. A v, v1, ..., vn szimbólumok változókat, az e, e1, ..., en szimbólumok pedig kifejezéseket jelölnek. A v, v1, ..., vn változók nem aktuális változóparaméterek, tehát lehetnek tömörített tömbök vagy rekordok elemei is.
Read(f,v1,...,vn)
ekvivalens abegin Read(f,v1); ...; Read(f,vn) end
utasítással.
Read(f,v)
ahol f nem szöveg típusú állomány, ekvivalens abegin v:= f^; Get(f) end
utasítással,
Write(f,e1,...,en)
ekvivalens abegin Write(f,e1); ...; Write(f,en) end
utasítással.
Write(f,e)
ahol f nem szöveg típusú állomány, ekvivalens abegin f^:= e; Put(f) end
utasítással.
11.4.2. Dinamikus helyfoglaló eljárások
A dinamikus helyfoglaló eljárások segítségével hozhatunk létre (New) és szüntethetünk meg (Dispose) új mutatóértékeket és ezek dinamikus változóit. Az alábbi leírásokban p mutatóváltozó, q mutatókifejezés, c1, ..., cn, k1, ..., kn pedig konstansok. Vegyük észre, hogy p nem aktuális paraméter, tehát tömörített tömbnek vagy rekordnak is lehet eleme.
New(p) létrehoz egy új, p-vel azonos típusú mutatóértéket, és azt p-hez rendeli. A p^ dinamikus változó teljesen határozatlan. New(p,c1,...,cn) Dispose(q) törli a q mutatóértéket. Hibát okoz, ha q értéke nil. Csak a New eljárás első (rövid) alakjával létrehozott q értékekre alkalmazható, különben hibát okoz. Dispose(q,k1,...,kn) törli a q mutatóértéket. Hibát okoz, ha q értéke nil. Csak akkor alkalmazható, ha a q értéket a New eljárás második (hosszú) alakjával hoztuk létre, és a k1.....kn konstansok ugyanazokat a változatokat jelölik ki, mint a mutatóérték létrehozásakor; különben hibára vezet.
11.4.3. Adatátviteli eljárások
Jelöljön U egy tömörítetlen, S1 indextípusú és T elemtípusú tömbváltozót. Jelöljön P egy tömörített, S2 indextípusú és T elemtípusú tömbváltozót. Jelölje B és C az S2 típus legkisebb és legnagyobb értékét. Jelöljön K egy új, (másképp nem hozzáférhető) S1 típusú, J pedig egy új, S2 típusú változót. Ingyen végül I egy S1-gyel kompatibilis kifejezés.
Pack(U,l,P)
ekvivalens abegin
K:= I;
for J:= B to C do begin
P[J]:= U[K];
if J <> C then K:= Succ(K)
end
endutasítással,
Unpack(P,U,I)
pedig abegin
K:= I;
for J:= B to C do begin
U[K]:= P[J];
if J <> C then K:= Succ(K)
end
endutasítással. Mindkét részletes leírásban az U is és a P is egyetlen változót jelöl a for utasítás valamennyi iterációs lépése során.
11.5.1. Aritmetikai függvények
Legyen x tetszőleges valós vagy egész kifejezés. Abs és Sqr eredmény típusa megegyezik x típusával. A többi aritmetikai függvény eredménytípusa valós.
abs(x) eredménye x abszolút értéke. sqr(x) eredménye x négyzete. Hibát okoz, ha az adott rendszerben az x szám négyzete nem létezik. sin(x) eredménye x szinusza, ahol az x értéket radiánban értjük. cos(x) eredménye x koszinusza, ahol az x értéket radiánban értjük. exp(x) eredménye a természetes logaritmus alapszámának x-edik hatványa. ln(x) eredménye x természetes logaritmusa. Hibára vezet, ha x kisebb vagy egyenlő, mint 0. sqrt(x) eredménye x négyzetgyöke. Hibát okoz, ha x negatív. arctan(x) eredménye x arkusz tangensének radiánban kifejezett főértéke.
11.5.2. Logikai függvények
Legyen i tetszőleges egész kifejezés, f pedig tetszőleges állományváltozó. Valamennyi logikai függvény eredménye Boolean típusú.
odd(i) ekvivalens az (abs(i) mod 2 = 1) kifejezéssel. eof(f) hibát okoz, ha f határozatlan; máskor viszont eof(f) eredménye igaz, ha f generálási módban van, vagy ha túlléptünk az f-beli sorozat utolsó elemén. Ha nincs paraméterlista, az eof függvényt az Input programparaméterre alkalmazzuk. eoln(f) hibás, ha f határozatlan, vagy ha eof(f) értéke igaz. f-nek szöveg típusú állománynak kell lennie. Az eoln(f) eredménye igaz, ha az f-beli sorozat aktuális eleme egy sor vége jel. Ha nincs paraméterlista, az eoln függvényt az Input programparaméterre alkalmazzuk.
11.5.3. Konverziós függvények
Jelöljön r egy valós kifejezést. E függvények eredmény típusa mindig Integer.
trunc(r) eredménye olyan érték, hogy ha r >= 0, akkor 0< = r-trunc(r) < 1, ha pedig r < 0, akkor -1 < r-trunc(r) <= 0. Hibát okoz, ha ilyen érték nem létezik. round(r) eredménye olyan érték, hogy ha r > = 0, akkor round(r) = trunc(r+0.5), ha pedig r<0, akkor round(r) = trunc(r-0.5). Hibát okoz, ha ilyen érték nem létezik.
11.5.4. A megszámlálható típusokon értelmezett függvények
Legyen i egész kifejezés, x pedig tetszőleges diszkrét kifejezés.
ord(x) eredménye x rendszáma. chr(i) eredménye az a Char típusú érték, amelynek rendszáma i. Hibát okoz, ha ilyen érték nem létezik. Ha c egy karakterérték, akkor mindig igaz, hogy chr(ord(c)) = c. succ(x) eredménye x után következő érték, ha ilyen létezik. Ilyenkor ord(succ(x)) = ord(x)+1. Hibát okoz, ha nem létezik a rá következő érték. pred(x) eredménye az x-et megelőző érték, ha ilyen létezik. Ilyenkor ord(pred(x)) = ord(x)-1. Hibát okoz, ha nem létezik x-et megelőző érték.
12. Szöveg típusú állományok be- és kivitele
Az olvasható szövegek be- és kivitelének alapegységei azok a szöveg típusú állományok (l. a 6.2.4. pontot), amelyeket egy Pascal programba programparaméterekként (l. a 13. fejezetet) viszünk be, és amelyek a program környezetébe tartozó valamilyen input vagy output egységhez, például terminálhoz, képernyőhöz, mágnesszalaghoz vagy sornyomtatóhoz kapcsolódnak. A szöveg típusú állományok kezelésének megkönnyítésére három további standard eljárást (a Readln, a Writeln és a Page eljárásokat) vezetünk be. két, már tárgyalt standard eljárás (a Read és a Write; l. a 11.4.1. pontot) érvényességét pedig kiterjesztjük. Azoknak a szöveg típusú állományoknak, amelyekre ezeket az eljárásokat alkalmazzuk, nem kell feltétlenül input/output egységekhez kapcsolódniuk, lehetnek lokális állományok is. Az említett eljárások aktuális paraméterlistáira nem a szokásos szabályok vonatkoznak (l. a 11.3. szakaszt), lehetőség van többek között arra is, hogy a paraméterlistán változó számú paraméter álljon. Még a paramétereknek sem kell szükségképpen Char típusúaknak lenniük, tartozhatnak bizonyos más típusokhoz is. Ilyenkor azonban az adatátvitel mellett automatikus adatkonverzióra is sor kerül. Ha az első paraméter egy állományváltozó, akkor ezt az állományt kell beolvasni vagy kiírni. Ha nem, akkor a gép az Input és Output standard állományokat (l. a 13. fejezetet) használja, mégpedig olvasás esetén az előbbit, írás esetén pedig az utóbbit.
12.1. A Read utasítás
Ha a Read eljárást szöveg típusú állományra alkalmazzuk, az alábbi szabályok szerint kell eljárnunk. Jelöljön f egy szöveg típusú állományt, v1, ..., vn pedig a Char vagy az Integer típusokhoz (vagy ezek valamely résztartomány-típusához), esetleg a Real típushoz tartozó változókat.
Read(f,v) hatása attól függ, hogy v milyen típusú.
12.1.1. Karakter beolvasása
Ha v a Char típussal kompatibilis típusú változót jelöl, a Read(f ,v) eljárás ekvivalens a
begin v:= f^; Get(f) end
utasítással, ahol f végig egyetlen változót jelöl. Ha eoln(f) igaz volt a Read(f,v) eljárás végrehajtása előtt, akkor utána igaz lesz, hogy (v = ' ').
12.1.2. Egész típusú szám beolvasása
Ha v az Integer típussal kompatibilis típusú változót jelöl, akkor a Read(f,v) eljárás hatására az f-ből kiolvasott karaktersorozat egy előjeles egészt (l. a 4. fejezetet) alkot, és az így jelölt egész érték lesz v új értéke. Az értéknek értékadás-kompatibilisnek kell lennie v típusával. Az elöl álló szóközöket és a sor vége jeleket átugorjuk. Hiba, ha az előjeles egész számot nem lehet megtalálni.
12.1.3. Valós típusú szám beolvasása
Ha v Real típusú változót jelöl, akkor a Read(f,v) eljárás hatására az f-ből kiolvasott karaktersorozat egy előjeles számot (l. a 4. fejezetet) alkot, és az így jelölt érték lesz v új értéke. Az elöl álló szóközöket és a sor vége jeleket átugorjuk. Hiba, ha az előjeles számot nem lehet megtalálni!
12.2. A Readln utasítás
Jelöljön f egy szöveg típusú állományt, v1, ..., vn pedig a Char vagy az Integer típusokhoz (vagy ezek valamely résztartomány-típusához), esetleg a Real típushoz tartozó változókat.
Readln(v1, ..., vn) ekvivalens a
Readln(g,v1,...,vn)
eljárással, Readln pedig a Readln(g) eljárással, ahol g az Input standard szöveg típusú állományt jelöli.
Readln(f,v1,...,vn) ekvivalens a
begin Read(f,v1,...,vn); Readln(f) end
utasítással, ahol f mindvégig egyetlen változót jelöl.
Readln(f) ekvivalens a
begin
while not eoln(f) do Get(f);
Get(f)
end
utasítással, ahol f végig egyetlen változót jelöl.
12.3. A Write utasítás
Ha a Write eljárást szöveg típusú állományra alkalmazzuk, az alábbi szabályok szerint kell eljárnunk. Jelöljön f egy szöveg típusú állományt, p, p1, ..., pn a WriteParaméter-eket, e egy kifejezést, m és n pedig egész kifejezéseket. A Write eljárás aktuális paraméterlistájára a következő szintaktikus előírások érvényesek:
WriteParaméterlista = "(" (Állományváltozó | WriteParaméter) { "," WriteParaméter) ")".
WriteParaméter = Kifejezés [ ":" EgészKifejezés [ ":" "EgészKifejezés]]
A Write(p1.....pn) eljárás ekvivalens a Write(g,p1,...,pn) eljárással, ahol g az Output standard szöveg típusú állomány.
A Write(f,p1,...,pn) eljárás ekvivalens a
begin Write(f,p1); ...; Write(f,pn) end
utasítással, ahol f mindvégig egyetlen változót jelöl.
Write(f,p) hiba, ha f határozatlan, vagy nem generálási módban van.
Egy Write paraméter formája az alábbi három forma valamelyike:
e
e:m
e:m:n
Itt e jelenti az f-be beírandó értéket, m és n pedig az ún. mezőszélesség-paraméterek. Hibát okoz, ha akár m, akár n nem pozitív, e lehet Integer, Real, Char, Boolean vagy füzér típusú. Az n kifejezés csak akkor szerepelhet, ha e Real típusú (l. a 12.3.3. pontot). Ha az m kifejezést elhagyjuk, a gép egy alapértékkel dolgozik. Az alapértéket a rendszer definiálja, ha e Integer, Real vagy Boolean típusú. Char típus esetén ez az alapérték 1, füzér típus esetén pedig a füzér elemeinek száma.
Ha e értékének ábrázolásához m-nél kevesebb pozícióra van szükség, akkor az értéket megfelelő számú szóköz előzi meg úgy, hogy pontosan m számú karakter íródjon ki, e értékének ábrázolása e típusától függ.
12.3.1. A Write utasítás karakter típus esetén
Ha e Char típusú, akkor a Write(f,e:m) eljárás ekvivalens a
begin
for J:= 1 to m-1 do Write(f,' ');
f^:= e; Put(f)
end
utasítással, ahol f végig egyetlen változót jelöl, J pedig egy új (másként hozzáférhetetlen) egész változó.
12.3.2. A Write utasítás egész típus esetén
Ha e Integer típusú, a Write(f,e:m) eljárás először egy '-' karaktert ír ki, ha e < 0, majd ezt követően kiírja abs(e) értékének tízes számrendszerbeli alakját, e értéke előtt annyi szóközt helyez el, hogy pontosan m számú karakter kiírására kerüljön sor.
12.3.3. A Write utasítás valós típus esetén
Ha e Real típusú a Write(f,e:m:n) eljárás e értékét fixpontos számábrázolással írja ki, n jegyet írva a tizedespont után; a Write(f,e:m) eljárás viszont lebegőpontosán írja ki ugyanezt az értéket. A "**" műveletijei a hatványozást jelöli.
12.3.3.1. Fixpontos ábrázolás
Legyen w nulla, ha e nulla, egyébként pedig legyen w az e abszolút értéke kerekítve, majd az n-edik tizedesjegynél levágva, w < 1 esetén legyen d = 1, egyébként pedig legyen olyan, hogy 10^(d-1) <= w < 10^d teljesüljön, d a tizedesponttól balra eső jegyek száma. Legyen továbbá s = ord((e < 0) and (w <> 0)). Az érték negatív, ha s = 1. Legyen végül k = (s+d+1+n); k a kiírandó nem szóköz karakterek száma.
Ha k< m, akkor a szám előtt m-k darab szóköz áll. e fixpontos ábrázolása az alábbi k karakterből áll:
12.3.3.2. Lebegőpontos ábrázolás
A Pascal rendszer előírja, hogy a lebegőpontos ábrázolás karakterisztikájában ("E részében") hány számjegynek kell állnia; jelölje ezt a számot x. Legyen k az m és az x+6 számok nagyobbika. A kiírandó értékes jegyek száma k-x-4, éspedig ezek közül egy áll a tizedespont előtt, d pedig utána (és így d = k-x-5). Legyen w és s nulla, ha e értéke nulla. Ha e értéke nullától különböző, akkor legyen s olyan, hogy 10.0^s< = abs(e) < 10. 0^(s+ 1) és legyen w = (abs(e)/10.0^s) + 0.5 * 10.0^(-d). Ha ekkor w >= 10.0, módosítsuk w-t és s-t úgy, hogy s:= s+1 és w:= w/10.0 legyen. Végül vágjuk le w-t a d-edik tizedesjegynél!
Az e lebegőpontos ábrázolása a következőkből áll:
12.3.4. A Write utasítás logikai típus esetén
Ha e típusa Boolean, akkor a Write(f,e:m) eljárás a true és a false szavak valamelyikét írja ki. Az eljárás ekvivalens az
if e then Write(f,'true':m) else Write(f,'false':m)
utasítással, attól eltekintve, hogy a rendszer határozza meg, kis- vagy nagybetűkkel ír-e.
12.3.5. A Write utasítás füzér típus esetén
Ha e k hosszúságú, füzér típusú érték, akkor m > k esetén a Write(f,e:m) eljárás m-k darab szóközt ír. Ezután következnek e elemei, indexeik növekvő sorrendjében. m < k esetén e-ből az utolsó k-m darab karakter nem íródik ki.
12.4. A Writeln utasítás
Jelöljön f egy szöveg típusú állományt, p1, ..., pn pedig write paramétereket.
Writeln(p1,...,pn) a Writeln(g,p1,...,pn) eljárással, Writeln pedig a Writeln(g) eljárással ekvivalens, ahol g az Output standard szöveg típusú állományt jelöli.
A Writeln(f,p1,...pn) eljárás ekvivalens a
begin Write(f,p1,...,pn); Writeln(f) end
utasítással, ahol f mindvégig egyetlen változót jelöl.
Writeln(f) egy sor vége jelet illeszt az f állományban elhelyezkedő sorozat végére. Hibát okoz, ha f határozatlan, vagy f nem generálási módban van.
12.5. A Page utasítás
A Page(f) eljárás hatását az f szöveg típusú állományra a rendszer definiálja úgy, hogy az f-be ezután írt szöveg az f nyomtatásakor a következő oldal elejére kerüljön. Ha f nem üres és a benne elhelyezett sorozat utolsó eleme nem sor vége jel, akkor a Page(f) eljárás egy implicit Writeln(f) eljárást is végrehajt. Ha nincs paraméterlista, a gép az Output standard szöveg típusú állománnyal dolgozik. Hiba, ha f határozatlan, vagy nem generálási módban van.
Rendszerfüggő, hogy milyen hatással van egy olvasó eljárás egy olyan állományváltozóra, amelyre előzőleg a Page eljárást alkalmaztuk.
13. Programok
Egy Pascal program egy programfejből és egy blokkból áll.
Program = Programfej ";" 'Blokk "."
Programfej = "program" Azonosító [ProgramParaméterlista].
ProgramParaméterlista = "(" Azonosítólista ")".
A program alapszó után álló azonosító a program neve; ennek a programon belül már nincs jelentősége. A program paraméterlistáján szereplő azonosítókat programparamétereknek nevezzük. Ezek a programon kívül, attól függetlenül létező - és ezért külsőnek (external) nevezett - objektumokat jelölnek. A program ezeken keresztül tart fenn kapcsolatot a környezetével.
Amikor egy programot hívunk, minden programparaméter ahhoz a külső objektumhoz kötődik, amelyet jelöl. Azon programparaméterek esetén, amelyek állományváltozók, ez az összeköttetés a rendszer által definiált; a többi programparaméter esetén rendszerfüggő.
Az Input és az Output kivételével minden programparamétert deklarálni kell a programblokk változódeklarációs részében. Az Input és az Output esetében az azonosító felvétele a program-paraméterlistára automatikusan a programblokkbeli szöveg típusú állományként deklarálja az azonosítót, és a program minden hívásakor automatikusan végrehajtja a Reset(Input) vagy a Rewrite(Output) eljárásokat.
A rendszer határozza meg, milyen hatásuk van a Reset és a Rewrite eljárásoknak, Input vagy Output állomány esetén.
Példák programra:
program ValosMasolas(F,G);
{TuroPascal}
var F,G: file of Real;
R: Real;
begin
Reset(F);
Rewrite(G);
while not Eof(F) do begin
Read(F,R);
Write(G,R)
end
end {ValosMasolas}.program Szovegmasolas(Input,Output);
{MS Pascal}
begin
while not Eof(Input) do begin
while not Eoln(Input) do begin
Input^:= Output^;
Put(Output);
Get(Input)
end;
Readln(Input);
Writeln(Output);
end
end {Szovegmasolas}.
14. Illeszkedés az ISO 7185 szabványhoz
Egy program összhangban van az ISO Pascal szabvánnyal [11], ha a nyelvnek csak a szabvány által definiált jellemzőit alkalmazza, és nem támaszkodik a rendszerfüggő konstrukciók speciális megvalósítási módjára. Azt mondjuk, hogy a program 0 szintű, ha nem használ illeszkedőtömb-paramétereket, és 1 szintű, ha használ.
A processzort a szabvány úgy definiálja, mint "olyan rendszert vagy mechanizmust, amelynek inputja egy program. A processzor ennek végrehajtását készíti elő, és az így meghatározott eljárást adatokkal végrehajtva szolgáltatja az eredményt." Egy processzor akkor van összhangban a szabvánnyal, ha az alábbi feltételek mindegyikének eleget tesz.
A nyelv minden részletét a szabvány által definiáltan fogadja el. 0 szintűnek mondjuk, ha nem fogad el illeszkedőtömb-paramétereket és 1 szintűnek, ha igen.
Ahhoz, hogy a nyelv valamely konstrukcióját megvalósítsa, nincs szükség a nyelv más, helyettesítő elemeire.
Képes a szabvány által leírt szabályok hibának nem minősülő áthágását észlelni, és ezt jelzi a felhasználónak. Ha a processzor nem vizsgálja végig az egész programot, hogy történt-e benne ilyen szabálytalanság, ezt a tényt is jeleznie kell.
Minden, hibának minősülő szabálytalanságot az alábbi négy mód valamelyikén kezel:
(a) Dokumentációjában az áll, hogy a hibát nem jelzi.
(b) A program előkészítése során jelzi, hogy hiba előfordulhat.
(c) A program előkészítése során jelzi, hogy hiba fog előfordulni.
(d) A program végrehajtása során jelzi, hogy hibát talált.
Hibaként tud feldolgozni minden olyan esetet, amikor a program a nyelv valamely bővítését vagy rendszerfüggő vonását alkalmazza.
Kísérő dokumentuma az alábbiakat tartalmazza:
(a) A rendszer által definiált valamennyi jellemző definícióját.
(b) Azon hibák felsorolását, amelyet a processzor nem jelez (l. 4. (a) pont.). Ha valamely bővítés egy olyan feltételt használ ki, amelyet a szabvány hibának tekint, és a processzor a hibát emiatt nem jelzi, a dokumentumból ki kell derülnie, hogy ennek a hibának a jelzésére nem fog sor kerülni.
(c)
A rendszer által alkalmazott valamennyi bővítés leírását.
A. függelék: Standard eljárások és függvények
Abs(x)
Aritmetikai függvény, amely a valós típusú x paraméter valós típusú, vagy az egész típusú x paraméter egész típusú abszolút értékét számítja ki.
ArcTan(x)
Aritmetikai függvény, amely a valós vagy egész típusú x paraméter valós típusú, radiánban megadott arkusz tangensét (pontosabban annak főértékét) számítja ki.
Chr(i)
Megszámlálható típusú függvény, amely kikeresi azt a karaktert, amelynek rendszáma az i egész típusú paraméter. Chr(i) hibát eredményez, ha ilyen karakterérték nem létezik.
Dispose(q)
Dinamikus helyfoglaló eljárás, amely fölszabadítja a q^ dinamikus változó tárolóterületét és törli a q mutatóértéket. Dispose(q) hiba, ha q értéke nil, vagy határozatlan. A q értéknek a New eljárás rövid alakjával létrehozottnak kell lennie.
Dispose(q,k1,...,kn)
Dinamikus helyfoglaló eljárás, amely fölszabadítja a q^ dinamikus rekordváltozó tároló-területét és törli a q mutatóértéket. Dispose(q,k1,...,kn) hibát eredményez, ha q értéke nil vagy határozatlan. Az eljárás csak akkor alkalmazható, ha a q értéket a New eljárás hosszú alakjával hoztuk létre, a k1, ..., kn konstansok által kijelölt változatoknak pedig meg kell egyezniük azokkal, amelyeket q létrehozásakor alkalmaztunk.
Eof(f)
Logikai függvény, amely a true értéket veszi fel, ha az f állomány változó generálási módban van, vagy ha f feldolgozási módban van ugyan, de túlléptünk utolsó elemén, Eof(f) hibás, ha f határozatlan. Eof(f) minden más esetben a false értéket veszi föl. Ha az f paramétert elhagyjuk, a gép az Input standard állománnyal dolgozik.
Eoln(f)
Logikai függvény, amely a true értéket veszi fel, ha a feldolgozási módban lévő f szöveg típusú állomány aktuális elemén egy sor vége jel áll. Eoln(f) hibás, ha f határozatlan, vagy ha Eof(f) igaz. Eoln(f) értéke minden más esetben false. Az f paraméter hiányában a gép az Input standard állománnyal dolgozik.
Exp(x)
Aritmetikai függvény, amely az e (a természetes logaritmus alapszáma) alapú exponenciális függvény valós típusú értékét számítja ki a valós vagy egész típusú x paraméter által meghatározott helyen.
Get(f)
Állománykezelő eljárás, amelynek hatására az f-ben elhelyezkedő sorozat következő eleme (ha egyáltalán van ilyen) válik aktuálissá, f^ pedig az itt elhelyezett értéket veszi föl; ha az állományban nincs következő elem, Eof(f) igazzá, f^ pedig határozatlanná válik. Get(f) hibát okoz, ha f határozatlan vagy Eof(f) igaz. Az f paraméter hiányában a gép az Input standard állománnyal dolgozik.
Ln(x)
Aritmetikai függvény, amely a valós vagy egész típusú x paraméter természetes (e alapú) logaritmusának valós típusú értékét számítja ki, föltéve, hogy x > 0. Ha x <= 0, Ln(x) hibát eredményez.
New(p)
Dinamikus helyfoglaló eljárás, amely tárolóterületet foglal le az új, p főtípusához tartozó p^ dinamikus változó számára, továbbá létrehoz egy új, p típusú mutatóértéket és azt p-hez rendeli. Ha p^ változat részt is tartalmazó rekord, New(p) valamennyi változat tárolására elegendő helyet foglal le.
New(p,c1.....cn)
Dinamikus helyfoglaló eljárás, amely tárolóterületet foglal le az új, p^ dinamikus változó számára, p^ típusa a p változat részt is tartalmazó rekord típusa, amelynek n számú, egymásba ágyazott változat részéből a kijelölőmező c1, ..., cn értékei jelölik ki az aktuális változatot. Az eljárás létrehoz egy új, p típusú mutatóértéket is, és azt p-hez rendeli.
Odd(i)
Logikai típusú függvény, amelynek értéke true, ha az egész típusú i paraméter páratlan; a függvény ellenkező esetben a false értéket veszi föl.
Ord(x)
Egész típusú függvény, amely az x megszámlálható típusú paraméternek az x típusa által meghatározott értékkészletbeli (egész típusú) rendszámát veszi fel.
Pack(u,i,p)
Adatátviteli eljárás, amely az u tömörítetlen tömb tartalmát az i-edik elemtől kezdve a p tömörített tömbben helyezi el.
Page(f)
Állománykezelő eljárás, amelynek az f szöveg típusú állományparaméterre való hatását a rendszer definiálja úgy, hogy az f állományba ezután írt szöveg f nyomtatásakor a következő oldal elején kezdődjék. Ha f nem üres, és a benne elhelyezkedő sorozat utolsó eleme nem egy sor vége jel, a Page(f) eljárás implicit módon egy Writeln(f) eljárást is végrehajt. Paraméterlista hiányában a gép az Output standard állománnyal dolgozik. Page(f) hibát okoz, ha f határozatlan vagy nem generálási módban van.
Pred(x)
Megszámlálható típusú függvény, amely az x megszámlálható típusú paramétert megelőző diszkrét értéket veszi föl, ha az egyáltalán létezik: ord(pred(x)) = ord(x)-1. Pred(x) hiba, ha x típusának legkisebb értéke.
Put(f)
Állománykezelő eljárás, amely f^ értékét az f végére illeszti. Put(f) hibát okoz, ha f határozatlan vagy nem generálási módban van, továbbá ha az f^ pufferváltozó határozatlan. A Put(f) eljárás végrehajtása után f teljesen határozatlanná válik.
Read(f,v)
L. a Felhasználói Kézikönyv 9. és 12. fejezetét, továbbá a Jelentés 11.4. és 12.1. szakaszát.
Read(f,v1,...,vn)
L. a Felhasználói Kézikönyv 9. és 12. fejezetét, továbbá a Jelentés 11.4. és 12.1. szakaszát.
Readln
L. a Felhasználói Kézikönyv 9. és 12. fejezetét, továbbá a Jelentés 12.2. szakaszát.
Readln(f,v1,...,vn)
L. a Felhasználói Kézikönyv 9. és 12. fejezetét, továbbá a Jelentés 12.2. szakaszát.
Reset(f)
Állománykezelő eljárás, amely f-et feldolgozási módba állítja és f első elemét teszi aktuálissá. Ha f üres, Eof(f) igazzá, f^ pedig teljesen határozatlanná válik. Ellenkező esetben Eof(f) hamis lesz, f^ pedig fölveszi az f-ben elhelyezkedő sorozat első elemének értékét.
Rewrite(f)
Állománykezelő eljárás, amely f tartalmát törli, és f-et generálási módba állítja. Eof(f) az eljárás hatására igazzá válik.
Round(r)
Konverziós függvény, amely a r >= 0.0 feltételnek eleget tevő valós típusú r paraméter esetére a trunc(r+0.5) értéket, az r < 0.0 feltételt kielégítő valós típusú paraméter esetére pedig a trunc(r-0.5) értéket számítja ki, ha ilyen érték az Integer típusban létezik. Ellenkező esetben hibát okoz.
Sin(x)
Aritmetikai függvény, amely a valós vagy egész típusú x paraméter radiánban megadott értékének valós típusú szinuszát számítja ki.
Sqr(x)
Aritmetikai függvény, amely valós típusú x esetén a valós x*x értéket, egész típusú x-re pedig az egész típusú x*x értéket számítja ki. Hiba, ha ez az érték nem létezik.
Sqrt(x)
Aritmetikai függvény, amely az x >= 0 feltételnek eleget tevő, egész vagy valós típusú x paraméter valós típusú, nem negatív négyzetgyökét számítja ki. Hiba, ha x < 0.
Succ(x)
Egész típusú függvény, amely az x megszámlálható típusú paraméter után következő értéket veszi föl, ha az egyáltalán létezik: ord(succ(x)) = ord(x)+1. Succ(x) hibát okoz, ha x típusának legnagyobb értéke.
Trunc(r)
Konverziós függvény, amely r >= 0.0 esetén a valós típusú r paraméter értékét meg nem haladó legnagyobb egész típusú értéket, r < 0.0 esetén viszont a legkisebb olyan egész típusú értéket számítja ki, amely nem kisebb a valós típusú r paraméternél, feltéve persze, hogy ilyen érték az Integer típusban létezik. Ellenkező esetben hibát okoz.
Unpack(p,u,i)
Adatátviteli eljárás, amely a p tömörített tömb tartalmát az u tömörítetlen tömbben, annak i-edik elemétől kezdve helyezi el.
Write(f,v)
L. a Felhasználói Kézikönyv 9. és 12. fejezetét, továbbá a Jelentés 11.4. és 12.3. szakaszát.
Write(f,v1,...,vn)
L. a Felhasználói Kézikönyv 9. és 12. fejezetét, továbbá a Jelentés 11.4. és 12.3. szakaszát.
Writeln
L. a Felhasználói Kézikönyv 9. és 12. fejezetét, továbbá a Jelentés 12.4. szakaszát.
Writeln(f,e1.....en)
L. a Felhasználói Kézikönyv 9. és 12. fejezetét, továbbá a Jelentés 12.4. szakaszát.
B. függelék: A műveletek összefoglalása
Aritmetikai műveletek:
Műveleti jel Művelet Az operandusok típusa Az eredmény típusa + (unáris) azonosság egész vagy valós ua. mint az operandusé - (unáris) előjelváltás egész vagy valós ua. mint az operandusé + összeadás egész vagy valós egész vagy valós - kivonás egész vagy valós egész vagy valós * szorzás egész vagy valós egész vagy valós div egészosztás egész egész / valósosztás egész vagy valós valós mod modulus egész egész
Reláció:
Műveleti jel Művelet Az operandusok típusa Az eredmény típusa = egyenlőség egyszerű, füzér, halmaz, mutató logikai <> nem egyenlőség egyszerű, füzér, halmaz, mutató logikai < kisebb egyszerű, füzér logikai > nagyobb egyszerű, füzér logikai <= kisebb egyenlő vagy halmaztartalmazás egyszerű, füzér, halmaz logikai >= nagyobb egyenlő vagy halmaztartalmazás egyszerű, füzér, halmaz logikai in halmazhoz tartozás az első bármilyen megszámlálható alaptípus, a második ennek halmaztípusa logikai
Logikai:
Műveleti jel Művelet Az operandusok típusa Az eredmény típusa not negálás logikai logikai or diszjunkció logikai logikai and konjunkció logikai logikai
Halmaz:
Műveleti jel Művelet Az operandusok típusa Az eredmény típusa + unió bármely T halmaz típus T - differencia bármely T halmaz típus T * metszet bármely T halmaz típus T
A műveletek precedenciája kifejezésekben:
Művelet Műveletcsoport not logikai negálás * / div mod and multiplikatív műveletek + - or addiktív műveletek = <> > < >= <= in relációk
Érékadás:
jelölés Művelet Az operandusok típusa Az eredmény típusa := értékadás bármilyen hozzárendelhető típus nincs
Változók elérése:
jelölés Művelet Az operandusok típusa Az eredmény típusa [,] tömbindexelés tömb elemtípus [.] mezőkijelölés rekord mezőtípus ^ változókijelölés mutató főtípus ^ pufferelés állomány elemtípus
Generálás:
jelölés Művelet Az operandusok típusa Az eredmény típusa [,] halmazgenerálás alaptípus halmaz ' ' füzérgenerálás karakter füzér
Adattípusok:
Standard azonosítók táblája:
Konstansok: False, MaxInt, True
Típusok: Boolean, Char, Integer, Real, Text
Változók: Input, Output
Függvények: Abs, ArcTan, Chr, Cos, Eof, Eoln, Exp, Ln, Odd, Ord, Pred, Round, Sin, Sqr, Sqrt, Succ, Trunc
Eljárások: Dispose, Get, New, Pack, Page, Put, Read, Readln, Reset, Rewrite, Unpack, Write, Writeln
A standard azonosítók ábécésorrendben:
Abs False Pack Sin ArcTan Get Page Sqr Boolean Input Pred Sqrt Char Integer Put Succ Chr Ln Read Text Cos MaxInt Readln True Dispose New Real Trunc Eof Odd Reset Unpack Eoln Ord Rewrite Write Exp Output Round Writeln
Szimbólumok táblája
Speciális szimbólumok:
+ - * / = < > <= >= <> - , : ; := ( ) [ ] ^ ..
Alapszavak:
and end nil set array file not then begin for of to case function or type const goto packed until div if procedure var do in program while downto label record with else mod repeat
További lehetőségek a szimbólumok ábrázolására:
[ helyett (.
] helyett .)
^ helyett @
Direktívák: forward
Egy programozási nyelv szintaxisának a kiterjesztett Backus-Naur-formában való (EBNF) leírása szabályok sorozatából áll, amelyeket együttesen a nyelv mondatainak alakját leíró "nyelvtannak" nevezünk. Minden szabály egy nemterminális szimbólumból és egy EBNF-kifejezésből áll, amelyeket egy egyenlőségjel választ el. A szabályokat pont zárja le. A nemterminális szimbólum egy "metaazonosító" (egy szóval vagy egybeírt szókapcsolattal jelzett szintaktikus konstans), az EBNF-kifejezés pedig ennek definíciója.
Az EBNF-kifejezés terminális szimbólumokból, nemterminális szimbólumokból és az alábbi táblázatban összefoglalt metaszimbólumokból épül fel. Minden alkotórészből szerepelhet benne nulla vagy annál több.
Metaszimbólum Jelentése =
|
.
[X]
{}
(X|Y)
"XYZ"
Metaazonosítódefiniáljuk úgy, hogy.
vagy.
szabály vége.
X-nek 0 vagy 1 példánya.
X-nek 0 vagy több példánya.
vagy X, vagy Y.
az XYZ terminális szimbólum.
a Metaazonosító nemterminális szimbólum.
Az EBNF például saját szintaxisának definiálására is felhasználható:
Szintaxis = {Szabály}.
Szabály = Nemterminális "=" Kifejezés ".".
Kifejezés = Tag {"|" Tag}.
Tag = Tényező {Tényező}.
Tényező = Nemterminális | Terminális | "(" Kifejezés ")" | "["Kifejezés "]" | "{" Kifejezés "}".
Terminális = """" Karakter {Karakter)"""".
Nemterminális = Betű {Betű | Számjegy}.
Megjegyzések:
Hierarchikus EBNF-leírás
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 |
Program = Programfej ";" Blokk ".". Programfej = "program" Azonosító [ProgramParaméterlista]. ProgramParaméterlista = "(" Azonosítólista ")". ............. Blokk = CímkedeklarációsRész KonstansdefiníciósRész TípusdefiníciósRész VáltozódeklarációsRész EljárisÉsFüggvénydeklarációsRész Utasításrész. CímkedeklarációsRész = [ "label" Számjegysorozat {"," Számjegysorozat} ";" ]. KonstansdefiníciósRész = ["const" Konstansdefiníció ";" {Konstansáéfiníció ";"}]. {Konstansdefiníció ";"}]. TípusdefiníciósRész = [ "type" Típusdefiníció ";" {Típusdefiníció ";"}]. VáltozódeklarációsRész = [ "var" Változódeklaráció ";" {Változódeklaráció ";"}]. EljárásÉsFüggvénydeklarációsRész = {(Eljárásdeklaráció | Függvénydeklaráció) ";"}. Utasításrész = ÖsszetettUtasítás. ............. Konstansdefiníció = Azonosító "=" Konstans. Típusdefiníció = Azonosító "=" Típus. Változódeklaráció = Azonositólista "=" Típus. Eljárásdeklaráció = Eljárásfej ";" Blokk | Eljárásfej ";" Direktíva | Eljárásazonosítás ";" Blokk. Függvénydeklaráció = Függvényfej ";" Blokk | Függvényfej ";" Direktíva | Függvényazonosítás ";" Blokk. ............. Eljárásfej = "procedure " Azonosító [FormálisParaméterlista]. Eljárásazonosítás = "procedure" Eljárásazonosító. Függvényfej = "function" Azonosító [FormálisParaméterlista] ":" Eredménytípus. Függvényazonosítás = "function" Függvényazonosító. FormálisParaméterlista = "(" Formális Paraméterrész {";" Formális Paraméterrész} ")". FormálisParaméterrész = Értékparaméter specifikáció | Változóparaméterspecifikáció | Eljárásparaméterspecifikáció | Függvényparaméterspecifikáció. ............. Értékparaméterspecifikáció = Azonosítólista ":" (Típusazonosító | Illeszkedőtömbséma ). Változóparaméterspecifikáció = "var" Azonosítólista (Típusazonosító | Illeszkedőtömbséma). Eljárásparaméterspecifikáció = Eljárásfej. Függvényparaméterspecifikáció = Függvényfej. Illeszkedőtömbséma = TömörítettIlleszkedőtömbséma | TömörítetlenIlleszkedőtömbséma. TömörítettIlleszkedőtömbséma = "packed" "array" "[" Indextípusspecifikáció "]" "of" Típusazonosító. TömörítetlenIlleszkedőtömbséma = "array" "[" Indextípusspecifikáció {";" Indextípusspecifikáció} "]" "of" (Típusazonosító | Illeszkedőtömbséma). Indextípusspecifikáció = Azonosító ".."Azonosító ":" MegszámlálhatóTípusAzonosító. ............. Összetettutasítás = "begin" Utasítássorozat "end". Utasítássorozat = Utasítás {";" Utasítás}. Utasítás = [Címke ":"] (Egyszerűutasítás | StrukturáltUtasítás). EgyszerűUtasítás = ÜresUtasítás | ÉrtékadóUtasítás | Eljárásutasítás | GotoUtasítás. StrukturáltUtasítás = ÖsszetettUtasítás | FeltételesUtasítás | Ciklusutasítás | WithUtasítás. FeltételesUtasítás = IfUtasítás | CaseUtasítás Ciklusutasítás = WhileUtasítás | RepeatUtasítás | ForUtasítás. ............. ÜresUtasítás = . ÉrtékadóUtasítás = (Változó | Függvényazonosító) ":=" Kifejezés. Eljárásutasítás = Eljárásazonosító [AktuálisParaméterlista | WriteParaméterlista]. GotoUtasítás = "goto" Címke. IfUtasítás = "if" LogikaiKifejezés "then" Utasítás ["else" Utasítás]. CaseUtasítás = "case" EsetIndex "of" Eset {";" Eset} [";"] "end". RepeatUtasítás = "repeat" Utasítássorozat "until" LogikaiKifejezés. WhileUtasítás = "while" LogikaiKifejezés "do" Utasítás. ForUtasítás = "for" Ciklusváltozó ":=" Kezdőérték ("to" | "downto") Végérték "do" Utasítás. WithUtasítás = "with " RekordVáltozólista "do" Utasítás. RekordVáltozólista = Rekordváltozó {"," Rekordváltozó}. Esetindex = MegszámlálhatóKifejezés. Eset = Konstans {"," Konstans} ":" Utasítás. Ciklusváltozó = Változóazonosító. Kezdőérték = MegszámlálhatóKifejezés. Végérték = MegszámlálhatóKifejezés. ............. Típus = EgyszerűTípus | StrukturáltTípus | MutatóTípus. EgyszerűTípus = MegszámlálhatóTípus | ValósTípusAzonosító. StrukturáltTípus = ["packed"] TömörítetlenStrukturáltTípus | StrukturáltTípusAzonosító. MutatóTípus = "^" Főtípus | MutatóTípusAzonosító. MegszámlálhatóTípus = FelsoroltTípus | RésztartományTípus | MegszámlálhatóTípusAzonosító. TömörítetlenStrukturáltTípus = TömbTípus | RekordTípus | HalmazTípus | Állomány Típus. Főtípus = Típusazonosító. FelsoroltTípus = "(" Azonosítólista ")". RésztartományTípus = Konstans ".." Konstans. TömbTípus = "array" "[" Indextipus {"," Indextípus} "]" "of" Elemtípus. RekordTípus = "record" Mezőlista "end". HalmazTípus = "set" "of" Alaptípus. ÁllományTípus = "file" "of" Elemtípus. Indextípus = MegszámlálhatóTípus. Elemtípus = Típus. Alaptípus = MegszámlálhatóTípus. Eredménytípus = MegszámlálhatóTípusAzonosító | ValósTípusAzonosító | MutatóTípusAzonosító. Mezőlista = [(RögzítettRész [";" VáltozatRész] | Változat Rész) [";"]]. RögzítettRész = Rekordszakasz {";" Rekordszakasz}. VáltozatRész = "case" Változatszelektor "of" Változat {";" Változat}. Rekordszakasz = Azonosítólista ":" Típus. Változatszelektor = [Kijelölőmező ":"] KijelölőTípus. Változat = Konstans {"," Konstans} ":" "(" Mezőlista ")". KijelölőTípus = MegszámlálhatóTípusAzonosító. Kijelölőmező = Azonosító. ............. Konstans = [Előjel] (ElőjelNélküliSzám | Konstansazonosító) | Karakterfüzér. ............. Kifejezés = EgyszerűKifejezés [RelácíósJel | EgyszerűKifejezés]. EgyszerűKifejezés = [Előjel] Tag {AdditívMűveletiJel | Tag}. Tag = Tényező {MultiplikatívMűveletiJel Tényező}. Tényező = ElőjelNélküliKonstans | Határazonosító | Változó | Halmazgenerátor | Függvénykifejezés | "not" Tényező | "(" Kifejezés ")". RelációsJel = "=" | "<>" | "<" | "<=" | ">" | ">=" | "in". AdditívMűveletiJel = "+" | "-" | "or". MultiplikatívMűveletiJel = "*" | "/" | "div" | "mod" | "and". ElőjelNélküliKonstans = ElőjelNélküliSzám l Karakterfüzér | Konstansazonosító | "nil". Függvénykifejezés = Függvényazonosító [Aktuális Paraméterlista]. ............. Változó = TeljesVáltozó | Elemváltozó | AzonosítottVáltozó | Pufferváltozó. TeljesVáltozó = Változóazonosító. Elemváltozó = IndexeltVáltozó | Mezőkifejezés. DinamikusVáltozó = Mutatóváltozó "^". Pufferváltozó = Állományváltozó "^". IndexeltVáltozó = Tömbváltozó "[" Index {"," Index} "]". Mezőkifejezés = [Rekordváltozó "."] Mezőazonosító. Halmazgenerátor = "[" [Elemleírás {"," Elemleírás} "]". Elemleírás = MegszámlálhatóKifejezés [".." MegszámlálhatóKifejezés]. AktuálisParaméterlista = "(" AktuálisParaméter {"," AktuálisParaméter} ")". AktuálisParaméter = Kifejezés l Változó l Eljárásazonosító l Függvényazonosító. WriteParaméterlista = "(" (Állományváltozó | WriteParaméter) {"," WriteParaméter} ")". WriteParaméter = Kifejezés [":" EgészKifejezés [":" EgészKifejezés]]. Tömbváltozó = Változó. Rekordváltozó = Változó. Állományváltozó = Változó. Mutatóváltozó = Változó. EgészKifejezés = MegszámlálhatóKifejezés. LogikaiKifejezés = MegszámlálhatóKifejezés. MegszámlálhatóKifejezés = Kifejezés. ............. MutatóTípusAzonosító = Típusazonosító. StrukturáltTípusAzonosító = Típusazonosító. MegszámlálhatóTípusAzonosító = Típusazonosító. ValósTípusAzonosító = Típusazonosító. Konstansazonosító = Azonosító. Típusazonosító = Azonosító. Változóazonosító = Azonosító. Mezőazonosító = Azonosító. Eljárásazonosító = Azonosító. Függvényazonosító = Azonosító. Határazonosító = Azonosító. ElőjelNélküliSzám = ElőjelNélküliEgész | ElőjelNélküliValós. Azonosítólista = Azonosító {"," Azonosító}. ............. Azonosító = Betű { Betű | Számjegy). Direktíva = Betű { Betű | Számjegy). Címke = Számjegysorozat. ElőjelNélküliEgész = Számjegysorozat. ElőjelNélküliValós = ElőjelNélküliEgész "." Számjegysorozat ["e" Karakterisztika ] | ElőjelNélküliEgész "e" Karakterisztika. Karakterisztika = [Előjel] ElőjelNélküliEgész. Előjel = "+" | "-". Karakterfüzér = " ' " Füzérelem { Füzérelem } " ' ". Számjegysorozat = Számjegy {Számjegy}. Betű = "a" | "b" | "c" | "d" | "e" | "f" | "g" | "h" | "i" | "j" | "k" | "l" | "m" | "n" | "o" | "p" | "q" | "r" | "s" | "t" | "u" | "v" | "w" | "x" | "y" | "z". Számjegy = "0" | "1" | "2" | "3" | "4" | "5" | "6" | "7" | "8" | "9". Füzérelem ="''" | BármelyAposztróftólKülönbözőKarakter. |
Az EBNF-szimbólumok előfordulási helye a Jelentésben és a hierarchikus leírásban
| Előfordulási hely a Jelentésben |
Metaazonosító / Alapszó | EBNF kereszthivatkozások |
| 9. 11.3.2. 11.3.2. 6.2.3. 6.2.4 7.4. 4 6.1.1. 4. 4. 10.1. 9.2.2.2. 9.2.3. 9.2.3.3. 10.1.1. 10.1.1. 7.3. 4. 8. 8. 6.1. 9.1. 8. 6.2.1. 7.2. 11.1. 11.1. 11.1. 11. 11.1. 11.3.1.2. 9.1.2. 4. 4. 8. 4. 4. 11.2. 9.1.1. 11.2.1.1. 9.2.2.2 9.2.2.2. 6.1.1. 9.2.2. 11.3.1. 11.3.1 9.2.3.3. 6.3 11.2. 11.2. 11.2. 11.2. 8. 11.3.1.2. 4. 9.1.3. 8. 6.2.3. 11.3.1.1. 9.2.2.1. 11.3.1.1. 7.2.1. 7.2.1. 6.2.1. 11.3.1.1. 4. 4. 9.2.3.3. 8. 6.2.2. 6.2.2. 5. 5. 5. 5. 8. 8. 6.1. 6.1. 6.2.2. 7.2.2. 6.2.2. 8. 6.3. 6.3. 7.3. 9.2.1. 13. 13. 13. 7.4. 6.2.2. 6.2.2. 7.2.2. 9.2.4. 8. 9.2.3.2. 6.1.3. 6.2.2. 6.2. 6.2. 9.2. 4. 4. 8. 7.1. 8. 6. 6. 6. 6. 6.2.1. 7.2.1. 11.3.1.1. 6.2. 11.3.1.1. 9. 9. 9.2. 9.1. 6.1. 6.2.2. 6.2.2. 6.2.2. 7. 7. 7. 7. 11.3.1.1. 9.2.3.3. 9.2.3.1. 9.2.4. 12.3. 12.3. |
AdditívMűveleti Jel AktuálisParaméter AktuálisParaméterlista Alaptípus ÁllományTípus Állományváltozó Azonosító Azonosítólista BármelyAposztróftólKülönbözőKarakter Betű Blokk CaseUtasítás CiklusUtasítás Ciklusváltozó Címke CímkedeklarációsRész DinamikusVáltozó Direktíva EgészKifejezés EgyszerűKifejezés EgyszerűTípus EgyszerűUtasítás Elemleírás Elemtípus Elemváltozó Eljárásazonosítás Eljárásazonosító Eljárásdeklaráció EljárásÉsFüggvénydeklarációsRész Eljárásfej Eljárásparaméterspecifikáció Eljárásutasítás Előjel ElőjelNélküliEgész ElőjelNélküliKonstans ElőjelNélküliSzám ElőjelNélküliValós Eredménytípus ÉrtékadóUtasítás ÉrtékparaméterSpecifikáció Eset Esetindex FelsoroltTípus Feltételesutasítás FormálisParaméterlista FormálisParaméterrész ForUtasítás Főtípus Függvényazonosítás Függvényazonosító Függvénydeklaráció Függvényfej Függvénykifejezés FüggvényparaméterSpecifikáció Füzérelem GotoUtasítás Halmazgenerátor HalmazTípus Határazonosító IfUtasítás Illeszkedőtömbséma Index IndexeltVáltozó Indextípus IndextípusSpecifikáció Karakterfüzér Karakterisztika Kezdőérték Kifejezés Kijelölőmező KijelölőTípus Konstans Konstansazonosító Konstansdefiníció KonstansdefiníciósRész LogikaiKifejezés MegszámlálhatóKifejezés MegszámlálhatóTípus MegszámlálhatóTípusAzonosító Mezőazonosító Mezőkifejezés Mezőlista MultiplikatívMűveletiJel MutatóTípus MutatóTípusAzonosító Mutatóváltozó ÖsszetettUtasítás Program Programfej ProgramParaméterlista Pufferváltozó Rekordszakasz RekordTípus Rekordváltozó RekordVáltozólista RelációsJel RepeatUtasítás RésztartományTípus RögzítettRész StrukturáltTípus StrukturáltTípusAzonosító StrukturáltUtasítás Számjegy Számjegysorozat Tag TeljesVáltozó Tényező Típus Típusazonosító Típusdefiníció TípusdefiníciósRész TömbTípus Tömbváltozó TömörítetlenIlleszkedőtömbséma TömörítetlenStrukturáltTípus TömörítettIlleszkedőtömbséma Utasítás Utasításrész Utasítássorozat ÜresUtasítás ValósTípusAzonosító Változat VáltozatRész Változatszelektor Változó Változóazonosító Változódeklaráció VáltozódeklarációsRész Változóparaméterspecifikáció Végérték WhileUtasítás WithUtasítás WriteParaméter WriteParaméterlista and array begin case const div do downto else end file for function goto if in label mod nil not of or packed procedure program record repeat set then to type until var while with |
160 170 188 188 189 92 174 188 136 140 125 137 183 191 197 2 26 27 38 40 71 71 71 153 209 210 211 212 213 214 215 219 219 223 3 28 53 56 127 149 219 240 223 223 224 224 234 1 7 29 31 32 34 85 97 84 86 105 112 79 94 225 7 13 179 182 30 33 224 193 194 199 162 163 164 118 119 80 81 186 186 187 132 137 139 178 181 31 39 39 92 189 213 21 29 11 20 29 30 38 59 47 58 82 92 157 164 229 230 218 226 227 228 229 166 172 157 172 218 218 227 41 141 81 91 45 52 98 98 111 97 110 123 127 83 85 38 40 43 43 44 45 86 105 122 126 34 42 42 91 174 190 214 21 32 32 32 40 61 167 174 48 60 231 231 240 82 94 167 186 125 136 166 215 85 95 54 57 62 70 184 184 181 184 131 131 138 65 68 69 71 158 172 231 227 228 229 105 113 91 162 168 189 193 201 150 153 150 152 26 111 111 128 151 151 157 157 173 209 14 15 26 8 14 95 102 103 200 110 113 114 187 187 200 201 119 123 138 140 71 124 141 152 207 185 212 181 185 134 143 151 165 171 118 122 122 142 205 182 198 22 75 83 1 1 2 2 3 179 183 145 145 149 125 133 109 109 185 196 107 109 162 169 86 100 123 128 143 145 118 120 121 206 80 83 223 224 232 232 238 13 13 225 226 227 232 164 164 165 178 180 165 165 166 168 27 28 118 139 149 53 56 66 70 126 205 206 207 208 210 16 17 27 9 16 125 131 184 195 63 67 120 125 62 64 78 78 79 96 96 104 106 108 111 12 22 76 78 101 81 90 119 141 208 147 148 151 143 143 146 146 150 91 166 178 189 112 180 211 18 19 28 10 18 46 55 106 114 86 103 84 107 191 192 193 93 191 171 65 68 131 75 97 146 14 171 103 106 107 106 96 77 99 135 137 105 40 42 94 94 169 13 171 173 168 65 69 97 131 136 137 146 170 65 120 38 39 2 133 100 136 95 106 16 102 18 56 103 107 |
Az EBNF-szabályok ábécésorrendben
AdditívMűveletiJel = "+" | "-" | "or".
AktuálisParaméter = Kifejezés | Változó | Eljárásazonosító | Függvényazonosító.
AktuálisParaméterlista = "(" AktuálisParaméter {"," AktuálisParaméter} ")".
Alaptípus = MegszámlálhatóTípus.
ÁllományTípus = "file" "of"Elemtípus.
Állományváltozó = Változó.
Azonosító = Betű { Betű | Számjegy}.
Azonosítólista = Azonosító {"," Azonosító}.
Betű = "a" | "b" | "c" | "d" | "e" | "f" | "g" | "h" | "i" | "j" | "k" | "l" | "m" | "n" |
"o" | "p" | "q" | "r" | "s" | "t" | "u" | "v" | "w" | "x" | "y" | "z".
Blokk = CímkedeklarációsRész
KonstansdefiníciósRész
TípusdefiníciósRész
VáltozódeklarációsRész
Utasításrész.
CaseUtasítás = "case" EsetIndex "of" Eset {";" Eset} [";"] "end".
Ciklusutasítás = WhileUtasítás | RepeatUtasítás | ForUtasítás.
Ciklusváltozó = Változóazonosító.
Címke = Számjegysorozat.
CímkedeklarációsRész = [ "label" Számjegysorozat {"," Számjegysorozat} ";" ].
DinamikusVáltozó = Mutatóváltozó "^".
Direktíva = Betű { Betű | Számjegy}.
EgészKifejezés = MegszámlálhatóKifejezés.
EgyszerűKifejezés = [Előjel] Tag {AdditívMűveletiJel | Tag}.
EgyszerűTípus = MegszámlálhatóTípus | ValósTípusAzonosító.
EgyszerűUtasítás = ÜresUtasítás | ÉrtékadóUtasítás | Eljárásutasítás | GotoUtasítás.
Elemleírás = MegszámlálhatóKifejezés [".." MegszámlálhatóKifejezés].
Elemtípus = Típus.
Elemváltozó = IndexeltVáltozó | Mezőkifejezés.
Eljárásazonosítás = "procedure " Eljárásazonosító.
Eljárásazonosító = Azonosító.
Eljárásdeklaráció = Eljárásfej ";" Blokk | Eljárásfej ";" Direktíva |
Eljárásazonosítás ";" Blokk.
EljárásÉsFüggvénydeklarációsRész = {(Eljárásdeklaráció | Függvénydeklaráció) ";"}.
Eljárásfej = "procedure" Azonosító [Formális Paraméterlista].
Eljárásparaméterspecifikáció = Eljárásfej.
EljárásUtasítás = Eljárásazonosító [AktuálisParaméterlista | WriteParaméterlista].
Előjel = "+" |"-".
ElőjelNélküliEgész = Számjegysorozat.
ElőjelNélküliKonstans = ElőjelNélküliSzám | Karakterfüzér | Konstansazonosító |"nil".
ElőjelNélküliValós = ElőjelNélküliEgész "." SzámjegyekSorozata ["e" Karakterisztika ] |
ElőjelNélküliEgész "e" Karakterisztika.
Eredménytípus = MegszámlálhatóTípusAzonosító | ValósTípusAzonosító | MutatóTípusAzonosító.
ÉrtékadóUtasítás = (Változó | Függvényazonosító) ":=" Kifejezés.
Értékparaméterspecifikáció = Azonosítólista ":" (Típusazonosító | Illeszkedőtömbséma).
Eset = Konstans {"," Konstans} ":" Utasítás.
EsetIndex = MegszámlálhatóKifejezés.
FelsoroltTípus = "(" Azonosítólista ")".
FeltételesUtasítás = IfUtasítás | CaseUtasítás.
FormálisParaméterlista = "(" FormálisParaméterrész {";" FormálisParaméterrész} ")".
FormálisParaméterrész = Változóparaméterspecifikáció | Értékparaméterspecifikáció |
Eljárásparaméterspecifikáció | Függvényparaméterspecifikáció.
ForUtasítás = "for" Ciklusváltozó ":=" Kezdőérték ("to" | "downto") Végérték "do" Utasítás.
Főtípus = Típusazonosító.
Függvényazonosítás = "function" Függvényazonosító.
Függvényazonosító = Azonosító.
Függvénydeklaráció = Függvényfej ";" Blokk | Függvényfej ";" Direktíva | Függvényazonosítás ";" Blokk.
Függvényfej = "function" Azonosító [FormálisParaméterlista] ":" Eredménytípus.
Függvénykifejezés = Függvényazonosító [AktuálisParaméterlista].
Függvényparaméterspecifikáció = Függvényfej.
Füzérelem ="''" | BármelyAposztróftólKülönbözőKarakter.
GotoUtasítás = "goto" Címke.
Halmazgenerátor = "[" [Elemleírás {"," Elemleírás}] "]".
HalmazTípus = "set" "of" Alaptípus.
Határazonosító = Azonosító.
IfUtasítás = "if" LogikaiKifejezés "then" Utasítás ["else" Utasítás].
Illeszkedőtömbséma = TömörítettIlleszkedőtömbséma | TömörítetlenIlleszkedőtömbséma.
IndexeltVáltozó = Tömbváltozó "[" Index {"," Index} "]".
Indextípus = MegszámlálhatóTípus.
Indextípusspecifikáció = Azonosító ".."Azonosító ":" MegszámlálhatóTípusAzonosító.
Karakterfüzér = "'" Füzérelem {Füzérelem} "'".
Karakterisztika = [Előjel] ElőjelNélküliEgész.
Kezdőérték = MegszámlálhatóKifejezés.
Kifejezés = EgyszerűKifejezés [RelácíósJel | EgyszerűKifejezés].
Kijelölőmező = Azonosító.
KijelölőTípus = MegszámlálhatóTípusazonosító.
Konstans = [Előjel] (ElőjelNélküliSzám | Konstansazonosító) | Karakterfüzér.
Konstansazonosító = Azonosító.
Konstansdefiníció = Azonosító "=" Konstans.
KonstansdefiníciósRész = ["const" Konstansdefiníció ";" {Konstansáéfiníció ";"}].
LogikaiKifejezés = MegszámlálhatóKifejezés.
MegszámlálhatóKifejezés = Kifejezés.
MegszámlálhatóTípus = FelsoroltTípus | RésztartományTípus | MegszámlálhatóTípusAzonosító.
MegszámlálhatóTípusAzonosító = Típusazonosító.
Mezőazonosító = Azonosító.
Mezőkifejezés = [Rekordváltozó "."] Mezőazonosító.
Mezőlista = [(RögzítettRész [";" VáltozatRész] | Változat Rész) [";"]].
MultiplikatívMűveletiJel = "*" | "/" | "div" | "mod" | "and".
MutatóTípus = "^" Főtípus | MutatóTípusAzonosító.
MutatóTípusAzonosító = Típusazonosító.
Mutatóváltozó = Változó.
Összetettutasítás = "begin" Utasítássorozat "end".
Program = Programfej ";" Blokk ".".
Programfej = "program" Azonosító [ProgramParaméterlista].
ProgramParaméterlista = "(" Azonosítólista ")".
Pufferváltozó = Állományváltozó "^".
Rekordszakasz = Azonosítólista ":" Típus.
RekordTípus = "record"
Mezőlista
"end".
Rekordváltozó = Változó.
RekordVáltozólista = Rekordváltozó {"," Rekordváltozó}.
RelációsJel = "=" | "<>" | "<" | "<=" | ">" | ">=" | "in".
RepeatUtasítás = "repeat"
Utasítássorozat
"until" LogikaiKifejezés.
RésztartományTípus = Konstans ".." Konstans.
RögzítettRész = Rekordszakasz {";" Rekordszakasz}.
StrukturáltTípus = ["packed"] TömörítetlenStrukturáltTípus | StrukturáltTípusAzonosító.
StrukturáltTípusAzonosító = Típusazonosító.
StrukturáltUtasítás = ÖsszetettUtasítás | FeltételesUtasítás | Ciklusutasítás | WithUtasítás.
Számjegy = "0" | "1" | "2" | "3" | "4" | "5" | "6" | "7" | "8" | "9".
Számjegysorozat = Számjegy {Számjegy}.
Tag = Tényező {MultiplikatívMűveletiJel Tényező}.
TeljesVáltozó = Változóazonosító.
Tényező = ElőjelNélküliKonstans | Határazonosító | Változó | Halmazgenerátor |
Függvénykifejezés | "not" Tényező | "(" Kifejezés ")".
Típus = EgyszerűTípus | StrukturáltTípus | MutatóTípus.
Típusazonosító = Azonosító.
Típusdefiníció = Azonosító "=" Típus.
TípusdefiníciósRész = [ "type" Típusdefiníció ";" {Típusdefiníció ";"}].
TömbTípus = "array" "[" Indextipus {"," Indextípus} "]" "of" Elemtípus.
Tömbváltozó = Változó.
TömörítetlenIlleszkedőtömbséma = "array" "[" Indextípusspecifikáció
{";" Indextípusspecifikáció} "]" "of"
(Típusazonosító | Illeszkedőtömbséma).
TömörítetlenStrukturáltTípus = TömbTípus | RekordTípus | HalmazTípus | Állomány Típus.
TömörítettIlleszkedőtömbséma = "packed" "array" "[" Indextípusspecifikáció "]" "of" Típusazonosító.
Utasítás = [Címke ":"]
(Egyszerűutasítás | StrukturáltUtasítás).
Utasításrész = ÖsszetettUtasítás.
Utasítássorozat = Utasítás {";" Utasítás}.
ÜresUtasítás = .
ValósTípusAzonosító = Típusazonosító.
Változó = TeljesVáltozó | Elemváltozó | AzonosítottVáltozó | Pufferváltozó.
Változóazonosító = Azonosító.
Változódeklaráció = Azonosítólista ":" Típus.
VáltozódeklarációsRész = [ "var" Változódeklaráció ";" {Változódeklaráció ";"}].
Változóparaméterspecifikáció = "var" Azonosítólista (Típusazonosító | Illeszkedőtömbséma).
Változat = Konstans {"," Konstans} ":" "(" Mezőlista ")".
VáltozatRész = "case" Változatszelektor "of" Változat {";" Változat}.
Változatszelektor = [Kijelölőmező ":"] KijelölőTípus.
Végérték = DiszkrétKifejezés.
WhileUtasítás = "while" LogikaiKifejezés "do" Utasítás.
WithUtasítás = "with " RekordVáltozólista "do" Utasítás.
WriteParaméter = Kifejezés [":" EgészKifejezés [":" EgészKifejezés]].
WriteParaméterlista = "(" (Állományváltozó | WriteParaméter) {"," WriteParaméter} ")".
Szintaxisdiagramok
A Betű, Számjegy Azonosító, Előjel nélküli egész, Előjel nélküli szám és Karakterfüzér feliratú diagramok azt mutatják be, hogyan épülnek föl a szótári szimbólumok a karakterekből. A többi diagramból az olvasható le, hogyan állnak össze a szintaktikus konstrukciók a szimbólumokból.
Betű:

Számjegy:

Azonosító és direktíva

Előjel nélküli egész:

Előjel nélküli szám:

Karakterfüzér:

Konstansazonosító, Változóazonosító, Mezőazonosító, Határozóazonosító, Típusazonosító, Eljárásazonosító, Függvényazonosító:
![]()
Előjel nélküli konstans:

Konstans:
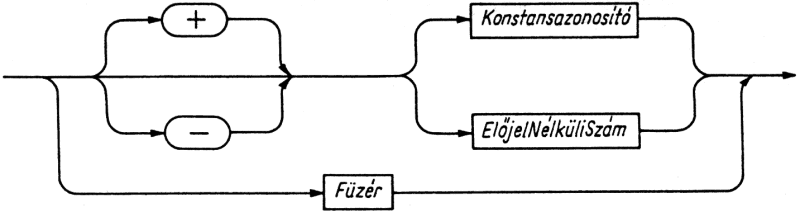
Változó:
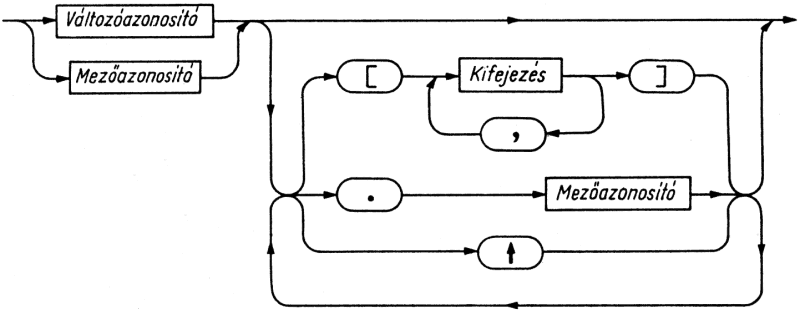
Tényező:
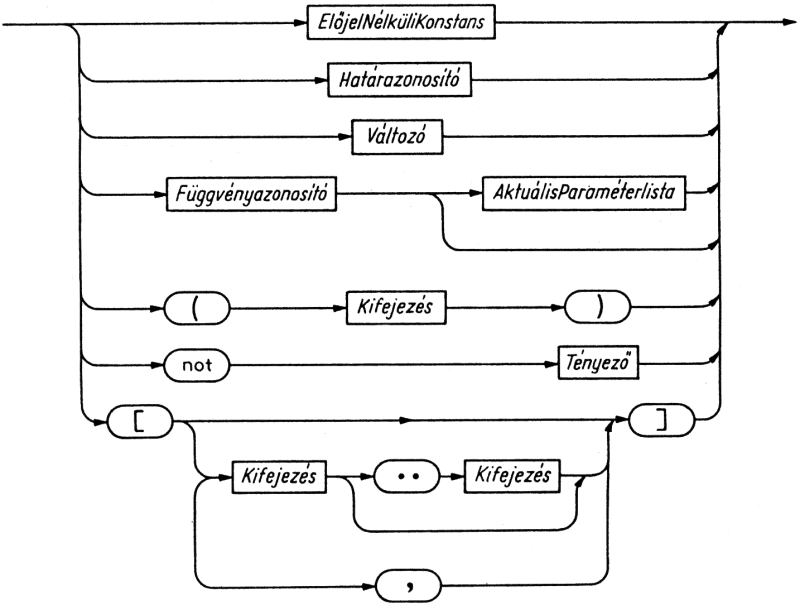
Tag:

Egyszerű kifejezés:

Kifejezés:

Aktuális paraméterlista:

Write paraméterlista:

Indextípus specifikáció:
![]()
Illeszkedőtömb séma:

Formális paraméterlista:

Eljárás vagy függvényfej:
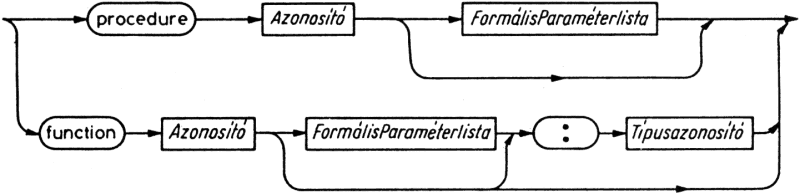
Megszámlálható típus:
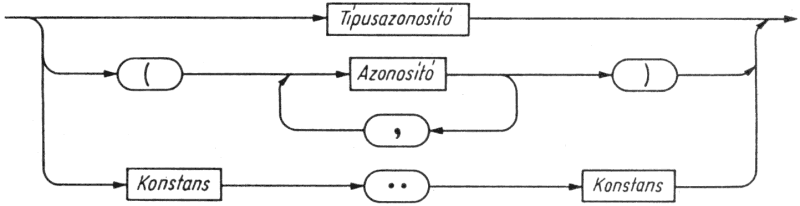
Típus:
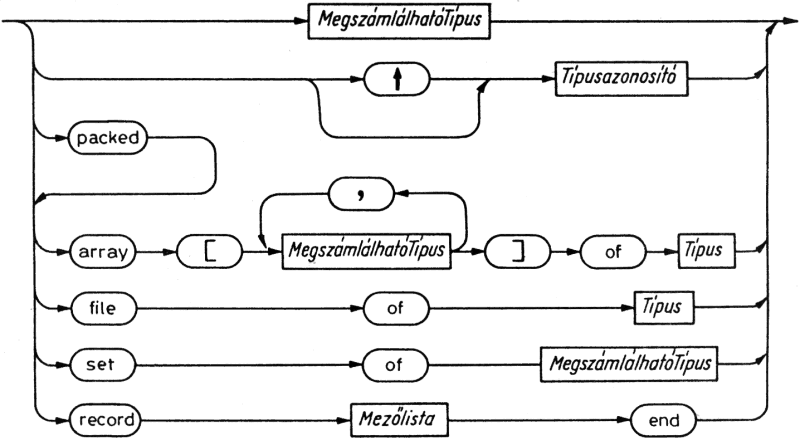
Mezőlista:
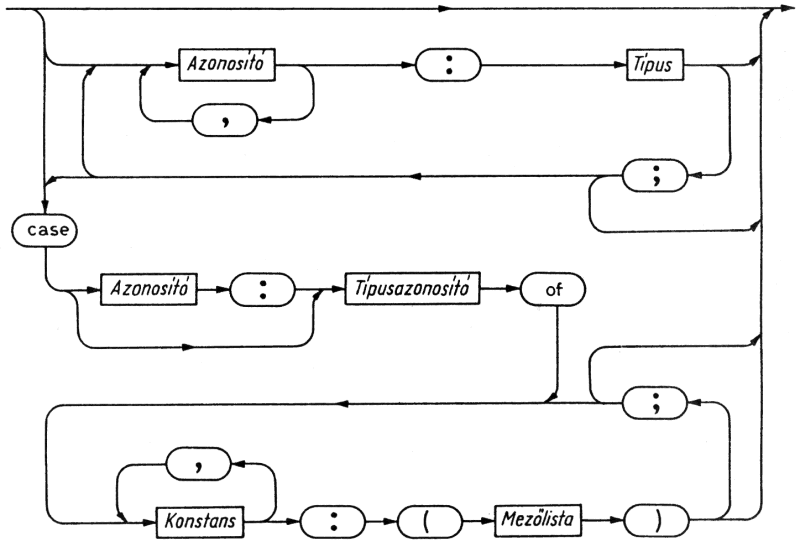
Utasítás:
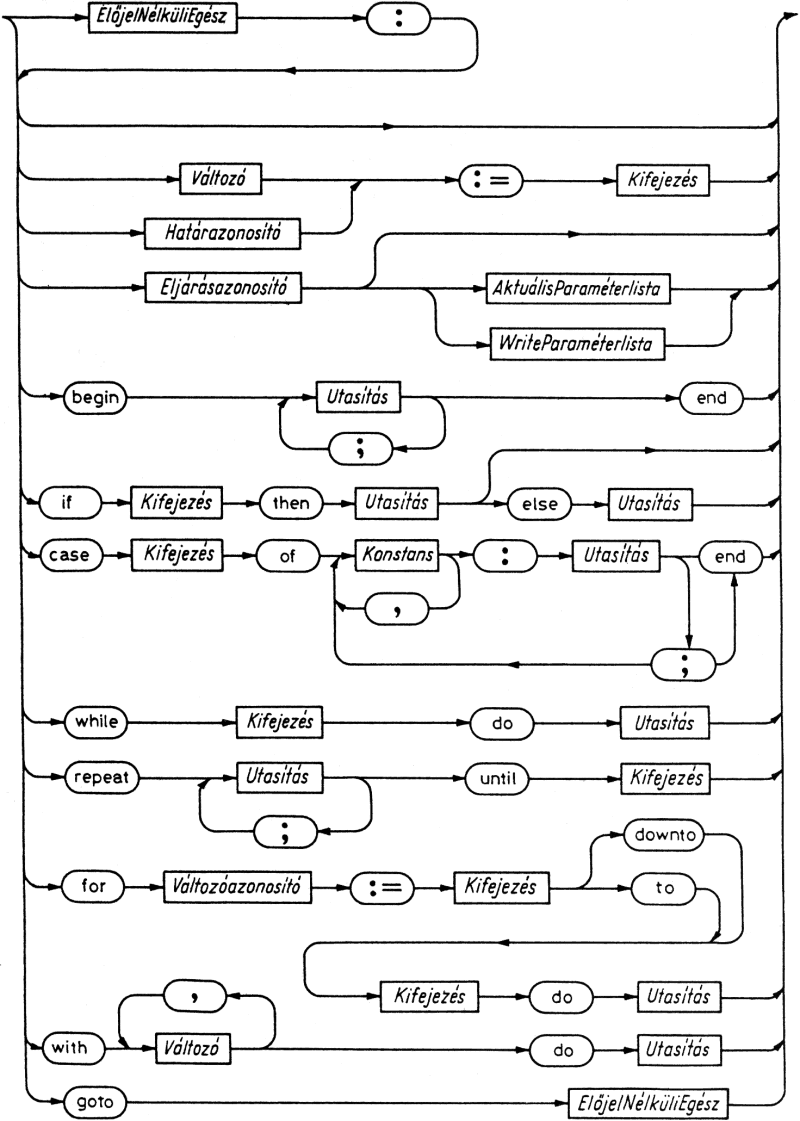
Blokk:
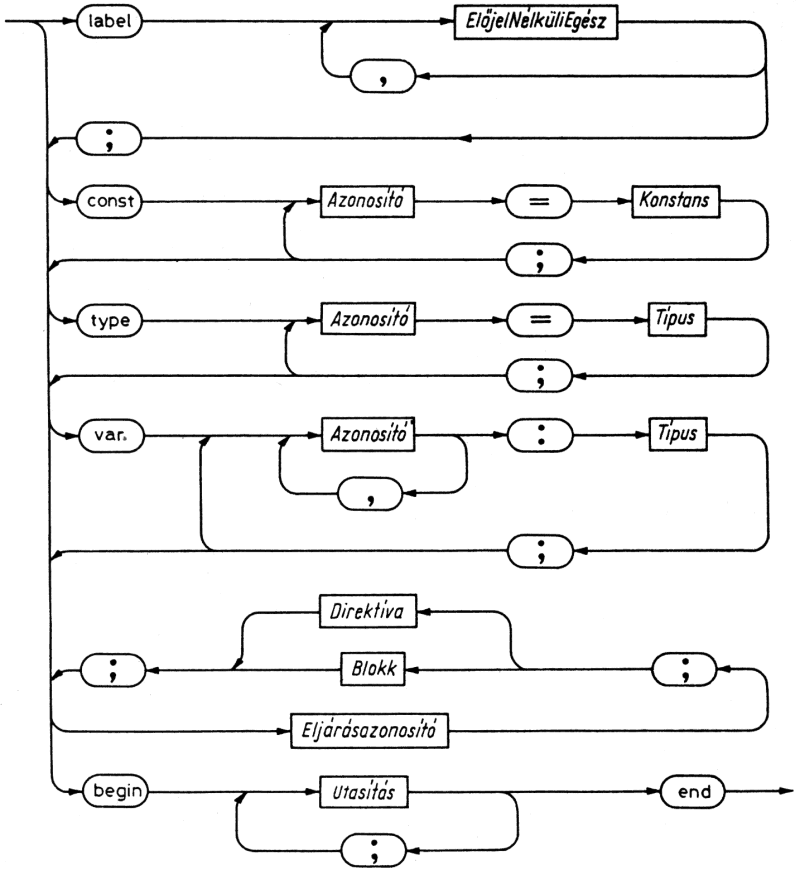
Program:

E. függelék: A mű első kiadásának eltérései az ISO 7185 szabványtól
Ez a függelék azokról a technikai jellegű módosításokról ad hozzávetőleges, korántsem teljes áttekintést, amelyeket a könyvön a harmadik (ISO szabvány) kiadásra való előkészítés miatt hajtottunk végre. Az összefoglaló azok számára lehet hasznos, akiknek az előző kiadások valamelyike birtokában van.
Jelentés, 3. Jelölésmód és terminológia
BNF helyett az EBNF-et használtuk.
Definiáltuk a hiba, a rendszer által meghatározott és a rendszerfüggő konstrukciók, továbbá a bővítés és a standard Pascal fogalmát, és a Jelentésben mindvégig következetesen alkalmaztuk őket.
Jelentés, 4. Szimbólumok és elválasztók
Megváltoztattuk a szintaxist leíró szabályokon belül az elválasztó- és határolójeleket.
Bevezettük a ".." szimbólumot.
A "[ , ]" és a "^" (eredetileg felfelé mutató nyíl) speciális szimbólumok jelölésére alternatív lehetőséget engedtünk meg.
Módosítottuk a magyarázatokra vonatkozó szintaktikus előírásokat; tilos a magyarázatok egymásba ágyazása!
Két azonosító különböző, ha karaktersoraik akárhányadik karakterben különböznek.
A szimbólumok új osztálya: a direktívák.
Jelentés, 5. Konstansok
Az új Jelentésben szerepel a MaxInt.
Jelentés, 6. Típusok
A skalár típusok helyett bevezettük a megszámlálható és a valós típusokat; definiáltuk a succ, pred és ord függvényeket és ezáltal egyszerűsítettük a tömbök indexelését, az esetválasztást, a résztartomány típust és a halmazok alaptípusát.
A típusok kompatibilitását neveik kompatibilitásával definiáltuk.
Bevezettük az értékadás-kompatibilitást és a hozzárendelhető típust.
A strukturált típusok tömörítése más szemantikus következményekkel jár.
A rekord típusok szintaxisát egy opcionális jellel egészítettük ki.
A rekordváltozatokban az egyes eseteket megkülönböztető címkéket most konstansoknak nevezzük.
A rekord típusokban a változat részek teljes specifikálására szükség van.
Az állomány típusok esetében megkülönböztettük a feldolgozási és a generálási módot.
A Text típus nem ekvivalens a Char elemtípusú (tömörített) állománytípussal.
Az állomány típusokat és az állomány típust tartalmazó típusokat (tehát a nem hozzárendelhető típusokat) nem engedjük állomány típusok elemtípusaként alkalmazni.
Bevezettük a mutató típusok főtípusát.
Jelentés, 7. Változók
Bevezettük a határozatlan és a teljesen határozatlan változók fogalmát.
Ha egy programban az Input és Output azonosítókat használjuk, azok implicit módon deklarált, szöveg típusú állomány-programparaméterek lesznek.
Jelentés, 8. Kifejezések
Tényezőnek tekintjük az illeszkedő tömb-paraméterek határazonosítóit is.
A kifejezések kiértékelésének sorrendjét rendszerfüggőnek tekintjük.
Módosítottuk a mod műveleti jel definícióját.
Egy halmazgenerátor típus lehet tömörített és tömörítetlen is.
Jelentés, 9. Utasítások
A goto utasításokkal elérhető címkékre vonatkozó szabályokat megszigorítottuk.
A case utasítás címkéit konstansoknak neveztük el.
A for utasítás ciklusváltozója csak lokális változó lehet.
Több korlátozást vezettünk be a for utasításra nézve, és pontosan definiáltuk az általa végrehajtott műveleteket.
Jelentés, 10. Blokkok, hatáskör, aktiválás
Definiáltuk a programpont; aktiválási pont, továbbá a címkék és azonosítók definíciójának vagy deklarációjának (bevezetésének) hatásköre fogalmát.
Pontosan definiáltuk a hatáskörre vonatkozó szabályokat, felszámolva a kétértelműségeket.
A címkéknek megfelelő egész számok értéke nem haladhatja meg a 9999-et.
Jelentés, 11. Eljárások és függvények
Bevezettük az eljárásokra és függvényekre vonatkozó direktívákat; a forward standard direktíva.
A paraméterek közé felvettük az illeszkedőtömböket; bevezettük az illeszthetőség fogalmát és az illeszkedő típust.
A formális eljárás- és függvényparaméterek (azaz a paraméterként alkalmazott eljárások és függvények) paraméterlistáit teljes egészükben meg kell adni; bevezettük a paraméterlisták kongruenciájának fogalmát.
Megtiltottuk a kijelölőmezők aktuális változóparaméterekként való alkalmazását.
Módosítottuk a pack és unpack eljárások tömbparamétereinek specifikációját.
Pontosan definiáltuk az állománykezelő eljárásokat és függvényeket, továbbá az állományváltozó és a pufferváltozó állapotát.
Jelentés, 12. Szöveg típusú állományok be- és kivitele
A page eljárás standard, állományparamétere opcionális; hatása módosult.
A write és writeln eljárások aktuális paraméterlistájaként bevezettük a WriteParaméter-listákat, és speciális szintaktikus szabályokat írtunk elő rájuk.
Az előírt formátummal dolgozó write és writeln eljárások mezőszélesség-paramétereit pontosan definiáltuk.
Jelentés, 13. Programok
A programparaméterek opcionálisak; tulajdonságaikat meghatároztuk.
Jelentés, 14. Összhang az ISO 7185-tel
Definiáltuk a szabvánnyal összhangban lévő program és processzor fogalmát. Kifejtettük, milyen követelményeket jelent az ISO Pascal-szabvánnyal való összhang.
F. függelék: Programozási példák
Két példát mutatunk be az alábbiakban: az első a programok lépésről lépésre történő kifejlesztését [2] illusztrálja, majd egy olyan eljárás következik, amely a többféle rendszeren futtatható programok számára szolgálhat modellként.
1. Példa: Program Palindrome
Olyan programot írunk, amelynek segítségével megkereshető valamennyi 1 és 100 közötti egész szám, amelynek négyzete palindrom. Például: 11 négyzete 121, ami palindrom.
Palindromnak valamely ábécé szimbólumaiból alkotott olyan füzért nevezünk, amelyet elölről hátra vagy hátulról előre olvasva ugyanazt a sorozatot kapjuk. Ismert magyar nyelvű példák (a szóközöktől és az írásjelektől eltekintve):
"goromba rab morog"
"erőszakos kannak sok a szőre"
"ólba rab dobál, de kenguru rúg neked lábodba, rabló"
1. Példa, 1. lépés:
program Palindrome(Output);
begin
KeressükAzon1És100KözöttiEgészeketMelyekNégyzetePalindrom
end {Palindrome}.
1. Példa, 2. lépés:
Pprogram Palindrome(Output);
{ Keressük azon 1 és 100 közötti egészeket, amelyek négyzete palindrom. }
const Maximum = 100;
type Egésztartomány = 1..Maximum;
var N: Egésztartomány;
begin
for N:= 1 to Maximum do
if Palindrom(Sqr(N)) then
Writeln(N, ' négyzete palindrom. ')
end {Palindrome}.
1. Példa, 3. lépés:
program Palindrome(Output);
{ Keressük azon 1 és 100 közötti egészeket, amelyek négyzete palindrom. }
const Maximum = 100;
type Egésztartomány = 1..Maximum;
var N: Egésztartomány;
function Palindrom (Négyzet: Integer): Boolean;
var NJegyei = 1..5 {5 = Log10(Sqr(Maximum)) + 1};
begin {Palindrom}
JegyekLevágása;
Palindrom: = Szimmetriavizsgálat(1,NJegyei)
end {Palindrom};
begin
for N:= 1 to Maximum do
if Palindrom(Sqr(N)) then
Writeln(N, ' négyzete palindrom ')
end {Palindrome}.
1. Példa, 4. lépés:
program Palindrome(Output);
{Turbo Pascal}
{Keressuk azon 1 es 100 kozotti egeszeketm melyek negyzete palindrom.}
const Maximum=100;
type Egesztartomany=1..Maximum;
var N: Egesztartomany;
function Palindrom(Negyzet: Integer): Boolean;
const Jegyek=5 {= Trunc(Log10(Sqr(Maximum)))+1};
type NJegyei=1..Jegyek;
EgyJegyu=0..9;
JegyVektor=array[NJegyei] of Egyjegyu;
var Szamjegyek: JegyVektor;
Meret: NJegyei;
procedure JegyekLevalogatasa;
begin
Meret:=1;
while Negyzet>9 do begin
Szamjegyek[Meret]:=Negyzet mod 10;
Negyzet:=Negyzet div 10;
Meret:=Meret+1
end;
Szamjegyek[Meret]:=Negyzet
end {Jegyeklevalogatasa};
function SzimVizsg(Bal,Jobb: NJegyei):Boolean;
begin
if Bal>=Jobb then SzimVizsg:=True
else if Szamjegyek[Bal]=Szamjegyek[Jobb] then
SzimVizsg:=SzimVizsg(Bal+1,Jobb-1)
else SzimVizsg:=false
end {SzimVizsg};
begin {Palindrom}
JegyekLevalogatasa;
Palindrom:=SzimVizsg(1,Meret)
end {Palindrom};
begin
for N:=1 to Maximum do
if Palindrom(Sqr(N)) then Writeln(N:2,' negyzete palindrom.')
end {Palindrome}.
2. Példa: Procedure Más Alapú Számrendszerben Ábrázolt Szám
Az alábbiakban egy olyan általános eljárást mutatunk be, amely bármely, 2 és 16 közé eső alapú számrendszerben ábrázolt egész szám beolvasására alkalmas.
MasAlapuSzamrendszerbenAbrazoltSzam végrehajtásánál feltételezzük, hogy az F szövegállomány olyan helyzetben van, hogy általánosított számjegyeknek egy olyan sorozatát lehet róla beolvasni, amely egy egész szám R alapút számrendszerben ábrázolt alakját adja.
Az általánosított számjegyek, növekvő sorrendben a kővetkezők: '0', '1', '2', '3', '4', '5', '6', '7', '8', ' 9', 'a', 'b', 'c', 'd', 'e', 'f'
A kisbetűk helyett a nekik megfelelő nagybetűket is használhatjuk.
Az E paraméter az alábbi hibák egyikének előfordulását jelzi:
type Alapszam = 2..16;
procedure MasAlapuSzamrendszerbenAbrazoltSzam
(var F: text; {ez tartalmazza a szamot}
var E: Boolean; {jelzi a hibat}
var X: Integer; {eredmeny, ha nincs hiba}
R: Alapszam {a szamrendszer alapja});
type Szamjegytartomany = 0..15;
var D: Szamjegytartomany;
V: Boolean;
S: 0..MaxInt;
procedure AltalanositottSzamjegyekAtvaltasa(C:Char; var V:Boolean; var D:Szamjegytartomany);
{Az eljárás megallapitja, hogy C altalanositott számjegye. Ezt V ertekevel jelzi, es ha V
igaz, D-nek az altalanositott számjegy numerikus értékét adja.}
begin {AltalanositottSzamjegyekAtvaltasa}
V:= C in ['0'..'9', 'a','b','c','d','e','f','A','B','C','D','E','F'];
if V then case C of
'0': D:=0; '1': D:=1; '2': D:=2; '3': D:=3; '4': D:=4;
'5': D:=5; '6': D:=6; '7': D:=7; '8': D:=8; '9': D:=9;
'A','a': D:=10; 'B','b': D:=11; 'C','c': D:=12;
'D','d': D:=13; 'E','e': D:=14; 'F','f': D:=15;
end
end {AltalanositottSzamjegyekAtvaltasa}
begin {MasAlapuSzamrendszerbenAbrazoltSzam}
E:=true;
AltalanositottSzamjegyekAtvaltasa(F^,V,D);
if V then begin
E:=false; S:=0;
repeat
if D<R then
if (Maxint-D) div R>=S then begin
S:=S*R+D;
Get(F);
AltalanositottSzamjegyekAtvaltasa(F^,V,D)
end
else E:=true;
else E:=true;
until E or not V;
if not E then X:=S
end
end {MasAlapuSzamrendszerbenAbrazoltSzam}
G. függelék: Az ASCII karakterkészlet
Az ASCII (American Standard Code for Information Interchange; az információcsere amerikai szabványkódja) az ISO (International Organization for Standardization: Nemzetközi Szabványügyi Szervezet) készletnek nevezett, hivatalosan elfogadott nemzetközi szabványkarakterkészlet amerikai változata. 128 karakter kódját tartalmazza. Az ISO karakterkód 12 szimbólumban engedélyez nemzeti változatokat (ilyen például a $ jel). A 128 közül 95 valamilyen alakzatot nyomtat ki, 33 pedig a különböző egységek vezérlésére szolgál. A backspace (visszalépés) vezérlőkarakter segítségével egyes kinyomtatott karaktereket lehet felülnyomtatni; így állíthatók elő például az egyes nyelvek számára szükséges ékezetes betűk.
A 33 vezérlőkarakter:
ACK
BEL
BS
CAN
CR
DC1
DC2
DC3
DC4
DEL
DLE
EM
ENQ
EOT
ESC
ETB
ETX
FF
FS
GS
HT
LF
NAK
NUL
RS
SI
SO
SOH
STX
SUB
SYN
US
VTAcknowledge
Bell
Backspace
Cancel
Carriage Return
Device Control 1
Device Control 2
Device Control 3
Device Control 4
Delete
Data Link Escape
End of Medium
Enquiry
End of Transmission
Escape
End of Transmission Block
End of Text
Form Feed
File Separator
Group Separator
Horizontal Tab
Line Feed
Negative Acknowledge
Null
Record Separator
Shift In
Shift Out
Start of Heading
Start of Text.
Substitute.
Synchronous Idle
Unit Separator
Vertical Tabvisszajelzés.
csengő.
visszalépés.
törlés.
kocsi vissza.
1. egység vezérlése.
2. egység vezérlése.
3. egység vezérlése.
4. egység vezérlése.
törlés.
kilépés az adatsorból.
közeg vége.
keresés.
átvitel vége.
kilépés.
átviteli blokk vége.
szöveg vége.
lapemelés.
állományelválasztó.
csoportelválasztó.
vízszintes tabulálás.
soremelés.
negatív visszajelzés.
nulla.
rekordelválasztó.
váltó be.
váltó vissza.
fejléc kezdete.
szöveg kezdete.
helyettesítés.
szinkron üresjárat.
egységelválasztó.
függőleges tabulálás.
A teljes, 128 karakterből álló készlet:
00 16 32 48 64 80 96 112 0 NUL DLE 0 @ P ´ p 1 SOH DC1 ! 1 A Q a q 2 STX DC2 " 2 B R b r 3 ETX DC3 # 3 C S c s 4 EOT DC4 $ 4 D T d t 5 ENQ NAK % 5 E U e u 6 ACK SYN & 6 F V f v 7 BEL ETB ' 7 G W g w 8 BS CAN ( 8 H X h x 9 HT EM ) 9 I Y i y 10 LF SUB * : J Z j z 11 VT ESC + ; K [ k { 12 FF FS , < L \ l | 13 CR GS - = M ] m } 14 SO RS . > N ^ n ~ 15 SI US / ? O _ o DEL
Egy karakter 7 biten ábrázolt kódja a sor és oszlop tetején álló szám összege. A G betű kódja tehát például 7+64 = 71.