A derékszögű és a polárkoordináták összefüggése
Mikroszámítógépes Grafika
Grafikai alogitmusok
Kepes János - 1987
Műszaki Könyvkiadó
Tartalom
| 1. Bevezetés 2. Előkészítés 2.1. Matematikai elemek 2.2 Programozási elemek 2.3. Grafikai elemek 3. Szabályos képek 3.1. Képek görbékből 3.2. Képek görbeseregekből 3.3. Képek pontokból 4. A véletlen képei 4.1. Véletlen vonalak 4.2. Képek véletlen vonalakból 4.3 Véletlen síkbetöltés 4.4. Véletlen síkfelosztások 4.5. Véletlen elágazások 4.6. Véletlen rétegződések 4.7. Véletlenszerű terjedés 4.8. Véletlen skatulyázás 4.9. Véletlen textúrák |
5. Térbeli képek 5.1. Perspektíva 5.2. Felület érzékeltetése görbeseregekkel 5.3. Takarás 5.4. Árnyékolás 6. Szimmetrikus minták 6.1. Hagyományos szimmetriák 6.2. Hasonlósági szimmetria 6.3. Ornamentális szimmetria 6.4. Belső szimmetria 7. Számítógéppel rajzolt képek 7.1. Tollrajzok 7.2. Tónusos rajzolás 7.3. Közelítő vonalrajzolás 8. Motívumokból képek 9. Mozgóképek 9.1. Kölcsönző-módszer 9.2. Relatív mozgás 9.3. Film néhány kockából |
"Mármost ahhoz, hogy egy szerzőt megértsünk..."
(B. Pascal)
A mikroszámítógépek elterjedésével alapvetően megváltozott az átlagember addig kicsit hűvös, kicsit idegenkedő, ugyanakkor némi csodálattal fűszerezett viszonya általában a számítógéphez. Ha eddig csak a beavatottak számára hozzáférhető, csak általuk szóra bírható varázseszközt látott benne (amiről éppen ezért nem is nagyon kell tudomást vennie), most a leghétköznapibb helyzetekben, munkahelyeken, iskolákban, sőt, a gyerekek játékai között nap mint nap találkozhat vele. Ennek a forradalmi változásnak egyik legszembetűnőbb jele - egyszersmind oka és következménye is - az ember és a számítógép közötti kommunikáció átalakulása. A szakemberek azelőtt (akár egy egzotikus vallás papjai) valami különös, titokzatos nyelven váltottak üzeneteket a számítógéppel. Ma viszont a gyerekek játékfigurákat, a tervezők még éppen csak megálmodott konstrukciók modelljét láthatják a számítógéphez kapcsolt képernyőn, és néhány billentyű lenyomásával mozgatni tudják vagy akár meg is változtathatják azokat. A mikroszámítógép tehát nem alfanumerikus kódokban, hanem közérthető képekben fejezi ki magát.
Ehhez persze hosszú elméleti és műszaki fejlődésnek kellett lejátszódni, amelynek során speciális ismeretek halmozódtak fel. Ezeket az ismereteket (amelyek tehát a számítógép képeken keresztül való kommunikációját alapozzák meg), számítógépes grafika néven szokás összefoglalni. A számítógépes grafika magában foglalja a grafikai célú eszközök egyre bővülő körének (különböző típusú képernyőknek, nyomtató- és rajzgépeknek) a készítéséhez és működtetéséhez szükséges ismereteket éppúgy, mint a korszerű grafikai programcsomagok és grafikára orientált programnyelvek ismeretét.
A számítógépes grafika - amellett, hogy hozzájárult a mikroszámítógépek korábban elképzelhetetlen mértékű elterjedéséhez - számtalan területen alkalmazható. Felhasználják a műszaki tervezésben, a tudományos kutatásban és az oktatás legkülönbözőbb szintjein, meteorológiai térképek készítésében, repülésszimulációban, nem is beszélve a számítógépes játékok sokaságáról. A számítógépes grafika egyik legnagyobb előnye, hogy segítségével szinte teljesen automatizált módon rajzolhatunk egyszerűen és gyorsan javítható, átalakítható képeket. A tervező a képernyőre pillantva azonnal látja, hol van szükség módosításra a tervezés alatt álló modellen, és ezt néhány utasítással, rövid idő alatt el is végezheti. Az ember és számítógép effajta gyors visszacsatoláson alapuló (ún. interaktív) együttműködésben elsőrendű szerepet játszanak a számítógépes grafikai módszerek.
Ez a könyv nem vállalkozik arra, hogy bevezesse az olvasót a számítógépes grafika szerteágazó problémakörébe. Grafikai algoritmusok egy gyűjteményét tartalmazza - tehát olyan, matematikai nyelven megfogalmazott, de számítógéppel kivitelezett eljárásokét, amelyeknek az is célja lehet, hogy valamilyen tárgyat többé-kevésbé híven ábrázoljanak, de akár az is, hogy érdekes, szép vagy egyszerűen csak szokatlan képeket rajzoljanak a számítógép képernyőjére. Eközben persze megoldást kell találnunk néhány általános számítógépes grafikai problémára is. Míg a közönséges mikroszámítógépek ábrázolási képességei viszonylag korlátozottak, szinte kimeríthetetlenül gazdag lehetőségek kínálkoznak a számítógépes grafika egy másik megközelítésében, ahol lemondunk az ábrázolás igényéről. Soha nem látott, minden valóságos referencia nélkül álló, de sokszor meglepő és izgalmas képeket rajzolhatunk ily módon, és egészen sajátos látványvilággal ismerkedhetünk meg a számítógép segítségével.
Azok a grafikai algoritmusok, amelyek matematikai szabályok láthatóvá tételével keletkeznek, mind ezt az utat követik. Az ábrázoló célú algoritmusok legjobb példái a tárgyak térbeli elhelyezkedését feltüntető háromdimenziós vagy térbeli grafikák algoritmusai. Az esetek jó részében viszont valamilyen vizuális jelenség fizikai, természeti motívum grafikai modelljéből indulunk ki, és ennek módosításával hozunk létre újabb képeket, miközben az ábrázolás szempontja egyre inkább háttérbe szorul.
Az ilyesfajta grafikai algoritmusok tehát egy kísérletező munka eredményei, és a könyv egyik fő célja, hogy az Olvasót hasonló kísérletezésre sarkallja. Ahelyett azonban, hogy iskolás módon feladatokkal, kísérleti célkitűzésekkel próbálnánk erre ösztönözni, célravezetőbbnek tartottuk, hogy maguknak a grafikai algoritmusoknak a leírásában mi-nél jobban hangsúlyozzuk a kísérleti jelleget, számbavéve a felmerülő alternatívákat és végigkövetve a lehetséges döntések hatását.
A számítógépes grafikai algoritmusok - természetükből adódóan - matematikai apparátust használnak, a könyvben tehát elég sok matematikáról lesz szó. A felhasznált matematika azonban ritkán lépi túl a középiskolai matematika szintjét és annak ismeretében mindig érthető lesz. Annak ellenére, hogy a könyv tekintélyes részét tölti ki, a matematikát mindig csak eszköznek tekintjük, amit csak a grafikai algoritmusok érdekében használunk. Ebből adódóan, bár minden matematikai eszközt vagy a 2. fejezetben, vagy a felhasználás helyén ismertetünk, ez sokszor nélkülözi a matematikában megszokott didaktikus felépítést és szabatosságot. A számítógép-képernyő véges geometriájához igazodva pl. lelkiismeretlenül leegyszerűsítettük az analízis egyes alapfogalmait: konvergencia helyett közelségről, derivált helyett különbségről, integrál helyett egyszerűen összegről beszélünk. A képernyő téglalapját gyakran síknak nevezzük, szomszédos pontokról beszélünk, stb. Abban reménykedünk azonban, hogy a cél az igényes matematikus Olvasó szemében is szentesíti az egyszerűsített eszközöket.
A grafikai algoritmusok egy része valamilyen fizikai vagy természeti jelenség ábrázolásából indul ki. A jelenség modellezéséhez azonban a fizika törvényeit sokszor már eleve hozzávetőlegesen alkalmazzuk. Az algoritmus módosításával kísérletezve ugyanis mihelyt lehetőséget találunk, megpróbáljuk a jelenséget kivonni a valóságos fizika törvé-nyeinek hatálya alól, amit sok esetben egy másfajta lehetséges világ irreális fizikájával helyettesítünk. Vagyis - az Olvasó utólagos engedelmével - a matematikához hasonlóan a fizika szabályait is önkényesen alárendeltük a grafikai célszerűségnek. A grafikai algo-ritmusokkal való kísérletezés (és ezzel együtt az egész könyv is) a következő általános célokat tűzheti ki maga elé: egyrészt az alapvető programozási jártasságot szerzett Olvasónak a grafikában egy rendkívül gazdag problémakört javasol, amelyben számtalan értelmes feladatot találhat önmagának. Másfelől a vizuális jelenségek grafikai modellezésével voltaképpen a látvány elemzésének eszközeit dolgozza ki. Harmadsorban pedig matematikai tanulságai is vannak a grafikai kísérleteknek, hiszen a matematikai szabályok alapján rajzolt képek egyúttal szemléleti alapot is szolgáltatnak e szabályok mélyebb megértéséhez. Az elmondottak szerint a könyv közönsége feltehetőleg elsősorban a matematika és grafika problémái iránt fogékony, programozási alapokkal rendelkező Olvasókból tevődik össze. Szeretnénk azonban, ha grafikai algoritmusaink a grafikában otthonos, de a számítógép által nyújtott újfajta látványra nyitott Olvasó fantáziáját is megragadná, hogy képet kapva a lehetőségekről (esetleg számítógépes szakemberekkel együttműködve) maga is kipróbálja ezt az új eszközt.
A véletlen (mint a legtöbb emberi tevékenységben), a számítógépes grafikai kísérletezések során is szerepet játszik - ráadásul többféle értelemben is. Egyrészt megtehetjük, hogy egyes algoritmusokban bizonyos változókhoz előre meg nem határozott, véletlen értéket rendelünk. Ezáltal ugyanazzal a programmal gyakorlatilag végtelen sok különböző képet rajzoltathatunk, amelyek között sokszor meglepő variációk fordulnak elő. Másfelől a véletlen megnyilvánulhat az algoritmus vagy a program megalkotása során elkövetett hibák képében is, és ha nem ragaszkodunk dogmatikus módon eredeti elképzelésünkhöz, sokszor bevallhatjuk önmagunknak, hogy csak nyertünk a cserén.
A könyvben szereplő képeket és programokat Sinclair Spectrum személyi számítógéppel készítettük. Ennek egyrészt az a jelentősége, hogy ezáltal talán azoknak is kedvet tudunk csinálni a grafikai kísérletezéshez, akiknek nincs nagyobb teljesítményű számítógépe. Másrészt ebből adódóan a könyvben leírt algoritmusok leírásához mindig a Spectrum által kínált lehetőségeket használtuk. Nem szeretnénk azonban, ha ez a könyv kizárólag Spectrum-tulajdonosok igényeit elégítené ki - éppen ezért nem is közlünk hosszabb programokat. Az algoritmusokat nagyrészt szóban ismertetjük. Mind a matematikai, mind a számítógépes kifejezéseket egységesen a Spectrum nyelvén adtuk meg. Ezt a nyelvet elég általánosnak, elég gazdagnak, ugyanakkor elég egyszerűnek tartjuk ahhoz, hogy más gépekre, más programnyelvekre, de a megszokott matematikai jelölésre is könnyen lehessen konvertálni. Ez a jelölés persze néhány kényelmetlen, és egy-két felemás megoldáshoz is vezetett (ahol a matematikai tartalmat körülményesebb volt számítógépes jelöléssel írni, ill. ahol egyáltalán nem volt meg a megfelelő Spectrum-kifejezés). Remélhetőleg azonban ez sehol nem okoz zavart a megértésben, és az Olvasó hamar hozzászokik ehhez a jelöléshez.
A 2. fejezetben a legalapvetőbb eszközöket készítjük elő a kísérletezéshez: egyrészt megadjuk a leggyakrabban használt matematikai fogalmakat, másrészt általános szerkezetű grafikai programsémákat és olyan grafikai elemeket sorolunk fel, amelyek hivatkozási alapul szolgálnak a konkrét algoritmusok programjainak leírásához.
A 3. fejezetben matematikai szabályokból kiindulva készítünk képeket, a fejezet végén pedig éppen azt a szabályt vizsgáljuk meg, amely a BASIC nyelv véletlenszám-generátorának a működését biztosítja.
A 4. fejezetben a véletlen (pontosabban a véletlenszám-generátor) segítségével rajzolunk. A véletlenszámok eközben annyira megszelídülnek, hogy biztosítani tudják, a görbe ne szaladjon le a képernyőről, a labirintus legyen mindig bejárható, és a kis körök tintapacára emlékeztető rendben helyezkedjenek el.
Az 5. fejezet a testek térbeli elhelyezkedésének ábrázolásával kapcsolatos problémákkal foglalkozik.
A 6. fejezet a szabályos ismétlődésekben megnyilvánuló szimmetriával kísérletezik.
A 7. fejezetben a számítógép mint speciális rajzeszköz jelenik meg.
Noha a könyv grafikai algoritmusaival nem áll szándékunkban művészi grafikákat készíteni, nem fölösleges az a törekvés, hogy az adott eszközökkel grafikáinkat minél szebbre rajzolhassuk meg. Ehhez ad tanácsokat a 8. fejezet.
Végül a 9. fejezetben olyan algoritmusokat ismerünk meg, amelyek segítségével, ha mégoly szűkös lehetőségek mellett is, de egyszerű animációs filmeket lehet készíteni.
"Mit lehet kezdeni a köddel, és miféle szerszámok valók hozzá?"
(Edward Stachura)
Ebben a fejezetben a könyvben legtöbbször felhasznált eszközöket, leggyakrabban visszatérő fogalmakat ismertetjük. A matematikai és programozási elemek ismertetésekor bizonyos jártasságot feltételezve adjuk meg a szükséges apparátust. A grafikai elemekről szóló részben viszont inkább hivatkozási alapot akarunk adni a későbbi képek, motívumok leírásához és osztályozásához. Természetesen ebben is csak az általánosabb eszközök kiemelésére szorítkozhatunk: egyes speciális fogalmak, matematikai vagy programozási ismeretek csak ott kerülnek említésre, ahol alkalmazásukra szükség lesz.
2.1. Matematikai elemek
A számítógépes grafika, mint látni fogjuk, elképzelhetetlen bizonyos matematikai ismeretek nélkül. A középiskolai matematikaanyag birtokában azonban már bátran elindulhatunk. Ebben a részben a felhasznált matematikai apparátust ismertetjük recept-szerűen, azaz rendszeres felépítés, bizonyítás nélkül, középiskolai szintű ismereteket feltételezve.
Koordináták, vektorok
A képernyő a sík téglalap alakú részletét jeleníti meg, amelynek bal alsó sarkában rögzítjük a derékszögű koordinátarendszer kezdőpontját (vagy origóját). A koordinátatengelyek a képernyő oldalaival párhuzamosak. A sík minden pontját egy (x,y) számpárral (vagy vektorral) adhatjuk meg - a képernyőre eső pontoknál speciálisan 0<=x<m, és 0<=y<n is teljesül (ahol m és n a számítógép által egy sorban, ill. egy oszlopban ábrázolható pontok száma).
Vektorokat nemcsak pontok, hanem irányok jelölésére is használhatunk: (x,y) jelölheti egyben az origót az (x,y) ponttal összekötő szakasz irányát is. Ugyanahhoz az irányhoz azonban különböző vektorok is tartozhatnak - a vektorokat az irányon kívül a hosszuk is jellemzi:
Pitagorasz tétele szerint az (x,y) vektor hosszát
|x,y| = SQR(x*x + y*y)
adja meg. Vektorok összegéről, különbségéről, valahányszorosáról az
(a,b) + (c,d) = (a+b,c+d)
(a,b) - (c,d) = (a-b,c-d) és
q*(a,b) = (q*a,q*b)
szabályok alapján beszélünk. Két vektor összegének szemléletes jelentése: egy olyan vektor, amely két egymáshoz csatlakozó vektor esetében az első kezdőpontjából a második végpontjába mutat. A kivonás itt is az összeadás fordított művelete: az előbbi helyzetben a második vektor lesz a harmadik és az első különbsége. Egy vektor q-szorosa ugyanolyan irányú, de q-szor olyan hosszú vektort jelent.
A térbeli képek leírásához háromdimenziós, térbeli koordináta-rendszert használunk. Itt a pontokat (és vektorokat) (x,y,z) számhármasokkal adjuk meg. A térbeli vektor hosszát analóg módon az
|x,y,z| = SQR(x*x+y*y+z*z)
kifejezéssel számíthatjuk ki. Vektorok összeadása, kivonása, számmal való szorzása szintén a kétdimenziós esethez hasonlóan végezhető el.
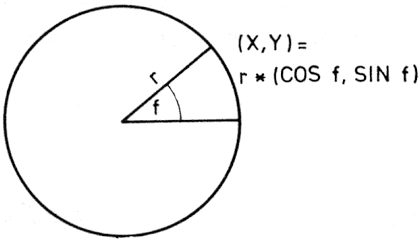
Használni fogunk még egy másik típusú koordinátarendszert is, ahol egy pontot az origótól vett r távolsága és az origóból húzott sugár vízszintessel bezárt f szöge határoz meg. Az (r,f) számpárt a pont polárkoordinátáinak nevezünk. A polárkoordinátákból a SIN és COS függvény definíciója alapján az
x = r*COS f, y=r*SIN f
képlettel számolhatjuk ki a derékszögű koordinátákat:

A derékszögű és a polárkoordináták összefüggése
Függvények, görbék, felületek
Adott f(x) függvénynél az [x, f(x)] koordinátájú pontok alkotják az illető függvény grafikonját. Egy f(x) függvény grafikonja tehát egy síkbeli görbe, amelynek alakja f választásától függ. Sok görbét adhatunk meg függvény-grafikon formában, de nem mindegyiket - a grafikonoknak ugyanis az a tulajdonságuk, hogy két különböző pontjuk sohasem kerülhet függőlegesen egy vonalba. Hiszen f minden x számhoz egyértelműen rendel egy f(x) értéket. Így pl. egy spirál nem lehet egyetlen függvény grafikonja sem.
Ha olyan görbét akarunk konstruálni, amely mindkét koordinátában szabadon változhat, mindkét koordinátában egy-egy függvénnyel ún. leképezést kell megadnunk.
Az [f(t), g(t)] koordinátájú pontok (ahol f és g egy-egy függvény) egy paraméteres görbét határoznak meg.
Ha egy függvénygörbénél vagy paraméteres görbénél a két koordinátában előforduló értékek nem a képernyőn megengedett határok közé esnek, akkor egy lineáris transzformációval érhetjük el, hogy mégis megjeleníthető legyen (I. a Geometriai transzformációk c. részben).
Kétváltozós f(x,y) függvényeknél az [x,y, f(x,y)] koordinátájú térbeli pontok egy felületet határoznak meg. Ezek sem teljesen általános felületek azonban - ugyanaz a hibájuk, mint az egyváltozós grafikonoknak: függőlegesen soha nem kerülhet egymás alá két pont, tehát pl. nem lehet gömbfelület (félgömb viszont már igen). Az általános felületeket szintén leképezésekkel adhatjuk meg, amelyeknek mindhárom koordinátájába kétváltozós függvényeket illesztünk:
[f(t,u), g(t,u), h(t,u)]
egy paraméteres felületet határoz meg.
Nézzük meg néhány konkrét esetben, hogyan lehet ismert görbéket, felületeket paraméteresen megadni (az első, második és harmadik koordinátafüggvény értékét most x, y, ill. z jelöli):
egyenes:
x = a*t+b, y = c*t+d, (t tetszőleges valós szám);
szakasz (a,b) és (c,d) végpontokkal:
x = a+(c-a)*t, y = b+(d-b)*t, ahol 0<=t<=1;
kör:
x = r*COS t, y = r*SIN t, ahol 0<=t<=2*PI (lásd ábra):
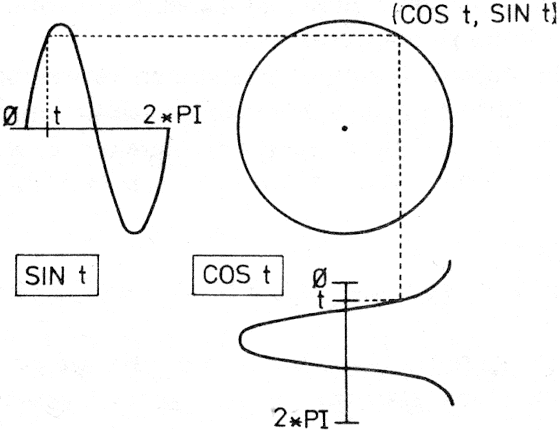
Kör paraméteres megadása
térbeli egyenes:
x = a*t+b, y = c*t+d, z = e*t+f, ahol t tetszőleges valós szám
gömb: x = r*SIN t * COS u, y = r*SIN u ,
z = r*COS t * COS u, ahol 0<= t,u <= 2 * PI; stb.
Ugyanazokat az alakzatokat természetesen különböző paraméteres leképezésekkel is megadhatjuk.
Alakzatok, egyenletek
Alakzatokat paraméteres leképezésen kívül más módon is meghatározhatunk. Többek között leírhatjuk őket olyan egyenletek segítségével, amelyek csak az illető alakzatok pontjaira teljesülnek. Például:
egyenes egyenlete a síkban:
a*x + b*y = c;
kör egyenlete a síkban:
(x-a)^2 + (y-b)^2 = r^2 [középpontja (a,b), sugara r];
sík egyenlete a térben:
a*x + b*y + c*z = d.
Egy térbeli egyenest csak két egyenlettel adhatunk meg:
a*x + b*y = c,
d*x + e*z = d,
(ilyenkor azt is fel kell tételeznünk, hogy x nem konstans).
Ilyen egyenleteket kaphatunk, ha a paraméteres görbéknél a t paramétert mindkét (vagy térbeli görbe esetén mindhárom) koordinátából kifejezzük, és ezeket egyenlővé tesszük. A kör egyenletében a
(COS t)^2 + (SIN t)^2 = 1
összefüggést használjuk ki, a sík egyenletét pedig a vektorok később ismertetetésre kerülő skaláris szorzásának tulajdonságai magyarázzák.
Az egyenlettel való megadás bizonyos értelemben kevesebbet jelent, mint a paraméteres leképezés rögzítése. Ahhoz ugyanis, hogy ebből valóban megkapjuk az alakzat pontjait, meg is kell oldanunk az egyenletet vagy egyenleteket. Ezek a megoldások azonban nem mindig egyértelműek. Például az origó körüli r sugarú kör esetében
x^2 + y^2 = r^2-ből
y = SQR(r^2 - x^2)-et vagy y = -SQR(r^2 - x^2)-et kapunk.
Az egyenlet előnye viszont, hogy könnyebb vele számolni. Például két egyenes metszéspontját könnyebben meghatározhatjuk az egyenesek egyenletéből:
a*x + b*y = c és d*x + e*y = f-ből
a kétismeretlenes egyenletrendszer megoldásával
x = (e*c - b*f)/(e*a - b*d),
y = (d*c - a*f)/(d*b - a*e)-t
kapunk, feltéve, hogy a nevező nem 0 (vagyis a két egyenes nem párhuzamos).
Pontok, vektorok kölcsönös térbeli helyzetének meghatározásához két újabb vektorműveletet használunk: a vektorok skaláris és vektoriális szorzatát.
Skaláris szorzat:
<(a,b,c),(x,y,z)> = a*x + b*y + c*z
Két vektor skaláris szorzata tehát egy szám. Erről a számról tudnunk kell, hogy a két vektor hosszának és az általuk közbezárt szög koszinuszának szorzatával egyenlő:
<(a,b,c),(x,y,z)> = |a,b,c|*|x,y,z|*COS f
ahol f a közbezárt szög. A koszinuszfüggvény tulajdonságaiból következik, hogy két (nem 0) vektor skaláris szorzata pontosan akkor 0, ha a két vektor egymásra merőleges.
Vektoriális szorzat:
(a,b,c)*(x,y,z) = (b*z - c*y, c*x - a*z, a*y - b*x)
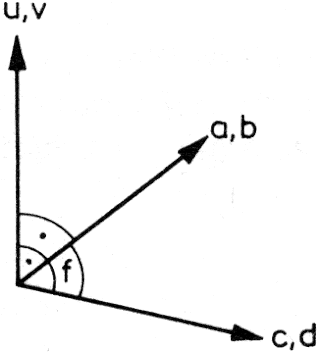
<(a,b),(c,d)> = a*c + b*d = |a,b|*|c,d|*COS f
(a,b)*(c,d) = (u,v)
|u,v| = |a,b|*|c,d|*SIN f
Két vektor vektoriális szorzata tehát egy harmadik vektor, amely merőleges a két vektor síkjára, hossza pedig a két vektor hosszának és a közbezárt szög szinuszának a szorzata:
|(a,b,c)*(x,y,z)| = |a,b,c|*|x,y,z|*SIN f
A skaláris és vektoriális szorzat többek között arra használható, hogy egy sík három pontjából meghatározzuk a sík egyenletét. A három (nem egy egyenesbe eső) pontból kettő-kettő meghatároz két különböző, de egyformán az adott síkba eső vektort. E két vektor vektoriális szorzata a síkra merőleges normálvektor lesz. Legyen a normálvektor (i,j,k), a három pont valamelyike (a,b,c) és a sík tetszőleges másik pontja (x,y,z). Ekkor az (x - a,y - b,z - c) vektor a síkban fekszik, tehát merőleges a normálvektorra, vagyis skaláris szorzatuk 0. Ily módon tehát
<(i,j,k),(x-a,y-b,z-c)> = 0
i*(x-a) + j*(y-b) + k*(z-c) = 0
vagyis
d = i*a + j*b + k*c-re i*x + j*y + k*z = d
egyenlet éppen a sík egyenlete lesz.
Geometriai transzformációk
A paraméteresen vagy egyenletekkel megadott alakzatok helyét vagy helyzetét néhány egyszerű szabály segítségével megváltoztathatjuk, és ez sokszor hasznunkra lesz a számítógépes grafikák készítésénél. Ilyen transzformációk a 6. fejezetben tárgyalt egybevágósági és hasonlósági transzformációk is, amelyek változatlanul hagyják az alakzatok alakját. A geometriai transzformációk a sík vagy a tér minden pontjára azonos módon hatnak, tehát az új pont koordinátáit egységes szabállyal tudjuk kiszámítani. Ily módon minden síkbeli transzformáció megadható azzal a szabállyal, ami egy (x,y) pont transzformáltjának koordinátáit adja meg.
A legegyszerűbb transzformáció az eltolás. Rögzítünk egy (u,v) eltolásvektort, és ezt az alakzat minden pontjának koordinátáihoz hozzáadva kapjuk meg az új pont koordinátáit:
(x+u,y+v)
Az eltolás nem változtatja meg az alakzat méretét és állását.
Ha minden pont helyvektorát ugyanazzal a számmal szorozzuk, nagyítást hajtunk végre. A nagyítás középpontja jelen esetben az origó. Az origótól különböző (a,b) középpontra vonatkozó c arányú nagyítás képlete:
(a,b) + c*(x-a,y-b)
A középpontos nagyítás megőrzi az alakzatok arányait, csak a méretét növeli vagy csökkenti attól függően, hogy c nagyobb vagy kisebb, mint egy. Ha c negatív, az ugyanolyan abszolút értékű nagyításhoz képest minden pontot tükröznünk is kell az origóra (azaz tőle ugyanolyan távolságban, de éppen ellentétes irányban kell elhelyezni).
Végezhetünk nagyítást csak az egyik vagy másik koordinátatengely irányában is, amit merőleges affinitásnak nevezünk. Ilyenkor csak a megfelelő koordinátát szorozzuk egy c számmal:
(c*x,y), vagy (x,c*y)
Ezáltal a kiinduló alakzat arányai, méretei is megváltoznak, a transzformáit alakzatból mégis visszakövetkeztethető, hiszen egy ugyanolyan típusú - 1/c arányú - transzformációval vissza is kaphatjuk.
A tengelyirányú nagyításoknak ez utóbbi tulajdonsága teszi lehetővé, hogy egy lineáris transzformáció segítségével tetszőleges arányú (de a koordinátatengelyekkel párhuzamos oldalú) téglalapot a teljes képernyőre vetítsünk. A lineáris transzformáció egy-egy tengelyirányú nagyítás és egy eltolás egymásutánjaként definiálható. Ha a kiinduló téglalap bal alsó sarka (a,b), jobb felső sarka pedig (c,d) (vagyis oldalai c-a, ill. d-b hosszúak), akkor x irányban (m-1)/(c-a), y irányban (n-1)/(b-d) arányban kell nagyítani ahhoz, hogy a képernyővel azonos nagyságú téglalapot kapjunk (m a képernyő oszlopainak, n a sorainak száma). A nagyítás előtt még egy -(a,b) eltolást végezve elérhetjük, hogy a téglalap bal alsó sarka az origóba menjen át - az ezután következő nagyítások most már pontosan a képernyőre vetítik a téglalapot. A transzformáció képlete tehát:
((x-a)*(m-1)/(c-a), (y-b)*(n-1)/(d-b))
A képletből látható, hogy ez a transzformáció az (a,b) pontot valóban (0,0)-ba, a (c,d)-t pedig (m-1, n-1)-be viszi át. A visszatranszformálás az
(x*(c-a)/(m-1)+a, y*(d-b)/(n-1)+b)
képlet alapján végezhető el:
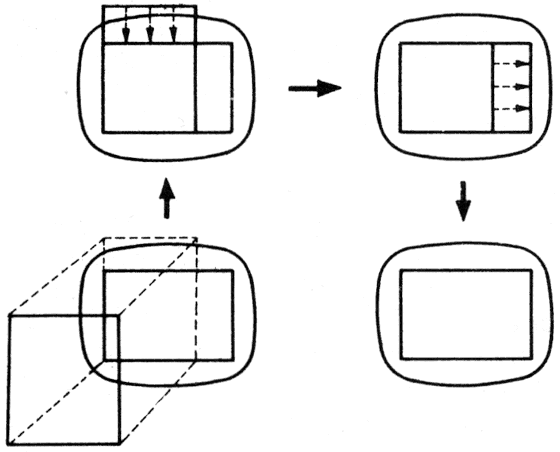
Lineáris transzformáció: eltolás + 2 merőleges affinitás
A tükrözés voltaképpen a nagyítás speciális esete, ahol a c arányt -1-nek választjuk. Ily módon egyszerű helyettesítéssel kapjuk a középpontos tükrözés
(a,b) - (x-a,y-b) = (2*a-x, 2*b-y)
és a tengely irányban való tükrözés
(-x,y), ill. (x,-y)
képletét. Ha tetszőleges origón átmenő ferde egyenesre akarunk tükrözni, a polárkoordinátás jelöléssel könnyebben boldogulunk. Legyen az egyenes (vízszintessel bezárt) szöge g, a pont polárkoordinátái (r,f) (vagyis közönséges koordinátái: r*(COS f, SIN f)).
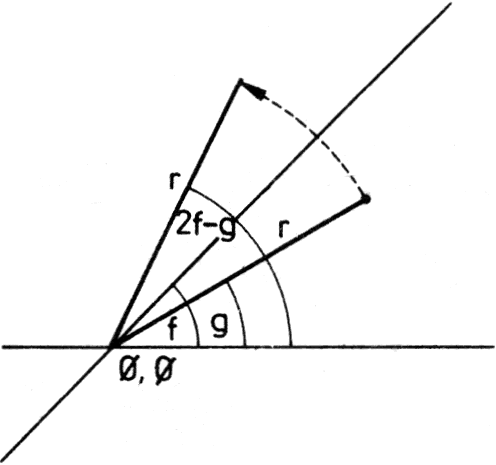
Tükrözés origón átmenő ferde egyenesre
Ekkor az egyenesre tükrözött pont polárkoordinátái (r,2*g-f) lesznek. Ezt visszaszámolva derékszögű koordinátákra r*(COS (2*g-f), SIN (2*g-f))-et kapunk. Felhasználva a COS és SIN addíciós képleteit,
COS (a+b) = COS a * COS b - SIN a * SIN b, ill.
SIN (a+b) = COS a * SIN b + SIN a * COS b,
g szögű egyenesre való tükrözés képlete:
(x * COS (2*g) + y * SIN (2*g), x * SIN (2*g) - y * COS (2*g))
Forgatás: ha egy (x,y) pontot az (a,b) körül g szöggel el akarjuk forgatni, ismét előnyösebb (x,y)-t (a,b) + r*(COS f, SIN f) alakban átírni. Ekkor az elforgatott pont egyszerűen
(a,b) + r*(COS (f+g), SIN (f+g))
lesz. Ismét az addíciós képletek alapján számolhatjuk vissza az új pont koordinátáit:
(a + (x-a) * COS g - (y-b) * SIN g, b + (x-a) * SIN g + (y-b) * COS g)
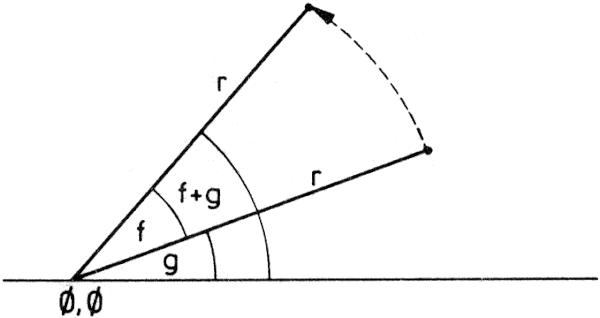
Origó körüli elforgatás
Ebből a képletből kitűnik, hogy a középpontos tükrözés nemcsak a nagyításnak, de a forgatásnak is speciális esete: éppen a PI szögű elforgatással azonos:
COS PI = -1, SIN PI =0
miatt PI szögű forgatásnál az előbbi képlet
(a,b) + (a-x, b-y) = (2*a-x, 2*b-y)
lesz. Érdemes még külön kezelni a PI/2 és -PI/2-szögű (azaz derékszögű) elforgatásokat - a
COS (PI/2) = 0, SIN (PI/2) = 1
értékek miatt itt is egyszerűsödnek a képletek (nem kell COS-szal és SIN-szal számolni):
(a,b) + (b-y, x-a) = (a+b-y, b-a+x)
ill.
(a,b) + (y-b, a-x) = (a-b+y,a+b-x)
Ebben a részben a könyv leggyakrabban használt programozásbeli megoldásait ismertetjük. Itt is feltételezünk bizonyos jártasságot a BASIC nyelvű programozásban. Mivel a különböző géptípusok a BASIC különböző változatait beszélik, és ez különösen vonatkozik a grafikai utasításokra, közös hivatkozási nyelvet kellett választanunk. Ahelyett, hogy egy általános ún. pszeudokódot használnánk, a Sinclair Spectrum BASIC nyelvjárásában írjuk le a megoldásokat, egyrészt, mert a könyv grafikái ilyen géppel készültek, másrészt mivel ennek egyszerű és hajlékony nyelve alkalmasnak tűnik a közös nyelv szerepére.
Grafikai utasítások
Egy számítógép grafikai teljesítőképességének egyik legalapvetőbb mérőszáma a képernyőfelbontás, vagyis hogy a képernyőn hány sorban és hány oszlopban lehet elemi képpontokat megjeleníteni. A Spectrum felbontása 192 sor X 256 oszlop. Egy képpontot a PLOT x,y utasítással lehet megjeleníteni (x az oszlop, y a sor száma). PLOT 0,0 a képernyő bal alsó sarkában rajzol be egy pontot. Egy szakasz megrajzolására alkalmas a DRAW u,v utasítás - a paraméterek azt jelölik, hogy a szakasz végpontja vízszintesen u, függőlegesen v ponttal tér el a kezdőpontjától. A kezdőpont az utoljára végrehajtott PLOT vagy DRAW utasítás utolsó pontja.
A POINT (x,y) függvény alkalmas az (x,y) koordinátájú pont vizsgálatára: értéke 1, ha azt korábban már berajzoltuk és 0, ha még nem.
Az elemi képpontokon kívül rajzolhatunk 8x8 pontból álló karaktereket is. Ilyen karaktereket választhatunk a gép megadott készletéből, de magunk is konstruálhatunk ún. definiálható karaktereket. A karaktereket PRINT utasítással írjuk ki. A képernyő karakterhelyeit egy-egy vonal- és háttérszínnel láthatjuk el, valamint választhatjuk villogónak és extra fényesnek is. A vonal- és háttérszín 8 lehetőség közül választható. Fekete-fehér képernyőn a különböző színek különböző tónusértékekként jelennek meg.
A képpontokat és karaktereket két speciális módon is berajzolhatjuk (a megszokotton kívül). Az INVERSE mód voltaképpen az érintett pontok törlését jelenti, az OVER mód pedig oda-vissza váltást a pont berajzolt, ill. törölt állapotai között.
Egyenesrajzoló algoritmus
A DRAW utasítás (és természetesen a PLOT) segítségével már bármilyen képet meg tudunk rajzolni. A DRAW kényelmes eszköz egyenes szakaszok rajzolására, sőt, amint később látni fogjuk, DRAW utasítások sorozatával görbéket is közelítően meg tudunk rajzolni. Most mégis érdemes egy kicsit vizsgálat alá venni ezt a DRAW utasítást, többek között, hogy a szakaszok megrajzolása közben figyelni tudjuk egyrészt, hogy az egyes pontok még a képernyőre esnek-e, másrészt, hogy az illető pontot nem rajzoltuk-e már be korábban (egy másik szakasz részeként). Mindkét problémára találunk példát, elsősorban a 4. fejezetben.
Egy olyan programtól, amely a DRAW utasítás működését szimulálja, a következőket várjuk: a megrajzolt szakasz pontjai lehetőleg minél kevésbé térjenek el az elméleti egyenestől. A szakasz legyen egyenletes vastagságú, az egyik végponttól a másik felé indulva minél jobban essen egybe a fordított változattal, a végpontok legyenek pontosak. Ahhoz, hogy a végpont a pontos helyére kerüljön az kell, hogy mind vízszintesen, mind függőlegesen összesen annyi egységet lépjünk, amennyi a koordináták eltérése. Az egyenletes vastagságot úgy garantálhatjuk, ha vagy minden oszlopba vagy minden sorba csak egyetlen pontot rajzolunk be. Ez úgy érhető el, hogy ha a kezdő és végpont két koordinátájának eltérése közül mondjuk a függőleges eltérés nagyobb, akkor függőlegesen minden ponttal egyet lépünk fölfelé, vízszintesen pedig a kisebb eltérés számát valamilyen módszer szerint egyenletesen beosztjuk a függőleges lépések közé. Az egyenletesség fogja garantálni, hogy a berajzolt pontok jól közelítenek az elméleti szakaszhoz.
Legyen a kezdőpont koordinátája (x,y), a végponté (u,v). Legyen az u-x és v-y eltérések közül (abszolút értékben) a v-y nagyobb. Ez azt jelenti, hogy függőlegesen minden lépésben 1-et fogunk lépni, v-y előjelétől függően fölfelé vagy lefelé. A vízszintes lépések beosztását a következőképpen végezzük el : az u-x eltérés abszolút értékét minden lépésben hozzáadjuk egy számlálóhoz, és amikor ennek a számlálónak az értéke meghaladja a v-y abszolút értékét, akkor lépünk vízszintesen (megintcsak az u-x előjelétől függően jobbra vagy balra). Ilyenkor a számláló értékét csökkentjük is ABS (v-y)-nal. Miután (a nagyobbik eltérés szerint) ABS (v-y) lépést teszünk, a számlálóhoz összesen ABS (v-y)*ABS (u-x)-et fogunk hozzáadni, ezt pedig éppen ABS (u-x)-szer csökkenthetjük ABS (v-y)-nal, ez garantálja, hogy vízszintes irányban is éppen a kellő számú lépést tegyük. A számláló túlcsordulásán alapuló léptetés pedig biztosítja a vízszintes lépések egyenletes beosztását. Ha ezenkívül még a számlálót nem is 0-ról, hanem ABS (v-y)/2-ről indítjuk, akkor, miután az utolsó lépés után is ABS (v-y)/2 lesz az értéke, azt is el tudjuk érni, hogy a megrajzolt szakasz nagyjából szimmetrikus lesz a kezdőpontra és végpontra nézve. Ezek után az algoritmus BASIC programja a következőképpen nézhet ki (a rövidség kedvéért a két esetet - amikor a vízszintes, vagy a függőleges eltérés nagyobb - közös sémában foglaltuk össze):
100 LET a=ABS (u-x): LET b=ABS (v-y)
110 LET c=SGN (u-x): LET d=SGN (v-y)
120 LET m=a: IF b>a THEN LET m=b
130 LET p=m/2: LET q=m/2
140 FOR i=1 TO m
145 PLOT x,y
150 LET p=p+a
155 IF p>=m THEN LET p=p-m: LET x=x+c
160 LET q=q+b
165 IF q>=m THEN LET q=q-m: LET y=y+d
170 NEXT i
Ez az algoritmus, mint látható, nem igényel szorzást-osztást, így gépi kódban, sőt, hardverszinten is viszonylag könnyen megvalósítható. Ha a sebesség növelésére törekszünk (a program némi meghosszabbítása árán), akkor az itt összefoglalt két esetet érdemes különválasztani, hiszen az x és y közül az egyik mindig automatikusan növelendő vagy csökkentendő, tehát a p és q számlálók közül is csak egyre van szükség. A b>a és b<=a esetekre tehát két külön ciklust kell írni.
Amint említettük, ezeknek a programoknak az az előnye az egyszerű DRAW utasítással szemben, hogy a PLOT x,y utasítások végrehajtása előtt különböző feltételeket ellenőrizhetünk - hogy x és y a megengedett határok közé esik-e, vagy hogy az illető pont nem volt-e korábban berajzolva. Ily módon megakadályozhatjuk, hogy a program rajzolás közben hibajelzéssel megálljon, vagy éppen ellenkezőleg, leállíthatjuk, ha szándékunk ellenére két vonal metszeni készül egymást.
Görberajzolás
Következő feladatunk, hogy akár a DRAW utasítás, akár saját szakaszrajzoló programunk segítségével megpróbáljunk görbéket rajzolni. Tetszőleges folytonos görbét jól közelíthetünk egymáshoz csatlakozó szakaszok sorozatával. Egy ilyen töröttvonalat mindig pontosan rekonstruálni lehet a szakaszok kezdő és végpontjait alkotó ún. osztópontok koordinátáival. Ily módon megadhatunk egy általános görberajzoló algoritmust, amelynek egy szubrutin adja az osztópontok koordinátáit, és ő ezek alapján megrajzolja a görbét közelítő töröttvonalat. Az algoritmus BASIC programja első közelítésben:
100 GOSUB 500: REM x,y kezdőpont
110 PLOT x,y: LET u=x : LET v=y
120 FOR i = 2 TO n
130 GOSUB 500: REM x,y osztópont
140 DRAW x-u,y-v
150 LET u=x: LET v=y
160 NEXT i
Ez a program azonban még több szempontból javításra szorul. Az első problémát a PLOT és DRAW utasítás paramétereinek kerekítése okozza. Vegyük pl. azt az esetet, amikor az 500-as szubrutin az i-edik (x,y) értékre (i,i/3)-at ad. Ekkor x-u mindig 1, y-v pedig 1/3 lesz. A kerekítésnél azonban az 1/3 0-ra változik, és így minden lépésben egy DRAW 1,0 utasítás hajtódik végre. Ez pedig egy vízszintes egyenest fog rajzolni az 1/3 meredekségű ferde egyenes helyett! Ennek orvoslására mi magunk végezhetjük el a DRAW utasítás paramétereinek kerekítését, ügyelve, hogy a kerekítési hibák ne halmozódjanak. A módszer rendkívül egyszerű: x, y, u és v minden PLOT - vagy DRAW-beli előfordulásánál az INT (egész-rész) függvényt használjuk, amely minden törtértéket lefelé, egészre kerekít:
110 PLOT INT x,INT y : ...
...
140 DRAW INT x-INT u,INT y-INT v
Ily módon a DRAW már nem hajt végre nemkívánatos kerekítéseket, és ha a kezdőpont (a,b), a végpont (c,d) volt, most (INT a, INT b) és (INT c, INT d) közé húzunk egyenes szakaszt. A szakasz minden pontjában legfeljebb 1 egységgel tévedünk lefelé. Még ezt a legfeljebb 1 egységnyi tévedést is felére tudjuk csökkenteni, ha pl. INT x helyett INT (x+0.5)-öt veszünk (és persze a többi változóval is így járunk el), az INT (x+0.5) kifejezés ugyanis a lehető leghelyesebben kerekít: 0.5-től kezdve fölfelé, az alatt pedig lefelé.
A másik probléma az, hogy ha a görbében éppen megrajzolandó szakasz végpontja már kívül esne a képernyőn, hogyan akadályozzuk meg, hogy a program hibajelzéssel leálljon, amikor még további görbéket is szeretnénk megrajzolni. Erre persze megoldásként kínálkozik a saját egyenesrajzoló algoritmusunk használata, amellyel figyelni tudjuk, hogy mely pontokat lehet még megrajzolni. Ennek viszont az a hátránya, hogy lassabban működik, mint a közönséges DRAW utasítás, de egyébként is érdekes kérdés, mennyit kell megrajzolni egy olyan szakaszból, amelynek a végpontja már kívül esik a képernyőn.
Legyen a kezdőpont (a,b), a rossz végpont (c,d) és most a könnyebb számolás kedvéért a és c essen -m/2 és m/2, b és d pedig -n/2 és n/2 közé (m, n az oszlopok, ill. sorok számát jelöli). A szakasz képernyőre eső részének (u, v) végpontját a következő algoritmussal kapjuk meg:
200 LET u=c-a: LET v=d-b
210 IF ABS (a+u)>m/2 THEN LET q=(m/2*SGN u-a)/u: LET u=q*u: LET v=q*v
220 IF ABS (b+v)>n/2 THEN LET q=(n/2*SGN v-b)/v: LET u=q*u: LET v=q*v
A program az első lépésben arányosan lekicsinyíti a szakaszt annyira, hogy x koordinátája már a képernyő szélére kerüljön. A második lépésben (ha szükséges), további kicsinyítéssel az y koordinátát is a megengedett határra csökkenti. Ezzel a módszerrel az eredeti szakasszal megegyező irányú szakaszt kapunk, amely éppen a képernyő széléig ér ki.
Még nagyobb nehézséget jelent az az eset, ha egy görbe rajzolását nem akarjuk abbahagyni, amikor kilép a képernyőről, mert lehet, hogy később még visszatéved (természetesen ilyenkor valami más kritérium alapján kell leállítani ennek a görbének a rajzolását). Most tehát lesznek olyan szakaszok mint az előbbi esetben, amelyek a képernyőn belüli pontot egy külső ponttal kötnek össze; lesznek olyanok, amelyek kívülről indulnak, és belül érnek véget. A legnehezebb esetben két külső pontot összekötő szakasznak is lehet a képernyőn látható részlete. Míg az első két eset az előbbi módszerrel kezelhető, olyan általános megoldást, amely a harmadik típusú szakaszra is érvényes, a Szakaszkivágó algoritmus c. részben mutatunk.
Grafikai programsémák
A könyvben szereplő grafikai algoritmusok jó része olyan programokkal valósítható meg, amelyek néhány egyszerű séma valamelyikébe illenek. Ilyen sémákat szeretnénk most bemutatni (voltaképpen már a görberajzoló program is egy ilyesfajta programséma volt). Ezek a programsémák persze nem oldják meg helyettünk a grafikai algoritmusok programozásának feladatát, mindegyikben olyan részletekre (szubrutinokra) hivatkozunk, amelyek a konkrét grafikákra, algoritmusokra jellemzők, így általánosságban semmit nem tudunk róluk mondani. Ezeknek a sémáknak tehát inkább csak az a jelentősége, hogy segítenek közös nevezőt találni a különböző grafikai algoritmusok között, segítenek azokat hozzávetőlegesen típusokba osztani. Az itt megadott sémák ráadásul egy összetett programnak csak egy-egy részletét tudják jellemezni, az egészet viszont esetleg éppen az előforduló algoritmustípusokkal jellemezhetjük.
Noha általában rövid programokról van szó, talán nem fölösleges az a fáradság, amit az ilyen programok áttekinthető, világos felépítésére fordítunk a későbbi érthetőség, javíthatóság, fejleszthetőség érdekében. Igaz ugyan, hogy a speciális grafikai utasítások könnyen felfedezhetők minden programban, de azok paramétereinek kiszámításához, a rajzolás feltételeinek meghatározásához esetleg bonyolult számításokra van szükség, és az ezeknek megfelelő programrészletek semmilyen módon nem utalnak arra a képre, amit a programmal meg szeretnénk rajzoltatni.
Érdemes a grafikai programok készítésekor az elképzelt kép struktúrájából kiindulni. Bontsuk fel a képet olyan részletekre, amelyekről tudjuk, hogy megrajzolásuk különböző típusú tevékenységet feltételez! Egy-egy ilyen tevékenységet egy-egy szubrutin végezhet el. A főprogram ezek után olyan szubrutinhívások (GOSUB utasítások) sorozatából állhat, amelyek a kívánt tevékenységeket a megfelelő sorrendben hatják végre. A szubrutinhívások mellé megjegyzésekben odaírhatjuk, hogy mi is a szubrutin feladata. Ezáltal (némi túlzással) új programnyelvet definiáltunk, amelynek az utasításai az általunk igényelt tevékenységeknek felelnek meg. Ha bizonyos részfeladatokat ismételten (ciklikusan) kell végezni, akkor a ciklust is érdemes a főprogramban feltüntetni, a ciklus végrehajtását vezérlő feltételekkel együtt. Ha egy szubrutint a programban több helyen is felhasználunk, különböző értékű paraméterekkel, akkor a paramétereknek a szubrutinhívást közvetlenül megelőzően kell értékeket adni. Sokszor külön szubrutinban érdemes kezdőértéket adni a program elején egyes változóknak a színek beállításával, a véletlenszám-generator beigazításával együtt. Mintaképpen egy (lehetséges) grafikai program főprogramjának szerkezete:
5 REM a rajz címe
10 GOSUB 100: REM input, kezdőértékek
20 INPUT a,b: GOSUB 200 : REM egy mintaelem
30 GOSUB 300: REM színezés
40 IF INKEY$="" THEN GOTO 20
50 STOP
Tudjuk, sokan úgy érzik, hogy az ún. strukturált programozás (amelyben a fentihez hasonló normákhoz kell igazodni) csökkenti az egyéni alkotókészség lehetőségeit. Valójában ez az aggodalom alaptalan, hiszen a programozói lelemény a feladatok kitalálásában, az alkalmas algoritmus megkeresésében vagy megalkotásában és az algoritmus optimális programozásában nyilvánul meg, nem pedig azokban a pusztán formai kérdésekben, amelyeket az efféle önként vállalt szabványok érintenek. Ez inkább ahhoz hasonlít, mint amikor egy programnyelv előírásaihoz alkalmazkodik az ember.
Lássunk tehát néhányat azokból a leggyakoribb programsémákból, amelyeket a számítógépes grafikák egy-egy elemének megrajzolására használni szoktunk (a főprogramból meghívott szubrutinokkal). A sémák sémajellege (azaz különböző módokon való megvalósíthatósága) a bennük szereplő szubrutinok konkrét tartalmának különböző lehe-tőségeiben nyilvánul meg. Mi e szubrutinokról csak annyit kötünk ki, hogy a megjegyzésben feltüntetett változókat állítja elő.
Soronként végigmegyünk a képernyő pontjain, és egyenként döntünk, hogy az aktuális pontot be kell-e rajzolni vagy sem. A döntés konkrét módszere határozza meg a kialakuló mintát.
100 FOR y=0 TO n-1: FOR x=0 TO m-1
110 GOSUB 500: REM o (a döntés)
120 IF o THEN PLOT x,y
130 NEXT x: NEXT y
Minden berajzolt pont után megadjuk azt az eltérésvektort, amelyet a pont vektorához hozzáadva megkapjuk a következő megrajzolandó pontot. Vigyázni kell, hogy minden pont a képernyőre essen, és meg kell adni a leállás feltételét.
100 LET x=p: LET y=q
110 PLOT x,y
120 GOSUB 600: REM a,b,o
130 LET x=x+a: LET y=y+a
140 IF o THEN GOTO 110
Egyenként adjuk meg a következő berajzolandó pontot, ill. a leállás feltételét.
100 GOSUB 700: REM x,y,o
110 PLOT x,y
120 IF o THEN GOTO 100
A bolyongó pontrajzolás algoritmusát úgy módosítjuk, hogy az egymás utáni pontokat szakasszal kötjük össze.
100 LET x=p: LET y=q: PLOT x,y
110 GOSUB 600: REM a,b,o
120 DRAW a,b: LET x=x+a: LET y=y+b
130 IF o THEN GOTO 110
Itt az ugráló pontrajzolás pontjait kötjük össze szakaszokkal.
100 GOSUB 700: REM x,y
110 PLOT x,y: LET u=x: LET v=y
120 GOSUB 700: REM x,y,o
130 DRAW x-u,y-v
140 IF o THEN GOTO 120
Itt egyenként adjuk meg az egymástól független eltérésvektorokat és kezdőpontjaikat.
100 GOSUB 800: REM x,y,a,b,o
110 PLOT x,y: DRAW a,b
120 IF o THEN GOTO 100
stb.
A 4. és 5. sémában, ahol egymáshoz csatlakozó vonalakból görbéket, vagy töröttvonalakat rajzolunk, a kerekítési hibák felhalmozódását megakadályozhatjuk, ha a görberajzolásnál megismert óvintézkedéseket megtesszük: a bolyongásban
DRAW a,b helyett DRAW INT (x+a) - INT x,INT (y+b) - INT y
az ugráló vonalaknál pedig
DRAW x-u,y-v helyett DRAW INT x - INT u,INT y - INT v-t írunk.
Természetesen ezek mellett más egyszerű grafikai programsémákat is el lehet képzelni, itt azonban csak a legegyszerűbbeket és leggyakrabban használtakat soroltuk fel. A könyv grafikai algoritmusait sokszor az itt megadott programsémák kombinációjával programozhatjuk a legkézenfekvőbb módon.
Rekurzív algoritmusok
A következő programsémák sokkal általánosabbak, mint az eddigi konkrét grafikai programok. Nem is kötődnek kifejezetten a grafikai programokhoz, másféle programokban éppoly jól használhatóak. Általánosságuk miatt sajnos még olyan pontos leírást sem lehet adni róluk, mint az eddigiekről. Olyan programrészletekről, helyesebben szubrutinokról lesz szó, amelyek a szubrutin belsejéből önmagukat hívják meg:
100... (a szubrutin eleje)
...
140 GOSUB 100
...
190 RETURN (a szubrutin vége).
Az ilyesfajta szubrutinokat rekurzív szubrutinoknak nevezzük. Használatuk ott indokolt, ahol a szubrutin által elvégzendő tevékenységben felfedezünk egy vagy több olyan részletet, amely (esetleg egy-két paraméter megváltoztatásával) ugyanabba a sémába szorítható, mint maga a teljes szubrutin. Egy példa: amikor egy fát akarunk rajzoltatni a géppel, úgy is eljárhatunk, hogy megrajzolunk egy függőleges törzset, majd annak végpontjában több, kisebb, törzsével ferdén induló fát rajzolunk, hasonlót a teljes megrajzolandó fához, csak valamivel kisebbet. Persze ez az algoritmus így még nem vezetne eredményre, hiszen végtelen sokáig kellene a faágakat kisebb fákkal helyettesítenünk - ezért meg kell adni egy feltételt arra, hogy a tovább-bontást mikor kell abbahagyni: példánkban ez elég természetesen adódik akkor, amikor a helyettesítendő fa mérete már egy bizonyos érték alá csökken.
Az előbbi programsémát tehát a példa tanulsága alapján ki kell bővítenünk egy feltételvizsgálattal, amely az egyik lehetséges esetben a szubrutinból való visszatéréshez vezet:
100 ...
...
120 IF ...THEN GOTO 190
...
140 GOSUB 100
...
190 RETURN
Természetesen az is lehetséges, hogy a szubrutin belsejéből többször is meghívjuk a 100-as szubrutint - a 140-es sorhoz hasonlóan másutt is szerepel a GOSUB 100 utasítás.
Ha készítünk egy olyan diagramot, amelyben a 100-as utasítás minden végrehajtásának (vagyis a szubrutin minden hívásának) egy-egy pontot feleltetünk meg, és két pontot akkor kötünk össze, ha az egyik szubrutinfutáskor hívtuk meg a másikat, ismét olyan ábrát kapunk, amely egy fára emlékeztet:
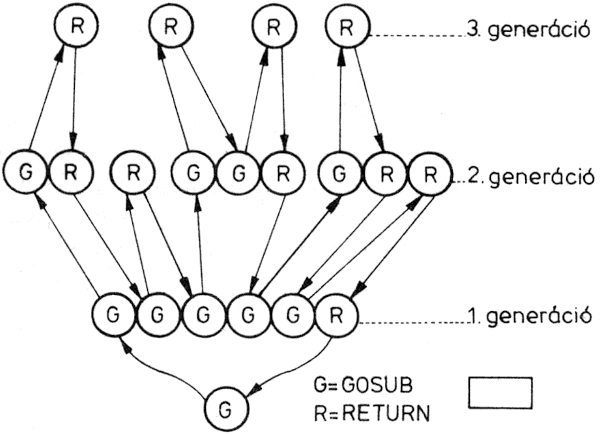
Rekurzív szubrutin fája
Nevezzük egy generációnak azokat a pontokat, amelyek egyforma távolságra vannak a 100-as szubrutin első meghívását jelképező kezdőponttól (az ábrán ezek vízszintesen egy vonalba esnek). Az ábráról leolvashatjuk, hogy a fa egy-egy pontjából több olyan ág is kinőhet, amely a következő generációhoz tartozó pontban végződik, és minden pontnak egyetlen őse van az előző generációban (ennyiben több ez a rekurzív programséma a közönséges ciklusnál - az olyan fának felel meg, amelynek minden pontjából egyetlen új pont felé vezet ág, természetesen a végpontot leszámítva). A rekurzív program futását ezek után a különböző generációk történeteként írhatjuk le: egy-egy generáció bizonyos feltételektől függően új egyedeket nemz, amelyek a következő generációhoz fognak tartozni, és más feltételek teljesülése esetén visszatér az előző generációba, megtér az ősökhöz. A pontok bejárásának sorrendje olyan, hogy először végigmegy az elsőszülött utódok során, egészen addig, amíg valahol meg nem szakad ez a sor; ezután addig megy vissza, ahonnan ismét új utódok származtak és így tovább.
Ne felejtsük persze, amikor pontokról beszélünk, hogy egy pont a szubrutin egyszeri hívásának felel meg. A továbblépés vagy a visszatérés feltételeit a szubrutin változóinak értéke határozza meg. Ezekkel a változókkal különös óvatossággal kell eljárnunk. Gondolnunk kell arra, hogy ugyanannak a változónak a GOSUB 100 utasítás előtt és után valószínűleg más lesz az értéke. Az ebből származó hibákat úgy kerülhetjük ki, hogy a szubrutin összes változója helyett ugyanolyan nevű tömbváltozókat írunk, amelyeknek indexébe az éppen aktuális generáció-sorszámot kell írni. Ezért szükségünk lesz egy változóra, amely mindig ezt a sorszámot jelöli, amit tehát a 100-as szubrutin legelső utasításában eggyel növelünk, és közvetlenül a RETURN utasítás előtt ismét eggyel csökkentünk. A programséma tehát eddigi legjobb tudomásunk szerint valahogy így néz ki:
100 LET n=n+1
...
120 IF ... THEN GOTO 190
...
140 GOSUB 100
...
190 LET n=n-1: RETURN
A program elején tehát deklarálnunk kell minden változóhoz egy annyi elemű tömböt, amennyi az elképzelhető legnagyobb generáció-sorszám. A szubrutinon belül (az n sorszámváltozót kivéve) minden változó olyan tömbváltozó, amelynek indexében n szerepel. Ha pl. a GOSUB 100 utasítás egy ciklusban fordul elő, a ciklus változóját is ilyen alakban kell használnunk.
A változók ilyen módon való kezelése a látszat ellenére rendkívül gazdaságos. Tegyük fel, hogy a szubrutinban mondjuk 10 változót használunk, és a generációk maximális száma 20. Ekkor összesen 10*20 = 200 változót kell lekötnünk. Ha viszont a szubrutin minden szinten kétfelé ágazik (kétszer hajtódik végre benne GOSUB 100 utasítás), akkor ez 10 * 2^20 féle értéket jelent, tehát minden változó átlagosan (2^20)/20, azaz több, mint 52 000 különböző alkalommal kap értéket.
A rekurzív szubrutin rendkívül hatékonyan használható olyan feladatok programozásánál, amelyek valamilyen fastruktúrához kötődnek. A gazdaságos változófelhasználás dacára azonban van egy hátránya ennek az algoritmustípusnak. Úgy viselkedik, mintegy szeszélyes gyerek, aki mindig azt csinálja, ami éppen az eszébe jut, nem képes arra, hogy a felmerült ötletek megvalósítását későbbre halassza. Következő algoritmussémánk ennek a hiányosságnak a kiküszöbölésére törekszik, és ezáltal olyan eszközt kapunk, ami rekurzív algoritmusoknál bővebb feladatosztály elvégzésére alkalmas. Igaz, gazdaságtalanabb lesz a változók kihasználása, viszont maga az algoritmus egyszerűbben programozható.
Határidőnapló
A következő sémát határidőnaplós sémának (vagy módszernek) nevezhetjük, mindjárt meg fogjuk látni, miért. Lényege ugyanis, hogy egy-egy lépésben az általa tárolt határidőnaplóból kiolvas egy bejegyzést (amely az előbbi értelemben vett generáció-sorszámot, és a hozzá tartozó változóértékéket tartalmazza), végrehajtja az esedékes feladatot, és ennek során új bejegyzéseket készít a határidőnaplóban. Ily módon egy időben különböző generáció-sorszámú elemek lesznek jelen a naplóban. Amikor viszont egy elem alapján az összes lehetséges továbblépést bejegyezte a naplóba (és a kívánt tevékenységet is rendben elvégezte), akkor ezt a bejegyzést ki is törli a naplóból - így nem fog egyszerre az összes élni.
A határidőnapló megvalósítására egy karaktertípusú változó a legalkalmasabb, amelyben a CHR$ függvény segítségével tetszőleges számértékeket tetszőleges helyen tárolni tudunk.
Ha az egyik bejegyzésnél felmerülő további bejegyzéseket sorban összefűzzük, és az egészet a határidőnapló legelejére írjuk be, miközben a bejegyzéseket mindig a napló elejéről olvassuk is ki, akkor a feladatok végrehajtásának a sorrendje pontosan ugyanaz lesz, mint a rekurzív szubrutinnál. Választhatunk azonban másféle sorrendbe fűzést is, ekkor esetleg a rekurzív programmal nem vagy csak nehezen megvalósítható megoldásokhoz juthatunk. Megtehetjük pl., hogy az aktuális bejegyzéseket véletlenszerűen olvassuk ki a naplóból.
Foltbetöltő algoritmus
A határidőnapló-módszer illusztrálására egy olyan programot választunk, amely egyébként is hasznos lehet. Ez a szubrutin egy zárt görbén belüli terület betöltésére szolgál. Paraméterként meg kell adni egy olyan (x,y) pontot, amely biztosan a görbe belsejébe esik. Ez a program valamivel bonyolultabb az eddigieknél - az érthetőség kedvéért ráadásul nem is a lehetséges legrövidebb vagy leghatékonyabb módon írtuk meg a programot.
Az algoritmus vízszintes vonalakkal próbálja betölteni a zárt területet. A határidő- naplóból kiolvassa egy belső pont (x,y) koordinátáit. Ekkor az (x,y) pontból jobbra, majd az (x-1,y) pontból balra haladva addig rajzolja be a vízszintes vonal pontjait, amíg már berajzolt ponthoz nem ér. Eközben figyeli az eggyel följebb és eggyel lejjebb levő vonal pontjait, és amikor ezeken a vonalakon (a haladás irányában) berajzolt pontot üres pont követ, az üres pontot felveszi a határidőnaplóba. Ily módon egy üres pont minden szomszédos üres pontja a következő menetben be lesz rajzolva, hiszen vagy maga is bekerül a naplóba, vagy egy ilyen pontból üres pontokon keresztül, vízszintes irányban elérhető. Ez pedig azt jelenti, hogy előbb-utóbb az egész zárt terület betöltődik.
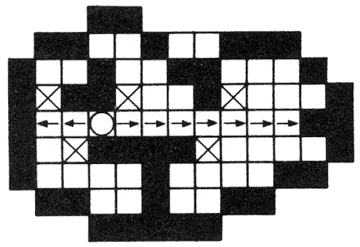
A foltbetöltő algoritmus működése
Lássuk tehát a programot:
| 500 FOR i=-1 TO 1 STEP 2 510 LET x=CODE a$(1)-(i-1)/2 520 LET y=CODE a$(2) |
A naplóból kivesszük a vonal kezdőpontját |
| 530 LET p=1: LET q=1: GOTO 580 540 PLOT x,y 550 LET r=POINT (x,y-1) 555 IF p>r THEN LET a$=a$+CHR$ x+CHR$(y-1) |
egy pont a vonalon ha az alsó, |
| 560 LET s=POINT (x,y+1) 565 IF q>s THEN LET a$=a$+CHR$ x+CHR$(y+1) 570 LET p=r: LET q=s |
vagy felső szomszédos vonalon berajzolt pontot üres követ, azt felvesszük a naplóba |
| 580 LET x=x+i: IF POINT (x,y)=O THEN GOTO 540 590 NEXT i 595 LET a$=a$(3 TO): IF a$>"" THEN GOTO 510 599 RETURN |
|
Szakaszkivágó algoritmus
Sokszor lesz szükségünk olyan algoritmusra, amely tetszőleges szakasznak meghatározza a képernyőre eső részét. Ennek az algoritmusnak a birtokában a görbéket nem kell a képernyő méretére transzformálni, ami főleg akkor jelent problémát, ha előre nem ismerjük pontosan a görbe által bejárt terület méreteit. Elég most már a görbe minden szakaszához meghatározni a képernyőre eső részt.
Legyen a szakasz két végpontja (a,b) és (c,d). A két ponton átmenő egyenest úgy fogjuk paraméterezni, hogy a két végpont a t=0, ill. t=1 értéknek feleljen meg:
x = a + (c-a)*t,
y = b + (d-b)*t
Ezután már a t-re kell olyan paraméterintervallumot megadni, ami a szakasz látható részének felel meg - ez nyilvánvalóan a (0,1) szakasz része lesz. Az ábra szerint vizsgáljuk meg, hogy milyen lehet a két ponton átmenő egyenes helyzete a képernyő szélein futó egyenesekhez képest.
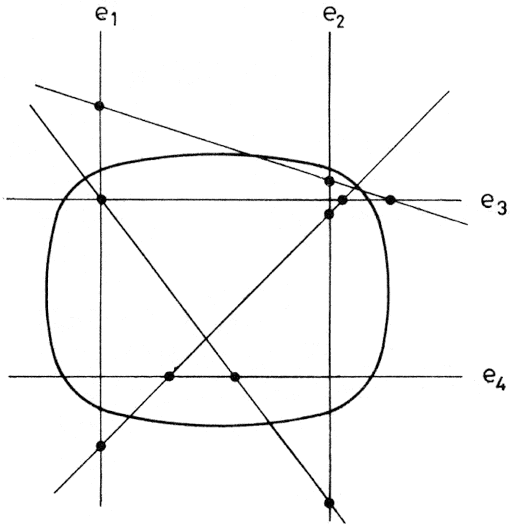
Általános egyeneseknek a képernyő széleihez viszonyított helyzete
Az ábráról kiderül, hogy ennek az egyenesnek csak akkor lesz a képernyőn látható szakasza, ha nem bontható két félegyenesre úgy, hogy az egyik csak a vízszintes, a másik csak a függőleges határegyeneseket metszi. Állapítsuk tehát meg a négy metszésponthoz tartozó paramétereket. A paraméterezésből kiolvasható, hogy az
x = 0 egyenessel való metszéspont paramétere:
t = -a/(c-a)
Hasonló módon az x = m-1, y = 0 és y = n-1 egyenesekkel vett metszéspontok paraméterei:
t = (m-1-a)/(c-a),
t = -b/(d-b), ill.
t = (n-1-b)/(d-b)
Legyen i = 1, 2, 3, 4-re az ei egyenessel való metszéspont paramétere ti. A metszéspontok sorrendjének megállapítása végett rendezzük a négy ti-t, legyen a nagyság szerinti sorrend ti1, ti2,... . Mivel ei1 és ei2 nem lehet egyformán vízszintes, vagy függőleges, (ahhoz, hogy az egyenes átmenjen a képernyőn), az kell, hogy 3 < i1 + i2 <7. Az ábráról az is leolvasható, hogy ebben az esetben a ti2 és ti3 közötti paraméterértékek határoznak meg képernyőre eső pontokat. A ti2, ti3 szakasz és a 0, 1 szakasz közös részét kell tehát megállapítanunk, hogy az eredeti szakasz képernyőn látszó részének paraméterintervallumát megkapjuk. Ez a közös rész 0 és ti2 nagyobbika, ill. 1 és ti3 kisebbike közötti szakasz lesz (amennyiben az első érték nem nagyobb mint a második - ez esetben megintcsak nincs látható részlet). Ezek után ezt a két értéket helyettesítjük t helyére az egyenes paraméteres egyenletében, és így kapjuk a megrajzolandó szakasz végpontjait.
Az algoritmus programját a következőképpen készíthetjük el:
300 DIM t(4): DIM i(4)
310 LET e=c-a+(c=a)/1000: LET t(1)=a/e: LET t(2)=(m-1-a)/e
320 LET e=d-b+(d=b)/1000: LET t(3)=-b/e: LET t(4)=(n-1-b)/e
330 FOR i=1 TO 4
335 LET i(i)=i
340 FOR j=1 TO i-1
350 IF t(j)>t(i) THEN LET s=t(j): LET t(j)=t(i): LET t(i)=s: LET s=i(j): LET i(j)=i(i): LET i(i)=s
360 NEXT j: NEXT i
370 LET s=i(1)+i(2): IF s=3 OR s=7 THEN RETURN
380 LET o=t(2)*(t(2)>0): LET p=t(3)+(1<t(3))*(1-T(3))
390 IF o<p THEN LET p=p-o: PLOT a+o*(c-a),b+o*(d-b): DRAW p*(c-a),p*(d-b)
399 RETURN
Véletlenszám-generátor
A grafikai programok némelyikében nagyon jó lehetőség kínálkozik a BASIC nyelv véletlenszám-generátorának használatára. A 4. fejezet csak ilyen programokat tartalmaz. A véletlenszám-generátor az RND beépített függvény hívásakor lép működésbe és egy 0 és 1 közé eső véletlen számot állít elő egyenletes eloszlásban. (Ez annyit jelent, hogy pl. az RND<0.7 feltétel éppen 0.7 valószínűséggel teljesül.) Valahányszor a programban egy olyan utasítás kerül végrehajtásra, amelyben az RND szerepel, a véletlenszám-generátor egy újabb 0 és 1 közé eső számot ad (pontosabban: a sorozat csak nagyon hosszú idő után kezdi ismételni magát). Ha viszont ugyanazt a programot egymás után kétszer úgy futtatjuk, hogy közben egyszer kikapcsoltuk a gépet, akkor pontosan megegyező véletlenszám-sorozatokat figyelhetünk meg. Ennek elkerülésére szolgál a RANDOMIZE utasítás. A RANDOMIZE utasítás a véletlenszám-sorozat első tagját állítja be a gép bekapcsolása óta eltelt időtől függően (amit 0.02 mp-es egységekben mér). Ily módon saját pontatlanságunk már garantálja, hogy különböző sorozatokat kapjunk.
Ha a RANDOMIZE utasítás után egy számot is írunk: RANDOMIZE n - akkor viszont a véletlenszám-sorozat kezdőértékét n-től függően választja. Ezzel azt tudjuk elérni, hogy a véletlenszám-sorozat tetszőleges, általunk választott rögzített sorozat lehessen - RANDOMIZE 15 után mindig ugyanaz a sorozat következik, de pl. RANDOMIZE 25 után mindig egy másik. Egy véletlen képet rajzoló program megadása után az előállítható képeket már egyértelműen azonosíthatjuk egy számmal, amit a program elején beolvasunk, és a RANDOMIZE utasítás paramétereként használjuk:
10 INPUT n: RANDOMIZE n
Ebben a részben olyan grafikai fogalmakat rögzítünk, amelyek a könyv számítógépes grafikáinak leírásánál, osztályozásánál hasznunkra lesznek. E fogalmak megvilágításához azonban sokszor előre kell utalnunk, a könyvben csak később szereplő grafikák példáira hivatkozva.
Pontok, pontfelhők
Abból indultunk ki, hogy minden kép ugyanazokból a pontokból építkezik. Ennek ellenére viszonylag ritkán készítünk képeket különálló pontokból - többnyire olyan algoritmusokat használunk, amelyek bizonyos kész alakzatokat rajzolnak, és ezekből állítjuk össze a számítógépes grafikákat. A 3. fejezetben azonban találunk pontonként megrajzolt képeket is. Viszonylag gyakoribbak lesznek az olyan algoritmusok, amelyekben sorrendben járjuk be a képernyő pontjait és egyenként rendelkezünk a berajzolásukról: erre példa a 3. fejezet RND-t leleplező mintája, akárcsak az almaemberke, ill. a sejtautomatával készített ábrák. Ide sorolható pl. a sokat alkalmazott véletlen betöltés algoritmusa is.
A pontonkénti rajzolás különös eseteinek tekinthetjük a 7. fejezet sörétes rajzolóalgoritmusá, amelyben kézzel célozzuk meg a berajzolandó pontok körülbelüli helyét, majd sörétszerűen ekörül szóródva jelennek meg a rajz pontjai.
Görbék, görbeseregek
A legtöbb képet vonalakból építjük fel, amelyek végső soron egyenes szakaszokból állnak, ill. egészen pontosan olyan pontokból, amelyek egyenes szakaszok közelítő képét alkotják. Ilyen vonalak lesznek tehát a könyv ábráinak legközönségesebb grafikai alapelemei. E vonalakból újabb gyakran alkalmazható elemeket szerkeszthetünk, ha azonos tá-volságban két-két párhuzamos vonalat rajzolunk, mint a 4. fejezet síkfelosztásában, (ez persze csak egyenes vonalakkal tehető meg), de hasonló hatást kelt a cső-vonal is. Új minőség alakul ki a görbére merőleges "szőrök" megrajzolásával is, bár ennek valószínűleg kevés helyen látjuk hasznát.
Gazdag lehetőségek nyílnak az olyan görbék megrajzolásával, amelyeket egymástól csak kevéssé eltérő paraméterek határoznak meg. Noha ez a meghatározás a legkevésbé sem alkalmas matematikai definíciónak, a matematikai szakirodalom is gyakran él a görbeseregek hasonló tartalmú, és hasonlóan körvonalazatlan segéd fogalmával. Mi is bátran beszélhetünk tehát görbeseregekről - erre többek között a gravitációs pályáknál, a mozgásegyenleteknél, a görbékkel megrajzolt térbeli felületeknél találunk példát.
Foltok, textúrák
A 2.2. szakaszban leírt foltbetöltő algoritmussal bármilyen zárt vonallal körülvett területet befeketíthetünk. Ennek az algoritmusnak apró módosításával olyan foltbetöltéseket is készíthetünk, amelyek dekoratívabbak, érdekesebbek, mint a folt egységes befeketítése.
A legegyszerűbb példa erre a csíkozás. Megtehetjük, hogy a foltbetöltés közben figyeljük az éppen soron következő pont y koordinátáját, és csak akkor rajzoljuk a pontot feketére, ha ez a koordináta páros. Ily módon egy-egy pont szélességű fekete-fehér csíkozással tölthetjük be a foltot. Ha viszont azt szeretnénk, hogy a fekete csík 3, a fehér 5 pont szélességű legyen, akkor az y koordináta paritása (párossága) helyett a 3+5 = 8-cal való osztás utáni maradékát vesszük (y-t modulo 8 tekintjük). Csak a 0, 1 vagy 2 maradék esetén rajzoljuk be a pontot - ezáltal éppen a kívánt szerkezetű csíkozást állítjuk elő.
A foltbetöltő algoritmus viszonylagos bonyolultságát (és következésképpen lassúságát) sok esetben kiküszöbölhetjük, ha tudjuk, egyszerűbb alakú foltot akarunk betölteni. Például egy kör vízszintes csíkozása úgy végezhető el, hogy végigmegyünk a függőleges átmérő pontjain, és az előbbi maradékvizsgálat után a 0, 1, 2 maradéknál jobbra és balra haladva addig rajzolunk be fekete pontokat, amíg a kör határához nem érünk (amit a már korábban megrajzolt fekete pont jelezhet számunkra).
Természetesen ugyanilyen módszerrel vizsgálhatjuk a pontok x koordinátáit, és állíthatunk elő különböző szélességű függőleges csíkozást is. További lehetőségek adódnak a két koordináta együttes figyeléséből: ha pl. az x koordináta 0, 1 maradékánál (modulo 5), és az y koordináta 0, 1, 2, 3 maradékánál (modulo 6) rajzoljuk be a pontokat. Ezzel a módszerrel a képzeletben 5x5-ös téglalapokra bontott képernyőn minden téglalap bal alsó részén egy 2x4-es kis téglalapot feketítünk be - a keletkező mintázat egyfajta raszterminta lesz. Még tovább bonyolítva a dolgot: választhatjuk feketének azokat a pontokat is (ugyanilyen téglalapbeosztásnál), amelyek x és y koordinátái egyszerre esnek a megadott határok alá vagy fölé (azaz x<2 mod 5 és y<4 mod 7 vagy x>1 mod 7 és y>3 mod 7). Ily módon aszimmetrikus sakktáblamintázatot kapunk, amelyben a 2x4-es téglalapok sarkaihoz 3x3-as négyzetek csatlakoznak.
A csíkozás, a raszterminták és a sakktáblaminták, amellett, hogy dekoratívak, bizonyos mértékben jellemzik is az általuk betöltött felületet - utalnak a felület anyagi minőségére. Az ilyen tulajdonságú felület-betöltéseket textúráknak nevezzük. A könyvben többféle textúrával fogunk találkozni. Az egyik alaptextúra a képernyőpontok véletlen döntés alapján való berajzolásával jön létre. Ezt a szemcsés felületre utaló mintázatot nevezzük a továbbiakban véletlen betöltésnek. A 4. fejezetben azután a sejtautomata egyik változatával foltos mintázatot készítünk ebből, ami viszont egzotikus állatbőrre emlékeztet. Érdekes textúrákat készíthetünk sejtautomatákkal csupa egyforma karakterrel betöltött képernyőből kiindulva is.
Másodlagos mintázatok
Vannak olyan minták, ahol a grafikai algoritmus által megrajzolt grafikai elemek összességéből végülis valamilyen másfajta motívum kerekedik ki, mint az alkotóelemek. Az 5. fejezetben pl. görbeseregekkel felületeket érzékeltetünk, és véletlenszerű pontbetöltéssel árnyékolunk. A sejtautomaták által megrajzolt pontrendszerek bonyolult szőnyegmintává állnak össze. A 7. fejezetben pedig elszórt pontokból, ill. különböző mértékben betöltött kis négyzetekből állítunk össze tónusos rajzokat. A 3. fejezet végén az egész képernyőn át húzódó egyenes vonalak adnak ki hullámzó görbéket. Ezekben az esetekben másodlagos mintázatokról beszélünk, hiszen az alkotóelemekből utólag, szinte másodlagosan alakul ki az, amit voltaképpen meg akartunk rajzolni. Az ilyen mintázatok mindig érdekesebbek, mint azok, amelyekben közvetlenül érünk célhoz - a szemlélő egyszerre érzékeli az alkotóelemek bonyolult összjátékát és az eredményként adódó formát.
"A kép megfelelhet egy látványnak, de nem lehet azonos vele."
(L. Wittgenstein)
A számítógépes grafika lehetőségeire gondolva első kézenfekvő ötletünk az lehet, hogy matematikai szabályok alapján készítsünk képeket. Tanulmányaink során a matematika amúgy is összekapcsolódott bizonyos típusú képekkel, ábrákkal, és a matematikai alapfogalmak közül soknak vizuális jelentése is van számunkra (pl. pontok, egyenesek, görbék, felületek, testek, koordináták vagy gráfok - ez utóbbiak még a nevükben is rokonságot mutatnak a grafikával). Ebben a fejezetben tehát ebből a megszokott (de még nem elég jól ismert) vizuális matematikából indulunk ki, miközben az egész könyvben arra törekszünk, hogy a számítógépes képek szerkesztésével, a látványok elemzésével, grafikai kísérletekkel megismerjük egyfajta matematikai vizualitás alapjait.
A 2. fejezetben megismert görberajzoló program olyan univerzális eszközt ad, amellyel tetszőleges görbéket meg tudunk rajzolni. A programba csupán be kell illeszteni egy szubrutint, amely sorban megadja a megrajzolandó görbe pontjainak koordinátáit, hogy a program előállítsa a görbét jól közelítő egyszerű töröttvonalat. Elég tehát azokkal a szabályokkal foglalkoznunk, amelyek alapján kiszámíthatjuk a görbe pontjait. Eleinte már ismert görbék definiáló szabályainak apró módosításaival kísérletezünk. Később előre elképzelt görbékhez is próbálunk szabályt keresni, amely azokat előállítja.
Változatok egy körre
Induljunk ki legelőször a kör paraméteres görbéjéből:
(x(t), y(t)) = (r*COS t, r*SIN t)
ahol r rögzített szám (a kör sugara), a t paraméter pedig a (0.2*PI) intervallumon fut végig.
Az első ötlet az lehet, hogy a két koordinátában az egyforma r helyett két különböző (p,q) értéket vegyünk:
(x(t), y(t)) = (p*COS t, q*SIN t)
Az így kapott görbe ellipszis, amelynek tengelyei az x és y tengellyel párhuzamosak. (p,q) különböző értékeihez természetesen különböző ellipszisek tartoznak.
Ezután próbálkozzunk meg azzal, hogy mindkét koordinátában azonos, de t-től függően változó r(t) sugarat választunk. A legegyszerűbb ilyen lehetőség, ha r(t)-t c*r*t-nek vesszük. Az eredmény, ahogy a képen látható, egy spirálvonal. Ezt a spirálvonalat, amelynél a sugár az elfordulási szöggel arányos, Arkhimédész-féle spirálnak nevezik.

Arkhimédeszi spirál
A program:
10 LET r=240: LET u=128: LET v=96
15 PLOT u,v
20 FOR t=0 TO 22.4*PI STEP .2
30 LET rr=.005*r*t
40 LET x=INT (128+rr*COS t): LET y=INT (96+rr*SIN t)
50 DRAW x-u,y-v
55 LET u=x: LET v=y
60 NEXT t
Ennél a spirálnál a sugár adott szögelfordulásnál adott mértékben nő meg. A másik lehetőség az, hogy adott szögelfordulásnál a sugarat adott arányban növeljük. Ekkor r(t) = c*r^t lesz. Az így megrajzolt logaritmikus spirált mutatja a következő kép.
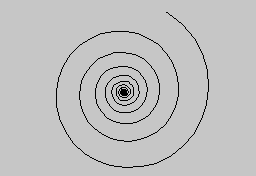
Logaritmikus spirál
Eddig mindkét koordinátafüggvényben változatlanul hagytuk a COS t és SIN t kifejezéseket. Ha a sugár változtatására nincs több ötletünk, ezek átalakításával is kísérletezhetünk. Tudjuk, hogy a COS t függvény felírható SIN (t + PI/2) alakban is. Ebből már adódik az ötlet, hogy a PI/2 helyett más d eltolási értéket is kipróbáljunk: rajzoljuk meg a
(x(t), y(t)) = (r*SIN (t+d), r*SIN t)
paraméteres görbét! Bármilyen d-re olyan ellipszist kapunk, amelynek a tengelyei 45 fokos szöget zárnak be a koordinátatengelyekkel, és amelyek belülről érintenek egy origó középpontú, 2*r oldalú négyzetet. (A paraméteres egyenletből az is kitűnik, hogy d = 0-ra egy 45 fokos szakaszt kapunk az y = x egyenesen, d = PI/2-re pedig ismét a körhöz jutunk, és hogy az ellipszisek d-ben 2*PI szerint periodikusan ismétlődnek.). A következő képen egy sor különböző d értékkel rajzoltuk meg ezeket az ellipsziseket.

Ellipszissereg
A program:
10 LET r=86
20 FOR d=PI/16 TO PI-.1 STEP PI/16
30 LET u=128+r*SIN d: LET v=88+r*SIN 0
40 PLOT u,v
50 FOR t=0 TO 2*PI+.1 STEP .1
60 LET x=128+r*SIN (t+d): LET y=88+r*SIN t
70 DRAW x-u,y-v
80 LET u=x: LET v=y
90 NEXT t
100 NEXT d
Ismét visszatérve a kiinduló kör paraméteres megadásához, a COS t és SIN t kifejezést benne COS (a*t)-vel és SIN (b*t)-vel kicserélve érdekes görbéket kapunk - ezeket Lissajous-görbéknek hívják.
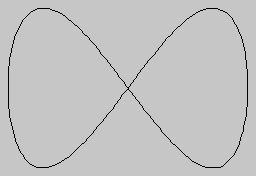
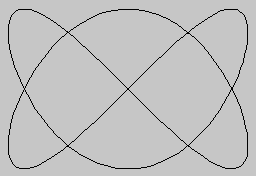
Az a és b valós értékeket eleinte kis egész számoknak választva megpróbálhatjuk kiismerni ezeknek a görbéknek a természetét. Durván azt mondhatjuk, hogy ha a és b egész számok, akkor a görbe függőlegesen a, vízszintesen pedig b púpot rajzol, mielőtt visszatérne a kezdőpontba. Most az is kérdéses, t-nek milyen határok között kell változni. Azt akarjuk, hogy a*t és b*t is 2*PI többszöröse legyen - ha d = (a,b) (a és b legnagyobb közös osztója), akkor t 0-tól 2*PI/d-ig futva a görbe biztosan visszatér a kezdőpontba. Hasonló módon, ha egész számok helyett a/c és b/c (közös nevezőre hozott) törtszámokat veszünk, t legnagyobb értéke 2*PI*c/d kell, hogy legyen (d ismét a és b legnagyobb közös osztója).
Szabályt keresünk görbékhez
Nehezebb feladatra vállalkozunk, ha elképzelt görbéhez keresünk olyan szabályt, amellyel előállíthatjuk. Elvileg most semmi nem is garantálja a sikert, a gyakorlatban azonban nehéz olyasmit elképzelni, amihez hasonlót már ne láttunk volna korábban, és aminek ne ismerhetnénk a szabályát. Ebben a részben is arra számítva próbálunk görbékhez szabályokat keresni, hogy valamely hasonló görbe hasonló szabályait átalakítva eredményhez juthatunk. A 7. fejezetben azután olyan algoritmust mutatunk be, amely minden görbéhez közelítő megoldást garantál, a görbe néhány jellemző pontjából kiindulva.
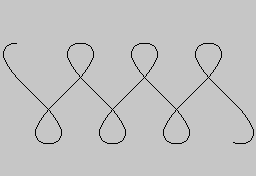
Sujtásminta
Keressünk először megfelelő szabályt a fenti sujtásmintájához. Ebben az esetben olyan görbével van dolgunk, amelyben ugyanaz a részlet periodikusan ismétlődik, az x tengely irányában eltolva. Ha a görbe paraméteres megadása (x(t), y(t)), (ahol az x és y függvény egyelőre ismeretlen), és két szomszédos sujtás között a távolság d, akkor x olyan periodikus függvény lehet, amelyre x(t+1) = x(t)+d minden t-re. Ilyen esetekben mindig érdemes megpróbálkozni azzal, hogy az x(t) függvény helyett olyan (hozzá hasonló) függvényt veszünk, amelyre mindig x(t+1) = x(t). Ez egyszerűen elérhető az x(t) - d*t átalakítással. Ez a görbénél azt jelenti, hogy (esetünkben vízszintes irányban) úgy nyomtuk össze, hogy az ismétlődő részletek pontosan egymásra essenek. Ha most ezt az egyetlen látható részletet már le tudjuk írni egy szabállyal, akkor az előbbi átalakítást fordított irányban elvégezve az eredeti görbét is paraméterezni tudjuk.
Az ábra sujtásmintáját az említett módon összenyomva egy nyolcast kapunk, amelyben felismerhetjük az egyik Lissajous-görbéjét. Ott a fekvő nyolcas alakú görbe képlete
(r*COS t, r*SIN (2*t)) 0 <= t <= 2*PI
volt. Ahhoz, hogy ezt nyolcassá alakítsuk, elég felcserélni a két koordinátafüggvényt:
(r*SIN (2*t), r*COS t)
A görbe kezdőpontja a nyolcas tetején lesz, és innen először jobbra fog kanyarodni, majd végül balról érkezik vissza ugyanoda. Ahhoz azonban, hogy a széthúzott görbe periódusonként csak egyszer metssze önmagát, ezt a nyolcast először tükröznünk kell az y tengelyre (vagyis az x koordinátákat -1-gyel kell szoroznunk):
(-r*SIN (2*t), r*COS t)
Ezután még meg kell állapítanunk, hogy x irányban milyen erősen kell széthúzni a görbét, hogy a kívánt sujtásmintát kapjuk. A nyolcas legbaloldalibb pontjának x koordinátája -r, a jobb szélsőé pedig r. Egy periódusban tehát a c*t eltolásnak 2*r-nél nagyobbnak kell lennie, innen pedig c > r/PI adódik (hiszen egy periódus hossza 2*PI).
Választhatunk pl. c = 3/2*r/PI-t, és ha azt akarjuk, hogy x(t) 1 szerint legyen periodikus (ahogy eredetileg kerestük), t-t 2*PI-vel kell szoroznunk. A sujtásmintát tehát végül az
r*(-SIN (4*PI*t) + 3*t, COS (2*PI*t))
paraméteres görbével rajzolhatjuk meg.
10 LET r=20: LET u=15: LET v=96+COS 0*50
20 PLOT u,v
30 FOR t=0 TO PI+.4 STEP .02
40 LET x=15+r*(-SIN (4*PI*t)+3*t): LET y=96+COS (2*PI*t)*50
50 DRAW x-u,y-v
60 LET u=x: LET v=y
70 NEXT t
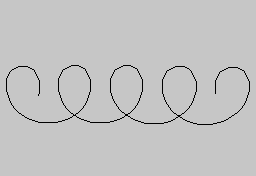
Csavarvonal
Pontosan ugyanezt a gondolatmenetet alkalmazhatjuk a fenti ábrán látható csavarvonalra - ott egy önmagán sokszor végigfutó körvonalat húzunk szét. A görbe tehát
r*(COS t + c*t, SIN t)
alakban adható meg. Ha c-t 1-nél kisebbre választjuk, akkor az ábrához hasonlóan önmagát metsző csavarvonalat kapunk, c>1-re viszont egyfajta aszimmetrikus hullámvonalat.
10 LET r=28: LET c=.3
20 LET u=10+r*COS 0: LET v=96
30 PLOT u,v
40 FOR t=0 TO 9*PI STEP .1
50 LET x=10+r*(COS t+c*t): LET y=96+r*SIN t
60 DRAW x-u,y-v
70 LET u=x: LET v=y
80 NEXT t
Spirográfnyomok
A körvonalból (mint legegyszerűbb görbéből) kiindulva egy újabb, gazdag variációkat rejtő görbecsaláddal ismerkedhetünk meg a következő módon. A kört most keréknek fogjuk fel. A legelső dolog, amit érdemes megpróbálni az, hogy egy ilyen keréken rögzítünk egy pontot, és megrajzoljuk ennek a pontnak a nyomát, miközben a kerék egy vízszintes vonalon (a képernyő alján) végiggördül. Az így kapott ciklois görbe alakja csak attól függ, hogyan választottuk ki a keréken a pontot, amely nyomot fog hagyni. Ezt pedig meghatározza egyrészt az illető pont és a kerék középpontja közti távolság, másrészt a kerék sugarának aránya. Ha ez az arány 0, a kapott görbe vízszintes egyenes, ha az arány 1, a görbe periodikusan ismétlődő csipkés vonal, a kettő közötti arányokra pedig aszimmetrikus hullámvonal (amennyiben a hullámhegyek és hullámvölgyek alakja nem egyforma). Az 1-től különböző arányokra a görbe mindenütt sima (azaz differenciálható lesz).
Ezeknek a görbéknek a paraméteres egyenlete a következő alakú:
(x(t), y(t)) = (r*t + s*COS t, s*SIN t)
ahol r jelöli a kiválasztott pont és a középpont távolságát, s pedig a kerék sugarát. Az egyenlet ismeretében most már megrajzolhatjuk egy olyan pont nyomát is, amely a középponttól távolabb van, mint a kerék sugara (r>s).
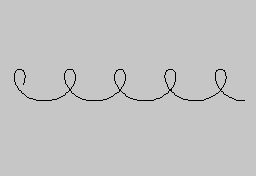
10 LET r=8: LET s=16
20 LET u=10+s*COS 0: LET v=96+s*SIN 0
30 PLOT u,v
40 FOR t=0 TO 9.5*PI STEP .1
50 LET x=10+INT (r*t+s*COS t): LET y=INT (96+s*SIN t)
60 DRAW x-u,y-v
70 LET u=x: LET v=y
80 NEXT t
Bonyolítsuk a helyzetet azáltal, hogy megváltoztatjuk a gördülő henger pályáját - eddig egyenes vonalban gördült, most járjon be egy körvonalat! Ezt a spirográf nevű eszközzel lehet megvalósítani, amelyben egy kisebb fogazott gyűrű gördül végig egy nagyobb, ugyancsak fogazott gyűrű belső falán, miközben a vele közös tengelyű tárcsát is forgatja. A tárcsa különböző pontjain fúrt lyukakba illesztett ceruza hegyével a legváltozatosabb alakú spirográf nyomokat rajzolhatjuk meg.
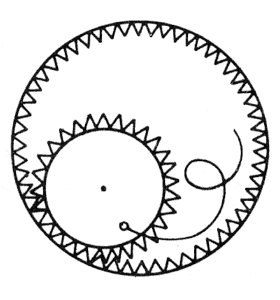
Rajzolás spirográffal
Próbáljuk meghatározni az ilyen módon megrajzolt spirográfpályák (ún. hipocikloisok) egyenletét. Vegyük a külső, nagyobb gyűrű sugarát r-nek, a benne forgó kisebb gyűrűét s-nek, míg a nyomot hagyó pont távolsága a kis gyűrű középpontjától legyen q. Jelölje t a belső, kis gyűrű teljes elfordulásának szögét a kiindulási helyzethez képest. Ekkor a kijelölt pont koordinátái a belső gyűrű középpontjához képest
(q*COS t, q*SIN t)
A gyűrű középpontjának a koordinátáit a következő meggondolással számíthatjuk ki: a kis gyűrű útja a nagy gyűrű belső falán s*t-vel egyenlő. A nagy gyűrűben viszont ez csak s*t/r szögelfordulást jelent. Mivel a kis gyűrű középpontja a nagy gyűrűétől mindig r-s távolságban van, a keresett középpont koordinátái:
((r-s)*COS (s*t/r), (r-s)*SIN (s*t/r))
(természetesen a nagy gyűrű középpontjához képest). Ehhez kell tehát hozzáadni a megrajzolandó pont előbb kiszámított koordinátáit. A képletekből kitűnik, hogy a görbe alakját r,s és q (sőt, voltaképpen már az r/s és s/q arány is egyértelműen meghatározza). Hogy t-nek milyen határok között kell változnia, az a Lissajous-görbék kapcsán felmerült problémához hasonlít: t-nek, és s*t/r-nek egyaránt 2*PI többszörösének kell lennie. Ha az s/r tört már nem egyszerűsíthető, akkor t-nek 0 és 2*r*PI között kell végigfutnia. A következő képen egy ilyen görbét rajzoltunk meg:

Spirográfnyomok
10 LET r=52: LET q=36
20 LET u=128+r*COS 0+q*COS 0
30 LET v=88+r*SIN 0+q*SIN 0
40 PLOT u,v
50 FOR t=0 TO 2*r*PI STEP .2
60 LET x=128+INT (r*COS (t/r)+q*COS t)
70 LET y=88+INT (r*SIN (t/r)+q*SIN t)
80 DRAW x-u,Y-v
90 LET u=x: LET v=y
100 NEXT t
Görbeseregnek nevezhetünk egy sereg olyan görbét, amelyek ugyanabból a szabályból kis módosítással keletkeznek. Például a már bemutatott ellipszissereg (r*SIN (x+d), r*SIN x) paraméteres görbék egy görbesereget alkotnak, ha d-t változtatjuk. Vagy ha a Lissajous-görbéknél (r*COS (a*t),r*SIN (b*t))-ben a-t és b-t variáljuk. Amikor a közös szabályban az eltérést képviselő paramétert (d-t, a-t vagy b-t) kis értékkel változtatjuk, általában a keletkező görbék is csak kevéssé térnek el, pályájuk nagyon hasonló. Sokszor éppen ezért bizonyos mértékben térbeli hatást keltenek - úgy néznek ki, mintha egy térbeli felületre rajzolt párhuzamos vonalak metszetei lennének. Ezt megfigyelve már szándékosan is használhatjuk az ilyen görbeseregeket a térbeliség jelzésére (l. az 5. fejezetet). Egyelőre azonban maradjunk az általános problémánál.
A spirográffal (vagy a spirográfot utánzó programmal) megrajzolt hipocikloisok voltaképpen egy csillag körül keringő bolygó holdjainak a pályái lehetnének (feltéve, hogy a bolygók és a holdak is körpályán keringenek). A nagy körben gördülő kis kör középpontja ugyanis szintén körpályán mozog a nagy kör középpontjához képest, és ez lesz a nyomot hagyó ceruzahegy pályájának a mindenkori középpontja. Ha rögzített nagy kör mellett több kis körrel rajzolunk spirográfnyomokat, az olyan, mintha az egyik bolygó körül több hold is keringene, ha viszont (ugyanabból a középpontból) különböző sugarú nagy köröket is használunk, akkor ezáltal a csillag több bolygóját is figyelembe vehetjük.
Egy bolygó egy holdjának pályáját a bolygó keringési sugara, a hold távolsága, és a két keringési sebesség aránya határozza meg. A keringési sebességeket természetesen előjellel kell tekinteni, mert másfajta pályákat kapunk, ha a hold a bolygóval azonos irányban, vagy vele ellentétes irányban kering.
Interferenciák
Az eddigi képeken a görbeseregek többnyire olyan vonalakból álltak, amelyek egymáshoz közel, egymástól nagyjából állandó távolságban haladtak. A vonalak metszése inkább csak kivétel volt, ami a szabályosság egyhangúságát fűszerezte. Ebben a részben viszont olyan vonalakból rajzolunk mintákat, amelyek helyenként metszik egymást vagy összeérnek, és éppen a vonalak ezáltal kialakuló megvastagodása alkotja a mintát.
Az alábbi képen egy meglepően egyszerű algoritmust követtünk: a képernyő keretének pontjait 3 egységnyi közönként összekötöttük az egyik belső ponttal. E szabály rögzítése után már csak a pont megválasztásával tudjuk szabályozni a konkrét mintát.
Két szomszédos vonal 3 pont távolságból indul, és ugyanabban a pontban végződik. Nagyjából a vonalak harmadolópontjainál ez a távolság két, ill. egy egységre csökken (természetesen a kerekítés miatt). A 3, 2 vagy 1 pont távolságban párhuzamosan futó vonalak rendszere azonban élesen eltérő mintázatot ad a képernyő összefüggő területeinek - ebből tevődik aztán ki a kép interferenciamintája.
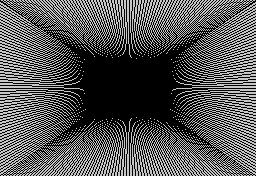
Interferencia
10 LET x=128: LET y=88: LET s=3
20 FOR i=0 TO 255 STEP s
30 PLOT i,0: DRAW x-i,y
40 PLOT i,175: DRAW x-i,-y
50 NEXT i
60 FOR i=0 TO 175 STEP s
70 PLOT 0,i: DRAW x,y-i
80 PLOT 255,i: DRAW -x,y-i
90 NEXT i
Gravitációs pályák
Az előbb naprendszermodellt készítettünk, most olyan görbeseregeket próbálunk megrajzolni, ahol az egyes görbék kiszámításánál szintén az égi mechanika szabályait alkalmazhatjuk. Gravitációs pályákat követünk végig, amelyek egy felület szabályosan elhelyezkedő pontjaiból azonos irányban vagy egy pontból szabályosan változó irányokban indulnak. A modellben véletlenszerűen elhelyezünk néhány égitestet (mondjuk három-négyet, mert ennél többre már túlságosan zavaros képet kapnánk), és egy űrhajót, amely köztük pusztán a gravitáció hatására mozog, saját hajtóművét nem működteti. Az egyszerűség kedvéért mind az égitesteket, mind az űrhajót a képernyő síkján helyezzük el, modellünk tehát csak kétdimenziós. Egy pontból adott kezdősebességgel, adott irányban elindítva az űrhajót addig követjük a pályán, amíg le nem tér a képernyőről, vagy bele nem zuhan valamelyik égitestbe. Ezután még elindítjuk ugyanabból a pontból ugyanakkora sebességgel az ellenkező irányba is. A többi pálya megrajzolásához a kezdőpontot és a kezdősebességet kétféle módszer szerint változtatjuk. Az egyik lehetőség, hogy a kezdőpontot a képernyő függőleges felezőegyenesén választjuk ki, egymástól azonos távolságokra. A másik esetben egyetlen kezdőponttal dolgozunk, de a kezdősebesség iránya változik egyenletes szögelfordulással.
Hogyan számítjuk ki a gravitáció hatását az űrhajó pályájára? Egyetlen égitest esetében a gravitációs erő az égitest felé mutat (mert vonzza az űrhajót), nagysága pedig a távolság négyzetével fordítottan arányos. Vagyis, ha ez a távolság r, a gravitációs erő hatására létrejövő gyorsulás c/r^2. Az űrhajó sebességét egy (u,v) vektor mutatja (u a vízszintes, v a függőleges irányú sebesség). Ugyanígy a gyorsulást is két komponensre (vízszintes és függőleges irányú gyorsulásra) kell bontani. A gyorsulásvektor az űrhajó pillanatnyi helyétől az égitest felé mutat: (x0-x, y0-y). Ezt a vektort azonban még meg kell szorozni egy számmal, úgy, hogy nagysága (abszolút értéke) az előbb megadott c/r^2 legyen, (ahol r értéke SQR ((x0-x)*(x0-x) + (y0-y)*(y0-y)). Mivel (x0-x, y0-y) abszolút értéke r, ezt a vektort c/r^3-nal kell szorozni, hogy c/r^2 abszolút értékű, de azonos irányú vektort kapjunk.
A valóságban persze a gyorsulás állandóan hat, így az űrhajó sebessége folyamatosan változik. Mi ezt nem tehetjük meg, ehelyett azonos időközönként megnöveljük az űrhajó helyét jelző koordinátákat a sebességvektor megfelelő komponenseivel:
x = x+u, y = y+v
a sebességvektort viszont a gyorsulásvektorral:
u = u + c*(x0-x)/r^3, v = v + c*(y0-y)/r^3
A c érték változtatásával növelhetjük vagy csökkenthetjük a gravitációs erőt (ez voltaképpen az égitest tömegének felel meg). Mindeddig egyetlen égitestről beszéltünk. Több égitest esetén a sebességet ugyanilyen időközönként az összesre külön-külön kiszámított gyorsulásvektorokkal növeljük meg.
Egy űrhajó pályáját addig követjük, amíg a képernyőn még látható marad. Ha viszont valamelyik égitestet túlságosan megközelíti (r egy adott értéknél kisebb lesz), akkor azt is megtehetjük, hogy ennél megakasztjuk, úgy tekintjük, hogy az űrhajó lezuhant.
A következő képeken több pontból azonos irányban, illetve egy pontból különböző irányokban elindított űrhajók pályáit látjuk.
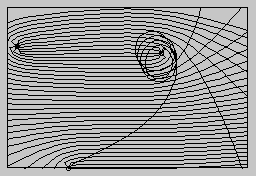
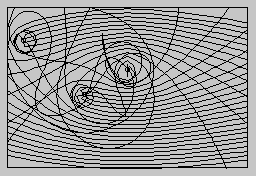
Párhuzamosan induló űrhajók pályálya
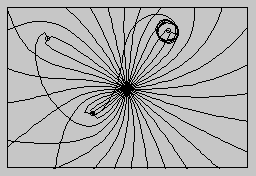
Sugarasan kilőtt űrhajók pályája
Ha alaposan megfigyeljük ezeket az ábrákat (és különösen saját programjainkat - lásd kazettamelléklet - működés közben), meglepő dolgokat tapasztalhatunk. Noha nagyon sok a szabályosság a képen, az egymáshoz közeli pontról induló űrhajók sokszor végig egymás melletti pályán futnak, a képet mégis kuszán elkalandozó vonalak szelik át. Néha az egészen hasonló feltételekkel elindított és kezdetben egyformán haladó pályák egészen különböző fordulatot vesznek, egymástól végletesen távol kerülnek. Míg a legtöbb űrhajó ugyanazokat az égitesteket ugyanannyiszor kerüli meg, mindig lesz egy-két deviáns, amelyik különös, kacskaringós pályán összevissza kószál az űrben, amíg végül valamelyik égitestbe zuhan, vagy elhagyja a látóteret.
Míg a gravitációs pályák kiszámításánál eddig igyekeztünk ragaszkodni a fizikai törvényekhez, a grafika céljaira tulajdonképpen engedhetünk a szigorú megkötésekből, ha nem akarjuk az előállított képet a valóság modelljének tekinteni. A gravitációs görbék esetében pl. olyan képzeletbeli világokat is vizsgálhatunk, ahol a gravitációs erő nem a távolság négyzetével, hanem valamilyen más hatványával fordítottan arányos. Azaz a gravitációs pályákat leíró képletben r^3-t valamilyen más r^n-nel helyettesíthetjük (ilyenkor a c-t is általában meg kell változtatni - c egy átlagos űrhajó - égitest távolság szóban forgó hatványával arányos). Ha n nagyobb, mint 3 akkor az égitestek kevésbé térítik el az űrhajót az egyenes pályáról, mindenesetre csökken a pályák bonyolultsága.
Mozgáspályák
A gravitációs pályák analógiájára másfajta szabályokat is kitalálhatunk, amelyek a pontonként megadott gyorsulással határozzák meg a mozgás pályáját. Ezzel a módszerre számtalan érdekes görbesereget kaphatunk. Most is egyenletes időközönként értékeljük ki a mozgást meghatározó paramétereket: az utat, a sebességet és a gyorsulást. Az összefüggés persze éppen fordított irányú, a mozgás egy adott pontján kiszámítjuk a ponthoz tartozó gyorsulást, ezzel megváltoztatjuk az eddigi sebességet, és ez határozza meg, hogy a következő vizsgált pillanatban hová jut el a görbe. A helyet, sebességet és gyorsulást most is vektorok tartalmazzák: (x,y) jelöli a pillanatnyi helyet, (u,v) a pillanatnyi sebességet és (a,b) a gyorsulást.
A gravitációs pályáknál az (x,y) helyhez tartozó gyorsulás
c/r^3 * (x0-x,y0-y) volt, ahol
r = SQR ((x0-x)*(x0-x) + (y0-y)*(y0-y))
A gyorsulást most a sokkal egyszerűbb (a,b) = (c*x, d*y) alakban keressük.
Hogy hogyan lesz az egyes görbékből görbesereg, arra nézve már a gravitációs pályáknál szerzett tapasztalatok lehetnek segítségünkre. Az egyik módszer szerint a képernyő valamelyik vízszintes vagy függőleges egyenesén haladunk végig egyenletes lépésközzel és ezekből a pontokból indítjuk el, mindig azonos kezdősebességgel, a megrajzolandó görbéket. Hogy ne legyenek a képernyőn olyan vonalak, amelyek egy pontban hirtelen megszakadnak, érdemes ugyanezekből a pontokból pontosan ellentétes sebességekkel is elindítani egy-egy görbét. A görbék addig haladhatnak, amíg a képernyő szélébe nem ütköznek. A képen egy ilyen görbesereget látunk:

Párhuzamos mozgáspályák
A görbék görbeseregbe való gyűjtésének másik módszere (akárcsak a gravitációs pályáknál), hogy egy pontból indítjuk az összes görbét, de a kezdősebességek különbözőek lesznek: egy közös vektor ismételt elforgatottjaival fognak megegyezni. A következő képen ilyen görbesereget látunk, amelynek az egyenlete:
(a,b) = 0.001*(-x,y)
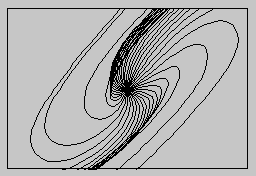
Sugaras mozgáspályák
A kezdőpont helye egyértelműen látszik a képen, a kezdősebességek viszont kettő abszolút értékű vektorok, amelyeket ismételten PI/40 szöggel forgattunk el.
Ezekről a görbékről is elmondható, ami a gravitációs pályánál tűnt fel: az egymáshoz közel haladó görbék sokáig nagyjából azonos pályát futnak be, mégis lesznek egymáshoz egészen közeliek, amelyeknek a sorsa a későbbiekben egészen különbözőképpen alakul.
Sem a gravitációs pályáknál, sem a további görbeseregeknél nem foglalkoztunk annak a lehetőségével, hogy a mozgó pont pályája önmagába visszatérő görbét alkot. Ilyen esetben az eddigi elveken felépített programok nem tudnak továbblépni a következő görbe megrajzolására. Ennek megoldására a képernyőről való letérés (és a gravitációs görbéknél az égitestekbe lezuhanás) vizsgálatán kívül azt is ellenőrizni kell, hogy egy görbe nem tért-e vissza egy korábbi pontjába, ráadásul ugyanolyan sebességgel. A kerekítési és számítási hibák miatt azonban ez esetleg csak nagyon sokára teljesül. A helymeghatározás tűrésére éppen a sebességvektort használhatjuk:
x-x0<u, y-y0<v
a sebességvektorok megengedett eltérését pedig tapasztalatilag adhatjuk meg valamilyen kis értékben. Persze a görbe összes korábbi pontjának hely- és sebességvektorát nem tudjuk megőrizni - ez a módszer csak akkor alkalmazható eredményesen, ha mindegyik görbénél van egy-két gyanús pont, amelybe a görbe esetleg visszatérhet, és ennek az adataival tudjuk összevetni a futó pont adatait.
Az (a,b) = (c*x, d*y) alakú mozgásegyenleteket sokféleképpen általánosíthatnánk. Például olyan egyenleteket is felírhatnánk, amelyek a gyorsulás kiszámításához a sebességet is figyelembe veszik. Vagy megadhatnánk a gyorsulást a hely bonyolultabb függvényeként.
Végül, a gyorsulásegyenletekkel megadott görbék helyett az egyenleteket felhasználhatjuk (különösen a gravitációs görbék esetében) erőterek megjelenítésére is. Noha most már nem görbeseregeket, hanem számtalan különálló vonaldarabot fogunk megrajzolni, a módszer nagyon hasonlít az eddigiekhez. Adott gravitációs térben végigmegyünk egy négyzetrács pontjain, minden pontot egy űrhajó kiindulási pontjának tekintünk, amelyben a kezdősebessége 0, és berajzoljuk az első időpontban kiszámított sebességvektorokat. Vagyis azt az irányt, amerre a tér adott pontján elengedett test elmozdulna, miközben a vektor hossza az elmozdulás nagyságát is jelzi. A következő képen láthatjuk három csillag által meghatározott gravitációs tér erővonalait:
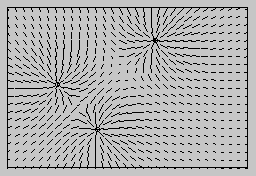
Három égitest gravitációs erőtere
Megtehetjük azt is, hogy az előbbi módon kiszámított elmozdulásvektorok PI/2 szöggel elforgatott változatait rajzoljuk be - ekkor az ún. ekvipotenciális vonalakat kapnánk meg, vagyis olyan vonalakat, amelyek mentén a gravitációs erő nagysága állandó:
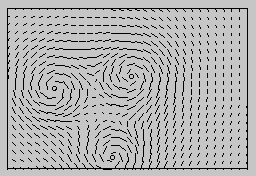
Ekvipotenciális vonalak három égitest gravitációs erőterében
Ebben a részben olyan algoritmusokat találunk, amelyek nem összetett képelemekből, hanem egyszerű pontokból építik fel a megrajzolandó mintát - bár a külön-külön kiválasztott pontok végül szabályos egésszé állnak össze -, ezért beszélhetünk mintákról.
Almaemberke
A 6.4. szakaszban olyan görbékkel foglalkozunk, amelyeknek a dimenziója nem 1, mint közönséges esetben, hanem 1 és 2 közé eső törtszám. Ezeket törtdimenziójú (vagy fraktális) görbéknek szokás nevezni. Most viszont egy olyan síkbeli alakzatot állítunk elő, amelynek a határa ilyen fraktális görbe.
Számunkra persze fontosabb az alakzat különös formája, minta határvonal dimenziója - mindenesetre érdemes tudnunk, hogy az említett ritka tulajdonsággal rendelkezik (és arról is híres).
Most tehát sorrendben történő pontberajzolással megrajzoljuk a szóban forgó ponthalmazt. Ezt a ponthalmazt a fraktális geometria egyik megalapítójáról Mandelbrot-halmaznak nevezik. Előállítása pedig a következőképpen történik: az x, y, a és b valós számokból kiindulva vesszük (x^2 - y^2 + a, 2xy + b) kifejezéssel meghatározott számpárt. Ezek után x és y helyére helyettesítsük a számpár első és második tagját, és végezzük el ugyanezt a műveletet! (Maga a művelet sokkal egyszerűbb a komplex számok körében - ha z = x+iy, u = a+bi, akkor egyszerűen a z^2 + u komplex szám képzéséről van szó, amelynek az eredményét ismét behelyettesítjük z-be.) Ha most az (x,y) számpárt egy síkbeli pont koordinátájának tekintjük, megfigyelhetjük, hogyan vándorol ez a pont, miközben a szóban forgó műveletet ismételjük. Kezdetben mindig a (0,0) pontból indulunk ki. A művelet ismétlése során (amely ezek szerint csak az (a,b) számpár megválasztásától függ), egyes esetekben korlátos pontsorozatokat kapunk, máskor a pontsorozat egyre távolodik a kiindulóponttól. Ez a sorozat azzal a tulajdonsággal rendelkezik, hogy ha valamikor legalább 2 egység távolságra kerül a kiindulóponttól, akkor már biztosan nem maradhat korlátos.
Az alábbi. képen az (a,b) pontot akkor rajzoltuk feketére, ha az (a,b)-vel meghatározott művelet 20 lépésén belül nem hoz létre olyan pontot, amely az origótól 2 egységnél távolabb van (természetesen az egység most nem 1, hanem kb. 100 képpont). Ha a 20 helyett nagyobb számot választottunk volna, pontosabban előállíthattuk volna a Mandelbrot-halmazt, azonban a számításhoz szükséges idő is arányosan megnövekedett volna. Már ez a 20 lépésből álló műveletsor is viszonylag jól közelíti az ismert almaemberke figuráját.

Almaemberke
Ha ennek a halmaznak egy-egy részletét kinagyítva rajzoljuk meg, majd ennek egy részét nagyítjuk fel stb., mindig az eredeti rajzhoz hasonlóan tagolt alakzatot látunk. Ez már önmagában is arra utal, hogy az alakzat határa az említett típusú, vagyis törtdimenziójú görbe.
Sejtautomaták
Aki úgy gondolja, hogy a képernyő pontról pontra való bejárása és egy minta pontonkénti berajzolása csak egészen egyszerű rajzok létrehozására alkalmas, annak figyelmébe ajánljuk a következő algoritmust. Az algoritmus maga rendkívül egyszerű, mivel azonban rendkívül sok műveletet igényel, ajánlatos gépi kódban programozni. Egy kb. 60000 pontból álló képernyő megrajzolása így durván 5 mp-t vesz igénybe - egyébként hosszú percekbe telhet - nekünk pedig a képernyő sokszori átrajzolására lesz szükségünk.
Az algoritmus (pontosabban algoritmusosztály) egy képernyőből kiindulva átrajzolja annak a pontjait. Minden egyes pont átrajzolásakor ugyanazt a szabályt követi. Megvizsgálja, hogy az illető pont körüli 3x3 egység oldalú négyzetben milyen színű pontok találhatók (természetesen most csak fekete és fehér pontokat engedünk meg). A 9 pont mindegyikén két lehetséges szín összesen 2^9 = 512 variációt jelent. E variációk függvényében határozzuk meg a pont színét a következő képernyőn. (Ügyelni kell arra, hogy minden pont szomszédjainak még az átalakítás előtti színét kell vizsgálni - ezért az aktuális pontot nem rajzolhatjuk azonnal át a kiszámított új színre, hiszen a fölötte levő sorban még eredeti színében kell számításba vennünk. Ezért minden kiszámított sort egy további sor meghatározásáig tárolnunk kell, és csak ha már 2 sorral feljebb tartunk, akkor rajzolhatjuk át.)
Ha az egy ponthoz tartozó 512 variációhoz tetszőlegesen választunk új színt, 2^512-féle átalakítási függvényt definiálhatunk - ezért beszéltünk algoritmusosztályról. Ez már nem is csillagászati szám - elképzelhetetlenül nagy érték. Valamivel csökkenthetjük a nagyságrendjét abban a szűkebb algoritmustípusban. Itt nem az számít, hogy egy pont szomszédjai közül minden egyes pont milyen színű, hanem, hogy hány szomszédja fekete. Ezt külön-külön vizsgáljuk meg fekete és fehér pont szomszédjaira.
Mind a fehér, mind a fekete pontoknál több különböző számot is megadhatunk (ami azt jelenti: ha a fekete szomszédok száma annyi vagy ennyi, akkor és csak akkor lesz ez a pont a következő képen fekete). Ily módon mind a fekete, mind a fehér pont átalakításához 2^9 féle szabályt adhatunk meg, ez összesen 2^18, azaz kb. negyedmillió. Egy átalakítást úgy definiálhatunk, hogy felsoroljuk a fekete és fehér pontoknál az "élethez" szükséges fekete pontok számát. Persze ezek közül is sok gyakorlatilag egyformán vagy pedig érdektelenül működik.
Ez az algoritmus a Neumann János-féle sejtautomata-fogalom speciális esete. Neumann János ennek segítségével bizonyította, hogy (elvben) lehetséges olyan automatát konstruálni, amely élőlény módjára önmagához hasonló, sőt, mutációval egyre tökéletesedő utódokat hoz létre. A sejtautomata név arra utal, hogy az automata olyan egyforma szerkezetű sejtekből áll, amelyeknek az állapota csakis a (pontosan és egységesen meghatározott) környezetének pontjaitól (szomszédjaitól) függ. A mi algoritmusunkban egy képpont jelent egy sejtet. Ebben az egyszerű esetben a sejteknek csak kétféle állapota van - feketék vagy fehérek, másképpen élők vagy holtak. Ez utóbbi szóhasználat sugallta az egyik ilyen típusú algoritmus Életjáték elnevezését. Itt a halott pont éppen három, az élő pedig két vagy három élő szomszéd esetén lesz élő. Ennek az algoritmusnak (vagy egyszemélyes játéknak) fantasztikus tulajdonsága van - bizonyos kiinduló alakzatokkal el lehet érni, hogy úgy működjön, mint egy számítógép, azaz (meghatározott alakú jelekkel és persze korlátlan nagyságú képernyőn) tetszőleges számítást el tudjon végezni. Az eredményt előre megadott jelek mutatják a gigantikus képernyőn.
Mi azonban olyan algoritmusokra koncentrálunk, amelyek szép minták készítésére alkalmasak. Ha a halott pontot egy élő szomszéd esetén feltámasztjuk, akkor (akár egyetlen kiinduló pont esetén is) a fekete pontok által kiadott minta egyre növekedni fog - persze minden újabb képen legfeljebb egy-egy pont vastagságú szegéllyel. Ha viszont a fekete pontokat nem tartjuk életben akárhány élő szomszéd mellett, akkor bizonyos idő után egyes pontok törlődni is fognak a képernyőről. Az algoritmus sokszori ismétlésével (matematikai nyelven iterációjával) ez a váltakozó törlés-berajzolás rendkívül izgalmas képeket hoz létre a képernyőn. Érdekes, hogy kiinduló alakzatnak elég a képernyő közepén egyetlen pont vagy az üres képernyő köré rajzolt keret.

Ha elnézzük pl. a fenti kép pontokból duplafalú keretből rajzolt mintázatát, érdekes következtetéseket vonhatunk le belőle, vagyis inkább valami misztikus érzésünk támadhat a számokkal, szabályokkal, a természet rendjével kapcsolatban. Kicsit megértjük a szám és a misztika valamikori szoros kapcsolatát. Hiszen ezek a képtelenül komplikált, díszítésekben burjánzóan gazdag minták ennyire egyszerű és egységes szabályok alkalmazásával jöttek létre! Ezek a szabályok éppoly egyszerűek, mint a fizika legáltalánosabb törvényei - és valóban, a kialakult minták bizonyos természeti analógiákat idézhetnek fel bennünk - pl. kristályok, hópelyhek, primitív élőlények képét.
Érdekes tanulsággal szolgálnak ezek a képek a szimmetria természetével kapcsolat-ban is. A tökéletes szimmetriában általában mesterséges beavatkozás jelét látjuk. Itt viszont a természettörvényekre emlékeztetően egyszerű matematikai szabályokkal hoztunk létre olyan mintákat, amelyek hibátlan szimmetriájukkal lepik meg a szemlélőt. Matematikailag ez persze nyilvánvaló. A képernyőn szimmetrikusan elhelyezett pontokból kiindulva, szimmetrikus átalakítási szabályokkal (hiszen a szomszédság figyelembevételénél egyik irányt sem tüntettük ki), nem is kaphattunk volna aszimmetrikus mintát. Mégis megdöbbentő, hogy miközben a minta bonyolulttá válik, szimmetriája mindvégig csorbítatlan marad.
Ha viszont akár csak egy hellyel is odébb választjuk meg a kiinduló pontot, a kez-detben szimmetrikusan fejlődő minta, mihelyt növekedésében eléri a képernyő szélét, aszimmetrikusan kezd viselkedni. Ennek az az oka, hogy a pont aszimmetrikus helyzetéből adódóan a növekvő mintázat nem egyszerre éri el a szemben fekvő oldalakat. Algo-ritmusunk pedig a képernyő szélén rendellenesen viselkedik, de nem is tehet másként, hiszen nem folytathatja korlátlanul a szomszédok vizsgálatát.
A minták matematikai viselkedéséről általában keveset tudunk. Nem is tudhatunk sok mindent, hiszen pl. az Életjáték bonyolultsága egy ideális számítógépével ér fel. Márpedig ismert matematikai tételek bizonyítják, hogy egy ilyen bonyolult rendszerrel kapcsolatban számtalan kérdés eleve nem dönthető el. Például nem mondhatjuk meg, hogy az Életjáték-számítógép valaha befejezi-e a működését, vagy hogy ezt vagy azt az eredményt fogja-e adni, no persze csak a végtelen képernyő esetében. A mi képernyőnkön így módosul az állítás; nem mondhatjuk meg, amíg ki nem próbáltuk az összes lehetőséget. Ezért aztán általában sem mondhatjuk meg, hogy ebben az algoritmusosztályban milyen kiinduló alakzatból mi mindent lehet elérni. Persze konkrét esetben találhatunk bizonyítható összefüggéseket - mint pl. a szimmetriára vonatkozó előbbi gondolatmenetben. Azt azonban tudhatjuk, hogy minden képsorozat, ha vég nélkül folytatjuk, ciklikusan viselkedik. Vagyis előbb-utóbb egy kezdeti kép visszatér. Ez már a lehetséges képernyő-konfigurációk véges számából is következik. A ciklusok hossza persze ennél a gyakorlatban lényegesen rövidebb. Azokat a (fekete vagy fehér pontokból álló) részleteket, amelyeknél a ciklus hossza 1 (azaz kialakulásuk után változatlanok maradnak), stabil alakzatoknak nevezhetjük. Kisebb stabil alakzatokat magunk is konstruálhatunk egyszerűen az átalakításfüggvény definíciójából kiindulva. Ha pl. az élő pontok 0,1, 2, a holtak pedig nem 3 fekete szomszéd esetén lesznek élők a következő menetben, akkor a fekete-fehér váltakozó sávok stabil alakzatot alkotnak. Ha viszont az élő pontok 8 fekete szomszéd hatására meghalnak, a holtak pedig 0 fekete mellett is feltámadnak, akkor nem lesz stabil alakzat, mert a képernyő felváltva lesz teljesen fekete és teljesen fehér - a ciklus hossza tehát 2.
| A szabályos véletlen | "Hulljon le a pel!" (I. Ferenc József) |
Mindeddig nem érdekelt minket, hogyan működik a véletlenszám-generátor. Most azonban figyelmünket a véletlenszám-generátor működésének konkrét mechanizmusára fordítjuk.
Először is jegyezzük meg - ezek csak ún. álvéletlen számok. Ez azonban nem jelent valamiféle csalást, értéktelen, selejtes megoldást. Az az igazság, hogy bár egy számsorozat véletlen voltát pontosan nem tudjuk definiálni, ha bármilyen szabály szerint is hozzuk létre a véletlennek szánt számainkat, egyszerűen meg tudjuk mondani, azok miért nem lehetnek véletlenek. Nevezetesen éppen a szabály miatt. Vagyis mindig meg tudjuk jósolni, mi lesz a sorozat következő eleme (elég csupán a szabályt követnünk). Ami pedig megjósolható, az biztosan nem véletlen, bármi legyen is a véletlen meghatározása. Ezért aztán nem szabad elégedetlenkednünk véletlen (vagy álvéletlen) számalkotó algoritmusunkkal, amely azonban sok esetben nagyon jól utánozza a véletlen viselkedést.
Hogyan állítható elő mármost ez a sorozat? Az elv a következő: vegyünk egy p prímszámot, és egy nála kisebb a számot. Ha a-t hatványozzuk és modulo p vesszük (a p-vel való osztás maradékát tekintjük), akkor egy ciklikus sorozatot kapunk. A ciklus hossza a p-1 osztója, de minden p prímszámhoz van olyan a szám, amelynél a ciklus hossza (úgy mondjuk: az a szám rendje) éppen p-1 (az ilyen a számot pedig primitív gyöknek nevezzük modulo p). A ciklus számai szeszélyesen ugrálnak az 1,2, ., p-1 értékek között, ezért lesznek jók a véletlenszámok előállításához. A véletlenszám-sorozatnál a p = 2^16+1 = 65 537-nek választjuk, és az a szám pl. a 75 lehet. Magát a véletlenszámot úgy kapjuk az a^i-kből, hogy 1-et kivonunk belőlük (így értékük most 0 és 65 535 között változik), és elosztjuk 65 536-tal, ily módon 0 és 1 közé eső számokat kapunk (0 lehetséges érték, de 1 nem).
Ennek a módszernek az ismerete sokszor hasznunkra válik, és persze más p és a számokkal is dolgozhatunk. Az egyik lehetséges felhasználási lehetőség, ha az 1,2, ..., n számoknak egy véletlen permutációját (sorbarendezését) akarjuk előállítani. Keressünk egy n-nél nagyobb, de lehetőleg hozzá közeli p prímszámot, és ahhoz egy a primitív gyököt (vagyis egy olyan számot, amelynek a hatványai moduló p éppen p-1 elemből álló ciklust alkotnak). Ekkor az a^i számok moduló p az 1, 2, ..., p-1 számok egy véletlen permutációját adják, és ezek közül az n-nél nem nagyobbak ugyanígy véletlen módon rendezik sorba az 1,2,...,n számokat. Persze ez a véletlen sorozat minden alkalommal ugyanazokat a számokat sorolja fel, tehát csak akkor használható, ha egyetlenegyszer kell összekavarnunk az első n számot.
"Ez nem véletlen, ez vélet."
(Karinthy Frigyes)
A 3. fejezetben matematikai szabályok alapján rajzoltunk, és bár a véletlenszám-generátor is szóba került, annak is csak a szabályosságával foglalkoztunk. Ebben a fejezetben viszont elfeledkezünk a véletlenszámok szabályos természetéről, és valóban véletlenszerűeknek tekintjük őket. Ezeket a véletlen értékeket írjuk azután az eddigi szabályos paraméterek helyére, és várjuk a sokszor önmagunknak is meglepetést okozó eredményt. Egy ilyen véletlenszámokkal tűzdelt program ugyanis (gyakorlatilag) sohasem működik kétszer egyformán, hiszen az RND függvény csak minden 65 536-ik alkalommal adja ugyanazt az értéket. Aki viszont attól tart, hogy a véletlen szerencsével megrajzolt kép már soha nem ismétlődik meg, a program elejére írt RANDOMIZE utasítással biztosíthatja magát - sőt, RANDOMIZE n alakban az n érték egyszerűen a program által előállítható különböző képek azonosítására is alkalmas lesz.
Ha kiinduláskor csak a szabályos paraméterekkel dolgozó programokba illesztettünk egy-egy véletlenszámhívást, később megtanulhatunk a véletlennel saját jogán bánni, olyan programokban, amelyek már eleve a véletlen kiaknázására szolgálnak. A véletlen paraméterek természetét kiismerve elérhetjük, hogy azok elképzeléseinknek megfelelően működjenek, megadott valószínűséggel állítsanak elő valamilyen motívumot, tereljék vissza a képernyő szélén tilosba tévedő vonalakat, vagy - az 5. fejezetben leírt módon - a fény-árnyék megoszlásnak megfelelően rajzoljanak világos és sötét pontokat. Amikor már az unalomig kiismertük a véletlen programok természetét, nem árt felvetni a kérdést, vajon nem tudnánk-e értelmes módon ismét szabályos paramétereket használni.
A véletlen felhasználásának egyik legkézenfekvőbb lehetősége, ha a különböző vonalrajzoló programsémákba helyettesítünk véletlen paramétereket. Ahhoz, hogy ezeket a vonalakat alkalmazni tudjuk számítógéppel készített képekben, foglalkoznunk kell azzal a problémával is, hogyan lehet őket a képernyő keretei között tartani, ill. mikor kell leállítani egy-egy vonal rajzolását.
Véletlen cikázás
Az alábbi kép a legegyszerűbb véletlen vonalat mutatja be, amely az ugráló vonalrajzolás sémájával programozható. Egymás után véletlenszerűen választott pontokat kötünk össze egyenes szakaszokkal.
Véletlen cikázás
Ha a képernyő felbontása m x n, akkor egy-egy pont koordinátáit az
(INT (RND*m), INT (RND*n))
kifejezéssel adhatjuk meg. Nem túlságosan sok pont összekötésével kapott képen érdemes az utolsó vonallal visszatérni a legelső ponthoz - így nem lesznek a képen szabadon lógó vonalvégek.
10 RANDOMIZE
20 LET u=INT (RND*256): LET v=INT (RND*176)
30 LET x1=u: LET y1=v
35 PLOT u,v
40 FOR i=1 TO 25
50 LET x=INT (RND*256): LET y=INT (RND*176)
60 DRAW x-u,y-v
70 LET u=x: LET v=y
80 NEXT i
90 DRAW x1-u,y1-v
Légy- és szúnyogmozgás
A véletlen vonalak népes családja származtatható a következő eljárásból. Olyan szakaszokat rajzolunk egymás után (és egymáshoz csatlakoztatva), amelyeknek az irányát mindig egy 0 és 2*PI között véletlenszerűen választott szög határozza meg. (Ilyen vonalakkal modellezhetjük egy folyadékrészecske ún. Brown-mozgását, amit a véletlenszerű irányból és sebességgel érkező többi részecskével való ütközése határoz meg.) Ennek a vonaltípusnak az egyik fajtáját azzal a további megkötéssel definiáljuk, hogy minden szakasz azonos hosszúságú. A következő képen látható vonal egy légy repülésére emlékeztet, ezért légymozgásnak is nevezhetjük.

Légymozgás
Ha ezt a megkötést elengedjük, és az egyes szakaszok hosszát is véletlenszerűen választjuk (persze adott határok között), akkor egy kicsit más jellegű vonalat kapunk. Ez a vonal megkülönböztetésképpen a szúnyogmozgás nevet kaphatja, mert a különböző irányú és hosszúságú szakaszok a szúnyog idegesítően szeszélyes, cikázó röptét idézik fel.
Mindkét fajta vonal előbb-utóbb elkerülhetetlenül le fog tévedni a képernyőről. Ez egyben természetes módon véget vet a vonal rajzolásának.
Mindkét vonaltípus (akárcsak az ezután következők) a bolyongó vonalrajzolás sémájával valósítható meg.
Madármozgás
Eddigi vonalaink csupa cikcakkból álltak. Aki pusztán ezek alapján ítél, azt hiheti, hogy a véletlen vonalak eleve nem is állhatnak olyan sima, lekerített ívekből, mint amilyet a szabályos görbék között láttunk. Ez azonban tévedés. A következő kép egy olyan tehetetlenséggel mozgó súlyos repülő test (talán egy nagyobb madár) útját ábrázolja, amely nem ötletszerűen, pillanatról pillanatra, hanem szép fokozatosan változtatja sebessége nagyságát és irányát.
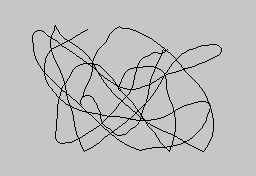
Madárröpte
Ilyen vonalat a bolyongó vonalrajzolás algoritmusával rajzolhatunk. A szomszédos pontokat összekötő (a,b) vektor tartalmazza a madár pillanatnyi sebességét, amit a madár pillanatnyi helyét megadó (x,y) vektorhoz minden újabb szakasz berajzolása után hozzáadunk. A sebességvektor koordinátáit minden lépésben kevéssel (mondjuk legfeljebb 1-gyel) változtatjuk meg, és ezáltal érjük el, hogy a madár harmonikus, lekerekített pályán repüljön, miközben a mozgás véletlenszerű jellege is szembeötlő.
A rajzolást elindítva most is előbb-utóbb azt tapasztaljuk, hogy a vonal a képernyő szélének ütközik. Hogyan lehetne ezt megakadályozni? Valahogy úgy kellene a sebesség vektort változtatni, hogy - a véletlenszerűséget megőrizve - a képernyő széleihez közeledve az irány mégis egyre inkább visszafelé, a belső területek felé mutasson. Eddig a se-bességvektor koordinátáit egyforma valószínűséggel növeltük, vagy csökkentettük 1-gyel. Most viszont megtehetjük, hogy a sebességvektor növelése vagy csökkentése a helyvektor vízszintes, ill. függőleges komponensével arányos valószínűséggel történjék. Vagyis a képernyő jobb oldali, ill. felső széléhez közeledve egyre nagyobb valószínűséggel -1-et, az alsó, ill. a bal oldali szélen +1-et adjunk a-hoz, ill. b-hez. A
LET a = a + SGN (RND*m- x), ill. LET b = b + SGN (RND*n- y)
utasítások pontosan ezt a hatást érik el.
Ezzel a módosítással a madár tovább fog repülni, mint eddig, de most sem lesz örökéletű. Ugyanis a szélekhez közeledve sebessége csak nagy valószínűséggel, de nem teljes bizonyossággal fordul a helyes irányba. Elképzelhető (sőt, előbb-utóbb biztos), hogy egyszer a kis valószínűségű szerencsétlen eset teljesül, és a madár a képernyő széléhez közeledve még jobban rákapcsol, és vesztére kirepül a képből. Ennek elkerülésére egy részt a sebességvektor mindkét komponensét egy rögzített korlát alatt kell tartanunk, másrészt, ha valamikor a gyorsítás már végzetes lenne a madár számára, kényszerítjük, hogy fékezzen le. Ha a megengedett maximális repülési sebesség d, (és a madár egy adott pillanatban valóban d sebességgel halad), akkor még fékezéssel együtt is legalább d + (d-1) + ... + 1 = d*(d+1)/2 távolságot tesz meg, mielőtt vissza tudna fordulni, így tehát a szélektől már d*(d+1)/2 távolságban már mindenképpen fékezni kell sőt, ha ettől még kevesebb, mint d távolsággal beljebb tartunk és gyorsítunk, szintén bajba kerülünk. Ily módon tehát csak a képernyő belső, m - d*(d+3), n - d*(d+3) nagyságú téglalapján választhatunk szabadon a gyorsítás és lassítás között. Az (a,b) sebességvektor új értékét meghatározó utasítások tehát a következők lehetnek:
LET a=a + SGN (RND*(m-h) + h/2 - x)
IF ABS a>d THEN LET a=d*SGN a
LET b=b + SGN (RND*(n-h) + h/2 - y)
IF ABS b>d THEN LET b=d*SGN b
(ahol h értékét már korábban beállítottuk d*(d+3)-ra).
Elvileg meg is engedhetnénk, hogy a megrajzolt vonal időnként lefusson a képernyőről, hiszen a 2. fejezetben megismert módszerekkel megoldhatjuk, hogy ilyenkor se álljon le a program. Elvégre később még visszatérhet a képernyőre, és elölről kezdhetjük a rajzolást, mintha mi sem történt volna. A véletlen programok esetében azonban nem ez a járható út, ugyanis a képernyőről letérő vonal nagy valószínűséggel előbb-utóbb reménytelenül eltávolodik, fölösleges volna tehát visszavárnunk.
Amelyik programnál viszont kivédtük azt az eshetőséget, hogy a vonal tilosba téved, külön kell gondoskodnunk a rajzolás leállításáról. Az egyik kínálkozó lehetőség ilyenkor az interaktív beavatkozás: egy billentyű lenyomásával jelezzük a programnak, hogy a vonal rajzolása befejeződött.
Miután amúgy is zavaró, ha egy véletlen vonal valamelyik vége a képernyő közepén látható, szerencsés megoldásnak ígérkezik, ha a vonalrajzolást olyankor állítjuk le, amikor éppen beleütközik egy korábbi pontba. (Ilyenkor a már említett módszer szerint a kezdőpontból újra elindítva a vonalat - ellentétes kezdősebességgel - elérhetjük, hogy mindkét vége le legyen zárva.) Ennek megvalósítására a saját egyenesrajzoló algoritmusunk a legalkalmasabb, amelyet kiegészítünk az éppen berajzolandó pont előzetes vizsgálatával.
Egy vonal azonban úgy is keresztezheti önmagát, hogy közben egyetlen berajzolt pontot sem érint (lásd ábra).

Ezért az előző módszert úgy javíthatjuk, hogy számoljuk a (regisztrált) metszéseket és a rajzolást akkor fejezzük be, amikor a számláló már elért egy megadott értéket. Ebben az esetben viszont már nem kell ragaszkodnunk a saját egyenesrajzoló rutinunkhoz sem, használhatjuk a (gyorsabb) DRAW utasítást is, a rajzolást addig folytatva, amíg valamelyik szakasz végpontja nem esik egy korábban berajzolt pontra.
Pillangómozgás
Visszatérve a véletlen vonalakhoz, most egy olyan algoritmust ismertetünk, amely a légymozgásból kiindulva rajzol lekerekített vonalat. Ott egymáshoz csatlakozó, azonos hosszúságú szakaszokat rajzoltunk, a szögeket 0 és 2*PI között véletlenszerűen választottunk. Most ezt az eljárást úgy módosítjuk, hogy két szomszédos szakasz szöge mindig ugyanannyival térjen el egymástól. Az eltérés szögét rögzített k-ra 2*PI/k alakban adjuk meg. A vonal véletlenszerűségét most az határozza meg, hogy az eltérés szögét egyforma valószínűséggel egyszer hozzáadjuk az előző szakasz szögéhez, egyszer levonjuk belőle. Ha k-t legalább 12-nek választjuk, az így keletkező vonal mintha csupa egyforma középponti szögű körívből tevődne össze. A véletlenszerű előjelű eltérések következtében az ilyen vonal egy ide-oda libbenő pillangó repülésére emlékeztet, ezért a továbbiakban pillangómozgás néven hivatkozunk rá.
A vonal letévedését most a következő gondolatmenet alapján akadályozhatjuk meg. Ha a szakaszok hosszát d-ben rögzítjük, próbáljuk meghatározni, hogy (a szögeltérések előjelét nem változtatva) a pillangó minimálisan mekkora sugarú szögben tud körbefordulni. Mivel a teljes 2*PI szöget k lépésben teszi meg, a kör kerülete durván k*d, innen pedig a sugara (közelítőleg) k*d/(2*PI). Amikor a pillangó a képernyő széléhez ennél közelebb kerül, tiltsuk meg az eltérésszög előjelének véletlenszerű változtatását - ezáltal ilyen sugarú körívben (tehát mindig a képernyőn maradva) visszatér a biztonságos területre. Az (a,b) sebességvektor ily módon a következő utasításokkal számítható ki:
IF x>r AND x<m-r AND y>r AND y<m-r THEN LET j=SGN (RND -.5)
LET i=i+j
LET a=d*COS (2*PI*i/k): LET b=d*SIN (2*PI*i/k)
(ahol r = k*d/(2* PI).
A képen ezzel az algoritmussal készült pillangómozgást látunk - a kép szélein megfigyelhetők a visszatérést biztosító hosszabb körívek.
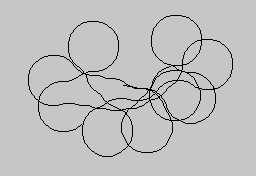
Pillangómozgás
4.2. Képek véletlen vonalakból
Ebben a részben az eddigi véletlen vonalakból kiindulva próbálunk grafikákat vagy egyszerűen csak összetettebb motívumokat készíteni.
Majomrajz
A következő kép ötletéből később további vonaltípusokat tudunk majd kikísérletezni. Az ötlet maga rendkívül egyszerű: a madárvonalat alkotó szakaszok végpontjában mindig megrajzolunk egy olyan szakaszt is, amely az adott vonaldarabra merőleges, és hossza egy rögzített szám. Az így kialakuló "szőrös" vonal majmok rajzaira emlékeztet.
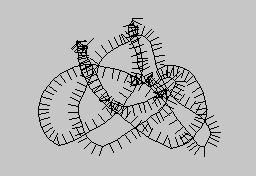
Majomrajz
A továbbfejlesztés több irányban kínálkozik. Az egyik kézenfekvő ötlet szerint pl. megpróbálkozhatnánk azzal, hogy ne csak a szakaszok végpontjaiba, hanem minden egyes pontba szőröket rajzoljunk - azt remélve, hogy ily módon véletlen vonalból véletlenszerűen kígyózó csövet tudunk készíteni. Ez a remény azonban nem válik be, mert ahol az eredeti vonal a cső belső ívét alkotná, ott a rá merőleges szőrök legyezőszerűen szétválnak, eloszlatva a csőszerűség illúzióját. A csőrajzoláshoz tehát más ötletre lesz szükség.
Véletlen ecsetvonás
Viszont az előbbi vonalnak egy egyszerűbb és mégis érdekesebb változatát készíthetjük el azáltal, hogy a minden pontban megrajzolt szőröket most nem a vonalra merőlegesen, hanem egységesen vízszintesen rajzoljuk meg. A szőrök hosszát azonban (szomszédos pontokban legfeljebb 1 eltéréssel) véletlenszerűen változtatjuk. E vonalfajta vastag ecset nyomára emlékeztet, amelyet rajzolás közben vízszintesen tartunk. E vonalfajta (ld. kép) vastag ecset nyomára emlékeztet, amelyet rajzolás közben vízszintesen tartunk.
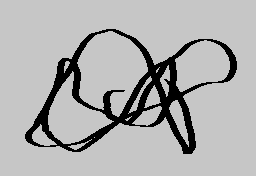
Véletlen ecsetvonás
Véletlen cső
A csőalgoritmus megvalósításához ismét a pillangómozgáshoz kell visszanyúlnunk, amelynél mindig adott hosszúságú szakaszokat fűztünk össze, egymáshoz képest adott szöggel jobbra vagy balra elforgatva. Illesszünk most a következő ábrához hasonlóan - az egyes szakaszok alá és fölé olyan egyenlőszárú háromszögeket, amelyeknek a csúcsában fekvő szöge éppen az adott elforgatási szöggel egyezik meg.
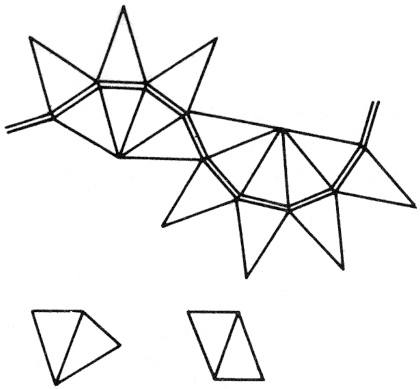
Azt tapasztaljuk, hogy minden szakasz valamelyik háromszöge egyik szárával érintkezik a szomszédos szakasz háromszögével - jobbra forduló szakasznál alul, balra fordulónál fölül. Ezek a háromszögek sugallják azt az ötletet, hogy ugyanilyen egyenlőszárú háromszögeket illesszünk össze, mindig a szárak mentén, de véletlenszerű választással egyszer úgy, hogy a csúcsok is összeérnek, máskor pedig éppen fordítva. Ebből az algoritmusból, némi meglepetésre, egy véletlenszerűen kanyargó cső rajzát kapjuk. Ennek a csőnek csak az az apró hibája, hogy egyes pontokban (ahol túl sok azonos állású háromszög csúcsa találkozik össze), kicsit megtörik. Ezen viszont könnyen segíthetünk, ha egyenlőszárú háromszögek helyett egyenlőszárú trapézokat veszünk.
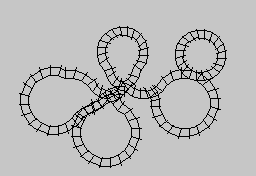
Véletlen cső
Labirintusok
Véletlen labirintusokat szeretnénk rajzolni a képernyőre. Erre nyilvánvalóan számtalan módszer képzelhető el - hogy ezeket valamennyire egységesíteni tudjuk, próbáljuk meg tisztázni, milyen feltételeket támasszuk a megrajzolandó labirintusokkal szemben:

A 2. feltétel szerint mondjuk a páratlan sorszámú sorokat és oszlopokat falnak választva a mindkét koordinátában páratlan négyzeteket feketére, a tiszta páros koordinátájúakat pedig szükségképpen fehérre színezzük. Választási lehetőség csak a vegyes koordinátájú négyzeteknél adódik (amelyeket a ábrán kérdőjellel jelöltünk). Minden labirintusrajzoló algoritmusnak tehát ezekről a kétséges négyzetekről kell rendelkeznie.
Az első lehetőség, hogy minden ilyen négyzetet véletlenszerűen választunk feketének és fehérnek. Ezt a labirintustípust olyan 2x2 kockából álló panelekből építhetjük fel, amelyeknek a bal felső sarka mindig fekete, a jobb alsó mindig fehér, a másik kettő pedig minden kombinációban előfordul. Tehát a 2x2 kombinációnak megfelelően összesen négy panelre lesz szükségünk, ezek közül mindig véletlenszerűen választunk egyet. A következő képen ilyen paneles labirintust látunk - a négy panelt most négy megfelelő grafikus karakterrel valósítottuk meg (de választhattunk volna 2X2 karakterből - fekete és fehér kockákból álló paneleket is).

Labirintus panelekből
Ez a rendkívül egyszerűen programozható labirintustípus, bár minden kétséget kizáróan megfelel a követelményeinknek, nem lesz teljesen kielégítő. Ugyanis olyan területeket is találunk benne, amelyeket mindenfelől fal vesz körül, senki nem tud se oda bejutni, se onnan kiszabadulni, esetleg a labirintus nem is átjárható. Megtehetnénk, hogy azokat a paneleket nagyobb valószínűséggel választjuk, amelyekben legfeljebb két kocka fekete - ezáltal gyakorlatilag kizárható az ilyen zárt részlabirintusok előfordulása. Ilyenkor viszont nagyon sok lesz az olyan fal, ami csak egy rövid szakaszon egybefüggő, a labirintus tehát túlságosan is átjárható lesz.
Ezeknek a hiányosságoknak az orvoslására vegyünk fel egy további megszorító feltételt az elfogadható labirintuskonstrukciókra:
Az egyértelmű összeköttetést két pont között persze csak úgy érthetjük, hogy az út egyetlen ponton se halad át kétszer. Nyilvánvalónak tűnik, hogy ez a követelmény globális, a labirintus egészére vonatkozik, tehát az előbbihez hasonló módszerekkel nem érhetünk célhoz, másmilyen ötletre van szükség.
A következő kép labirintusa a síkfelosztáshoz hasonló módszerrel készült.

Labirintus leválasztással
Az algoritmus egy-egy lépésben kiválaszt egy még osztatlan téglalapot és azt majdnem kettéosztja (azaz két szembenlevő fala között olyan falat épít, amely az egyiktől egy híján a másikig vezet). Eközben persze ügyelni kell arra, hogy korábbi kikötéseinkhez tartsuk magunkat, így tehát mindig csak páratlan sorszámú sorban vagy oszlopban építhetünk falakat. A majdnem-kettéosztás miatt a téglalap egyik feléből továbbra is át lehet jutni a másikba, de csakis a fal hézagán keresztül. Ha most ezt az eljárást mindaddig folytatjuk, amíg még egyáltalán van felosztható téglalap, akkor biztos, hogy a 3. feltételnek is megfelelő labirintust kapunk.
Ez az algoritmus természetesen a határidőnapló sémájával programozható, akárcsak a síkfelosztás, amiből kiindultunk.
A határidőnapló-sémával programozható a következő algoritmus is (amelyet rekurzív labirintus algoritmusnak nevezhetnénk). A naplóban most a fa (vagy labirintus) ágainak a pontjait jegyezzük fel. Egy-egy lépésben véletlenszerűen kiválasztunk egy pontot. Megvizsgáljuk, a négy lehetséges irány közül valamelyikben még továbbléphetünk-e belőle. Ha nem, töröljük a naplóból - egyébként pedig az egyik lehetséges irányba valóban továbbnövesztjük az ágat (több szabad irány közül természetesen véletlenszerűen választunk). Ilyenkor az új pont koordinátáit is felvesszük a naplóba. Előbb-utóbb elfogynak a folytatható ágak, és ekkor a labirintusrajzolás be is fejeződött. Ezzel a módszerrel készítettük tehát a képen látható labirintust.

Rekurzív labirintus
"Az, aki most Goljadkin úrral szemben ült,
Goljadkin úr része, Goljadkin úr szégyene,
Goljadkin tegnapi lidérce, egy szó, mint száz,
maga Goljadkin úr volt."
(F. M. Dosztojevszkij)
A szimmetria - csábító kutatási terület. Sokféle szempontból próbálhatjuk megközelíteni. Egyrészt tudjuk, hogy jelentősége alapvető a képzőművészetekben. Térben és időben távoleső kultúrák művészetében megfigyelhetjük, vizsgálhatjuk érzékelés-lélektani, esztétikai szempontból, alapvető fizikai, biológiai, természetfilozófiai kérdéseket vet fel, és végül mélyreható matematikai elemzések tárgya lehet. Számítógépes grafikai kísérletezésünk során természetesen a matematikai megközelítésnek vehetjük a legtöbb hasznát, de igyekszünk - legalább időnként - rámutatni a szimmetria másfajta vonatkozásaira.
A szimmetria is egyike azoknak a fogalmaknak, amelyeket szinte mindenki ismer, de senki nem tudna közelebbről meghatározni. Próbáljuk most mégis összeszedni, mit is értünk szimmetria alatt. A legelső jelentés, ami eszünkbe jut, valószínűleg a kétoldali szimmetria, a jobb-bal tükrösség, amivel a leggyakrabban találkozunk az élővilágban, az élettelen természetben, az építészetben és más képzőművészetekben, sőt bizonyos értelemben még a zenében is. A fizikusok régóta keresnek választ arra a kérdésre, hogy vajon a természetben van-e kitüntetett szerepe a jobb vagy bal (forgási) iránynak, vagy minden fizikai törvény érvényben marad a jobb és bal szerepének felcserélésével is. Nem tudjuk tehát, hogy a természet szimmetrikus-e ebben az egyszerű értelemben. A kérdést egyelőre nem sikerült véglegesen eldönteni.
A kétoldali tükrösség mellett gondolhatunk még a középpontosan tükrös, vagy forgásszimmetria példáira is, noha itt már kevésbé határozottan mondanánk, hogy szimmetriáról van szó. Pedig ezekből a példákból kiindulva juthatunk el egy szabatos matematikai meghatározáshoz is, amelyet azután még többé-kevésbé természetes módon meg is próbálhatunk kiterjeszteni. De még ezelőtt kíséreljük meg megfogalmazni, hogy mi a közös mozzanat a szimmetria eddigi példáiban. Némi nagyvonalúsággal azt mondhatjuk, a szabályos ismétlődés. Noha ez még nem elég a szimmetria fogalmának megértéséhez, mégis levonhatunk belőle néhány következtetést.
A szabályos ismétlődés részben már képes megmagyarázni a szimmetria érzékelés-lélektani vagy esztétikai jelentőségét. Ha egy mintában felismerjük, hogy egy kisebb részlet valamilyen szabály szerint ismétlődik benne, akkor ez nagy könnyebbséget jelent a minta megtanulásában, későbbi felismerésében. Ezáltal jelentős mértékben csökken ugyanis a mintában rejlő információmennyiség, amit meg kell jegyeznünk (más szóval: a minta fölös, redundáns információt tartalmaz). Elég megjegyeznünk most már az ismétlődő részletet és az ismétlés szabályát. Gondoljunk arra, milyen nehezen tudunk megtanulni, de akár csak pontosan megfigyelni is egy olyan mintát, amiben semmilyen szabályosság nincs. Az ismétlődés arra is lehetőséget nyújt, hogy ellenőrizzük, valóban jól ismertük-e fel a mintát, amikor először ránéztünk. Ez a bizonyosság pedig örömmel, megnyugvással tölti el a szemlélőt, talán ezért érezzük olyan harmonikusnak, megnyugtatónak a szimmetrikus formákat. No persze a természeti analógiák miatt is. Erre utal talán az is, hogy a tökéletes, maradéktalan szimmetriánál még egy kicsit élőbbnek, izgalmasabbnak érezzük az olyan formákat, mintákat, amelyekben az alapvető szimmetriát némi apró szabálytalanság, aszimmetria fűszerezi. Ha a szimmetriát szabályos ismétlésként fogjuk fel, akkor az is rögtön nyilvánvaló, hogy a számítógép itt sokban a segítségünkre lehet.
"Az emberiség két nagy csoportra osztható.
Egyik fele a tükör előtt azt mondja képmására, hogy "én",
a másik azt mondja, hogy "te".
Jómagam már gyerekkoromban külön csoportot alkottam: "ő"-nek neveztem tükörképemet."
(Eörsi István)
Miután ilyen bizonytalan kiindulópontból ilyen messzemenő következtetéseket vontunk le, próbálkozzunk meg a szabatos matematikai definícióval. Ehhez néhány alapvető fogalomra lesz szükségünk. Az első az egybevágósági transzformáció fogalma. Ez olyan térbeli mozgatás, amelynek során a testek nem változtatják meg méreteiket (és következésképpen változatlanok maradnak szögeik, arányaik, kölcsönös térbeli helyzetük stb.). Erre utal az egybevágóság szó. Ezek a mozgatások visszafordíthatok, mindegyiknek létezik egy inverze, amelyet közvetlenül utána végrehajtva visszaáll az eredeti helyzet. így pl. egybevágósági transzformáció az eltolás, tükrözés, elforgatás, (de a nagyítás már nem, hiszen az megváltoztatja a méreteket). A nagyítás az egybevágósági transzformációkkal együtt a hasonlósági transzformációk tágabb csoportjához tartozik. Két transzformáció kompozíciója (egymás utáni végrehajtása) is transzformáció, akárcsak az inverze. Egybevágóságok kompozíciója mindig egybevágóság, hasonlóságoké hasonlóság marad.
Következő alapfogalmunk az invariancia. Egy alakzat invariáns egy transzformációra nézve, ha (sem az alakja, sem a térbeli helyzete) nem változik meg általa. Például egy egyenes invariánsa vele párhuzamos irányú eltolásra, egy gömb a középpontja körüli elforgatásokra, egy négyzet az átlójára vonatkozó tükrözésre nézve. Ezek után szimmetrikusnak nevezhetünk egy formát, ha invariáns valamilyen egybevágósági transzformációra nézve (és az adott forma szimmetriájának mondjuk ezt a transzformációt). Így tehát egy test annyiféleképpen lehet szimmetrikus, ahányféle egybevágósági transzformáció létezik (persze egy fajtából is lehet több különböző szimmetriája). Beszélhetünk eltolási, forgási, tükrös szimmetriáról, ill. ezek kombinációiról. Az egész tér minden egybevágósági transzformációra nézve invariáns, tehát tökéletesen szimmetrikus. A legtöbb élőlény testében felfedezhetünk valamilyen szimmetriát - a növényeknél és az alacsonyabb rendű állatoknál gyakran forgás-, vagy középpontos tükörszimmetriát, a magasabb rendű állatoknál többnyire a jólismert kétoldali tükörszimmetriát.
Szimmetriák kompozíciója is szimmetria, pl., ha egy test invariáns a 30 fokos elforgatásra nézve, akkor ennek ismételt kompozícióira, azaz a 60 fokos, 90 fokos, ... , 330 fokos elforgatásra is biztosan szimmetrikus lesz. Néhány jól megválasztott transzformációból kompozíciókkal általában megkaphatjuk egy test (alakzat, minta) összes szimmetriáját.
Másfelől (az említett redundanciaelv alapján) mindig kiválaszthatjuk a szimmetrikus mintának egy olyan részletét, amelyet az alaptranszformációk mindig teljes egészében egy másik részbe visznek át, és amely maximális, azaz tovább nem bővíthető. Ez a részlet, és a megadott alaptranszformációk most már teljesen meghatározzák a mintát. Pontosan ez szolgáltatja az alapját annak a módszernek, amellyel szimmetrikus alakzatokat fogunk előállítani a számítógép képernyőjén. Először is kiválasztjuk a szimmetriákat (azokat az egybevágósági transzformációkat, amelyekre nézve invariáns alakzatot szeretnénk kapni). Ezután meghatározzuk, hogy milyen részen választhatjuk meg a mintát teljesen szabadon, anélkül, hogy a kívánt szimmetriatulajdonságokkal összeütközésbe kerülnénk. Ebből kiindulva a transzformációk segítségével már az összes többi részletet meg tudjuk rajzolni, mégpedig egyértelműen.
Nézzük meg tehát, hogy hogyan fest mindez a gyakorlatban: vegyük sorra az egybevágósági transzformációkat, először külön-külön, azután kombinálva, és készítsünk hozzájuk szimmetrikus alakzatokat!
Kétoldali szimmetria
A szimmetriának a legegyszerűbb válfajánál lesz a legkönnyebb dolgunk. A képernyőn kiválasztunk egy szimmetriatengelyt (legyen ez a függőleges felezőtengely, hogy jobb-bal szimmetriához jussunk). Ekkor a tengely egyik oldalán (mondjuk a képernyő jobb felén) teljesen szabadon választjuk meg a mintát, és azt ezután egyszerű tükrözéssel átmásoljuk a bal oldalra. Az átmásolást persze végezhetjük pontonként, vagy képelemekként, így még arra sincs szükség, hogy megjegyezzük, hova mit rajzoltunk. Egyszerűen minden
PLOT m/2+x,y vagy DRAW u,v
utasítás után végrehajtjuk a megfelelő tükörutasítást:
PLOT m/2-x,y ill. DRAW -u,v
A képernyő felének megrajzolásában persze gyakorlatilag ugyanakkora szabadságunk van, mintha az egész képre rajzolnánk - ezért általában a kétoldali szimmetriával rendelkező mintákról, formákról még nem mondhatunk túl sokat. Korlátozzuk figyelmünket most a függvénygörbékkel, görbeseregekkel előállítható kétoldali szimmetrikus mintákra!
Vannak olyan függvények, amelyeknek a grafikonja már magában is kétoldali szimmetriát mutat az y tengelyre mint szimmetriatengelyre. Ez a feltétel pontosan akkor teljesül, ha az origótól jobbra és balra azonos távolságra eső helyeken a függvényértékek megegyeznek, vagyis minden x-re
f(-x) = f(x)
teljesül. Az ilyen függvényeket páros függvényeknek nevezzük - talán azért, mert minden páros k számra az f(x) = x^k hatványfüggvény is ilyen lesz. Páratlan függvények az olyan függvények, amelyeknél minden x-re
f(-x) = -f(x)
ezek az origóra nézve középpontosan szimmetrikusak. Az említett hatványfüggvényeken kívül páros függvény még pl. a COS(x), és páratlan a SIN (x) függvény is. Az (f(t),g(t)) alakú paraméteres görbéknél, ha a t paraméter egy (-a,a) intervallumon fut végig, akkor nyilvánvalóan kétoldali szimmetriával rendelkező görbét kapunk, ha f és g közül az egyik páros függvény, a másik páratlan. Ha mindkettő páratlan, akkor viszont középpontosan szimmetrikus lesz a görbénk. Természetesen, ha olyan görbesereget veszünk, ahol az f(t) és g(t) függvény minden görbénél azonos típusú, (mondjuk f mindig páros, és g mindig páratlan), akkor az egész görbesereg olyan szimmetriatulajdonsággal fog rendelkezni, mint az egyes görbék.
Forgásszimmetria
A forgásszimmetrikus alakzatban mindig egy körcikk alakú részt választhatunk meg szabadon, és ennek elforgatásával kapjuk meg a teljes alakzatot. (Persze a körcikket sem kötelező teljes egészében kitölteni.)
Az alábbi képen, a szabadon megválasztható részletet véletlenszerűen töltöttük be, és ebből ismételt elforgatásokkal alakítottuk ki a szimmetrikus mintát.

A forgatást a középponton kívül egy f elforgatási szöggel tudjuk jellemezni, ennek értékét ajánlatos úgy választani, hogy a 2*PI (azaz 360 fok) osztója legyen (később majd látni fogjuk, miért). Ha f = 2*PI/n, akkor a kezdő körcikk minden egyes (választott) pontjának n db elforgatott pont fog megfelelni. Az (x,y) pont f szöggel elforgatott képe
(x*COS f - y*SIN f, x*SIN f + y*COS f)
lesz (ahogy a 2. fejezetben láttuk). Ezt a pontot ismételten f szöggel elforgatva, megkapjuk mind az n elforgatott pontot. Pontosan ugyanígy kell kiszámítani az elforgatott szakaszok (pontosabban a megfelelő DRAW utasítások) koordinátáit is a kiinduló értékekből.
A program:
10 FOR i=1 TO 600
20 LET y=RND*52: LET x=RND*y+10
30 FOR f=0 TO 2*PI STEP PI/6
40 LET cosf=COS f: LET sinf=SIN f
50 PLOT 128+x*cosf-y*sinf,96+x*sinf+y*cosf
60 NEXT f
70 NEXT i
Ha egy alakzat f szög szerint forgásszimmetrikus, akkor forgásszimmetrikus lesz minden k*f szöggel is (ahol k egész szám). Most derül ki, miért választottuk f-et 2*PI/n alakúnak. Egy 360°-nál nagyobb szöggel való elforgatás ugyanis pontosan megegyezik a nála 360 fokkal kisebb szögű elforgatással (hiszen már a szögek is egybeesnek). Ily módon, ha az eredeti f elforgatási szög nem osztója a 360 foknak, akkor valamelyik többszöröse már 360 foknál nagyobb lesz, de magánál f-nél kisebb. Jelöljük ezt a kisebb szöget f1-gyel. Ha egy alakzat szimmetrikus az f szögű elforgatásra, akkor az f1 szögűre is. Most f1-re ugyanúgy megkérdezhetjük: osztja-e a 360 fokot. Ha nem, újabb f2 forgásszimmetriát kapunk, amely most még f1-nél is kisebb szöggel adható meg. Ha az f és a 360 fok aránya irracionális, ez az eljárás az f szögű elforgatásból kiindulva végtelen sok forgásszimmetriát tud kimutatni. Persze a számítógépnél nincs igazán értelme irracionális számról beszélni - hiszen minden számot csak véges sok jeggyel tudunk megőrizni. Viszont nincs is szükség végtelen sok forgásszimmetriára sem ahhoz, hogy az egész képernyő fekete legyen! Próbáljunk meg a középpontból kiinduló egyetlen sugarat vagy ívet elég kis szögekkel elforgatni, hogy képet kapunk erről a jelenségről! Ha a kör teljes betöltéséhez a sugár hosszától függően a teljes szög néhány ezredrésze kell is, már néhány század körüli értékeknél is azt tapasztaljuk, hogy majdnem az egész körlap befeketítődik, és egy érdekes másodlagos minta alakul ki. Ez a minta ugyan szintén forgásszimmetrikus, de semmi köze nincs az eredeti elforgatási szöghöz, sokkal inkább a -90 fokos elforgatáshoz, a képernyő derékszögű rácsszerkezete miatt.
A forgásszimmetria speciális esete a középpontos tükörszimmetria (ami voltaképpen 180 fokos forgásszimmetriát jelent) és a 90 fokos forgásszimmetria. Az ilyen szimmetriával rendelkező formákat nem is érezzük forgásszimmetrikusaknak (bár szimmetrikusnak igen), mert nem találunk rajtuk kerek formákat, és amikor felfedezzük az egymásnak megfelelő pontokat, úgy érezzük, ezek nem elforgatással hozhatók fedésbe. Amint a 2. fejezetben láttuk, ezeknek a forgatásoknak a kiszámítása is egyszerűbb, mint általában: középpontnak az origót véve az (x,y) pont képe a 180 fokos elforgatásnál (-x, -y) lesz, a 90 fokos elforgatásnál pedig (-y,x) - nem kell tehát a COS és SIN függvényeket használnunk.
6.4. Belső szimmetria
Ebben a részben meglehetősen önkényesen próbáljuk általánosítani a szimmetria fogalmát. A definíciónkat természetesen nem szükséges elfogadnia annak, aki az itt szóba kerülő módszereket alkalmazni szeretné.
Abból indultunk ki, hogy a szimmetria az eddigi értelemben bizonyos minták külső tulajdonsága, amennyiben egyes részleteinek egymáshoz való viszonyával írható le. Most viszont egy alakzatnak önmaga részleteihez való (belső) viszonyára szeretnénk a szimmetria fogalmát kiterjeszteni.
Vegyünk egy szakaszokból álló nem zárt görbét (tehát töröttvonalat), és jelöljük meg egyes szakaszait, mint helyettesítendő, a többit pedig, mint összekötő szakaszokat. A helyettesítendő szakaszokkal pedig a következőképpen járjunk el: helyettesítsük őket az egész görbének egy olyan szögben elforgatott példányával, hogy a töröttvonal két végpontját összekötő szakasz az eredeti helyettesítendő szakasszal egyirányú legyen. A kez-deti töröttvonal összes helyettesítendő szakaszát helyettesítsük ily módon. Most persze újabb helyettesítendő szakaszok jelennek meg - a helyettesítendő szakaszok második generációja. A következő menetben ezeket helyettesítjük az eredeti töröttvonal alkalmasan elforgatott példányaival, a helyettesítendő szakaszok harmadik generációját hozva létre ezáltal stb.
Önhasonló görbék
Ha ezt az eljárást végtelen sokáig folytatnánk, miközben a kapott görbéket mindig úgy kicsinyítjük, hogy átmérőjük változatlan maradjon, akkor végül olyan görbéhez jutnánk, amely hasonló önmagának bizonyos részleteihez (éppen azokhoz, amelyek az eredeti töröttvonalban a helyettesítendő szakaszok helyén keletkeztek). Az ilyen görbéket önhasonlónak nevezhetjük. A következő képeken a sokak által ismert Koch-és Sierpinski-féle görbéket mutatjuk be.

Koch-féle görbe

Sierpinski-féle görbe
A Koch-görbe három, a Sierpinski-féle görbe pedig két azonos önhasonló görbéből tevődik össze, ráadásul a Sierpinski-félénél (akárcsak a kiinduló töröttvonalában) összekötő szakaszokat is be kellett rajzolnunk.
Természetesen a helyettesítéseket mi csak véges mélységben végeztük el, hiszen türelmünk is, de a képernyő felbontóképessége is korlátos. Ezek a görbék tehát csak utalnak ideális önmagukra. Ha ezzel mégis megelégszünk, az előbbi gondolatmenet alapján korlátlanul készíthetünk most már ilyen önhasonló görbéket. A programozáshoz ismét a rekurzív programséma kínálkozik. A rekurzív program egy szintjén menjünk végig a he-lyettesítendő szakaszok adott generációján, mindegyikhez számítsuk ki, hogy az eredeti töröttvonalat milyen szöggel kell elforgatni, hogy vele párhuzamos legyen, és hívjuk meg a következő szintet. Két helyettesítendő szakasz között persze mindig rajzoljuk be az oda-tartozó összekötő szakaszokat. A rekurzív hívás mélységét pedig előre rögzítsük - általában öt-, nyolcszoros mélység elég lesz.
Aki alaposan megfigyel egy ilyen vonalat (pl. a Sierpinski-féle görbét), az eldöntheti, vajon jogosan beszéltünk-e itt szimmetriáról. Mindenesetre szabályos ismétlődést éppúgy felfedezhetünk benne, mint harmóniát, nyugalmat. Ez persze a minta hagyományos szim-metriatulajdonságaival is bőven magyarázható, mi mégis úgy érezzük, hogy a belső szimmetria kifejezéssel érdemes megkülönböztetni az olyan alakzatokat, amelyek önmaguk részleteihez hasonlóak.
Az önhasonló görbéket előállító rekurzív programot úgy fejleszthetjük tovább, hogy már kiindulásképpen is többféle töröttvonalat veszünk fel, és mindegyiken a helyettesítendő szakaszokat megjelöljük aszerint, hogy melyik kiinduló töröttvonallal kell majd helyettesíteni.
Még egy rövid matematikai kitérő az önhasonló görbékkel kapcsolatban: ezek a legegyszerűbb példák az olyan görbékre, amelyeket a matematikusok fraktális (azaz törtdimenziójú) görbéknek neveznek. Vegyük pl. a Koch-féle görbe kiinduló töröttvonalát. Képzeljük el, hogy a vonalat azonos nagyságú körökkel kell lefedni. Ha a kör átmérőjének a töröttvonal két szélső pontja közti távolságot választjuk, akkor egyetlen körrel le tudjuk fedni a töröttvonalat. Ha viszont az átmérőt a harmadára csökkentjük (hogy most éppen egy helyettesítendő szakaszt érjen át), akkor nyilvánvalóan négy körre lesz szükség a lefedéshez. Miután az egész görbe ennek a töröttvonalnak az egyre kisebb arányú példányaiból áll, általában is igaz, hogy ha az eredő önhasonló görbét (a Koch-görbét) azonos méretű körökkel akarjuk lefedni, akkor harmadakkora átmérőjű körökből négyszer annyira lesz szükség.
Egy közönséges görbénél (amelynek a dimenziója 1), a körök átmérője és száma fordítottan arányos. Háromszor kisebb körből háromszor többet kell vennünk. Így nyilvánvalóan az ilyen önhasonló görbék nem 1 dimenziójúak. A dimenzió egyik lehetséges definíciója szerint, ha a-szor kisebb átmérőjű körökből b-szer többre van szükség, akkor a görbe dimenziója LOG b/LOG a. (Ez egybevág a megszokott dimenziófogalommal, pl. egy négyzet lefedéséhez a-szor kisebb átmérőjű körökből a^2-szer többet használunk, a képlet így: LOG (a^2)/LOG a = 2-t ad.)
7. Számítógéppel rajzolt képek
"Nem én vagyok-e a kormányos - kiáltottam."
(Franz Kafka)
Azok számára, akik a fejezet címét meglepőnek találják, tegyük hozzá, az eddigi képeket megkülönböztetésül számítógép által rajzolt képeknek nevezhetnénk. Eddig ugyanis általában arra próbáljuk megtanítani a számítógépet, hogyan tud élvezhető képeket előállítani a saját feje után, vagy többé-kevésbé pontos utasításainkat követve. Valahogy úgy, ahogy egy előkelő úr képet rendel a festőtől, akinek a tehetségében ugyan megbízik, mégis kiköt egyet 's mást az elkészítendő festménnyel kapcsolatban. Ezzel szemben most magunk lehetünk a festők, megpróbálva a számítógépet egyszerűen egy sajátos rajzeszközként alkalmazni. Másképpen megfogalmazva: csökkenteni szeretnénk a számítógép önállóságát, lehetőséget biztosítva, hogy időről időre beleavatkozzunk a rajzkészítés folyamatába, miközben a gépre csak egyszerű, mechanikus részfeladatokat bízunk. Menet közben, ha úgy látjuk, hogy a rajz nem felel meg a várakozásunknak, lehetővé kell tenni a javítást, módosítást, esetleg bizonyos részletek törlését. A számítógép ilyesfajta felhasználását interaktivitásnak szokás nevezni, természetesen nemcsak a grafikában, hanem más területeken is. Mindössze annyit értünk ezalatt, hogy a gép és működtetője állandó kapcsolatban, párbeszédben állnak, és így együtt jutnak el a kitűzött feladat megoldásához.
A fejezet első részében rajzolóprogramokról lesz szó, amelyekben a számítógépnek viszonylag kevés önállóság jut - voltaképpen a ceruza vagy ecset szerepére kárhoztatjuk. Ezt persze önmagában sohasem tekinthetjük célnak - nem érdemes a számítógépet olyasmire használni, amit mondjuk egy ceruzával jobban meg lehet oldani. Erre inkább annak van szüksége, aki az ily módon készített rajzokat még további számítógépes felhasználásra szánja - pl. animációs filmet akar összeállítani belőlük - vagy olyasvalakinek, aki a számítógép folyamatos korrigálásával jobban tud rajzolni. Hiszen a számítógépes grafika számtalan előnyének egyike éppen az, hogy rendkívül könnyűvé teszi a javítást, változtatást a félig elkészült rajzokon.
A fejezet későbbi részében viszonylag nagyobb önállóságot biztosítunk a gépnek (vagyis az eddig megszokott felhasználási mód felé közelítünk), csak egy-egy INPUT értékkel szabályozzuk működésének részleteit, és természetesen időnként döntünk, hogy az eddigiek megfelelnek-e az elképzeléseinknek, vagy bizonyos részleteket újra kell rajzolni.
Az interaktivitás előbbi értelmezésére gondolva észrevehetjük, hogy végül is eddig is többször készítettünk grafikákat a géppel együttműködve. Például megesett, hogy a rajzolást külső beavatkozással állítottunk le, vagy hogy a program elején INPUT paraméterek megadásával határoztuk meg a rajzolás menetét. A különbség inkább csak annyi, hogy eddig összesen egyszer avatkoztunk bele a gép működésébe a futás elején vagy végén, nem gyakoroltunk részletről részletre ellenőrzést fölötte. Ezáltal a keletkező képet is vagy mindenestül elfogadtuk, vagy az egész rajzolás kezdődhetett élőiről. Most, hogy az interaktivitást szem előtt tartva készítjük a programokat, kevesebb fáradsággal, munkával tudunk célhoz érni.
Pontonkénti rajzolás
A legegyszerűbb interaktív rajzolóprogrammal mindig egymás melletti pontokat rajzolhatunk be. Azt a helyet, ahol éppen tartunk (vagyis a ceruza hegyét) kurzornak nevezzük. A kurzor mozgatását előre rögzített billentyűkkel végezzük - pl. megállapodhatunk, hogy az "5" billentyű egy ponttal balra, a "6"-os eggyel lefelé, a "7"-es fölfelé és a "8"-as jobbra mozdítja el a kurzort. Természetesen mindegyik irányba csak akkor lehet továbblépni, ha még nem értük el a képernyő szélét - bár azt is megtehetjük, hogy a képernyőt tóruszfelületként fogjuk fel, vagyis a jobb széléről egyetlen lépéssel a bal szélére, az aljáról a tetejére jutunk és fordítva. Akit nem elégít ki a négy lehetséges lépés, további négy billentyűt (mondjuk az "1", "2", "3" és "4"-et) leköthet a ferde irányokba való elmozdításra.
Már ennél az egyszerű rajzolóprogramnál felmerül az interaktív rajzolás néhány általános követelménye. Az egyik, hogy a kurzor helyét akkor is jeleznie kell a programnak, amikor éppen egyik vezérlő billentyűt sem nyomjuk. Erre az egyik kézenfekvő lehetőség, hogy ilyenkor OVER üzemmódban a kurzor helyén egy kis keresztet rajzolunk, majd másodszori megrajzolással le is töröljük, nehogy a kurzor elmozdítása után is ottmaradjon. A másik követelmény, hogy a kurzor ugyanolyan mozgatása mellett a programnak háromféle vonalat kell tudnia rajzolni. Egyrészt természetesen fekete vonalat, amely ténylegesen a rajzhoz tartozik. Másrészt fehér vonalat, amely az útjába eső fekete pontokat törli. Végül transzparens vagy áttetsző vonalat, amely csak a kurzor mozgatására szolgál, az útközben érintett pontok változatlanok maradnak. Ezáltal oldhatjuk meg, hogy felemelt ceruzával is lehessen mozogni a képen, tehát ne kelljen az egész képnek egyetlen összefüggő vonalból állnia. (Igaz, ezt már a fehér vonallal is el lehet érni, csak jóval kényelmetlenebb módon.) Ezzel a rajzolóprogrammal most már bármilyen vonalas rajzot el tudunk készíteni, csak éppenséggel nem túl hatékonyan. Következő rajzolóprogramjaink nem lesznek ennyire általánosak, de gyorsabban, könnyebben lehet majd velük rajzolni.
Szakaszonkénti rajzolás
Ez az algoritmus nem egyes pontokból, hanem egész szakaszokból építi fel a rajzot - ahogyan pl. a görberajzoló programnál láthattuk. A kurzort természetesen most is pontonként mozgatjuk, az előbb kiválasztott billentyűket is megtarthatjuk. A leglényegesebb különbség a pontonkénti rajzoláshoz képest az, hogy most egy speciális (mondjuk a "0") billentyűvel rögzíteni tudunk egy pontot, és ettől kezdve mindig innen húzunk egyenes szakaszt a kurzor aktuális helyéig. A rajzolást vezérlő ciklus elején OVER 1-gyel mindig megrajzoljuk a szóban forgó szakaszt. Ez azonban valójában törlést jelent, mert, mint látni fogjuk, most másodszor (vagy páros alkalommal) kerül sor ennek a szakasznak a megrajzolására. Ezután végezzük el a lenyomott billentyűk megfigyelését és ha kell, a kurzor elmozdítását. A ciklus végén az előbbivel megegyező utasítással berajzoljuk a szakaszt, vagy a kurzor új helyéig, most először, vagy a változatlan helyre, páratlanszor (tehát most úgy, hogy a szakasz valójában megjelenjen). Ennek az lesz a hatása, hogy amikor nem nyomunk egyetlen billentyűt sem, az éppen megrajzolandó szakasz egyenletesen villog. Ha ismét a "0" billentyűt nyomjuk meg,akkor OVER 1 nélkül (tehát véglegesen) berajzoljuk a szakaszt, majd az új szakasz kezdőpontját a kurzor jelenlegi helyével azonosítjuk, és minden kezdődhet élőiről.
A szakasz villogása most fölöslegessé teszi a kurzor helyének külön jelzését. A fekete vonal - fehér vonal megkülönböztetést most is ugyanúgy érdemes megtenni, mint a pontonkénti rajzolásnál (egy állapotjelző változó értékének átállításával), a transzparens vonal helyett azonban elég, ha a szakasz kezdőpontját a kurzor helyére állítjuk anélkül, hogy előtte véglegesen megrajzoltuk volna az előző szakaszt.
Bár a fehér vonal most is rendelkezésünkre áll, mint törlési lehetőség, a már megrajzolt vonaldarabok törlésére hatékonyabb eszközt kell keresnünk. Fehér vonallal ugyanis csak akkor tudunk maradéktalanul letörölni egy rosszul megrajzolt szakaszt, ha mind a kezdőpontját, mind a végpontját teljesen pontosan sikerült beállítanunk - ellenkező eset-ben a képernyőn marad néhány pont, aminek a törléséről külön gondoskodni kell.
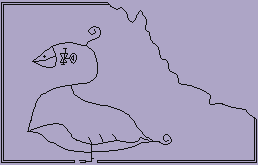
Vonalas rajz
Szakaszonkénti rajzolás kódolással
Hogy valóban interaktív rajzolásról beszélhessünk, rugalmasabb eszközt kell biztosítanunk a már részben megrajzolt kép módosítására, bővítésére vagy részletek törlésére. Erre alkalmasnak ígérkezik egy ötlet, amely később, a mozgókép-sorozatok készíté-sénél is felhasználható lesz. A kiindulópontot az eddigi (fehér vonallal való) törlés módszerének az elégtelensége jelentheti. Ha csak úgy lehet kielégítően törölni egy szakaszt, ha a végpontokat pontosan megtaláljuk, mennyivel egyszerűbb, ha a végpontok koordinátáit menetközben mindig tároljuk egy változóban! Ekkor nincs többé szükség arra, hogy kézzel próbáljuk megközelíteni a törlendő szakaszt. A végpontok koordinátáinak tárolására pl. egy karakteres változót használhatunk. A változó első két karaktere (azaz byte-ja) a rajzolás kezdőpontjának x és y koordinátáját tartalmazza. Valahányszor a rajzolás során befejezünk egy szakaszt, a végpontok koordinátáit egy-egy karakterben a változó végére biggyesztjük. Ily módon egy k pontból álló töröttvonal kódolására 2*(k+1) byte-ot használunk: az első kettőt az első szakasz kezdőpontjának, a többi 2*k byte pedig az első, második, n-edik szakasz végpontjának a koordinátáit tartalmazza. Amikor új kezdőpontból akarunk töröttvonalat indítani, a megelőző kódsorozatot egy (0, n+1) byte-párral zárjuk le - ezt megtehetjük, hiszen a n+1 már nem jelölhet ténylegesen előforduló y koordinátát. Hasonlóképpen (0, n+2) kódokkal jelezhetjük a fekete, és (0, n+3)-mal a fehér vonal kezdetét - ilyenkor azonban nem szükséges az aktuális töröttvonalat (sőt, a szakaszt sem) megszakítani.
Ily módon a töröttvonalakból álló rajz teljes információmennyisége kódolva tárolható egy karakteres változóban, és ezt használhatjuk fel a rajz módosításában.
A módosításhoz szükséges, hogy a változóban jobbra, balra tudjunk mozogni (természetesen kétbyte-os lépésekkel). Ezt szintén egy-egy billentyű megnyomásához köthetjük. Ilyenkor ugyanazok a műveletek, amelyekkel az új szakaszokat rajzoltuk, a régi szakaszokat meghatározó értékek módosítására lesznek jók. A kurzorral együtt az éppen vizsgált szakasz végpontját (és azzal együtt a következő szakasz kezdőpontját) állítjuk - ezzel párhuzamosan persze mindig meg kell rajzolni a szakaszok új képét. A törlés (ugyanúgy, ahogy a rajz végén a töröttvonal megszakítása), a (0, n+1) byte-pár beiktatásával történik - ezáltal a vizsgált szakasz eltűnik a képről. Ha pedig egy új szakaszt akarunk berajzolni a régi helyére, akkor a végpontjától kezdve az összes byte-ot két hellyel jobbra kell tolni, a keletkező üres helyen pedig megismételni a kezdőpont koordinátáit - majd a módosítás üzemmódban a kurzort a megfelelő helyre visszük, és így alakítjuk ki a szakasz végső koordinátáit.
Rajzolás a száguldó autó nyomában
Az előző két rajzolóalgoritmus nagy hátránya, hogy a rajzolás csak olyankor halad, amikor valamelyik gomb megnyomásával mi magunk adunk utasítást erre. Nem lehet azt mondani a gépnek: "most haladj tovább ebben az irányban" vagy "folytasd tovább ezt az ívet, amíg másfajta utasítást nem kapsz". Most következő algoritmusunk ezt a hiányosságot igyekszik kiküszöbölni. Valahogy úgy kell majd irányítani, ahogy autót vezet az ember: egy-egy billentyűvel lehet a rajzolás sebességét fokozni (gázt adni) vagy csökkenteni (fékezni), és két másik billentyűvel jobbra, ill. balra kormányozni. Amikor viszont semmilyen utasítást nem ad az ember, a gép adott sebességgel és egyenletes szögelfordulással folytatja a rajzolást. Ezért aztán állandóan résen kell lennünk, nehogy az autónk letérjen az elképzelt útról - ezt némi gyakorlat birtokában elsősorban a sebesség alkalmas megválasztásával érhetjük el.
Az autó egy-egy lépésben
t/k * (u,v)
szakaszt fut be. A k érték egy rögzített szám (mondjuk 8), t pedig 0 és k között változhat (gázadásnál eggyel nő, fékezésnél eggyel csökken, feltéve, hogy a határok között marad). Az (a,b) elmozdulásvektort minden lépésben adott szöggel elforgatjuk. A szöget a kormány balra fordítása egy rögzített kis szöggel (mondjuk PI/20-szal) növeli, a jobb ráfordítás pedig ugyanekkorával csökkenti. Itt is kikötjük, hogy ez az elfordulási szög ne haladjon meg egy rögzített értéket (mondjuk PI/4-et). Ahelyett, hogy a szögből minden alkalommal viszonylag lassan kiszámítanánk a COS és SIN értékeket, megtehetjük, hogy minden elforgatás helyett közvetlenül az elforgatott szög koszinuszát és szinuszát számítjuk ki: legyen tehát c és s a mindenkori elforgatási szög COS-a és SIN-a, c0 és s0 pedig a rögzített COS(PI/20), ill. SIN(PI/20) értékek. Ekkor bal oldali kormánymozdulatnál:
LET p=c*c0-s*s0: LET q=c*s0+s*c0
IF p>ABS q THEN LET c=p: LET s=q
jobb oldalinál pedig ugyanezt a képletet -s0-lal alkalmazzuk. A p>ABS q feltétel azt fejezi ki, hogy a kormány elforgatási szöge nem haladta meg a PI/4-et (azaz 45 fokot). Az átigazított c és s értékekkel azután minden lépésben elforgatjuk az aktuális (a,b) elmozdulásvektort:
LET w=u*c-v*s: LET v=u*s+v*c: LET u=w
Ezt az elmozdulásvektort azonban a megrajzolás előtt még megszorozzuk a (0 és 1 közé eső) t/k értékkel, amely az autó pillanatnyi sebességének felel meg. Ily módon pl. elérhetjük, hogy egészen kis ívben tudjunk fordulni az autóval: t értékét fékezéssel 1-re kell csökkenteni. Sőt, ha t-t 0-ra csökkentjük, ezután elforgatjuk a kormányt, majd ismét gázt adunk, akkor az is lehetségessé válik, hogy az autó álló helyzetből más irányba induljon el, mint amilyenben odaérkezett.
Itt is értelmes a fekete, fehér és áttetsző vonal megkülönböztetése, amelyet a megszokott módon egy-egy billentyűvel állíthatunk át. Miután azonban az autó nyomán való rajzolás nem olyan egyszerű, mint az eddigi módszerek, a törlésről, javításról most le kell mondanunk. Az interaktivitás itt tehát csak az autó folyamatos irányítását jelenti.
A másik lényeges megjegyzés, hogy most a billentyűk figyelése nehezebb, mint az eddigi programokban. Azt szeretnénk ugyanis, hogy legalább két billentyű (egy sebességszabályozó - fék vagy gáz - és egy kormánybillentyű) megnyomása egy időben legyen érzékelhető. Erre a BASIC nyelv GET utasítása vagy az INKEY$ függvény már nem nyújt lehetőséget - a megoldás viszont géptípusonként változó. A Spectrum esetében az IN 254 kifejezés 0., 1., 2., 3. vagy 4. bitje jelzi, hogy a gép billentyűzetén valamelyik sorban a szélről számított 1., 2., 3., 4. vagy 5. billentyű be van-e nyomva, ráadásul szimultán, vagyis az egyik billentyű benyomása nem befolyásolja a másikra vonatkozó bit értékét.
Az itt leírt módszerek inkább festésre, mint rajzolásra emlékeztetnek - segítségükkel különböző tónusú foltokat lehet a képernyőn egymás mellé állítani, és ezekből felépíteni az ábrázolandó figurát.
Rajzolás sörétes puskával
A legelső rajzolóalgoritmushoz hasonlóan a kurzort négy billentyű segítségével négy irányban mozgathatjuk, és aktuális helyét mindig egy villogó kereszt jelzi. Két speciális karakterrel a kurzor köré véletlenszerűen fekete, ill. fehér pontokat szórhatunk, nagyjából úgy, mintha sörétes puskával lőnénk egy céltáblára. A sörétek száma adott - mondjuk egy-egy lövés húsz sörétet szór el a pontos cél körül. Persze a véletlenszerű szórás eredményeképpen megeshet, hogy egy-egy sörét ugyanarra a helyre csapódik be. Ha a kurzor elmozdítása nélkül egymás után többször lövünk (fekete söréttel), akkora célpont körüli 5 egység sugarú körben még több fekete pont lesz, ami egy sötétebb tónusú foltot eredményez. Ha viszont rájöttünk, hogy túlságosan sötét lett az illető terület, fehér sörétek kilövésével gyengíthetjük a tónust. Ahhoz, hogy az egész kör alakú területet megtisztítsuk, 5-10 alkalommal is rá kell lőni fehér sőrétekkel.
Egy x,y pont körüli lövésnél a sörét pontos helyét az
x + r*COS f,y + r*SIN f
képlet adja meg, ahol
r = 5*RND, f = 2*PI*RND
Miután azonban egy lövésnél húsz ilyen pont koordinátáit kell kiszámítani, és ez a COS és SIN függvény húszszori hívását jelenti, nem ajánlatos ezeket az értékeket minden alkalommal újra kiszámítani. Sokkal gyorsabban ki tudunk lőni egy-egy adag sörétet, ha mondjuk száz ilyen
(r*COS f, r*SIN f)
értékpárt beírunk egy tömbbe, és minden lövésnél ezek közül veszünk ki véletlenszerűen választott helytől kezdve egymás után húszat. Ezeket a kurzor (x,y) helyvektorához adva kapjuk meg az egyes sörétek aktuális helyét.
A képen egy ilyen módszerrel készített arcképet láthatunk. Noha a söréttel való rajzolás elég fáradságos, eddigi rajzolóprogramjainkkal szemben ez végre valami olyasmi, amit számítógép nélkül jóval nehezebb lenne megrajzolni.
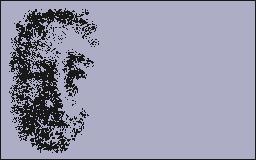
Arckép söréttel
Rajzolás kockákkal
A tónusos rajzolás ötletét olyan módszerekkel is megvalósíthatjuk, amely nem tartalmaz véletlen elemet. (Voltaképpen az árnyékolás különböző módszereit használhatjuk fel tónusos rajzok készítéséhez - az 5. fejezetben szereplő árnyékolási módszerek mind használhatók.) Most viszont eddig nem alkalmazott árnyékolási technikákat fogunk alkalmazni (amelyek viszont a térbeli képekre is átvihetők volnának).
A következő módszer képernyőt egyenletes négyzetrácsra osztja, és egy-egy négyzeten belül változtatható nagyságú kis négyzetet feketít be. A rajzolóprogram irányítására néhány számbillentyűt használunk. A kurzort ugyanazokkal a billentyűkkel, ugyanolyan módon mozgatjuk, mint a pontonkénti rajzolásnál. Valahányszor a kurzor új helyre kerül, OVER 1 választással először a régi, aztán az új helyre fekete négyzetet rajzolunk (aminek tehát az lesz a hatása, hogy a négyzeten látható minta átfordul feketéről fehérre és vissza). Ily módon a kurzor nem villog fölöslegesen, csak amikor változtatjuk a helyét. Az is teljesül, hogy minden helyen páros sokszor (pontosan kétszer) rajzolunk OVER 1-gyel fekete négyzetet, tehát amikor odébbállunk, az illető helyen visszaáll az eredeti helyzet. Míg az "5"-"8" billentyűkkel a kurzort mozgatjuk, az "1"-"4" billentyűkkel 4 különböző nagyságú négyzetet rajzolhatunk a kurzor alatti rácsnégyzet közepére (mindig úgy, hogy a széle ne érjen egészen a szomszédos mezőig). Ezt már nem lehet OVER 1 választással rajzolni (hiszen akkor egy esetleges javításnál a kisebb négyzet lyukat ütne a nagyobbik közepén). Ezért először az egész mezőt törölni kell, majd be kell rajzolni annak a négyzetnek az inverzét, amit végül is ott szeretnénk látni - hiszen a kurzor arrébb vitelekor az illető mező tartalma még egyszer átfordul. Ily módon tehát tetszőleges sorrendben végigmehetünk a képernyő rácsnégyzetein, és a megfelelő nagyságú négyzet berajzolásával különböző tónusértékeket állíthatunk be. Maga a kurzor természetesen nem változtatja meg az útjába eső négyzeteket. Ha viszont az "1"-"4" billentyűkkel egy négyzetet akarunk belerajzolni, akkor felülírjuk korábbi tartalmát.
Ennek a technikának (az egyszerű programozhatóság mellett) hátránya, hogy a nagy rácsnégyzetbe írható kis négyzetek nem képviselnek egyenletesen erősödő tónusskálát. A másik hibája viszonylag könnyebben javítható - nevezetesen az, hogy csak négy különböző négyzettel (következésképpen tónussal) tudunk operálni. Ha az "1"-"4" billentyű helyett az ábécé betűit használjuk, akkor elvileg akárhányféle négyzetet is előállíthatunk - mivel azonban a rácsnégyzeteket 8*8-asnál nagyobbnak nem ajánlatos választani, ebből gyakorlatilag legfeljebb hét lehetőséget használhatunk ki.
Rajzolás raszterelemekkel
A nagyjából egyenletes tónuseloszlás a következő módon valósítható meg. A képernyőt 4*4-es rácsnégyzetekre osztjuk, és minden mezőt nyolcféleképpen töltünk be pontokkal háromszög alakban, a következő. ábra szerint:

4*4 pontból álló raszterelemek
Amint látjuk, a teljesen betöltött és a teljesen üres négyzet között viszonylag folytonos átmenetben választhatók az egyes betöltések - miután a rácsnégyzet kicsi, a nyolcféle betöltési lehetőség gyakorlatilag minden tónusérték megvalósítására alkalmas.
A program az előzőhöz hasonló elven működik. Megtehetjük, hogy az előző programban csak a konkrét betöltést végző szubrutint cseréljük ki (és persze a rácsnégyzetek méretét 4*4-ben rögzítjük). Adódik azonban egy-két javítási lehetőség is. Az egyik azon alapul, hogy a kurzor által megjelölt mezőn nem a számgombokkal adjuk meg a betöltés konkrét értékét, hanem egy gomb (pl. a "0") többszöri megnyomásával egyre sötétebb tónusú betöltéseket választhatunk, majd a legutolsó (azaz a teljes betöltés) után visszatérünk a legelsőhöz, a teljesen üres négyzethez. Ily módon már rajzolás közben láthatjuk, milyen tónust helyes választani az adott helyen - igaz, ez némi gyakorlatot igényel, hiszen a kurzor alatt éppen a tényleges betöltés inverzét látjuk.
A másik javítási lehetőség pedig az, hogy tetszőleges választásnál egy konkrét betöltést ismételhetünk, pusztán a kurzormozgató és a "0" billentyű használatával. Ezt pl. úgy valósíthatjuk meg, hogy kétfajta üzemmódot engedünk meg a program működésében, amelyeket pl. az "1" billentyű megnyomásával válthatunk át egymásra. Az első üzemmód az előbb leírt módon működik. A másik üzemmódban viszont megtiltjuk a különböző tónusértékű betöltések ciklikus váltogatását, most a "0" billentyű megnyomására mindig egyféle betöltést rajzol a program - az utolsót, amelyet az üzemmódváltás előtt használtunk. Ennek az az értelme, hogy egy-egy rajznál sokszor kell nagyobb területeket egyenletes tónusban betölteni - a leggyakoribb a teljesen fekete betöltés (pl. a háttér jelzésére) vagy a teljesen fehér négyzet ismétlése (törléskor).
"Ha cserben hagy az értelem, a tapasztaláshoz folyamodunk."
(Montaigne)
Ebben a részben olyan algoritmusról lesz szó, amely az interaktivitásban nagyobb önállóságot szán a számítógépnek. Mi interaktív módon pontokat jelölünk meg a képernyőn, majd a gép saját maga rajzolja meg azt a görbét, amely ezeken a pontokon átmegy (vagy, a másik esetben megközelíti őket). Ezután, ha az eredménnyel nem vagyunk elégedettek, módosítjuk a kiinduló pontok elhelyezését, a gép ismét rajzol stb., amíg az elképzelt formához nem jutunk. Ennek a módszernek, viszonylagos lassúsága ellenére előnye, hogy egyrészt nem számít a programmal rajzolni kívánó ember kézügyességére, másrészt, hogy a keletkező vonalak az őket meghatározó pontokkal egyszerűen kódolhatók, és így könnyen módosíthatók.
A kiinduló pontokat a már megszokott módon a kurzor mozgatásával jelöljük ki. A kurzor helyén most is egy keresztet villogtathatunk. Amikor a "0" gombot megnyomjuk, a kurzor adott helyén felveszünk egy pontot, köré kis kört rajzolunk, és egy karakteres változóban tároljuk a koordinátáit. A kurzort tovább mozgatva, további "0" gombnyomásokra újabb pontokat vehetünk fel.
Ha módosítani akarunk a már megadott pontokon, az "1" gomb megnyomására a kurzor a legelső pont koordinátáit veszi fel, és a karakteres változónak is a legelejére állítunk egy mutatót. A kurzor mozgatása most az adott pont koordinátáinak módosítását jelenti, ami a "0" paranccsal véglegessé is válik, és a mutató a következő pontra áll rá, és a kurzor ennek a helyén jelenik meg. A "2" gombbal törölni lehet az aktuális pontot, a "3"-assal pedig beszúrni elé egyet, természetesen a pontokat kódoló karakteres változót is megfelelően átalakítva.
A "9" gomb hatására kezdődik a számítógép érdemi munkája: a megadott pontokat görbével köti össze. Erre két algoritmust is megadunk. Az első az interpolációs polinomok segítségével működik. Olyan f(t) és g(t) polinomokat konstruálunk, amelyekre
(f(i),g(i)) = (xi,yi)
éppen az i-edik pont koordinátáit adja meg. Ha n pontunk van, akkor t 1 és n között fog futni. Az f(t) és g(t) polinomokat a következő
hi(t) = (t-1)*(t-2) * ... * (t-i+1)*(t-i-1) * ... * (t-n)
polinomokból építjük fel. A definícióból nyilvánvaló, hogy hj(t) értéke t = 1,2,..., i-1, i+1,..., n-re 0, de t = i-re nem 0. Most hi(t)/hi(i) t=i-ben 1-et, a többi 1 és n közötti egész számra pedig 0-t ad. Ha tehát f(t)-t és g(t)-t a következőképpen definiáljuk:
f(t) = X1*h1(t)/h1(1) + ... + xn*hn(t)/hn(n)
g(t) = y1*h1(t)/h1(1) + ... + yn*hn(t)/hn(n)
akkor i = 1, ..., n-re valóban f(i) = xi és g(i) = yi lesz. Ily módon tehát olyan (f(t),g(t)) paraméteres görbét definiálhatunk, amely a megadott sorrendben átmegy a kijelölt pontokon.
Annak ellenére, hogy az interpolációs polinomokkal definiált görbe pontosan a megadott pontokon halad át, az elképzelt görbét nem mindig tudjuk jól közelíteni vele. Ha ugyanis a jobb közelítés érdekében még több pontot veszünk fel, a görbe a pontok között egyre nagyobb kanyarokat alakít ki. A következő módszerrel definiált görbék, bár nem érintik a megadott pontokat, több pont felvételével egyre jobb közelítést tesznek lehetővé. Az f(t) és g(t) függvényeket most is polinomok (az ún. Bernstejn-polinomok) összegével adjuk meg. A
i. Bernstejn-polinom azzal a tulajdonsággal rendelkezik, hogy míg értéke az [1,n] intervallum nagy részében kicsi, t = i környékén n^n közelébe szökik fel. Ha tehát az (f(t),g(t)) paraméteres görbét az
f(t) = (x1*b1(t) + ... + xn*bn(t))/n^n, és
g(t) = (y1*b1(t) + ... + yn*bn(t))/n^n
definícióval adjuk meg, akkor a t = i-re jól megközelíti az (xi,yi) pontot, különösen akkor, ha a szomszédos pontokat egymáshoz viszonylag közeli helyen választottuk.
A "9" gomb megnyomásakor tehát a számítógép letörli a képernyőt, és interpolációs vagy Bernstejn-féle polinomokkal megrajzol egy (közelítő) görbét. Ha most még változtatni akarunk, a kurzormozgató billentyűk hatására ismét megjelennek a pontokat reprezentáló kis körök, és az említett módszerrel új helyre vihetjük át őket, hogy elképzeléseinknek jobban megfelelő görbét kapjunk.
"Eppur si muove..."
(Galilei)
Azt hihetnénk, hogy az animáció (vagyis képsorok megelevenítése) tipikusan a számítógépnek való feladat - ez azonban, mint látni fogjuk, csak félig-meddig igaz. Ahhoz, hogy egy képsorozat valóságos mozgás érzetét keltse, másodpercenként tízszer-húszszor egymástól csak kevéssel eltérő képeket kell vetíteni. Ez rengeteg mechanikus munkát igényel - ha tudjuk, hogy egy-egy jellemző pillanatban a képen szereplő figurák milyen helyzetben vannak, a közbeeső időpontokban szinte gépiesen meg tudnánk rajzolni az ún. fázisrajzokat. Valójában azonban eközben is hasznát vesszük a figurák természetére, az anyag és mozgás törvényeire vonatkozó ösztönös tudásunknak, amit pedig még megfogalmazni is bajos volna, hát még megtanítani egy számítógépnek.
Másfajta problémák is vannak. A rajzfilm számítógépesítésének elvileg két lehetősége van. Vagy valamilyen programmal magunk készítjük el az összes fázisrajzot, a memóriában egymás mellé elhelyezve azokat, és a vetítés során gyors egymásután előhívva őket, vagy olyan szabályt táplálunk be a gépbe, aminek alapján minden alkalommal gyorsan újra tudja rajzolni a szükséges fázisrajzokat. Az első esetben nagyon hamar beleütközünk a memória korlátaiba: pl. a Spectrum központi memóriájába összesen 6-7 képernyő fér el - ez (másodpercenként 10 képet számolva) még egy másodpercnyi filmet sem jelent. A második módszernek a gép sebessége szab határt - egy-két tizedmásodperc alatt nem lehet nagyon bonyolult képeket megrajzolni. (A sebesség persze az első esetben is szerepet játszik, hiszen a kész kép átmásolása a memóriából a képernyőterületre szintén időbe kerül. Ez akadályozza meg azt is, hogy a képeket külső adattárolókon helyezzük el. A második lehetőség pedig szintén igényel memóriát, hiszen a képek megrajzolásához szükséges információt is tárolni kell.)
Ha tehát (egy közönséges, elterjedt mai személyi számítógéppel) mozgóképeket akarunk készíteni, elkerülhetetlenül kompromisszumokra kényszerülünk. Megpróbáljuk a mozgás illúzióját kelteni úgy, hogy a képen egyszerre csak egy kis részletet változtatunk meg. Vagy pedig azáltal, hogy egyes képrészleteket egészben áthelyezünk, megváltoztatjuk a kép alkotóelemeinek viszonyát. Ehhez hasonló trükkök alkalmazásával megpróbálunk néhány olyan képsorozatot előállítani, amely - igaz, kicsit sután, kicsit együgyűen, de mégis - mozog!
Ha eddig pesszimista módon csak az animációval kapcsolatos nehézségekre fordítottunk figyelmet, most jegyezzük meg, hogy bizonyos értelemben mégis viszonylag könnyen készíthetünk mozgóképeket. Anélkül, hogy akár a legkisebb mértékben is törekedtünk volna rá, tulajdonképpen már eddig is létrehoztunk élvezhető animációt. Legtöbb grafikánknak volt ugyanis valamilyen története, időbeli fejlődése vagy változása, ami (különösen a véletlen programok esetében) még a programozónak is meglepetéseket okozott. Érdekes volt tehát végignézni, hogyan alakult ki a végső kép, amely esetleg önmagában nem is volt különösebben izgalmas. Például a gravitációs pályák kusza sokasága sokkal kevesebbet mond, mint amikor egyenként figyelhettük végig, hogyan alakul egy-egy űrhajó sorsa. Vagy amikor önhasonló görbéket paraméterezünk és sokáig csak szurkolhatunk, vajon az előre elképzelt görbét sikerült-e szabályba foglalni. Ezek jelenthetik tehát az első lépést a mozgóképkészítés felé, amellett, hogy ötleteket adhatnak a komolyabb animációhoz is.
A mai ember megszokta, hogy ha autón vagy vonaton utazik, és az ablak mozdulatlan keretei között elsuhan a táj, azt (helyesen) a jármű mozgásaként érzékelje. Vagy ha a filmvásznon egy álló repülőgépet lát, amely mögött folyamatosan, egy irányban mozognak a felhők, tudja, hogy ez inkább a repülő mozgásának jelzésére szolgál. Az egymáshoz képest mozgó tárgyak viszonylagosságát csak a valóságos helyzet ismerete szünteti meg, maga a kép nem ad támpontot. Amikor a képen egy ember és egy hegy közeledik egymáshoz, automatikusan az embert fogjuk fel mozgásban levőnek - csak akkor esünk zavarba, ha tudjuk, hogy ez az ember Mohamed.
Ez az érzékelés-lélektani adottság is kapóra jön, amikor egyszerű animációs filmet akarunk készíteni: ha azt akarjuk ábrázolni, hogy egy bonyolult figura mozog egy viszonylag egyszerűbb háttér előtt, megtehetjük, hogy ehelyett a hátteret mozdítjuk el a stabil figurához képest - úgy fog tűnni, mintha a nézőpont (vagyis a kamera) a figurával párhuzamosan haladna.
A háttér mozgatására alkalmas módszer a képernyő SCROLL-ozása. Ez azt jelenti, hogy fölfelé vagy lefelé, jobbra vagy balra egy sorral eltoljuk az egész képernyőt. (Ahhoz persze, hogy ez az eltolás elég gyorsan történjen, a SCROLL programot gépi kódban kell írni.) Ha mondjuk jobbra SCROLL-ozunk, a képernyő bal oldalán egy olyan új sor keletkezik, amiről eddig még semmit nem tudunk. Ezt választhatjuk teljesen fehérnek vagy teljesen betöltöttnek, ebbe a sorba rajzolhatunk olyasmit, amit aztán be akarunk úsztatni a képernyő közepére, de azt is megtehetjük, hogy ide áthozzuk azt a túlsó sort, ami egyébként elveszne. Ez utóbbi esetben az egész kép ciklikusan ismétlődni fog, miután annyit SCROLL-oztunk, amennyi a sorok száma (a SCROLL irányában). Ez utóbbi műveletet megkülönböztetésül ROLL-nak szokták nevezni.
Chicago
Az alábbi kép egy film egyik kockáját mutatja. Egyszerűen három autót látunk egy amerikai város - mondjuk Chicago - egyik széles útján végigsuhanni, miközben a háttérben a város látképe vonul végig folyamatosan.
Chicago
A megvalósítás technikája is egyszerű: a város, a képernyő felső kétharmadában időközönként egyet jobbra SCROLL-ozik. A bal oldalon keletkező üres sorban megrajzoljuk az aktuális ház egy vonalát - a ház magasságát néha véletlenszerűen megváltoztatjuk, és ilyenkor esetenként rövidebb-hosszabb szünetet iktatunk be két ház közé. A házak előtt egy fasor húzódik - a lombkorona alsó és felső kontúrját a tehetetlenséggel mozgó véletlen görbe algoritmusával változtatjuk - a görbe y irányú sebessége mindig 1/2-del nő, vagy csökken, és a növekedés vagy csökkenés valószínűségét az y érték és a lehetséges maximális kiterjedés hányadosa adja. A lombkorona alá időnként a fatörzseket is berajzoljuk.
Az egész képernyőt jobbra kell SCROLL-ozni, hogy az autóútra festett szaggatott vonalak is a házakkal egyformán formán mozogjanak. Ettől viszont a három autó is elmozdul jobbra - ennek megakadályozására minden lépésben újból be kell rajzolni őket ugyanazokra a helyekre. Hogy az előző lépésben jobbra csúszott autók jobb széle ne lógjon ki, az őket definiáló 2*3 karakter jobb szélső oszlopát teljesen feketének (betöltöttnek) kellett választanunk - ez, ha kicsúszik is, nem üt el az út hátteréről.
A házak és fák függőleges csíkozását úgy oldjuk meg, hogy a ház függőleges vonalát csak olyankor rajzoljuk be, amikor a SCROLL-okat számláló változó értéke 3-mal osztható - a fáknál pedig éppen fordítva. A fatörzsek egységes háromszoros vastagságát úgy érjük el, hogy véletlenszerűen választott időpontokban egy számláló értékét mondjuk 7-re állítjuk. Ettől kezdve minden SCROLL-ozás után eggyel csökkentjük (amíg a nullát el nem éri), de a fatörzset csak addig rajzoljuk be, amíg a számláló értéke 3-nál is nagyobb. Ezáltal azt is megakadályozzuk, hogy két fatörzs egymásra nőhessen.
Az autóút szaggatott vonalai úgy keletkeznek, hogy minden öt SCROLL-ozásból egymás után háromban az adott sorokba egy-egy fehér pontot rajzolunk. Ezek a szaggatott vonalak azonban az autókba ütközve elnyelődnének, ha tőlük jobbra is, az első öttel osztható x koordinátájú pontban ugyanebben a ritmusban nem rajzolnánk pontokat.
Összegezzük tehát, mi mindent kell egy-egy SCROLL-ozás után elvégeznünk: legyen s a SCROLL számlálója, h a házak közötti hézag, és f a fatörzsek számlálója. Ekkor
A fejezet elején szinte rögtön elvetettük azt a lehetőséget, hogy a memóriában egymás mellé helyezett képek levetítésével készítsünk animációs filmet, hiszen a memória nagyon szűk korlátokat szab az ilyen megközelítésnek. Most mégis arra mutatunk példát, hogyan lehet - az egész fejezet jellemző kompromisszum-készséggel - legalább rövid ideig élvezhető animációs filmet készíteni a memóriában elhelyezhető néhány képből.
A teljes képernyő (attribútumok nélkül is) 6K memóriát igényel. Ebből a program mellett legfeljebb öt db férne el a memóriában. Ha azonban a képernyőt vízszintesen három egyforma sávra tagoljuk, és a középső sáv bal oldali negyedétől a jobb oldali negyedéig terjedő részét vesszük, ez az egész képernyőnek mindössze 1/6-a, tehát 1 K memóriában elfér. Ilyen képekből tehát már 20-30-at is el tudunk helyezni a Spectrum memóriájában. 20-30 kép azonban, ha folyamatosan levetítjük, valós sebességgel, 1-2 másodpercnyi filmet szolgáltat. Ez pedig már a mi céljainkra sem lehet elég! Kézenfekvő a következtetés - egy-egy képet többször is fel kell használni a filmben. Erre a legegyszerűbb lehetőséget az olyan képsorozatok szolgáltatják, amelyek egy ismétlődő mozgássorozat képeiből épülnek fel, és így a képek ciklikusan egymás után vetítve lesznek felhasználhatók. Ezzel a módszerrel megnyújtható az az idő, amíg az adott képkészletből élvezhető mozgóképsorozatot állíthatunk össze.
Beszélő
A következő film az alábbi képeken látható kockákból épül fel.
A képeket nem ciklikusan egymás után vetítjük, hanem véletlenszerű sorrendben de persze nem akárhogyan. A képek, mint látjuk, egy arc különböző helyzetű és kifejezésű változatait mutatják. A tíz kép több kisebb ciklusba sorolható. Mindegyik ciklus kezdőpontja az 1. kép. Itt egy viszonylag közömbös kifejezésű arc látható. A 2. és 3. kép egy olyan ciklust alkot, amelyben az arc (lehunyt szemmel) jobbra elfordul. Ha ezeket 1, 2, 3, 2, 1 sorrendben vetítjük le, akkor a film főszereplője egyszer jobbra fordítja a fejét, majd visszatér a kiinduló helyzetbe. Pontos tükörképe a 2. és 3. képnek a 4. és 5. kép - ezek tehát egy balra elfordítás és visszafordítás ábrázolására alkalmasak. A 6., 7. és 8. képen az illető úr egyre izgatottabb lesz - szája és szeme egyre kerekebbre nyílik. Az 1, 6, 7, 8, 7, 6, 1 ciklus során viszont az izgalmi hullámzás során visszajut a kezdeti egykedvű állapotba. Végül a 9. és 10. kép egy olyan ciklust alkot, amely során hősünk elkomorul, és a 10. képen egy fenyegető, vagy intő kézmozdulatot is tesz. A képeket alkalmasan paraméterezett DRAW és PLOT utasítások segítségével készítettük el - ebben tehát nincsen semmi általánosan hasznosítható. Annál inkább a vetítési sorrend megszervezésében.
Az eddigiekből is kitűnt, hogy a tíz kép négy kisebb ciklusba szerveződik. Minden ciklus az 1. képpel indul, aztán két vagy három képen keresztül eljut a végső fokozatába, majd ugyanazon az úton visszatér az első képhez. Az első képben aztán véletlenszerűen választjuk meg, hogy következőre melyik ciklus képein kelljen végighaladni. De azért nem teljesen egyforma valószínűséggel. A választási valószínűségeket úgy állítjuk be, hogy pl. egy balra fejfordítási ciklust a többinél nagyobb valószínűséggel kövessen egy jobbra fejfordítás - így egy ideig csak ingatja a fejét. Ezeknek a valószínűségeknek a konkrét megválasztása hosszas kísérletezést igényel, és apró eltérésekre is elég kényes. Az sem kívánatos, hogy egy fejfordítás után túlságosan sokáig csakis fejcsóválás következzen, de az se jó, hogy az egyik irányú fejfordítást sokszor nem követi a másik. Egyébként az első kép után az egyes ciklusokat egyforma valószínűséggel választja a program. A képek sorrendjének ezenkívül csak egy különlegessége van: a 8. (izgatott) képből bizonyos valószínűséggel nem a 7. képhez fordul vissza, hanem átugrik egy másik ciklusba a 10. (fenyegető) képhez, és ugyanígy visszafelé. Ezáltal a vetítési sorrend még egy kicsit szabálytalanabb lesz, és a film még egy darabig szórakoztató marad.
Még egy megjegyzést a rajzolásról: a képernyőnek az a részlete, amelyet az előbb leírt módon a memóriából hozunk be, túlságosan kicsi ahhoz, hogy az egész arc ráférne, így világosan el kell különíteni azokat a részleteket, amelyek az összes képen ugyanazok, és ezt csak egyszer, a program elején kell megrajzolni. Esetünkben az arc kontúrja, és természetesen a (rajzolt) tv-képernyő már kilóg a változó területről.