
Etűdök személyi számítógépre
1984 - Fried Katalin, Kepes János Sztókay Kálmán, Török Turul
Szerkesztette: Votisky Zsuzsa
Szaklektorok: Andor Csaba, Szlékely Jenő, Zémbori Zoltán
Tartalom
Hat évvel ezelőtt még csak a szakemberek tudtak arról, hogy új irány nyílt a számítástechnika fejlődésében. Bizonyára maguk sem gondolták, hogy a méretek csökkenése és az azt követő rohamos árcsökkenés olyan népszerűvé avatja a személyi számítógépet, hogy az amerikaiak öt év múltán, 1982-ben, nemhogy az év gépének, hanem - rájuk jellemző módon - az év emberének fogják megválasztani.
Itthon is gyors ütemben peregnek az események, közülük az egyik legjelentősebb, hogy az 1982-83-as tanév végéig minden középiskola hozzájutott a hazai gyártású iskolai számítógéphez (magyar nevén: a HT-1080Z Iskola computerhez). Irodákban, klubokban, otthonokban ismerkednek egyre többen az új gépekkel. Most tehát, amikor az anyagi, tárgyi feltételek megteremtődtek, sokak számára nyílik alkalom, hogy a gépek mellé üljenek, és kipróbálják, mi mindenre képesek.
Ezzel a könyvvel az első lépések megtételében szeretnénk az olvasót segíteni. Azt szeretnénk, hogy saját gyakorlatával hódítsa meg a sokszor misztifikált új technikai csodát, a számítógépet. Saját maga essen át az első programírás, javítgatás, futtatás tűzkeresztségén. A könyv fejezetei mindehhez felfedező utakat kínálnak: problémákat vetnek fel, program- és programozási ötleteket adnak. Az effajta stílus nem állt távol a könyv közreműködőitől, hiszen mindnyájan ilyen-olyan módon a problémamegoldó matematika-tanítás hívei.
Reméljük, hogy a hazai számítástechnikai kultúra kialakításáért és elterjedéséért valamit ezúton is tehettünk.
Itt mondunk köszönetét a Gondolat Könyvkiadónak, hogy átvállalta az Országos Pedagógiai Intézettől a kiadás gondjait.
Surányi János
Az első találkozás a személyi számítógéppel sokféle lehet: például több órás elméleti tanulás után papíron kidolgozott programmal ülünk a számítógép elé, vagy ügyes kezek néhány billentyű lenyomásával meghökkentő ábrákat varázsolnak a képernyőre, vagy kazettás magnóról beolvasott program indít el a gép segítségével egy játékot, vagy éppen a gépkönyv tanulmányozásával kezdődik az ismerkedés. Ebben a fejezetben az önálló próbálkozásokhoz igyekszünk segítséget nyújtani olyan egyszerű gyakorlatokkal és játékokkal, amelyekhez nincs szükség különösebb alapképzettségre. Ne felejtsük el azonban, hogy - tekintettel a személyi számítógépek közti nagy különbségekre - a fejezet nem helyettesítheti a géphez mellékelt "gépkönyv"-et. Inkább csak a gépkönyvtől különböző megvilágításban mutatja be ugyanazokat a dolgokat. Leírásunkban a XZ SPECTRUM gépet vettük alapul.
A programírás alapelveiről
Ha hozzálátunk egy program megírásához, legegyszerűbb, ha szerkezeti egységekre bontjuk, mégpedig olyan kis részekre, amelyeket már meg tudunk fogalmazni a gép nyelvén. Olyan ez, mint amikor az egyszerű tőmondatból bővítgetéssel építjük föl a teljes mondatot. Megszerkesztjük a program vázát, aztán összetartozó egységenként hozzáírjuk minden mondanivalónkat. Ez a legfontosabb elv, ezt kell mindig szem előtt tartanunk. Az ilyenfajta programozás a szerkezetre épül, ezért strukturált programozásnak nevezik. Legelőször a gép nyelvével kell megismerkedni, amiben néhány játékos program is a segítségünkre lesz.
A gép "logikája"
A bekapcsolt gép "figyel", másodpercenként többször is megvizsgálja, hogy milyen billentyűt ütöttünk le. Várja tőlünk a parancsokat, és amit kérünk, azt elvégzi. A parancs a számítógép vezérlésének egyik módja, amelyet - szemben az utasítással - azonnal végrehajt a gép (az utasításokat csak megjegyzi, és a program indítása után hajtja végre). Az utasítások egy része parancsként is kiadható; a megkülönböztetés alapja, hogy sorszámmal kezdődik-e a sor vagy sem. A PRINT 4+4 parancs, amelynek hatására a képernyőn megjelenik a 8 felirat, míg pl. a 120 PRINT 4+4 utasítás, s a 8 eredményt csak akkor írja ki a gép, ha a programot elindítottuk, s az eljutott a 120-as sorra.
Hogy mikor kezdheti földolgozni azt, amit kértünk, azt onnan tudja meg, hogy visszaadjuk a "vezérlést". Erre a gépeken javarészt jobboldalt található Enter, Return, New Line, CR gombot használhatjuk. A sokféleséget elkerülendő, jelöljük ENTER-rel.
Kiíratás: PRINT
Minden személyi számítógép egyben számológép is; elvégzi a megszokott műveleteket. Ha beütjük, hogy 5+8, akkor elvégzi az összeadást, vagy szintaktikai hibát jelez. Csakhogy semmit sem látunk az eredményből. Ahhoz, hogy megtudjuk, mennyi is az 5+8, kérnünk kell, hogy írja ki. Erre az angol PRINT szót használják. PRINT 5+8 parancs után (ne felejtsük el visszaadni a vezérlést a gépnek!) már megjelenik a 13.
Ennél azonban sokkal többet is tud a személyi számítógép. Nagy előnye a számológéppel szemben, hogy egyrészt "változókat" tud kezelni, másrészt "szövegekkel" is képes dolgozni. Változónak vagy azonosítónak nevezzük az olyan - a mikroszámítógépeken használatos BASIC nyelvben többnyire csak két jelből, de legalább egy betűből álló: betű, két betű, betű-szám-jelcsoportokat, amelyekhez értékeket rendelhetünk, és ezekre az értékekre a változó nevével hivatkozhatunk. A változó értéke lehet szám, de "szöveg" is. Itt a szöveg annyit jelent: jelsorozat. Állhat betűkből vagy akármilyen jelből, amelyet a gép le tud írni. Ezeket karaktereknek hívjuk, és idézőjelek közé tesszük. A karakteres változó angolul string (ejtsd: sztring, jelentése: füzér), ami arra utal, hogy a karakterek egymás után következnek.
Nemcsak számítási eredményeket írathatunk ki, hanem a változók értékét is. Legyen ismét az I változó értéke 5+8, a BASIC-ben ez így szól: LET I=5+8; sok gépen (de a Spectrumon nem) el is hagyható a LET szócska: I=5+8. Ezután a PRINT I paranccsal megkapjuk az eredményt. Használhatjuk a PRINT-et stringek kiíratására is. A BASIC a szöveges és a numerikus változókat (azonosítókat) úgy különbözteti meg egymástól, hogy a szöveges változó neve mindig $ jellel végződik. Például: A$. Legyen tehát LET A$="NAGY TIBOR". A PRINT A$ parancsra a gép kiírja: NAGY TIBOR. (A pontot nem, azt mindkét esetben csak a magyar helyesírási szabályok követelték meg.)
Az idézőjelnek fontos szerepe van a karakteres változóknál, hiszen a PRINT "JO" és a PRINT JO két teljesen különböző dolog. Az első kiíratja, hogy JO, míg a második a JO nevű változó értékét írja ki (ha korábban nem használtunk ilyen nevű változót, akkor 0-t; egyes gépek - így a Spectrum is - pedig hibát jeleznek ilyenkor). Próbáljuk ki!
A legtöbb személyi számítógépen e két vagy több utasítást meg lehet adni egy sorban,de el kell választanunk - mégpedig kettősponttal - őket. PRINT "JO": PRINT JO. A több utasítást tartalmazó sort utasítássornak hívják. A képernyőn látható sor nem azonos a számítógép által egy sorként kezelt egységgel. Ez utóbbi minden esetben sorszámmal kezdődő és egymástól kettősponttal elválasztott utasítások sorozata. A sor hossza azonban általában korlátozott; a legtöbb számítógép két vagy három képernyő sornyi utasítást hajlandó egy sorként elfogadni. Az is előfordulhat, hogy nagyon sok utasítást akarunk adni, vagy hogy ugyanazt az utasítást sokszor el akarjuk végeztetni. A program éppen arra való, hogy megjegyeztessük az utasításokat a géppel, és így ne kelljen annyit gépelnünk.
Hogyan lesz utasításokból program?
A BASIC nyelvben elég (de egyúttal szükséges is!) egy számot írni az utasítássorok elé, amelyek egyúttal a sorok közti sorrendet is meghatározzák. A számoknak nem fontos egyesével növekedniük, sőt a későbbi beszúrásokra lehetőséget teremtve általában tízesével következnek:
10 PRINT "jo"
20 PRINT jo
Amikor ezeket a sorokat (ENTER-rel) beadjuk, látszólag semmi nem történik, ilyenkor jegyzi meg azonban a gép, hogy mit kell majd csinálnia. Tehát míg a parancsok eltűntek, addig ezek megmaradnak a memóriában. Ha "elő akarjuk hívni", vagyis ki szeretnénk íratni a képernyőre, akkor LIST (ejtsd: liszt, jelentése: lista) parancsot kell adnunk. A program utasításait pedig a RUN (ejtsd: ran, jelentése: fut) parancs hatására végzi el. (Most se feledkezzünk el az ENTER-ről.)
A lefuttatott program kiírja, hogy "jo" és 0-t vagy pedig hibát jelez, aszerint, hogy a gép hogyan kezeli a változókat.
Még egyszer PRINT
Mint már láttuk, a legtöbb gépen két utasítás is lehet egy sorban. A PRINT azonban egy olyan speciális utasítás, hogy még azokon a gépeken is írhatunk két kiíratást egy sorba, amelyeknél más utasításra ez nincs megengedve (pl. ZX 81). Mindössze annyit kell tudnunk, hogy a PRINT ...; formában megadott kiíratásban a pontosvessző miatt a legközelebbi kiírató utasításnál a gép folytatólagosan ír, és a pontosvessző után elég csak megadni, hogy mit akarunk kiíratni. Például: PRINT "jo";jo. Most a két kiírt karaktersorozat közvetlenül egymás mellé került.
Ha kicsit távolabbra akarjuk íratni őket, akkor vesszővel kell elválasztanunk: PRINT "jo",jo. A távolság gépenként változó. Próbáljuk ki, mi történik, ha két vesszőt írunk egy helyett: PRINT "jo",,jo. Nézzük meg azt is, hogy hány vesszőt kell írnunk ahhoz, hogy az előbbi PRINT "JO":PRINT JO sorral megegyező eredményt kapjunk. (Itt is érvényesek az előbbi megjegyzések az értékadás nélküli változókról.)
Mi történik, ha a pontosvesszőkből is többet írunk? Sajnos semmi, ami akkor is zavaró, amikor két szöveges változót íratunk ki. PRINT "JO";"JO" végeredménye: JOJO. (Van ennek előnye is természetesen.) Ahhoz, hogy eggyel távolabb kerüljön a két szó, szóközt kell közé tennünk, mégpedig mindig az idézőjelen belül: PRINT "JO ";"JO", vagy külön karakterként: PRINT "JO";" ";"JO".
És hajtsa végre újra...
Legyen az A$ értéke újra a Nagy Tibor név, és legyen egy szóköz a végén. LET A$="NAGY TIBOR ". írassuk ki kétszer közvetlenül egymás után, tehát pontosvesszővel elválasztva. De próbaképp mégis két külön sorba írjuk a két PRINT utasítást:
10 LET A$="NAGY TIBOR "
20 PRINT A$;
30 PRINT A$
Az eredmény: NAGY TIBOR NAGY TIBOR, vagyis a pontosvessző ottléte miatt folytatólagos a kiírás.
Az egyes utasítások végrehajtása automatikusan, sorszám szerint halad. Vannak azonban úgynevezett ugró-utasítások, amelyekkel, legalábbis a végrehajtás szempontjából, átrendezhetjük a sorokat. Ilyen a GO TO - más gépeken GOTO - (az angol go to kifejezésből, ejtsd: gótu, jelentése: menj ... -hez), amit az a sorszám követ, ahová ugrik a program.
Ha a fenti programban a 30-as sor helyére GO TO 10-et írunk, akkor azt kérjük ezzel, hogy menjen a 10-es sorra, és hajtsa végre újra. Azt várjuk, hogy a futtatás eredménye ugyanaz lesz, mint az imént (hiszen a 10-es sorban kiírja a nevet, rámegy a 30-asra, onnan visszaküldjük a 10-esre, és újra kiíratjuk az A$-t). Amikor azonban azt látjuk, hogy a harmadik név is megjelenik, sőt a negyedik, az ötödik stb., míg tele nem lesz a képernyő, akkor már nyilvánvaló, hogy a kör bezárult: a másodszori kiírás után újra rámegy a 30-as sorra, aztán újra kiír stb. A gépünket - ha nem állt még le hibajelzéssel - a BREAK gomb lenyomásával állíthatjuk le.
A feltételes leállás
Számoltassuk a géppel, hányszor írta ki ezt a nevet, és a tizenharmadiknál állítsuk le. A számolásra használjuk az I változót: először értéke legyen 0. Valahányszor az A$-t kiíratjuk, az I értékét növeljük eggyel, vagyis I helyébe 1+1 kerüljön: LET I=I+1. Mivel l-t mindig akkor növeljük, amikor kiírunk egy nevet, ezért I épp akkor lesz 13, amikor az A$-t tizenháromszor írtuk le. Ha I=13, akkor vége. Ez angolul így hangzik: IF I=13 THEN STOP. (Más gépeken STOP helyett az END utasítás szolgál erre a célra.) Szó szerint ez lesz az egyik programsor is. Ellenkező esetben visszamegyünk arra a sorra, ahol növelünk és kiírunk. (E két utasítást azért rakjuk egy sorba, mert logikailag szorosan kapcsolódnak. Azokon a gépeken, ahol ez nem lehetséges, a 30-as sort kétfelé tagoljuk, és a második felét beírjuk 35-ös sornak.)
10 LET I=0
20 LET a$="NAGY TIBOR"
30 LET I=I+1: PRINT a$
40 IF I=13 THEN STOP
50 GO TO 30
A ciklus
A BASIC nyelvben a ciklikusan ismétlődő programrészeket, eljárásokat egyszerűb-ben is meg tudjuk adni: az úgynevezett FOR-NEXT utasításpárral. A FOR utáni "ciklusváltozónak" kezdőértéket adunk, és a TO utasítás után írjuk a végső értéket: FOR i=1 TO 13.
(Itt az I nem 0-ról indul, de az előző programban is az I=1 értékkel léptünk be a ciklusba.)
A FOR ... TO ... utasítást követő sorokat (az úgynevezett ciklusmagot) a gép végrehajtja, míg a NEXT I (jelentése: következő I, értsd: az I következő értéke) lezárási utasítást meg nem találja. Tehát a program:
10 LET a$="NAGY TIBOR"
20 FOR i=1 TO 13
30 PRINT a$
40 NEXT i
Futtassuk le, az eredmény ugyanaz. Az egyetlen különbség, hogy most az I értéke 14, ezt a PRINT I utasítással ellenőrizhetjük. Az előbb 13-nál hagytuk abba a futtatást, ezért I értéke végül 13 volt.
A két szerkezet tehát nem azonos. Az utóbbinál a NEXT I növel, és a FOR vizsgálja, hogy a ciklusváltozó túlment-e a fölső korláton. Ha nem, akkor visszamegy a kiíró sorra (a 30-as utasításra). (Egyébként a FOR nem a 20-as sorban vizsgál, ott csak értéket ad, hanem a 40-esben. Így a ciklusnak megfelelő szerkezet a következő:
10 LET a$="NAGY TIBOR"
20 LET i=1
30 PRINT a$
40 LET i=i+1: IF i<=13 THEN GO TO 30
Más szöveg
Ha a programíráskor még nem tudjuk, hogy mi is A$ értéke, illetve későbbre hagyjuk, a "felhasználóra" bízzuk a szöveget, akkor INPUT utasítást kell használnunk. így a program futása közben is lehet akár numerikus, akár szöveges adatokat beolvasni.
Az INPUT (ejtése: kivételesen ugyanaz, ahogy olvassuk, jelentése: bemenet) hatására a program megszakítja a futást, vár egy bemenő adatot (ENTER-rel kell beadnunk), amit az INPUT után álló változóhoz rendel, és folytatja a futást.
10 INPUT a$
20 FOR i=1 TO 13
30 PRINT a$
40 NEXT i
Most már akár azt is megadhatjuk (egy másik INPUT-ban), hogy hányszor írja le az adott szöveget:
10 INPUT a$
15 INPUT n
20 FOR i=1 TO n
30 PRINT a$
40 NEXT i
A program futtatása kényelmetlen, mert nem tudjuk, mikor vár számot és mikor szöveget (Spectrumon a megjelenő idézőjel jelzi, ha szövegfüzért vár a program), ezért jobb, ha kiíratjuk az INPUT előtt, hogy milyen adat szükséges. Az első két sor tehát így módosul:
10 INPUT "Mi a neved? ";a$
15 INPUT "Hanyszor irjam le? ";n
20 FOR i=1 TO n
30 PRINT a$
40 NEXT i
Más BASIC nyelvjárásokban általában nem tud szöveget megjeleníteni az INPUT utasítás, ott a következő alak használható:
10 PRINT "MI A NEVED? ": INPUT A$
20 PRINT "HANYSZOR IRJAM LE? ": INPUT N
Karakteres változók
Próbáljuk ki a következő programot:
10 LET a$="KEL"
20 LET b$="KAPOSZTA"
30 PRINT a$+b$
Azt tapasztaljuk, hogy a gép valóban összeadja, vagyis összerakja a két szót: ez az egyetlen szokásos művelet, amit karakteres változókon is végre lehet hajtani. A kivonást már más utasítás helyettesíti, amellyel az utolsó karakterekből annyit lehet levágni, amennyit akarunk (persze nem többet, mint amennyi van).
A szó vége a jobb oldali karaktert jelenti. Angolul a jobb RIGHT (ejtsd: rájt), és az A$-nak a jobb oldali, vagyis utolsó N karaktere pedig RIGHT$(A$,N). A bal oldali karaktereknek, vagyis az első N a karakternek LEFT$(A$,N) felel meg. (LEFT jelentése bal.) Kiemelhetjük a szöveg belsejét is. Ha a K-adiktól N hosszon át van rá szükségünk, akkor a MID$(A$,K,N) adja ezt meg. Más gépeken - így a Spectrumon is - csak egy utasítás van, A$(K TO N) a K-adiktól az N-edikig adja meg a szöveg karaktereit. Az A$ szöveg hosszát minden gépen a LEN(A$) határozza meg. Így ez utóbbi jelöléssel az első, illetve az utolsó N karakter ez lesz:
A$( TO N) vagy A$(1 TO N)
A$(LEN(A$)-N+1 TO ) vagy A$(LEN(A$)-N+1 TO LEN(A$))
Szóépítés
Az elmondottak alapján próbáljunk olyan programot írni, amely kiírja a diákok év végi kedvenc feliratát:
O
IO
CIO
ACIO
KACIO
AKACIO
VAKACIO10 LET a$="VAKACIO"
20 FOR i=LEN (a$) TO 1 STEP -1
30 PRINT A$(i TO )
40 NEXT i
Más gépeken ugyanez a program:
10 A$="VAKACIO"
20 FOR I=1 TO LEN(A$)
30 PRINT RIGHT$(A$,I)
40 NEXT I
Ha jobbra akarjuk igazítani a kiírást, akkor minden kiíratás elé a megfelelő számú szóközt írunk:
10 LET a$="VAKACIO"
20 FOR i=LEN (a$) TO 1 STEP -1
30 PRINT " "(1 TO i-1);a$(i TO )
40 NEXT i
Ezek után nem lesz nehéz az a program, amely INPUT-tal bekér egy karakteres változót, majd visszafelé kiírja:
10 INPUT a$
20 FOR I=LEN (A$) TO 1 STEP -1
30 PRINT A$(I);
40 NEXT I
Más gépeken ugyanez a program:
10 INPUT A$
20 FOR I=1 TO LEN(A$)
30 PRINT MID$(A$,LEN(A$)+1-I,1);
40 NEXT i
Nemcsak jobbról balra, mint a VAKACIO szóval tettük, hanem visszafelé is építhetünk szavakat. A betűpiramis nevű nyelvi játék olyan szavakat keres, amelyeknek első néhány betűjét összeolvasva már értelmes szót kapunk, és ha tovább ragasztgatjuk ehhez az értelmes szóhoz az alapszó egymás utáni betűit, akkor is csupa értelmes szó jön ki; ilyen szó például az ADOMA.
Titkosírás
A gép leírása többek közt egy úgynevezett kódtáblázatot is tartalmaz. Ebből tudjuk meg, hogy a különböző karaktereket milyen kódok "képviselik". Például az A betű többnyire a 65-ös kódú jel, a Z kódja 90. E két érték között helyezkednek el sorban az angol ábécé betűi. Elég is ennyit tudni ahhoz, hogy megalkossuk a titkosírást. Két lehetőség is van. Az egyik a betűket egyszerűen a kódjukkal helyettesíti (vagyis a beírt betűsorra egy számsort ad ki); a másik már kicsit bonyolultabb: megnézi a betűsor elemeinek kódját, és például az eggyel nagyobb kódú jeleket írja ki. A szóközöket mindkét esetben meghagyjuk szóközöknek.
Tudnunk kell, hogy egy jel kódját a CODE (más gépen az ASC) függvény árulja el, vagyis egy szövegként kezelt karakterhez a kódját rendeli, például: CODE "A" = 65. A CODE nem feltétlenül csak egy karakteren értelmezhető. Bármilyen hosszú szöveget beírhatunk, de ilyenkor csak az első karakter kódját adja meg. A CODE függvény fordítottja a CHR$, amely a 0 és 255 közé eső kódhoz tartozó karaktert mondja meg. Például: CHR$(67) = "C".
Tehát az A$ I-edik karakterének kódja:
CODE a$(i)
más gépeken:
ASC(MID$(A$,I,1))
míg az ennél eggyel nagyobb kódú karakter:
CHR$ (CODE a$(i)+1)
más gépeken:
CHR$(ASC(MID$(A$,I,1))+1)
Így az első titkosírásnak megfelelő program:
10 INPUT "Mi a szoveg? ";a$
20 FOR i=1 TO LEN a$
30 IF a$(i)=" " THEN PRINT " ";: GO TO 50
40 PRINT CODE a$(i);" ";
50 NEXT i
Ugyanez más gépeken:
10 PRINT "MI A SZOVEG? ":INPUT A$
20 FOR I=1 TO LEN(A$)
30 IF MID$(A$,I,1)=" " THEN PRINT " ";:GOTO 50
40 PRINT ASC(MIS$(A$,I,1));" ";
50 NEXT I
A második titkosírásnak megfelelő programot úgy kapjuk, hogy az előbbi programba a CODE a$(i);" " helyett CHR$ (CODE a$(i)+1)-et írunk.
Madárnyelv
A titkosírás után jöjjön most a titkos beszéd: a madárnyelv. (Tuvudsz ivigy beveszévélnivi?) A szabály a következő: ha a magánhangzóhoz érünk, akkor egy v-t ejtünk, és újra ugyanazt a magánhangzót. Így lesz például az "a"-ból "ava". A programban tehát csak azt kell figyelnünk, hogy magánhangzónál tartunk-e. B$-ban a vizsgált (éppen soron következő) karaktert tároljuk.
10 INPUT "MI A SZOVEG? ";a$
20 FOR i=1 TO LEN (a$)
30 LET b$=a$(i): PRINT b$;
40 IF b$="A" OR b$="E" OR b$="I" OR b$="O" OR b$="U" THEN PRINT "V";b$;
50 NEXT i
Figyeljünk, hogy a program jelenlegi állapotában csak nagybetűvel írt szövegfüzérekkel működik. Hogy kisbetűket is elfogadjon, a 40. sorban a feltétel vizsgálatot kell kiegészíteni.
Érdekes és nem is túl nehéz probléma annak a programnak a megírása is, amely a madárnyelven írt szöveget "visszafordítja", ezért ezt az olvasóra hagyjuk.
Néha jó lenne, ha programfutás közben letörölhetnénk a már kiírt információkat. Sok gépen e célra van egy olyan karakter (például a 12-es kódú), amelynek kiíratásakor a képernyő kitisztul. Tehát a PRINT CHR$(12) utasítás letörli a képernyőt. A Spectrum erre az egyszerű CLS (CLear Screen = töröld a képernyőt) utasítást használja.
Minták
Az utolsó játék a PRINT-tel egy szöveg grafikus jelekké való átkódolása. Minden betűnek megfeleltetünk egy grafikus jelet a karakterkészletből. Nem feltétlenül fog minden betűhöz más jel tartozni, de ez nem baj, mert most nem az a célunk, hogy titkosítsuk a szöveget, hanem hogy mintát rajzoljunk a segítségével. A legtöbb gépen elég az ábécé betűinek kódjait valamennyivel eltolni ahhoz, hogy grafikus jelek legyenek belőlük. Spectrum-on például az ábécé kódok 65-tel kezdődnek, és a grafikus jeleké 129-cel, akkor 64-et kell a betűkódokhoz hozzáadni. Ha nem megy ilyen egyszerűen, mert nincs annyi grafikus karakter, akkor egy egyszerű összefüggést kell keresnünk, amely megfelel a célra.
A második titkosírás-programból kapjuk a grafikus programot. Csak most az CODE a$(i)-et nem eggyel növeljük, hanem például 65-tel, vagy pedig elvégezzük ezt a bizonyos általunk talált egyszerű átalakítást.
Nemcsak szöveget, hanem számokat is átkódolhatunk mintákká. Például egy bűvös négyzetet vagy egy latin négyzetet. A latin négyzetet a következő tulajdonság jellemzi - vegyünk például egy 6x6-os méretűt az első hat szám mindegyikéből hat darab van benne, minden sorban és oszlopban pontosan egy. Már 6x6-os latin négyzet is nagyon sok van, de készíthetünk más méretűt is.
Példa 6x6-os latin négyzetre:
| 1 | 2 | 3 | 4 | 5 | 6 |
| 6 | 1 | 2 | 3 | 4 | 5 |
| 5 | 6 | 1 | 2 | 3 | 4 |
| 4 | 5 | 6 | 1 | 2 | 3 |
| 3 | 4 | 5 | 6 | 1 | 2 |
| 2 | 3 | 4 | 5 | 6 | 1 |
Ezt a 6x6 számot úgy tárolhatjuk az A$-ban, mintha folytonosan olvasnánk: A$="123456612345561234456123345612234561". A$-t egy "kettős ciklussal" fogjuk lebontani. Az I a sorokat sorszámozza, a J a szám sorszáma az l-edik sorban. Most mindkét változó 1-től 6-ig megy. Az l-edik sor J-edik eleme az A$-nak (I-1)*6+J-edik karaktere, hiszen I-1 teljes soron jutottunk túl, míg az l-edikbe értünk, azaz (I-1)*6 számon. Ebben az l-edik sorban pedig J karakternyit megyünk előre.
Hat jelet szeretnénk egymás mellé kiíratni, erre a PRINT ...; típusú utasítást használjuk. Ezután új sort kezdünk. Az utolsó PRINT ...; pontosvesszőjének hatását azzal oldhatjuk föl, hogy beírunk egy "üres" PRINT utasítást, ami nem ír ki semmit, csak új sort kezd. A program tehát (legyen most a számok és a grafikus jelek kódjai közt a különbség 86 - csak mert így kapunk érdekes mintát):
10 LET a$="123456612345561234456123345612234561"
20 FOR i=1 TO 6
30 FOR j=1 TO 6
40 LET n=(i-1)*6+j
50 PRINT CHR$ (CODE a$(n)+86);
60 NEXT j
70 PRINT
80 NEXT i
Így készíthetünk "véletlen mintákat" is. Például:
10 RANDOMIZE
20 PRINT CHR$ INT (RND*16+128);
30 GO TO 20
Az RND függvényről a II. fejezet Véletlen elemek című szakaszában és a III. fejezet Valószínűség című szakaszában részletesebben is beszélni fogunk.
A latinnégyzet-programnál a hat sort vehetjük hat külön stringnek, hat adatnak, amit egymás után kell majd földolgozni, így a kibontás képletét elkerüljük. Adatokat a DATA (DATA jelentése: adatok) utasítással tárolhatunk, amelyeket a program futása közben "olvasunk be" a READ (ejtsd: ríd, jelentése: olvasni) utasítás segítségével. Ez lehet a program:
10 FOR i=1 TO 6
20 READ a$
30 FOR j=1 TO 6
40 PRINT CHR$ (CODE a$(j)+86);
50 NEXT j
60 PRINT
70 NEXT i
80 DATA "123456","612345","561234","456123","345612","234561"
A DATA - ahogy mondani szokás - "nem tartozik a BASIC-hez": ez annyit jelent, hogy a programban bárhol elhelyezhető. Például megadhattuk volna az iménti program 5-ös sorában is. A READ utasításra a gép végiglépked a DATA soron, és minden értéket kiolvas, de csak egyszer. Ha az adatokra többször is szükség volna, akkor a RESTORE (ejtsd: risztor, jelentése: helyreállít) utasítást kell adnunk, pontosabban RESTORE (sorszám) alakú utasítást, ahol a megfelelő DATA sor számát kell megadnunk. Ügyelnünk kell azonban arra, hogy mely adatokat akarjuk ismételten beolvasni: ilyenkor célszerű az értékeket több sorban elhelyezni.
A gép memóriájába a PEEK (ejtsd: pík, jelentése: kukucskálni, belesni) - kicsit bonyolult, de igen érdekes függvény - valamint a hozzá szorosan kapcsolódó POKE (ejtsd: pók, jelentése: belökni) utasítás segítségével lehet betekinteni.
A memóriahelyek meg vannak számozva, hogy mettől meddig, az a géptől - illetve annak memóriakapacitásától - függ. Minden helyen (ezeket címeknek hívják) egy 0 és 255 közötti szám áll. (A gépi információ számokra épül.) A PRINT PEEK 20000 utasítás a 20000-es helyre kukucskál be, és kiírja a tartalmát. A POKE 20000,65 a 20000-es helyre 65-öt lök be. Ez a két utasítás szédületes lehetőségeket rejt magában. Lényegében uralkodni tudunk a memórián. Például meg tudjuk tréfálni a gépet: ha tudjuk, hogy hol tárolja a programot, akkor át tudjuk javítani az egyik programsor számát jóval kisebbre.
Azt a nyelvet, amely a BASIC-nek ezt a két utasítását használja, Controlled BASlC-nek hívják, amit magyarra Ellenőrzött BASIC-nek fordíthatnánk.
Végül még egy hasznos tanács a programíráshoz. Érdemes egy sorba írni a logikailag szorosan összetartozó utasításokat, de legalábbis úgy számozni őket, hogy a számok legfeljebb az egyesekben térjenek el. Hasonlóképp az alprogramok utasításainak sorszáma egymástól csak az egyes és tízes helyi értékeken álló számokban térjenek el. Ezzel is fel tudjuk tüntetni a szerkezet lényegét.
Bevezetés
A személyi számítógépek többsége monitor vagy közönséges tv-készülék képernyőjén jeleníti meg a program által előállított számértékeket, szövegeket, ábrákat stb. A képen számítások eredményei jelennek meg, esetleg a bekért adatokra vonatkozó emlékeztető szövegek, vagy pedig olyan táblák és pályák, amelyeken különféle játékokat lehet lejátszani, egyszóval mindig olyasmi, ami valamilyen további célt szolgál. Miért ne lehetne a megjelenítés célja maga a kép, pusztán a szépség vagy érdekesség kedvéért? Természetesen lehet. .A nagy számítógépekhez kapcsolt sornyomtatókkal és rajzgépekkel már régóta készítenek komputeres grafikákat. Ki is alakult a grafikának egy ága, amelyet "Computer Art"-nak neveznek.
A személyi számítógépek némelyike még jobb lehetőséget nyújt grafikai alkalmazásokra, mint a hagyományos nyomtató- és rajzolóeszközökkel ellátott számítógépek: színes képernyőn finom rajzolatú színes ábrák és mozgó képek készíthetők velük.
Ebben a fejezetben személyi számítógépes grafikai programokról lesz szó. Az első részben az eszközökről, az ilyen programok készítéséhez szükséges alapvető ismeretekről és programozási fogásokról, a másodikban pedig néhány konkrét grafikai ötletről olvashat az érdeklődő. Az első rész lényegében nem számít több programozási ismeretre, mint amit az első fejezetből is el lehet sajátítani - a másodikban némi gyakorlatot tételezünk fel grafikai programok készítésében, amelyhez remélhetőleg az első részben leírtak is valamelyest hozzájárulnak. Mindenesetre azt az olvasót, akit e fejezet megírásakor magunk elé képzeltünk, inkább jellemzi az érdeklődés és kísérletező kedv, mint a magas fokú programozási készség; az itt leírtakkal pedig ahhoz akarjuk hozzásegíteni, hogy a maga ízlésének és elképzeléseinek megfelelő grafikai programokat tudjon készíteni személyi számítógépén.
Kicsit másfajta örömet nyújt az ilyesfajta programok írása, mint a népszerű interaktív (a géppel párbeszédben játszott) ügyességi, nyelvi, logikai játékoké. Itt nagyobb hangsúly kerül az ötletre és a megvalósítás módjának felfedezésére, mint magára az eredményre. Ha már sikerült elképzelésünket megvalósítani, nem sok lehetőség marad a beavatkozásra - csak annyi, hogy gyönyörködjünk az elkészült grafikában. A nagy mű kész, az alkotó pihen.
Nem lehet persze sokáig élvezni egy olyan programot, ami mindig pontosan ugyanazt csinálja, mondjuk mindig ugyanazt a képet állítja elő. Ezért olyan módszereket is le fogunk írni, amelyek némi változatosságot vihetnek ezekbe a programokba, részben véletlen, részben a "néző" beavatkozásától függő mozzanatok felhasználásával. Azzal is érdekesebbé tehetjük programjainkat, ha egy ötlet különböző variációit közös sémába foglaljuk, amelyből aztán tetszés szerint kiválaszthatjuk, mikor melyiket szeretnénk megjeleníteni.
Az itt leírt programok BASIC nyelven készültek. Sajnos a különböző számítógépek némileg eltérő BASIC "nyelvjárást" használnak, és a legnagyobb eltérések éppen a grafikai utasításokban vannak. Ezért elsősorban a két viszonylag elterjedt gépről, a Sinclair ZX 81 és Sinclair Spectrum típusú számítógépekről fogunk írni, a közölt programok mindig e két gép valamelyikén működnek, csak helyenként utalunk arra, hogyan lehet hasonló feladatokat más típusú gépeken (például HT 1080Z) megoldani. Mivel amúgy sem az a célunk, hogy kész programokat adjunk az olvasónak, hanem hogy felkeltsük érdeklődését a grafikai programok iránt és ehhez eszközöket és módszereket javasoljunk, amelyeket saját gépén éppolyan jól fel tud használni, remélhetőleg nem riasztjuk el a másfajta gépek tulajdonosait és ismerőit sem.
Akkor hát - fogjunk hozzá!
A képernyő
Minden személyi számítógéppel lehet karaktereket (betűket, számokat, írásjeleket és műveleti jeleket, és még egy sor speciális jelet) írni a képernyőre. Ha lefuttatjuk a következő rövid programot:
10 PRINT "A";
20 GO TO 10
megfigyelhetjük, hogy a gép szép szabályosan, sorokba és oszlopokba rendezetten, "A" betűkkel írja tele a képernyőt. A sorokat és oszlopokat megszámlálva megállapíthatjuk, hogy a számítógép hány karakterrel tölti ki a képernyőt. A School-computer képernyőjén 16 sor és 64 oszlop jelenik meg. Sinclair gépeknél 22 sort és 32 oszlopot találunk (illetve még két sort a képernyő alján a gép által kiírt üzenetek számára). Ez tehát összesen 22x32 = 704 (illetve 24x32 = 768) karakterhelyet (pozíciót) jelent a ZX 81-nél. Minden karakternek a memóriában egy tárolóhely, más szóval 1 byte (azaz 8 kettes számrendszerbeli helyi érték) felel meg. Ezen az 1 byte-on az adott karakterhelyen álló karakter kódját találjuk - összesen 2^8 = 256-féle különböző kód valamelyikét (amelyek közül persze nem mindegyik felel meg különböző karakternek.
A képernyő tartalmát tehát a memória egy összefüggő területe írja le. Ha tudjuk, hogy ez a memóriaterület hányadik byte-on kezdődik, akkor ki tudjuk számítani, hogy mondjuk az 5. sor 20. karaktere hányadik byte-nak felel meg. A School-computernél az első byte sorszáma 15360, ehhez 4x64+19 = 275-öt kell hozzáadni - az eredmény 15635, és ha ebbe a byte-ba a POKE 15635,65 utasítással a 65 kódot visszük be, akkor az 5. sor 20. helyén megjelenik a megfelelő karakter, az "A" betű. Ha pedig a PEEK (15635) függvény értékét kiíratjuk, az adott helyen álló karakter kódját kapjuk vissza.
A ZX 81-nél bonyolultabb a helyzet. Először is a képernyő első byte-jának sorszáma nem állandó - a PEEK 16396+256*PEEK 16397 kifejezés adja meg. Másrészt a sorok sem állandó hosszúságúak - minden sor végét egy speciális - 118 kódú - Newline (Új sor) karakter jelzi, amellyel együtt maximálisan 33 byte felel meg a képernyő egy-egy sorának. Egy CLS (képernyőtörlés) utasítás végrehajtása után minden sor egységesen ilyen hosszú lesz - ekkor az első byte sorszámához 4x33+19-et kell hozzáadnunk, hogy oda 38-at POKE-olva (a ZX 81-nél más a kódrendszer!) "A" betűt írhassunk a kívánt helyre (az 5. sor 20. karaktere helyére). (A BASIC nyelvben a CHR$ függvény alakítja át a kódokat karakterekké, így például a ZX-81-en a CHR$ 38 az "A" karaktert jelöli; fordított irányban a CODE függvény áll rendelkezésünkre karakterek kódjának előállítására: CODE "A" = 38.) Ha pedig a PEEK (sorszám) függvény értékét kiíratjuk, azt a kódot kapjuk meg, ami az adott sorszámú memória-byte-on a megfelelő karakterhely tartalmát írja le.
POKE-kal és PEEK-kel a memória bármelyik byte-ját (nemcsak a képernyőt leíró memóriaterület byte-jait) módosíthatjuk, illetve kiolvashatjuk. (Természetesen ez csak azokra a memóriaterületekre vonatkozik, amelyek "írhatók" és "olvashatók" (ún. RAM memória). De pl. a BASIC értelmező tartalmát csak olvasni tudjuk (ún. ROM memória), megváltoztatni nem. Vannak emellett olyan memóriák is, amelyeknek a tartalma megváltoztatható, ám ha PEEK paranccsal vagy utasítással próbálkozunk, mindig 0-t jelez a gép, ezek tehát írható, de nem olvasható memóriák.) A képernyő adott karakterhelyének átírására van viszont egy egyszerűbb lehetőség is: ZX 81-nél PRINT AT 4,19;"A" (a számozás 0-tól kezdődik), a School-computernél PRINT @ 275,"A" utasítással közvetlenül az 5. sor 20. helyére írhatunk egy "A" betűt. Egy karakterhely tartalmának kiolvasására viszont a ZX 81-nél csak a PEEK függvénnyel operálhatunk: (PEEK (PEEK 16398 + 256*PEEK 16399)).
A Spectrumnál az egyes karaktereket nem egy-egy byte-ban kódolva találjuk. A SCREEN$(i,j) függvény azonban közvetlenül megadja az i. sor és j. oszlop metszésébe írt karaktert, beleírni pedig szintén a PRINT AT i,j; karakter utasítással lehet.
A későbbiekben, amikor karakteres kijelzési módról beszélünk, az olyan szerkezetű képernyőre, azokra az utasításokra és függvényekre gondolunk, amelyekről ebben a részben volt szó.
Félgrafikus kijelzés
A PRINT-tel kiíratható karakterek között vannak olyan speciális, úgynevezett "grafikai karakterek" is, amelyek a képernyő egy-egy mezejét 2x2 (más gépeknél 3x2) részre osztják, és ezek közül például a HT School-computernél minden lehetséges variációban egyeseket feketén, másokat fehéren jelenítenek meg. Az ilyen karakterek száma tehát 2^(2x2) = 2^4 = 16, illetve 2^(3x2) = 2^6 = 64.
Ezek használatát úgy kell elképzelni, mintha a gép a képernyőt a ténylegesnél kétszer (vagy háromszor) több sorra, és kétszer több oszlopra osztaná, és az egyes sorok és oszlopok kereszteződésében álló kis négyzeteket külön-külön be tudná feketíteni.
Egy kis négyzet befeketítése a PLOT l,J utasítással történik, ahol l (ZX 81-nél) 0 és 63, J pedig 0 és 43 közé esik. Például a PLOT 15,23 utasítás a képernyő bal alsó sarkából számított 16. oszlop és 24. sor metszésében jelenít meg egy kis négyzetet. UNPLOT 15,23 hatására ugyanez kitörlődik.
A School-computernél a PLOT l,J utasítás funkcióját a SET (l,J) utasítás látja el, ahol I a 0 és 127, J pedig 0 és 47 közé esik, az UNPLOT-nak a RESET felel meg. Ugyanakkor itt a POINT (l,J) függvény használható, amely 1-et, illetve 0-t ad aszerint, hogy az I. oszlop és J. sor metszésében található négyzet be van-e töltve vagy nincs. Ez a függvény a ZX 81-nél hiányzik.
Finom felbontású képernyő
Sok személyi számítógép (köztük a Spectrum) olyan sok pontra osztja be a képernyőt, hogy finom rajzolatú ábrák megjelenítésére is alkalmas. A Spectrum például 256 oszlopban és 176 sorban képes pontokat kirajzolni. A memóriában minden pontnak 1 bit (egyetlen kettes számrendszerbeli helyi érték) felel meg, amely azt jelzi, hogy az adott pont ki van-e gyújtva vagy nem. Ez összesen 256x176 bitet, azaz 5,5 Kbyte-ot jelent. A Spectrumnál egy pont kigyújtása a PLOT i,j utasítással történik, ahol i a 0 és 255, j pedig 0 és 175 közé eshet.
A finom felbontású képernyőhöz speciális utasítások tartoznak, amelyek természetesen gépenként különböznek. Egyetlen utasítással egyenes szakaszt lehet húzni adott pontból kiindulva, a tőle vízszintesen és függőlegesen megadott távolságban elhelyezkedő ponthoz. A DRAW 15,-40 utasítás hatására például a gép összeköti az utoljára berajzolt pontot a tőle 15 egységgel jobbra és 40 egységgel lefelé elhelyezkedő ponttal. Harmadik paraméterként megadhatunk egy radiánban vett szöget is, ekkor a két végpont között egy olyan körív rajzolódik ki, amelynek központi szöge a megadott szög, természetesen PLOT-tal ekkor is meg kell adni a kezdőpontot. Például a DRAW 150,-40,.52 ezt rajzolja, előtte mondjuk egy PLOT 50,100 utasítást kell végrehajtani:
10 PLOT 50,100
20 DRAW 150,-40,-.52
30 CIRCLE 160,128,40

A CIRCLE utasítás adott sugárral kört rajzol egy két koordinátával megadott pont körül: például CIRCLE 160,128,40 egy 40 egység sugarú kört a 160,128 pont köré.
Természetesen a DRAW és a CIRCLE utasítás nem rajzol egészen pontos szakaszt, illetve kört - mindkettő kerekített értékkel dolgozik, az adott 256 -176-os négyzetrács pontjaiból próbálja a kívánt alakzatot összeállítani. Ha az összekötendő pontok nincsenek egészen közel, vagy a kör sugara nem túl kicsi, ez nem okoz észrevehető hibát, ám - amint a későbbiekben látni fogjuk - még ezt a kis hibát is ki lehet használni grafikai programok készítésében.
Speciális megjelenítési lehetőségek
Az említetteken kívül a Spectrum még több olyan lehetőséget ad, amely a grafikában hasznunkra válhat. Noha ilyen lehetőségek sok gépen adottak, megvalósításuk annyira eltérő lehet, hogy teljes általánosságban szinte semmit nem mondhatnánk róluk.
Azon a memóriaterületen kívül, amely a képernyőn kigyújtott pontok információját tárolja, a Spectrumban van egy másik memóriaterület, amely speciális képi lehetőségek megvalósítására szolgál. A ZX 81 karakteres képernyőjéhez hasonló beosztásban (de fix helyen, rögzített hosszúságú sorokkal) 704 byte-on a képernyő 704 karakterhelyének tulajdonságait (attribútumait) írhatjuk le.
Minden karakterhelynek (8x8 elemi pontból álló négyzetnek) két színe lehet: egy alapszín (azoknak a pontoknak a színe, amelyek egy karaktert kiadnak) és egy háttérszín (azaz a többi pont színe). Mindkét szín 8 lehetőség közül választható.
Az egy karakterhelyet leíró byte-ban 3-3 bitet köt le a két szín kódolása (2^3 = 8), és 1-1 további bitet a villogás és fényesség jelölése.
A karakterhelyek tulajdonságait megadhatjuk külön utasításokban: ilyenkor minden olyan karakterhelyre érvényesek lesznek, amelyre valamit írunk (akár PRINT, akár másmilyen grafikai utasításokkal). A karakter alapszíne INK szám utasítással adható meg, ahol a szám 0 és 9 közé eshet (0-tól 7-ig a különböző színeket, 8-cal az eredeti szín állítható vissza, 9-cel pedig a háttérrel kontrasztban álló színt - feketét vagy fehéret választhatunk).
A háttérszín PAPER n utasítással jelölhető ki, n most 0 és 7 közé eshet. A felsorolt utasítások mindegyike közvetlenül "beépíthető" az ismert grafikai utasításokba; például a PRINT PAPER 6; INK 4; AT 5,5; "*" az 5,5 karakterhelyen sárga alapra zöld csillagot rajzol. Másutt a színezés ettől teljesen független lehet.
Karakterdefiníció
A Spectrumon lehetőség van arra, hogy a programozó maga definiálta karaktereket írhasson a képernyőre. A definiálható karakterek a 144 kódú "A" karaktertől a 154 kódú "U"-karakterig terjednek. Már tudjuk, hogy minden karakter egy 8x8 pontból álló rácsban rajzolható meg. Nyolc külön utasítással kell megadni minden karakter mind a nyolc sorát (persze ha a nyolc sor valamilyen közös szabállyal adható meg, vagy mindegyikbe INPUT-tal visszük be az értékeket, akkor egy ciklusban is megoldhatjuk a definiálást). Például az "A" billentyűvel meghívott karakter 5. sorát így adhatjuk meg: POKE USR "A"+4,érték. (Az USR "A"+ 4 kifejezés jelenti az "A" karakter 5. sorát - a számozás ugyanis itt is 0-tól kezdődik.) Az érték szó helyére vagy egy kettes számrendszerbeli számot adunk meg a BIN alapszó után írva, amelyben az 1-es jegyek jelölik a karakterben alapszínnel megjelenítendő pontokat (például BIN 11110000 olyan sort határoz meg, amelynek a négy bal oldali pontja van kigyújtva), vagy pedig ugyanennek a kettes számrendszerbeli számnak a tízes számrendszerbeli értékét (ami az előző példában 240 lenne).
0 0 0 1 0 0 0 0 0 0 1 0 1 0 0 0 0 0 1 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 0 0 1 1 1 1 0 1 0 0 1 0 0 0 0 0 1 1 0 0 0
POKE "A", BIN 10000 (16) POKE "A"+1, BIN 101000 (40) POKE "A"+2, BIN 101000 (40) POKE "A"+3, BIN 110000 (48) POKE "A"+4, BIN 100111 (36) POKE "A"+5, BIN 10100100 (103) POKE "A"+6, BIN 11000 (164) POKE "A"+7, BIN 11000 (24)
Néhány példa:
100 FOR i=0 TO 7
110 POKE USR "C"+i,2^i-1
120 NEXT i
130 PRINT CHR$ 146;: GO TO 130
Ez a program háromszögletű karakterekkel írja tele a képernyőt.
Ha a 110-es utasításban a 2^i-1 kifejezés helyére ezt írjuk: 85*(1+i-INT(i/2)*2), akkor a definiált karakter fekete pontjai sakktáblaszerüen helyezkednek el, a karakter szürkének fog tűnni. Ezt a módszert használhatjuk a színek keverésére is, például narancssárga hatást kelt, ha beépítjük a 130-as sorba a PAPER 6; INK 2; utasításokat. (Ugyanis 85= BIN 01010101, és ezt szorozzuk 1-gyel, ha i páros, 2-vel, ha i páratlan, amikor is a kapott érték 170= BIN 10101010.)
10 FOR i=0 TO 7
20 POKE USR "C"+i,68*(i=0)
30 NEXT i
40 PRINT AT 10,10;"o": PRINT OVER 1;AT 10,10;CHR$ 146
SCROLL
A ZX 81-en ezzel az utasítással az egész képernyőt egy sorral feljebb tudjuk tolni, így a legfelső sor elvész, legalul pedig egy üres sor keletkezik.
10 FOR I=0 TO 31
20 SCROLL
30 PRINT TAB I; "*"
40 NEXT I
50 GO TO 10
A program ferde csíkokat rajzol a képernyőre karakterekből, amelyek folyamatosan fölfelé vándorolnak.
A Spectrumon nincs SCROLL, helyette a POKE 23692,2 utasítást használhatjuk. A School-computernél, ha már teleírtuk a képernyőt, automatikusan egy sorral följebb tolódik, mihelyt újabb PRINT utasítást akarunk végrehajtani.
A Spectrumnál a betelt képernyőre a gép nem hibajelzéssel válaszol, hanem a "Scroll?" üzenetet írja ki. Ha erre bármelyik gombot megnyomjuk, a gép az egész képernyőt eltolja annyi sorral, amennyi a képernyőre ráfér, hogy helyet csináljon az újabb kiírások számára - kivétel a Break vagy az "N" billentyű, amelyek hatására a program leáll.
Pontok
Pontnak fogjuk nevezni azt a kis négyzetet, amit a PLOT vagy SET utasítás megjelenít, akár félgrafikus, akár grafikus (finom felbontású) képernyőről van szó. Megvizsgáljuk, hogyan lehet a PLOT utasításban megadott koordináták változtatásával a pontokat a képernyőn mozgatni - ez alapvető a grafikai programok szempontjából, hiszen a legtöbb ábra ilyen pontokból áll össze. Írjunk egy pontot a képernyőre, ami a ZX 81 géphez kapcsolt képernyő bal alsó sarkában lévő origótól számított (25,21) koordinátájú pontot rajzolja ki.
10 PLOT 25,21
a következő utasítás pedig legyen
20 PLOT 35,21
Azt tapasztaljuk, hogy a második pont az elsőtől 10 egységgel jobbra helyezkedik el. Ennek a koordinátákban az felel meg, hogy az utóbbi pont első koordinátája (amely a vízszintes elmozdulásért felelős) 10-zel nagyobb, mint az első ponté. Ha most a 20-as utasításban az első pont koordinátái közül mondjuk a másodikból levonnánk 7-et,
20 PLOT 35,14
akkor a második pont az első alatt 7 egységgel jelenik meg (a második koordináta határozza meg ugyanis a függőleges irányú helyzetet).
Bármilyen ferde irányú eltolást is létrehozhatunk a koordináták variálásával:
10 INPUT a
20 INPUT b
30 PLOT 25,21
40 PLOT 25+a,21+b
Most a program elején beadhatjuk az A vízszintes és B függőleges eltolási értékeket: A pozitív értéke jobbra, negatív értéke pedig balra, B pozitív értéke fölfelé, negatív értéke pedig lefelé való eltolást jelent. Az eltolás nagysága vízszintes irányban A, függőlegesen B abszolút értékével egyenlő.
Más gépeken a SET(X,Y), DOT(X,Y), SETDOT(X,Y) utasítások valamelyikével lehet képpontokat előállítani. A Sinclair gépektől eltérően a legtöbb személyi számítógép esetében X azt jelöli, hogy (0-tól kezdve és felülről lefelé számítva) hányadik sorban, Y pedig azt, hogy (szintén 0-tól kezdve és balról jobbra haladva) hányadik oszlopban kívánjuk a képpontot meg-jeleníteni.
Most nagyítsunk, ill. kicsinyítsünk. Ehhez kell egy hasonlósági középpont és egy hasonlósági arány. A középpont legyen a már szereplő (25,21) pont; egy INPUT utasítással fogjuk bevinni a hasonlóság C arányát, és a hasonlósági transzformációval odábbviendő pont A és B koordinátáját.
10 INPUT c
20 INPUT a
30 INPUT b
40 PLOT a,b
50 PLOT 25+c*(a-25),21+c*(b-21)
Ha C-nek 2-t adunk meg, a program a beadott pontot a középponttól kétszeres távolságra viszi; ha 0.5-öt, akkor meg fele távolságra. C = -1-re tükrözést végez a középpontra.
Ha az 50-es utasításban csak az egyik koordinátát változtatjuk meg az (A,B) ponthoz képest, akkor a középponton átmenő merőleges tengelyekre vonatkozó vetítést (nagyítást-kicsinyítést) tudunk végrehajtani. C = -1-re most tengelyes tükrözés jön létre.
Adott ponthoz viszonyított derékszögű elforgatás a következőképpen valósítható meg:
10 INPUT a
20 INPUT b
30 PLOT a,b
40 PLOT 25+(b-21),21-(a-25)
vagy a másik irányba:
40 PLOT 25-(b-21),21+(a-25)
Azaz az új pont két koordinátájának eltérését a középpont koordinátáitól felcseréljük, és valamelyiket negatív előjellel vesszük.
Ha valamilyen T szöggel akarunk elforgatni egy pontot a középpont körül (az óra járásával ellentétes irányban), a következőképpen járhatunk el:
10 INPUT a
20 INPUT b
30 INPUT t
40 LET c=COS t
50 LET s=SIN t
60 PLOT a,b
70 PLOT 25+c*(a-25)-s*(b-21),21+s*(a-25)+c*(b-21)
A PLOT utasításban ezúttal egy olyan bonyolult kifejezés szerepel, ami megérthető ugyan a középiskolában tanult sinus és cosinus addíciós képletekből, de a példa analógiájára az is használhatja, akit nem érdekel, pontosan hogyan is működik.
Ne lépjünk le a képernyőről!
Néha, amikor egy pontot el akarunk tolni, egy másikból vetíteni vagy elforgatni, azt tapasztaljuk, hogy a gép hibajelzéssel megáll - a kiszámolt koordináták ugyanis már nem esnek a képernyőre. Pontosabban azt vehetjük észre, hogy kilépve a képernyőről felfelé és jobbra, hibajelzést kapunk, az alsó, illetve bal oldali széltől pedig visszatükröződik a pont, a gép a koordináták abszolút értékét veszi. Ezzel grafikai programok készítésénél mindig számolni kell, és meg kell találni a megfelelő védekezési módot.
Ha PLOT kifejezés1,kifejezés2 alakú utasítással rajzoljuk ki a pontokat, célszerűbb helyette előbb egy LET X = kifejezés1, és LETY = kifejezés2 utasítást írni, hogy aztán X és Y értékének ellenőrzése után írhassuk: PLOT X,Y. A legegyszerűbb, ha megvizsgáljuk, hogy X és Y megengedett értékeket vesznek-e föl, és csak ekkor engedjük meg a PLOT végrehajtását. Például ZX 81 esetében:
IF 0<=X AND X<=63 AND 0<=Y AND Y<=43 THEN PLOT X,Y
A másik lehetőség, hogy a képernyő bal oldalán kicsúszott pontot jobb oldalon, az alul "letévedt" pontot pedig fölül hozzuk vissza (és természetesen fordítva is). Ez annyit jelent, hogy X értékéből csak a 64-gyel, Y-éból pedig a 44-gyel való osztás maradékát tekintjük.
LET X=X-64*INT(X/64)
LET Y=Y-44*INT(Y/44)
Ekkor X automatikusan 0 és 63, Y 0 és 43 közé esik, így minden ellenőrzés nélkül PLOT X,Y-t írhatunk.
Megtehetjük azt is, hogy ha a pont valamelyik oldalon kívül esnék a képernyőn, akkor azon a szélen megállítjuk. Ezt a következő átalakítással érhetjük el:
X*(0<X AND X<64)+63*(X>63)
Y*(0<Y AND Y<44)+44*(Y>44)
A zárójeles kifejezés - mint az előbb is - +1 -et vagy 0-t ad eredményül attól függően, hogy a kijelölt reláció (=, <, <= stb.) teljesül-e vagy sem. Így az átalakítás után X értéke 0 lesz, ha korábban 0-nál kevesebb volt; 63, ha eredetileg nagyobb; egyébként pedig változatlan marad - Y átalakítása is hasonló módon történik. A PLOT utasítást itt is ellenőrzés nélkül kiadhatjuk.
Függvényábrázolás
A személyi számítógépekkel egyetlen utasítással megkaphatjuk néhány úgynevezett beépített függvény (SIN, COS, TAN, LOG, EXP, SQR stb.) értékét, és DEF FN utasítással még továbbiakat is definiálhatunk. Grafikai utasítások segítségével ezeknek a függvényeknek a görbéit megjeleníthetjük a képernyőn. A függvénygörbék (X; f(X)) koordinátájú pontokból állnak. Kézenfekvőnek látszik tehát, hogy PLOT-tal ezeket rajzoljuk be. A legtöbb függvény esetében azonban csalódni fogunk, ha ilyen egyszerű megoldással próbálkozunk. Ha például a SIN függvény jellegzetes hullámait a Spectrumon ezzel a programmal akarjuk kirajzoltatni:
10 FOR x=0 TO 255
20 PLOT x, SIN x
30 NEXT x
akkor csak egy recés vonalat kapunk a képernyő legalján, ami a tükrözés miatt ráadásul | sin x | görbéje. Túl kicsik lesznek a hullámok, és az sem jó, hogy alul helyezkednek el. Ezért följebb kell tolni, függőlegesen és vízszintesen "szét kell húzni" a görbét. Ha mondjuk a képernyő középvonaláig akarjuk föltolni, és függőlegesen-vízszintesen 50-szeresére nagyítani, akkor a 20-as utasítást így kell átalakítanunk:
20 PLOT x,88+50*SIN (x/50)
Világos, hogy a második koordinátát 50-nel megszorozva függőleges irányban 50-szeresére nagyítottuk a görbét, és hogy ehhez még 88-at hozzáadva föltoltuk a középvonalig. Az talán nem magától értetődő, hogy a vízszintes irányú nagyítást miért úgy értük el, hogy a SIN után X/50-et írtunk. Érthetőbb volna, ha ezt írnánk: PLOT 50*X, SIN X. Csakhogy ekkor a FOR utasítás határait kellene úgy megváltoztatni (és olyan lépésközt megadni), hogy az 50*X értékek ugyanazok legyenek, mint amelyeket az előbb x-szel jelöltünk. (FOR X = 0 TO 5.1 STEP .02). Ehelyett a PLOT utasításban X-et mindkét helyen X/50-nel helyettesítettük, a FOR utasításban pedig 50-nel szoroztunk minden értéket, így az előbbi 10-es utasítást meghagyhattuk, a 20-asban viszont a SIN után X/50 szerepel.
Általában, ha egy FN f(X) függvényt akarunk ábrázolni a képernyőn, ki kell választanunk az értelmezési tartományának (az X értékeknek) egy szakaszát, amit meg akarunk jeleníteni. Legyen ez mondjuk a 15,32 szakasz (a képernyő bal oldala tehát feleljen meg a 15, jobb oldala pedig a 32 X-értéknek). Ezután meg kell állapítanunk egy alsó és felső korlátot a függvényértékekre ezen a szakaszon. Legyen ez most -500 és 1000. Miután a képernyő oszlopait 0-tól 255-ig számozhatjuk, a 100-as utasítás mindig jó kezdés lesz, és a PLOT utasítás ekkor PLOT X,... alakú kell hogy legyen. f(...)-en belül olyan kifejezést kell írni, hogy az X-értékek 15 és 32 közé essenek: f(15+x*17/255) lesz a jó kifejezés, itt a 17 = 32-15 miatt került a képletbe. Másrészt, ha a függvényértékekhez hozzáadunk 500-at, akkor biztosan nem lesznek negatívak (0 és 1500 közé fognak esni), ha pedig ezután megszorozzuk 175/1500-zal, akkor éppen 0 és 175 közti értékeket kapunk a PLOT utasításban szereplő második kifejezésre.
PLOT x,(500+FN f(15+17*x/255))*175/1500
Egyenesrajzolás
A Spectrum egyetlen DRAW utasítással egyenes szakaszt tud rajzolni. Ugyanakkor félgrafikus képernyőn is szükség lehet arra, hogy a PLOT-tal megrajzolható pontokból szakaszt állítsunk össze - a későbbiekben sokszor fel fogjuk használni ezt a lehetőséget. Amikor például különböző görbéket akarunk megrajzolni, sokszor célravezetőbb, ha nem egyenként számítjuk ki a görbe pontjait, hanem közülük csak bizonyosakat, amelyeket azután szakaszokkal kötünk össze. Szükség lesz tehát egy olyan programra, amely grafikus karakterek segítségével egyenest rajzol.
Természetes megoldásként kínálkozik, hogy az egyenest függvénynek tekintjük (például egy DEF FN E(X)=2*X/3+1 utasítás után mint FN E(X)-re hivatkozunk rá, vagy egyszerűen FN E(X) helyére mindenütt 2*X/3+1-et írunk). Ez sokszor jó is lesz, például ZX 81-nél a
10 FOR X=0 TO 63
20 PLOT X,46*X/63
30 NEXT X
program be fogja rajzolni a képernyő egyik átlóját. Olyankor van csak baj, ha a megrajzolandó szakasz meredeksége (azaz X szorzója) nagyobb 1-nél vagy kisebb -1-nél. Például:
10 FOR X=0 TO 21
20 PLOT X,2*X
30 NEXT X
olyan egyenest fog húzni, amelynek csak minden második pontja látszik a képernyőn. Ennek az az oka, hogy amíg az X koordináta 1-gyel nő, az Y (vagy második) koordináta 2-vel. Nekünk az kellene, hogy egy lépésben mindkét koordináta legföl-jebb 1-gyel nőjön, hogy mindig szomszédos négyzeteket tudjunk berajzolni. Az előző program például úgy javítható ki, hogy a 10-es utasítás végére STEP 0.5-öt írunk, ekkor az X koordináta 0.5-tel, az Y pedig 1-gyel fog nőni. Lényeges ugyanis, hogy legalább az egyik koordináta pontosan 1-gyel nőjön, egyébként a megrajzolt vonal helyenként túl "vastag" lesz, egymás mellett két négyzetet is befeketít. Aki nem hiszi, próbálja ki ezt a programot!
10 FOR X=0 TO 63 STEP .5
20 PLOT X,X*2/3
30 NEXT X
Ezek után lássunk egy megoldást erre a feladatra:
1000 LET R=C-A
1010 LET S=D-B
1020 LET E=ABS R
1030 IF ABS S>=E THEN LET E=ABS S+(S=0)
1040 FOR X=0 TO 1 STEP 1/E
1050 PLOT A+R*X,B+S*X
1060 NEXT X
1070 RETURN
A program A,B és C,D pontok között húz szakaszt. Azáltal, hogy egy RETURN utasítással zártuk le, bármilyen programból egy GOSUB 1000 utasítással meghívható (előzőleg A, B, C és D értékét megfelelően beállítva), elvégzi feladatát, majd a RETURN hatására visszatér oda, ahonnan meghívtuk. Az ilyen GOSUB-bal meghívott és RETURN-nel lezárt programrészleteket szubrutinoknak hívjuk - segítségükkel jelentős mértékben lerövidíthetők az olyan programok, amelyekben több helyen kell hasonló tevékenységeket elvégezni.
Kör
Ha tudunk függvényeket ábrázolni a képernyőn, akkor kört is kell tudnunk rajzolni. Erre több módszer is kínálkozik, itt most a függvénygörbeként való előállítást írjuk le. Ha a képernyő 32,22 koordinátájú pontja körül 15 sugárral akarunk kört húzni, a megfelelő függvény: 22+SQR(225-(X-32)*(X-32)) - ez azonban csak a felső félkört adja meg, az alsó félkörnél a 22 után "-" jel áll. (SQR a négyzetgyököt jelenti!) Az ábrázolásnál azonban ki kell kerülni egy problémát: ha az X értékeket 32-15 (kb. 17)-től 32+15 (kb. 47)-ig futtatnánk, a széleken kevés pontot kapnánk, csak középen lennének elég sűrűén a kör pontjai. Ezért azt csináljuk, hogy csak a felső félkör középső pontjait rajzoljuk be, azokat viszont a középpont körül derékszöggel egymás után háromszor elforgatjuk. így elegendő X-nek 32-15/SQR 2 =22-től 32+15/SQR 2 =42-ig futnia, hogy a felső félkör középső negyedkörét megkapjuk. A Pontok c. részben már foglalkoztunk a derékszögű elforgatással, ennek alapján érthetjük meg az alábbi körrajzoló programot:
100 FOR X=22 TO 42
110 LET A=SQR (225-(X-32)*(X-32))+22
120 PLOT X,A
130 PLOT 10+A,54-X
140 PLOT 64-X,44-A
150 PLOT 54-A,X-10
160 NEXT X
Görbék
A függvényábrázolásnál a PLOT utasításban szereplő első koordináta mindig X volt - egyszerűen végigfutott a képernyő oszlopain, és mindegyikbe egy pontot rajzolt, amelynek második koordinátáját valamilyen függvénykifejezéssel határoztuk meg. Azt is megtehetjük azonban, hogy mindkét koordináta valamilyen változó függvénye legyen - a közös változót paraméternek, az így előállítható vonalakat pedig paraméteres görbéknek nevezzük. A függvénygörbéknél változatosabb vonalakat lehet velük rajzolni, hiszen itt nem kikötés, hogy minden oszlopban csak egy pont szerepelhet.
Legegyszerűbb példaként itt is a körrajzolást említhetjük, és ez már csak azért sem lesz haszontalan, mert rajta keresztül azt is meg tudjuk mutatni, hogyan használhatjuk fel egyenesrajzoló szubrutinunkat a görbék pontjainak összekötésére. A ZX 81 félgrafikus képernyőjén 31,21 középponttal és 20 sugárral szeretnénk kört rajzolni. A megfelelő függvények a COS T és SIN T alkalmas átalakításai: itt konkrétan 31+20*COS T és 21+20*SIN T kell, a T paraméter 0 és 2*PI között változik. A lépésközt (a körív két pontja közötti elfordulási szöget) PI/10-nek választjuk - azaz a valóságban nem kört, hanem szabályos húszszöget rajzolunk. A program a következő (az 1000-es sorszámtól kezdve az egyenesrajzoló szubrutin következik):
10 LET A=51
20 LET B=21
30 FOR T=PI/10 TO 2*PI STEP PI/10
40 LET C=31+20*COS T
50 LET D=21+20*SIN T
60 GOSUB 1000
70 LET A=C
80 LET B=D
90 NEXT T
1000 LET R=C-A
1010 LET S=D-B
1020 LET E=ABS R
1030 IF ABS S>=E THEN LET E=ABS S+(S=0)
1040 FOR X=0 TO 1 STEP 1/E
1050 PLOT A+R*X,B+S*X
1060 NEXT X
1070 RETURN
Mindig A-ban és B-ben tároljuk a szakaszok kezdőpontjainak koordinátáit, a 40-es és 50-es utasításokkal számítjuk ki a végpont koordinátáit, az 1000-es szubrutin segítségével összekötjük őket, majd az eddigi végpontot tekintjük kezdőpontnak, kiszámítjuk az új végpontot, és így tovább, amíg a T szög a 2*PI-t el nem éri, azaz a pontok körbe nem futnak.
Egészen kis módosítással az előbbi programot spirál rajzolására is képessé tehetjük. Egyszerűen a sugarat kell a szögelfordulás arányában növelni, és a körülfordulás szögét megnövelni - hiszen a spirál éppen attól spirál, hogy sokszor körülfordul a középpont körül. A szükséges módosítások:
10 LET A=31
30 FOR T=PI/10 TO 7*PI STEP PI/10
40 LET C=31+(1+T)*COS T
50 LET D=21+(1+T)*SIN T

A BASIC nyelv lehetőséget ad arra, hogy véletlen elemeket építsünk be a programjainkba, és így előre ki nem számítható variációkat valósíthassunk meg velük. (Valójában a személyi számítógépek álvéletlen (pszeudo-véletlen) számokat állítanak elő, amelyek azonban statisztikai szempontból jól közelítik a véletlen számokat.) Az RND függvény (az angol "random" - véletlenszerű, találomra vett jelentésű - szó rövidítése) véletlen számot állít elő 0 és 1 között (ami annyit jelent, hogy valahányszor a programban RND szerepel - pontosabban valahányszor egy RND-t tartalmazó utasítás végrehajtódik -, a gép olyan számot vesz helyette, amiről csak azt lehet előre tudni, hogy 0 és 1 közé esik). 10*RND persze 0 és 10 közötti véletlen számot jelent, INT(10*RND) pedig találomra valamelyiket a 0, 1, 2, ..., 9 számok közül.
Hogyan lehet a véletlen számokat grafikai programok készítésében felhasználni? Ugyanúgy, ahogy a többi függvénnyel kiszámolt értékeket! Az ábrákat a program által kiszámolt számértékek határozzák meg, és ezek között lehetnek véletlen értékek is. Kiválaszthatjuk például véletlenszerűen azt a helyet, ahova egy karaktert kiírunk:
10 PRINT AT INT(RND*22),INT(RND*32);"O"
20 GO TO 10
A PRINT AT... utasítás első koordinátájában a sort, a másodikban az oszlopot adtuk meg véletlenszerűen - ezáltal találomra helyeztünk el egy "O" betűt a képernyőn. A program azután ezt a végtelenségig ismétli - amit látunk (legalábbis eleinte, amíg a kép még nincs túlságosan tele), az úttestre hulló esőcseppek mintájára emlékeztet. Előbb-utóbb azonban egyre inkább betelik a képernyő, a karakterek szabályos elrendezése elnyomja a minta eredetileg véletlenszerű jellegét.
Véletlen (random) betöltés
Ha meg akarjuk őrizni a minta véletlenszerűségét, másképp kell eljárnunk: pédául végigmegyünk a képernyő összes karakterhelyén, és véletlenszerűen döntjük el, melyikre milyen jel kerüljön. A legegyszerűbb, ha csak kétféle karakter, mondjuk a "*" és "0" karakter közül választunk, amelyek kódja 23, illetve 52 (a ZX 81-en). Ekkor a 23+29*(RND>.5) kifejezés véletlenszerűen és egyenlő valószínűséggel állítja elő a kétféle kódot, a következő program pedig véletlenszerűen betölti a képernyőt a kétféle karakterrel:
10 FOR I=1 TO 704
20 PRINT CHR$(23+29*(RND>.5));
30 NEXT I
Spectrumon a két karakter kódja 42 és 79, ezért a 20 sor így alakul:
20 PRINT CHR$(42+37*(RND>.5));
A 20-as utasításban az (RND>.5) kifejezés értéke - a korábbiakhoz hasonlóan - 1 vagy 0 aszerint, hogy RND nagyobb-e .5-nél vagy sem. A CHR$ függvény adott kódú karaktert állít elő. A kétféle karakter előfordulási aránya nagyjából 50-50%, hiszen az RND>.5 reláció 0.5 valószínűséggel teljesül.
Véletlen (random) bolyongás
Ha nem sorban megyünk végig a képernyő karakterhelyein, hanem a képernyő közepéről elindulva mindig a továbblépés irányát választjuk meg véletlenszerűen, olyan mozgást láthatunk, amelyet random bolyongásnak szoktak nevezni. Az INT(RND*4) kifejezés segítségével véletlenszerűen állítjuk elő a 0, 1, 2 vagy 3 értékek valamelyikét, és ettől függően jobbra, balra, fölfelé vagy lefelé lépünk egy "kockával":
10 LET X=16
20 LET Y=11
30 PRINT AT Y,X;"*"
40 LET R=INT(RND*4)
50 LET X=X+(R=0)-(R=1)
60 LET Y=Y+(R=2)-(R=3)
70 GO TO 30
Az 50-es és 60-as utasításban a már jól ismert fogást alkalmaztuk: felhasználva, hogy például az (R=0) kifejezés értéke 1, ha R=0 és 0 egyébként, az X értékét 1-gyel növeltük, ha R=0 volt, és 1-gyel csökkentettük, ha R=1. Hasonló módon R=2, illetve R=3 esetén az Y értékét növeltük, illetve csökkentettük 1-gyel.
Ebben a programban nem lesz sok örömünk, amíg meg nem akadályozzuk, hogy a berajzolandó pont letévedjen a képernyőről - a Pontokról szóló részben leírt megoldások valamelyikével ezt elkerülhetjük.
A véletlen bolyongás egyszerűbb válfaja a véletlen imbolygás, amikor csak az X koordináta változik véletlenszerűen, az Y koordináta minden lépésben 1-gyel nő. Az előbbi programban csak néhány változtatást kell végrehajtanunk, hogy ezt a mozgást is megjeleníthessük: az Y kezdőértéke 0 lesz, a 40-es utasításban RND szorzója 2 (hiszen most csak két lehetőség - a jobbra vagy balra lépés között kell választanunk), a 60-as utasítás pedig LET Y=Y+1-re egyszerűsödik. A program egy olyan imbolygó vonalat fog rajzolni, ami leginkább egy kanyargó folyóra emlékeztet. Ha valahova a 30-as és 70-es utasítás közé beszúrunk egy SCROLL utasítást (ami az egész képernyőt egy sorral följebb viszi), azt is elérhetjük, hogy a folyó nem áll meg a képernyő alján, hanem vég nélkül tovább folydogál.
10 LET X=16
20 LET Y=0
30 PRINT AT Y,X;"*"
40 LET R=INT(RND*2)
50 LET X=X+(R=0)-(R=1)
60 LET Y=Y+1
70 GO TO 30
Véletlen bolyongás tehetetlenséggel
A random bolyongásnak egy olyan változatát is beprogramozhatjuk, ahol a vonal nem változtatja minden szabályosság nélkül az irányát, hanem egyfajta "tehetetlenséggel" mozog; ha már elindult valamilyen irányba, akkor csak sebességének fokozatos megváltoztatásával fordulhat egy másik irányba. Ezáltal a mozgó pont nyoma nem cikcakkos vonalat, hanem lekerekített ívekből álló görbét alkot. Ezt a programot finom felbontású képernyőre írtuk, de a félgrafikus képernyőn is érdemes megvalósítani.
Az előbb a mozgó pont koordinátáit (illetve ezek változását) adtuk meg véletlenszerűen. Most a pont sebességét (a koordináták egy lépésben való megváltoztatását) változtatjuk meg véletlenszerűen (a mozgás úgyszólván másodfokon random - nem a koordináták eltérései, hanem a koordináták eltérésének eltérései változnak meg véletlenszerűen). Ahogy eddig X-ben és Y-ban tároltuk az éppen berajzolt pont koordinátáit, most ezeken kívül két további változóra (mondjuk u-ra és v-re) lesz szükségünk, hogy a pontok sebességének vízszintes és függőleges összetevőit is feljegyezzük. A program a következőképpen nézhet ki Spectrumon:
100 LET x=128: LET y=100
110 PLOT x,y
120 LET u=0: LET v=0
130 LET u=u+SGN(RND-.5)
140 LET v=v+SGN(RND-.5)
150 DRAW u,v: LET x=x+u: LET y=y+v
160 GO TO 130
Akárcsak korábban, most is meg kell oldani azt a problémát, hogy a pont előbb-utóbb le fog térni a képernyőről. Itt a védekezés körülményesebb, mint az előző programban, mert a DRAW utasítás közben lépnénk túl a megadott határokat. Ilyenkor (ha azt a módszert választjuk, hogy a képernyő másik oldalán folytatjuk a rajzolást) még a DRAW végrehajtása előtt ellenőrizni kell, hogy a végpont koordinátái megengedett értékek-e, és ha nem, a megrajzolandó szakasznak csak egy részét húzhatjuk be, ki kell számolni a megmaradó darab koordinátáit, PLOT-tal a túloldalon meg kell rajzolni egy pontot, és onnan folytatódhat a vonal rajzolása.
Egyszerűbb, ha a programot addig hagyjuk futni, amíg ez a hiba elő nem áll, akkor pedig elölről kezdjük. Ennek a résznek a végén viszont leírunk egy olyan módszert a tehetetlenséggel mozgó pont véletlen bolyongásának programozására, amely - amellett, hogy könnyen programozható - még szebb vonalat is rajzol.
A valószínűség szabályozása
Az eddigi példákban az RND-t mindig úgy használtuk, hogy a kapott véletlen értékek a megadott lehetőségek között mindig egyenlően oszlanak meg. Például a random betöltésnél fele-fele valószínűséggel írtunk minden helyre "*" vagy "O" karaktert; a random bolyongásnál 1/4 - 1/4 valószínűséggel léptünk jobbra-balra, fölfelé vagy lefelé stb. Azt is megtehetnénk pedig, hogy ezeket a valószínűségeket nem automatikusan egyformának állítjuk be, hanem egyenlőtlenül osztjuk el a különböző lehetőségek között - másrészt függővé tehetjük a képernyő adott helyétől, a program indítása óta eltelt időtől stb.
Ha a random betöltés programjában a 20-as utasításban az RND-t nem 0.5-tel, hanem más számmal hasonlítjuk össze, akkor megváltozik a képernyőn a kétféle karakter előfordulási aránya. Például 1/3-nál az "O" karakter előfordulási valószínűsége 1/3 lesz, a "*"-é következésképpen 2/3, így a képernyőn nagyjából 1:2 arányban fognak előfordulni. A program elején elhelyezhetünk egy 5 INPUT Y utasítást, és az RND-t ezzel az Y-nal hasonlíthatjuk össze - ekkor megfigyelhetjük, hogyan függ a karakterek előfordulási aránya a megadott értéktől.
Az így módosított programnak is megmarad az a tulajdonsága, hogy a képernyő minden részén nagyjából egyforma lesz a kétféle karakter aránya. Ha a képernyőt úgy járjuk be, hogy közben számon tartjuk, melyik oszlopban és melyik sorban járunk, lehetőség nyílik arra, hogy a helytől is függővé tegyük az egyes karakterek előfordulási valószínűségét.
10 FOR I=0 TO 21
15 FOR J=0 TO 31
20 PRINT AT I,J; CHR$ (23+29*feltétel)
25 NEXT J
30 NEXT I
Spectrumon a 20. sor: 20 PRINT AT I,J; CHR$ (42+37*feltétel)
Ha a "feltétel" szó helyére ezt írjuk: (RND>J/31), akkor olyan képet kapunk, ahol a bal oldalon az "O", a jobb oldalon a "*" karakter lesz túlsúlyban, középen pedig kiegyenlítődik az arány. (Ha ugyanis J kicsi, az RND értéke nagy valószínűséggel nagyobb, mint J/31, és ez a valószínűség fokozatosan csökken a 0-ig, ahogy J a 31-hez közeledik.) Az (RND>I/22) feltétellel ugyanez az alsó és felső térfélre teljesül. Ha a ">" jeleket mindenütt "<" jelre cseréljük, a kétféle karakter előfordulási aránya megfordul - ahol eddig sok volt, most sok "O" lesz, és fordítva.
Az (RND>ABS(I/11-1)*ABS(J/16-1)) feltétellel olyan képet kapunk, ahol a képernyő közepén csoportosulnak az "O"-k.
Még egy változtatást érdemes kipróbálni: helyettesítsük a fenti példák bármelyikében RND-t RND*RND-vel! Most azt vehetjük észre, hogy az átmenetek (mondjuk a több "*"-ot tartalmazó területről a több "0"-t tartalmazóra) kevésbé lesznek fokozatosak, mint eddig. Egy ideig túlnyomórészt az egyik lesz többségben, majd hirtelen átbillen az arány. Ha viszont RND helyett SQR(RND)-t írunk, elvileg az ellenkezője kell, hogy történjen: még finomabb átmeneteknek kell előállniuk - ez a különbség azonban gyakran alig észrevehető.
Egy példa olyan programra, ahol a valószínűség az időtől függ: a Véletlen elemek elején szereplő, a képernyő találomra vett helyeire "O"-t író programot alakíthatjuk át úgy, hogy amikor a képernyő már nagyjából tele van, elkezdünk egyre több "*" karaktert írni, így fokozatosan megtisztítjuk a képet, majd minden kezdődhet elölről. Az eddigi egyetlen "O" karakter helyett tehát most két karaktert a "O"-t és a "*"-t használjuk. Ha N helyre írunk találomra, akkor nagyjából N*LOG N lépésre van szükség, hogy mindenhova legalább egy jelet tegyünk - ez az N=704-nél körülbelül 5000 lesz. Ez nagyon lassú lenne, ezért csak 9x11-es téglalapra írunk. Olyan kifejezéssel kell tehát összehasonlítanunk az RND-t, amely 0-val indul, körülbelül 500 lépésben 1-hez közelít, majd megint 0-ra csökken, 500-as periódusban. Erre az (1+SIN(L/150+1.5))/2 kifejezés lesz a legalkalmasabb, ahol L a lépésszámot jelöli.
10 FOR L=1 TO 1000000
20 PRINT AT INT(RND*9)+5,INT(RND*11)+6; CHR$(23+29*(RND>(1+SIN(L/150))/2))
30 NEXT L
A 10-es utasításban szereplő 1000000-s érték hatására a program nagyon hosszú ideig fut, hogy közben akárhányszor megfigyelhessük a megmutatni kívánt váltakozást.
Ami a random bolyongást és random imbolygást illeti, ott is lehetőség van a valószínűség "szabályozására". Amúgy is kényelmetlen volt, hogy külön utasításokkal kellett védekeznünk az ellen, hogy letérjünk a képernyőről. Egy egyszerű gondolat álapján úgy módosíthatjuk a programot, hogy erre ne kerülhessen sor. Tegyük ugyanis függővé a jobbra vagy balra fölfelé vagy lefelé) lépés valószínűségét attól, hogy mennyire közelítettük már meg a képernyő jobb vagy bal oldali (fölső vagy alsó) szélét. Minél közelebb kerültünk valamelyik oldalhoz, annál kisebb valószínűséggel lépjünk abba az irányba! Ennek megfelelően a random bolyongás programjában az 50. és 60. utasítást a következőképpen fogjuk átalakítani:
50 LET X=X+SGN (RND-X/31)
60 LET Y=Y+SGN (RND-Y/21)
(A 40. utasításra ekkor nincs is szükség). Az SGN az előjelfüggvényt jelöli; ha RND>X/31 (ami kis X-re nagyon valószínű, X=31-re pedig már lehetetlen), akkor az SGN (RND-X/31) kifejezés 1-et ad, ellenkező esetben -1-et. Elvileg RND=X/31 is előfordulhat, amikor a kifejezés értéke 0 lesz, X-et se nem növeljük, se nem csökkentjük - ennek valószínűsége azonban elhanyagolhatóan kicsi. Így X értékét kis X-re nagy valószínűséggel növeljük, nagy X-re nagy valószínűséggel csökkentjük - hasonlóképpen határozzuk meg Y új értékét is.
Ez a mozgás kissé másmilyen jellegű lesz, mint előbb, részben, mert a kockák most "sarkosan" érintkeznek (hiszen minden lépésben X és Y értékét is megváltoztattuk). Az olvasóra bízzuk, hogy olyan megoldást találjon, amellyel ebben a módosított programban is biztosíthatja, hogy az egymás után berajzolt négyzetek a korábbi módon, oldalaikkal érintkezzenek.
A lényeges újdonság azonban az, hogy a random imbolygó pont most érdekes módon elkerüli a széleket, a képernyő közepén szeszélyesen cikázik, de a szélekhez közeledve lendülete egyre csökken, majd újra visszafordul közép felé.
A "tehetetlenséggel" való random bolyongás esetében a valószínűség szabályozása még meg is könnyíti a helyzetünket - egyébként csak nagyon körülményesen tudtuk megakadályozni, hogy a vonal elhagyja a képernyőt. Az alapgondolat itt is a random bolyongás egyszerűbb esetében alkalmazott megoldásra emlékeztet: a pont sebességét aszerint csökkentjük vagy növeljük, hogy milyen közel van a képernyő széléhez. Például ahogy a képernyő jobb szélét megközelíti, egyre nagyobb valószínűséggel választjuk a vízszintes sebesség csökkentését, amíg aztán az negatívvá nem válik, és a pont el nem indul visszafelé, a képernyő középső területére. Példánkban (I. véletlen bolyongás tehetetlenséggel) u jelölte a vízszintes sebességet, és amikor ezt elkezdtük csökkenteni, még u + (u-1) + (u-2) + ... + 2 + 1 = u*(u+1)/2 hosszú utat kell megtennünk előre. Ha viszont nem csökkentjük, akkor még legalább (u+1)*(u+2)/2 lépés van hátra. (Ha u negatív, és a képernyő bal oldali széle felé közeledünk, ugyanezt a képletet ABS u-val kell kiszámolnunk.) Így például ha x+u > 255-(u+1)*(u+2)/2, akkor már feltétlenül "fékezni", azaz u értékét csökkenteni, ugyanígy, x < (-u+1)*(-u+2)/2 esetén u-t mindenképp növelni kell. Ennek megfelelően a szóban forgó program 130-as utasítása "környékén" a következő módosításokat kell végrehajtani:
130 LET w=(ABS (u)+1)*((ABS (u)+1)+1)/2
135 LET u=u+SGN (RND*(255-2*w)+w-x)
140 LET z=((ABS (v)+1)*(ABS (v+1)+1))/2
145 LET v=v+SGN (RND*(175-2*z)+z-y)
A 135-ös utasításban az RND*(255-2*w)+w kifejezés egy w és 255-w közé eső véletlen értéket állít elő - ezt hasonlítjuk össze x értékével - ugyanez a 145. utasításban szereplő, hasonló kifejezés titka.
Ezzel elérjük, hogy a mozgó pont idejében "fékezzen", ne fusson le a képernyőről.
Beavatkozik a néző
Véletlen elemek alkalmazásával érdekesebbé, többször nézhetővé tettük grafikai programjainkat. Gyakran a program készítőjét is meglepik azok a véletlen kombinációk, amelyek a véletlenszám-generátor (RND-függvény) alkalmazásával kijönnek.
Ahogy a fejezet elején is említettük, van egy másik módszer is a programok "fogyaszthatóságának" javítására: a "néző" beavatkozása.
A beavatkozásra lényegében kétféle lehetőség van: az egyik, ha paramétereket (bemenő adatokat) adunk a programnak INPUT utasítással, amelyeket az beépít a képet meghatározó értékek rendszerébe. Erre már eddig is láttunk példát (például a pont mozgatását leíró részben), a továbbiakban (például a Lissajous-görbéknél) is támaszkodunk erre a megoldásra. Igazából kevés olyan program van, ahol valami-lyen paramétert nem adhatnánk meg változtatható módon az INPUT segítségével. A véletlen elemekkel operáló programok is jól tudják használni az INPUT-tal meg-adott változtatható paramétereket (például egyes valószínűségi értékeket adhatunk meg, mint a képernyő random betöltésénélm a valószínűség szabályozása részben, vagy az alábbiakban a Labirintus rajzolásakor).
Arra is szinte korlátlan lehetőség nyílik, hogy INPUT-tal a program futása közben (nemcsak a legelején) adjunk meg értékeket, amelyekkel folyamatosan változtathatjuk és meghatározhatjuk a kialakuló kép jellegét.
Az utóbb leírt típusú beavatkozásra (menet közben, a program eddigi futásának eredményeit már felhasználva) a BASIC nyelv speciális lehetőséget biztosít, amely nem igényli a program futásának megszakítását az INPUT utasítás végrehajtásakor. Az INKEY$ függvény mindig az éppen lenyomott gomb tartalmát (mint egyetlen karaktert) tartalmazza. Amikor egy gombot se nyomunk le, az INKEY$ tartalma: "" (az üres karaktersorozat). Ha a programunkat úgy írjuk meg, hogy helyenként felhasználjuk az INKEY$ függvény aktuális értékét, akkor kívülről egy-egy gomb megnyomásával (anélkül, hogy futásában megakasztanánk) befolyásolni lehet működését.
A grafikai programok készítésének "tudománya" voltaképpen abban áll, hogy a megvalósítani kívánt képeket számokkal tudjuk meghatározni, más szóval, kódolni tudjuk őket. Mondhatjuk tehát, hogy ez a fejezet teljes egészében a kódolás problémájával foglalkozik - akkor viszont miért kell külön részben kitérni rá? Nos azért, mert néha nem az elképzelt kép beprogramozásában, hanem magán a programon belül lesz szükség képek vagy képrészletek kódolására. A program mint adatot tekinti az előállított képet vagy annak egy részletét. A legvilágosabb példa a fejezet végén szereplő rajzfilmvetítő program, amely egymás után képeket másol át a képernyőre.
Töröttvonal kódolása a$-ban
Ha a finom felbontású képernyőn a DRAW utasítással szakaszokat rajzolunk egymás után, a keletkező töröttvonal "megjegyzéséhez" elég a sorban végrehajtott DRAW utasítások paramétereit tárolni. Miután a maximális megengedett érték 255, egy DRAW utasítás két paramétere két byte-on tárolható. A legelső DRAW utasítás előtt PLOT utasítást kell végrehajtani, hogy a töröttvonal kezdőpontját megadjuk. Egy karakter típusú változóban (mondjuk a$-ban) sorban rögzíthetjük az egy-egy byte-os számpárokat a CHR$ függvény segítségével. Amikor a$-t megfelelően feltöltöttük, a következő programmal rekonstruálhatjuk a kódolt töröttvonalat:
100 FOR i=2 TO LEN a$ STEP 2
110 IF i=2 THEN PLOT CODE a$(i-1),CODE a$(i)
120 IF i>2 THEN DRAW CODE a$(i-1),CODE a$(i)
130 NEXT i
Alkalmasan választott szögpontokkal tulajdonképpen bármilyen görbét kódolhatunk ily módon - persze csak akkor érdemes, ha az nem sok apró kanyarból áll, így a$-ban nem kell nagyon sok pontot tárolni.
Egyetlen karakteres változóban több össze nem függő vonalat is kódolhatunk. Ekkor szükségünk lesz egy olyan speciális jelre, amely két vonalat elválaszt egymástól. Ez például a pont második koordinátájában álló 200 kódú karakter lehet: ezen a helyen egyébként maximum 175 állhatna. A 110. és 120. utasítást most más feltételtől kell függővé tennünk: például egy c változó 1-es értéke jelzi, ha új vonalat kell kezdenünk, értéke egyébként 0. Ekkor a 110. utasítás így kezdődik: IF c = 1 ... a 120. pedig: IF c = 0 ... Az előbbi programba három új utasítást kell beszúrni:
90 LET c=1
105 IF CODE a$(i)=200 THEN LET c=1: GO TO 130
125 LET c=0
Ugyanennek a programnak a félgrafikus képernyőre működő változatát is elkészíthetjük, felhasználva a már leírt egyenesrajzoló szubrutint, amelyet ismét 1000-es sorszámtól kezdve helyeztünk el. A$-ba ezúttal valóban a szögpontok koordinátáit helyeztük el (az előbbivel ellentétben, amikor az első pont koordinátáit a DRAW-ban szereplő paraméterek követték). Mivel itt minden karakterben maximum 63-as kód áll, a 128-as kódú fekete négyzetet használhatjuk a vonalak elválasztására.
100 IF A$(3)=" " THEN LET A$=A$(4 TO )
110 LET A=CODE A$(1)
120 LET B=CODE A$(2)
130 LET C=CODE A$(3)
140 LET D=CODE A$(4)
150 GO SUB 1000
160 LET A$=A$(3 TO )
170 IF LEN A$>3 THEN GO TO 100
A DRAW utasítással dolgozó változatnak megvolt az az előnye, hogy az a$-ban tárolt első két byte (a kezdőpont koordinátáinak) megváltoztatásával az egész vonalat eltolhattuk a képernyő bármelyik másik pontjába, mint kezdőpontba. Ha ezt a félgrafikus képernyőn működő programmal is meg akarjuk valósítani, az egyenesrajzoló szubrutint kissé át kell alakítani: ne A, B, C és D értékekkel számoljon, hanem csak R-rel és S-sel, ami most a C-A és D-B különbségeket tartalmazza. A és B értékét adottnak veszi, és minden szakasz berajzolása után megnöveli R-rel, illetve S-sel (ekkor az egyenesrajzoló szubrutin pontosan úgy fog működni, mint a DRAW utasítás, az A$-ba tehát az első byte-páron a kezdőpont koordinátáit, a továbbiakban a vízszintes és függőleges eltérést kell tárolni).
Ha nagyon sok cikcakkot tartalmaz az a vonal, amit a$-ban kódolni akarunk, akkor a szögpontonként való kódolás nem elég gazdaságos, hiszen minden pont két byte-ot foglal el. A görbe minden pontját egyetlen byte-on is kódolhatjuk, ahol az a byte az előző ponttól való eltérésének irányát tartalmazza a 0-7 számok valamelyikével kódolva (0 jelöli a jobbra lépést, 1 a jobbra-föl, 2 a fölfelé lépést és így tovább). Az első két byte-on ismét a kezdőpont koordinátáit tároljuk. Ha a$-ban már előállítottuk a görbe kódolását, a következő program végezheti el a megrajzolást:
10 LET i=CODE a$(1): LET j=CODE a$(2): PLOT i,j
20 FOR k=3 TO LEN a$
30 LET q=CODE a$(k)
40 LET i=i+(q=0)+(q=1)+(q=7)-(q=3)-(q=4)-(q=5)
50 LET j=j+(q=1)+(q=2)+(q=3)-(q=5)-(q=6)-(q=7)
60 PLOT i,j
70 NEXT k
Ennek a kódolásnak nagy előnye, hogy ugyanannak a görbének 45 fok többszöröseivel való elforgatását teszi lehetővé. Valamilyen kezdőértéket adva q-nak (ami az elforgatási szöget határozza meg 45 fokos egységekben), a 30-as utasításban CODE a$(k)-t relatív (elforgatási) szögként értelmezzük. A beszúrandó és módosított utasítások:
5 LET r=...
30 LET q=r+CODE a$(k): LET q=q-8*(q>7)
Ugyanennek a kódolási módnak egy egyszerűbb változata, amikor a szomszédos pontok csak oldalaikkal érintkezhetnek (sarkosan nem), így a q értéke 0, 1, 2 vagy 3 lehet. (Ezt a kódolási módot alkalmazzuk majd a Kígyó mozgatásánál.)
A képernyő mint memória
Néha nincs szükség arra, hogy külön változóban kódoljuk a képernyő tartalmát - magáról a képről le tudjuk olvasni a szükséges információt. A képernyő c. részben már szóltunk róla, hogy ZX 81-en hogyan lehet PEEK-kel olvasni a képernyőről és POKE-kal írni rá. (A Spectrumnál a PRINT AT ... utasítás és a SCREEN$ függvény látja el ezt a feladatot.) Ez tehát a kódolásnak a legegyszerűbb válfaja - a kép "magáért beszél".
A későbbiekben többször élünk ezzel a lehetőséggel: például a Labirintusban, amikor új falakat húzunk, a képernyőről olvassuk le, milyen hosszú lehet, hogy még ne ütközzön bele a keresztbe futó falba; az Életjátékban, ahol minden pontot a szomszédaival együtt megvizsgálunk, hogy milyen színűek vannak köztük többségben. Végül a rajzfilmprogramok is memóriának használják a képernyőt, amelyről átmásolják a képeket a memória más területeire, hogy aztán megfelelő sebességgel tudják őket a képernyőre visszahozni.
Miután a legalapvetőbb fogásokat megpróbáltuk áttekinteni, vázlatosan ismertetünk néhány teljes grafikai programot. Viszonylag hosszabb programokról lévén szó, itt már listákat nem tudunk közölni, hanem csak algoritmusokat, amelyek alapján az olvasó maga is el tudja készíteni a leírt - vagy azokhoz hasonló - programokat. Az első részben képekről lesz szó, azaz olyan programokról, amelyek egy-egy érdekes, szép képet állítanak elő. A második csoportba tartozó programoknál fontos a mozgás is, ahogy a képek előállnak vagy folytonosan átalakulnak. A harmadik részben arról lesz szó, hogyan lehet a ZX 81 segítségével egészen egyszerű rajzfilmeket készíteni - olyan képsorozatokat, amelyek pillanatról pillanatra teljes egészükben megváltoznak.
1. Sakktábla
A legegyszerűbb grafikai program, amivel valószínűleg minden kezdő megpróbálkozik. Végigmegyünk a képernyő sorain és oszlopain, és ha a sor és oszlop számának összege páros, akkor fekete, ha páratlan, akkor pedig fehér négyzetet nyomtatunk. Ha I a sorszámláló, J az oszlopoké, a fehér mező kódja 0, a feketéé pedig 128, akkor a
PRINT CHR$ (128*(i+j-INT ((i+j)/2)*2));
utasítás mindig a megfelelő színű négyzetet rajzolja be. Az i+j-INT((i+j)/2)*2 kifejezés ugyanis 1-et ad, ha l+J páratlan, és 0-t, ha páros - emiatt a CHR$ után álló érték 128-cal vagy 0-val egyenlő, az előállított karakter pedig a fekete vagy a fehér négyzet. Így az egész képernyőt bekockáztuk, nemcsak a sakktáblának megfelelő 8x8-as táblát.
Ha mégis a sakktábla fontos, akkor nagyobb négyzeteket érdemes rajzolni. Mondjuk 2x2 kis négyzetből álló nagyobb négyzetekhez l-t és J-t 0-tól 15-ig kell futtatni, és az előző PRINT utasításban helyettük olyan K, L változókat használni, ahol K=INT(i/2), L=INT(j/2).
A példaprogramban a 32-es ASCII kódú (szóköz), és a 143-as kódú fekete kockát használjuk:
10 FOR i=1 TO 22
20 FOR j=1 TO 32
30 PRINT CHR$ ((111*(i+j-INT ((i+j)/2)*2))+32);
40 NEXT j
50 NEXT i

2. Függvényábrázolás csíkokkal, kockákkal
A Függvényábrázolás c. részben pontokkal rajzoltuk meg egyes függvények grafikonját, ami persze sokszor jól jön, de mint látvány, nem annyira érdekes. Kicsit érdekesebbé tehetjük a következő módon:
3. Interferenciaképek
A finom felosztású képernyőn rajzolt egyenes szakaszok (az Egyenesrajzolás algoritmusához hasonlóan) természetesen nem pontosak, hiszen egy négyzetháló pontjaiból állnak össze. Ha távol állnak egymástól, ez nem is tűnik fel - ha viszont sok egyenes szakaszt rajzolunk egymás mellé, az apró szabálytalanságok együttesen, felerősödve mutatkoznak meg, interferenciaképek keletkeznek. Nézzünk néhány példát erre:
Végiglépdelünk a képernyő legalsó és legfelső során, mondjuk minden negyedik pontot PLOT-tal berajzoljuk, majd DRAW-val összekötjük a szemben fekvő szakasz két végpontjával (azaz a képernyő két távolabbi csúcspontjával). (Ld. kép, példaprogram)
A képernyő függőleges középvonalának alsó és felső végpontját összekötjük a legalsó és legfelső sor minden harmadik vagy negyedik pontjával. Ugyanezt megtehetjük a vízszintes középvonal végpontjaival is.
A legalsó és legfelső sor pontjait összekötjük a függőleges középvonalnak egy-egy pontjával, amelyet a következőképpen határozunk meg: ha az alsó sorból indulunk ki, a két szélén levő pontot a középvonal alsó, a középen levő pontot pedig középső pontjával kötjük össze, a kettő között a SIN függvény valamilyen alkalmas átalakításával számolunk: -87*SIN (i*PI/255) lesz a megfelelő második koordináta, ahol i az alsó (vagy felső) sorban levő kezdőpont vízszintes koordinátája. Az első pont koordinátái: (0,0), a másodiké 127,87*SIN (i*PI/255), illetve (i,175),(127/175-87*SIN (i*PI/255) A felső sor pontjainál 175-ből vonjuk le ezt az értéket, ez határozza meg a velük összekötendő pont második koordinátáját.
A legalsó sor pontjait kössük össze a képernyő középpontja körül 40 egység sugárral rajzolt kör felső félkörének pontjaival úgy, hogy miközben az alsó sorban balról jobbra végigmegyünk, a félkörön jobbról indulva az óra járásával ellentétes irányban jussunk el az átmérő másik végpontjába.
INPUT-tal vegyünk be egy n számot a program elején, i most fusson 0-tól 2*PI-ig PI/60 lépésközzel, és a képernyő bal oldali oszlopának 88+80*SIN i második koordinátájú pontját kössük össze a jobb oldali oszlop 88+80*SIN (i+PI/n) második koordinátájú pontjával! Futassuk le a programot, n-nek 1, 2, ..., 8 értéket adva!
Az előző ponthoz hasonlóan olvassunk be egy értéket n-be, i-vel 0 és 2*PI között futva rajzoljuk meg egy 68,88 középpontú és 60 sugarú kör pontjait, majd kössük össze a 120 egységgel jobbra eltolt körnek azzal a pontjával, ahol a szögelfordulás PI/n-nel nagyobb (tehát az első pont koordinátáiban COS i és SIN i, a másodikéban COS (i+PI/n) és SIN (i+PI/n) szerepel!
Kössük össze a képernyő két középvonalából álló kereszt pontjait úgy, hogy a függőleges középvonal alsó és a vízszintes középvonal jobb oldali pontjából indulunk (azokat összekötjük), és egyenletes léptékkel haladva átérünk a kiválasztott pontokhoz, a megfelelő pontpárokat mindig szakasszal összekötve.

10 FOR i=0 TO 255 STEP 4
20 PLOT i,0: DRAW 128-i,175
30 PLOT i,175: DRAW 128-i,-175
40 NEXT i
Természetesen még számtalan hasonló "interferencia"-programot lehet készíteni. Érdekesebbek azok, amelyek - mint az 5) és 6) pontban leírtak - valamilyen bevitt értéktől függően variálhatók.
4. Szövetminta
A Spectrumnál lehetőség van arra, hogy saját magunk definiáljunk speciális karaktereket. A szóban forgó program erre a lehetőségre támaszkodik, bár ennek hiányában minden olyan karakter megfelel, amely nem egyetlen színnel tölt be egy mezőt, tehát alapszínnel és háttérszínnel színezhető.
Vegyünk ugyanis egyetlen ilyen karaktert (ha magunk definiálhatjuk, akkor például legyen olyan, amely egyik átlója mentén két háromszögre bontja a kis négyzetet), és töltsük meg vele az egész képernyőt. Ezek után menjünk végig a sorokon, és minden sorban egy véletlenszerűen választott színnel egységesen adjuk meg az ott található karakterek alapszínét. Majd ugyanígy véletlenszerűen (de az egyes oszlopokon belül egységesen) határozzuk meg az oda tartozó karakterek háttérszínét. Ha két ciklusban megyünk végig a képernyőn (a külső a sorokat, a belső az oszlopokat járja be), akkor a 32 oszlopnak megfelelően egy 32 elemű tömbben tárolhatjuk az egyes oszlopokhoz tartozó háttérszíneket (amit a program elején RND-vel betöltünk), a sorhoz tartozó egységes alapszínt elég azelőtt beállítanunk egy változóba, mielőtt végigmennénk a sor elemein.
Ez a rendkívül egyszerű program nagyon szép és változatos mintákat állít elő, amelyek gyakorlatilag soha nem ismétlődnek meg. fekete-fehér tv-n is élvezhető lesz, hiszen a különböző színeknek ott különböző tónusok felelnek meg.
5. Labirintus
Sokan találkozhattak már olyan számítógépes játékkal, amelyben egy labirintuson kellett végigmenni - itt is érvényes azonban, amit a fejezet elején mondtunk: például az a labirintus, amelyet ez a program állít elő, önmagában is olyan szép, hogy érdemes megcsinálni; persze semmi akadálya, hogy ezt is egy játék pályájaként használhassuk.
A program a ZX 81 karakteres képernyőjén működik, POKE utasításokkal és a PEEK függvény alapján rajzolja meg a labirintus falait. Könnyen megvalósítható persze minden olyan gépen, amely közvetlenül írni-olvasni tud a képernyőn (ponto-sabban a megfelelő memóriaterületen). Csak kétféle karakterrel dolgozik: a "blank" vagy "üres" karakterrel és inverzével, a teljesen befeketített négyzettel. Az utóbbi alkotja a labirintus falait, az előbbi pedig a köztük vezető járatokat. A falak és a járatok is egy karakter szélességűek lesznek, így a labirintust körülvevő falakkal együtt páratlan sok karakter szélességű lesz minden oldala. Először is körülvesszük a képernyőt (pontosabban: annak maximális páratlan oldalhosszúságú - a ZX 81-nél 31x21-es - téglalap alakú részét) egy fallal, amelyen csak két helyen hagyunk nyílást: a felső sorban balról, az alsóban pedig jobbról a második mezőben. Labirintusunk ugyanis olyan lesz, hogy a bal felső sarokból mindig el lehet jutni a jobb alsóba.
Minden második sorba és oszlopba fogunk falakat húzni. Véletlenszerűen kiválasztunk egy sort vagy egy oszlopot, majd azt is véletlenszerűen eldöntjük, hogy (sor esetében) jobbról vagy balról, illetve (oszlop esetében) alulról vagy felülről kezdjük-e építeni. Megeshet, hogy ebből az irányból már korábban elkezdtünk falat húzni: ekkor az adott sorban (oszlopban) kettesével addig lépünk tovább, amíg üres helyhez nem érkezünk. Innen kezdjük berajzolni az új fal kockáit, és addig megyünk előre, hogy éppen neki ne ütközzünk egy keresztbe húzódó falnak, tehát az általunk húzott falrészlet ne vágjon ketté egyetlen területet se - így a labirintus belseje összefüggő területet alkot, bármelyik pontjából bármelyik másikba el lehet jutni.
Ha a keresztbe húzódó fal az egész labirintus egyik szélső fala (ezt onnan tudhatjuk, hogy valamelyik koordinátája maximális), akkor az összes sor és oszlop számontartására alkalmas tömbben feltüntetjük, hogy az aktuális sor (oszlop) betelt - ha legközelebb a véletlen választás megint erre esne, itt már ne próbálkozzunk.
Ugyanakkor egy számláló értékét eggyel növeljük, amiből megtudhatjuk, hány sor és oszlop telt már be teljesen.
Amíg ez a számláló kevesebbet mutat, mint az összes berajzolandó sor és oszlop száma, addig próbálunk keresni olyan helyeket, ahova új falakat rajzolhatunk. Végül olyan labirintust kapunk, amelyben még el lehet jutni az egyik sarokból a másikba, de már egyetlen új kockát nem rajzolhatnánk be úgy, hogy ez továbbra is teljesüljön.
Arra is van lehetőség, hogy a most leírt labirintust még valamivel bonyolultabbá tegyük, sőt bonyolultsága egy általunk megadott értékkel még szabályozható is legyen. Az előző algoritmusnál mindig olyan hosszú falat húztunk, amilyet csak lehetett - ameddig bele nem ütköztünk egy másikba. Ehelyett megtehetjük, hogy a program elején INPUT-tal bekérünk egy 0 és 1 közé eső értéket, mondjuk egy Y nevű változóba, és ezentúl minden kocka berajzolását csak Y valószínűséggel végezzük el - azaz, előtte megvizsgáljuk, hogy az RND<Y reláció teljesül-e, és ha nem, abbahagyjuk az aktuális fal rajzolását. Y=1-re az előző típusú labirintust kapjuk, Y=0.5-re viszont egy sokkal zegzugosabbat. 0.5-nél kisebb értéket nem érdemes megadni, mert ez a futási időt jelentős mértékben megnöveli, de a labirintus már nem lesz sokkal bonyolultabb.

6. Fa I
Az első változatban karakteres képernyőn megvalósítható véletlen fát írunk le, amelynek az ágai - kissé absztrakt módon - derékszögben nőnek. Mindenesetre nagyon dekoratív lesz.
A fa egymásból kinövő ágak nemzedékeiből épül fel, az egyes nemzedékek felváltva csupa vízszintes, illetve csupa függőleges ágakból állnak, az egy ágból kinövő új "hajtások" pedig felváltva indulnak el jobbra és balra (függőleges ágnál), illetve fölfelé és lefelé (vízszintes ágnál). Valahogy gondoskodni kell arról is, hogy az ágak "ne kuszálódjanak össze", egy ilyen durva léptékű rajzon az nem mutatna túl jól.
Egy karakter típusú változóban tárolva az egy nemzedékhez tartozó ágak "rügyeinek" koordinátáit (azaz az olyan pontokét, amelyekből a következő nemzedék ágai fognak kinőni), egyszerű szubrutint készíthetünk, amely végigmegy az aktuális generáció összes ágán, megkeresi a rügyeket, azokból kiindulva új ágakat rajzol, és rajtuk véletlenszerűen rügyeket választ, és azok koordinátáit följegyzi. Minden új pontnál ellenőrzi, hogy az még a képernyőn lesz-e, illetve hogy a négy szomszédja közül csak egy legyen már berajzolva (tudniillik, amelyiket az előbb rajzoltuk be). Egy új ág befejezése után a haladási irányt ellentettjére (1-szeresére) változtatjuk. Amikor egy egész ágnemzedék minden rügypontján végighaladtunk, azok koordinátáit törölni lehet a karakteres változó elejéről, az ágak növekedési irányát meg kell változtatni függőlegesről vízszintesre, vagy fordítva. Ezt a szubrutint, amely egy egész generáció ágait berajzolja és a szükséges feldolgozásokat elvégzi, addig ismételjük, amíg egy nemzedékben már egyetlen új rügyet sem jelöltünk be.
Most is, mint a labirintusrajzolásnál, megadhatunk INPUT utasítással a program elején egy valószínűségi értéket (0 és 1 közé eső számot), hogy az ágak növekedése ne addig tartson, ameddig egyáltalán lehetséges, hanem amíg az (RND < megadott érték) reláció teljesül. Itt 0.9 körüli értékeket érdemes megadni. Ezzel a módosítással általában szebb fákat rajzol a program, mint az, amelyikkel nem végeztettünk ilyen ellenőrzést.
7. Fa II
Hasonló elv alapján sokkal élethűbb fát lehet rajzolni finom felbontású képernyőre. Az ágak most már nem kell hogy derékszögben nőjenek. Most minden ágat egy karakteres változó négy byte-jában kódolunk, ahol az első két byte a kezdőpont koordinátáit, a második kettő pedig a végpont tőle számított vízszintes és függőleges eltérését tárolja. Miután ez a rajz úgyis sokkal bonyolultabb lesz, mint az előző, elég, ha áganként legföljebb egy rügyet veszünk föl, amit az ág berajzolása közben véletlenszerűen választunk. Az egy ághoz tartozó négy adatból mindig ki lehet számítani a vízszintessel bezárt szögét, és ehhez képest (megadott határokon belül) szintén véletlenszerűen határozzuk meg az új ág elhajlásának szögét, kiszámítjuk és tároljuk a végpontok koordinátáit, illetve eltéréseit.
Az ágak megrajzolása itt a DRAW utasítással történik, így még annak végrehajtása előtt ellenőrizni kell, hogy mindkét végpont a képernyőre kerül-e. Ennek biztosítására korlátozhatjuk az új nemzedékek számát és egy ág maximális hosszát úgy, hogy a legrosszabb esetben se érjen el a képernyő széléig. A másik lehetőség, hogy minden új nemzedékben az ágak hossza az előzőeknek mondjuk maximálisan a 2/3-a - ekkor a fa legnagyobb átmérője sem lehet az első ág (a törzs) hosszának háromszorosánál több.
8. Pitypang
Láttuk, hogyan kell egy pontot adott középpont körül adott szöggel elforgatni. Ezt a tudást most egy olyan programban fogjuk felhasználni, amely pitypangot rajzol, véletlenszerű mozzanatok felhasználásával.
Aki már látott pitypangot, tudja, hogy egy magból sugarasan kinövő kis szálakból, és azokból ernyőszerűen szétálló pelyhes szálakból áll. Egy ilyen száracska a hozzá tartozó ernyővel együtt kb. így néz ki:

Mi is egy ilyen alakzatból fogunk kiindulni (amely térben is így helyezkedik el), és ezt fogjuk a tér különböző irányaiba elforgatni a szár bal oldali vége, mint középpont körül. Térbeli forgatásról eddig ugyan még nem volt szó, az azonban mindig megvalósítható két síkbeli forgatás egymásutánjaként. A pitypang pontjait a térben három koordinátával jellemezhetjük: a vízszintes és függőleges helyzetet megadó x, illetve y koordinátával, illetve a mélységet jelölő z koordinátával. Ha az elforgatandó kis elemi alakzat sugara 20 egység, az ernyőé pedig 10, akkor jellemző pontjainak koordinátahármasai a következők:
ahol u 0 és 2*PI közé esik, mondjuk k*PI/4 alakú, ahol k = 0, 1, ..., 7 lehet. Ha olyan forgatást akarunk megvalósítani a térben, amely a szár jobb oldali végét (szemből nézve) mondjuk a 140,100 pontba viszi, akkor először az x-y síkon elforgatjuk addig, amíg az első koordinátája 140-re nem esik, ezután szembe, az y-tengelytől a z-tengellyel ellentétes irányban (tehát magunk felé) fordítjuk addig, amíg az y koordináta 100-at nem vesz fel.
Módszerünk azonban nem a szár jobb oldali végpontjának adott pontos forgatása, hanem
A második esetben ügyesen kell megválasztani mind a szögelfordulások lépésközét, mind az RND-vel összehasonlított számértéket, hogy egyrészt elég sok szárat és ejtőernyőt berajzoljunk, másrészt mégse túl sokat, hogy az egyes futtatásokkor a rajzok észrevehetően különbözzenek, és hogy a program ne fusson túlságosan hosszú ideig.
Amikor képeket rajzoltatunk a programokkal, egy időben mindig egy új pont (vagy - szinte egyszerre - egy szakasz, vagy egy körív összes pontja) jelenik meg a képernyőn - ez azonban eddig lényegtelen volt, csak a végeredményként előálló kép számított. Az újonnan megjelenő pontokat (esetleg bizonyosak törlésével) ugyanakkor arra is fel lehet használni, hogy olyan képeket készítsünk, amelyeknek a mozgás is lényeges alkotóeleme. A most következő részben néhány ilyen programötletet sorolunk fel.
1. Kígyó
A véletlen bolyongás továbbfejlesztett változata, a ZX 81 karakteres képernyőjére. A képernyő középső sorában megjelenik egy fekete kockákból álló csík, a bal oldalán egy inverz (fekete alapon fehér) csillag, a jobb oldalán pedig egy inverz "X" betű: ez lesz a kígyó. Ezután a kígyó feje véletlen bolyongásba kezd, a teste követi, és amerre elhalad, valamilyen speciális karakterből álló nyomot húz maga után. Minden lépésnél megvizsgáljuk, hogy a fej a képernyőn marad-e, illetve, hogy nem érinti-e a teste valamelyik másik pontját (azaz hogy a továbblépésre kiválasztott új mező nem tartozik-e már a kígyóhoz - saját nyomába természetesen újból beléphet). Ily módon, ha elég hosszú a kígyó - mondjuk tíz kockából áll -, előbb-utóbb a saját maga által bekerített területre ér, és nem tud továbblépni - addig azonban keresztül-kasul sokszorosan bepásztázza a képernyőt.
A fej véletlenszerű mozgását a Véletlen bolyongás c. részben leírt módon programozhatjuk, az említett ellenőrzéssel bonyolítva. Hogy a kígyó farkát hogyan töröljük minden lépésben a nyomot jelképező karakterrel helyettesítve, és hogyan visszük át a teste - előző lépésben még - utolsó előtti pontjába - egy érdekes kódolási problémát vet fel. Tudnunk kell ugyanis minden lépésnél, hogy melyik karakterhelyen található a kígyó feje, a második, harmadik stb., utolsó pontja, és ezt minden lépésben át kell igazítani. Nagyon körülményes volna mindezt magáról a képernyőről leolvasni. Egy viszonylag egyszerű megoldás a következő: külön tároljuk egy-egy változóban a kígyó fejének és farkának helyét a képernyőn, ezenkívül egy karakteres változóban a teste pontjainak egymáshoz képest vett irányát az 1, 2, 3 és 4 számok-kal kódolva. Amikor meghatároztuk a fej új helyét, akkor a régihez viszonyított iránynak megfelelően beírunk ennek a karakteres változónak az elejére egy új kódot. Amikor viszont a farkát akarjuk "áthelyezni", az utolsó helyen álló kódnak megfelelően számítjuk ki az új helyet, majd ezt a kódot töröljük a változó végéről. Ily módon mindig ugyanolyan hosszú marad a kígyó, és az az érdekes, hogy mozgásának sebessége egyáltalán nem függ a hosszától, hiszen minden lépésben csak a fejével és a farkával foglalkozunk.
2. Életjáték
A közismert életjáték egyik változatát a következőképpen programozhatjuk be személyi számítógépre. A képernyőt véletlenszerűen betöltjük fekete és fehér négyzetekkel. Ezután a képernyő legszélső sorainak és oszlopainak kivételével minden mezőt meghatározott módon átalakítunk - olyan színre írjuk át, amilyen korábban a belőle és négy szomszédjából álló területen többségben volt.
Az átalakítást ugyanakkor úgy kell végrehajtani, mintha minden mezőn egy időben történne, azaz nem szabad, hogy valamelyik átalakításnál a már átalakított szomszédot vegyük figyelembe. Ezért amikor egy soron végighaladunk, az átalakításokat nem végezzük el rögtön, hanem csak valahogy megjegyezzük, melyik mezőt milyen színűre kell majd átalakítani, és a tényleges átírással addig várunk, amíg az adott mezőt már az alatta levő sor átalakításához is figyelembe nem vettük. Erre az egyik lehetséges megoldás, hogy amikor egy mezőt (és a szomszédjait) megvizsgálva azt találtuk, hogy a következő menetben feketének kell lennie, akkor a jelenlegi alapszínnek megfelelő jelet (mondjuk egy "X"-et) teszünk oda. Így a tőle jobbra és lefelé eső mezők ellenőrzésénél csak a szomszédok alapszínét szabad figyelembe venni. Amikor pedig már az alatta fekvő karakter ellenőrzése megtörtént (tehát más mező ellenőrzésénél már nem fog szerepelni), akkor ezt a mezőt is át lehet írni, ha "X" szerepelt benne, akkor feketére, egyébként fehérre.

Kérdés lehet még, hogyan végezzük el a mezők ellenőrzését. ZX 81-nél ez egyszerűen megoldható a kódok összegzésével. Az üres mező kódja 0, a feketéé 128, ha "X"-et írunk rájuk, akkor 61-gyei növekszik. Így elég azt ellenőrizni, hogy az öt mezőn álló karakterek kódjainak összege eléri-e a 3x128 = 384 értéket - ekkor az adott mező legközelebb fekete lesz, egyelőre "X"-et írunk bele.
A Spectrumnál a színeket külön lehet ellenőrizni az úgynevezett attribútummezőkben - a fehér alapon fekete karakterek színkódja 56, a fekete alapon fehéreké pedig 7. Ha az öt szomszédos mezőre összesen 3x56-ot= 168-at kapunk, akkor a következő menetben itt fehér kocka áll - most a fordított esetben jelölhetjük meg a vizsgált mezőt "X"-szel.
3. Lissajous-görbék
Finom felbontású képernyőre egyszerű és érdekes programot lehet írni, amely egy egész görbecsalád megjelenítésére képes. A kör paraméteres görbéjét a COS t és SIN t függvények megfelelő átalakításával rajzoltuk meg. Ha most a körrajzoló programba COS(a*t)-t és SIN(b*t)-t írunk, akkor a és b értékeitől függően egészen különböző jellegű görbéket kapunk: ezeket nevezik Lissajous-görbéknek. Ha a és b tört értékek, akkor a görbe nem zárul be, mire t a 0-tól 2*PI-ig elfut - egyszerűbb, ha felső határként mondjuk 1000000-t írunk, és a programot addig futtatjuk, amíg COS(a*t) az 1-et, SIN(b*t) pedig a 0-t eléggé meg nem közelíti.

10 LET r=80: LET u=128+r*COS 0: LET v=96
20 LET a=.24: LET b=.96
30 PLOT u,v
40 FOR t=0 TO 8.4*PI STEP .2
50 LET x=INT (128+r*COS (a*t)): LET y=INT (96+r*SIN (b*t))
60 DRAW x-u,y-v
70 LET u=x: LET v=y
80 NEXT t
4. Gravitációs görbék
Véletlenszerűen elhelyezünk néhány csillagot a képernyő rögzített helyeire, majd valahonnan útnak indítunk egy űrhajót. A gravitáció hatására az űrhajó sebessége és iránya állandóan változik, és változatos pályákat ír le a csillagok között.
Az űrhajó helyzetét mindig hat adat írja le: kettő a pillanatnyi helyének koordinátáit, egy-egy a vízszintes és függőleges sebességét, és egy-egy a vízszintes és függőleges gyorsulását. A gyorsulás minden pillanatban változik, egy csillag esetében az űrhajó és a csillag vízszintes eltérését elosztjuk a távolság valamilyen rögzített hatványával (a fizikai törvényekhez való hűség a 3/2-ik hatványt diktálná - így jönne ki a tömegvonzás a távolság négyzetével fordított arányban -, ám a képernyő méretei miatt nem feltétlenül ez adná a legszemléletesebb görbét, másfajta hatványkitevővel próbálkozva talán nagyobb szerencsével járunk). Több csillag esetén mind a vízszintes, mind a függőleges irányú gyorsulást csillagonként összegezzük.
Amikor kiszámítottuk az új gyorsulásokat, a vízszintes sebességet megnöveljük a vízszintes gyorsulással, a függőlegeset a függőlegessel. Hasonlóképp a vízszintes koordinátához hozzá kell adni a vízszintes sebesség (új) értéket, a függőleges koordinátához pedig a függőleges sebességet. Így megkapjuk az űrhajó pályájának egy újabb pontját, amelyet az előzővel összekötve fokozatosan megrajzolhatjuk az egész pályát.
Megeshet, hogy helyenként a sebesség értékére olyan nagy szám jön ki, hogy az űrhajó "kirepül" a képernyőről - vagy pedig a pálya két szomszédos szakasza éles szögben találkozik. Ennek kiküszöbölésére alkalmas módszer, ha a sebességet mindig állandó nagyságúnak vesszük (azaz mind a vízszintes, mind a függőleges sebességkomponenst elosztjuk a kettő négyzetének összegéből vont gyökkel) - ekkor viszont a gravitációs erőt meghatározó kifejezésben kisebb hatványkitevőt kell venni -, ismét a fizikai valóság némi "átfogalmazásával".
Érdekes megfigyelni, hogy különböző helyekről vagy ugyanarról a helyről különböző irányokban vagy különböző sebességekkel elindított űrhajók milyen pályákat futnak be. Nagyon szép képeket kapunk, ha ezeket a pályákat egyszerre megőrizzük a képernyőn, miközben egy sor hasonló helyzetű űrhajót indítunk útnak egymás után. Többféle szabály szerint adhatjuk meg az űrhajók kezdeti helyzetét, például:
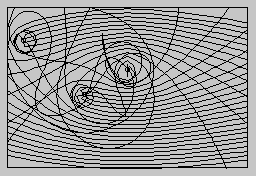
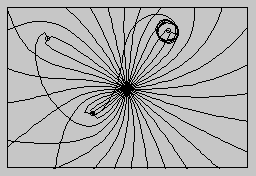
5. Összefonódó csíkok
Már tudunk olyan programot készíteni, amely egy pont véletlen bolyongását jeleníti meg, és tehetetlenséggel (nem cikcakkosan, hanem lekerekített ívekben) halad előre. Azt is megtehetjük, hogy ahol az előbb egyetlen pontot rajzoltunk, most néhány karakterből álló vízszintes csíkot jelenítünk meg. Amikor a csík eléri a képernyő alját, egy SCROLL utasítással egy sorral följebb toljuk az egész képet, így az imbolygó csík, mint egy folyó, végtelen sokáig folytatja kígyózó útját.
Elindíthatunk két ilyen csíkot is (amelyek különböző karakterekből állnak, hogy ahol összeérnek, jól el lehessen különíteni őket). Nagyon érdekes mozgást kapunk akkor, ha a keresztezéseknél nem mindig az egyik csík fedi a másikat, hanem felváltva. Ezt úgy lehet elérni, hogy mindkét csíkhoz prioritást vagy rajzolási sorrendet rendelünk: a kereszteződéseknél nyilván az lesz felül, amelyiket másodszor rajzoltuk be. Ha eredetileg a jobb oldali csík volt nagyobb prioritású, amikor keresztezi a másik útját, és a jobb oldali széle is balra kerül annak legbaloldalibb pontjától, akkor megcseréljük a prioritásukat, amelyik eddig első volt a kirajzoláskor (és így a másik alá került), most második lesz.
Nehezebb az az algoritmus, amellyel kettőnél is több csík fedési viszonyait (vagy kirajzolási prioritását) határozzuk meg. Míg az előbb röviden úgy fogalmazhattuk volna meg a fedési algoritmust, hogy a jobb oldali csík kerül felülre egészen addig, amíg teljes terjedelmében a másiktól balra nem kerül (tehát a másik nem lesz a jobb oldali) - most ezt az eljárást azért nem követhetjük, mert három csík (nevezzük őket A-nak, B-nek és C-nek) elhelyezkedhet úgy is, hogy az eredetileg teljesen a jobb szélen levő A csík már balra kilóg a másodikból, B-ből, de még nem került egészen balra tőle (tehát még nem cserélődött meg a prioritásuk), és ugyanez a helyzet az eredetileg középső B és bal oldali C csíkok között, viszont az A csík a C-től már teljes egészében balra került. Magyarul: az A jobbra van a B-től, a B a C-től és a C az A-tól. Ennek alapján pedig nem lehet a prioritást meghatározni.
A megoldás az, hogy két csík között a prioritási sorrend csak akkor változik meg, ha a nagyobb prioritású teljesen balra kerül a másiktól, és nincs közöttük "harmadik", azaz nincs olyan csík, amely a prioritási rendben a kettő közé esne, viszont mindkettővel érintkezne.
Hátravan még, hogy hogyan kell meghatározni az eredeti prioritási rendet. Erre többféle lehetőség kínálkozik; a legegyszerűbb, ha balról jobbra vesszük sorra a csíkokat. Sokkal változatosabb képet ad viszont az a rend, amit például öt csíknál így adhatunk meg: 1,3,5,2,4, ahol az "1" jelöli a legbaloldalibb csíkot, "2" a másodikat, és így tovább.
Vonzó lehetősége a személyi számítógépeknek, hogy egyszerű "animációs" vagy rajzfilmeket lehet készíteni velük. Olyan programokra van szükség, amelyek másodpercenként tízszer-hússzor átrajzolják az egész képernyőt. Ehhez a BASIC programok túlságosan lassúak, azokkal legfeljebb egy-egy pontot lehet másodpercenként tízszer-hússzor átírni. Gépi kódban írt programokkal persze korlátlan lehetőségek nyílnak rajzfilmprogramok készítésére (különösen finom felbontású képernyőn) - viszont a gépi kódú programozás körülményes, nehéz ellenőrizni és javítani ezeket a programokat. Ezért most egy olyan lehetőséget írunk le, amely (igaz, csak ZX 81-re, amely legalább 16 kbyte-os RAM-mal ki van egészítve) egészen könnyűvé teszi egyszerű rajzfilmek készítését. Persze a ZX 81 grafikai lehetőségei nem olyan jók, mint akár a Spectrumé, ám ez itt azt is jelenti, hogy a memóriában a képernyőnek meg-felelő terület nem egészen 1 kbyte nagyságú (szemben a Spectrum 5,5 kbyte-jával, ami más, finom felbontású képernyővel dolgozó gépeken is szükségképpen legalább ekkora), és ehhez képest a 16 kbyte RAM-kapacitás viszonylag sok.
Azt fogjuk csinálni ugyanis, hogy BASIC-ban írt programokkal megrajzoljuk a rajzfilmben szereplő képernyőket ("fázisrajzokat"), majd egy egészen rövid gépi- kód-programmal tároljuk őket a memória különálló területein. Ha a képernyőből csak fél kbyte-ot használunk fel (ami 15 teljes sornak felel meg a maximális 22 helyett), akkor ilyen képekből kényelmesen tudunk tárolni, mondjuk, húszat. Amikor minden képet megrajzoltunk és tároltunk, az előző gépikódú program egyetlen byte-ban módosított változatával egymás után sorban be tudjuk hívni a képernyőre az egyes képeket, és ezzel "levetíteni" 1-2 másodperc időtartamú rajzfilmünket. Mivel ez nagyon rövid idő, úgy érdemes megszervezni a képeket, hogy ciklust alkossanak, azaz az utolsó után a legelső megint vetíthető legyen, így addig nézhetjük az ismétlődő mozgást, amíg meg nem unjuk, sőt - ahogy az utolsó példában látni fogjuk - még ebbe az ismétlődésbe is vihetünk némi változatosságot.
Itt közöljük az említett gépikódú programot (működésének részletezése nélkül):
decimális kód: ld de,NN
.0.
.0.
ld hl,(NN)
12
64
inc hl
ld bc,NN
0
2
nop
ldir
ret17
0
0
42
12
64
35
1
0
2
0
237, 176
201
Ezt a gépikódú programot a BASIC program legelején egy REM utasításban kell elhelyezni:
Az üres kocka a space jele, a többi keretezett jel grafikus karakter. Ekkor például egy RAND USR 16514 utasítással meghívható. Futtatása előtt egy POKE 16516,K utasítást kell kiadni, ahol K 78 és 120 közötti páros értékeket tartalmazhat. Hatására a képernyő első 512 byte-ját, ami valamivel több mint 14 sornak felel meg, kiviszi a memória 256*K címétől kezdődő területre. Ha azt akarjuk, hogy fordítva működjön (tehát a 256*K címtől kezdve 512 byte-ot behozzon a képernyőre), akkor a gépikódú program meghívása előtt egy POKE 16524,235 utasítást kell kiadni - ezután a REM-ben egy "FOR" karakter jelenik meg a "GOSUB" előtt. A BASIC program tehát a következő lehet:
1 REM ...
10 POKE 16524,0
20 FOR I=80 TO 120 STEP 2
30 GOSUB 200
40 POKE 16516,1
50 RAND USR 16514
60 NEXT I
70 POKE 16524,235
80 FOR I=80 TO 120 STEP 2
90 POKE 16516,I
100 RAND USR 16516
110 NEXT I
ahol 200-tól következik az l-nek megfelelő képet előállító szubrutin.
Megkönnyíthetjük a rajzfilmhez szükséges képeket megrajzoló program írását azáltal, ha olyan szubrutint írunk, amely (az egyenesrajzoló algoritmus segítségével) egy karakteres változóban kódolt pontsorozatot szakaszokkal összeköt a Kódolás c. részben leírt módon. Így nem kell minden rajzfilmnél külön programot írnunk a képek megrajzolására: a változó rész csak az lesz, amelyik a megfelelő karakterpárokat tárolja a kijelölt karakteres változóba.
Lássunk tehát néhány rajzfilmötletet! (A megvalósításnál ne feledjük, hogy - legalábbis az itt megadott gépikód programmal - csak a képernyő felső 14 sora vehető igénybe. A rajzolást persze PLOT-tal végezzük, így ez valójában 28 sort jelent.)
1. Nagy hal - kis hal
A képernyő jobb felére rajzolunk egy nagy halat - nagyjából egy rombuszt. Ez az alak végig változatlan lesz - kivéve, hogy a száját ki fogja tátani, majd megint becsukja. (Tehát a hal balra néző fejrészének két változatát kell megrajzolnunk: egy nyitott szájút és egy csukott szájút.)
A képernyő bal oldaláról egy kis hal (kisebb rombusz alakú figura) közeledik képenként a nagy halhoz, aki csukott szájjal várja. Amint a kis hal hozzáérne a szájához, kitátja, addig vár, amíg az beúszik, majd megint becsukja. Ezután még néhány képig mozdulatlanul áll, majd megint minden kezdődik elölről.

2. Galamb
Elölnézetből egy nagy madár (mondjuk egy galamb) szárnymozgását jeleníthetjük meg a következőképpen. A madár törzse a képernyő közepén mozdulatlanul áll - ezt csak egyszer kell megrajzolnunk. A szárnyai szimmetrikusan mozognak. Mindkét szárnya három-három csuklóból áll, középen a törzshöz rögzítve. Az első csukló mozgó végpontja valamilyen SIN függvény szerint mozog, ha húsz képet rajzolunk, akkor SIN(I*PI/10) valahányszorosa lesz a pontos függvény - ez biztosítja, hogy húsz kép alatt éppen a kezdeti helyzetbe ér vissza. A második és harmadik csukló is ugyanilyen periódusú SIN függvény szerint mozog, csakhogy a szög mindkettőnél egy-egy lépésközzel lemarad - SIN((I-1)*PI/10), illetve SIN((I-2)*PI/10) valamilyen transzformáltja lesz a csuklók végpontjainak második koordinátáit leíró függvény.

3. Légynéző
A képernyő közepére egy arcot rajzolunk, az orr, a szemek és a szemöldökök sematikus vonalával. Az arc előtt ellipszispályán (amelynek vízszintes tengelye mondjuk a szemek vonalában helyezkedik el) egy légy kering. A légy megjelenítése nagyon egyszerű: három pont képenként váltakozva "V", illetve lefelé fordított "V" alakban. Ha húsz képet rajzolunk, a légy az ellipszispálya egyenletesen elhelyezkedő húsz pontján tűnik fel.
Miközben a légy kering, az arc utánafordul: az orr töröttvonala hegyével a légy vízszintes kitérésének megfelelően jobbra-balra elfordul; a szemek pedig (a mozdulatlan szemöldökökhöz képest) egy kétszer két pontból álló négyzetnek éppen a légyhez legközelebb eső pontjában helyezkednek el.
A rajzfilm "levetítésénél" most egy újabb kézenfekvő lehetőség adódik: nem mindig ugyanabban a sorrendben hívjuk elő a memóriából a képeket, hanem olyan sorozatokban, amelyeknek második végpontját a húsz közül mindig véletlenszerűen választjuk. Ehhez az eredeti BASIC programban néhány változtatásra van szükség:
73 LET U=80
75 LET V=80+2*INT(RND*240)
80 FOR I=U TO V STEP 2*SGN(V-U)
120 LET U=V
130 GOTO 75
Például elindulunk az első képpel, aztán véletlenszám-generátorral kiválasztjuk a 13-at - ekkor az 1-től a 13-ig vetítjük le őket -, utána mondjuk 7-et választunk, tehát a 13-tól a 7-ig vetítjük őket, most visszafelé, és így tovább. Ha nem is lehet túl sok olyan motívumot kitalálni, ami ehhez hasonlóan ötletszerűen oda-vissza játszva is élvezhető lesz, néhány esetben ezzel is enyhíthetjük a rajzfilmek szűk terjedelme okozta egyhangúságot.

Bevezetés
A számítógépnek az iskolában betöltött szerepét sokféleképpen megfogalmazták már. Volt oktatási segédeszköz ("olcsó" fizikaszertár), megismerendő objektum (fel kell készíteni a jövő szakembereit), adminisztrációs munkaerő (csináljon órarendet) és sok egyéb. Ki-ki érdeklődése és érdekeltsége szerint tört lándzsát valamelyik funkció kizárólagos volta mellett, és elég sok energiát emésztett fel az ürügyek keresése.
Mégis - kicsit durván fogalmazva - azt lehet mondani, hogy egyelőre szinte teljesen mindegy, mire használnak egy gépet az iskolában, a lényeg, hogy minél többen használják. Pontosabban: ki-ki használja arra, amire neki tetszik: ebből a sokféleségből előbb-utóbb biztosan körvonalazódik a számítógép iskolai státusa. Mindenekelőtt azonban két tévhitet szeretnénk eloszlatni:
Ezt a két gondolatot érdemes kicsit bővebben is kifejteni.
A számítástechnika hovatartozásáról. Kb. húsz évvel ezelőtt hazánkban az első programozók szinte kivétel nélkül matematikus-fizikus végzettségűek voltak, elvétve akadt még közöttük néhány mérnök. Ennek akkor is csak részben volt az az oka, hogy azok az emberek igényelték leginkább a komputer segítségét, és őhozzájuk állt legközelebb a számítógépes gondolkodás. Lényegében ugyanilyen fontos volt az a tény is, hogy sokuk számára igen kedvező elhelyezkedési lehetőséget kínált az új terület. Természetesen egy pillanatig sem vitás, hogy a számítástechnikában (a programozásban) használható ismeretek a természettudományokhoz és a matematikához állnak legközelebb. Talán úgy is fogalmazhatnánk, hogy a számítástechnika ezekre a tudományokra épül, de csak oly mértékben, mint a fizika a matematikára, a biológia a fizikára, mint ahogyan a pszichológia mögött közvetlenül is ott áll egy csomó más diszciplína.
A gépek felhasználásának lehetőségei tágabbak ennél. Napjaink közhelye, hogy a számítógép az élet minden területére betör. Ez ellen nehéz bármit is tenni, ezt tudomásul kell venni. Egyes szakírók az elektronikai forradalom eredményeit olyan jelentősnek és olyan hatásúnak tartják, mint az írni tudás tömeges térhódítását. Mi is arról szeretnénk - egyebek között - meggyőzni az olvasót, hogy legyen bármilyen is az érdeklődési területe, a számítógépben partnerre, segítségre találhat. Nyilván nem egyforma szinten és mértékben, de a számítógép intellektuális kihívására minden alkotó gondolkodású embernek fel kell figyelnie.
A következőkben tehát egy "általános olvasót" képzelünk el: mindegy, milyen korú, képzettségű, és mi iránt érdeklődik. Szemléletünk mégis meglehetősen "tananyagcentrikus" lesz. Ennek több oka is van. Egyrészt iskolába mindenki járt vagy jár, így a feladatok témája mindenkinek ismerős, másrészt az iskolás korosztály, mint a fenti számvetés is mutatja, igen fogékony. Végül, de nem utolsósorban a régóta remélt iskolagépek megjelenése - érzésünk szerint - ebben a korosztályban ébreszti a legnagyobb igényt.
Mint már említettük, sokat lehet arról vitatkozni, hogy mi legyen a gépek szerepe az iskolában. Mi fontosabb: a gyermekek tanuljanak meg programozni vagy a gép segítse a pedagógusokat a tanításban? Az alábbiakban szándékosan nem választjuk szét a két dolgot. Valószínűleg a szépírást is sokkal célszerűbb a helyesírással együtt gyakorolni: már első általános végén többet ér 10-20 bonyolultabb helyesírású szót leírni gyakorlásul, mint százszor azt, hogy "baba".
Pontosabban, átmenetet képzelünk el pár soros gyakorlóprogramoktól a profik által írt "technikás", sokoldalú oktatórendszerekig. Optimista szemünk előtt tanulók által írt sok száz program sorakozik, amibe ki-ki saját egyéniségét is beleviszi, és ez adja igazi értéküket. A kétkedőknek csak annyit, hogy Amerikában a világ legismertebb oktatórendszerének, a gigászi PLATO-nak kb. 10 000 órányi tananyagát 90%-ban tanulók írták.
Itt és most - a semmiből indulva - a szórványos "amatőr" kísérleteknek is örülni kell. Évek alatt ezekből, ezek alapján és velük párhuzamosan didaktikailag profi rendszerek lesznek kidolgozhatok. Sőt egy rózsaszínű szemüvegen keresztül felsejlik a jövő, amikor az egész oktatási rendszert módosítani, de legalábbis segíteni tudják a számítógépek. Olyan anyagrészek elemei kerülhetnek be a 12 osztály anyagába, mint az integrálszámítás, differenciálegyenletek, optimalizáció, statisztikai módszerek, szimuláció stb. És mindez "könnyed", élvezetes, játékos módon. Ezek után már a fizika, kémia, biológia, nyelvtan, irodalom, idegen nyelv stb. is sokoldalúbban tárgyalható.
Mégis kiknek és milyen céllal íródott ez a rész?
Azt javasoljuk, az olvasó ne igyekezzék gyorsan túljutni a fejezeten. Tapasztalataink alapján úgy próbáltunk fogalmazni, hogy egy átlagos tizennégy éves gyerek az írottak nagy részét megérthesse. Mégis eleinte mindenki próbáljon érdeklődésének megfelelő témakört találni, majd miután meggyőződött róla, hogy nem boszorkányság a dolog, akkor már nagyobb sebességgel mehet tovább. Okvetlenül érdemes "gépközelben" olvasni és rövid időn belül (például az iskolában) kipróbálni a leírottakat. A sikerélmény feltétlenül gyorsítja a haladást.
Végül szeretnénk hozzájárulni ahhoz, hogy a komputer az iskolában ne csak egy gyors függvénytáblázat legyen vagy a tesztszerű kikérdezés türelmes eszköze, hanem jó barát, akivel értelmesen játszani és akitől játszva tanulni lehet. Reméljük a legjobbakat.
Időmérés, vezérlés
Bármily meglepő, a címbeli magas szintű tevékenységek ellátására is alkalmas a legtöbb gép BASIC-je. INKEY$-vel jelezzük azt a függvényt, ami egyetlen karakter bevitelét teszi lehetővé, de az INPUT-nál ravaszabb formában. Az INPUT utasításra ugyanis a komputer konokul és tétlenül vár addig, amíg nem felelünk. Az INKEY$ sokkal megértőbb: ha éppen nem kap választ, akkor vállvonással folytatja egyéb te-vékenységét (tovább számol, rajzol stb.). A
10 FOR i=1 TO 1000
20 IF INKEY$="S" THEN PRINT "s";: GO TO 40
30 PRINT "C";
40 NEXT i
program hatására annyi S betű jelenik meg, ahányszor lenyomjuk a billentyűjét, különben C betűkkel lesz teli a képernyő. Érdemes kipróbálni, a legádázabb nyomkodás mellett is kb. 10-szer annyi C lesz, mint S. Ez azt jelenti, hogy a gépi műveletekhez képest ilyen nagyságrendű a reakcióidőnk.
Figyelni kell arra, miszerint az INKEY$ nem azonosító, tehát értéke olvasáskor eltűnik! Célszerű LET a$=INKEY$-vel "megfogni", és ezután már A$-ben kitörlésig ott van a beütött karakter.
Egyik alkalmazási lehetőség, hogy időt mérjünk.
5 LET k=0
10 FOR i=1 TO 26
20 IF INKEY$ <> CHR$(96+i) THEN LET k=k+1: GO TO 20
30 PRINT CHR$(96+i);
40 NEXT i
50 PRINT: PRINT k
program azt teszteli, hogy hány időegység alatt (K) tudjuk az ábécét begépelni. K<800 már kiváló eredmény, érdemes versenyezni.
Egy másik vonzó terület a láthatatlan manipuláció. Például rajzolni lehet ily módon. Helyezzünk el egy pontot a képernyőn. Legyen az O - balra, P - jobbra, Q - fel, A - le megfeleltetéssel elérhető, hogy bármelyik billentyű lenyomásakor a megfelelő szomszédos pont is kivilágosodjék. Így tetszőleges folytonos vonal jeleníthető meg.
10 LET x=128: LET y=88: PLOT X,Y
20 LET b$=INKEY$
30 IF b$="" THEN GO TO 20
40 IF b$="o" AND x>0 THEN LET x=x-1
50 IF b$="p" AND x<255 THEN LET x=x+1
60 IF b$="q" AND y<175 THEN LET y=y+1
70 IF b$="a" AND y>0 THEN LET y=y-1
80 IF b$=" " THEN STOP
90 PLOT X,Y: GO TO 20
Megoldható az is, hogy a billentyűk "láthatatlanul" mozgassák a pont helyét, és a kivilágítást egy további gombbal (F) kelljen kérni. Így már bármi, nem csak folytonos vonal rajzolható a képernyőre. Vegyük észre, az igények és adminisztrációjuk sehol sem fogja zavarni a képet. INPUT-tal ez nem lenne elérhető!
Még elegánsabb, ha az O, P, Q, A billentyűk csak "elindítják" a pontot a megfelelő irányba, és az addig halad arra, míg egy másik billentyűvel meg nem állítjuk.
Kódolás
Azt a tevékenységet nevezzük kódolásnak, amikor egy tulajdonságot valamilyen jellel (általában számmal) helyettesítünk. Például az 5-ös osztályzat jelentése: hibátlanul tudod a leckét. Természetesen a kódok egyértelműségét nem könnyű biztosítani, de ezzel nem foglalkozunk, inkább arra mutatunk néhány ötletet, hogyan lehet "kis helyen" minél több információt tárolni.
Képzeljük el, egy osztály (30 fő) érdemjegyeire van szükségünk öt tárgyból. Ez látszólag 150 számmal oldható meg: ennyi 1-5 közötti számot kell a gépbe vinni, ami ott 150 adatnyi helyet foglal el. Ennél sokkal tömörebb (és egyszerűbb is), ha például X. Y. jegyeit (mondjuk, 4,3,5,4,4) egyetlen ötjegyű számként, 43544 alakban tároljuk. Ez csak 30 számot jelent, igaz, hosszabbakat. Hogy valóban értékelni tudjuk a megoldást, gondoljunk arra, hogy 1000-1200 fő osztályzataira van szükségünk. Ezt az 5-6000 adatot már kevés gép képes "megenni".
A kérdés az, hogy egy ötjegyű számból hogyan lesznek osztályzatok? Kicsit általánosabban fogalmazva, egy több jegyű egész (A) K-adik jegyét szeretnénk előállítani. Célszerű a jegyek sorszámozását jobbról kezdeni. Ily módon egy tetszőleges A szám K-adik jegye az
INT (a/10^(k-1))-10*INT (a/10^k)
formulával adódik. A fenti esetben (A=43544), a harmadik jegy (K=3): INT (43544/100) = 435, illetve 10*lNT(43544/1000) = 430 különbsége valóban 5 lesz! Ezt bármilyen típusú gép elfogadja - esetleg a ^ helyett kell más jelet írni -, és így egy viszonylag gyorsan számolható kifejezéssel könnyen történhet a visszakódolás. Ha gépünkön kétváltozós függvény is definiálható - a Spectrum ilyen -, akkor FN(a,k) hivatkozás még gyorsabban szolgáltatja a kívánt értéket.
Másik - még tömörebb - lehetőség, ha a számot ötös számrendszerbelinek képzeljük. Az előbbi 43544 nem vehető számnak az ötös számrendszerben, ezért vagy 32433, vagy 43044 értékké kell alakítani. Ezt tízes számrendszerbelire átírva még rövidebb (2243, illetve 2899) alakot kapunk. Ennek a módszernek az igazi előnyei olyankor látszanak, ha kevés lehetőség közül lehet választani. Ha pedig tíznél több lehetőség volna, akkor próbálkozhatunk betűkkel, és a visszakódolás karakteres függvényekkel történhet.
Gyakran élünk azzal a lehetőséggel is, hogy két - közepesen hosszú - számot (A és B) "egybeolvasztunk" A egész és B tizedestörtté (C=A.B módon). Ilyenkor triviális, hogy
A=INT(C) és B=C-A
A fenti tömörítési eljárásokat úgy is megfogalmazhatjuk, hogy egyetlen azonosítóban (memóriahelyen) több információt rakunk el. Ez igen gazdaságos megoldás, és csak apró többletfáradsággal jár: vissza kell nyerni az eredeti, a számunkra fontos információt. Gondolni kell azonban arra is, hogy gép csak bizonyos pontossággal veszi figyelembe az értékeket, nem képes akárhány értékes jegyet (általában csak 6-10-et) megjegyezni. Ez bármely komputernél hamar kideríthető.
A PRINT 2/3 hatására a pont után valahány hatos és egy hetes jelenik meg. Ennyi jegyet nyugodtan rábízhatunk a gépre, az így tárolt információ vissza is szerezhető.
Példaként felsorolunk néhány későbbi szakaszt, ahol ezek az eljárások alkalmazást is nyernek:
Valószínűség
A komputer, pontosabban a BASIC nyelv látszólag kiszámíthatatlan értékek előállítására is képes. Ez nem helytelen reakciót jelent, hanem az előírásszerű működés közben adódó "véletlen" elemeket.
Szinte minden gép - illetve minden BASIC-változat - ismeri az RND(x) függvényt. Ez legtöbbször egy "véletlen" számot ad meg 0 és 1 között.
A véletlen ebben az esetben azt jelenti, hogy egy elég bonyolult aritmetikai kifejezésből származik az eredmény, előre nem sejthető, sőt BASIC-en keresztül ki sem ismerhető az algoritmus. Általában pszeudovéletlennek (álvéletlennek, majdnem véletlennek) nevezik az ilyen számokat. A jelzők arra utalnak, hogy nem teljesen véletlen számokról van szó (függvénykapcsolat van köztük), de mint látni fogjuk, elég jól szolgálják azt a célt, hogy kívánt helyeken váratlanná, kiismerhetetlenné tegyék a programot. Sőt kifejezetten hasznosak bizonyos véletlen törvényszerűségek tanulmányozásakor. Igen érdekes feladat olyan programot írni, amely "teszteli" a generátort, pontosabban azt vizsgálja, vajon eléggé "véletlen"-e.
Az RND(x) függvény szinte minden személyi számítógépen megtalálható, apró eltérések vannak csak. Az értékek általában a (0,1) intervallumba esnek úgy, hogy sem 0, sem 1 nem fordul elő köztük. Az úgynevezett egyenletes eloszlást követik, ami azt jelenti, hogy a (0,1) bármelyik részintervalluma előbb-utóbb sorra kerül. Más szóval, ha egy csomó számot generálunk egymás után, akkor ezek elég egyenletesen beborítják a (0,1) intervallumot. Még precízebben fogalmazva: ha egy tetszőleges (a,b) részintervallumot választunk, akkor megfelelően sok szám generálása után az (a,b)-be esők hányada éppen b-a lesz. Kevés kivétellel az RND(x) függvény argumentuma (az x érték) nincs közvetlen hatással az eredményre, így általában közömbös, mit írunk oda, sőt előfordul, hogy nincs is argumentum, mint a ZX gépeknél. A továbbiakban mindig RND-t írunk.
A véletlengenerátor használata sok előnye mellett egy kis kényelmetlenséggel is jár. Eléggé megnehezíti a program "belövését", vagyis azt a fázist, amikor a késznek vélt és már begépelt programot helyes működésűvé tesszük. Gondoljuk meg, minden kísérletnél más és más számok szerepelnek.
Sok gépen kétféle véletlengenerátor is van. Az egyik minden futásnál ugyanazokat az értékeket adja azonos sorrendben, mintha egy táblázatba lennének beírva "véletlen" számok, és ebből a sorozatból venné a gép a számokat, mindig a következőt, a futás elején az elsővel kezdve. A másik (RANDOMIZE) a "kevert" változat, általában az első érték megválasztásában különbözik: a gépnek egy sűrűn változó állapotától függ. A pontos megoldást nem érdemes részletezni, lényeg az, hogy céljainkra mindig megfelel. (A második fejezet "Véletlen elemek" című részében olvasható erről még néhány szó.) Nyomatékosan hangsúlyozzuk azonban, hogy ha mindkét változat létezik a gépünkön, akkor a belövés okvetlenül a táblázatossal történjék és csak ha helyesen működik, akkor keverjük meg a generátort - akkor viszont feltétlenül érdemes.
A mindennapi életben viszonylag ritkán van szükség véletlen törtekre, így ezeket a 0 és 1 közötti véletlen számokat általában transzformálni kell. Egy tetszőleges (A.B) intervallumba eső véletlen értéket állíthatunk elő a
A+(B-A)*RND
kifejezéssel. Az M és N közötti egészeket pedig az
INT(M+RND*(N-M+1))
szolgáltatja. Ebben az esetben M-től N-ig az összes egész szám egyforma eséllyel fordul elő, az M és N határokat is beleértve.
Gyakran van szükség "nem egyenletes" eloszlásokra is, erről a későbbiekben részletesen is lesz szó.
Keverés
Legyen az a feladat, hogy N elemet (számot, nevet, kérdést stb.) véletlen sorrendbe kell állítani, és ilyen kevert sorrendben kiíratni. Az első ötlet általában az szokott lenni, hogy sorra generálunk egy csomó véletlen (sor)számot, amivel megadjuk a sorrendet:
110 FOR i=1 TO n
120 LET a=INT (RND*n+1)
130 PRINT u(a)
140 NEXT i
Eleinte megy is a dolog, de hamarosan ismétlődések következnek, és bizonyos elemek kimaradnak. Ez még orvosolható egy
122 FOR j=1 TO I-1
124 IF a=v(j) THEN GO TO 120
126 NEXT j
128 LET v(i)=A
betéttel, de így már jóval lassúbb (N>100 esetén elviselhetetlen) lesz a futási idő.
Mutatunk egy igen gyors módszert, mely ha nem is tökéletesen, de céljainknak megfelelően "keveri össze" az elemeket. Tegyük fel, hogy N dologról van szó. Válasszunk egy tetszőleges M<N számot, hogy (M,N) = 1 teljesüljön (közös osztójuk egy, vagyis relatív prímek). Ezután válasszunk egy tetszőleges K<N egészet: 90 LET K=INT (RND*N). Könnyen látható, hogy a
110 FOR i=1 TO l
120 LET k=k+m: IF k>n THEN LET k=k-n
130 PRINT a$(k)
140 NEXT i
program L<=N darabot "eléggé" véletlenül sorsol ki, ismétlődés nélkül. Célszerű M-et eleve prímnek választani, és ekkor csak az M N feltétel kell teljesüljön. Általában a 2/3*N < M < 9/10*N választás igen kedvező. A relatív prím követelménye igen lényeges, mert különben nem minden elem kerül sorra. Például 15 elemen hármasával végigmenve - bárhol is kezdjük - az elemeknek csak a harmadát kapjuk meg, ötösével haladva pedig csak az ötödét! Egyetlen fogyatékossága a módszernek, hogy bizonyos sorozatok eleve nem adódhatnak! Ha nem az a cél, hogy mind az N! lehetőség egyforma eséllyel kerüljön sorra, csak egy keverést óhajtunk végrehajtani, akkor megfelel ez a gyors és egyszerű módszer.
Sokkal egyenletesebb megoldás, ha véletlenül kiválasztunk két elemet, és meg-cseréljük őket. N/5-N/2 ilyen csere szintén elég jól "véletlenszerűsít", N csere már tökéletes.
A minden igényt kielégítő változat valószínűleg a két utolsó között van: kombinálni kell a kettőt. Először néhány csere (kb. N/10), majd következhet a gyors eljárás.
Elemi valószínűségszámítás
Természetesen a véletlen témakörében is rengeteg fokozat képzelhető el. Legegyszerűbb esetben csak "szimulálja" a véletlen jelenséget a komputer, vagyis tömegesen előállítja az egyes eredményeket. Például a
100 DIM a$(2)
110 LET a$(1)="I": LET a$(2)="F"
120 FOR i=1 TO 20
130 LET a=INT (RND*2+1): LET b=INT (RND*6+1)
140 PRINT a$(a),b
150 NEXT i
program pár másodperc alatt "feldob" 20 pénzérmét és 20 játékkockát, és kiírja az egyes dobások (kísérletek) eredményeit. Még ennél is gyorsabb, ha az eredményeket nem dobásonként közöltetjük, hanem a program végén összesítve.
100 DIM a$(2): DIM p(2): DIM k(6)
110 LET a$(1)="I": LET a$(2)="F"
120 FOR i=1 TO 20
130 LET a=INT (RND*2+1): LET b=INT (RND*6+1)
140 LET p(a)=p(a)+1: LET k(b)=k(b)+1
150 NEXT i
160 PRINT p(1);a$(1),p(2);a$(2): PRINT
170 FOR i=1 TO 6: PRINT i,k(i): NEXT i
Ezzel a módosítással akár 100, sőt több ezer dobás is végezhető. Egyrészt az egész kísérletsorozat eredménye elfér a képernyőn, másrészt másodperceket kell csak várnunk. Hasonló programok (több kockával dobunk, urnából golyókat húzunk, lottózunk, céltáblákra lövöldözünk stb.) kiválóan szolgálják a valószínűségszámítás eseményeinek gyors bemutatását.
Érdemes összehasonlítani a két kocka egyidejű feldobásának alábbi három változatát. A programsorok különböző módokon "cinkelik" a kockát.
30 LET a=INT (RND*11+2)
30 LET a=2*INT (RND*6 +1)
30 LET a=INT (RND*6+1): LET b=INT (RND*6+1)
35 LET c=a+b
Ez egyrészt egy kezdőknek nem triviális valószínűségszámítási probléma, másrészt a véletlenszám-generátor használatát is jól gyakoroltatja. Akik pedig már jártasak egy kicsit az elméletben, azok ellenőrizhetik a generátor "jóságát": mennyire igazolja a könnyen kiszámítható valószínűségeket, eloszlásokat.
Az előbb említett program több korosztály számára is újat jelenthet, és segíthet a mélyebb összefüggések megértésében. Az alábbi diagrammal illusztráljuk a különböző állomásokat, amelybe egy konkrét futtatás eredményét is beírtuk.
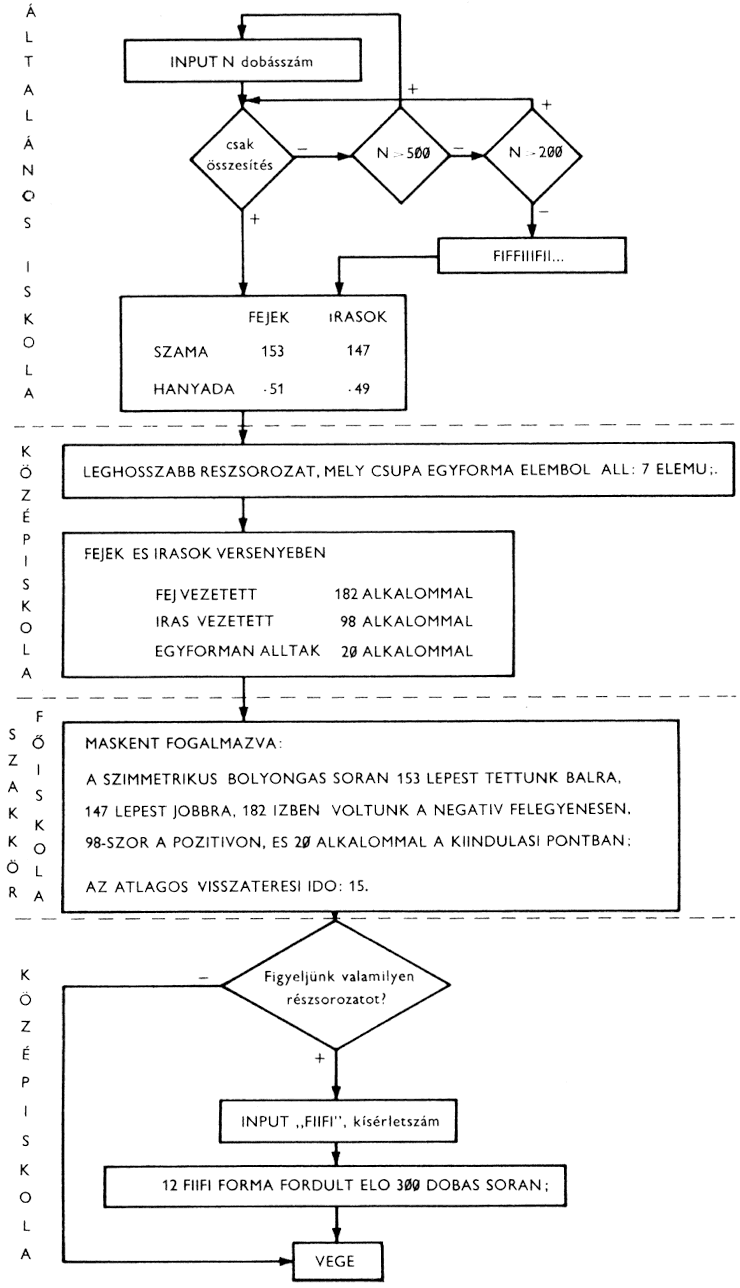
Galton-deszka
A szimmetrikus egydimenziós bolyongást (vö. az előző fejezetben a Véletlen bolyongás c. szakasszal és az előző grafikonnal) az úgynevezett Galton-deszkával szimulálhatjuk. Az n-edik szinten n elágazás van. Ezek mindegyikénél egyforma valószínűséggel terelődik jobbra vagy balra a felül beejtett golyó. A legalsó szint alatt tartályokban összegyűlnek a labdácskák. Kérdés, melyik dobozban hány darab lesz N számú útnak indított golyóból?

A szimuláló program, miután megkérdezi a deszka magasságát (szintek számát), illetve az átbocsátandó labdák számát, szép lassan elindítja a "pontokkal" ábrázolt golyókat, s azok hangjelzéssel kísérve potyognak a tartályokba. Egy idő után már csak a koppanás hallatszik, és alul sebesebben nőnek a halmok. Ha valamelyik doboz "betelt", léptékváltás történik: öt eddigi pontnak egyetlen felel meg, így még tovább folytatódhat a töltődés. A Galton-deszka szoros kapcsolatban áll a közismert Pascal-háromszöggel:
| 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 |
Az egyes elágazási pontokhoz a közvetlenül felette jobbra vagy balra levő utakból juthatunk. Lefelé pedig ismét 1/2 - 1/2 valószínűséggel mehetünk jobbra, illetve balra. Ha p(k,N) annak a valószínűsége, hogy az N-edik szint (balról számítva) k-adik urnájába pottyan egy golyó, akkor a
összefüggés alapján
ami megfelel a Pascal-háromszög N-edik sorában a k-adik helyen levő elemnek. A p(k,N) valószínűségeket k= 1,2,..., N mellett binomiális eloszlásnak nevezik. Ez korántsem egyenletes eloszlás, hiszen középen lényegesen nagyobbak az értékek, mint a széleken.
Az ábra azt mutatja, hogy a Galton-deszka N= 8, illetve 12 szintjéhez milyen eloszlás rajzolható ki, akár a képernyőn is.

A binomiális eloszláson mutatjuk be, hogyan lehet egyenletestől eltérő eloszlásokat vizsgálni. Eddigi ismereteink alapján is tudnánk a Galton-deszkát szimulálni: útjukra bocsátjuk a golyókat, és minden szinten pénzfeldobásszerűen küldjük azokat jobbra vagy balra. Ez egy tökéletes, pontos, szemléletes megoldás, de elég lassú. (Száz golyó végigkísérése tíz szinten már több percig tart, tehát előbb-utóbb unalmassá válik.)
Minthogy ismerjük azt a valószínűséget, amivel egy golyó valamelyik urnába kerül, közvetlenül eszerint is dönthetünk a golyók végállomásáról. Ezt hiba lenne
INT (RND*n)+1
választással szimulálni, hiszen - mint említettük - az N/2 környékén levő urnák "esélyesebbek". Akkor járunk el igazságosan, ha a (0,1) intervallumba egymás után rendre bejelöljük a p(k,N) valószínűségeket, és generálva egy (0,1)-beli egyenletes eloszlású véletlen számot, a megfelelő urnát választjuk.

A kívánt programhoz először képezzük a (0,1) intervallum megfelelő osztópontjait:
Q(K)=P(0)+P(1)+...+P(K)
ahol P(K) = p(k,8)
Ezután a
10 FOR k=1 TO 100
20 LET a=RND
30 FOR i=0 TO N
40 IF a>q(i) THEN GO TO 60
50 LET v(i)=v(i)+1: LET i=n+1
60 NEXT i
70 NEXT K
programmal száz golyó útját lehet végigkísérni a deszkán. Ez gyorsabb megoldás, és közvetlenül a binomiális eloszlást közelítő értékeket állít elő. Tanulságos lehet mindkét szimulációt összevetni a p elméleti értékekkel!
Születésnap
Aki nem ismeri, azt könnyen meglepheti az alábbi kérdésre adott válasz: Mi a valószínűsége, hogy egy 35 fős osztályban van két gyerek, akik (napra) pontosan egyidősek.
Legyen pn annak a valószínűsége, hogy n személy közül legalább kettő az évnek pontosan ugyanazon a napján született. Ha eltekintünk a szökőnapon születettektől, akkor sem nehéz belátni, hogy
p2 = 1 - 364/365
p3 = 1 - (364/365)*(363/365)
pn = 1 - (364/365)*(363/365) ...*((365-n+1)/365)
hiszen a szorzat azt mutatja meg, hogy mi a valószínűsége annak, hogy mind az n ember más napon született.
Ennek az összefüggésnek a segítségével ki lehet a géppel számoltatni, hogy például 35 gyerek esetén milyen valószínűséggel fog kettőnek ugyanarra a napra esni a születésnapja, illetve, hogy hány személy esetén lesz 99% valószínűséggel kettőnek egy napon a születésnapja.
A számítógépes program először "tesztelheti" a P(N) (diszkrét) függvényről alkotott fogalmainkat: különböző N-hez tartozó függvényértékeket kell megbecsülni. Ha elképzeléseink hamisak, akkor kirajzolja a görbét is, illetve tetszőleges intervallum-ban közli a pontos értékeket. Ezután kívánságra szimulálja a jelenséget: INPUT-tal megadott létszámhoz véletlenszerűen generálja a születésnapi dátumokat. Ezeket egy előre megrajzolt naptárban pöttyökkel jelzi. Ha egy dátum ismétlődik, hang- és fényjelzéssel tudatja, és kommentálja.
A tesztelés
1. Egészen kezdőknek az egyik leginkább ajánlott feladatkör. Legegyszerűbb változataihoz szinte csak az IF utasítás ismerete szükséges. Egy ilyen "lineáris" séma:

Ennek alapján N kérdés feltehető és elbírálható egy kb. 5*N utasításból álló programmal. Kezdőktől ez értékelhető teljesítmény, de rögtön látszik néhány fogyatékossága is: kicsit fárasztó a sok hasonló utasítás bepötyögése, elég hamar kiismerhető, és igen kényes a válaszra (például "nagy" helyett "hatalmas" vagy "nagy méretű" nem lesz jó, hogy más szinonimákról ne is beszéljünk). A feleletek merev elbírálása alkalmasan választott témakörnél nem jár sok gonddal. Történelmi évszámok, földrajzi adatok, kétnyelvű szótár, vegyületek képletei, műalkotás szerzője, helyesírás stb. esetén az adatszerű INPUT nem nagyon okozhat meglepetést.
2. A kérdéseket és válaszokat célszerűbb egyaránt tömbökben célszerű tárolni, az egymáshoz tartozó párokat azonos sorszám alatt:
A$(1)="ARANYBULLA", A$(2)="MOHÁCSI VESZ'',...
A(1)=1222,A(2)=1526
Így egy FOR ciklus segítségével egy, az előbbinél jóval rövidebb program már 20-200 elemű készletet is "adminisztrál". A kérdések és (helyes) feleletek - a továbbiakban adathalmaz - nyilván DATA-ban tárolódnak, és csupán ezek cseréjével "új" programot kaphatunk.
100 PRINT "Ird a kerdojel utan a megfelelo evszamot"
120 FOR i=1 TO n
130 READ a$(i),b(i): NEXT i
135 FOR i=1 TO n
140 PRINT A$(i);
150 INPUT X
160 IF x=b(i) THEN PRINT "BRAVO": LET h=h+1: GOTO 180
170 PRINT "TEVEDTEL, ";B(i);" a helyes valasz!"
180 NEXT i
190 PRINT n;" Kerdesbol ";H;" helyes valasz"
3. Az előző változat azzal színesíthető, hogy a kérdések véletlenszerűen következnek egymás után. Az imént háromféle keverési eljárást ismertettünk, ezek közül bármelyik választható. Megjegyezzük, hogy a leggyorsabb változat (ahol relatív prímmel lépkedünk) tökéletesen megfelel a célra.
4. Megtehetjük, hogy az előzők szerint véletlenül választott kérdés mellé több "feleletet" íratunk, és ezek közül kell a helyeset kiválasztani (teszt jelleggel). Ez különösen hosszabb válaszok esetén vonzó, hiszen a sok karakter bevitele helyett egyetlen (sor)szám is elegendő. Jó, ha a valódi válasz is megjelenik (természetesen nem kötelező), a többi 2-5 lehetőség véletlenszerűen adódhat.
Megjegyezzük, hogy a 3. és 4. változat egyetlen programban is kombinálható: ugyanazt az adathalmazt felhasználva véletlenszerűen változhat a kétféle kérdés:
a) Mi Franciaorszag fovarosa? (b$(i)-t várja a gép.)
b) Minek a fovarosa Roma? (1-4 között egy számot vár a gép.)
1 - Svajc
2 - Olaszorszag
3 - Anglia
4 - Vatikan
Egy másik lehetőség, amikor rossz válasz esetén egy másik típusú kérdés segítséget ad. Ha például Svédországhoz Oslót rendeli a válasz, a gép jelzi a tévedést, és tesztszerűen visszakérdezi: Minek a fővárosa Osló?, majd ugyanígy: Mi Svédország fővárosa?
5. További feladatot ró a programozóra, ha a kiértékelést súlyozva óhajtja végeztetni. Nyilván kisebb tévedés, ha a Dózsa-felkelést 1524-re datálja valaki, mintha 1912-re. Numerikus adatoknál könnyű az eltérés nagyságrendje szerint elbírálni, de szöveges válaszoknál ez sokkal nehezebb.
Definiálhatjuk a kérdések és válaszok tulajdonságait, és ezek alapján adódik, mennyire összetartozó elemeket kapcsolt össze a válaszadó. Például, ha valaki Beethovennek tulajdonítja a Mona Lisát, akkor nemcsak a műfajt tévesztette el, de a kort és a színhelyet (nemzetiséget) is. Hasonlóan CH2O2 és a Ca(OH)2 közül az első szerves, sav és nincs fémes komponense, míg a másikról mindez nem mondható el; viszont mindkettőben van oxigén, hidrogén, sőt hidroxilgyök is.
A tulajdonságok tárolása elég memóriaigényes, jártasságot kíván a téma (szak)tantárgyában, így 20-50 elemű adathalmazra érdemes kidolgozni ezt a változatot.
Barkochba
Általában csak az a lehetőség oldható meg, ha a gép kérdez, és a válaszok alapján egy előre megadott készletből kiválasztja a megfelelőt. Legegyszerűbb esetben ez egy ún. gráfbeli fa bizonyos ágainak végigkövetését jelenti. Valamilyen négyszögre gondolva például:
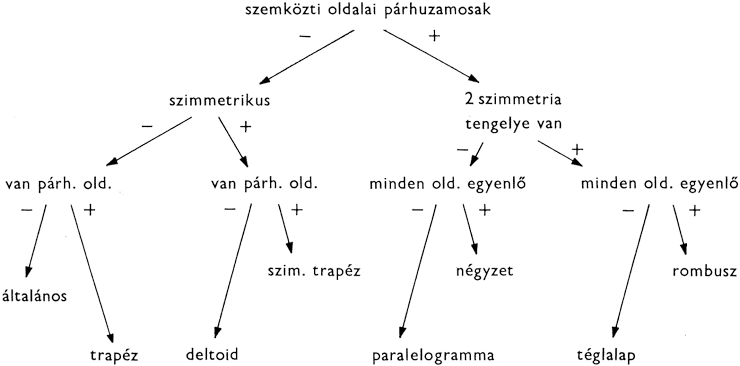
Igaz, hogy csak három kérdés hangzik el minden futás során, de hét lehetőségre kell felkészülni. Egy N elemű készlethez a fenti program kb. 5*N utasítás. Ezek nagyon hasonlítanak a kérdés-felelet játék legegyszerűbb változatához, csak most a li-neáris jelleg helyett rengeteg GO TO teszi a programot nehezen áttekinthetővé! 20-30 elemhez már kell egy kis gyakorlat.
Korántsem egyszerű az a megoldás, amikor a második és harmadik kérdésre adott válaszokat egyszerre értékeli ki a gép. A - -, - +, + - és + + válaszvariációk megkülönböztetésével valóban csak 5 kérdést kell tartalmaznia a programnak, viszont az elbírálás is bonyolultabb. Az ilyen vegyes megoldás még nem mindig éri meg igazán a fáradságot, de gyakorlásként tanulságos lehet.
Egy ügyes barkochbázónak van rá esélye, hogy N elemű készletből kb. INT(LOG(N)/LOG(2))+1 kérdéssel kitalálja a gondolt elemet; a képletet a mindjárt ismertetendő intervallum-felezéses eljárással lehet levezetni. Számítógép ritkán versenyezhet ezzel a teljesítménnyel, de például a fenti nyolc síkidomot a következő három kérdéssel minden esetben meg lehet különböztetni:
Ha 1 jelzi az "igen" választ, 0 az ellenkezőjét, akkor a különböző idomok így kódolhatók:
| idom | válaszok | 2-es számr. | 10-es számr. |
| általános | 0,0,0 | 0 | 1 |
| trapéz | 0,0,1 | 1 | 2 |
| deltoid | 0,1,0 | 10 | 3 |
| szimm. tr. | 0,1,1 | 11 | 4 |
| paralelogr. | 1,0,0 | 100 | 5 |
| négyzet | 1,0,1 | 101 | 6 |
| rombusz | 1,1,0 | 110 | 7 |
| téglalap | 1,1,1 | 111 | 8 |
Ez a sorrend automatikusan választja ki a feleleteknek eleget tevő négyszöget. Továbbá, ez a bonyolultabb változat képes kikeresni egy esetleges rossz választ is! Ha például a komputer deltoidot talál ki, de mi rombuszra gondoltunk, akkor máris kész a diagnózis: "A szemközti oldalai mind párhuzamosak?" kérdésre IGEN lett volna a helyes válasz! (Hiszen 010 és 110 az első feleletnél eltér.) Célszerű mind a kérdéseket, mind a lehetséges elemeket karaktervektorban tárolni. Ezeket az adatokat nem számítva, ez az intelligensebb változat alig hosszabb az elsőnél.
Sokkal izgalmasabb, hogy például Európa országait (36 elem) 7 kérdéssel szintén szétválogatja egy 50 soros program, míg a triviális módszerhez 100-nál biztosan több utasítás kellene, hogy a program egyszerűbb struktúrájáról ne is szóljunk!
A készletet érdemes a futás elején felsorolni, ez további 5 utasítás, és így sok csalódásnak vehetjük elejét. Ezek figyelembevételével említünk néhány hálás témakört:
Egy feladat megoldásánál elkülönül az előkészítés (kódolás) és a program megírása. Az utóbbi sokkal egyszerűbb: tulajdonképpen csak egyszer kell elvégezni, a tesztekhez hasonlóan csak az adatok változnak. A kérdések összeválogatása és a kódolás már inkább az illető szakterületen igényel jártasságot. 15-25 elemű halmazra az előkészítés még könnyűnek mondható, 50 elem felett viszont általában már komoly teljesítmény.
Kicsit túlmutat a kezdeti célkitűzésen, de gyakorlottak megpróbálhatnak olyan programot írni, amely elvégzi az előkészítést vagy legalábbis segíti! INPUT-tal sorban bejuttatva a kérdéseket, illetve az elemeknek megfelelő válaszokat, a program vizsgálja meg, mennyire csoportosítanak jól a kérdések. Redundanciavizsgálat alapján esetleg módosíthatjuk a kérdéseket (újabb INPUT). Sőt a gép ajánlatot tehet, milyen elemeket lehet még a készlethez hozzávenni, hogy a kérdések továbbra is egyértelműen válasszák szét a lehetőségeket.
Innen már csak egy lépés az intelligens keresőrendszerek (katalógus) létrehozása. Például egy programkatalógusé. Egy ilyen katalógusból, mondjuk, egy biológiai tárgykörű, 7-8. osztályosok részére csoportos bemutató céllal ABC-80 típusú gépre készült játékos programot szeretnénk kikerestetni, ekkor a számítógép néhány címmel válaszol, és megadja a hozzáférési utalást.
Egy speciális esettel külön is érdemes foglalkozni, egyszerűsége miatt. Az elterjedt számkitalálós játék is barkochba, ha "kisebb-e A-nál" típusú kérdésekkel szűkítjük a lehetőségek körét.
A legegyszerűbb - meglepő módon a szöveges barkochbánál is egyszerűbb -, ha a gép gondol egy véletlenszerű (egész) számot, mondjuk 1 és 100 között. A játékos pedig egy számmal kérdez, és a gép "igen" felelete azt jelenti, hogy a gondolt szám kisebb a kérdezettnél, míg a "nem" nagyobb-egyenlőt jelez. Ettől lesz a kérdezgetés barkochba.
Picit bonyolultabb, amikor a játékos gondol egy A és B közötti egész számra és a komputer találgat a fentiek szerint. Gyakorlott személy f(B-A) = INT(LOG(B-A)/LOG(2))+1 kérdésből biztosan kitalálja a gondolt számot, és erre a teljesítményre egy ügyes program ugyancsak képes. Módszere: minden alkalommal a még szóba jövő intervallumot lehetőség szerint minél pontosabban elfelezi, és ez a felezőszám lesz a következő kérdés.
Különösen hatásos, ha a számítógép versenyre hívja az embert: mindketten gondolnak is, találgatnak is. Egy kis csellel olyan programot írhatunk, hogy a gép soha nem kaphat ki. A "gondolásnál" a következő taktikát választja: nem gondol eleinte semmire, hanem mindig úgy válaszol, hogy a kérdező dolgát nehezítse. Például ha a pillanatnyilag elképzelhető intervallum [X,Y] és a kérdés Z, akkor Z-X>Y-Z esetben igent válaszol (a gondolt szám kisebb Z-nél, azaz [X,Z-1] intervallumba esik).
Így biztosan nem keveredik ellentmondásba, és a végén - amikor már csak [X,X] "szakasz" jöhet szóba - nyilván X-et tekinti "gondolt" számnak. Ezáltal a játéknak ebből a részéből kiküszöbölte a szerencsét, és garantált a fenti f(B-A) számú kérdés. A másik oldalon (amikor a játékos gondol) a komputernek lehet szerencséje, és kevesebb próba is elég!
Újabb lehetőség - már nem egészen barkochba jellegű, ha a találgatás egyszerre két számmal történik, és a lehetséges válaszok: kisebb, közte van, nagyobb. A fenti ötletek az f(B-A) = INT(LOG(B-A)/LOG(3))1+1 módosítással ide is meg-felelnek.
Keresés a képernyőn
A játék a következő: a számítógép eldug valamit a képernyőn, és az a dolgunk, hogy megkeressük. Vagy koordináták megadásával, vagy egy villogó pont (karakter) mozgatásával lehet próbálkozni. Az utóbbi úgy történik, hogy bizonyos billentyűk jobbra-balra, le-fel viszik a pontot, amire a legtöbb gépen kényelmes lehetőség van (INKEY$), de az INPUT is megfelel. A komputer elbírálja a próbálkozásokat: jelzi, hogy mennyire járunk közel az elrejtett ponthoz. A jelzés történhet több módon:
Számtalan ötlet valósítható meg ilyen típusú játékként, kb. 20-25 különböző változat ismeretes. Különösen a megjelenítés hálás téma, de az információszolgáltatás is sok lehetőséget kínál. Példaként három programot részletesebben is ismertetünk, igyekeztünk több ötletet is összesűríteni bennük.
1. Tűz-víz (6-12 éveseknek)
A képernyőn (maximum 40x60-as négyzetrácson) valahol el van rejtve egy karakter. Kezdetben a bal felső sarokban villog egy kereső csillag. Az I, J, K, M billentyűk hatására a csillag elindul felfelé, ill. balra, jobbra, lefelé. Változtatható sebességgel mindaddig halad, amíg - a helyköz lenyomásával - meg nem állítjuk. A játékos a P gombot lenyomva jelezheti, hogy a csillag mostani helyén sejti az elrejtett karaktert. Válaszként a csillag helyén egy szám jelenik meg. minél közelebb vagyunk a rejtekhez, annál nagyobb számjegy.
2. Legyek (inkább gimnazistáknak)
Egy 10x10-es négyzethálón négy légy rejtőzik. Koordináták begépelésével kell megkeresni őket. Minden kísérlet után megjelenik a lövés és az egyes legyek távolsága (egytizedes pontossággal), illetve a lövés helye a céltáblán. Ha egy legyet megtaláltunk, némi dicséret a részünk, és a képernyőn megkülönböztető jelzés kerül a helyére. Amennyiben csak a legutolsó (két) lövéshez tartozó távolságok maradnak a képernyőn, akkor kicsit nehezebb a játék.
Az ügyesek hat próbálkozásból mind a négy legyet megtalálják. Ennél kevesebb kísérlethez szerencse is kell. 10-nél több lépés után már hümmögni is lehet.
A program tanító változatában egy-egy nem éppen jófelé leadott lövés után a gép jelezheti a célzás következetlenségeit. Például tegyük fel, hogy az (5,5) kísérlethez tartozó távolságok 1.4 és 1 (már csak két légy van). Ezután a komputer mondjuk csak olyan próbálkozásokat fogad el, amelyek koordinátái legfeljebb eggyel térnek el az (5,5)-től [(4,5), (5,6), (6,4) stb.].
Pontosabb értékelést tesz lehetővé, ha minden lövésnél (a harmadiktól kezdve) előre közölni kell, melyik légyre vadásztunk leginkább. Ilyenkor csak olyan lövés fogadható el, amelyik - erre a kiválasztott légyre vonatkozóan - összeegyeztethető az előző lövésekkel.
Adhat a komputer nehezebb feladatokat is. Sokkal bonyolultabb például, ha a pont egy megadott irányban lassan elmozdul. Az irányt célszerű az elején kijelölni. Még egy dimenzióban is nehéz lehet egy mozgó pontot eltalálni. Valaki 0-30 között gondol egy egészet, és ezt minden tippnél növeli a következőképpen: Ha a tipp kisebb a (pillanatnyilag) aktuális értéknél, akkor a különbséggel megnöveli ezt az aktuális értéket, ha meg nagyobb, akkor a különbség kétszeresével. Például ha a gondolt szám 17 és a tipp 13, akkor 21 lesz az új érték; míg ha a tipp 21, akkor az új érték 25 lesz. A játék nem könnyű, nem érdemes megengedni, hogy a mozgó szám túllépje a százat, mert akkor már amúgy is elég reménytelen az ügy. A játéknak létezik nyerő stratégiája, legfeljebb 6 próbálkozásból ki lehet találni a gondolt számot. Az előbbi légyvadászatot azzal is bonyolíthatjuk, hogy a válaszok típusa programon belül változik a 4 lehetőség szerint, vagy ha nem jelenik meg minden alkalommal a teljes (mind a négy légyre vonatkozó) információ (például a legyeknél először az 1-től, majd a 2-től, 3-tól stb. való távolság elmarad). Térbeli esetben a nyilvántartás is nehezedik, a megjelenítés pedig különösen izgalmas.
Ha a játékos a rejtő fél és a komputer keres, akkor a programíráshoz a koordinátageometriában való jártasság szükséges, és a program nem egyszerű. Célszerű ilyenkor szubrutinokat összeállítani a különböző (céltáblaszerű) alakzatok egyenletében szereplő együtthatók meghatározására és az ilyen egyenletek megoldására is. Kisebb céltáblán, vagy ha a lehetőségek már csak szűk területre korlátozódnak, akkor érdemes egyenként megvizsgálni a még szóba jövő pontokat - összhangban vannak-e az eddigi információkkal. Ezzel a kizárásos módszerrel előbb-utóbb célhoz érünk, bár a futás így igen hosszú is lehet. A programot viszont sokkal könnyebb megírni.
3. (Föld)rajzolás
A képernyőn való keresgélés egyik tanulságos alkalmazása a térkép-, pontosabban a vaktérképrajzolás. A grafikáról írt második fejezetre támaszkodva, különbséget teszünk a kb. 100 pontból, illetve a több száz pontból álló rajzok között. Ez lényegében a durva, illetve a finom felbontású grafika szétválasztását jelenti.
A finom felbontásnál - tehát több száz pontból áll a vonal - kiválasztunk néhány (10-30) jellegzetes töréspontot, és ezek koordinátáit egyetlen adatként tároljuk - 86.29 jelentése 86; 29 -, már csak össze kell kötni a pontokat. Az ábra könnyen nagyítható, sőt a forgatás sem okoz komoly gondot (I. a Képelemek c. részt). A töréspontok kiválasztása természetesen befolyásolja az ábra "hűségét", minél több és alkalmasabb pontot szemelünk ki, annál jobban rá lehet ismerni a rajzra.
Más jellegű a durva rajzok készítése, itt ugyanis valamennyi pont tárolható a következő elrendezésben:
8 1 2 7 X 3 6 5 4
Az X-szel jelzett pozíció szomszédjait a fenti módon kódoljuk, és minden számjegy azt fogja mutatni, merre kell lépni a következő alkalommal.
Egy vonaldarab kódolása pl. 3,4,4,3,3,5,6. Ezt a törtrész-módszerrel .3443356 alakban tömörítjük, és ily módon 100 pont 12-17 adatban tárolható. Nyilván gondoskodni kell a kezdőpont megadásáról, célszerű negatív számokat alkalmazni a megkülönböztetésre.
Az ábrát nehéz nagyítani, de a 90 fok többszöröseivel történő elforgatás igen könnyű. Vegyük észre, hogy 1-3, 2-4, ..., 7-1, 8-2 megfeleltetés éppen az óramutató járása szerinti derékszögű elforgatást eredményez. Nyilvánvalóan a kezdőpont megváltoztatásáról külön kell gondoskodni. Más szöggel való elforgatás már elég bonyolult.
Ezekkel az eszközökkel könnyen megvalósítható a következő program: A képernyőn megjelenik egy vaktérkép néhány villogó ponttal, és néhány városnév. Ez utóbbiak közül ki kell választani a villogó pontoknak megfelelőt. Nehezítésként az ábra esetleg elforgatható, sőt egyes határvonalai elhagyhatók (bizonyos pontok vagy szakaszok a megjelenés után azonnal törlődnek is). Például közepes térképismeretnél egy-egy adatelem csak 0.1 eséllyel törlődik azonnal, a kiválóaknál ez az ér-ték 0.5.
Csak mellesleg jegyezzük meg, hogy az ötlet tovább fejleszthető. A memóriában tárolt térkép megrajzolásával a felhasználó maga is kísérletezhet (I. vezérlési), majd a gép összehasonlítja az elkészült alakzatot az ideálissal. Itt az elbírálás jelent igazából gondot. Képzeljük el, hogy egy tökéletesen sikerült ábra egészében el van tolva a tárolt adatokhoz képest. A különbség ilyenkor már igen jelentősnek tűnhet az "ostoba" komputer számára. Célszerű ezért néhány pontot - tájékoztató jelleggel - előre megadni, és ezután annál rosszabbnak ítélni az ábrát, minél több a hiba. Hang- vagy egyéb jelzéssel a kezdődő eltéréskor figyelmeztethetjük a rajzolót, és csak a további (már jelentősebb) tévedést minősítjük hibának.
Fizika
Kísérleteink azt mutatják, hogy a számítógépes oktatásban ez a leghálásabb terület. Szinte kimeríthetetlen, és igen szellemes lehetőségeket kínál a tárgy kezdőknek, a megvalósítás látványossága, igényessége még a haladóknak is izgalmas lehet.
Ámde nem kívánjuk kimerítő részletességgel boncolgatni a fizika és a számítógépek kapcsolatát, inkább ízelítőt próbálunk adni a fentiek illusztrálására. Néhány ötletet vázolunk, ahol a hangsúly azon van, hogy egy-egy fizikai apróságot (képletet, összefüggést) hogyan lehet látványosan köríteni, esetleg játékos formában feldolgozni.
Természetesen ezeket az ötleteket főleg olyanoknak szánjuk, akik kedvelik a tárgyat. A megvalósításhoz több-kevesebb fizikatudásra lesz szükség, bizonyos dolgok megértése pedig biztos jártasságot igényel (potenciáltér, űrhajók).
Arkhimédész
"Minden vízbe mártott test
a súlyából annyit veszt,
amennyi az általa
kiszorított víz súlya."
Ezt a versikét már az általános iskolában is fújják a gyerekek, fizikai tartalma azonban nem mindig, nem mindenkinek egyértelmű. Mindenekelőtt pontosítsunk: nemcsak víz, általában folyadék.
Arkhimédész törvényének megtanulása után, annak szemléletes gyakoroltatására készülhet a program. Egy állandó térfogatú kádban, egy állandó térfogatú figura ül. Induláskor a gép a figura súlyát és a kiömlő folyadék fajsúlyát kérdezi meg. A kettőt együtt vagy külön-külön változtatva, az úszás bekövetkezésének körülményeit vizsgálja a program. Az egyszerűség és a későbbi grafika kedvéért a folyadék nem folytonosan ömlik a kádba, hanem valamilyen egységenként (poharanként). Minden pohár után meg kell vizsgálni az úszást. Arkhimédész törvénye szerint ez akkor következik be, ha X*F=G, ahol G a test súlya. F a csapból ömlő folyadék fajsúlya, X pedig a folyadékba merülő test térfogata. Ez utóbbit mindig újra kell számolni, hiszen a beömlő folyadék egyre jobban ellepi a figurát. Egy téglatestnél ez igen könnyű, de egy emberke figuránál kicsit bonyolultabb. Lássuk tehát a program fizikai magját:
200 FOR j=1 TO j9
210 LET v=v+1: LET x=x+1
220 IF f*x>=g THEN PRINT "USZAS VAGY LEBEGES": STOP
230 IF v=a(j) THEN LET v=0: GO TO 250
240 GO TO 210
250 NEXT j
ahol J9 a kád magassága, A(J) a J-edik szinten elférő poharak száma.
Tanulságosabb az az aktív változat, amikor a folyadék, mondjuk, tízpoharanként ömlik a kádba, és minden alkalommal tippelni lehet: van-e úszás vagy sem? Elképzelhető, hogy a tanuló tetszőleges mennyiségű folyadékot kér, annak beömlése után tippel, majd ismét kér stb. Az a cél, hogy minél kevesebb kérdéssel minél pontosabban találja el a lebegést.
Kuriózumként említjük a feladat térbeli kidolgozását. A program magja nem változik (csak az A(J) értékek módosulnak esetleg), az illusztráció azonban érdekes lehet!
Radioaktív bomlás
A bemutatásra kerülő programban a felezési idő és a radioaktivitás egyéb jellemzőinek ismeretében kell a tanulónak meghatároznia a különböző időtartamok alatt még el nem bomlott részecskék számát. A program némileg játékos formában íródott.
A játékbarlangban a 0 időpillanatban 100 000 radioaktív "zseton" van, melyek felezési ideje 10 perc. A játékosnak kezdetben 1000 Ft-ja van, a banknak pedig N millió (N véletlen!). T időnként bizonyos pontossággal meg kell tippelni, hogy hány zseton maradt. A következő fogadási lehetőségek vannak:
(p a zsetonok pontos száma, t a tipp).
A tét mindenkor a játékos pénzének a fele. A fogadási lehetőségeket úgy kell értelmezni, hogy ha például 9000 Ft-ja van a fogadónak, akkor 4:1-es fogadás után vagy 4500 Ft-ja marad, vagyis veszít, vagy 22 500 ( = 4500 + 4*4500) lesz a nyereménye. A játék célja, mint rendesen: bankot robbantani.
Potenciáltér
Az elektrosztatikus tér ekvipotenciális görbéit rajzolja meg a program. Az elektrosztatikus tér erővonalai (gondoljunk a hasonló mágneses vasreszelékes kísérletekre) és az ekvipotenciális görbék merőlegesek egymásra a metszőpontokban. Az ekvipotenciális görbe minden pontjában ugyanakkora az egységnyi töltés potenciális energiája.
A program úgy kezdődik, hogy a képernyő közepén villog egy pont. A már jól ismert (I, J, K, M) billentyűk segítségével nyomtalanul mozgatható. Ily módon elhelyezünk néhány pontszerű töltést (a töltés nagyságát is megadva), majd egy tetszőlegesen megadott kezdőponttól indulva a gép kirajzolja az ekvipotenciálist.
Gombnyomásra a rajzolás megszakad, és a kezdőpontból az ellenkező irányba folytatódik. Újabb gombnyomásra ennek az ekvipotenciálisnak a rajzolása véget ér, és ismét villog a pont: újabb vonal kezdőpontját jelölhetjük be stb.
A rajzolás mechanizmusa a következő: Ha valameddig kész a vonal, akkor a gép megvizsgálja az utolsó pont "elülső" öt szomszédját:
Ezek közül azt gyújtja ki, amelyben a potenciális energia értéke legközelebb van a kezdőpontra kiszámított értékhez. Lehetőség van gyorsításra is, ilyenkor eggyel távolabbi szomszédokról (ismét csak ötről) kell dönteni:

Gyorsított esetben az összekötés természetesen folytonos szakaszokkal történik. Lassítható is az eljárás, ilyenkor közelebbi szomszédokat vizsgál. A gyorsító-lassító funkciók igazából csak finomabb grafikáknál jönnek szóba.
A fenti demonstrációs változat könnyen alakítható "oktatóvá". Miután a gép kivilágította egy vonal kezdőpontját, villogtatni kezd egy tetszőleges pontot. Csak I-M (vagy csak J-K) segítségével olyan pozícióba kell vinni, hogy a kezdőponttal azonos ekvipotenciálison legyen. A tippet kiértékeli a gép. Szélsőséges esetben maga a tanuló is megpróbálhat teljes vonaldarabokat rajzolni [l. még a (Föld)rajzolást). Itt az ellenőrzés (elbírálás) különösen nehéz feladat.
Meg kell jegyezni, hogy ez a program - bonyolultságával, sokoldalúságával - talán kicsit kilóg a kollekcióból. Nyilvánvalóan csak gyakorlottaknak való feladat, könnyített változatait is elég nehéz elképzelni. Mégis megemlítettük, ugyanis egy másodikos (!) gimnazista gyerek készítette, a maga erejéből. Kitalálta a feladatot, elképzelte és megvalósította.
Hajítás - bolygók - űrhajók
Kezdőknek nagyon ajánlott feladat a ferde hajítás (grafikus) szimulációja. A kilövési szög (A) és a kezdősebesség (V) függvényében igen egyszerű kiszámítani és megrajzolni a pont (az elhajított test) T időpontbeli helyzetét.
100 LET c1=v*COS A: LET c2=v*SIN A
110 FOR t=1 TO 60
120 LET x=t*c1: LET y=c2*t-9.81*t*t
130 PLOT x,y
140 NEXT t
ahol X,Y a pont vízszintes és függőleges koordinátája. Nyilvánvalóan - géptől függően - külön kell gondoskodni arról, hogy a test ne szálljon ki a képernyőről (I. a II. fejezetet)!
Az ábrázolás mellett oktató jelleget is adhatunk a programnak, ha egy véletlen pontot kell eltalálni a megfelelő A és V értékek megadásával. Tovább nehezíthető a feladat, ha akadályt helyezünk a cél elé, vagy ha figyelembe vesszük a közegellenállást is.
Bonyolultabb mechanikai összefüggések is gyakorolhatók bolygók, (mesterséges) holdak pályájának szimulálásával. Például mekkora kezdősebességgel kell kilőni egy mesterséges holdat ahhoz, hogy visszaessen a Földre, hogy keringjen vagy hogy elhagyja a Naprendszert (pályája ekkor parabolikus, elliptikus vagy hiperboli-kus)? Létezik oktatóprogram a Kepler-törvények illusztrálására is. Itt ismét igen érdekes a térbeli mozgás megjelenítése.
Nehezebb játék, és persze nehezebb program is, ha egy űrhajó útját kell követni. Célul tűzhetjük ki egy Holdra szállás megtervezését. Mivel a Hold felé mozgó test össze fog ütközni a Holddal, fékezni kell a sima leszállás érdekében. Itt a tömegvonzás és energiamérlegek mellett a fékezési energia hatását is figyelembe kell venni, elég bonyolult összefüggések írják le, milyen stratégiát érdemes követni.
Egy lehetséges megoldás, hogy a gép - véletlenszerűen - megadja az űrhajó pályájának paramétereit, az űrhajó tömegét és az útra vitt üzemanyag mennyiségét. Bizonyos időközönként lehetőség van beavatkozni: változtathatjuk az éppen fékezésre szánt energiát, eszerint a gép módosítja a sebességet és az ettől függő-paramétereket, és jelzi a változásokat. Végül kiderül, hogyan érkeztünk a Hold felszínére, mekkora krátert ütött a járművünk.
Egy műholdpályát kirajzoló programot be is mutatunk. Ezt is gyerekek írták, mégpedig a HT 1080Z iskolaszámítógépre.
Néhány magyarázat a listához:
A 2. sorban a PRINT CHR$(23) hatására a számítógép ritkítottan ír. Ezt az üzemmódot a képernyő törlése (CLS utasítás) szünteti meg.
A PRINT utasításokban a @ után álló szám a nyomtatás helyét határozza meg, az első sor karaktereinek 0-tól 63-ig, a másodiknak 64-től 127-ig stb., az utolsó, 16. sornak 960-tól 1023-ig terjednek a számai.
Az alapvető rajzolási eszköz a SET(X,Y) utasítás, amely a függőlegesen 48, vízszintesen 128 négyzetből álló háló koordinátákkal megadott képelemét jeleníti meg. A RESET(X,Y) utasítás hatására a SET utasítással megjelenített képelem eltűnik. A pályamódosításkor beírt értéket a program karakterenként olvassa be, a new-line karakterig. A képernyőn itt nem közvetlenül jelenik meg a begépelt karakter, hanem az INKEY$-t követő PRINT hatására. A (billentyűnyomásra) várakozást az INKEY$ függvénnyel lehet megoldani.
A NEXT utasításban nem kell kiírni a ciklusváltozót. Ha a NEXT utasításban kiírjuk a ciklusváltozót, akkor egy NEXT utasítás több ciklus végét is jelezheti, mint azt a 120. sorban látjuk.
2 CLS: PRINT CHR$(23): PRINT @276, "MUHOLD PALYAK"
6 PRINT @516,"EZ A PROGRAM MUHOLD PALYAKAT": PRINT @591,"SZAMOL ES ABRAZOL"
7 PRINT @704,"A MUHOLD PALYALAT AZ M BILLENTYU"
8 PRINT @768,"MEGNYOMASA UTAN LEHET MODOSITANI"
11 IF INKEY$="" THEN 8
15 CLS: PRINT @716,"A PROGRAM A KOVETKEZO ADATOKAT IRJA KI:"
16 PRINT @832,"X,Y KOORDINATAK X,Y IRANYU SEBESSEGEK"
17 PRINT @896,"SEBESSEG MAGASSAG IDO"
18 IF INKEY$="" THEN 18
19 CLS: PRINT @776,"A PALYAMODOSITAS AZ X IRANYU SEBESSEG (VX) ERTEKENEK": PRINT @852,"VALTOZTATASAVAL TORTENIK";
20 DATA 40,300,0,6500,9.5,0,398000
25 READ DT,KT,X,Y,VX,VY,K
40 FOR SZ=0 TO 6.28318 STEP .3142
42 SET(63+12*COS(SZ),10-6*SIN(SZ))
44 NEXT
46 PRINT @221,"FOLD";
48 R=SQR(X*X+Y*Y)
50 FOR T=0 TO 100000 STEP KT
60 PRINT @960,"X=";X;" Y=";Y;" VX=";VX;" VY=";VY;
65 PRINT @2,"V=";V;"KM/SEC M=";M;"KM T=";T;"SEC ";
70 XK=X/500+63: YK=10-Y/1000
72 IF XK<0 OR XK>127 OR YK<0 OR YK>47 THEN 79
75 SET(XK,YK)
79 V=SQR(VX*VX+VY*VY)
87 IF R<6370 PRINT @659," M E G S E M M I S U L T !";: END
90 A$=INKEY$: IF A$<>"M" THEN 100
91 SET(63,12): PRINT @920,"PALYAMODOSITAS? ";
92 C$=""
93 B$=INKEY$: IF B$="" THEN 93
94 C$=C$+B$: PRINT B$;
95 IF ASC(B$)<10 OR ASC(B$)>13 THEN 93
97 VX=VX+VAL(C$): RESET(63,12)
100 FOR I=0 TO KT STEP DT
110 X=X+VX*DT: Y=Y+VY*DT: R=SQR(X*X+Y*Y)
114 RR=R*R*R
115 VX=VX-K/RR*X*DT: VY=VY-K/RR*Y*DT
118 M=SQR(X*X+Y*Y)-6370
120 NEXT I,T
130 END
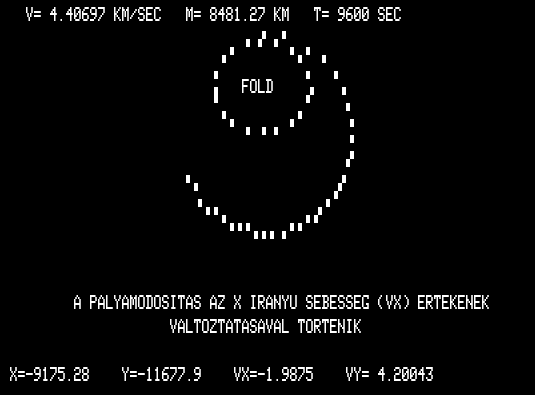
Végül felsorolunk még néhány lehetőséget:
A szimuláció
Azt hiszem, erre a szóra minden számítástechnikusnak bizseregni kezd vagy a szíve, vagy a tenyere. Rengeteget írtak már a (számítógépes) szimulációról, és valóban a komputernek mindenképpen az egyik legizgalmasabb, legszínesebb alkalmazási területe ez. Sok szinten lehet művelni, de igazából művészi fokon űzve izgalmas.
Ahelyett, hogy definícióval kísérleteznénk, hogy vajon mi tartozik ide, inkább néhány példát mutatunk, amelyekből azután ki fog tűnni, mit tekintünk szimulációnak.
Meg kell itt említenünk, hogy léteznek úgynevezett szimulációs programnyelvek (CSL, GPSS, SIMSCRIPT, SIMULA 67 stb.), amelyek általában nagy számítógépeken érhetők el. Ezek használatához nemcsak a nyelvet, hanem a gépek eléggé bonyolult konvencióit is meg kell tanulni. A következőkben csak azt szeretnénk illusztrálni, hogy az igen egyszerű BASIC nyelv is alkalmas ilyen jellegű tevékenységre. Ezáltal lehetőség van arra, hogy kezdők is megismerkedhessenek a szimuláció lényegével, és főleg a felhasználás területeivel. Már eddigi példáink között is bőven akadt szimuláció, kezdve a pénzfeldobástól a legutóbb tárgyalt ferde hajításig; most nagy vonalakban bemutatunk néhány biológiai, illetve gazdasági jelenséget szimuláló programot.
Rókák - nyulak
A program három populáció (róka, nyúl, fű) együttéléséből adódó konfliktust szimulál. A biológiában populációnak nevezik az egy fajhoz tartozó, egymással szoros kapcsolatban álló egyedek csoportját. A program tehát egy olyan összetett rendszer viselkedését írja le, amelyikben az egyes fajok populációi egymással kölcsönhatásban élnek: a nyulak füvet esznek, a rókák nyulakat, és mindketten trágyázzák a talajt, és például a nyulak rókák nélkül túlságosan elszaporodnának. Az állatfajok egyedeinek száma a két faj létszámának szorzatától függően is változik. Az ilyen - kölcsönhatásban változó - rendszerek viselkedését differenciálegyenletekkel szokták leírni, amelyekből rekurzív összefüggések adódnak:
Nk+1 = Nk(a-bRk),
Rk+1 = Rk(c+bNk),
ahol Ni a nyulak, Ri, a rókák i-edik időpontbeli száma, ezek értéke függ a megelőző időpontbeli értékektől és a folyamat paramétereitől (a, b, c - étvágy, túlélési arány).
Lehetőség van arra, hogy R0 és N0 kezdeti értékekből kiindulva rendre kiszámítsuk az időben változó Nk és Rk mennyiségeket. Elég nagy k esetén már látszik a folyamat lényege: adott paraméterek mellett elképzelhető valamelyik faj kihalása (például b>0.3, a=0.8, c=1 esetben a nyulak hamarosan kipusztulnak), de lehetséges egy "békés" egyensúlyhoz való közeledés is.
Ennél lényegesen látványosabb lehetőség a következő: A képernyő K sorban és M oszlopban KxM mezőre van osztva. Kiinduláskor INPUT-tal megadjuk a nyulak (N) és rókák (R) kezdőszámát. Rókákkal és nyulakkal rajzoltatunk tele tehát R és N mezőt, a többibe füvet rajzol a gép. Ugyancsak megadjuk az egyes állatok étvágyát (E1 és E2) is. Ezután minden időpontban véletlenszerűen kiválasztódik egy mező, és az éppen ott levő élőlény megváltozhat:
Bonyolultabb, de jóval valósághűbb a szimuláció, ha a valószínűségek (E1, E2) függnek a "környezettől" is. Például fűből csak akkor lesz nyúl, ha van már nyuszi a szomszédban (van, ami szaporodjon!)
Ezek alapján a "tájkép" elég gyorsan változik, és a fenti rekurzív formula misztikus paraméterei helyett minden jól áttekinthető tényezők szerint történik. Érdemes külön tömbben tárolni az egyes időpontok N(K) és R(K) létszámát, és ezeket a függvényeket időnként gombnyomásra megjeleníteni. Nagyon tanulságos lehet a két modellt (a rekurzív egyenleteket és KxM mezőt) összehasonlítani. Ezáltal az a, b, c elméleti meggondolásokból adódó paraméterek értelmezése is megvilágosodhat. Ugyancsak érdekes a különböző N, R, E1, és E2 értékre adódó N(K) és R(K) függvények eltérése, sőt azonos paraméterek mellett a véletlen okozta különbözőségek magyarázat.
Marhafarm
Tipikus gazdasági játék. A Rókák-nyulak-hoz hasonló, de aktívabb és játékosabb program. A játékos egy marhafarm tulajdonosa lesz, kezdetben 100 fiatal, 100 felnőtt és 100 öreg állata van. Ezek meghatározott szabályok szerint szaporodnak. A játék elején a farmer szerződést köt egy marhakereskedővel N esztendőre úgy, hogy minden évben meghatározott számú fiatal, felnőtt és öreg állatot ad át neki. Ezt a három számot be kell gépelni. Megválasztásuknál figyelembe kell venni a szaporodást és az elhalást is.
A lehetséges állapotváltozások:

A k+1-edik évben a különböző korú állatok száma a következő:
x1(k+1) = a*x2(k)+b*x3(k)
x2(k+1) = x1(k)
x3(k+1) = x2(k)+c*x3(k)
(ahol a, b a felnőttek és öregek szaporodási aránya, 1-c az öregek elhalásáé).
A szerződés végén a program gazdasági mérleget készít az N év eredményéről. Rossz vállalkozásnak számít, ha valamelyik évben nem sikerül átadni a vállalt számú állatot, illetve ha az állatok túlságosan elszaporodnak (túl sok takarmány fogy!), vagy kihalnak. A fő cél, hogy minél nagyobb legyen az eladásból származó bevétel (a különböző korú állatoknak az áruk is különböző!).
A játékban tehát egy ismert, de elég összetett rendszer viselkedését kell előírt határok közé szorítani, illetve valamilyen optimumra törekedni.
A feladat általában csak ismételt próbálgatásokkal oldható meg, különösen nehéz, hogy az N év elején kell állandó eladási arányt megadni.
Evolúció
Az egyedek szaporodásában alapvető jelentőségű az átöröklés, vagyis az, hogy az utódok sok tekintetben ugyanolyanok, mint az ősök. Gyakran előfordulnak kisebb eltérések is, tulajdonképpen ez biztosítja az egyediség sokszínűségét, vagyis végső soron a fejlődés lehetőségét. Ezt a jelenséget mutációnak hívják. Például a szürkepettyes araszoló utódai is szürkepettyes araszolók lesznek, azonos számú szárnnyal, csáppal stb. Mégis előfordulnak világos (fehér) és sötétebb (barnás) színű formák, meglehetősen véletlenszerű módon. Ha nagyobb populációt vizsgálunk (pár ezret), akkor a következő néhány évben kialakuló helyzet egyrészt függ a lepkék kezdeti eloszlásától, másrészt a környezet alakulásától (például melyik formának kedvez jobban az éghajlat vagy a növényzet stb.). Az ezzel kapcsolatos tömegjelenségeket és statisztikákat szintén lehet szimulálni.
Világmodell
A személyi számítógépek elterjedése azt is lehetővé teszi, hogy az oktatásban eddig nélkülözött témák, például a futurológia, vagyis a jövőtudomány is megjelenjék.
Például a Római Klub jelentésén alapuló Forrester-féle világmodell öt változó között fennálló visszacsatolások pontos megadásán alapul. Az öt világváltozó, amelyre a modell épül:
A népesség (populáció) alapvető változásait a születési arány (pozitív visszacsatolás) és a halálozási arány (negatív visszacsatolás) befolyásolja. Mindkettő exponenciális változással jár.
A tőke keletkezésének mértéke elsősorban a népesség számának alakulásától függ: több ember több tőkét tud létrehozni. De alacsony életnívó mellett kisebb a tőkefelhalmozódás. Az egy főre jutó tőke növekedésével nő a tőkeberuházási arány, ez pedig fokozza az anyagi életszínvonalat.
A tőkeberuházási aránytól elsősorban a környezetszennyeződés mértéke függ.
A népesség és az anyagi életnívó növekedése fokozza a természeti erőforrások felhasználási arányát. Ezek a források nem megújuló jellegűek (nyersanyagok, energiahordozók), nincs "inputjuk", csak "outputjuk" van. Meg lehet tippelni, hogy ez a visszacsatolás milyen veszéllyel jár a jövő szempontjából.
A népesség számának növekedésével csökken a tőkeberuházási arány, ezzel csökken a mezőgazdasági tőkeberuházás is, ez pedig az élelem mennyiségét is csökkenti. A kevés élelem csökkenti a születések és növeli a halálozások számát. Kevesebb ember viszont kevesebb tőkét termel, ..., és már gyakorlatilag vissza is jutottunk a modell 1. alrendszeréhez, amely folytatódik tovább, egészen a "világ végéig".
A világmodellt szimuláló program az alrendszereken belüli és egymás közötti függvénykapcsolatok, kezdőértékek és normálási értékek felhasználásával készült. E számértékek kulcsfontosságúak, mert ha az adatok módosulnak, a modell egészen másfajta tendenciákat mutat.
A Föld fejlődésének 1900-tól 1970-ig tartó szakaszáról pontos adataink vannak, az előbbi és a későbbi változóértékek és a normálási tényezők megválasztása elég önkényes. A cél nem csupán egy helyesen működő modell, hanem az is, hogy a számítógép jellemzőit kihasználva látványos, színes, a képernyő méreteit betartó grafikus eredményeket produkáljunk. A vízszintes tengely az időt jeleníti meg 1900 és 2100 között, a függőleges tengely mentén sorakoztatjuk fel a népesség-, a tőke-, az erőforrások-, az életminőség- és a szennyezés-görbéket. A program ezeket az adatokat évenként számolja ki, de a grafika lassúsága miatt csak ötévenként rajzolja fel. A különböző grafikonokat különböző színekkel vagy különböző vastagságú vonalakkal lehet megrajzolni.
A program elején meg lehet adni, hogy melyik időtartamban milyen változtatásokat akarunk végrehajtani a kezdeti értékekhez képest, és "standard" futást kérünk-e, vagy ha van a számítógéphez csatolt kézi irányító (pedál, joystick stb.), akkor menet közben is be lehet avatkozni. A modell működtetéséhez nem kell túl nagy számítási feladatot elvégezni: húsz egyszerű aritmetikai kifejezést kell kiértékelni. A legtöbb időt a szakaszosan megadott függvények interpolálása igényli.
Nézzünk egy példát:
ekkor ?t idő múlva a k+1-edik évi populáció:
nk+1 = nk+s*?t-h(nk)*nk*?t
A világmodell több változatban történő lefuttatása az egész Földre kiterjedő érdeklődésre, gondolkodásra, áttekintésre neveli a diákokat, hiszen a grafikonok "életbevágóak".
Az előző szakasz elején azt bizonygattuk, hogy a személyi számítógépet oktatásra a fizikában lehet a legtöbbféleképpen felhasználni. A legnagyobb hatású lehetőségek viszont a többi természettudományban körvonalazódnak. Pontosabban a személyi számítógépek közreműködésével alapfokon is megismerhetünk olyan matematikai eszközöket (differenciálegyenleteket, statisztikát, szimulációt), amelyek segítségével a kémia, biológia mesélős, leíró jellegét valóban meggyőző kísérletek, illetve szimulációk támaszthatják alá. Illusztrációként felsorolunk még néhány példát.
Kereső eljárások
Először egy eléggé összetett gráfrajzoló programot ismertetünk, amelynek a részletei önmagukban is érdekesek lesznek. Majd aprólékosan elemzünk egy több néven is ismert igen hasznos eljárást: backtrack, legkisebb mélységű keresés vagy branch and bound. Végül az eljárást a betűszámtanra alkalmazzuk.
Gráfok
A program először 4-10 pontot rajzol a képernyőre, majd ezek közül véletlenszerűen szakaszokkal köt össze bizonyosakat. Ezáltal egy gráf keletkezik, melynek minden pontjáról meg kell állapítanunk a fokszámát (vagyis hogy hány él indul ki az adott pontból). Ha ez sikerrel megtörtént, a gép felteszi a kérdést: Megrajzolható-e a gráf egyetlen vonallal, a "ceruza" felemelése nélkül? Az adott és a helyes válasz négyféle variációja szerint a következő változatok lehetségesek:
A gép természetesen figyel az esetleges "tévedésekre", jelzi, ha egy él nem húzható meg (illetve ha nem törölhető). Meg kell jegyeznünk, hogy durva grafikával már 8 pont összekötése is nehezen ábrázolható, mert összemosódnak a vonalak. Érdemes ilyenkor néhány élt szaggatva rajzolni, különösen a csúcsok környékén. Az ábra változásait pedig célszerű "szövegben" is követni a pontok sorszámainak kiírásával.
A legkisebb mélységű keresés
Nézzük meg, hogyan lehet a megfelelő ismétlődés nélküli utat megkeresni a gráfban! Az ismertetett eljárásnak az az alapja, hogy az összes utat valahogyan sorba rendezzük, mégpedig éppen az érintett pontok szerint.
Egy egyszerű gráf lehetséges útjai, ha 1-ből indulunk:
ha 2-ből indulunk:
A pontos algoritmust egy nagyobb gráfon részletezzük:

Egy alkalmas kirándulást választunk: legyen ez 1 (lehetne még 2 is, más viszont nem). Ezután vesszük az innen elérhető legkisebb sorszámú pontot: 1 - 2 (1 nem jöhet szóba a második helyen)! Ismét a lehető legkisebb értéket véve: 1 - 2 - 3 (2 után se 1, se 2 nem következhet már)! Így folytatjuk, amíg csak lehet: 1 - 2 - 3 - 4 - 2. Ha elakadunk, még mielőtt minden éllel végeznénk, akkor megváltoztatjuk az utolsó számot - ha lehet. Ha nincs rá mód (4-ből már csak 2-be mehetünk), akkor egyet visszalépve próbálunk cserélni. [Sajnos 3-ból se mehetünk máshová: újabb visszalépés (jelöljük V-vel).]
Ha tudunk változtatni, akkor megtesszük (kétszeri V után: 1 - 2 - 4). Folytatjuk az utat erre, amíg csak lehet: 1 - 2 - 4 - 3 - 2, de ismét elakadtunk. Négy visszalépés viszont már jó lesz: 1 - 5 - 6 - 1 - 2 - 3 - 4 - 2.
Egy megfelelő utunk így már van, de ha akarjuk, folytathatjuk tovább, és még az 1 - 5 - 6 - 1 - 2 - 4 - 3 - 2 (két V), az 1 - 6 - 5 - 1 - 2 - 3 - 4 - 2 (hat V), és az 1 - 6 - 5 - 1 - 2 - 4 - 3 - 1 (két V) utakat is megkaphatjuk.
Ha már az első helyen sem lehet változtatni (1-ből már sehova máshova nem tudunk lépni), akkor az eljárás véget ért, és megkaptuk az összes elfogadható utat. Ezek száma persze lehet nulla is! Esetünkben négy volt 1-ből való indulással, és ugyanennyi lett volna 2-es kezdéssel is.
A fenti eljárás éppolyan, mintha felírnánk az összes sorozatot (utat), amelyben megfelelő számban fordulnak elő 1-től 6-ig az értékek, az 1 és 2 két ízben, a többi csak egyszer. Ez nyolc elem összes kombinációja, ahol kettő kétszer megegyezik: 8!/(2!2!) kb. 10 000 eset! Ezeknek a sorozatoknak csak elenyésző töredéke jöhet igazából szóba, például az 1-4... kezdetű változatok egyike sem megfelelő. Módszerünk ebből a sorozatból párszor tíz lépésben kiválogatta az összes alkalmas utat.
Összefoglalva az eljárás lényegét, egy módszeres alapossággal végrehajtott keresésről van szó, ez azt jelenti, hogy a sorban generált utakat végigpróbálgatjuk, és egy utat akkor tekintünk elfogadhatónak, ha egy adott feltételrendszer teljesül. Ez persze többféleképpen is lehetséges, de azonnal szembetűnik a szóban forgó algoritmus két előnye. Egyrészt a "hátulról" történő változtatás révén csak útdarabokat kell generálni, például 1 - 2 - 4 - 5 - 6 - 4 esetben először csak az utolsó három helyen lesz változás, az eleje marad a régi. Másrészt, ha egy útszakaszról kiderül, hogy alkalmatlan, akkor ezzel nemcsak egyetlen lehetőséget vetünk el, hanem az összes ezzel kezdődőt is. Példánkban a kb. 10 000 változatot sikerült "végignéznünk" mindössze nyolc útfelépítéssel és további kb. 100 elemi (egyetlen élt érintő) cserével!
Betűszámtan
Az iménti algoritmus felhasználási köre igen tág. Keresésre szinte mindig alkalmazható, igazából csak a célszerűsége lehet kérdéses. A kérdést lényegében az dönti el, hogy mennyire fogalmazható meg a komputer számára jól a feltételrendszer, és hogy a gép milyen gyorsan hajtja végre a módszeres vizsgálatot. Az egyikhez rendszerint csak a másiktól távolodva lehet közelebb jutni. Nézzünk erre egy újabb példát.
Jól ismertek a
típusú feladatok; ezeknél a betűk helyére úgy kell számokat írni, hogy az összeadás helyes legyen. A különböző betűk különböző számjegyeket jelentenek, és például az E betű mindháromszor ugyanazzal helyettesítendő. Ez a lényegében nyolcismeretlenes egyenletrendszer egyetlen - bár eléggé összetett - feltétele: a két négyjegyű szám összege az ötjegyű. Ez kiválóan ellenőrizhető, de hosszadalmassá teszi a dolgot. Ha generáljuk az összes lehetséges számnyolcast, majd ezekből a három számot (illetve szót), és végül megnézzük az eredmény helyességét, mindez bizony 10!/2! > 1,8*10^6 vizsgálat, amin az se igen segít, ha felismerjük az M = 1 összefüggést. Ez egy átlag gépnek sokórás feladat.
Sokkal célszerűbb négy részre bontani a feltételt: számjegyenkénti összeadásra. Az iskolában tanult "oszloponkénti" összeadásra alapul a következő -HT 1080Z iskolaszámítógépre készült - program: megadja, mit kell az egyes betűk helyére írni.
10 DIM A$(10)
20 FOR D=0 TO 9
30 A(D)=1
40 FOR E=0 TO 9
50 IF A(E)=1 THEN 410 ELSE A(E)=1
60 FOR Y=0 TO 9
70 IF A(Y)=1 THEN 390 ELSE A(Y)=1
80 IF Y<>D+E AND Y<>D+E-10 THEN 380
90 IF Y=D+E THEN X1=0 ELSE X1=1
100 FOR N=0 TO 9
110 IF A(N)=1 THEN 370 ELSE A(N)=1
120 FOR R=0 TO 9
130 IF A(R)=1 THEN 350 ELSE A(R)=1
140 IF E<>N+R+X1 AND E<>N+R+X1-10 THEN 340
150 IF E=N+R+X1 THEN X2=0 ELSE X2=1
160 FOR O=0 TO 9
170 IF A(O)=1 THEN 330 ELSE A(O)=1
180 IF N<>E+O+X2 AND N<>E+O+X2-10 THEN 320
190 IF N=E+O+X2 THEN X3=0 ELSE X3=1
200 FOR S=0 TO 9
210 IF A(S)=1 THEN 310 ELSE A(S)=1
220 FOR M=0 TO 9
230 IF A(M)=1 THEN 290 ELSE A(M)=1
240 IF O<>M+S+X3 AND 0<>M+S+X3-10 THEN 280
250 IF O=M+S+X3 THEN X4=0 ELSE X4=1
260 IF M<>X4 THEN 280
270 PRINT 1000*S+100*E+10*N+D: PRINT 1000*M+100*O+10*R+E: PRINT 10000*M+1000*O+100*N+10*E+Y: PRINT
280 A(M)=0
290 NEXT M
300 A(S)=0
310 NEXT S
320 A(O)=0
330 NEXT O
340 A(R)=0
350 NEXT R
360 A(N)=0
370 NEXT N
380 A(Y)=0
390 NEXT Y
400 A(E)=0
410 NEXT E
420 A(D)=0
430 NEXT D
Végül említünk még néhány példát, ötletet, ahol jól használható a backtrack algoritmus:
Szólánc
Több néven is ismert játék; egy - mondjuk, hárombetűs - szóból szintén hárombetűs szavakon át úgy kell eljutni egy másik hárombetűs szóhoz, hogy az egymás utáni szavak csak egyetlen betűben különbözzenek az előzőtől. Így a JÉG-ből nemcsak olvadással lehet VÍZ, hanem a JÉG-VÉG-VÍG-VÍZ szóláncon keresztül is. Leginkább 3-4 betűs szavakkal szokták játszani, és néha érdemes további megszorításokat is alkalmazni. A továbbiakban a magánhangzókat G-vel, a mássalhangzókat S-sel fogjuk jelölni.
Ha a magyar ábécét 32 betűsnek tekintjük: 14 G és 18 S (a kettős betűket, és Q-t, W-t nem számítottuk), akkor ez 32^3 - (19^3 + 14^3) kb. 26 000 elméletileg lehetséges variációt jelent, melyek közül kb. 1000-nek lehet jelentést tulajdonítani. Nyilvánvaló, hogy őrületes munka valamennyi szót figyelembe venni, hogy a láncépítés mikéntjéről ne is beszéljünk. A láncra az ideális algoritmus az lenne, ha minden szót egy gráf szögpontjának tekintenénk, és ha állhatnak egymás után (egyetlen betűben különböznek), akkor összekötnénk őket. Egy ilyen gráfot programmal is meg lehet konstruáltatni, de ez is nehéz. A gráfban utat keresni szintén érdekes feladat. A legnagyobb hátránya mégis az, hogy igen sok adatot igényel, és a keresés is elég hosszadalmas.
Ajánlunk egy gyors és egyszerű megoldást. Egyrészt először csak SGS alakú szavakra szorítkozunk. Másrészt, minthogy a komputerek általában nehezen birkóznak meg az ékezetekkel, csak A, E, I, O, U hangokat veszünk figyelembe. Végül, az előbb említett gráfban nem próbálunk maximális számú élt meghúzni, csak egy maggal tesszük ezt:
1 2 3 4 5 6 1 0 0 0 3 3.4 3.4 2 0 0 0 3 3.4 3.4 3 0 0 0 0 4 4 4 3 3 0 0 0 0 5 4.3 4.3 4 0 0 0 6 4.3 4.3 4 0 0 0
A 6x6-os táblázat az átmeneteket jelzi. Például KOS-ból KIS közvetlenül (0) elérhető, KAN csak a KAS-on keresztül (3), és KEN pedig csak a KAS és KAN (3.4 jelentése 3 és 4!) útján.

A többi szó a mag szavaira felfűzhető. Olyat sosem szerepeltetünk egy ágon, amelynek középső magánhangzója eltér a kezdetitől:

Ezeket a további elemeket valamilyen rendszer szerint sorszámozzuk. Minden szóhoz egy külön tömbben azt a sorszámot rendeljük hozzá, amelyiken keresztül közeledhetünk a maghoz:
FIA-26, FIX-25, MIX-24, MIK-23, HIT-28, MIT-28, FAJ-74
stb.
Ezek után az algoritmus a következő:
Tetszőleges két szóból kiindulva a kódvektor segítségével a magba "lépkedünk", ahol a haladást a 6x6-os táblázat határozza meg.
Elegáns dolog megnézni, nincs-e felesleges szó a láncban? Például a FAJ FAR KAR KAN KAR VAR VAD sorozat közepe kihagyható. Az ilyen eseteket egy szubrutinnal lehet kiszűrni.
Többféle változatban készíthető program.
Kb. 100-150 szót - amelyek összefüggő gráfot alkotnak - kiírunk a képernyőre. Az összekötendő szavakat (INPUT-ba vagy véletlenszerűen) villogtatja a gép, a lánc közbülső elemei mellé csillag kerül.
Ha nagyobb szókészlettel próbálkozunk, akkor csak a lánc elemeit kell kiirtani. Kívánságra segíthet a gép az összekötésben oly módon, hogy először csak néhány elemet ír ki (lehetőleg ritkább szavakat).
Érdekes versenyre kelni a géppel, illetve az algoritmussal. A játékos a gép által választott szavak közé építi a láncot, és fordítva, INPUT-tal lehet a gépet kérdezni. Meglepő módon a számítógép általában rövidebb idő alatt talál megoldást, bár az sokszor hosszabb, mint a "humán" összekötés.
Minthogy a mag köré többféle fastruktúrát lehet készíteni (például VAJ FAJ FAR KAR és VAJ VAD VAR KAR), bizonyos szavakhoz többféle kód is rendelhető, és ezekből véletlenszerűen választhat a komputer. A 72.74 jelentése, hogy a szóban forgó elem mind 72, mind 74 szavakon keresztül kapcsolódik a maghoz. Ha a szavak 10-15%-a ilyen, ezzel szinte "kiismerhetetlenné" tehető a program.
Természetesen idegen szavakkal is lehet játszani. Sőt angol nyelven még könnyebb, ugyanis az angolban igen gyakoriak a hárombetűs szavak. A 26 betűből (5 G és 21 S) elméletileg is csak kb. 8000 variáció állítható össze, amiből több mint 500-nak lehet értelmet tulajdonítani (vagyis arányban többet, mint a magyarban), és közülük 300 közismert. A lényeges azonban nem ez, hanem hogy szinte valamennyi szó összefüggő gráfot alkot! Igen gyakori az SGS-SGG átmenet (TEN-TEE, BED-BEE), és más váltások is könnyen megoldhatók (EYE-BYE, ANY-ANN stb.). Ennek köszönhetően a középiskolák angol szókincsét kicsit kibővítve kb. 150 szó közül bármelyik kettő összeköthető. A kb. 300 leggyakrabban használt szó közül pedig 95-97% összefüggő gráfban helyezkedik el!
Beszámoló
Szinte mindenki írt már ilyen-olyan rutinszerű beszámolót vagy levelet. Tudjuk, hogy ezeknek nagy része gépies, majdnem semmitmondó. Ezeket a tulajdonságokat kihasználva készültek a beszámoló-, illetve levélíró programok. Szavakból és ki-fejezésekből ügyesen összeállított szótár alapján a számítógép véletlenszám-generátorának segítségével egy alig ismétlődő, változtatható méretű szöveget lehet íratni.
A "szótárban" (memóriában) elhelyezkedő szavak, szócsoportok, mondatrészek 11 csoportba sorolhatók:
1. időhatározó
2. módhatározó
3. helyhatározó
4. állítmány
5-6. birtokos
7. birtok (alany)
8. kötőszó
9. - beszúrás -
10. jelző
11. bővítmény ("tekintetében" stb.)
Az azonos szerkezetű mondatrészekből kb. 10-15 darabot tartalmaz a szókészlet, ezekből véletlenszerűen választ a gép, és eltérő szerkezetű - egyszerű és összetett; rövid, normál és hosszú - mondatokat képes alkotni.
Például tetszőleges témakörben életszerűen "hivatalos" szöveget állít össze az adott szókészletből. A program - miután megkérdezi, hogy hány oldal legyen és kinek készül a beszámoló vagy levél - a szöveget 3-6 mondatonként bekezdésekre tördeli, és 3 bekezdés ad ki egy oldalt.
Az egyes mondatok szerkesztésének menete:

A zárójelben levő mondatrészek elhagyása nem befolyásolja a mondat értelmességét. Egy véletlen szám dönt, szerepeljen-e vagy sem.
Kicsit nehezebb változat az, ha bizonyos valószínűséggel egy mondat részei (például alanya) megegyeznek az előző mondat egyes részeivel.
Érdekességként említjük, hogy eddig a következő "beszámolókat" rendelték meg:
Eleinte külön programok készültek minden alkalommal, de a kapacitáshiány kikényszerítette a következő változatot: Mindössze az 5., 6., 7. szócsoportokat kell az adott terminológiának megfelelőre cserélni, és ezután a program tetszőleges témakörben ontja a szöveget.
Levél
A beszámolókészítő programhoz hasonló felépítésű ez a program is. Két kérdésre kell mindenekelőtt válaszolni: kinek készül és ki írja? Az első kérdésre adott válaszból, különböző jelzőkből és egyes szám első személyű birtokviszonyból alakul ki véletlenszerűen a megszólítás.
Az aláírás a második válaszból adódik, egyes szám második személyes birtokviszonnyal fűszerezve, amely szintén véletlen: például "SÓVÁRGÓ KEDVESED", "UTÁNAD EPEKEDŐ SZERELMED" stb.
A levél "szókincse", a beszámolóéhoz hasonlóan, szintén több csoportba sorolható:
A szótártól és szókincstől függően különböző hangulatú leveleket lehet a program segítségével szerkeszteni: csak a szerelmes levél kategóriáján belül is lehet odaadót, szakítót, szemrehányót, és ki tudja, még hányfélét? Érdekes kísérlet lehet kipróbálni, hogy melyik címzett veszi észre, hogy számítógéppel írt levelet kap az aláíró "egyéni stílusú" levele helyett!
Idealisztikus elképzelések - rózsaszínű álmok
Talán lesznek olyan olvasók, akik szerint az egész fejezet a fenti cím alá kívánkozik. Védekezésül a már említett tapasztalatokat lehet csak megismételni, nevezetesen: szakköri környezetben a felsorolt példák nagy része tárgyalható, sőt számos példát maguk a diákok találtak ki.
A személyi számítógépek megjelenése az iskolában nyilván hatással lesz a tanított anyagrészekre is. Természetesen ma még nehéz megmondani, hogy pontosan miként, hiszen nem tudjuk megjósolni, milyen új gépek, milyen új feladatok lesznek a jövőben. Az iskolai alkalmazások változatos lehetőségeire az 1980-81-ben tartott számítástechnikai verseny győztes diákjainak a programjait említjük még meg. A rendes tananyagtól ezek a példák valóban távol állnak, a távlatok bemutatására azonban igen alkalmasak.
Az első díjat egy zöldhullám-kiértékelő program nyerte. Az akkor 17 éves szerzőnek jogosítványa nem volt, csak olvasta valahol, miszerint ez egy hálás téma. Ugyanekkor a Hivatal főilletékese úgy nyilatkozott, hogy "a közlekedés számítógéppel történő tervezése teljesen reménytelen, nem is érdemes vele foglalkozni. Több ilyen rendszert vettünk már külföldről, de rengeteg baj van velük." A versenyprogramnak természetesen voltak hibái, de működött, és jól érthető visszajelzéseket adott a zöldhullám lámpáinak összehangoltságáról.
A verseny másik kiemelkedő programja a Kalevala három magyar műfordítását vetette egybe az eredetivel, különböző hangzástani szempontokat figyelembe véve (rímek, magánhangzó-eloszlások, alliterációk száma és helye a sorokon belül stb.). Ugyancsak izgalmas dolog lenne például Ady verseiben ritka, szokatlan szókapcsolatokat keresni, és ezek számát figyelni a költő különböző korszakaiban. El lehet képzelni olyan programot is, amely egy versre teljes formai elemzést végez.
Még mindig a versenynél maradva, szerepelt egy lakáscserét szervező program is. Nem tudott igazán sokat, de az ötlet figyelemre méltó volt. Ugyancsak ekkortájt dúlt nagy vita, érdemes-e a Hirdetőnek valami hasonlóval foglalkoznia. Azóta már számítógép segítségével is közvetítenek lakáscserét, de a hasonlóan bonyolult informatikai feladatok megoldása hazánkban nem tekint nagy múltra vissza. Természetesen ezek a problémák nem kapcsolódnak az alapoktatáshoz, de jól mutatják, hogy az érdeklődő diákok igen messzire eljutnak.
Összefoglalva:
Az iskolai számítógépek bizonyára sok tekintetben meg fogják változtatni az oktatást. Mi nem a pedagógiai területeket mutattuk be, hanem nagy vonalakban a lehetséges (tan)tárgyi alkalmazásokat igyekeztünk bemutatni. Reméljük, a felsorolt példák, gyakorlatok indíttatást adnak a hasonló programok elkészítéséhez, és egy kis idő múlva az itt leírtak már túlhaladottak lesznek.
Egy nagy horderejű változás kezdetén vagyunk.
Kétségtelen, hogy a személyi számítógépek egyik legnagyobb vonzereje a játékprogramokban rejlik. Ebben a fejezetben csoportosítjuk a játékokat, és néhány példával segítjük az olvasót a megfelelő típusú játékprogramok megírásában.
A gép is játékos
Legelőször is olyan játékokról szólunk, amelyeket a gép is "játszhat". A legtöbb ilyen program megírása ugyan bonyolult matematikai problémához vezethet, hiszen olyan stratégiát kell kidolgoznunk, hogy ne lehessen egykönnyen fölülmúlni. Példa rá egy igényesebb sakk- vagy bridzs-program. Persze vannak nagyon egyszerűek is: öröknaptár, bioritmuskészítés. A legnépszerűbbek pedig a NIM, számkitalálós játék (I. a III. fejezet Barkochba c. szakaszában).
A nehéz programoknál lemondhatunk arról, hogy a gép is játsszék. Vagyis meghagyjuk csak játékvezetőnek. Lássunk erre egy példát: a szópókert. Szabályai: az egyik játékos gondol egy ötbetűs szót. A másik értelmes ötbetűs szavakkal találgat. Ha egy kérdezett szó valahányadik betűje megegyezik a gondolt szó ugyanannyiadik betűjével, akkor az egy találatot jelent. Az első játékos minden kérdezett szó után megmondja a találatok számát. Ezekből az információkból kell kitalálnia a második játékosnak, hogy mi volt a gondolt szó. Érezhető, hogy nehéz lenne olyan algoritmust írni, amellyel a gép bármely gondolt szót ki tud találni. Könnyű viszont annak a programnak a megírása, amelyben a gép "gondol" (azaz kiválaszt egyet, mondjuk, ötven előre beírt szó közül), a találgatásra információt ad, s végül jelzi az eredményt. A programban a harminc szót közvetlen egymás után írjunk a D$-ral jelölt szövegváltozóban (10. sor). Lássuk tehát a programot:
10 LET D$="kutyamalaczebramajomfagyi..."
20 LET x=INT (RND*30): LET a$=d$(5*x+1 TO 5*x+5)
30 CLS : PRINT "Gondoltam, lehet talalgatni!"
32 PRINT "Ha abba akarod hagyni, akkor"
34 PRINT "azt ird be, hogy: feladom": LET s=0
40 INPUT b$
45 IF LEN b$<>5 THEN PRINT "5 betus szavakat kerek!": GO TO 40
47 LET s=s+1: LET u=0
50 IF b$="feladom" THEN PRINT a$: GO TO 100
60 FOR Q=1 TO 5: IF a$(q)=b$(q) THEN LET u=u+1
70 NEXT q
80 IF u=5 THEN PRINT "Kitalaltad ";S;" talalgatassal!": GO TO 100
90 PRINT " ";u;" talalat": GO TO 40
100 INPUT "FOLYTATJUK? (i/n)",v$
110 IF v$="i" THEN GO TO 20
Néhány javaslat, olyan szavakra, amiben ékezetes karakter sincs:
| ablak arany beteg bunda cukor ember |
fagyi fotel iroda kalap kalap karaj |
kocka kukac kutya lakat leves majom |
malac meggy munka posta retek sonka |
sport szita torta villa vonal zebra |
Ennél a játéknál sokan úgy próbálják becsapni a számítógépet, hogy értelmetlen szavakkal találgatnak, és így hamarabb jutnak az eredményhez, megkönnyítik a játékot. Érdemes tehát betenni egy olyan programrészt, ami véletlenszerűen időnként kicseréli a kérdezett szót egy már bentlévővel. (Ha a kérdezett szó értelmetlen, úgy nehezebb lesz kitalálni, ha a gép majd ezt választja ki mint gondolt szót.) Legegyszerűbb annak a szónak a helyére beírni, amelyiket éppen akkor találgatja a játékos.
Természetesen olyan egyszerű játékok is ebbe a csoportba tartoznak, mint például a Ki nevet a végén. A játékszabályokra igen egyszerűen "megtaníthatjuk" a gépet, azonban a játék akkor érdekes igazán, ha táblát is rajzolunk a képernyőre, és minden információt a gép kezel. Ez viszont már túl sok munka ahhoz képest, hogy milyen hamar meg lehet unni a játékot. Végül arra egyszerűsödik a program, hogy a dobásokat generáljuk. Akkor már érdekesebb az a játék, amelyben a gép néhány játékos helyett dob, és megnézi, hogy ki dobta a legnagyobbat. Esetleg több dobás átlagát veszi. A programot azzal kezdjük, hogy megkérdezünk néhány dolgot: hányan játszanak (legfeljebb 6 játékost engedjünk meg), játszhat-e a gép, hogy hívják a játékosokat. Ezt a részét a programnak (ahol tehát föltálaljuk a választási lehetőségeket) menünek hívják. Lépései a program 10-90 soraiban találhatók. Ezután generáljuk a kockadobásokat az RND függvénnyel. Minden játékos dobását és addigi dobásainak összegét tároljuk, valamint számoljuk, hogy hányadik körnél tartunk.
10 CLS : PRINT "KOCKADOBAS"
20 INPUT "En is jatszhatok? (i/n)",a$
30 INPUT "Hany jatekos lesz (1-6)",n
40 IF a$="i" AND n=0 THEN GO TO 100
50 IF n<1 OR n>6 THEN PRINT "Helytelen valasz!": GO TO 10
60 DIM k$(n+1,12): DIM d(n+1): DIM s(n+1)
70 FOR i=1 TO n
80 PRINT "Hogy hivjak a ";i;" jatekost?": INPUT k$(i)
90 NEXT i
100 IF a$="i" THEN LET n=n+1: LET k$(n)="A gep"
110 FOR q=1 TO N: LET s(q)=0: NEXT q: LET j=1
120 LET m=0: LET g$="": CLS
130 FOR q=1 TO n
140 LET d(q)=INT (RND*6+1)
145 IF d(q)>m THEN LET m=d(q): LET g$=k$(q): GO TO 155
150 IF d(q)=m THEN LET g$=k$(q)
155 PRINT k$(q);" dobasa: ";d(q): LET s(q)=s(q)+d(q)
160 PRINT k$(q);" ATLAGA: ";s(q)/j
165 PRINT
170 NEXT q
175 PRINT "Nyert ";g$;" ";m;"-vel"
180 INPUT "Folytassuk? (i/n)",v$
190 IF v$="i" THEN LET j=j+1: GO TO 120
200 INPUT "Kezdjuk ujra? (i/n)",v$
210 IF v$="i" THEN GO TO 10
Ez a program már "kisajátítja" a játékot, a játékosok csak nézői az "előadásnak".
A gép mint játékeszköz
Sok program viszont még annyira sem vesz részt a játékban, mint a szópókernél. Egyszerűen csak valamilyen eszközt ad hozzá. Például a dobásgenerálás a Ki nevet a végén játékban. Hasonló a szerepe egy olyan programnak, amely néhány elemet kever össze (I. a III. fejezet Keverés c. szakaszában). De készíthetünk egy egyszerű labirintust, amelyben kedvünkre barangolhatunk.
10 FOR i=1 TO 640
20 LET p=INT (RND*2)+1
30 IF P=1 THEN PRINT "/";
40 IF P=2 THEN PRINT CHR$ 92;
50 NEXT i
Ez a program 50-50% valószínűséggel rajzol \-t, és /-t.
Ugyanebbe a csoportba tartozik az a program, amely 10 véletlenül kiválasztott betűt ad meg (mint a tv-ből ismert Játék a betűkkel játékban), hogy ebből a játékosok a lehető legtöbb értelmes szót állítsák össze. Bevehetünk a betűk közé esetleg egy jokert is, amely például az "A" betű előtti karakter ("@") lehet. Ha az A kódja 65, akkor ez lesz a betűgenerálás programja:
10 FOR i=1 TO 10
20 PRINT CHR$ (64+INT (RND*27));" ";
30 NEXT i
Míg a játékosok gondolkodnak, a gép mérheti az időt valamilyen módon, és egy bizonyos idő elteltével minden játékos leteszi az írószert. Most lehet összeszámolni, hogy ugyanannyi idő alatt ki rakott ki több szót.
Mint már láttuk, nemcsak a véletlen betűket, hanem a véletlen számokat is föl tudjuk használni: kockadobást generálhatunk. A kockapóker-játékban azonban döntéseket kell hozni, így a teljes játékprogram megírása (legalábbis, ha színvonalas ellenfelet akarunk) kicsit bonyolult. Ha azonban a döntéseket elvégezzük a gép helyett, akkor már egyszerűbb. A program teljes összeállítását az olvasóra bízzuk.
Az ilyen típusú (segédeszköz) programok közül talán a varázstévé az egyik legkellemesebb feladat, és ez adja az egyik legérdekesebb játékot is. Az eredeti játékon két csavarógombbal tudtunk irányítani egy rajzolófejet függőleges, illetve vízszintes irányban. Ha a gépünkön van PLOT utasítás, akkor hasonlót varázsolhatunk a tévénkre.
Első lépésként kitisztítjuk a képernyőt, a "rajzolófejet" a 0,0 pontba állítjuk, és INKEY$ -ral várjuk, hogy merre induljunk. Készítsük el azt az egyszerűbb változatot, amely nem vizsgálja, hogy túlmentünk-e a képernyő keretein, hanem egyszerűen leáll hibajelzéssel. Az "A" és "Z" karaktereket a föl-le, az "M", "N" karaktereket a jobbra-balra irányú mozgatásokhoz használjuk.
10 LET x=0: LET y=0
20 LET a$=INKEY$: IF a$="" THEN GO TO 20
30 IF a$="a" THEN LET y=y-1: GO TO 70
40 IF a$="m" THEN LET x=x+1: GO TO 70
50 IF a$="n" THEN LET x=x-1: GO TO 70
60 IF a$="z" THEN LET y=y+1
70 PLOT x,y
80 GO TO 20
Ennek a játéknak az az egyik hátránya, hogy csak folyamatosan tud rajzolni. Megcsinálhatjuk azt is, hogy ha a "SHIFT" gombbal együtt nyomjuk le a megfelelő betűt, akkor ugyan elmegy a megfelelő irányba, de nem rajzol vonalat.
Hasonló típusú érdekes játék még a reakcióteszt (I. a III. fejezet Időmérés, vezérlés c. szakaszát) program. Ellenőrizhetjük a memóriánkat is, a következő játékkal. A gép megjelenít egy kétjegyű számot, vár egy darabig, majd a szám eltűnik. A feladat: írjuk vissza a látott számot. Ha elsőre eltaláljuk, akkor a számjegyek száma növekszik eggyel, a felvillantási idő pedig csökken. Ha csak másodikra találjuk el, akkor csak a számjegyek száma nő, míg ha csak harmadszorra, akkor egyik sem változik. Ha ennyi találgatásra sem sikerül, akkor a gép megmutatja, hogy mi volt a szám, és megkérdezi, hogy a játékosnak van-e kedve újra próbát tenni a memóriajátékban.
A gép nekünk játszik
Vannak olyan játékprogramok is, amelyeknek a megírása az igazi feladat, a gép játszik helyettünk is. Például, ha a Játék a betűkkel betűgenerálása után rögtön megoldásokat is ad a gép. Ennek a programnak a megírása már meglehetősen bonyolult, komoly számítástechnikai ismereteket igényelhet egy-egy frappáns megoldás. De van ennél jóval egyszerűbb játék is. Például kirajzolunk egy szövegkeretet úgy, hogy fölül, illetve baloldalt rendesen, alul és jobboldalt visszafelé legyen olvasható:
100 INPUT a$
110 PRINT a$
120 FOR i=1 TO LEN a$-2
130 PRINT a$(i+1);
140 FOR j=1 TO LEN a$-2
150 PRINT " ";
160 NEXT j
170 PRINT a$(LEN a$-i)
180 NEXT i
190 FOR i=LEN a$ TO 1 STEP -1
200 PRINT a$(i);
210 NEXT i
A "szövegnégyzetet" a képernyőn természetesen máshol is elhelyezhetjük. Arra azonban vigyáznunk kell, hogy kiférjen.
Egy másik - a játékos számára hasonlóan passzív, de igen mulatságos - játék a versírás. Minden verssor nyelvtani szerkezete megegyezik a "Három kutya sétál a széles híd mellett" mondatéval. Az első szó egy névelős melléknév vagy egy számnév, ugyanez a negyedik is. A második - csakúgy, mint az ötödik - egy ragozatlan főnév. A harmadik egy egyes szám harmadik személyű ige, míg a hatodik egy névutó. Az első típust az A$ szövegváltozó-vektorban, a másodikat a B$-ban, a harmadikat a C$-ban, a negyediket a D$-ban tároljuk. Legyen mindegyikből 20. Programrészlet:
100 LET i=INT (RND*20+1)
110 LET j=INT (RND*20+1)
120 LET k=INT (RND*20+1)
130 LET l=INT (RND*20+1)
140 LET m=INT (RND*20+1)
150 LET n=INT (RND*20+1)
200 PRINT a$(i);" ";b$(j);" ";c$(k);" ";a$(l);" ";b$(m);" ";d$(n)
210 GOTO 100
Próbáljunk meg minél líraibb és ritmikusabb szavakat beírni. (A szövegváltozók beírására a 100-as sorszámig hagytunk helyet.)
Néhány tisztán matematikai probléma megoldása is ide sorolható. A számelméletben például sok olyan algoritmus van, amelyek gépre vitele érdekes feladat, még ha ismert is az eredmény. Ilyen például az a prímszámkereső algoritmus, amelyet Eratoszthenész szitájának hívnak. Az a lényege, hogy az összes számok közül kihúzunk minden másodikat, harmadikat (negyediket már nem kell, mert azokat kihúztuk, amikor minden másodikat kihúztunk), minden ötödiket stb. De benthagyjuk a legelsőket, vagyis a kettőt, a hármat, az ötöt stb. A bentmaradtak éppen a prímszámok. Természetesen nem tudunk minden számon végigmenni, de nézzük meg például az első százat. (Az A vektorban fogjuk ezeket jelölni.) Elég lesz ekkor az első tíz számmal "szitálni", mert ha egy összetett számnak csak tíznél nagyobb prímtényezői vannak, akkor az biztos nagyobb, mint száz. Az A(I)-ben 1-es lesz, amíg ki nem szitáltuk, amint kiesik, nulla kerül az egyesek helyébe. Így végül majd azokat a számokat kell kiírni, amelyekhez tartozó vektorelemben egyes áll.
10 DIM a(100)
20 FOR i=2 TO 100: LET a(i)=1: NEXT i
30 FOR p=2 TO 10
35 IF a(p)=0 THEN GO TO 65
40 FOR i=p+p TO 100 STEP p
50 LET a(i)=0
60 NEXT i
65 NEXT p
70 FOR i=2 to 100
80 IF a(i)=1 THEN PRINT i,
90 NEXT i
Amellett, hogy a játékoknál is használható, érdekes matematikai probléma adatok nagyság szerinti rendezése, sorba rakása. Ez akkor szükséges például, amikor meg akarjuk mondani egy játszma után a sorrendet: ki az első, második stb. Íme egy egyszerű rendezőprogram, amely az A(1), ..., A(10) változókat rakja sorba úgy, hogy az A(1) változóba kerül a legnagyobb érték, az A(2)-be a második stb., az A(10)-be a legkisebb:
100 FOR i=1 TO 9
110 FOR j=i+1 TO 10
120 IF a(j)>a(i) THEN LET s=a(j): LET a(j)=a(i): LET a(i)=s
130 NEXT j
140 NEXT i
Álljon itt egy trükk, hogy hogyan lehet rögtön a játékosok nevét is tárolni az eredményekkel. Ha az egyik játékos neve például EMIL, a pontszáma 16, akkor legyen a neki megfelelő változó "EMIL+16". Ez szövegváltozó, így az értékét a VAL függvény segítségével kapjuk meg.
Más matematikai algoritmust is beprogramozhatunk, például két szám legnagyobb közös osztóját vagy legkisebb közös többszörösét is megkaphatjuk egy-egy érdekes programmal.
Néhány szó a kalandjátékokról
Kétségtelen, hogy a legnépszerűbb játékok az Adventure Game-ek (Kalandjátékok). Ezek egy része olyan játékokat modellez, amelyeket már réges-régen is játszottunk papíron. Például a torpedójáték vagy az autóverseny. Négyzetrácsos papírra rajzolt kacskaringós útszalag a pálya. Egyik vége a start, a másik a cél. Minden autót egy-egy pont képvisel.
Az előrejutás szabályai: először is pályán kell maradni, s ha valaki mégis kirepül, akkor ugyanott kell visszatérnie, ahol kifutott. Minden pontnak nyolc szomszédja van; a nyolc hozzá legközelebb eső rácspont. Minden lépésnél az autó lépésútját egy nyíllal jelöljük, azaz összekötjük a pontokat, amiken az autó áthalad. Az első lépés a kiindulópont egyik szomszédjába visz. A következő lépést úgy tesszük meg, hogy "majdnem" ugyanolyan nyilat rajzolunk, mint az előzőben, de a végpont valamelyik szomszédjába kell átlépni végül is.
Az ugyanabban a körben megtett lépések vonalát keresztezni szabálytalan (vagyis tilos az ütközés). Természetesen az nyer, aki legelsőnek fut át a célon.
A program szinte kizárólag grafikai megoldásokat igényel, az adminisztrációs részek a szokásosak:
A kalandjátékok programját nem könnyű megírni. Ez olyan feladat, amelyre csak néhány hónapos aktív tanulás után vállalkozhatunk. Nehéz lenne itt minden részletre kitérni. A kalandjátékok lelke majdnem mindig a grafika. Azt tanácsoljuk, hogy első lépésként egyszerű grafikus karaktereket mozgassunk a képernyőn, később egy véletlenszerűen mozgó karaktert is odarajzolhatunk. Harmadik lépés lehet például annak az ellenőrzése, hogy a két karakter ütközött-e.
Azért is nehéz feladat ezekről általánosan beszélni, mert a grafika gépenként nagyon eltérő. Mindössze néhány rendszerező tanáccsal szolgálhatunk azok számára, akik ilyen programot szeretnének írni:
A BASIC nyelv története az 1960-as évek elejére nyúlik vissza. Ekkor jelentek meg az olyan nagyszámítógépek, amelyek képesek voltak arra, hogy időosztásos (time-sharing) üzemmódban egyidejűleg sokan használhassák ugyanazt a számítógépet. A számítógépek sebessége ekkor már akkora volt, hogy a gép "munkaidejét" egészen kis időegységekre (time-slice-okra) bontva el lehetett érni, hogy az ugyanazt a számítógépet egyidejűleg, egymástól teljesen függetlenül használó emberek mind úgy érezzék, hogy a gép csak az ő feladatukkal foglalkozik.
Az időosztásos rendszer lehetővé tette, hogy a számítógépet alkalmazó ember a terminálján keresztül közvetlen kapcsolatban legyen a számítógéppel: követhesse programjának futását, a program futása közben adatokat adhasson meg és eredményeket kapjon vissza. Az első olyan programnyelv, amely ezeket az új lehetőségeket kihasználta, a dartmouthi főiskolán a magyar származású John Kémény és munkatársai által kifejlesztett BASIC nyelv volt.
A dartmouthi főiskolán 1963-ban helyezték üzembe azt az időosztásos nagy számítógépet, amely egyidejűleg száz felhasználót is képes volt kiszolgálni. John Kémény és munkatársai a FORTRAN nyelvvel szerzett sokéves tapasztalatuk alapján olyan nyelvet igyekeztek létrehozni, amelyet az emberek milliói könnyen elsajátíthatnak. Így született meg a FORTRAN alapján a BASIC programnyelv, amelynek egyszerűsége mellett az ember és a számítógép közötti közvetlen kapcsolat lehetősége, az interaktivitás volt a legfőbb erénye. Mai szemmel, az olcsó interaktív személyi számítógépek világából nézve a BASIC interaktivitása talán nem is tűnik olyan jelentős dolognak, a maga korában azonban ennek úttörő jelentősége volt, hiszen abban az időben csak drága, nagy számítógépek voltak, amelyek költségessége csak időosztásos rendszerekben tette lehetővé az interaktív alkalmazásokat.
A BASIC sokkal egyszerűbb nyelv, mint a FORTRAN. Például a BASIC nyelvben az INPUT és a PRINT utasításokhoz nem kell olyan részletességgel megadni, hogy az információ milyen formátumú legyen, mint a FORTRAN nyelv FORMAT utasításában. Így a BASIC nyelv megjelenése - egyrészt egyszerűsége, másrészt a közvetlen ember-gép kapcsolatot jelentő felépítése folytán - minden értelmes ember számára elérhető közelségbe hozta a számítógépek alkalmazásának lehetőségét.
A BASIC nyelv szerepe, jelentősége a személyi számítógépek megjelenésével tovább növekedett, ugyanis a BASIC nyelvet általában sokkal kevesebb memóriában el lehet helyezni, mint más, bonyolultabb nyelvek fordítóprogramjait, így a számítógép ára is sokkal alacsonyabb lehet, mint más nyelvek alkalmazása esetén volna. Nyilvánvaló, hogy olcsóbb egy 8 Kbyte memóriában elhelyezett BASIC nyelvet tartalmazó személyi számítógép előállítása, mint egy 64 Kbyte memóriát igénylő PASCAL nyelvű gép előállítása.
A BASIC viszonylagos olcsóságának azonban komoly ára van. A kis memóriában elférő BASIC értelmező - amely, ellentétben a fordítóprogramokkal, a gépi kódot nem a futtatás előtt, hanem a futtatás közben, utasításról utasításra állítja elő - általában lassú működésű, hiszen ugyanazt a programrészt általában többször kell értelmeznie, így egy BASIC program futási ideje sokszorosa lehet az ugyanazt a feladatot más nyelveken megoldó programok futási idejének. Különösen lassúak azok a személyi számítógépek, amelyek a BASIC utasítások formai ellenőrzését is a program futása közben végzik.
A személyi számítógépek előállítási költségeinek a BASIC nyelv alkalmazásának árán történő csökkentése szélesebb kör számára tette elérhetővé ezeket a gépeket, ugyanakkor megnehezítette annak lehetőségét, hogy a csaknem húsz évvel ezelőtt valóban komoly fejlődést jelentő BASIC nyelv szerepét átvegye egy korszerű, a szá-mítástudomány azóta elért eredményeit felhasználó, az emberi gondolkodáshoz kö-zelebb álló programnyelv.
A BASIC nyelven nagyon sokféle programozási feladatot meg lehet oldani, és jól használható a programozás tanításakor első programnyelvnek. A BASIC lehetőségei azonban korlátozottak, a hosszabb BASIC programok a nyelv szerkezete következtében szinte elkerülhetetlenül a GOTO utasítások labirintusai lesznek. Igen nehezen lehet jól áttekinthető hosszabb BASIC programot írni. A BASIC nyelvet könnyű megtanulni, egyszerű programozási feladatokat könnyű BASIC nyelven megoldani, a BASIC értelmezőt könnyen el lehet helyezni kis memóriában, viszont bonyolultabb feladatokat BASIC nyelven nem lehet szépen, strukturáltan megoldani. A személyi számítógépek körében a BASIC nyelv egyeduralmát inkább a gépek szempontjai indokolják, mint az embereké - a BASIC nyelv a gépnek könnyű. Ugyanakkor az elmúlt években több olyan nyelvet fejlesztettek ki, amelyek közelebb állnak az emberi gondolkodáshoz, és világosabb szerkezetű programok írását teszik lehetővé, mint a BASIC nyelv.
A számítástudomány fejlődésével, a személyi számítógépek lehetőségeinek bővülésével - a kisebb személyi számítógépek nemrég legfeljebb 16 Kbyte memóriával készültek, ma már sok gépnek 32 Kbyte, sőt 64 Kbyte memóriája van - a BASIC értelmezővel készülő gépekhez FORTH, LOGO, PASCAL stb. fordítóprogramok jelentek meg, és készülnek olyan gépek is, amelyek beépített nyelve nem BASIC, hanem például FORTH. Az említett nyelveken kívül vannak olyan, nagyobb memóriát igénylő korszerű nyelvek - például APL, ADA, C stb. amelyek a személyi számítógépek mai fejlettségi szintjén még nem jelenhettek meg ezeken a gépeken.
A következőkben két olyan nyelvvel ismerkedünk meg, amelyekkel - a nem is olyan távoli jövőben - személyi számítógépeinken is találkozhatunk majd.
A FORTH és a LOGO modern eljárásnyelvek. Ezekben a nyelvekben egy programozási feladat megoldása nem úgy történik, hogy egy hosszú programot írunk, hanem úgy, hogy a feladatot kis részekre bontjuk, és mindegyikre külön egy önálló kis program-eljárást írunk, majd ezeket az eljárásokat újabb eljárásokban aleljárásokként felhasználva jutunk a programozási feladat megoldását adó eljáráshoz. Másképp szólva, a programozási nyelv szókincsének - parancskészletének - felhasználásával új szavakat - új eljárásokat - definiálunk, ezzel kiterjesztjük a nyelv szókincsét, majd a továbbiakban erre a bővített szókincsre alapozva újra és újra kiterjesztjük a nyelvet egészen addig, amíg a programozási feladat megoldása a nyelv egyetlen új szavának - egy általunk írt eljárásnak - meghívását jelenti. Ily módon az eredeti, bonyolult programozási problémát egyszerűbb problémák megoldására vezetjük vissza, és magát a problémát igen tömör formában tudjuk kifejezni.
A programok független eljárásokból történő felépítésére sok hagyományos programozási nyelvben is van lehetőség, a BASIC nyelv azonban éppen nem ilyen. A BASIC nyelvben csak szubrutinok szervezésére van lehetőség, ez azonban sokkal gyengébb eszköz, mint az igazi eljárás, ugyanis a BASIC szubrutin nem önálló program - FORTH és LOGO eljárásai önállóak - továbbá a BASIC szubrutinnak inputot csak a főprogramból, értékadó utasításokkal adhatunk.
Az eljárásnyelvek moduláris felépítése lehetővé teszi, hogy az egyes eljárásokat előre lefordítva tároljuk, és így a futtatás közben az értelmezőnek sokkal kevesebb tevékenységet kell végeznie, mint BASIC nyelvű programok futtatásakor, így a FORTH és LOGO nyelvű programok az azonos problémát megoldó BASIC nyelvű programhoz képest kétszer-háromszor tömörebbek lehetnek, futási idejük pedig a BASIC program futási idejének ötöde-tizede lehet.
Az alábbiakban a FORTH nyelvű programozásba a FORTH egyszerű aritmetikai feladatokra való alkalmazásával, a LOGO nyelvű programozásba a LOGO grafikus rendszerének ismertetésével vezetjük be az olvasót.
A FORTH bemutatása
A FORTH nyelvben a számok tárolásának alapvető módszere az adathalom (stack, ejtsd: sztek, jelentése: verem). Például, ha sorra a
10 4 5
számokat gépeljük be, akkor az adathalomban ez a három szám lesz, az első a halom alján, az utolsó a halom tetején. A halomban levő számokkal különböző műveleteket lehet végezni, Például a DUP szó (duplicate - ejtsd: duplikeit, jelentése: megkettőz) hatására a halom tetején levő számból egy újabb példány kerül a halom tetejére, a DROP szó (drop, jelentése: elejt) hatására a halom felső eleme eltűnik, a SWAP szó (swap - ejtsd: szvap, jelentése: cserél) hatására a felső két elem megcserélődik, az OVER szó (over = át, fölé) hatására a felülről számított második elemből kerül egy újabb példány a halom tetejére. Előző adathalmunk a DUP szó hatására a
10 4 5 5
számokat fogja tartalmazni. Ha most DROP-ot mondunk, akkor eltűnik a felső elem, a halom újra csak a
10 4 5
számokat tartalmazza. Ha most a SWAP szót gépeljük be, akkor a halomból
10 5 4
lesz, és ebből az OVER szóval a
10 5 4 5
halmot kapjuk. Úgy képzelhetjük el, mintha a számokat kártyákra írtuk volna fel, és a FORTH szavak a kártyák elhelyezését, átrendezését jelentik.
Az aritmetikai műveleteket meghatározó FORTH szavak a halomban levő számokkal végzik a műveleteket. A négy alapműveletnek az egy jelből álló + - * / FORTH szavak felelnek meg. így például a
+
FORTH szó hatására a halom tetején levő két szám összeadódik, a két összeadandó helyett a halom tetejére az összeg kerül. Előző példánknál maradva a
10 5 4 5
halomból a + szó hatására
10 5 9
lesz, majd ebből a halomból egy újabb + szó hatására a
10 14
halmot kapjuk, amiből egy újabb + szó hatására a
24
egyelemű halom adódik. Egyszerre több adatot és FORTH szót is megadhatunk, így például ha a halom éppen üres, akkor a
10 4 5 SWAP OVER + + +
számok és szavak begépelésének hatására ugyanaz történik, mint amit az előbb lépésenként csináltunk. A BASIC nyelv PRINT utasításának a FORTH nyelvben a . (pont) szó felel meg, amelynek hatására a halom legfelső eleme kiíródik a képernyőre, és törlődik a halomból. Így ha kíváncsiak vagyunk arra, hogy milyen szám van a halom te-tején, de nem akarjuk elrontani a halmot, akkor a
DUP .
szavakat kell begépelnünk, a kiíratás számára másodpéldányt készítünk a halom legfelső eleméből, a kiíratás során ez a másodpéldány tűnik el. Ha a halom felső két elemét akarjuk kiíratni, akkor az
OVER . DUP .
szavakat kell begépelnünk. Ha a halomban a
10 4 5
számok vannak, akkor az OVER DUP . szavak hatására a képernyőn a 4 és 5 jelenik meg, a halom változatlan marad. Ha most a + DUP . szavakat adjuk meg, akkor a képernyőre kiíródik a felső két szám összege, vagyis a 9, a stackben pedig a
10 9
számok lesznek.
Két szám, mondjuk 10 és 4 összegét a BASIC nyelvben a
PRINT 10+4
paranccsal írathattuk ki, FORTH nyelven ugyanehhez a következőket kell begépelnünk:
10 4 + .
Ez a fordított sorrend talán kissé szokatlan, mégis logikusabb, mint a BASIC nyelvből megszokott sorrend, és jól mutatja, hogy valójában mit és milyen sorrendben csinál a számítógép - elhelyezi a memóriájában a két számot, összeadja őket, végül kinyomtatja az összeget.
A FORTH szavak felhasználásával újabb FORTH szavakat - eljárásokat - definiálhatunk. Az új szavak definiálásának kezdetét a : (kettőspont), végét a ; (pontosvessző) FORTH szó jelzi. Például egy szám, mondjuk a 10 négyzetét a következőképpen nyomtathatjuk ki:
10 DUP * .
Ha több szám négyzetét is ki szeretnénk számítani, akkor nem érdemes annyiszor beírnunk ezt a három FORTH szóból álló parancssorozatot, jobban járunk, ha definiálunk egy új szót, "megtanítjuk" a számítógépnek, hogy mondjuk a NEGYZET szó jelentse azt, amit a fenti három szó egymásutánja jelent:
: NEGYZET DUP * . ;
Hasonlóan, a halom felső két elemének kiíratására definiálhatjuk mondjuk a FENT szót:
: FENT OVER . DUP . ;
Az új szavak definiálásával bővített FORTH szókincs felhasználásával legelső példánknál, a halomban levő
10 4 5
számoknál maradva, a FENT újonnan definiált FORTH szó segítségével megtudhatjuk, hogy a halom felső két száma 4 és 5, majd a
NEGYZET FENT
szavak begépelésének hatására a képernyőn először a legelső szám négyzete, vagyis 25 jelenik meg, utána a halomban maradt számok közül a felső kettő, tehát a 10 és 4 jelenik meg.
Ha el akarjuk dönteni, hogy a halom tetején álló két szám között milyen reláció teljesül, akkor az = < > FORTH szavak közül a megfelelőt használhatjuk. Ezek hatására az összehasonlított két szám eltűnik a halomból, és a halom tetejére 1 kerül, ha a reláció igaz volt, 0 kerül, ha a reláció hamis volt. Például, ha üres halommal indulunk és a következőket írjuk be:
2 3 =
akkor a halomban 0-t találunk, a
2 3 <
begépelése után a halomban viszont 1-et fogunk találni. A 0= 0< 0> FORTH szavak a halom tetején álló számot 0-val hasonlítják össze - az eredmény ugyanaz, mint ha a 0-t is elhelyeznénk a halomban, és az előzőkben szerepelt = < > FORTH szavak közül a megfelelőt alkalmaznánk.
Az IF, ELSE, THEN szavak hasonló hatásúak, mint a BASIC nyelv IF utasítása, a FORTH fordított logikájának megfelelően azonban a következőt jelentik:
ha a halom tetején álló szám igaz (nem nulla), akkor az IF után álló szavak következnek, ha nem igaz, akkor az ELSE után álló szavak következnek, az IF illetve ELSE után álló szavak feldolgozása után a THEN után álló szavak következnek.
Példaként definiálunk egy olyan FORTH szót, amely a halom tetején álló számból egy másodpéldányt készítve megvizsgálja, hogy a szám negatív vagy nem negatív, és a vizsgálat eredményét kiírja a képernyőre:
: MILYEN
DUP 0<
IF
." NEGATIV"
ELSE
." NEM NEGATIV"
THEN
;
A MILYEN szó definíciójában szereplő ." FORTH szó az utána álló szöveget nyomtatja ki a következő idézőjelig. Az IF és ELSE ágak a THEN szónál találkoznak, példánkban a THEN után rögtön befejeződik a MILYEN szó.
Mielőtt egy példát mutatnánk a MILYEN szó alkalmazására, térjünk vissza az előzőekben definiált NEGYZET szóhoz, és változtassuk meg azt a következőképpen:
: NEGYZET DUP * DUP . ;
(a különbség annyi, hogy most a szám négyzetéből a halom tetején marad egy pél¬dány).
Most az
5 MILYEN
begépelésekor a
NEM NEGATIV
szöveg, a
-5 MILYEN
begépelésekor a
NEGATIV
szöveg, a
-5 NEGYZET MILYEN
begépelésekor a
25 NEM NEGATIV
szöveg fog a képernyőn megjelenni.
Látjuk, hogy miközben új FORTH szavakat definiálunk, vagyis új eljárásokra tanítjuk meg a számítógépet, arra is gondolhatunk, hogy megtanítsuk magyarul "beszélni" - ehhez csak annyit kell tennünk, hogy minden FORTH szót újra definiálunk, valahogy így:
: CSERE SWAP ;
: ELDOB DROP ;
: HA IF ;
: EGYEBKENT ELSE ;
: AZUTAN THEN ;
és ezzel közelebb hozhatjuk a számítástechnikát azokhoz, akiknek gondot okoz az angol nyelv ismeretének hiánya. A magyarítás a FORTH nyelvben tehát igen egyszerűen, kevés munkával megoldható, a BASIC átírása összehasonlíthatatlanul nehezebb feladat volna.
Következő példánkban olyan FORTH szót fogunk definiálni, amely a halom tetején álló szám faktoriálisát számítja ki (a definícióban szereplő ?DUP szó megduplázza a halom tetején álló számot, ha az nullától különböző, ha nulla, akkor nem csinál semmit sem, az 1- szó pedig 1-et kivon a halom tetején álló számból):
: FAKTORIALIS
?DUP
IF
DUP 1- FAKTORIALIS *
ELSE
1
THEN
;
A ?DUP szó elkészíthető pl. így:
: ?DUP
DUP 0 >
IF
DUP
ELSE
THEN
;
Azt az ügyes módszert, hogy a FAKTORIALIS definíciójában önmaga is szerepel, rekurziónak nevezzük. A FORTH nyelvben az eljárások önmagukat hívhatják, egy bonyolult problémát így vissza lehet vezetni önmagának egyszerűbb változataira.
A FAKTORIALIS szóról valószínűleg sosem derül ki, hogy hibás, viszont más hasonló, rekurzív definíciójú szavak hamar bajt okozhatnak. A FORTH ugyanis az eljáráshívásokat feljegyzi egy visszatérési halomba, és az eljárás végén - vagyis a szó feldolgozása után - e bejegyzés alapján visszatér a hívó eljárásba, és ekkor törli a visszatérési halomból a bejegyzést. A rekurzív eljárás során ezek a bejegyzések nem törlődnek, a visszatérési halom véges számú ismétlés után betelik, és a program futása megszakad. A FAKTORIALIS szó esetében, hacsak nem adunk meg túl nagy számot, ez nem fog bekövetkezni, más esetekben viszont a rekurzív definícióba beépített R> DROP szavakkal - a visszatérési halomból az adathalomba átvive és onnan eldobva - törölhetjük a bejegyzést.
A FORTH nyelv DO ... LOOP ciklusutasítása hasonló a BASIC nyelv FOR ... NEXT utasításához, így például a FORTH nyelven definiált
: CIKLUS 100 0 DO LOOP ;
megfelel a BASIC nyelv
10 FOR I=1 TO 100
20 NEXT I
utasításainak, a
: CIKLUS 100 0 DO I . LOOP ;
pedig a BASIC nyelv
10 FOR I=1 TO 100
20 PRINT I
30 NEXT I
utasításainak.
A FORTH nyelvnek még sok olyan lehetősége van, amelyek bemutatására ebben a fejezetben - ahol nem a nyelv megtanítása, csupán a nyelv szemléletének megismertetése a célunk - nincs helyünk.
Azok számára, akik már ismernek valamilyen nem strukturált programnyelvet, a FORTH nyelv nehezebben megtanulhatónak tűnhet, mint a BASIC nyelv. Aki azonban nem riad vissza, és eljut a FORTH szemléletének megértéséhez, az könnyűnek fogja találni ezt a nyelvet. Míg nem strukturált BASIC programokat közvetlenül a számítógép mellett ülve, szinte a feladat előzetes átgondolása nélkül is lehet írni, a FORTH programokat jobb előre megtervezni, szavanként megírni, majd magát a programot a már működő részekből egyetlen szó definiálásával összeállítani. Aki megismerkedett a FORTH nyelvvel, annak nem fog nehézséget jelenteni más, nagygépes strukturált nyelvek elsajátítása sem.
Nem elhanyagolható szempont a FORTH nyelv tömörsége és gyorsasága sem. Mint említettük, a FORTH nyelvű program az ugyanazt a feladatot megoldó BASIC nyelvű programnál ötször-tízszer gyorsabb lehet, ami éppúgy fontos lehet egy inter-aktív játékprogramnál, mint egy olyan számítógépnél, amelynek használatára sokan várakoznak. A FORTH nyelv viszonylag kis memóriában megvalósítható, így természetes, hogy a BASIC értelmezővel készülő személyi számítógépek legnagyobb részéhez - így például a nálunk legelterjedtebb VIC20, TRS80, ZX81 gépekhez - lehet FORTH nyelvet vásárolni.
A LOGO nyelv a mesterséges intelligencia körébe tartozó kutatások céljaira kidolgozott LISP nyelvhez hasonló, de oktatási célokra tervezett korszerű programnyelv. A LOGO nyelv a FORTH-hoz hasonlóan strukturált, önkiterjesztő nyelv. A programírás mindkét nyelvben új szavak definiálásával, vagyis a nyelv kiterjesztésével történik, így miközben a gyerekek a LOGO-t "tanítják" új dolgokra, maguk is felfedezéseket tesznek, tanulnak.
A LOGO bemutatása
A LOGO nyelv grafikus rendszere különösen alkalmas arra, hogy már a legkisebbeket is bevezesse a számítástechnika gondolatvilágába. A LOGO grafikus rendszerében a rajzolás egyik eszköze a képernyőn megjelenő, teknősbékának nevezett, háromszögű alakzat, amelyet néhány egyszerű parancs segítségével lehet mozgatni. Például a FORWARD parancs hatására a teknősbéka előremegy az orra irányában - a teknősbéka orra a háromszögű alakzat meghatározott csúcsa. A FORWARD 50 parancs hatására a teknősbéka 50 teknőclépéssel előremegy. A RIGHT parancs hatására a teknősbéka a megadott szöggel jobbra, a LEFT parancs hatására a megadott szöggel balra fordul el. A teknősbéka egy tollat cipel magával, amely nyomot hagyhat a képernyőn. Ha a teknősbéka lerakja a tollat, akkor nyomot hagy a képernyőn (PENDOWN parancs), ha felemeli a tollat, akkor nem hagy nyomot (PENUP parancs). Ha kész a rajz, akkor el lehet tüntetni a teknősbékát (HIDETURTLE), majd ha szükséges, újra láthatóvá lehet tenni (SHOWTURTLE). Az ábrán néhány példát láthatunk arra, hogy a megismert parancsok hatására milyen nyomot hagy a képernyőn a teknősbéka.

A teknősbékával rajzolás jó játék ezekkel az egyszerű parancsokkal is, de igazán érdekessé akkor válik, ha új szavakra kezdjük tanítani a számítógépet. Az eddigi parancsokkal így rajzolhattunk négyzetet:
FORWARD 50
RIGHT 90
FORWARD 50
RIGHT 90
FORWARD 50
RIGHT 90
FORWARD 50
ez azonban még négyzetnél is unalmas és csúnya, hát még mondjuk 24-szögnél. Tanítsuk hát meg a teknősbékát arra, hogy négyzetet úgy rajzolhat, hogy négyszer megismétli a FORWARD 50 RIGHT 90 parancssorozatot. Ezt LOGO nyelven így lehet leírni:
TO SQUARE
REPEAT 4 [FORWARD 50 RIGHT 90]
END
Vagyis négyzetet rajzolni úgy kell, hogy 4-szer meg kell ismételni azt, hogy előre 50-et és jobbra 90-et - magyarul persze ezt nem így fogalmaznánk. Ezzel egy LOGO eljárást definiáltunk. A definíció kezdetét, amelyet a FORTH-ban : jelzett, itt a TO szó jelzi. Az utána álló szó - itt a SQUARE - az eljárás neve, amely most már benne lesz a számítógép szótárában, így ha ezentúl bármikor azt mondjuk a teknősbékának, hogy SQUARE, akkor ugyanilyen négyzetet fog rajzolni. Az eljárás további része azt adja meg, hogy milyen utasításokat kell a számítógépnek végrehajtania, ha a SQUARE parancsot adjuk ki. Az eljárás definíciójának végét az END szó jelzi (az újabb angol szavak jelentése: to a főnévi igenév képzője, square ejtsd: szkver; négyzet, repeat ejtsd: ripit; ismétel, end: vége). Adhattunk volna az eljárásnak bármilyen más, a LOGO szótárában még nem szereplő nevet, például NEGYZET-et vagy akár CIRCLE-t, az eljárás hívásának eredménye ugyanez a négyzet lenne. Ha az eljárás definiálása előtt próbáltuk volna a SQUARE parancsot kiadni, akkor a "TELL ME HOW TO SQUARE" üzenetet ("Mondd meg, hogyan kell SQUARE-t rajzolni") kaptuk volna.
A SQUARE szó hatására a teknősbéka most mindig 50 teknőslépés hosszúságú négyzetet rajzol. A FORWARD szó rugalmasabb, meg lehet mondani neki, hogy mennyit menjen előre a teknősbéka. A SQUARE eljárást is módosíthatjuk úgy, hogy inputot várjon, a
TO SQUARE : SIZE
REPEAT 4 [FORWARD :SIZE RIGHT 90]
END
módosított eljárásnak már meg lehet - sőt meg kell - mondani, hogy mekkora négyzetet rajzoljon (size ejtsd: szájz, jelentése: méret). Például a
SQUARE 100
100 oldalhosszúságú négyzetet, a
SQUARE 50
pedig 50 oldalhosszúságú négyzetet fog rajzolni. Az inputot az eljárás fejrészében álló, kettősponttal kezdődő név jelzi, ahol az eljárás definíciójában ez a név szerepel (a kettősponttal együtt), oda a számítógép az eljárás hívásakor megadott input értéket helyettesíti be.
A már definiált eljárást természetesen felhasználhatjuk újabb eljárások definícióiban, például:
TO MINTA
REPEAT 6 [FORWARD 20 RIGHT 60 SQUARE 75]
END
A követező eljárás a SQUARE-hez hasonlóan megadott oldalhosszúságú négyzetet rajzol:
TO NEGYZET :SIZE
FORWARD :SIZE
RIGHT 90
NEGYZET :SIZE
END
Bár az eredmény ugyanaz a négyzet, a két eljárás mégis nagyon különböző. A SQUARE eljárás hívásakor a teknősbéka megrajzolja a négyzetet, majd megáll pihenni, a NEGYZET hatására viszont ugyanazon a vonalon újra és újra végigmegy egészen addig, amíg meg nem állítjuk a számítógépet, hiszen ha kiadjuk mondjuk a NEGYZET 100
parancsot, akkor a teknősbéka előremegy 100 lépést, jobbra fordul 90 fokkal, majd újra a NEGYZET 100 parancsot kapja, és ez így folytatódik, amíg közbe nem avatkozunk.
A négyzetet rajzoló eljárást átalakíthatjuk úgy, hogy a szöget is inputként kelljen megadni:
TO NEGYZET :SIZE :ANGLE
FORWARD :SIZE
RIGHT :ANGLE
NEGYZET :SIZE :ANGLE
END
A LOGO nyelv egyes változataiban - például a TI LOGO-ban - a mindentudó teknősbéka mellett törpék is szerepelnek. A törpéknek van helyük, irányuk és sebességük, de nem tudnak rajzolni. A képernyőn megjelenő alakzatokat (például fiú, lány, kutya, part, csónak, kocsi, ház, repülő, nap, csillag, tölgyfa, fenyőfa stb. - egyszerre 25 különböző tárgy lehet) magukkal vihetik, és bárhol letehetik azokat. A tárgyak és élőlények mozoghatnak lassan vagy gyorsan, úszhatnak, repülhetnek, nagyíthatók, kicsinyíthetők, 16 színre átfesthetők, így a törpék segítségével érdekes mikrovilágot lehet a képernyőre varázsolni.
A LOGO nyelv grafikus lehetőségei játszva vezetnek be a számítógépek világába. A teknősbéka-grafika parancsai egyszerűek, hatásuk a képernyőn rögtön látható, egészen egyszerű programok is adhatnak igen látványos, néha váratlan eredményeket. A LOGO nyelvnek ezzel a kis részével a gyerekek hetekig szívesen eljátszanak, szép mintákat készítenek, és közben olyan matematikai problémákkal próbálnak megbirkózni, mint például hogy a megadott szög hogyan határozza meg az alakzatot, vagy hogy mikor adnak az ismétléseket tartalmazó programok szimmetrikus rajzokat.
